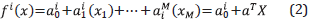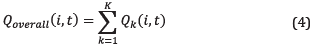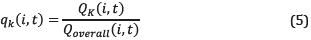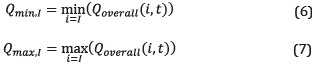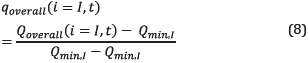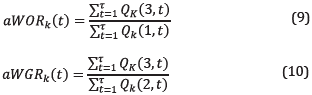1. INTRODUCTION
Due to technological advances such as diversity on high capacity sensors and computation performance, today it is possible to access a wide range of data from oil fields. Petroleum engineering is using such data to monitor the operation in oil production fields and to ensure production demand at the lowest possible cost 1]-(3]. However, classical data analysis techniques, where the analyst's experience plays an important role, are not adequate to manage the large generated databases (big data). Hence, tasks such as optimal operation and recovery must be performed through computer-aided techniques as Asodallahi 4] presented. Currently, the number of available computer-aided options is large, ranging from traditional statistical tools to modern artificial intelligence (AI) tools.
In this research, two AI models to predict oil, water and gas production in a Colombian oil field were developed. The novelty of this proposal is the use of a procedure for pre-processing the existing production data using an AI data imputation algorithm. A combined use of fuzzy logic (FL) and artificial neural networks (ANN) tools in data mining is implemented independently, extending an adaptive pattern classification procedure 5]. The modeling procedure uses FL to determine the most useful variables or parameters to be considered in each well model 6]. Next, ANN is used to obtain predictive models after the data mining processing. The combined use of both AI tools allows for an iterative process on any oil field model to enhance it until a specified accuracy level is reached by the model at large. This work is organized as follows: Section 2 describes the main concepts of ANN and FL. Section 3 presents a review of the use of AI tools in petroleum engineering. The proposed modeling methodology is explained in Section 4. The results are shown in Section 5 and, lastly, conclusions are presented in Section 6.
2. THEORETICAL FRAME
ARTIFICIAL INTELLIGENCE TECHNIQUES IN BRIEF
Artificial Neural Networks (ANN), Fuzzy Inference Systems (FIS) and Fuzzy-Neural-Networks have been increasingly used with success for predicting complex non-linear systems 7]-10]. ANN and FIS are artificial tools developed to provide machines with man inspired logical procedures. Although there are differences between ANN and FIS structures and operation, their ranges of application are similar in modeling, forecasting and estimating tasks. The main difference between ANN and FIS stems from their basis. While an ANN imitates the human brain in its structural configuration, a FIS imitates the human brain in its reasoning method. As a first approach, it could be said that ANN (especially feedforward networks) have their optimum performance when pattern recognition tasks are required, while FIS (especially Takagi-Sugeno fuzzy models) are suitable for function approximation. There has been growing interest in the development of Neuro-Fuzzy systems, taking advantage of both, ANN and FIS models, to enlarge the range of application of the resulting model. However, inherent learning complexity of that hybrid tool has limited its use in real models in spite of several reported applications in academic field 11]-16], so present work does not follow this strategy. As a common practice for identifying empirical models as ANN or FIS, a normalization procedure must be applied to the input and output variables to avoid scale differences. Thus, normalized databases have values in the hyper-cube [0,1]. Due to its linear nature, the normalization procedure has an inverse function, which is used to recover the original scale of predicted variables given by the model.
ARTIFICIAL NEURAL NETWORKS (ANN)
An artificial neuron is a mathematical formulation receiving signals from other artificial or external neurons. The output signal from a neuron is calculated by applying a function (called activation function) to the neuron inputs [17],[18],[10]. The signals are transferred through artificial connections with associated weights, equivalent to natural connections in the human brain. A group of connected artificial neurons are called ANN.
The ANN has the ability of learning from examples, with or without supervision. Such learning is attained by tuning the weights associated to the connections between neurons. Usually, two phases are recognized in ANN applications: the training phase, where the ANN learns the hidden relationship in data, and the forecasting phase, where the ANN is used to predict new results from input data not used during the training phase. For the training phase, it is possible to use different optimization algorithms including conjugated gradients, generalized delta rule, genetic algorithms, simulated annealing and evolutionary strategies, as presented in, [19]-[23], all based on ANN prediction error. The main characteristic of the ANN approach is its capability to discover hidden relationships in data, and to predict new results in presence of input data with noise, uncertainty or incompleteness. The simplest ANN is a feedforward, which could be understood as a multiple regressor model where the independent variables are the inputs of the ANN and the dependent variables are the outputs of the ANN. This network has on input layer, one or more hidden layers, and one output layer.
In this work, a feed-forward network trained with the back propagation algorithm for training was used by Chen, et al. [17]. The activation function used in each neuron was a sigmoid (S-shaped) function evaluated as the quotient between 1 and [1+exp(-a * (x-c)], with a and c function parameters and x the input to the sigmoid function [18]. Only one hidden layer was necessary to model well production. The number of neurons in the hidden layer is found by trial and error, with the number of neurons providing the smaller mean squared error over the training set. For this model, seven (7) neurons in the hidden layer presented the best approximation to the available data set.
FUZZY INFERENCE SYSTEMS (FIS)
A Fuzzy Inference System (FIS) is a linguistic tool that performs mapping S:X⊂=RN → Y ⊂RM using a Fuzzy Logic (FL) strategy. When this mapping is used as a model, the FIS is called a Fuzzy Model (FM). In this tool, the knowledge about the relationship between input domain X⊂RN and output domain Y ⊂RM is encoded as a set of IF -THEN rules. The antecedent and consequent of the rule may contain linguistic terms linked by logical operators: And, Or, Not, etc. In order to conform the antecedent, any FIS defines a set of linguistic terms A¡ in the domain of each input variable i. This set of terms A i = [A 1 ,A 2 ,...A S] is known as a fuzzy partition on the variable X. The number of linguistic terms in A¡ (granularity) is strongly related to FIS precision when it is used as a model. The other FIS rule component is the consequent, which is directly related to the output variable Y. The rule output may be a fuzzy set (Linguistic FIS, Relational FIS) or a numerical function (Takagi-Sugeno FIS). The final element in FIS is the inference machine, which operates over the rules set to map a set of input values to output values. This static mapping is augmented with the dynamic behavior of the system being modeled using external delays applied to the model input vector. Thus, the information of model inputs (regressor) is constituted by current and delayed values of the system inputs [24].
Usually, most of FIS operates with an explicit antecedent partition, but it is possible to use an implicit partition. A multidimensional fuzzy set A ¡j [25]-[27] can be used. In this case, all the individual fuzzy sets in the antecedent of each rule are transformed into a single multidimensional fuzzy set. In spite of the loss of linguistic meaning that occurs during this procedure, the multidimensional fuzzy set obtained results more compact. Therefore, the tasks related to FIS model design and tuning (model identification) result easier than same task for other kind of FIS and ANN. Additionally, a fuzzy clustering is performed over the data to obtain a first guess of the final number or rules. This approach guarantees the existence of a Takagi-Sugeno Fuzzy Model (TSFM) with multidimensional fuzzy sets in the regressor space (inputs X). The TS-FM uses as consequent a linear function of the input variables, which simplifies the model parameter identification. This model is able to represent a general class of static or dynamic nonlinear systems using rules with the form:
where x = [x 1 ,x 2 , ...x N] are the N inputs of the FM, B ¡ (x) is a N-dimensional fuzzy set and y ¡ is the output for the rule i defined by the function f i (x). Generally, this function is expressed as an affine linear function of input variables:
where 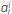 are tunable parameters. It should be highlighted that a¿ term acts like the bias neuron in the ANN. The consequent parameters are those being used by the function f
i (x) and the antecedent parameters are those that define a multimensional fuzzy partition of the input space. The normalized model output, y
n, is calculated as a weighted average of the contribution of each rule
are tunable parameters. It should be highlighted that a¿ term acts like the bias neuron in the ANN. The consequent parameters are those being used by the function f
i (x) and the antecedent parameters are those that define a multimensional fuzzy partition of the input space. The normalized model output, y
n, is calculated as a weighted average of the contribution of each rule 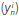 :
:
where w ¡ =g(x n) is the membership value of the normalized input vector x n to the input fuzzy set of the rule i [28].
In this work, a TS-FM with multidimensional fuzzy sets is used. In the FL approach, the model performs a function approximation opposed to the pattern recognition performed by the ANN. The TS-FM was attained maintaining the link between the minimum number of clusters and the best performance. After a sensitivity analysis, it was found that six (6) clusters equivalent to six fuzzy rules provide the best results.
3. EXPERIMENTAL DEVELOPMENT
MODELLING PETROLEUM PRODUCER FIELDS WITH AI
By developing computer data acquisition technologies, the management of big data bases made necessary to have more efficient data analysis tools. AI approaches got many possibilities for building those analysis tools. Simultaneously, the access to such large quantity of information turns the identification of deterministic models into a hard task due to the inherent complexity of the models and the conventional use of expertise supported methodologies for model construction. The implementation of AI techniques for information processing in petroleum engineering can be identified since 1989, with the use of Artificial Neural Networks (ANN) by Halliburton to model total porosity and lithofacies [29]. Also, AI was used to configure a predictive decline curve in the field of West Virginia [30]. Adaptations of AI tools were introduced continuously to meet the requirements of oil production analyses. That necessity has been recognized over time. In that sense, one of the first works using AI is [31], where a Fuzzy Inference System (FIS) model is developed in FORTRAN to evaluate economic feasibility in enhanced oil recovery processes. Similarly, in the work of Boomer [32] two analyses were compared for the same field: one using professional experience, and the other using ANN. The accuracy achieved with the last one was superior than the accuracy using professional experience, and it demonstrates the usefulness of AI techniques in modeling oil producer fields.
Early in the 21st century, and taking advantage of high computer processing speeds, a successful coupling of AI techniques was possible. In [29], ANN and FIS techniques are used to develop an accurate model to forecast oil production of a petroleum field. Fuzzy Logical rules are used to analyze noise signals and to select the variables for improving forecasting capabilities of ANN models. Further, in [33], both AI technologies are used to characterize fractured reservoirs, due to their capacity to manage high data volumes, and to identify relationships among variables.
After the use of AI to model, its use was explored to optimize oil field operations. In [34], a genetic optimization algorithm is used to evaluate different scenarios for several gas producer fields, resulting in a solution to the proposed production problem. The work [35] integrates AI with the six-sigma norm to adjust oil production according to market demand. Also, using classical optimization algorithms, in [36], an optimal operation is found using numerical models and ANN. With the coupling of AI tools, the forecast task takes less time and required less computational efforts when thousands of scenarios are tested. This premise is also defended in [37], which recognizes that the main difficulty in the optimization process is the high demand of computational resources even to simulate simple operational conditions with deterministic models frequently used for oil fields. In this same vein, the use of AI emerges as a useful strategy because those tools allow the identification of simple but robust models through ANN and FIS. There are results that show successful applications of those techniques to optimize a multi-well field operation [38].
As a consequence of its successful application in modeling, AI started to be used not only to obtain predictive models. The parametric identification of petrophysical properties was the next step. In the work of Al-Fattah and Al-Naim [39] an ANN model is used to represent the complex and non-linear phenomena of fluid transport and to predict water-oil relative permeability in a field. Similarly, in [40] authors use AI to analyze a set of data looking for trends to predict the behavior of oil and gas offshore assets.
With the access to big data bases, the priority evolved to analyze that information and extract useful knowledge about the oil field. Thus, [41] obtains an accuracy model using ANN without a-priori assumptions on the geological properties of the field. In spite of the heterogeneous properties of the treated field, the identified model is obtained only from historical data. Using ANN, [42] couples that AI tool with the nodal analysis to identify a reliable model in production allocation. Both techniques enable gathering the necessary data from available data to develop individual well models. Going a little further, in [43] an AI-based model was developed using data mining over historical data to predict the performance and to plan operational strategies for an oil field.
In view of the foregoing, traditional and AI methodologies have been coupled to obtain accurate models in petroleum engineering. An example of that is the technique named Top-Down Intelligent Reservoir Modeling (TDIRM), which integrates traditional engineering analysis with AI and Data Mining [44]. This technique has been used recently in the work of Dahaghi et. al. [45] to estimate petrophysical parameters, remaining hydrocarbon reserves, new well performance and other analysis directly performed on field data. The most commonly reported AI tool is the ANN, but FIS have participated in petroleum engineering too. Some reported uses in petroleum engineering could be checked in [46]. Regarding data mining, a general approach was proposed and tested in [6] for industrial processes. The adaptive resonance theory [5] is added to determine the operative modes in dynamic processes. Then, such dynamic modes are used for big data processing using AI tools. Improved data bases retain the main characteristics of the production field, avoiding false or wrong production values.
Recent works are related to complex engineering tasks. In [47], AI is used to model unconventional reservoirs. ANN and FIS with genetic algorithms have been used to find the production profile under a given operation, or solve the contrary problem, given a desired production profile to find the operation. In [48], a production history matching is made using AI. Hence, the model parameters are adjusted according to available data seeking to improve model accuracy. The result is a successful identification process for three heterogeneous field cases reported in the literature. Finally, in [46] FIS and Genetic Algorithms optimization are used in history matching processes to obtain accurate parameters identification for a production field.
A MODELLING METHODOLOGY FOR PRODUCER FIELDS
A petroleum producer field is a set of wells arranged in order to produce oil and gas from a reservoir or asset conformed by one or more formations. As it was mentioned before, having an interaction model among wells during production will provide a valuable tool to optimize producing field operations. In this regard, and looking for using artificial intelligence (AI) tools capabilities, a combined modeling strategy using artificial neural networks (ANN) and fuzzy inference systems (FIS), is presented herein. The major challenges to overcome were: i) to complete an available big data base looking for a complete data base containing all behaviors of an oil field, ¡¡) to mine the available big data in order to find wells' interaction and other operating effects over production, and iii) to obtain a model for each mass flow from each operative well in the oil field.
The used big data base is directly taken from an automatic data acquisition system of the oil field operator. The first challenge is solved using a simple algorithm to data fault detection and data imputation, obtaining a data base without lost data. The proposed algorithm operates through a data imputation procedure to detect data absences or data inconsistencies [6]. The second challenge is overcome using a FIS model as a well-clustering detector. An iterative FIS model identification detects when a regressor configuration is optimal for a well production model. Such regressor contains all wells affecting the modeled well. A simple analysis of all regressions obtained for all wells' models shows out the wells interaction in the field. The last challenge is overwhelmed identifying an ANN model and a FIS model for each mass flow for any fluid phase in each well. Next, models are selected in accordance with their prediction capabilities (minimum error over past data). This is the mechanism to attain the best AI model for each substance flow per well. When a batch of new data is available every six months, the re-selection of the "best model" is performed. It was found that some substances at some wells are better predicted by an ANN model, while others are better forecasted by a FIS model. Finally, the model of the oil field as a whole is a net of AI models (ANN and FIS) formed by the model for each well individual mass flow. Each individual AI model provides the forecast to be used as input by all other individual models to provide the next step forecasting.
DATA IMPUTATION IN DATA BASE
In order to complete the data fault in the available big data and taking into account a previous data set that represents the natural behavior of the wells, a data imputation procedure is proposed [6]. During the procedure, all changes in the original data base are recorded to contrast the real data set and each new reconstructed data set. Data imputation is required because natural field behavior must be totally reconstructed for modelling the field production with a low error margin. The purpose of this modeling work is to represent the natural behavior of the wells, but under current data fault, it is necessary to reconstruct data in order to correct those points where the field did not operate as it does normally or no-data exist, as it said by Buuren [49].
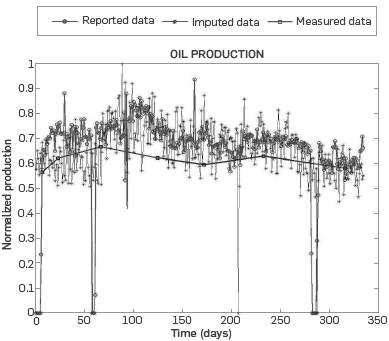
The proposed methodology first computes the average value of each mass flow on a moving time horizon. Two limit values are selected in accordance to direct values obtained from the data base to determine the tolerance for production variables. Next, the deviation for each data within this time window is calculated. Those values that are out of the select range are imputed with a random value of the data generated inside the range. In this work, a period of 67 days was used as moving horizon and a restricted range of x ±0.03 was selected for all normalized variables [0, 1]. Figure 1 shows the data imputation result for only one production well and one substance (oil). Similar results were obtained for the rest of wells of the modeled production field. The thick line with squares represents real measured data, as taken by human operators. The thin line with circles indicates the reported data from production completed by expert engineers using current estimative models available in the oil industry. Finally, the thin line with asterisks shows the results of the proposed imputation procedure, which was the database used for model identification and validation.
After the application of the foregoing procedure, a smoother behavior is observed over all mass flow on most of the wells. Obviously, such data imputation procedure minimizes the sudden changes caused by human intervention over a well, but preserves original well behavior.
NORMALIZATION
To find a model regressor (model inputs), a data clustering algorithm operating with fuzzy c-means principle detects the effect of different inputs on a specific mass flow in a well. As for oil, gas and water production for each well is reported in volumetric measurements, requiring data normalization of all variables into [0, 1] interval. A good normalization procedure must be: i) a linear operator with known inverse and easily computed and ii) able to maintain records of used limits to denormalize any datum to obtain the original value with its original units. Oil, gas and water production can be compared only in original units, non at normalized units, given their different original measuring units. However, using normalized data is possible to check when a well mass flow makes a significant contribution to overall field production.
The overall production is calculated with (4):
by adding up the production of all wells for the substance: i: 1=oil, 2=gas, 3=water. The percentage of participation of each well regarding total production is evaluated according to (5):
where q is calculated for the k-th well and process started for the substance i at time t. Finally, it is made the normalization of the overall production too with (6), (7), and (8).
As was previously said, normalized variables are all within the range [0, 1].
AUXILIARY VARIABLES DETERMINATION
With the aim to use variables containing extra information about the physical properties of the well, it is proposed to calculate the accumulative water-oil ratio (aWOR) and the accumulative water-gas ratio (aWGR). If oil, gas and water flows can be described by Darcy's law, those ratios provide a comparison of the relative permeability of porous media, pressure gradient and length of the trajectories for each substance. Therefore, those ratios make it possible to identify the wells that are more likely to produce one of the substances compared with other wells, keeping in the model the intrinsic flow nature of well to be modeled.
The accumulative ratios were selected over instantaneous ratios for two reasons: ¡) instantaneous ratio is a simple function of flow variables, not providing extra information, and ii) due to the noisy nature of the measured flow, the ratio computation will give some extra noisy variables, hindering the real flow trends. In this regard, and avoiding extra-noise over the data set, variables with smooth profile are used in the proposed model. A cumulative calculation acts as a smoother due to the effect of summation of variable variations over time. Based on that concept, aWOR and aWGR were calculated by (9) and (10):
keeping in mind that Q k (¡,t) for k the well, ¡: 1=oil, 2=gas, 3=water and t the time index. It is important to highlight that except for t=1, aWOR and aWGR do not have a direct relationship with the respective substance flows. In fact, those auxiliary variables provide information about the historic behavior of the well production.
MODEL INPUTS (REGRESSOR) SELECTION
After applying the above processes, each register at database for a k well have five entries or variables (oil, gas and water flows, in addition to WOR and WGR). Thus, it is necessary to determine which of all variables for other wells are adequate to model the flow of different substance at the current well. Two procedures for input variables selection are used. These are explained below:
Descriptive relation among variables
This process is aimed at determining what variables provide relevant information for a specific well substance-production model. It identifies the relationship among variables that will provide good model accuracy. In this sense, it selected the next model regressor structure for each well production flow in real time, q k (¡,t), produced flow one day ago, q k (¡,t-1), current cumulative aWOR k (t) and current cumulative aWGRk (t). Rember that cumulative variables provide information about relative production ratios of different substances inside the historical production profile of each well. In spite of the possibility of using a longer time lag (>2 days) for model regressor, to use data lagging only one day was enough to achieve good model precision. This prevents the uncertainty and noise introduced when a longer delay is used in the regressor. Obviously, if low-noise data were available, to include a longer time lag will improve model accuracy. Also, to model a given substance production, data of the same substance production for all wells are used. With their regressor selection, two objectives are fulfilled: i) obtaining a set of model inputs (regressor) with more information to model identification, and ii) avoiding noise variables into the regressor. When variables to be used for modelling are already selected, the next step is to determine the wells that may provide useful information to improve the accuracy of model. It will be explained in the next section.
Relation among all wells
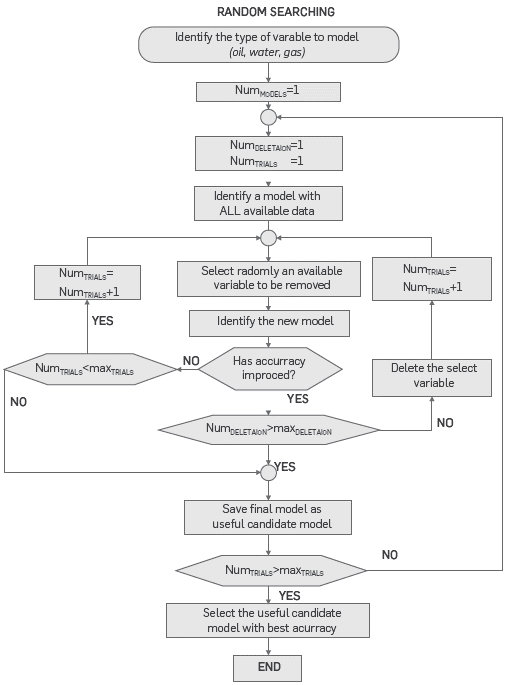
As it was mentioned before, the aim is to determine the variables of a specific group of wells that provide useful information to model a specific mass flow. This process is carried out with a two-step random search.
(I) Double random selection of model inputs. This step provides the input variables to be taken into account in each model (model regressor). The suggested procedure is:
a) With all variables indicated previously as model regressor to identify a patron model. In model identification, 70% of the available data is used in the identification process. The rest of data is used for validation purpose to allow the accuracy model quantification through the difference between predicted and real datum. The identification and Validation data sets are randomly selected from the complete imputed data base.
b) Randomly, one of all input variables is not considered in the model regressor. A new model is obtained, and its validation error is calculated. If current validation error is better than patron model, the selected variable is removed definitively from the regressor and the new model is the patron model. If this is not the case, the selected variable is returning to regressor and a new randomly selected variable is removed from the regressor.
c) The number of admissible deletions and the number of admissible trials are set as a priori parameters. If any of those admissible values are reached, the random search process stops and the current patron model is saved as a candidate for useful model. The process restarts from the beginning (starting with the identification of a new first patron model taking into account all variables) until reaching the maximum number of trials, or the admissible number of deletions. Thus, the useful candidate models are obtained.
(II) Best model selection: According to recorded validation error for each candidate to useful model, the best model is selected as the one offering best accuracy. At the end of this procedure, a model for one variable is available. The procedure is repeated until all variables to be modeled have their respective model.
Figure 2 presents the proposed random search algorithm. Inner iterative process performs searching task, deleting variables one-by-one until finding which should be eliminated to enhance the accuracy of the model. Second, an iterative process deletes the selected variable and restarts the search until reaching the maximum number of deletions, assuring that models with just one variable do not persist there. An outer iterative process allows for obtaining different candidates for final models to forecast well behavior. Once the regressor is determined, the ANN and FIS models are identified.
4. RESULTS
This work is conducted based on information of a Colombian oil producer field. The field has three producing formations, the main one with 23 active producer wells at 2013. The producer wells in the main formation are widely distributed along the field. The wells in the main formation produce by natural flow; however, with the aim of pressurizing the reservoir, natural gas is injected through 15 special wells. All wells in the field produce water, oil and gas. The field operation data available includes daily production of each well, distributed as water, oil and gas flows. Records contain the produced flow across all productive period of each well. For the purposes of this work, only data corresponding to 2013 is used for model construction and validation. The objective is to identify model parameters using 300-day data and validate the model forecasting over the last 35 days of the year. In this way, an indicative of the model accuracy is obtained.
Five wells were selected to apply the proposal algorithm looking for a group of interacting wells directly identified from AI tools. The selection was made according to geo-location information to ensure that selected wells had a high inter-related behavior Fuzzy clustering was applied on operational data to verify assumed wells interaction and discover some new interactions. It is worth mentioning that some FIS findings when applied to well interaction detection resulted contrary to the geo-localization indication However, after consulting with company production and reservoir expert engineers, the FIS results were confirmed by the presence of rock discontinuities among field formations. Two gas injector wells were included in the set as they are placed in the selected area
Following the procedure described above, models for six interconnected wells were identified. The overall algorithm was configured with just one day of delay in all variables avoiding cumulative error during predictions. Total data set corresponds to 336 days of field operation. 300 days of this set of data were used to identify the model, and the other 36 days were used to validate the model. For FIS models, 4 clusters were selected as inference If-Then rules structure. The ANN models have 3 neurons in the hidden Layer, and 3 total layers (input, hidden and output).
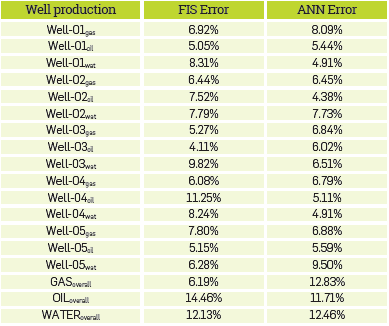
After the model identification process, the accuracy of each model is assessed by comparing the model predicted value and the real value of the validation data set. Table 1 shows forecasting errors for FIS and ANN models of several wells. The results are grouped according to the corresponding well production. At the end of the table, the relative errors for the models that predict the overall production of water, oil and natural gas of all producer field are shown. As it was mentioned before, the overall production data is required to interpret the contribution of each well in overall production.
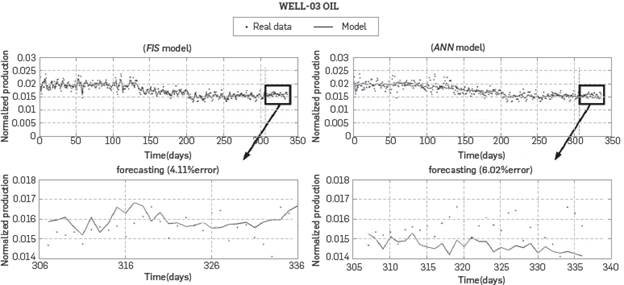
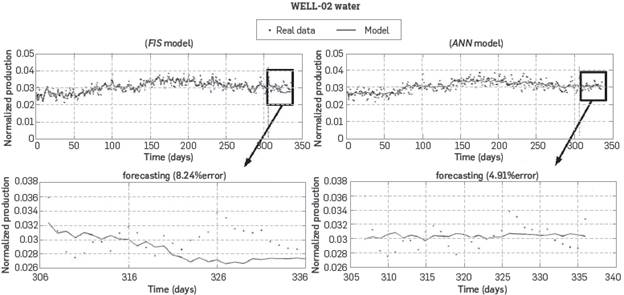
The forecast task is run for FIS and ANN models. For this purpose: models start with the last "known" data (data from day 302), and the prediction is performed. Forecasting continues running using past prediction values, i.e., all values predicted by the model are used as valid past data for future prediction. This fact could conduct to an error cummulative effect, whenever the model parameters are wrong. Therefore, to use past model predictions for future prediction is a critical task for any model. As it can be seen from forecast results, the current models have shown good behavior regarding real data. In Figure 3 and Figure 4, the results of forecasting for FIS and ANN models of two producer wells (WELL 01 and WELL 02 respectively) are shown. Each figure compares the results for both AI tools. Such comparison is used later as a criterion to select the model providing the best forecast. Thus, both models are solved in parallel to rely on the better forecast as the valid prediction for the next-time step. In Fig. 3, the FIS model showed better performance than the ANN model, but in Fig. 4, the behavior is opposite. It shows that forecasting performance is not determined by the AI tool, but for the quality of data. Then, it is proved that the algorithm has a non-arbitrary behavior.
In addition, after reviewing Table 1, it is possible to state that there is not a best model between FIS and ANN for all the wells. It is possible so state that the FIS models capture specific behavior of the production while the ANN models represent an average trend of well production. This fact enables using both kinds of AI models to obtain a better well production forecast. Hence, the best performance of each AI tool is provided in accordance with available data for each forecast. The specific behavior capture and average trend modeling are complementary tasks that contribute to improve the final forecast. It should be noted that the model forecast could be an average or a specific prediction regarding the use of ANN or FIS. However, the global performance seems an average from the combination of both tools. This action produces a filtering effect resulting in softer predictions with a trend to real data of each production stream. Furthermore, the input transfer from inputs to model prediction of the inherent noise present in the data set is significantly reduced.
CONCLUSIONS
This work proposes a methodology to identify a combined FIS and ANN model to predict well production in an oil field. The methodology includes a novelty pre-processing of data in order to impute data at absent or erroneous registers in the original database. The aim of that imputation is to obtain the most precise information representing natural dynamic behavior of the field taking into account the available production information. The data imputation previously applied to the data base avoids identify specific operational policies, which are totally unpredictable in a typical oil production field. Conversely, data imputation used hereon operates from the core dynamic behaviors of the production field
A random search is used to find the significant variables to be used as model input (regressor) for each well model. This process deletes a variable randomly and compares the validation error with previously Identified models. The random search is carried out a finite number of times. At the end of that procedure, the model with best accuracy to represent just one producer well is selected.
For each well, a FIS and an ANN model are identified for each produced substance. The FIS models are capable of predicting specific behaviors, while the ANN models are able to forecast an average behavior. Those properties make them an interesting tool to combine each forecast result and obtain the best accurate prediction of the fluid phase production.