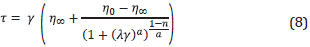1. INTRODUCTION
The enhanced oil recovery (EOR) methods are a group of techniques applied in reservoir management with the purpose of improving the oil recovery factor that today can be applied at any stage of reservoir development. The EOR methods are divided into three broad categories [1]-[4], thermal, miscible and chemical (CEOR) methods. The last group consists in adding chemical products to the injection fluids. It encompasses polymer, surfactant/polymer (SP), alkali/surfactant/polymer (ASP) or gel floodings. However, among them, polymer flooding is the most used method in large scale, while the SP and ASP applications are limited for technical reasons, such as the difficulty to design and predict the process behavior in the field, the excessive formation of carbonate or silicate scales, and the formation of strong emulsions in production facilities [5].
A surfactant-polymer (SP) process consists in the addition of surfactant products, to achieve significant interfacial tension reduction and, thus, produce a high capillary number. Also, a polymer solution is used as control mobility agent seeking an increase of areal efficiency [6],[7].
Characterizing the chemical products to be injected and understanding their interactions are key factors for the effectiveness and dynamic performance of the CEOR process [8]-[11]. Therefore, the design of the optimum formulation demands previous studies related to the rheological behavior of the selected polymer, the capability of the chosen surfactant to reduce the IFT, as well as the solution phase behavior evaluation.
Therefore, this study is focused on the assessment of the injection blend using Flopaam 3230S and SDS as polymer and surfactant, respectively. It seeks to found an SP formulation suitable to develop an EOR process encompassing a detailed rheological study to determine the influence of temperature, salts and surfactant concentrations on different polymer solutions. Furthermore, phase behavior tests aim to determine solubilization parameters, optimal salinity, type of micro-emulsion and IFT values through Chun Huh equations.
2. STATE OF THE ART
The residual oil mobilization mechanisms associated with CEOR process has been linked to a decrease of the capillary forces[12] due to the reduction of IFT [13] and thus, increase of the capillary number. This condition is achieved when interfacial tension reaches values ranging between 10-3 and 10-4 (dynes/cm]. Additionally, changes in rock wettability have been documented [14],[15].
Different definitions related to the SP process have been used [4],[16],[17]. The main difference lies in the surfactant concentration, and the way in which the polymer is used during the process. For this work, an SP flooding is characterized for the use of low surfactant concentrations (0.1% to 2% wt) and the addition of polymer in the same solution to increase its viscosity and overcome the viscous instability of low interfacial tension [18]. This approach differs from the Micellar flooding as in that case, the surfactant concentration is 2% up to 12% wt higher, and also from the surfactant flooding where the surfactant is added only on the aqueous phase. Another injection scheme considers a surfactant slug driven by a polymer solution to improve the sweep efficiency and reservoir pressure maintenance [19].
The surfactants are amphiphilic molecules, i.e., they have both hydrocarbon portion (nonpolar) or "tail" and an ionic portion (polar) or "head" [4]. Therefore, they are soluble in both, organic solvents and water. Usually, they are referred to as surface-active agents [20]. At low concentration, they are adsorbed on the surface, or concentrated at the fluid/fluid interface and thus, reduce the surface energy per unit area required to develop the interface between two immiscible fluids, also called IFT. This effect takes place directly due to the replacement of solvent molecules at the interface by surfactant molecules i.e., the micelles have solubilized a phase that is immiscible with the solvent. These aggregates in solution are named micro-emulsions (ME).
Surfactant dissolved in either water or oil phase tends to partition in some degree into the other phase. It depends on its capability of solubilizing between phases. i.e., a hydrophilic surfactant tends to be preferably soluble into water without excluding that part of it can also solubilize in oil. The partitioning can be characterized by the partitioning coefficient (Ke), which is defined as:
Where  and
and  are the concentration of the solute in the oleic and aqueous phase, respectively.
are the concentration of the solute in the oleic and aqueous phase, respectively.
The partitioning coefficient depends on temperature, surfactant composition at the interface, ionic strength, pH, oil type and cosolvents used [21],[22]. A partitioning coefficient equal to a unity corresponds to the same solubilization of both fluids within the micro-emulsion. This condition is associated with the Winsor III behavior and the minimum IFT of the system.
The Bancroft's Rule is an entirely phase-based qualitative method, where an emulsifier is more soluble and, constitutes the continuous phase [23]. Therefore, hydrophilic surfactants tend to generate oil in water (o/w) emulsion, whereas lipophilic surfactants will make water in oil (w/o) emulsion. The use of this rule has been recently reported [24].
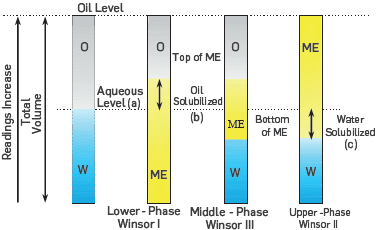
Several authors [24],[26],[27] have associated micro-emulsions with a high solubilization of oil and water with the low IFT values required to improve the oil recovery. The formation of a micro-emulsion is influenced by different factors such as surfactant nature, brine salinity, temperature, co-solvent types, etc [6],[28]. Hence, three different kinds of micro-emulsion are usually reported in CEOR processes. The first, known as Winsor I or Lower-phase micro-emulsion is present when the surfactant exhibits good aqueous-phase solubility, and a small quantity of oil is solubilized in the cores of the micelles, i.e., the ME characterizes by an excess oil phase (O) without surfactant and a water-external micro-emulsion phase [29]. In the second case, named Winsor II or Upper-Phase micro-emulsion, the system separates into an oil-external micro-emulsion containing some solubilized water and an excess of water phase (W). The Last system, called Winsor III or middle-phase micro-emulsion, is more complex due to the existence of a three-phase region consisting of excess oil, micro-emulsion, and excess water [28], This region is saturated with both oil and water at the temperature and overall composition of the system, and it is important due to the associated ultralow IFT's values [16]. A schematic representation of the micro-emulsion types is shown in Figure 1.
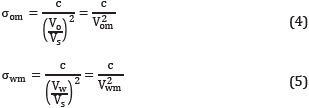
The micro-emulsion behavior as a function of different variables of interest (Water/oil Ratio-WOR, salinity, surfactant and co-surfactant concentrations) have been studied through phase behavior tests. These tests are conducted in pipettes, and the primary objective is to find a chemical formula with high solubilization ratios of oil and water volumes, and to determine the optimum salinity, i.e., the salt concentration where the lowest IFT value is obtained. According to [4],[27], to reach an ultra-low IFT, the solubilization ratio must be greater than 10. One way to quantify the solubilization ratio parameters is shown in equations (2) and (3)
Where A is the aqueous level, B and C are the oil and the water-solubilized level, respectively. The Figure 1 includes the schematic representation of these variables.
The IFT values between the micro-emulsion and the fluid phases can be obtained according to Chun Huh [30] based on the solubilization ratio parameters, as follows:
For the above equations, Huh, found that in EOR process these expressions are consistent with values of c near 0.3. A reasonable agreement between these equations and measurements carried out with a spinning drop are reported [26],[31].
The phase behavior has been extensively studied. Healy et al. [28] explored some physico-chemical properties of multiphase micro-emulsion systems viewing toward understand immiscible aspects of micro-emulsion flooding and develop systematic screening procedures useful for optimal flood design. The relationship between interfacial tension and phase behavior were exposed Moreover, they showed that the addition of polymer to the brine did not affect the interfacial tension behavior in a significant manner In addition, Reed & Healy [32] presented a complete and detailed study on the effects of salinity, brine composition, temperature, surfactant structure, cosolvent, and oil aromaticity on the phase behavior, Interfacial tension, and solubilization parameters. Table 1 summarizes the results.
Table 1 Summary of Influence of Some Variables on Phase Behavior, Interfacial Tension, and Solubilization Parameters.

Salager [33] also presented a detailed study of the phase behavior micro-emulsion formation, and Interfacial tension. This author presented detailed experimental procedures to characterize the surfactants and to develop the phase behavior tests. The evaluated variables Included: surfactant concentration, structure, and composition; aqueous phase salinity; oil structure through the alkane carbon number (ACN) for alkane series, and effective Alkane Carbon Number (EACN) for other hydrocarbons or mixtures; the alcohol type and concentration, WOR and temperature. The process was considered not very sensitive to pressure changes. Table 2 shows the phase behavior results for anionic surfactants.
Micro-emulsion viscosity measurements were conducted for Bennett, Davis, Macosko, & Scrlven [34], observing that at a fixed shear rate or shear stress and during the transition to Winsor I→III→II, The micro-emulsion viscosity presented two maximum points and a minimum closer to optimal salinity. Close to these maximum values, the ME exhibited non-Newtonian behavior, whereas far away from these points, the micro-emulsion behaved as a Newtonian fluid. On the other hand, Thurston, Salager, & Schechter [35] showed a Newtonian behavior of the viscosity In a Winsor I→III→II transition. They also proposed that the birefringence and viscosity are maximized near the salinity that a transition of phase behavior occurs. Similarly, Lopez Salinas [36] performed the micro-emulsion viscosity measurements using a falling-viscometer with multiple ring-shaped and inductive proximity sensors. The micro-emulsion viscosity presented a Newtonian behavior. Moreover, the micro-emulsion viscosity in function of the salinity exhibited two local maxima and a local minimum. The latter In Itself is near optimal salinity.
Using mixtures of surfactant (anionic and nonlonic), polymer, alcohol, water, oil and sodium chloride, Pope, Tsaur, Schechter, & Wang [37] performed static measurements of phase volumes, Interfacial tension, viscosities, and phase concentration. They observed a phase behavior transition of Winsor l-HII-HI for mixtures with and without polymer. They also noted that the anionic surfactants appear to be more compatible with polymers than nonionic ones. Moreover, they reported a little difference in the IFT values with and without polymer. According to them, the polymer only increased the viscosity of the water-rich phase, with little effect on the micro-emulsion phase.
Alvestad et al. [10] presented the dynamic behavior of some surfactant systems for EOR applications. They conducted phase behavior studies and core flood recovery process. The surfactant used was synthesized for seawater and heptane at 70°C. Dueto this optimization, a cosurfactant not was required. The phase behavior was determined at WOR equal to 20, 10, 4, 2, 1, 1/2 and 1/3 for surfactant concentrations between 0 to 3 [%wt]. The results showed a Winsor II→III→I transition.
The micro-emulsion transition shown In the Figure 1 is considered an Ideal representation of the phase behavior, I.e., those multiphase regions are uniquely defined. The real phase behavior Is more complex than that since several middle-phase compositions are founded rather than a single point. The presence of a precipitate in equilibrium with a rich oil micro-emulsion and several liquid crystalline structures with birefringent properties are some indicators of a not typical phase behavior. A complex experimental behavior Is reported by Salter [38].
The phase behavior of water/oil/surfactant systems and the basic principles of low-energy emulsification was reported by Nishimi [39] According to this study, the surfactants SDS and Disulfosuccionate Sodium Salt (AOT) exhibited only two phases with a phase transition Winsor INI at all salt concentrations. Also, pointed out that even at the point of balance between hydrophllicity and lipophillcity, a three-phase state was not observed.
Y. Wang [40], presents the results of over forty core flooding test assessment of a surfactant-polymer process in homogeneous and heterogeneous porous media. The IFT behavior for the different formulations evidenced that a tendency associated with the polymer concentration In the solution Is non-existing and the IFT values presented a small difference. Nevertheless, in general, the order of magnitude of these values was maintained.
Sagi et al., [41], presents an evaluation of surfactants at 25°C for a CEOR process in a carbonate reservoir with salinity of 11.000 ppm of total dissolved solids (TDS). The phase behavior tests showed a transition of Winsor I→II without observing Winsor III behavior. Hence, they proposed some criteria to determine de optimal salinity based on the solubilization parameters and assuming that all the surfactant was in the micro-emulsion phase.
On the other hand, synthetic polymers and biopolymers have been used in the petroleum Industry. The conventional synthetic polymer used is partially hydrolyzed polyacrylamide (HPAM), and a common biopolymer Is Xanthan gum [42], The HPAM Is used for most field projects due to its costs and large-scale production [43], The HPAM is a copolymer of polyacrylamide (PAM), which is obtained by partial hydrolysis of PAM or by copolymerizatlon of sodium acrylate with acrylamide [44], The hydrolysis of PAM consists in converting some of the amide groups (CONH2) to carboxylate groups (COOM). It reduces the adsorption on mineral surfaces. In commercial products, the hydrolysis usually ranges from 15% to 35%.
When a monovalent salt (i.e., NaCl, KCl) Is added in a homogenous HPAM solution, the carboxyllc group is surrounded by the cations, which shield the charge and reduce the carboxyllc group repulsion the hydrodynamic volume becomes smaller and therefore, the viscosity decreases [4], When divalent salts are present (i.e. MgCl2.6H20, CaCl2.2H20) in an HPAM solution, their effect is more significant on the viscosity reduction. At high hydrolysis, the solution viscosity decreases sharply until the precipitation of a complex mix of hydrolyzed products and divalent cations occurs [45],[46], Due to their higher positive charges, divalent Ions are more effective in shielding negative charges on the polymer chain than the monovalent ions. Consequently, the polymer coils up at Lower divalent Ions concentration, and the hydraulic radius of the polymer chain reduces, diminishing the degree of polymer chain entanglement [47],[48],
Temperature also influences the rheological behavior of the polymeric solution. Significant changes are reported for 60 and 90 °C [49], Different authors [50]-[52] documented that the relationship between the apparent viscosity of polymeric solution and temperature satisfies the Arrhenlus equation:
where η is the apparent viscosity of the polymeric solution, A Is the frequency factor, T is the absolute temperature, ∆Eη is the viscous activation energy or the activation energy for flow, and R is the universal gas constant.
Several models describe the rheological behavior of pseudo-plastic fluids under the majority of variable conditions [53]. Nevertheless, the most commonly used is the power law model, also called as Ostwald-de Waele law [4], which describes the pseudo-plastic region. Mathematically, the formula is:
where τ is the shear stress (Pa), y is the shear rate (s-1), n is the flow behavior index (dimensionless), and k is the consistency index (Pa*s). For pseudaplastic fluids, n < 1. The equation describes with good accuracy only the pseudo-plastic regime and cannot be applied for high and low shear rates [20].
A more satisfactory model for the complete shear rate range, capable of fitting data in the three regions of the characteristic curves of thinning fluids, is the Carreau-Yasuda model [4],[54].
where η∞ is the limiting viscosity at the upper shear rate and is generally taken as water viscosity [4], n is the same as power law index, Á is a time constant generally taken as 2 [4], n0 is the viscosity at very low shear rates or stress.
Nasr-El-Din, Hawkins, Green, & Inst [55] developed an experimental study to determine the effects of various alkalis, surfactants and brine on the viscosity of dilute aqueous solutions of Alcoflood 1175L and HPAM. They evidenced that the presence of ionic species (NaCl, CaCl2), and anionic surfactants reduced the hydrodynamic size of the polymer molecule (physical change), inducing a detrimental effect on the solution viscosity. They observed that nonionic species presented a negligible effect on the viscosity behavior. The effect of alkalis on rheological behavior is complex as they affect the polymer chain physically (charge shielding) and chemically (hydrolysis).
Samanta et al. [11] described the anionic surfactant effects on the rheological behavior. They observed a detrimental effect on the viscosity of HPAM solutions when adding SDS. They confirmed that the apparent viscosity of polymer decreases with an increase in the surfactant concentration. Also, Shupe [56] exposed a reduction of viscosity of polyacrylamide solutions and attributed this effect to the increased ionic strength of the surfactant solutions, caused by the content of anionic surfactants themselves and significant amounts of sodium sulfate.
Another important property that must be considered during the design of a CEOR process that includes polymer for operations is the visco-elasticity. Laboratory results have reported an increase in oil recovery when using visco-elastic polymeric solutions [57],[58]. This improvement has been attributed to the elastic properties of the polymeric solutions, and their effects on the displacement efficiency increase [59]-[61] through the expansion and contraction of the polymeric solutions inside the porous ganglia.
Urbissinova et al. [61] investigated the effect of both polymer solutions with similar shear viscosity, but different elastic characteristics elucidating a later breakthrough time and higher oil recovery when the polymer with higher elasticity was used.
Wei et al. [62] presented a review of the oil displacement mechanism in polymer flooding. They related the elastic properties with a pull effect, stripping and oil thread (column flow) as a mechanism to reduce oil residual saturation.
Xia et al. [63] compared the displacement efficiencies of visco-elastic HPAM solution and viscous glycerin solutions by flooding at visual macroscopic glass models. The results elucidated the gradual increase of the displacement oil residual efficiency as the viscoelasticity of HPAM solutions and the viscosity of glycerin solutions rises.
Zhang et al.[64] showed that the oil recovery of visco-elastic polymer flooding can be enhanced by larger displacement efficiency due to its microscopic roles. Therefore, the injection pressure required increases accordingly if the elastic effect is significant.
Clarke et al. [65] demonstrated the existence of a phenomenon called elastic turbulence. The presence of elastic turbulence will generate a fluctuating pressure field that is observed to destabilize trapped oil drops and thus, recover more oil. Based on the above, this study is aimed at analyzing the behavior of the storage modulus (G'), also named elastic modulus, which is related to Hooke's law [53]. It is associated with "memory" or elasticity of the polymer solution, which means that the material returns to its original configuration when any deforming force is removed. Moreover, the changes caused on the loss modulus (G''), known as viscous modulus [66], provides information about the viscous properties of the solution. If G' and G': exist simultaneously and are horizontally parallel in an amplitude sweep test (AST), it can be stated that the material has a linear visco-elastic region (LVR) [53],[67].
In the light of the above discussion, we can state that for a successful surfactant-polymer flooding, an entirely rheological behavior study and phase behavior tests of the solutions should be carried out on target conditions to evaluate and determine the better chemical and the corresponding amount should be used. Thus, allowing a better understanding of mechanisms acting during the CEOR process.
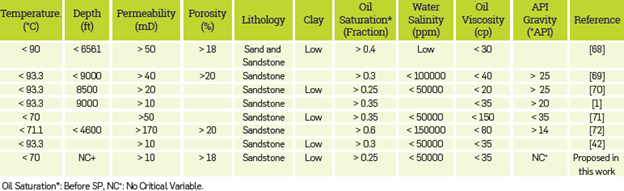
The target conditions for this work were determined through a previous screening of the method (Table 3). Based on these criteria, the reservoir conditions, petro-physics and fluid properties of the San Francisco (SF) field were selected as references to develop this study.
The SF field was discovered in 1985 and is located 20 km northwest of the city of Neiva in the Upper Magdalena Basin (Colombia). The San Francisco Field is an example of a mature field producing under a mature water-flooding project, with water cut above 90%, an unfavorable mobility ratio [73],[74]. The SF field is considered a good candidate for a CEOR process.
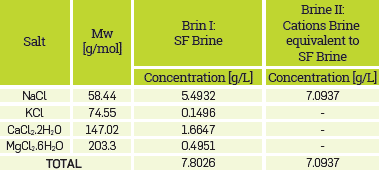
The reservoir temperature is 50 °C, with an initial pressure of 1100 [Psia], at depth of 3000 [ft], a permeability and porosity range of 20-2000 [mD] and 12 - 23 %, respectively and a residual oil saturation closer than 0.25. The oil viscosity was determined at reservoir temperature and corresponds to 18.4 [cP]. The reservoir brine composition is shown in Table 4.
The information related to the field was supplied by the Project "Advanced image techniques for reservoir characterization and improvement of the oil recovery factor," developed by Universidad Industrial University of Santander (UIS), Ecopetrol S.A and Colciencias. It is important to highlight that the reported information is only a reference for the properties to be experimentally recreated to conduct this work.
3. EXPERIMENTAL DEVELOPMENT
MATERIALS.
A viscosity of 16 - 20 [cP] guided the selection of the oleic phase, which consisted in a mixture of Marlim Field dehydrated oil and Kerosene 28,6 [%wt], A rheological study determined the proportion of each fluid. The last was aimed at keeping the target oil viscosity. The oil density and viscosity were measured as 0.881 [g/cm3] and 18.5 ± 1 [cP], respectively, at atmospheric pressure and a temperature of 50 °C.
The selected polymer was Flopaam 3230S® from SNF Floerger, which is a synthetic HPAM with an Mwof 5 x 106 [g/mol], 30% of hydrolysis degree, and water content of less than 1%[75].
The Sodium dodecyl sulfate (SDS) from LabSynth with MW of 288.373 [g/mol], with purity of 99.23%, was chosen as the surfactant.
The polymer was selected because the molecular weight of HPAM is directly related to the permeability of the porous media, and it is threrefore the polymer to be used [76], On the other hand, the SDS already has been evaluated as a useful surfactant for a CEOR process, with similar oleic phase composition [77],[78]
POLYMER SOLUTION PREPARATION.
The polymer solution preparation followed API RP 63. A stock HPAM solution containing 5000 ppm of the polymer was prepared using the synthetic brines (SB) described in Table 4. The brines were deairated using a vacuum pump, and the HPAM was added to the solutions while agitating them with a magnetic stirrer. The agitation continued for (5-7) h until the solution reached a homogeneous aspect, and it did not have Insoluble particles (fisheyes). All the HPAM solutions were prepared carefully with the minimum degree of agitation to avoid mechanical degradation of the long-chain molecules. The stock solutions were left still overnight to ensure full hydration.
Then, the stock solutions were diluted with SB up to desired concentrations (eleven different levels). The new solutions were put into a beaker and homogenized with a magnetic stirrer at low speed (120 rpm) for 10 minutes. All HPAM solutions were stored in closed containers to minimize oxygen uptake.
The preparation of Surfactant-polymer Blend solutions differs from the process exhibited previously, only regarding the kind of solution used to prepare the polymer stock solution and dilute it. In this case, the solution has a mixture of brine and surfactant. The SDS and HPAM concentrations analyzed were 0.5, 1, 1.5 and 2 [%wt] and 5000, 2000,1500 and 1000 ppm, respectively.
RHEOLOGICAL FLUIDS CHARACTERIZATION.
In this part, the work was divided into two steps. The first one focused on the examining the temperature (50 °C) and salts (tests conducted at laboratory temperature aiming to minimize the temperature effect) effects on the rheological and viscoelastic behavior of polymer solutions prepared with both reference field brines. Therefore, this step aims to select one of them to develop the following activities.
The second evaluation study focused on the Investigation of the surfactant effect on the rheological behavior of the aqueous solutions. This analysis was conducted only with the brine selected previously.
RHEOLOGICAL AND VISCOELASTIC ASSESSMENTS.
The rheological and viscoelastic parameters were measured using a rheometer HAAKE MARS III, which is a high precision instrument. The sensor used was the coaxial cylindrical (DG41), whichis preferable for low viscous fluids. The temperature was controlled by a THERMO HAAKE C25P refrigerated bath with a Phoenix II controller. A new sample was used for each test, and every data analyzed was within the measuring range of the equipment and was compared with the rheological behavior of a fluid pattern (IPT-83). The flow curves were recorded at shear rates between (10-1 and 103) s-1 with 20 measurement points. These flow curves were used to evaluate how the shear stress and temperature affect the viscosity of the solutions.
The viscoelastic behavior was determined with frequency sweep tests (FST) covering a range of 0.062832 - 628.32 rad/s with 25 measurements points. For this study, it was necessary to choose a shear stress within the LVR of amplitude sweep tests (AST) conducted between 0.001 - 100 Pa, with 30 measurements points. These measurements were carried out, at least in duplicate using fresh samples, at 50 °C and atmospheric pressure to ensure the repeatability of the results.
PHASE BEHAVIOR TESTS
This analysis was used to determine solubilization parameters, optimal salinity for different surfactant concentrations, the type of formed micro-emulsion and the IFT values at the desired salinity varying the surfactant concentration. The fundamental assumptions made in this development were:
Isothermal conditions at 50 °C;
There is no free gas into the oleic phase;
The effect of divalent cations and alcohol on surfactant phase behavior is currently not investigated;
Polymer content does not affect surfactant phase behavior;
The effect of pressure on surfactant phase behavior is neglected;
WOR = 1.
Similar assumptions have been reported in the literature [79].
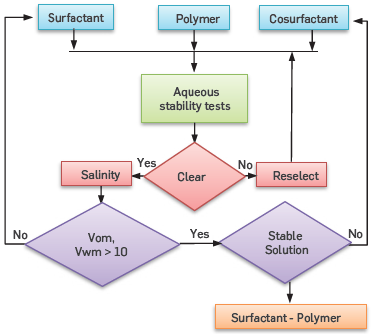
These tests were based on salinity scans at different surfactant concentration. The strategy used for this step is presented in Figure 2. The solutions were prepared according to Salager (33). Its method is based on the development of highly concentrated surfactant and brine solutions, followed by dilution up to the desired concentration values.
Different borosilicate pipettes of volumetric capability of 5 [ml] were filled separately up to 2 [ml] with solutions containing SDS at 0.5, 1, 1,5 and 2 [%wt], and variating the NaCl concentration of 0.2, 0.5, 0.7, 0.9, 1.2, 1.5, 2 and 3 [%wt]. Then, the pipettes were heated until the investigation temperature and, then, agitated. Finally, pipettes were sealed and left still overnight to observe the occurrence of any precipitation. This procedure was defined as an aqueous stability test. To avoid precipitation of some compounds during pipettes filling is recommendable to spill the fluids as follows: 1) Brine, 2) Distilled water, 3) Surfactant Solution.
Later, 2 [ml] of the oleic phases were placed inside the pipettes. They were sealed and balanced at constant temperature. Then, the pipettes were inverted six times every two hours for a total of 8 hours. The last step was repeated the next day. The registration of the volumetric and properties changes started 24 hours after the mixture process finished.
The test ended when the system reached the equilibrium point. According to Per Healy & Reed [6], this occurs when no further macroscopic changes (volumes or number phases, color, transparency, and others) takes place in a micro-emulsion.
4. RESULTS
SHEAR STRESS AND SHEAR RATE CURVES.
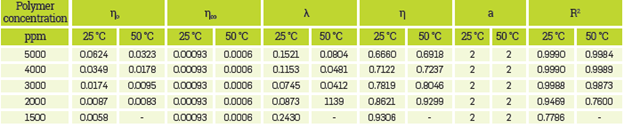
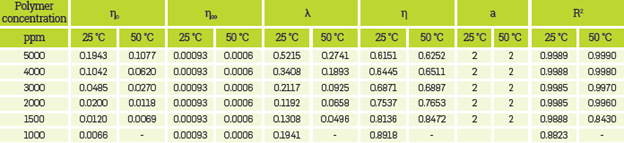
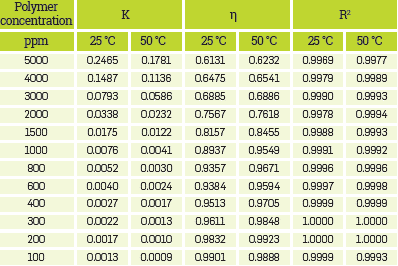
This section shows the results for shear stress-shear rate data of the prepared HPAM solutions with different polymer and salts concentration obtained at reservoir temperature. The solutions with high polymer concentration present the first plateau and the pseudo-plastic behavior. In these cases, both regions can be fit using the Carreau-Yasuda model. Adjusted curves showed good accuracy (R2 values showed in Appendix A are closer to 1).
While under low polymer concentrations, the fit provided by Carreau-Yasuda model became similar to Ostwald-de Waele law. This happens when the value of n°° becomes close to the value of no. In this case, the calculation to obtain the Carreau-Yasuda constants implied greater uncertainty, i.e., the R2 gets away from 1. Figure 3 shows the fits obtained for HPAM Solution with Brine I at 50°C. For Carreau-Yasuda model n« corresponded to 0.93 and 0.6 for 25°C and for 50°C, respectively. These values are the SB I viscosity at these temperatures.
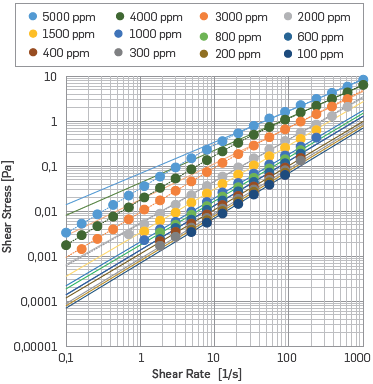
Figure 3 Shear Stress vs. Shear Rate for HPAM Solution with Synthetic Brine I and different polymer concentrations at 50 °C. Dashed lines: Carreau-Yasuda fits, continuous lines: Ostwald-de Waele fits.
All samples showed good fits to the theoretical models (R2 >0,9800) and showed that when as more diluted the solution, the closer to the Newtonian fluid behavior (n=1), presenting negligible changes in the shear rate.
As the polymer concentration increases, the consistent index decreases. i.e., the higher the polymer content, the greater is the resistance to the solution flows. Therefore, at a fixed shear rate, the solution exhibits larger shear stress, as presented by other authors [50],[67],[80],[50],[67]. This resistance increase is related to increased e intermolecular entanglement [48],[53].
The parameters for the best fits using the mentioned models for all HPAM solutions are presented in Appendix A.
Figure 4a,b shows the viscosity against shear rate for polymer solutions with both SB compositions at different HPAM concentrations. The viscosity of the solutions decreased with decreased polymer concentration and, therefore, have a low shear stress, as expected. In addition, when shear rate increases, the solution viscosity decreases, suggesting that the HPAM solutions exhibit shear thinning behavior as has been mentioned by other authors [11],[66], This behavior Is due to uncoiling and aligning of the polymer chains upon exposure to shear flow.
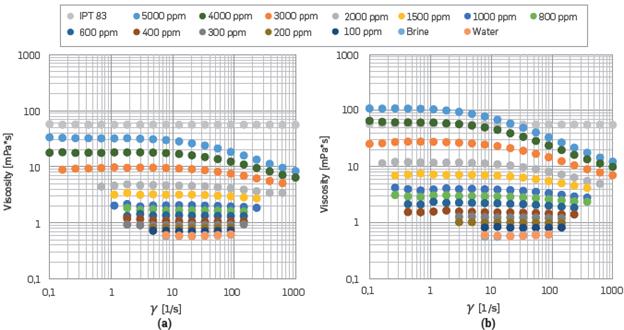
Figure 4 Viscosity vs. Shear Rate for Polymer Solution with different HPAM concentrations at 50 °C using (a) Synthetic Brine I (b) Synthetic Brine II. The water viscosity is plotted as well.
SALTS AND TEMPERATURE EFFECTS ON THE RHEOLOGICAL BEHAVIOR OF POLYMERIC SOLUTIONS.
Figure 5 summarizes the salts Influence on the solution viscosity at laboratory temperature (25 °C). On such grounds, one can see that the ions influences are more evident for low shear rate and high HPAM concentrated solutions. Additionally, higher divalent cations content Included in the SB I caused a more negative effect on the polymer solution than that of the SB II. The more diluted the polymer solutions are, less is the influence of ions on the polymer chain. Despite the brine composition, HPAM concentrations below 1000 ppm were less affected by the ions content.
The presence of Na+ generates shrinkage on the hydrodynamic volume. The effective neutralization of negative charges promotes a compression of the flexible chains. As the salt content increases, the coiling of the polymer increases generate a detrimental effect on viscosity. Other authors have presented a similar performance [4],[11],[53], On the other hand, the divalent cations (Ca+2, Mg+2) Interact with negative loads, thus neutralizing the effect of molecular expansion [75],[81].
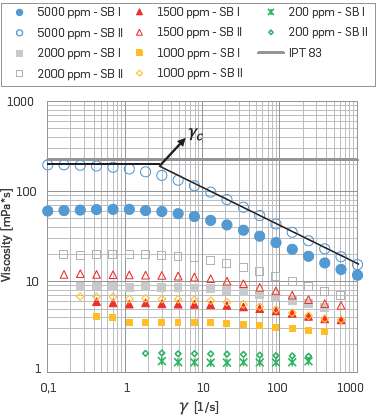
Figure 5 Comparison of Viscosity vs. Shear Rate for HPAM solutions with different SB ions content (SB I: Na+, Cl-, K+, Ca+2, Mg+2; SB II: only Na+, Cl-) at 25 °C.
The critical shear rate (γ c) represents the transition between the Newtonian behavior or Initial plateau and the beginning of the shear-thinning behavior (see Figure 6). The reduction of the hydrodynamic volume results in a higher critical shear rate. Accordingly, the Newtonian behavior will extend over a wider range of the shear rate. The cations effects explained above also occur at 50 °C. As it Is well known, the temperature raise generates an increment on the average speed of the molecules within the liquid; therefore the interaction time with neighboring polymer molecules decreases. As the temperature increases, the average Intermolecular forces decrease. Similar behavior has been reported [11],[67].
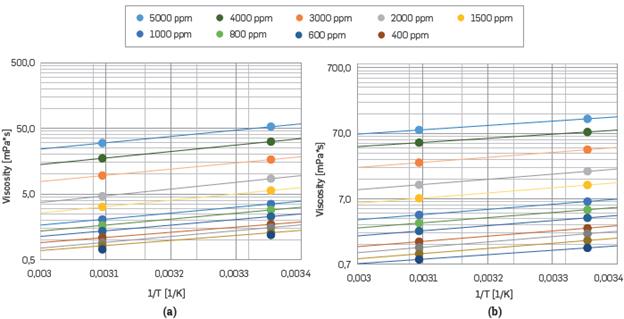
Figure 6 Arrhenius plot of viscosity at different HPAM concentration with shear constant, γ=7.8 s-1. (a) polymer Solution with SB I; (b) polymer solution with SB II.
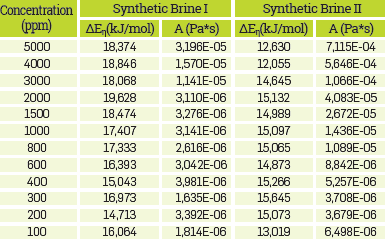
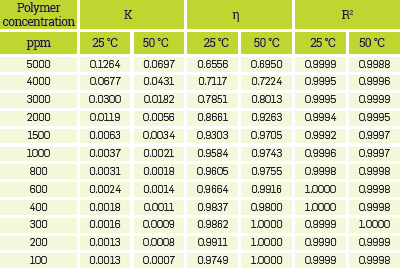
The Arrhenius equation was used for correlating the effect of temperature on the viscosity of HPAM solutions. For this purpose, a reference shear rate of 7.8 s-1 was selected, which Is approximated to the shear rate applied to the fluid in the reservoir [75],[82], Table 5 shows the fit parameters for all polymer solutions. Also, Table 5, shows that the change in the AE, value is not meaningful, regardless of the change on HPAM concentration. This result means that the viscous activation energy Is almost Independent of the polymer concentration, corresponding to similar behaviors reported [50],[51] Otherwise, the ∆E, value is related to the influence of temperature on the viscosity of polymer solutions [11].
In addition, Arrhenius plot exhibited in Figure 6a,6b shows the detrimental temperature effect on polymer solutions. The temperature is expressed in absolute units.
In Figure 6a,b, it can be observed that polymer solutions prepared using SB I and HPAM concentrations below 1000 ppm were more affected by the temperature variation, presenting viscosity values close to the brine viscosity at 50°C.
Nevertheless, the viscosity reduction will influence the displacement flooding efficiency at laboratory and field operations. The largest contribution to that significant reduction at shear rates close to those typical of flow through the reservoir caused by the presence of divalent ions and temperature.
VISCOELASTIC BEHAVIOR OF POLYMER SOLUTIONS.
Increases in oil recovery due to viscoelastic HPAM solutions have been attributed to the phenomena of expansion and contraction of the fluid during the flow through porous media [61]. This effect modifies the forces (capillary and viscous) that maintain oil trapped and induces the movement of part of the residual oil [57].
Initially, tests aimed at analyzing the salt effects on viscoelastic behavior were conducted at 25°C, with the purpose of minimizing the temperature effect on visco-elastic properties. Thus, Amplitude Sweep Tests (AST) were carried out for all polymer solutions. Figure 7 shows a comparison of AST results for polymer solutions with SB and SB II at HPAM concentrations, where a Linear Viscoelastic Region (LVR) exists.
Figure 7 exhibits a smaller LVR when the solution includes divalent ions. This occurrence correlated with higher ionic strength seems to reduce the strength of intermolecular interactions [83]. Also, the LVR reduces as the HPAM concentration decreases. Similar performance has been reported [67]. For the polymer solution with SB I (the highest divalent ions content) the LVR was present up to 4000 ppm of HPAM, whereas polymer solution with SB II has LVR up to 3000 ppm of HPAM.
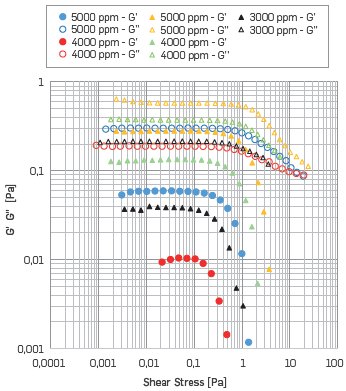
Figure 7 AST results. G' G'' vs. Shear stress at 25 °C, where the Circle represents HPAM solutions with SB I, the triangle represents HPAM solutions with SB II.
Then, a shear stress value of 0.1 [Pa] was selected to execute the FST. This value was chosen to guarantee that the tests execution are within the LVR. The results are shown in Figure 8. It is noted that the G' is more affected when the solution includes divalent ions than the G'' modulus. Thus, the measured value of elasticity decreased earlier at lower shear stress values for polymer solutions with SB I than for polymer solutions with SB II. Similar performance has been reported [61].
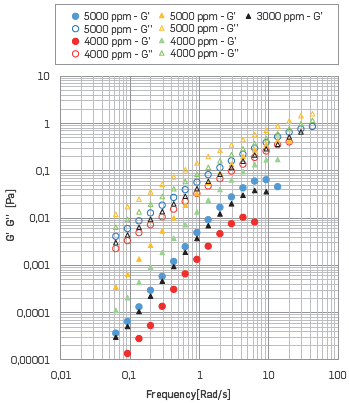
Figure 8 G' G'' vs. Frequency at 25 °C, where the Circle represents HPAM solutions with SB I, the triangle represents HPAM solutions with SB II.
Now, analyzing the temperature effect on visco-elastic behavior, the LVR disappears for polymer solutions with SB I at 50°C. (See Figure 9).
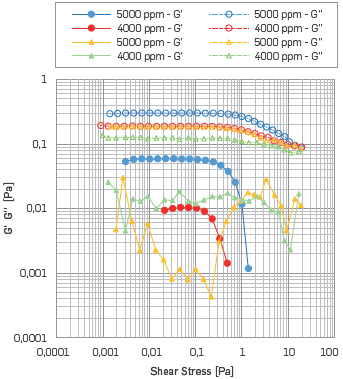
Figure 9 AST results. G' G" vs. Shear Stress of HPAM solution with SB I. The Circles correspond to 25 °C, while the triangles correspond to a temperature of 50 °C.
On the other hand, for polymer solutions with SB II, the reduction of LVR occurred when the temperature increased. LVR was present up to 4000 ppm at 50 °C. Beyond that, G'' was predominant, and G' began to diminish. The above discussion allows to infer that for HPAM concentrations of less than 4000 ppm, the solution will have a predominant viscous behavior. (See Figure 10a, 10b). Therefore, it was concluded that polymer solutions with SB II showed the best rheological and viscoelastic behavior.
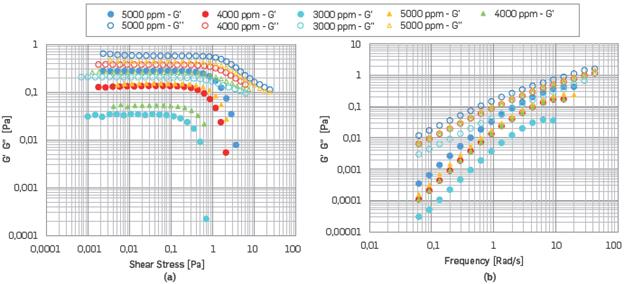
Figure 10 (a),(b) Comparisons AST results and FST results for polymer solutions with SB II, respectively. The Circles correspond to 25 °C, while the triangles correspond to a temperature of 50°C.
For the above reasons, the SB II was selected as Brine reference to pursue activities in this work.
SURFACTANT EFFECTS ON RHEOLOGICAL BEHAVIOR.
This work is aimed at designing fluids for a subsequent assessment of oil recovery enhancement using a surfactant-polymer blend with constant salinity, i.e., the fluid injected will have the capacity to improve the mobility ratio, while reducing the interfacial tension between the fluids in the rock. Hence, through the analysis of the flow curves, HPAM solution concentrations of 2000,1500 and 1000 ppm were selected as possible polymer concentrations to be used.
The decision was based on the attainment of a target viscosity ratio. The surfactant effects on polymer solutions were analyzed for SDS concentrations of 0.5,1,1.5 and 2 [%wt]. The results are shown in Figure 11.
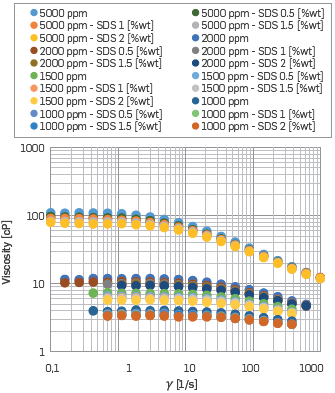
Figure 11 Viscosity vs. Shear Rate for Polymer Solution with different HPAM and SDS concentrations at 50 °C using Synthetic Brine II.
The viscosity of polymer-surfactant blend solutions decreased as the surfactant concentration increased; however, the effect became negligible at high shear rates. The anionic surfactants act to increase the ionic strength and reduce the hydrodynamic size of the polymer molecule. This mechanism is similar to that caused by an increase in monovalent cations.
PHASE BEHAVIOR TESTS.
The phase behavior observed corresponds to a transition Winsor l-H without finding some Winsor III micro-emulsion. Due to the SDS hydrophillc nature, this behavior was not expected, probably as a result of the presence of natural surfactants in the oil phase able to solubilize some quantity of water Into an external oil phase. Salager [33] pointed out that this behavior corresponds to a reversal status of the surfactant, I.e., a significant change of the partition coefficient value induced for the alteration of some variable exhibit In Table 1, Although Winsor III is associated with the lowest Interfacial tension reduction, It Is considered that the absence of Winsor III can be defined as a challenge, as once achieving a low IFT, the reduction of the residual oil is possible. Therefore, we do not consider it necessary to obtain the maximum Interfacial tension reduction or an ultra-low FT value to alter the capillary forces.
Most of the surfactant concentrations studied with low salt content exhibited W/O micro-emulsions. However, as the surfactant and salt concentration Increases, the hydrophillc condition of the surfactant rises. This effect is derived from the fact range that the Winsor I was actually diminished. The Bancroft's rule was a useful tool at this point for recognizing qualitatively changes in the type of micro-emulsion formed. It will be a Winsor I (O/W) or Winsor II (W/O).
Some criteria for the optimum salinity selection were proposed in this work. A similar analysis was conducted by [41]. The criteria proposed are shown below:
In salinity scans of 0.2 or 0.3 [%wt] NaCl salinity intervals and after reaching a clear inversion Winsor II to Winsor I, optimal salinity is taken as that where the maximum value of Vo/Vs was measured.
For salinity intervals greater than 0.2 or 0.3 [%wt] NaCl, optimal salinity was selected at mid-point of the interval at which the criteria defined previously is applied.
The phase behavior results obtained after 26 days of balancing and some additional details are presented below (Figure 12a, 12b, 12c, 12d). For 0.5 [% wt] of SDS, weak w/o micro-emulsion are present. At same surfactant concentration and for a 0.7 [%wt] of NaCl, one can observe that a solution with high oil content is surrounded by the water without some physically visible change over time. The term weak is used to express the facility in which the micro-emulsion spreads into a water phase.
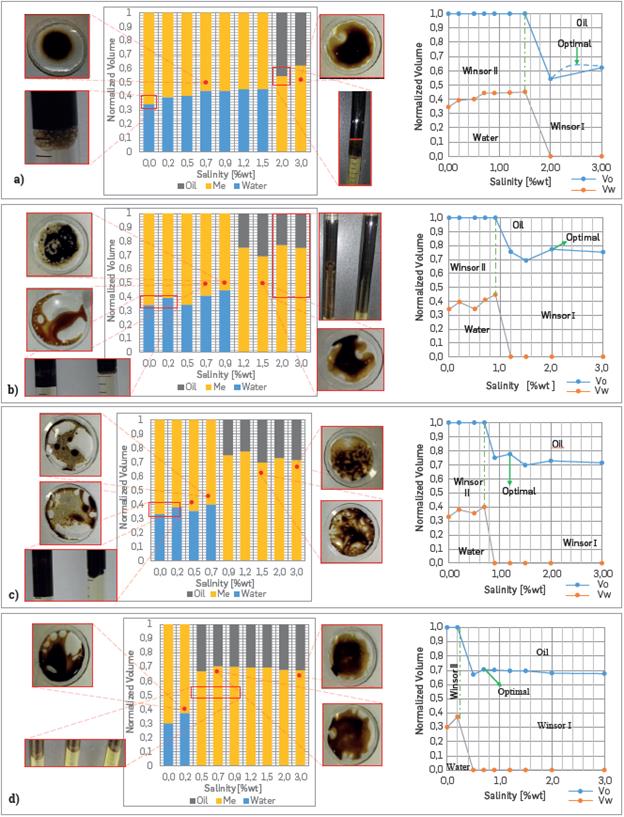
Figure 12 Salinity Scan and Phase behavior results for Solutions with: (a) 0.5 [%wt] SDS, b) 1 [%wt] SDS, (c) 1.5 [%wt] SDS and (d) 2 [%wt] SDS.
However, when the SDS concentration rises to 1 [%wt], the w/o micro-emulsion are easier identified. For 0.7 [%wt] of NaCl, a significant quantity of oil has solubilized a relatively low volume of water. This condition is evident because of the w/o micro-emulsion does not spread easily within the water. Whereas that, when the NaCl content is increased up to 0.9 [%wt] the water-solubilized diminish, elucidating a high dark nature of the micro-emulsion caused by a higher amount of oil solubilized. Besides that, at NaCl concentrations above of 1.2 [%wt], the water content into the micro-emulsion rises, making the micro-emulsion to spread easier into a water phase than with lower salinity.
Solutions with 1.5 [%wt] of SDS up to NaCl concentration close to 0.7 [% wt] presented similar behavior. Moreover, as surfactant concentration increased, the partition coefficient changes were more pronounced as can be observed in the images obtained from Bancroft's rule application. In other words, the high hydrophilic nature of the surfactant starts to control the phase behavior as the surfactant concentration increases.
Finally, at 2 [%wt] SDS, the hydrophilic nature of the surfactant is remarkable generating o/w micro-emulsion for salinities above 0.2 [%wt]. Likewise, the presence of a white-beige precipitate is observed in the interface between the fluids at salinities close to optimal salinity.
The performance described coincides with that observed by Salager [33], who showed that for low concentration of anionic surfactants or in the absence of alcohol, this leads to a direct Winsor II-I transition. Also, the same author states that these systems exhibit three-phase behavior, but often appear as a precipitate or a gel rather than a micro-emulsion.
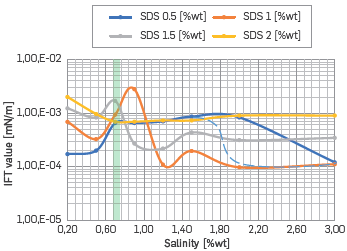
The IFT values were obtained through the Chuh Huh equations. A comparison of these values depends on the salinity and surfactant concentrations presented in Figure 13.
In Figure 13, the dashed line is used to represent a possible case of the IFT behavior between 2 to 3 [%wt] of NaCl when applying the proposed criteria to select optimum salinity. These values were not salinity discretized as they are very far from the salinity sought. Additionally, Figure 13 shows the results for the desired salinity at all SDS concentrations, which generated IFT reduction up to values ranging between 10-3 and 10-4, i. e., these solutions reached the IFT reduction required to improve the oil recovery factor.
It was evidenced also that close to the Winsor II-I transition there is an inflection point of the IFT value caused by a step change in the phase behavior, endorsing the lack of Winsor III micro-emulsions. Therefore, the value used to estimate the IFT value by Chuh Huh equations changes significantly, i.e., for salinities where the Winsor II is present, the IFT value is estimated using Vwm and when the transition to Winsor I occurs, the IFT value is calculated with Vom.
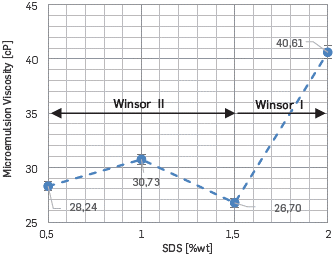
On the other hand, at the salinity of interest for this work, the lowest interfacial reduction was obtained using SDS concentrations of 0.5 or 2 [%wt]. Finally, the micro-emulsion viscosity at 50 °C was measured at a salinity of interest exhibiting a Newtonian behavior for all surfactant concentrations. Furthermore, the viscosity is maximized near to phase behavior transition (2 %wt SDS), evidencing substantial change in the formation and aggregation of the micelles (Figure 14). A similar behavior was reported [34],[35]. Also, the micro-emulsion viscosity behavior shows local minimum near to the optimal salinity, as proposed by other authors [34]-[36]. We interpreted it as a check of the behavior elucidated and the criteria proposed.
Due to the high micro-emulsion viscosity obtained with 2 [%wt] of SDS, this surfactant concentration was discarded for the core-flooding tests.
CONCLUSIONS
Based on the work performed and on literature support, we can highlight the following conclusions:
The polymer solutions studied were mainly affected by the divalent cations content and the range of investigated temperature. However, both factors generated a detrimental effect on its rheological and viscoelastic behavior.
The polymeric solution with synthetic Brine II (without divalent content) presented a more extended Linear Viscoelastic Region, and higher viscosity values. Therefore, it shows the best rheological and viscoelastic performance.
The carreau-Yasuda model satisfactorily adjusted the experimental data obtained for highly concentrated polymer solutions. On the other hand, the use of Ostwald-de Waele Law was enough to fit the data for the solutions with polymer concentration below 1000 ppm.
The observed phase behavior corresponds to a Winsor II→I transition, without finding any Winsor III micro-emulsion. The Bancroft Rule was used as qualitative verification tool of the type of formed micro-emulsion. This behavior corresponded to a reversal status of the surfactant. Therefore, some criteria for the selection of optimal condition were proposed.
Most of the surfactant concentrations studied with low salt content exhibited w/o micro-emulsions. As the surfactant and salt concentration increases, the hydrophilic condition of the surfactant rises. However, at 2 [%wt] SDS, the hydrophilic nature of the surfactant is remarkable generating o/w micro-emulsion for salinities above 0.2 [%wt].
Regarding the lowest interfacial tension reduction at target salinity, the surfactant concentration to be used in future core-flooding tests was 0.5 [%wt] of SDS. However, similar IFT values are obtained using 2 [%wt] SDS; at this concentration, the micro-emulsion viscosity reaches the highest viscosity value.