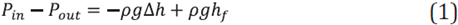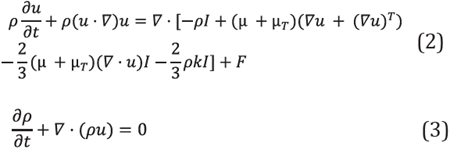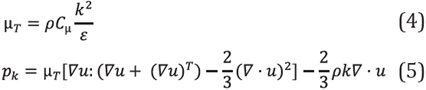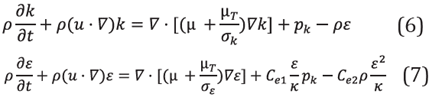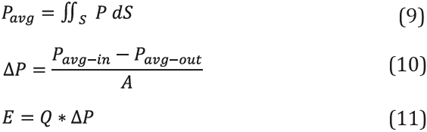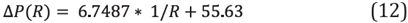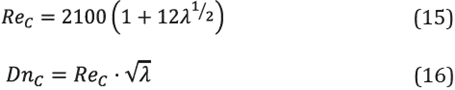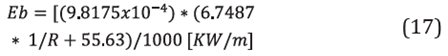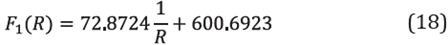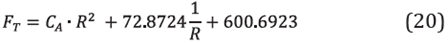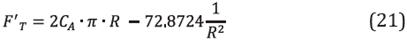1. INTRODUCTION
Microalgae culture is a promising biobased and sustainable process able to reduce the excess of carbon dioxide to produce various types of products with application in pharmaceutical, biofuels, and food industries [1]. Microalgae production is performed in open ponds or closed units called PhotoBioReactor (PBR). Nowadays, microalgae culture in open ponds is a common practice. Nevertheless, this type of process is prone to contamination that affects culture yield. Thus, variables are hard to control, while PBRs allow for variables control and, therefore, high productivity and high yield [2]. Nonetheless, Tubular PBRs need high energy uptake to obtain biomass products and, hence, this increases operational costs. Zhu et al. [3] developed an economic analysis for microalgae oil production; they state that the PBR must be improved with the correct design of light penetration and mixing, using less energy input. Additionally, [2] found that PBRs can improve their economic performance by reducing the mixing energy uptake, which will have a high effect on total energy consumption.
Computational Fluid Dynamics (CFD) has been used as a tool to evaluate mixing conditions in PBRs. Furthermore, some authors have used CFD to design mixing conditions that will increase productivity using less energy uptake [4]. For example, Gómez-Pérez et al. [5] proposed to use wall turbulence promoters to maintain some mixing conditions while average velocity is low. Thus, energy consumption was 34% less than in its initial condition. Gómez-Pérez et al. [6] proposed a twisted tubular PBR configuration to enhance light-dark cycles in microalgae, which will increase productivity and, at the same time, improve mixing conditions with low energy consumption. Wongluang, et al. [7] designed the bend shapes of elbows in tubular PBRs, seeking to avoid death zones and energy loss. However, tubular pilot-scale PBR still uses conventional elbows with high energy consumption [1],[8].
Helical PBRs is a promising design as it allows a larger ratio of surface area for the culture volume to receive illumination effectively, and thus the incident light energy input per unit of volume is high [9],[10]. Helical PBRs has been used in literature as an experimental PBR for microalgae culture evaluation given its high yield [11],[12]. However, since curvature affects energy uptake, it is important to obtain an efficient helical PBR design to assess an appropriate curvature that can minimize the energy consumption in the PBR.
This paper intends to develop a helical tubular PBR configuration design that avoids energy consumption by bends shape design. First, we introduce the analysis by assessing the energy uptake because of the bend-shape of Tubular PBRs. This section is used to justify the application of helical PBRs in algae culture. Section 2 explains the mathematical models. Then, we analyze the curvature effect on pressure drop and propose an optimization problem to find the optimal curvature. We finish with a discussion on results and conclusions. The assessment contained herein can be used to design helical PBRs based on energy and area costs
2. THEORETICAL FRAME
HELICAL PBR DESIGN VARIABLES FOR ENERGY UPTAKE MINIMIZATION
High energy consumption in tubular PBRs has a high impact on operation costs [2]. Hence, any kind of energy-saving is material for the culture economy. Tubular PBRs at the pilot-scale use different types of elbows to change the culture flow direction. PBRs are using U bend-shape with high energy consumption [8], and tubular PBRs with elbow bend-shape [1]. Some pilot PBRs use elbows, like the AlgaePARC tubular PBR [1]. Furthermore, it is possible to find helical tubular PBRs configurations [13]. Helical tubular PBRs have certain advantages vis-à-vis other types of tubular PBRs. As regards the flow direction change, helical PBRs have the advantage that it is possible to use the radios of curvature as a design variable to avoid energy loss. Other studies have been carried out that take into account the various designs of PBR, such as helical, open tanks, plates, and tubes. These analyses have shown greater cell growth in helical PBRs compared to open-tank PBRs. Carvajal-Oses et al. [14] use a helical PBR for the production of Spirulina platensis, Isochrysisgalbana, Skeletonema costatum, and Chlorella vulgaris. It was determined that this type of PBRs can benefit from microalgal biomass for more days, and also require a smaller area and operating costs are lower in the medium term. Da Silva et al. [15] also compared the growth of Arthrospira platensis (Spirulina) in different PBRs and different lighting conditions, where it was observed that helical PBRs perform better the first seven days.
This is because of their high surface and volume ratio (S/V). In the study conducted by Romero Maza et al. [16], various PBRs were used to produce pigments from Arthrospira maxima, where it was established that to obtain higher fat-soluble pigment contents, it is advisable to use helical PBRs during the exponential phase.
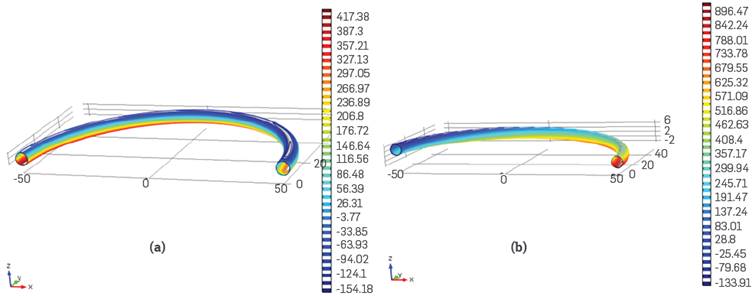
Helical PBRs main variables for energy uptake are the curvature radius and the coil pitch. We ran a first simulation using the κ-ε model (Section 3) and Bernoulli equation to evaluate the effect of these variables. In this case, we prepared a semicircular tube, with tube radius is 2.5 cm, and the radius of curvature is 50 cm. inlet average velocity is 0.5 m/s and the pressure outlet is supposed to be 0 Pa. Using these conditions, we evaluated two kinds of geometry, a semicircular tube with coil pitch, and without coil pitch. Figure 1 shows the results.
Using gravitational forces, it is noted that pressure profiles take values consistent with the height. It was found that the pressure drop of the semicircular tube with a coil pitch is 675 Pa, while the pressure drop without coil pitch is 187 Pa. If we evaluate the Bernoulli equation between the flow inlet and outlet, the following equation is obtained:
Here, P is the pressure (Pa),p is the density (Kg/m3), g is the gravity constant (m/s2). Δh is the height difference (m), and h f the energy head Loss (m). Supposing that there is no energy dissipation, the pressure drop will be determined by the height difference, from the geometry, Δh=5 cm, which corresponds toa pressure drop of 490 Pa, If we subtract this value from the pressure drop with coil pitch, the result is 185 Pa. Therefore, the obtained pressure drop is equivalent to the dissipation because of the flow direction change and the coil pitch. We repeated the previous experiment, but in this case, we did not consider the gravitational forces. Semicircular tube with coil pitch pressure drop is 111.02 Pa, while the pressure drop without coil pitch is 111.6 Pa. This means that most of the energy dissipation is caused by the flow direction change, and the coil pitch does not have extra energy dissipation. The Bernoulli equation shows that the height has an important pressure drop in Helical PBRs. Hence, the coil pitch must be the minimum possible to obtain low energy consumption. As the energy dissipation is related to the radius of curvature of the flow direction change, this paper is focused on the radius of curvature of the helical tube (R), as the important design variable for the optimization of the mixing and energy consumption in microalgae cultures.
κ-ε Model.
This work uses COMSOL Multiphasics® to assess the tubular PBR fluid dynamics. The κ-ε model is used to evaluate turbulence behavior. This model, which is well known in the industry, uses the average Navier-Stokes equations and two additional equations to evaluate the turbulence behavior. Average Navier Stokes equations solve the average velocity and pressure profile [17].
Where u is the average velocity (m/s), t is the time (s), µ is the dynamic viscosity (kg/(m-s)), P is the pressure (Pa), k is the turbulent kinetics energy (m 2 /s 2 ), k is the turbulence kinetic energy dissipation, F is a volumetric force (kg m/s 2 ) and I is the turbulence intensity, which is defined as I = u'/u, where u' is the quadratic average fluctuations of the average velocity [17], Cµ and σk are model parameters.
The turbulent kinetic energy and kinetic energy dissipation are obtained from equations 6 and 7 respectively.
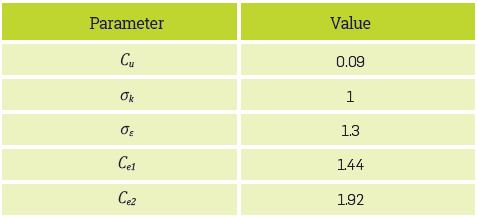
Model parameter values were obtained from the literature [17], as shown in Table 1.
HELICAL TUBULAR PBR RADIUS OF CURVATURE COST FUNCTION
A cost function is proposed taking into account the pumping energy consumption and the occupied area used to build the PBR; both terms of the cost function depend on the radius of curvature. Where, a is the parameter that takes into account the price of energy in the city of Medellin. β is the parameter that links the lease price per square meter in Medellin. f ΔP (R) is the pumping energy consumption as a function of the radius of curvature. f A (R) is the occupied area by the helical PBR, which is also a function of the radius of curvature. Intuitively, as the radius of curvature increases, Dumping energy consumption should decrease; on the other hand: the occupied area cost will increase as it must occupy more area, Hence, there should be an optimal radius of curvature. In this work: the pumping energy consumption fΔP (R) will be identified based or the CFD results (Section 6) to build the cost function for the helical PBR design.
3. EXPERIMENTAL DEVELOPMENT
The parameters and conditions implemented in the simulation are explained hereunder.
PARAMETERS FOR CFD SIMULATION
Equation (11), shows the energy consumption in PBR, (10) shows the pressure drop in the PBR, and (9) shows the average pressure in the cross-sectional area.
Where S is the cross-sectional area of the pipe (m2), P_avg is the pressure average obtained by the simulation results (Pa). ΔP is the pressure drop per length (Pa/m), Q is the volumetric flow (m 3 /s), E is the pumping flow power consumption per length (J/s∙m).
MESH EVALUATION
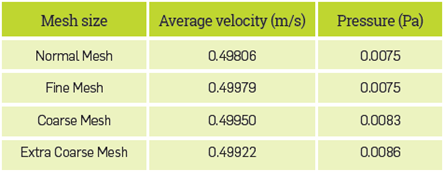
A mesh convergence study is carried out to obtain an accurate solution of the model. Different types of mesh are compared by assessing the output average velocity and the final average pressure, Variables are obtained from the evaluation of pressure and velocity simulation results at the output of the tubular PBR.
The Table 2 shows the simulation results with different mesh sizes. The results are similar among them and this enabled us to determine that the values converge and any type of mesh can be used for this analysis. We opted for a Normal mesh to perform the simulations, as it lowers the computational cost as compared with finer meshes.
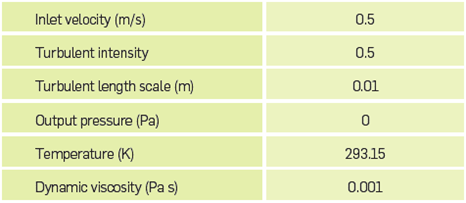
BOUNDARY CONDITIONS
Water properties were used to characterize the simulation fluid in COMSOL®. This fluid in the simulation is a correct approximation because microalgae's density in an aqueous medium is close to the density of water. The operation average inlet velocity is 0.5 m/s, which represents a turbulent regime. The output pressure is 0 Pa. and the tubular pipe is modeled as a (smooth) wall where the velocity is 0 m/s. A coarse mesh was computed using the COMSOL® mesh generation. The pressure drop was evaluated using equation ¡10); other properties are set by default from the software.
SIMULATION DESIGN
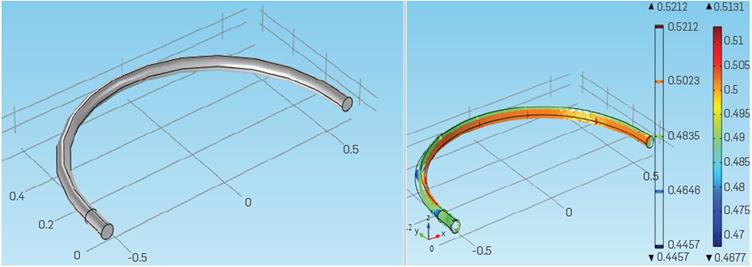
Ten simulations in COMSOL® Muitiphysics software were performed to evaluate the radius of curvature effect on pressure drop. The value of the radius of curvature ranges from 10 cm to 100 cm. The tubular PBR internal radius is 2.5 cm. Figure 3 shows the geometry and the velocity profile results of a simulation where the radius of curvature is 0.5 m.
4. RESULTS ANALYSIS
PRESSURE DROP AS A FUNCTION OF RADIUS OF CURVATURE
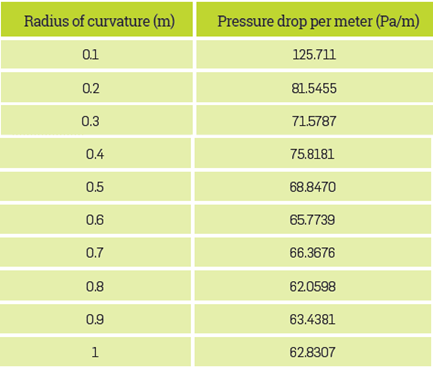
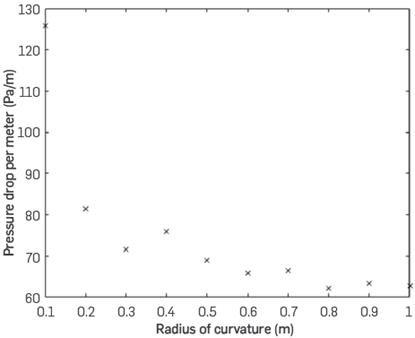
Values were obtained for pressure at the Input and output of the pipe in each simulation. In order to stabilize the flow profile before entering to the curve pipe, the simulation considers a fraction of a straight pipe, 10 cm long. The pressure average was measured in the union between the straight pipe and the curve pipe. Then, we calculated the pressure average and obtained a pressure drop by equation (9). As the length of the curve tube changes, we evaluated the pressure drop related to the tube length. Table 4 shows the results of pressure drop per meter with different radius of curvature.
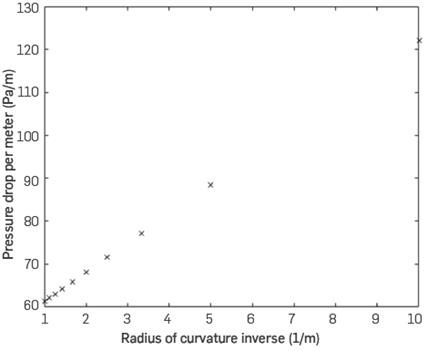
Figure 4 shows that in a small radius of curvature, the pressure drop will be significant. When the curvature radius is more than 70 cm, the pressure drop tends to be a limit constant value. The previous behavior was assessed on the basis of several interpolation functions. However, none of them seems to represent pressure drop behavior. Nevertheless, when the pressure drop was evaluated using the inverse curvature radius, a linear function was obtained (Figure 5)
Linear function enabled us to evaluate extrapolation values. The Linear function to evaluate the pressure drop is:
CFD RESULTS VERIFICATION AND VALIDATION
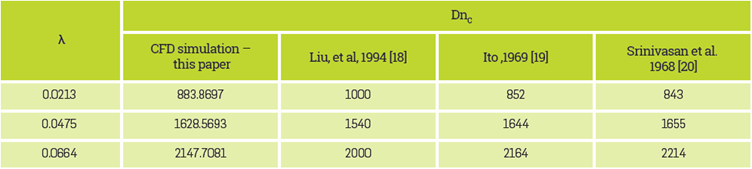
In this subsection, we conducted an analysis for the verification of CFD simulations, using the Liu, Afacan et al. [18] study about helical tubes for results comparison. The authors use the following equation for helical tubes fluid dynamics characterization.
Where H'=(H/a) and R'=(R/a), a is the radius of the tube, H is the coil pitch and R is the radius of the curvature. λ is a dimensionless number that characterizes the helical tube geometry. Using the number λ, it is possible to calculate the Dean number:
The Dean Number is an index that relates inertial and centripetal forces to viscous forces. This number is important in helical tubes as it relates to energy consumption and flow mixing. To compare our results with the results from Liu, Afacan et al. [18], we calculate the critic Dean Number using the following equations:
They used this particular value to compare their results with other correlations found in the literature. In this paper, our simulation results are compared with three correlations found in the literature (Table 5).
The results show that the CFD simulation is not very far from the correlations obtained from the literature. Hence, CFD results are validated for the optimization design of helical tubes.
ENERGY CONSUMPTION AS A FUNCTION OF THE RADIUS OF CURVATURE
It was found the relationship between the cost of the area used and the cost of energy consumed for the pump. The price for the energy required is 572.85 COP (0.14 $) per kWh [21]. The pressure drop is represented by equation (12) when the average velocity is 0.5 m/s. and the energy consumed by the pump is:
Assuming PBR will operate 192 hours per month, multiplying the previous function by the total length of the pipe (100 meters) and the energy cost in Colombia, the following equation is obtained.
F1 is the equation that indicates the energy consumption price as a function of the curvature radius.
OCCUPIED AREA COSTS AS A FUNCTION OF THE RADIUS OF CURVATURE
The average lease price in Medellin according to the needs for the operation of the PBR is between 10000 to 25000 COP (2.5-6.25 Dollars) per square meter. Multiplying equation (10) by the price per square meter (C A ), results in the following equation, which relates the average price of leasing as a function of the radius of curvature
COST FUNCTION EVALUATION
Adding up Fl and F2, the following equation is generated, which relates the cost of the area and the energy of the pump as a function of the radius.
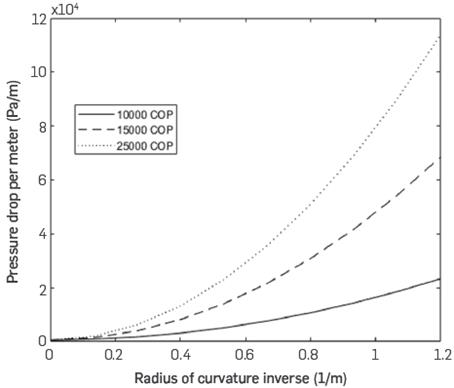
The previous function is evaluated in the Figure 6 to analyze possible minimum values. It is observed that if the lease price increases, the cost function increases as expected.
The lower value of the price in the three curves does not change considerably, but there is a significant difference as of 0.3 meters in the radius of curvature. The picture shows that the value of the area has a significant influence on the total price of the design, and therefore, it is important to minimize the area used in the design.
The optimal point of the cost function was found with an unconstrained newton method
The result of the optimization consisted in two complex roots and one real root. The following values are the optimal points of each cost function that varies the area price.
Analyzing the behavior of the cost function with three different area prices, the cost function shows that there is a variation of the minimal point of each function. It is evident that the cheaper the area, the higher the optimal radius of curvature. Previous results showed that a higher radius of curvature decreases the energy consumption and the pressure drop. Based on such results, it can be concluded that If the reactor is built on a cheap ground, it Is possible to build a bigger reactor, with lower energy consumption.
CONCLUSION
From the study of the fluid dynamics of a tubular PBR, a structure was defined, which can reduce losses for the change in flow direction, reaching a mathematical expression that relates the radius of curvature with the pressure drop. Using that expression to evaluate the energy consumption and taking into account the costs for the helical tubular PBR occupation, a possible range of radius of curvature was established, which is ideal for the design of the tubular helical PBR. The design method used in this paper enabled us to identify a structure with minimum energy consumption as the losses associated with the change of direction by bend-shape are minimized.