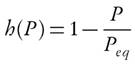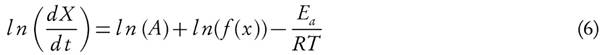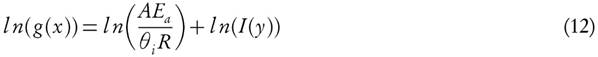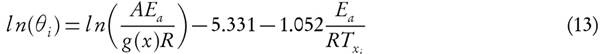Introduction
Chir pine (Pinus roxburghii) forests are predominately found at 500 to 2 000 m of the Himalayan range of India, Bhutan and Nepal, therefore it is indispensable to identify their attributes as a new alternative source of energy. Uttarakhand, one of the Northern states of India, has been the sole contributor of 2 million tonnes of pine needles annually through 17 forest divisions located in 12 different districts [1]. The ample forest waste is available for energy generation; hence, assuming it as a rubbish on the forest floor is unethical and uneconomical. In addition to that, if forest wastes are used, these may curtail the exploitation rate of the conventional fuel resources: coal and wood. For the sustainability of our ecosystem, it is also beneficial to maintain equilibrium between environment and the energy requirements.
The detrimental effect caused by pine needles is reviewed in literature [2].
Besides exploiting the residual wastes for daily use, using them as a mixing constituent of the co-firing plants make them ancillary resource to the energy industries. Some thermo-chemical tests must be conducted in order to recognise the hidden potential of pine needles. One of thermal-chemical transformations is pyrolysis, defined as a thermal decomposition of bio-materials that occurs at elevated temperature in the absence of oxygen, which induces simultaneously chemical and physical phase transformations. In a broad perspective, bio-waste can be converted into the high calorific biofuel, but the thermal conditions are not yet explored. This high calorific secondary fuel can be a good replacement of gasoline in the internal combustion engine, or gas turbine after passing through intermediate stages [3].
The thermal degradation process relies on the competitive reactions which are controlled through several state-variables, such as heating rate, temperature, pressure, residence time, moisture and composition characteristic of the biomass material. To perform any thermal analysis, it is necessary to examine the chemical interaction among constituent biomass species in the presence of inert environment. Thus, the thermal biomass behaviour can be correlated with their chemical behaviour. There are several kinetic models proposed to analyze pyrolysis mechanism. In this manner, the optimization of gasifier plant as well as the study of the engine behaviour propelled by the producer of gas can be simplified [4]. To process the information about the thermal biomass behaviour, thermogravimetric analysis (TGA) is the most promising way to analyze the kinetics of pyrolysis at the microscopic level. There are some literatures about implementation of TGA analysis for thermal degradation of different materials at non-isothermal conditions [5].
Dhaundiyal and Gupta [2] conducted a comprehensive parallel testing for knowing the thermal capabilities of destructive coniferous species, chir pine. They have examined the pine needles at different size of reactors (120kW-h and 10 kW-h gasifiers). It is observed through the evolved gas composition that the thermo-chemical process is accompanied with the formation of combustible gases, which is mainly dominated by carbon monoxide (14 %), carbon dioxide (14 %) and hydrogen (4.58 %). They have successfully designed a low emission thermal power plant powered by pine waste, despite the work is devoid of chemical aspect of pine needles, which is an intrinsic factor to govern the evolved gas composition. They overlooked the intermediate stages of the gasification process and the whole study was carried out to fulfil the thermal aspect of the process. Later, Dhaundiyal and Tewari [1, 6] worked on the designing aspects of the gasifier reactor as well as the relative importance of pine needles to coal gasifier. The feed rate is estimated to be 21 kg/h for the 10 kW power plant [1], whereas the rice husk gasifier requires 28 kg/h [7] at the same rated power. Therefore, it is necessary to examine the chir pine behaviour with varying thermal conditions. The objective of this study is to investigate devolatilisation characteristic of pine needle. The effect of the reaction heterogeneity on kinetics of thermal decomposition is one of such attributes to assess. Moreover, the chemical kinetics emphasises the proposition that pine needles must rather be used for energy generation. However, ash formation and resinous nature limited its application for direct use in the pilot size power plants. But the proper pre-treatment may alleviate this problem. The subsequent sections are focussed on the suitable kinetic modelling for recognising the characteristic of biomass pyrolysis.
Materials and methods
Chemical kinetics
Chemical kinetics describes the rate at which chemical structure transforms into other forms. It can either be governed by quantum mechanics or the phenomenological model (semi-empirical law derived from simplified physical model). According to the perspective of biomass application, the engineering kinetics or semi-empirical law-based modelling suits the requirement to carry out analysis task. Hence, it is necessary to examine the models critically before their implementation.
The interdependent nature of pressure, conversion and temperature are inextricably linked when discussing the chemical kinetics of material [8]. The chemical reaction pathway is mainly expressed in the form of differential equations that governs reacted and formed fraction of reactants and products. The rate for the condensed state can either be expressed in the product formation rate or reactant decomposition rate with suitable exponents or reaction orders.
Model-fitting and model-free schemes are mainly used to solve the kinetic problems of condensed phase reactions. Both have some merits and demerits over each other. Model-fitting methods are based on the force-fitting of non-isothermal thermo-analytical data to phenomenological model. Kinetics parameters represented by the integral form g(X) are based on the pseudo-reaction schemes. In addition, temperature and conversion (X) vary simultaneously with time; therefore, it is difficult to obtain a unique solution. The model-based scheme is unable to demarcate temperature dependence of rate constant from the conversion. Thus, any assumed model that simulates the thermoanalytical data shows a huge deviation between the assumed model and the mathematical model. Model-fitting method follows tenets of black-box modelling that reduces computational time, but accuracy is iffy. Because of drastic variation, the model-based methods provide vague solution of differential rate equation. The activation energy estimated by model-fitting methods is an implicit function of temperature and conversion. However, the activation energy represents the average value for the overall pyrolysis process. The derived value is assumed to be invariant to the reaction mechanism and kinetics of process, which vary with temperature and extent of conversion [9]. Hence, the iso-conversional methods have provided weightage over model-based schemes to overcome drawbacks of inconsistent values. One of model-fitting methods, Coats Redfern [10], is also used in evaluating kinetics parameters. This method derives Arrhenius parameters from a single heating rate. This scheme is highly inaccurate. It is suggested that the kinetic analysis should not be based on the single heating rate [8, 11]. Furthermore, thermal decomposition of weed indicates that the results obtained from Coats-Redfern are highly incoherent as compared to model-free scheme [12]. However, this method can be transformed into iso-conversional method through rearrangement of the conventional form of Coats-Redfern equation (1) [8]. Even the approximation of Coats-Redfern model provides an activation energy value which is invariant of conversion. But the model-free scheme can easily incorporate dependency of activation energy, E, on conversion, X .
On the contrary, the isoconversional methods are not supposed to be free, but these assume that the same reactions, independent of temperature, occur in the same ratio at a given extent of reaction. However, a reaction network of parallel independent reactions can be constructed whose relative reactivity changes as a function of temperature due to different activation energies [13]. Moreover, the competitive reactions with different activation energies make the overall reaction pathway to be different at a different temperature [14].
Nonetheless, some of the isoconversional methods work more effectively than other methods and provide a robust kinetic modelling [15]. These methods were developed 50 years ago, and Kujirai and Akahira [16] were the first to devise an empirical isoconversional equation to assess influence of temperature upon the decomposition of material at isothermal condition. Later, Friedman developed the differential method [17]. On the other hand, Ozawa, and Flynn and Wall separately developed their own integral methods [9, 18]. Friedman stated that function f (1-X) remains constant at a given value of (1-X) if the chemical pathway is invariant of temperature. But, as discussed before, it is possible to develop a reaction pathway that does not obey the isoconversional scheme. The overlapping of parallel reactions leads to a variation of activation energy which is addressed by the model of Miura et al. [19], who reported that the overlapping of parallel reactions cause reactivity distribution that can be encountered by replacing the effective-fraction-reacted from the actual-fraction-reacted in iso-conversional method. The same concept led to the formation of distributed reactivity model.
The concept states that the complex reactions are followed by a distribution of independent parallel reaction, explained through surface-catalysed reactions. These surface-catalysed reactions cause compensatory effect in A-E evaluation due to various attacking-sites on the surface of material. Consequently, it leads to distribution of activation energies that governs the reaction profile [20]. In 1943, Vand proposed reactivity distributed model for irreversible variation of electrical resistance upon annealing of evaporated metal film [21]. The parallel reaction scheme is popularised by the work of Pitt [22] and Hanbaba [23] in the coal pyrolysis. Furthermore, Anthony and Howard [24] introduced the reactivity distribution through density function of Gaussian distribution. However, it is not necessary that the distribution follows symmetrical behaviour. It is found that Rayleigh distribution may impart reactivity distribution far better fitting than Gaussian [25]. Dhaundiyal et al. [26] attempted to solve distribution of activation energy through bi-variant function. It is a well-known fact that pyrolysis is not only governed by a single-step and there is existence of competitive reactions that make modelling more complex. However, heat of reaction, grain orientation, particle size, reaction scheme and residence time play the major roles to decide the reaction pathway. Lewellen et al. [27] reported that the residence time of volatile products within the pyrolyzing matrix is extremely important in determining conversion; they provided a more detailed description of possible pathways that led to weight loss during pyrolysis. Despite all those efforts of implementing a logistical distribution to fit the reaction profile, it does not yield realistic kinetic parameters that meet modelling requirements. However, some of them may provide good curve-fitting to thermo-analytical data. It can be useful for pre-processing reaction scheme to filter the suspicious values, but it must be realized that the derived parameters compromise with each other to converge the numerical solution to a finite value. Therefore, it is critical to know how effectively the approximated scheme work for the complex thermal histories.
Among model-free methods, Kissinger's method [28] is relatively precise and non- iso-conversional method; however, it is usually close to it. It relies on the unique solution rather than finding activation energies at each successive conversion point. It considers the temperature value at which the rate of reaction (as function of heating rate) is maximum, so that Arrhenius parameters can be derived. It is very robust and isoconversional for first-order reactions [29]. It is a promising technique for those reaction schemes which are based on nth- order [30], nucleation-growth [31], and distributed reactivity reactions [32]. However, KAS method is related to Kissinger’s method, but it absolutely relies on isoconversional principle. This methodology allows to identify the activation energy from DTG peaks temperature at different heating rates. Furthermore, there are ample sources that support application of Kissinger's method, KAS, Vyazovkin's method and FWO for analysing sigmoidal reactions (biomass decomposition) [33]. However, the modified version of Coats-Redfern for multiple heating rates may also be used for analysis purpose, but here the analysis is confined to recommended methods of chemical analysis. In a systematic study of isoconversional methods for a complex process (including competitive or independent reactions), Elder [34] and Dowdy [35] concluded that the application of isoconversional methods are reliable to analyse the multi-step processes. Therefore, it can be useful to apply the same methodology to analyse thermochemistry of bio-waste. In the subsequent sections, model-free schemes are discussed succinctly.
Modelling of biomass pyrolysis
The model-free scheme is adopted for the kinetic analysis, which follows the isoconversional principle. Accordingly, the f (x), function of temperature can be assumed to be constant at a given extent of conversion. Isonconversional methods are valid to analyze both isothermal (where the temperature changes) and non-isothermal (where heating rate changes) pyrolysis. In non-isothermal (where heating rate changes) kinetics, various isoconversional methods were suggested in the 1960s [9, 17, 36]. These methods are based on the multiple heating rates and it is impossible to conclude any proposition at a single ramp rate. Some of them are discussed at the subsequent sections.
To investigate the kinetics of condensed phase pyrolysis, the model-free approach has been studied analytically. A single step kinetic equation is represented by equation 2 [37].
where, h(P) is pressure dependence and it is assumed to be unity for model-free scheme. Here, P is partial pressure of the gaseous product and Peq is the vapour pressure at equilibrium state
According to Arrhenius equation, temperature relationship with rate constant is expressed as
Here ‘X' represent conversion and it can be obtained from thermograms of TGA analysis. By the definition,
Here m0 is the initial mass of pine needles in mg, mt is instantaneous mass at the given temperature and mr is the residual mass at the end of the heating process.
where Ea is the apparent activation energy (kJ mol -1 ), T is the absolute temperature (K), Ris the gas constant (8.314 JK -1 mol -1 ) and A is the frequency factor or pre-exponential factor (min -1 ).
The explicit temperature dependency of the rate constant k(T) is brought by replacing it from equation (2) with Arrhenius equation (3), which provides equation (5)
Taking natural logarithm of equation (5), therefore it can also be stated as
It has been assumed that the term l n( f(X)) could be neglected, therefore the value of Ea and ln(A) can be computed by plotting 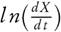 against 1/T. They have also reported that the error observed, while estimating Ea values, is around 15 % to 20 % [38]. However, demerit of equation (6) came into light. It has been put into a group of methods which allow evaluating the kinetic parameters at the single heating rate. Criado et al. [39] also reported the drawbacks and suggested a detail calculation of the errors in E
a
resulting from this assumption. The kinetic term f(X) mainly depends on the state variables (P, T) and stage of reaction and it is usually expressed as (1-X) if it is first order reaction [40].
against 1/T. They have also reported that the error observed, while estimating Ea values, is around 15 % to 20 % [38]. However, demerit of equation (6) came into light. It has been put into a group of methods which allow evaluating the kinetic parameters at the single heating rate. Criado et al. [39] also reported the drawbacks and suggested a detail calculation of the errors in E
a
resulting from this assumption. The kinetic term f(X) mainly depends on the state variables (P, T) and stage of reaction and it is usually expressed as (1-X) if it is first order reaction [40].
For nonisothermal conditions, the explicit time-related dependence of conversion (X) can be revised for the given problem by introducing heating rate 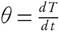 into equation (5) and it is expressed as,
into equation (5) and it is expressed as,
The function 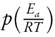 has no analytical solution, therefore it can be estimated by numerical approximations [41].
has no analytical solution, therefore it can be estimated by numerical approximations [41].
Kissinger Method
This method provides information about the kinetic parameters of a solid-state reaction without considering the reaction mechanism. In 1956, Kissinger [30] provided a proposition with mathematical evidence by stating that model- free and non-isothermal method do not require to estimate E for each conversion 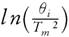 against 1000/T
m
for a series of experiment performed at different heating rates (θ
t
), where T
m
represents the temperature at which peak differential thermal analysis deflection occurs (illustrated in Fig. 6). At peak temperature, the second derivative of conversion is zero.
against 1000/T
m
for a series of experiment performed at different heating rates (θ
t
), where T
m
represents the temperature at which peak differential thermal analysis deflection occurs (illustrated in Fig. 6). At peak temperature, the second derivative of conversion is zero.
Differentiating equation (1) with h(P ) = 1 and putting it equal to zero.
For first order reaction, 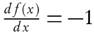 , so after the rearrangement of equation (9), it is obtained
, so after the rearrangement of equation (9), it is obtained
Thus, activation energy is estimated as a slope of the equation (10), which is equal to 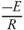 .
.
The activation energy (E) is grouped along with frequency factors and the resultant equation exhibits a linear behaviour. The intercept of the linear equation and the slope of that equation are used to estimate the kinetic parameters.
The nature of isoconversional methods is to recognise the possibility of reaction heterogeneity, although it is difficult to identify through model-fitting schemes. It implies that different intermediate products may be formed at different stages of the global conversion. These schemes are robust enough to provide global measure of rate or extent of a process. It comprises the several elementary reactions having different activation energies. Moreover, they can more easily relate dependence of activation energy (Ea) with frequency factor (A) than other methodologies. But Kissinger's method [28] cannot be grouped with the other isconversional schemes, as the value of Tm , the onset point of deflection of conversion that varies with the heating rate [42].
Isoconversional methods based on FWO and KAS assumptions
Behaviour of activation energy with the degree of conversion was originally investigated by Flynn and Wall [36]. They applied an isoconversional scheme to non-isothermal data set of multi-step kinetics. Later, their work is supported in Dowdy's work [35], whichstated that the differential scheme provides the kinetics results of multi-step reaction process, which shows the activation energies dependency with conversion. The original isoconversional methods (e.g. Friedman [17], Ozawa [9]) are unable to evaluate frequency factor or the reaction model directly. Flynn suggested that the reaction followed the reaction model of (1-X)n , and at X = 0, the intercept of equation (6) resulted in the values of ln(A). Once ln (A) is estimated, the value of reaction order (n) can be computed through plotting ln(f (X) versus X [43]. In the same sequence, FWO and KAS are derived below.
The FWO method [9, 18] based on the computation of kinetic parameters through cartesian plot of natural logarithms of heating rates, ln(θt) versus 1000/Txi, which exhibits the linear relation with reactivity degree at different ramp rates. Primitive and prime of conversion functions, f (X ) and g(X ), are defined as
where I(y) represents the temperature integral and 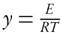
Hence,
The method of Ozawa [9] and Flynn and Wall [18] based on the approximated form of equation (10). Therefore, Doyle's approximation [44] of the temperature integral is adopted to yield the results.
Substitute the value of l n(I(y)) in equation (12),
or
Equation (13) is the required expression for FWO method. Subscript ‘Xi ' represents conversion at given heating rate.
Note: Equation (13) is only valid if  [36].
[36].
The KAS method is derived by using equation (14), which is valid in the given interval 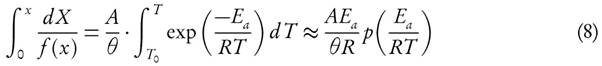 [45]
[45]
In KAS method, the temperature is related to the heating rate by equation (15)[30]
The apparent activation energy can be estimated from a plot of 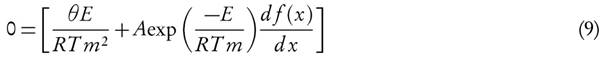 versus
versus 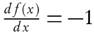 for a given value of conversion, X, where the slope is equal to
for a given value of conversion, X, where the slope is equal to 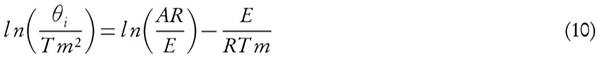 .
.
Forest waste
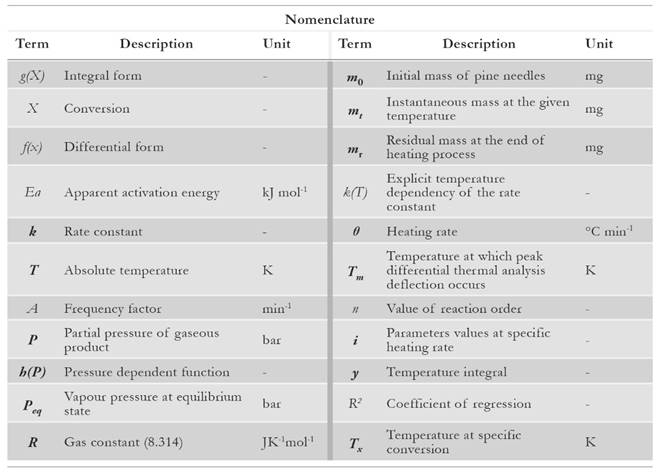
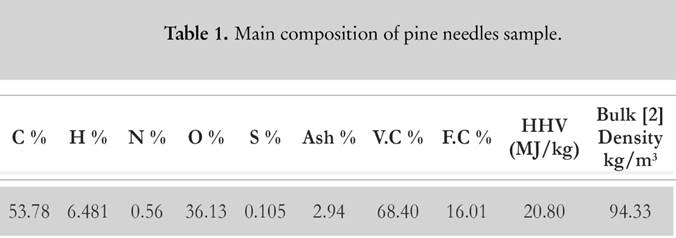
For evaluation purpose, the samples of pine needles are collected from Chakrata forest division of Uttarakhand. Pine needles samples are mechanically grinded into powder form for the experimental process. The powder is sealed in an air tight bottle to prevent ingression of moisture as pine needles are highly hydrophilic [2]. The elemental detail about pine needles is illustrated in Table 1 [2]. CHNS-O analyser (vario MACRO) (Fig. 1) is used to evaluate the chemical composition of pine needles. Before using the CHNS-O analyzer, the furnace is heated up to 1 473 K for 30 min. Once it gets heated, the capsule forms of the sample are fed into the slot of rotating disk. The flow of oxygen maintains the catalytic combustion, whereas helium gas acts as a carrier gas stream so that the volatile gases with water (CO2, SO2, NO2 and H2O) can be absorbed at different reduction columns. These tubes are in-between the combustion chamber and the detection unit (computer-based software). The gas mixture is separated into its components through purge or trap chromatography. Thereafter, each component is separately detected by thermal conductivity detector (TCD). The gases CO2, H2O and SO2 are absorbed in a sequence, whereas N2 passes through all the three columns, and it is finally detected by TCD. TCD generates the electrical signal that is proportional to the concentration of elementary components of biomass. There is a post combustion furnace followed by the main furnace chamber to ensure the complete combustion of the sample. Once the combustion is completed, the gases are passed through the reduction tube made up of copper or tungsten (for non-sulphurous mode). The reference material is considered to be powder of birch leaf. The moisture content (Fig. 2) is deducted from the calculated results to obtain the chemical composition at dry basis. The bomb calorimeter (Fig. 3) at constant volume is used to measure the calorific value of pine needles.
TG Method
Thermal analysis of pine needles is conducted on thermogravimetric analyser (SII 6300 EXSTAR) at IIC, Indian Institute of Technology, Roorkee. To attain pyrolysis conditions, an inert gas (Nitrogen) is used. The inert medium of nitrogen is considered to purge the chamber and prevent the micro-balance from intrusion of possible pollutants. The volumetric flow rate of nitrogen is maintained at 200 mL min-1 to scavenge the product gases. To prevent the buoyant effect at elevated temperature, the horizontal differential balance is put into practice. Each pine sample of 10.54 mg is examined within the temperature interval of 308 K to 1 173 K at different heating rates. A crucible pan of Al2O3 is used to hold the sample. Thermocouple type ‘R' is employed to measure the sample temperature with respect to time.
Results and Discussion
Thermal Analysis
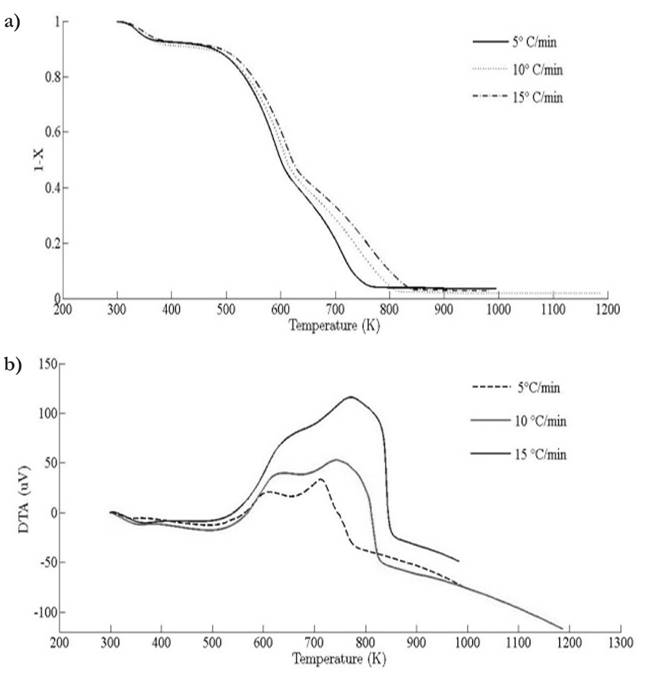
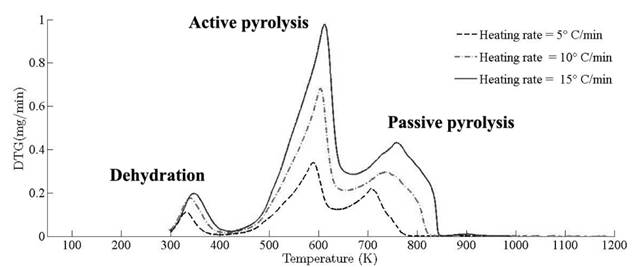
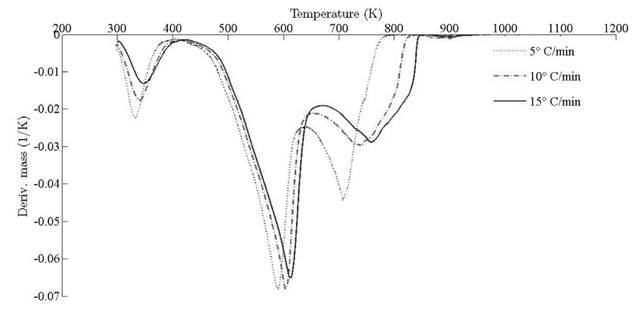
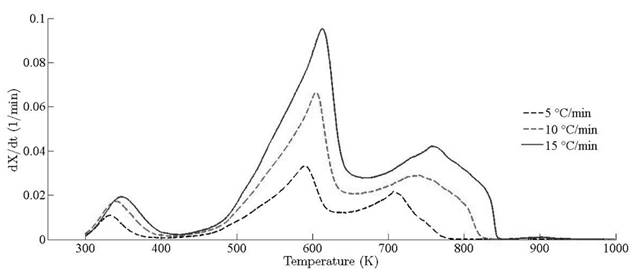
Thermograms at different heating rates are depicted in Fig. 4(a). As it is observed from the plot, the pyrolysis process initiates at about 400 K and the rapid mass decrease with increasing temperature encountered until 800 K. Thereafter, the decrease in the remaining mass fraction (1 - X ) slows down until reaching the final temperature. The solid residual yield is nearly 6 % for pine needles. DTA curves at different heating rates are depicted in Fig. 4(b). Differential thermogravimetric (DTG) of pine needles pyrolysis for different heating rates 5 ◦ C min-1, 10 ◦ C min-1, 15 ◦ C min-1 is illustrated in Fig. 5. Demarcated regions have exhibited the temperature range at which dehydration, active and passive pyrolysis occurred. The domain of first region lies in the temperature span of 300 K to 400 K, which is related to the drying or moisture extraction from the given sample of pine needles. Primary pyrolysis reactions take place in an interval of 500 K to 650 K at low heating rate, while the same reactions initiate at elevated temperature range of 600 K to 750 K for high heating rate. In addition, there are two peaks [46] that provide information related to degradation of hemicellulose and cellulose; whereas lignin decomposes in the regions of active and passive pyrolysis with characteristic peaks as lignin percentage is nearly about 43 % in pine needles [47]. The effect of heating rate is shown in Fig. 6, Fig. 7 and Fig. 8. The change in heating rate affects TG curves position, maximum decomposition rate and location of maximum Tm peaks deflection illustrated in DTG of pine needles (Fig. 6), with increase in heating rate, temperature range of active and passive pyrolysis (Fig. 6 and Fig. 8). The water evaporation regime does not vary with heating rate for each analysis (Fig. 5).
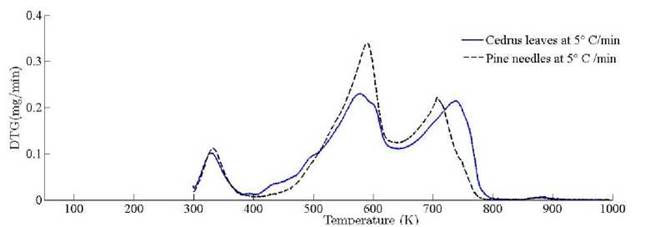
The location ofmaxima and minima of DTG curves get drifted as temperature increases. The reason for anomality of DTG curves is owing to heat transfer limitation between the sample and the furnace. Due to rapid variation in the instantaneous thermal energy of the system, the inert medium (nitrogen) takes a long time to attain asymptotic stability with the sample temperature at low heating rates. Conversely, the same allocated time span has been reduced at higher heating rate, thus reaction time decreases. Therefore, for the same time and temperature regime, the temperature required to decompose the sample is also increased [48]. To ensure that the same heating rate leads to drift in the curves, comparative DTG plots of coniferous species (Pinus roxburghii and Cedrus deodara) at 5 ◦C min-1 have been drawn, concluding that there is no appreciable shift for the same heating observed in Fig. 9.
Kinetic Analysis
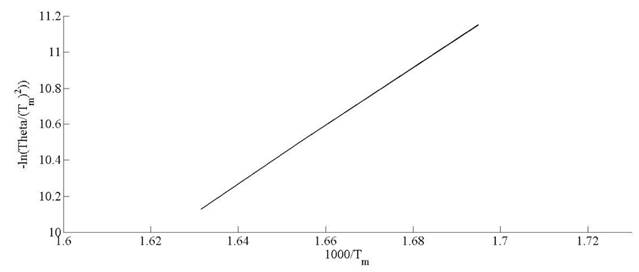
Kinetic parameters of thermal decomposition of pine needles are calculated on the basis of model-free approach. The activation energy (Ea ) and pre-exponential factor (A) are estimated by using Kissinger, KAS and FWO methods. The equations (10), (13) and (14) are used to calculate the activation energy and pre-exponential factor. In case of Kissinger method, the peak temperature, Tm represents the maximum mass loss peaks. The activation energy and pre-exponential factor. In case of Kissinger method, the peak temperature, Tm represents the maximum mass loss peaks. The peak temperatures are estimated in Fig. 6. Kissinger plot of ln 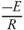 versus 1000/T (K
-1
) for pine needles is depicted in Fig. 10. The activation energies (E
a
) and preexponential factor (A ) are estimated from the slope and intercept of linear relationship among thermal parameters, respectively. The activation and frequency factors obtained through Kissinger method are 132 kJ mol
-1
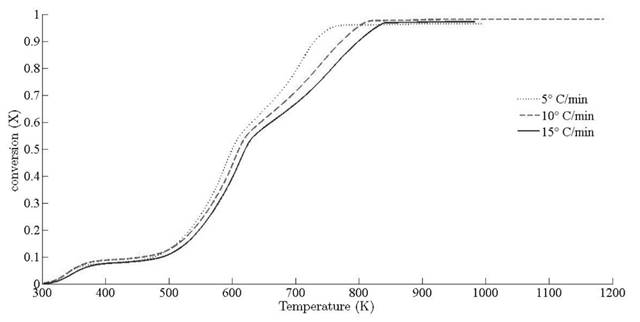
and 13.15 x 107 min-1, respectively. Deviation of conversion extent with respect to sample temperature is illustrated for different heating rates in Fig. 7.
versus 1000/T (K
-1
) for pine needles is depicted in Fig. 10. The activation energies (E
a
) and preexponential factor (A ) are estimated from the slope and intercept of linear relationship among thermal parameters, respectively. The activation and frequency factors obtained through Kissinger method are 132 kJ mol
-1
and 13.15 x 107 min-1, respectively. Deviation of conversion extent with respect to sample temperature is illustrated for different heating rates in Fig. 7.
To demonstrate the approach, similar values of X ranging from 0.05 to 0.7 are chosen to obtain the corresponding temperature at different ramp rates. According to thermal study of pine needles for different gasifier reactors [1, 2], it has been found that the residence time of volatile content triggers some autocatalytic reactions which somehow influence the intermediate stages [26, 49]. The large size of particles makes the fluid residence time sufficiently, resulting in secondary reactions of generated volatile during primary pyrolysis [50]. The product of primary pyrolysis influences the heat reaction and may lead to overlapping of endothermic and exothermic reactions at higher heating rates; therefore, the primary focus is to analyze the behaviour of pine needles pyrolysis at the beginning and intermediate stages, so that variation of activation energy can be recorded at the beginning and finishing boundaries of devolatilisation stage.
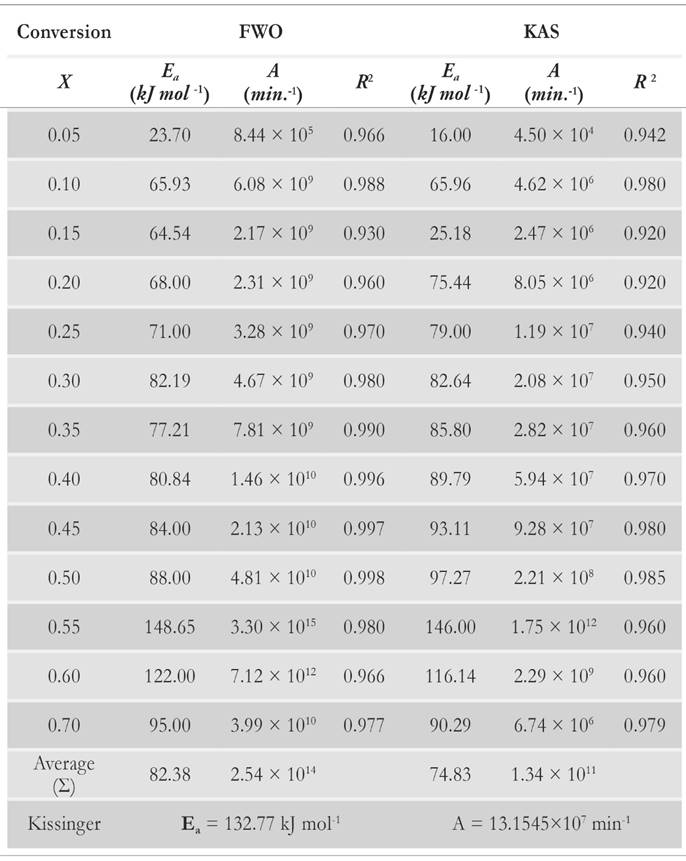
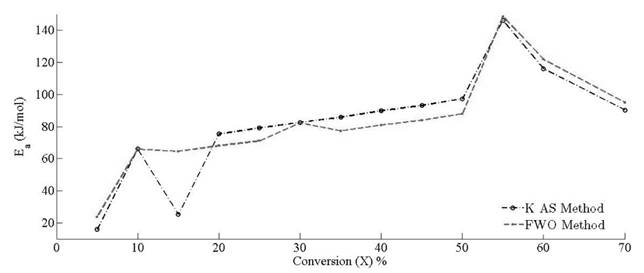
The apparent values of Arrhenius parameters are obtained along with the correlation coefficient (R2) (Table 2) at different conversion points. The calculated square values of correlation coefficient vary from 0.92 to 0.998 in all the cases.
Variation of apparent activation energies with conversion percentage is depicted in Fig. 11. It is observed that the apparent activation energy value is inconsistent for predefined conversion range, which insinuates that there is an existence of a complex and non isoconversional reaction sets formed in the solid state. The apparent values of activation energy obtained by FWO method vary from 23.70 to 148.65 kJ mol-1. It is about 16 to 146 kJ mol-1 for KAS method. It implies that the reaction scheme is not similar for the whole pyrolysis process. Therefore, the activation energy is largely relying on the conversion and heating rate. At x = 0.55 , it is clearly visible that there is an overlapping of the competitive reactions, which leads to drastic variation of activation energy. Both methods explain the existence of the concurrent reaction that leads to the formation of reactivity distribution with respect to the activation energies. However, the variation of activation energy in KAS method is more uniform for the conversion range of 20 % - 50 %, whereas FWO provides uniformity of activation energies at conversion ranges of 15 % to 25 % and 35 % to 50 %. Both methods provide the common solution at conversion values of 30 % and 50 %. It is clearly visible through analysis that there is existence of some intermediate stages that disturb the equilibrium of the activation of energy with respect to conversion. It may be possible that the activation energy has either linear or nonlinear implicit functions of conversion and temperature, causing perturbance as the extent of conversion varies with the time. It also indicates that decomposition of pine needles does not just follow acceleratory reactions but passes through deceleration phase reactions (i.e. Sigmoidal). These reactions are mostly affected by autocatalytic behaviour of volatile matter. Pine needles have relatively high volatile content to other biomasses [51]. Therefore, the devolatilisation effect of pine needles pyrolysis makes the undulation higher than other biomasses [12, 52]. Moreover, it is also clear that there is no cut-and-dried inference between Aand E a . The frequency factor may or may not increase proportionally with activation energies. The reason for the incoherence among Arrhenius parameters is the dependency of frequency factors upon temperature as well. Therefore, the frequency factor can be the implicit function of (T , E a ). The mass loss as well as the heat evolution with the overlapping of different heat reactions (endothermic and exothermic) during the intermediate stages made the isoconversional kinetics to be more complex and difficult to analyze for a material.
The model-free approach allows calculating Arrhenius parameters as a conversion function without any preposition about reaction model, thus it delineates the presence of multi-step kinetics. On the contrary, Kissinger method provides a unique solution for E a of the whole decomposition event, but the mechanism is undefined [53]. Activation energy estimated with the help of Kissinger method is independent of conversion and uniform with the value range obtained through the FWO and KAS methods. However, the derived solution for the activation energy and pre-exponential (frequency) factor also depends on the type of purge gas which is being used for the experimental purpose. The values of activation energy in air are higher than E a for the inert atmosphere of nitrogen [54]. Dhaundiyal and Singh [55] used the multi-reaction model and obtained 80 kJ mol-1 as an activation energy for pine needles in the presence of nitrogen atmosphere, which is very close to the average values obtained by using FWO and KAS methods. The difference in kinetic parameters shows a complicated nature of pine needles species, namely cellulose, hemicellulose, lignin and extractives Additionally, the different experimental conditions and different calculation procedures cause the calculated kinetic parameters to vary in magnitude for the same class of biomass. The obtained results are compared with thermal decomposition of weed [12], rice husk [51], red pepper [56] and another coniferous species, cedrus deodara [49]. Kinetic parameters are within permissible variation limits of kinetic parameters for coniferous species. To validate the results, the estimated value of activation energy is compared with mathematical model, and the results found are obtained for the activation energies [26].
Conclusion
In this work, thermogravimetric and kinetic analyses were performed in the presence of an inert medium at ramp rates of 5 ◦C min-1, 10 ◦C min-1 and 15 ◦ C min-1. Thermal decomposition of pine needles is demarcated by different regimes: evaporation, passive and active pyrolysis. It is concluded that the pyrolysis reactions take place within temperature range of 400 K to 750 K. Influence of the ramp rate on TG and DTG curves is also discussed and it has been assessed that the temperature required for decomposing biomass elevates with incremental change in the heating rate. Kinetic parameters were estimated with the help of model-free methods. Activation energy and pre-exponential factor derived from Kissinger method are consistent for the whole pyrolysis process, whereas the apparent kinetic parameters estimated from FWO and KAS methods rely on the conversion. They exhibit the presence of complex reaction mechanisms that occur during the pyrolysis process. The estimated values of activation energy and pre-exponential factor obtained by using Kissinger methodare 132.77 kJ mol-1 and 13.15 x 107 min-1 respectively. Whereas 82.38 kJ mol-1 and 25.42 x 1013 min-1,74.833 kJ mol-1 and 13.44 x 1010 min-1 are the apparent averaged values of activation energy and pre-exponential factor, for FWO and KAS, respectively.
Determined results depicted that computed kinetic parameters are in good agreement and the model-free approach describes the complexity of the pyrolysis process. For a better insight of pine needles, analysis of its constituent species is required.