Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Cuadernos de Contabilidad
versión impresa ISSN 0123-1472
Cuad. Contab. vol.14 no.34 Bogotá ene./jun. 2013
Mercado Integrado Latinoamericano (MILA): análisis de correlación y diversificación de los portafolios de acciones de los tres países miembros en el período 2007-2012*
Latin American Integrated Market (MILA): A Correlation and Diversification Analysis of the Stock Portfolios of the Three Member Countries in the Period 2007-2012
Mercado Integrado Latino-americano (MILA): análise de correlação e diversificação dos portfólios de ações dos três países membros no período 2007-2012
Yaneth Patricia Romero-Álvarez1
Fabián Hernando Ramírez-Atehortúa2
Diana Sirley Guzmán-Aguilar3
1Docente, Institución Universitaria CEIPA, ingeniera industrial, especialista en finanzas y evaluación de proyectos, aspirante a maestría en finanzas, Universidad de Medellín. Correo electrónico: yaneth.romero@ceipa.edu.co
2Docente, Universidad de Medellín; economista, magíster en administración, Universidad de Medellín; estudiante de doctorado en administración, Universidad EAFIT. Correo electrónico: framirez@udem.edu.co
3Docente, Universidad de Medellín; estadística, magíster en ciencias estadísticas. Correo electrónico: dsguzman@udem.edu.co
*Artículo escrito para optar al título de maestría en finanzas, Universidad de Medellín.
Fecha de recepción: 6 de septiembre de 2012 Fecha de aceptación: 28 de enero de 2013
Para citar este artículo
Romero-Álvarez, Yaneth Patricia; Ramírez-Atehortúa, Fabián Hernando & Guzmán-Aguilar, Diana Sirley (2013). Mercado Integrado Latinoamericano (MILA): análisis de correlación y diversificación de los portafolios de acciones de los tres países miembros en el período 2007-2012. Cuadernos de Contabilidad, 14 (34), 53-74.
Resumen
En este trabajo se analizan los factores en común de los mercados accionarios de los países pertenecientes al Mercado Integrado Latinoamericano, MILA: Chile, Colombia y Perú, con el fin de explorar la existencia de una posible integración financiera que afecte los beneficios de diversificación para los inversionistas. Para ello, se investigan los rendimientos históricos diarios de las 15 acciones más negociadas en cada uno de ellos, en el período de enero de 2009 a junio de 2012, sobre los cuales se realizan dos evaluaciones: primero, se obtiene el portafolio óptimo en cada país y otro del mercado en conjunto; y segundo, mediante un análisis de componentes principales en cada país, se determinan el número de factores de riesgo compartidos y la incidencia de cada país en su variación. Encontramos una alta correlación entre los activos de los países, lo cual evidencia una integración financiera que repercute en que los beneficios de una diversificación de portafolios para un inversionista se minimicen. Se espera continuar con la aplicación de metodologías novedosas relacionadas con los mercados integrados teniendo en cuenta variables fundamentales que incidan en los resultados.
Palabras claves autor: Harry Markowitz, diversificación, análisis de componentes principales, integración de mercados de capitales.
Palabras claves descriptor: Markowitz, Harry, 1927-, acciones, activos (Contabilidad), análisis de costos, portafolio de inversiones.
Códigos JEL: G15, C10, C20
Abstract
The present paper analyses common factors in the stock markets of the member countries of the Latin American Integrated Market (MILA), Chile, Colombia and Peru, with the purpose of exploring the existence of a possible financial integration that would affect diversification benefits for investors. For that purpose the daily historic performances of the fifteen most negotiated stocks in each of them was studied, in the period between January 2009 and June 2012. Two evaluations were performed on these performances: first, through principal component analysis in each country, the number of shared risk factors and the impact of each country in its variation were determined. A high correlation between the countries' assets was found, which evidences a financial integration the effect of which is the minimisation of the benefits of portfolio diversification for an investor. We hope to continue to apply new methodologies related to integrated markets considering the fundamental variables affecting the results.
Key Words author: Harry Markowitz, Diversification, Principal Component Analysis, Integration of Stock Markets.
Key Words plus: Markowitz, Harry, 1927-, actions, assets (Accounting), cost analysis, investments portfolio.
Resumo
Este trabalho analisa os fatores em comum dos mercados acionários dos países pertencentes ao Mercado Integrado Latino-americano, MILA: o Chile, a Colômbia e o Peru, com o objetivo de explorar a existência de uma possível integração financeira que afete os benefícios de diversificação para os investidores. Para isso, pesquisaase sobre os rendimentos históricos diários das quinze ações mais negociadas em cada um deles, no período entre janeiro de 2009 e junho de 2012, sobre os quais se realizam duas avaliações: primeiro, obtém-se o portfólio ótimo em cada país e outro do mercado em conjunto; e segundo, mediante análise dos componentes principais em cada país, determina-se o número de fatores de risco compartidos e a incidência de cada país em sua variação. Encontramos alta correlação entre os ativos dos países, o que evidencia uma integração financeira que repercute em que os benefícios de uma diversificação de por-tfólios para um investidor estão a minimizar-se. Espera-se continuar com a aplicação de metodologias inovadoras relacionadas com os mercados integrados levando em conta variáveis fundamentais que incidirem nos resultados.
Palavras-chave autor: Harry Markowitz, diversificação, análise de componentes principais, integração de mercados de capitais.
Palavras-chave descritor: Markowitz, Harry, 1927-, ação, ativo (Contabilidade), análise de custos, investimento em carteira.
Introducción
El objetivo de esta investigación es determinar si existe integración financiera entre los países pertenecientes al MILA y se enfoca en dos aspectos: primero, la obtención del portafolio óptimo diversificado de una combinación de las 15 acciones más bursátiles de cada uno de los países pertenecientes al MILA, Chile, Colombia y Perú en comparación con la combinación óptima de un portafolio diversificado reproducido mediante el Modelo de Harry Markowitz con los índices de la bolsa de cada uno: el IPSA (Índice de Precio Selectivo de Acciones, Chile), IGBC (Índice General de la Bolsa de Valores de Colombia, Colombia) y el IGBVL (Índice General de la Bolsa de Valores de Lima, Perú), tal como explican Zvi Bodie, Alex Kane y Alan J. Marcus (2011), con el criterio de que a menor integración, mayor diversificación de portafolios. El segundo enfoque indaga si existe integración de los mercados accionarios tal como lo proponen los autores Steven L. Heston, Roberto E. Wessels y K. Geert Rouwenhorst (1995) y David Morelli (2010), mediante el análisis de los factores en común de estos países, bajo la premisa de que, si existe integración, los activos de todos los países tienen el mismo comportamiento en un alto grado; para ello, usamos el método estadístico de análisis de componentes principales como lo utilizan Alan Harper y Zhenhu Jin (2012); por último, contrastamos los resultados y efectos de la integración en la diversificación.
Desde hace ya varias décadas, en Latinoamérica se ha buscado un proceso de integración; sin embargo, esto ha sido más desde un punto de vista económico mediante convenios multilaterales, políticas regulatorias o incentivos de intercambio de bienes y de flujos de capital, con esquemas comerciales de carácter multilateral y amplio ámbito geográfico (Aragão, 1993). La integración que se analiza en este artículo es financiera, específicamente del mercado de capitales en el MILA, Mercado Integrado Latinoamericano, que inició sus operaciones el 30 de mayo de 2011 para lograr un mercado único latinoamericano que les brinde a inversionistas nacionales e internacionales mayores oportunidades de diversificación de sus portafolios y satisfaga sus necesidades de inversión y, de igual forma, otorgue beneficios a los emisores internacionales.
Una integración de este tipo es un proceso gradual que toma muchos años con reversas ocasionales, exige grandes reformas del sector financiero, la economía y los procesos políticos y la habilidad de los inversionistas extranjeros para hacer inversiones directas (Carrieri, Errunza & Hogan, 2007). Los beneficios que se obtienen son múltiples, en especial económicos, ya que la integración permite acelerar el crecimiento de las economías de los países integrantes, contar con un soporte en épocas de crisis (Asness, Israelov & Liew, 2011) y lograr la disminución de los costos transaccionales (Thapa & Poshakwale, 2010). Pero financieramente, para los inversionistas en búsqueda de oportunidades de inversión, los beneficios de diversificación esperados en sus portafolios pueden verse disminuidos en la medida en que los mercados de capitales se vayan integrando, ya que los activos van tomando un mismo comportamiento.
La integración es entendida generalmente como una situación en la cual no hay barreras de ninguna clase para las transacciones transfronterizas (Ayuso & Blanco, 2001), como un lugar donde no hay oportunidades de arbitraje ni prevalece la ley del arbitraje (Federico, 2007), los activos de idénticos tipos de riesgo esperan retornos similares independientes de su domicilio (Bekaert & Harvey, 2003) y a la vez muestran el mismo riesgo ajustado a los rendimientos esperados (Lence & Falk, 2005). Es un estado en el que diferentes mercados de capitales brindan a los inversionistas oportunidades de inversión en un portafolio más amplio de activos bajo una misma expectativa de riesgo y rentabilidad, ya que comparten factores de riesgo en común y a la vez no se da lugar al arbitraje.
En los estudios de la integración financiera de mercados internacionales, los autores se han centrado en determinar el grado de relación de las variabilidades de los activos y el fácil acceso a carteras internacionales en ausencia de restricciones (Fernández & Matallín, 2000). Tal como sostienen Andy Naranjo y Aris Protopapadakis (1997), la integración de mercados como el MILA, la inclusión de más países y la adopción de nuevas políticas de negociaciones transfronterizas deben tener en cuenta el grado de integración de los activos tanto domésticos como internacionales, es decir, este grado de integración se debe medir con un modelo que permita determinar de una forma más acertada la integración de mercados de capitales y el éxito o fracaso de integraciones, como la de Chile, Colombia y Perú que conforman el MILA.
La base de medición del grado de integración de dos o más mercados utilizada por muchos autores es el análisis de los factores de riesgo compartidos, lo que permite establecer si estos países se enfrentan a un mismo mercado, con acceso a los mismos instrumentos y servicios, además de las mismas reglas y el mismo marco político. Por ejemplo, Zhenhu Jin (2005) estudió el grado de en la integración entre las economías principales de la Gran China: Shangai, Hong Kong y Taiwán, por medio de la correlación entre los retornos de sus índices de mercado, la compara con la integración de sus economías y hace hallazgos interesantes de una mayor correlación entre Hong Kong y Taiwán, que son los mercados que mejor explican la economía china, a diferencia de Shangai. Cabe aclarar que la integración financiera es positiva si no hay movimientos conjuntos entre sus precios, es decir, si existe independencia a largo plazo entre los mercados (Fernández & Matallín, 2000).
En estudios tempranos, Heston, Wessels y Rouwenhorst (1995), bajo la premisa de que dos mercados son integrados si la rentabilidad de los activos es la misma y si se encuentran en las mismas condiciones de riesgo, probaron que era posible medir la integración al examinar los retornos de dos portafolios de acciones, uno de cada país, perfectamente correlacionados; indican que la variación de los retornos obedece a una variación a un factor, en este caso una prima de riesgo. Otros autores se han centrado en evaluar la integración financiera teniendo en cuenta modelos de valoración multifactorial, como el modelo Arbitrage Pricing Theory, APT, aplicado por Werner Kristjanpoller y Mauricio Morales (2011), sobre acciones individuales del mercado accionario chileno para el período 1996-2006, al determinar las sensibilidades de sus retornos a factores macroeconómicos propios de este país. Por otro lado, Anthony Chambet y Rajna Gibson (2008) estimaron el nivel de integración financiera de 25 países emergentes en la década de los noventa, al desarrollar un modelo de valoración de activos de tres factores y encuentran que los países latinoamericanos aún se encontraban muy segmentados.
Este concepto de que hay al menos un factor de riesgo internacional compartido que incide en los retornos de las acciones en el mercado internacional fue probado más recientemente por Kim Hiang Liow y James R. Webb (2009), lo que permite medir el impacto de inversiones foráneas en mercados locales. Así mismo, Juliana Caicedo-Llano y Thomas Diony-sopoulos (2008) propusieron como medida de integración, el uso de una proxy de un factor compartido de riesgo proyectado en el tiempo, de tal forma que protegiera estrategias de portafolios de pérdidas importantes en mercados a la baja. Más recientemente, David Morelli (2010) examinó la integración de 15 países europeos que toman parte en la Unión Europea bajo el contexto de un modelo de valoración de activos CAPM [Capital Asset Pricing Model]; al asumir que los retornos siguen una estructura con k factores, encontró que estos países comparten varios factores en común y que sí existe un grado de integración entre ellos.
En América Latina, la mayoría de los estudios se centra en los aspectos económico y comercial y deja rezagado el campo financiero en el análisis de la integración que permitiría proyectar los factores de riesgo que comparten los países y establecer con éxito la estabilidad de las integraciones de mercados, como el MILA. Gongmeng Chen, Michael Firth y Oliver Meng Rui (2002) analizaron la interdependencia de los mercados bursátiles de países latinoamericanos como Argentina, Brasil, Chile, Colombia, México y Venezuela, mediante un modelo de cointegración y técnicas de corrección de errores de vectores autorregresivos (VAR); en la conclusión de esta investigación sugieren que el potencial para diversificar el riesgo de un inversionista en diferentes mercados de Latinoamérica es limitado; aunque parte de esta teoría fue debatida por Frank de Jong y Frans A. de Roon (2005), quienes señalaron que en las últimas décadas los mercados emergentes se han mostrado menos segmentados del mercado mundial, lo que ha producido una disminución en el costo del capital, pero también una notable disminución en los retornos esperados de los activos. Por su parte, Panayiotis F. Diamandis (2009) examinó la existencia de tendencias estocásticas comunes entre los mercados capitales de Argentina, Brasil, Chile y México, con un mercado desarrollado como el NYSE (New York Stock Exchange) y encontró una relación estadísticamente significativa de cointegración entre los cinco mercados de valores y que hay por lo menos cuatro factores compartidos que dirigen los resultados en el largo plazo.
Tal vez el estudio más reciente en cuanto a integración financiera en Latinoamérica es el de Abdelmounaim Lahrech y Kevin Sylwester (2011), quienes examinaron en qué medida los mercados accionarios de Argentina, Brasil, Chile y México se han ido integrando en el tiempo, con una medida de integración empírica, al hallar la correlación dinámica condicional entre cada mercado y el de Estados Unidos y usar un modelo GARCH [Generalized AutoRegressive Conditional Heteroskedasticity] multivariable; estos autores encontraron que cada vez es mayor el grado de correlación pero la velocidad del incremento varía de acuerdo al tipo de país.
Otros estudios similares de medición de integración de mercados son en Asia, el de Ip Wing Yu, Kang Por Fung y Chi-Sang Tam (2010); en la Unión Europea, el de Usha R. Mittoo y Sergiy Rakhmayil (2009) y entre Estados Unidos y la eurozona, el de Christos S. Savva y Nektarios Aslanidis (2010).
En cuanto a la técnica de Análisis de Componentes principales para la medición de la integración financiera de mercados y su efecto sobre portafolios de inversión, la literatura es escasa y muy reciente. Entre estos estudios encontramos a Ilhan Meric, Larry Prober, Benjamin Eichhorn y Gulser Meric (2009), quienes basados en el principio de que una baja correlación entre mercados nacionales es prueba de un potencial beneficio de diversificación y al estudiar las correlaciones de 25 índices nacionales de mercado de economías emergentes pertenecientes al S&P500, encontraron que hay un gran potencial para los inversionistas que desean diversificar, debido al hallazgo de cinco diferentes componentes principales cuya carga factorial variaba en sus propios países.
Más recientemente, autores como Alan Harper y Zhenhu Jin (2012) también estudiaron el acceso a la diversificación de portafolios de inversionistas con acciones de la India y sus principales socios comerciales y encontraron que se maximizan más los retornos al invertir más en acciones locales que extranjeras. Contemporáneamente, Ilhan Meric, Joe H. Kim, Linguo Gong y Gulser Meric (2012), mediante la técnica de componentes principales, analizaron los comovimientos de los retornos de los países asiáticos desde enero de 2001 a enero de 2011 y encontraron que los mercados más influenciados por el mercado asiático son Singapur, India y Japón por sus altas correlaciones mientras que Filipinas y Corea del Sur son los menos correlacionados.
La diversificación de portafolios internacionales brinda confianza a los inversionistas nacionales y extranjeros con apetito de rentabilidad pero aversos al riesgo y ha sido uno de los principales temas investigados en el ámbito mundial. De los estudios más tempranos del tema, quizás los más conocidos son el de Herbert G. Grubel (1968) y el de Bruno H. Solnik (1974), citados por Clifford S. Asness, Roni Israelov y John M. Liew (2011), quienes se centraron en demostrar los beneficios de la diversificación internacional basados en la disminución del riesgo. Un portafolio diversificado implica que un portafolio compuesto de activos de mercados internacionales esté sujeto a un retorno ajustado a su riesgo, superior a los retornos de los países individuales. Otra ventaja de la diversificación de portafolios internacionales es la ampliación de la cartera de activos potenciales que no están sometidos a los diferentes factores propios de cada país, lo que hace el ambiente propicio para diversificar, entre más independientes sean los mercados en la formación de sus precios, mayor será la diversificación de su portafolio (Fernández & Matallín, 2000).
En general, cuando se habla de integración de mercados financieros internacionales, se espera que la cartera conformada por los diferentes activos tenga una mayor rentabilidad esperada y un menor riesgo que cada cartera de forma individual. De hecho, autores como Joshua D. Shackman (2006) han demostrado que hay una relación positiva entre el grado de integración y el valor esperado de los retornos en exceso ajustados al riesgo de los países emergentes en comparación con mercados desarrollados como Estados Unidos, en un estudio realizado con 18 países incluidos de economías emergentes, entre ellos los integrantes del MILA.
En esta investigación se analiza entonces la integración financiera de mercados capitales, mediante la técnica estadística de Análisis de Componentes Principales, aunque el punto de partida no se centra en las operaciones que se hayan llevado a cabo en la reciente conformación del MILA y el comportamiento del nuevo índice creado por Standard & Poors, el S&P MILA 40, sino en la información histórica de las acciones de los diferentes países y los índices principales de las bolsas de valores de cada uno, el IPSA en Chile, el IGBC en Colombia, el IGBVL en Perú, sometidos en conjunto a un factor de riesgo compartido relacionado con los retornos de un portafolio único compuesto de activos del MILA. El principal hallazgo detectado en este estudio es que al parecer los mercados accionarios de los países integrantes al MILA se encuentran integrados y que la diversificación se ve afectada.
1. Datos
Para este estudio se utilizaron los retornos diarios de las 15 acciones más negociadas en las bolsas de valores de Colombia, Chile y Perú para el período de diciembre de 2009 a junio de 2012, de acuerdo con los principales índices de cada país, para un total de 954 datos, teniendo en cuenta cubrir los históricos de las principales acciones que se cotizan en cada bolsa, ya que el índice de la Bolsa de Valores de Perú y de Colombia están conformados por acciones líquidas pero emitidas recientemente, es decir, con históricos de menos de 2 años. Esta restricción de los datos se detalla en las delimitaciones del trabajo.
Los históricos diarios de los precios para cada uno de los países fueron tomados de Bloomberg para el período diciembre de 2009 a junio de 2012. Para cada una de las acciones, se construyó una matriz de retornos en dólares y de excesos de retorno por cada país utilizando la tasa libre de riesgo de Estados Unidos. La tabla 1 muestra los estadísticos descriptivos de cada uno de los países del MILA.
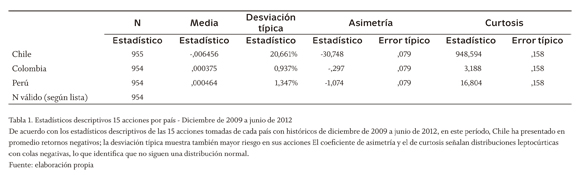
En un panorama general, Perú parece representar un portafolio de inversiones más atrayente para los inversionistas, debido a una mayor rentabilidad promedio (0,046%) aunqu con un riesgo del 1,347% superior al de Colom bia con una desviación estándar del 0,937%; si embargo, no se puede dejar de lado que estos datos provienen de 15 acciones para las misma fechas, por lo que para ser más precisos y tener en cuenta el mercado de forma más global, se utilizó la información de los estadísticos descriptivos del índice principal de bolsa de cada país, como se muestra en la tabla 2 en el mismo período, es decir, para el período diciembre de 2009 a junio de 2012. Así, observando la media y la desviación estándar de cada uno, podemos inferir que los países se muestran má equilibrados en cuanto al riesgo-rentabilidad esperados.
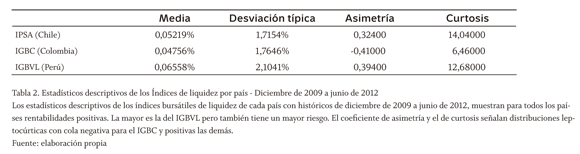
Los anteriores datos de la tabla 2 cambian entonces el panorama a un ambiente de riesgo - rentabilidad más favorable para Chile con una rentabilidad promedio (media) del 0,05219% y un riesgo asociado del 1,7154%.
2. Metodología
Modelo de Diversificación Eficiente de Portafolios
La teoría moderna de portafolios, desarrollada inicialmente por Harry Markowitz y William Sharpe (1952), ambos premios Nobel en Economía en 1990, junto con Merton H. Miller, establece que hay un portafolio óptimo diversificado que representa un conjunto de carteras que maximizan la rentabilidad esperada en cada nivel de riesgo, en el cual la tasa de rentabilidad rp es la media ponderada de la rentabilidad de los valores con las proporciones de inversión como ponderaciones (ecuación 1), la tasa de rentabilidad esperada E(rp) es una media ponderada de la rentabilidad esperada de los valores compuestos con la misma proporción de cartera de las ponderaciones ω. (ecuación 2) y la varianza del portafolio s2p depende de esa proporción y la interrelación entre sus rentabilidades (ecuación 3) (Bodie, Kane & Marcus, 2011):
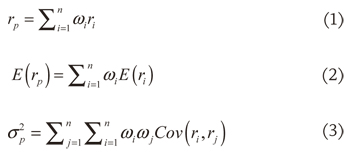
Donde ω. representa la proporción del activo . en el portafolio y r. la rentabilidad histórica de cada uno en el mismo período.
La relación dada en un portafolio por su riesgo y rentabilidad es usualmente medida por un indicador de desempeño denominado la Ratio de Sharpe (1966, 1975, 1994) citado por John Douglas Opdyke (2007), que provee una medida del retorno por unidad de volatilidad (ecuación 4) y divide el rendimiento esperado de una cartera superior a la tasa libre de riesgo de su desviación estándar esperada:

En la práctica financiera, es usual encontrar que la Ratio de Sharpe es calculada con el promedio de los retornos esperados de un portafolio, su riesgo como la desviación estándar y la tasa de los bonos del Tesoro de Estados Unidos como la tasa libre de riesgo (Best, Hodges & Yoder, 2007), entonces a mayor ratio de Sharpe, mejor será la recompensa de los retornos que se esperan por el riesgo asumido y este resultado es el que se espera obtener al combinar activos, por ejemplo, acciones, con diferentes promedios de retornos esperados, diferentes niveles de riesgo y en nuestro caso de diferentes mercados financieros.
Cuando se establece para cada nivel de riesgo de una cartera la máxima Ratio de Sharpe, entonces se va construyendo un conjunto de combinaciones óptimas de riesgo-rentabilidad para el inversionista denominado frontera eficiente.
Construcción de la frontera eficiente y portafolio óptimo MILA
Un mercado financiero puede tener múltiples combinaciones de activos financieros que dan lugar a múltiples portafolios, cada uno con su propia relación riesgo-rentabilidad, y el procedimiento que se sigue al construir una frontera eficiente es el de establecer los portafolios más eficientes, dado un nivel de riesgo formulándolo de la siguiente forma: dado un valor esperado (ecuación 2), calcular las proporciones ω. que hacen que se cumpla:

El resultado obtenido son las proporciones en las que se debe invertir en cada activo para lograr un nivel esperado de rentabilidad y mínimo riesgo. Al variar el nivel de riesgo esperado, se pueden hallar las combinaciones (E(rp), σp) que serían los puntos que conforman la frontera eficiente, además del portafolio óptimo y el portafolio de mínimo riesgo, por debajo del cual se encuentra el conjunto de portafolios ineficientes para ese mercado (Buenaventura & Cuevas, 2005).
En países emergentes como los estudiados en esta investigación, al construir la frontera eficiente y calcular el portafolio óptimo, además de las anteriores relaciones también se debe tener en cuenta que están prohibidas las ventas en corto, por lo que se debe incluir la restricción:
ω ≥ 0 (7)
Aunque se ha establecido en anteriores investigaciones como las de Gur Huberman (2001) y Mark Grinblatt y Matti Keloharju (2001), investigadores citados por Joost Driessen y Luc Laeven (2007), que los inversionistas locales prefieren carteras locales a las carteras extranjeras, al momento de minimizar riesgos, la diversificación internacional es mucho más importante para estos que para los extranjeros.
En aras de analizar este potencial beneficio de una integración financiera consideramos los portafolios óptimos y las fronteras eficientes de cada país integrante del MILA de forma separada, teniendo en cuenta las 15 acciones seleccionadas para cada país, con condiciones similares en todos los sectores económicos involucrados en los portafolios y para comparar estadísticamente los resultados con el modelo factorial.
3. Resultados de la diversificación
Con los históricos de los retornos de las 15 acciones seleccionadas para cada uno de los países, hallamos las combinaciones de riesgo-rentabilidad óptimas y de mínimo riesgo para un inversionista local en cada uno de los países que se muestran en la tabla 3.
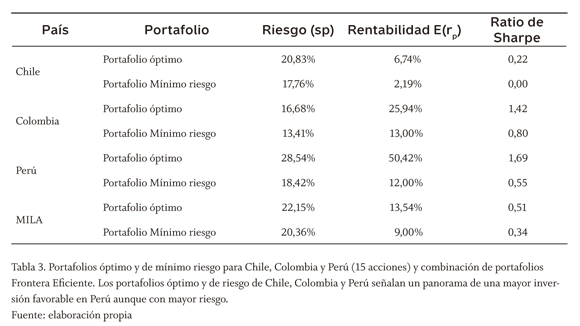
De acuerdo con los resultados de la tabla 3, al invertir en Chile, se puede obtener una rentabilidad promedio óptima del 6,74% sometido a un riesgo de perder su dinero por las variaciones en los precios de estos activos del 20,83%, un inversionista colombiano, en forma óptima puede obtener una rentabilidad del 25,94% bajo un riesgo del 16,68%, es decir, mayor rentabilidad esperada que un portafolio chileno mirado de una forma individual, y también a un menor riesgo y en el caso de Perú, el mercado peruano se muestra un poco más conservador que Chile y que Colombia, ya que su portafolio óptimo presenta un riesgo del 28,54% —pero a la vez esto representa una menor rentabilidad 50,42%—, considerado muy alto.
En resumen, para Chile, Colombia y Perú de forma individual se cumple el enunciado "A mayor riesgo, mayor rentabilidad" y cada país muestra una perspectiva diferente para un inversionista local. Para el MILA en conjunto, cada activo representa el promedio ponderado de los excesos de retorno de cada país simulando un único índice, aunque cabe la pena resaltar que según Philippe Jorion (1985, 1992), estos estimadores presentan errores de estimaciones comunes y pueden ser calculados con más precisión, pero generalmente son aceptados.
La figura 1 muestra la frontera eficiente conformada por portafolios de activos de los tres países, para unas diferentes combinaciones de riesgo-rentabilidad. Al contrastar estos resultados con los individuales, en el caso de Chile, resulta beneficioso pasar de una rentabilidad promedio esperada óptima de 6,74 a 13,54%; claro está, pasando de 20,83 a 22,15% del portafolio MILA. En los casos de Colombia y Perú, el beneficio de diversificación disminuye notablemente, ya que sus rentabilidades esperadas promedio óptimas son de 25,94 y 50,42%, respectivamente.
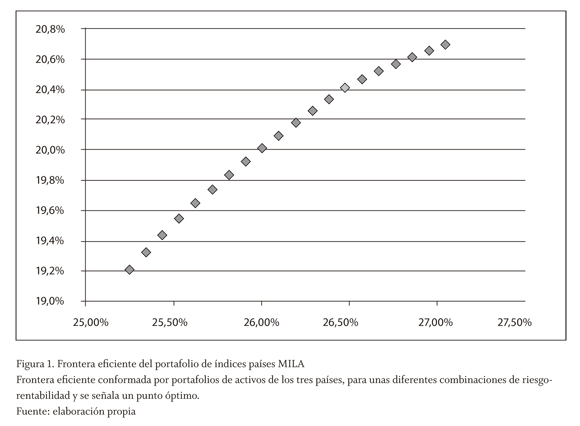
4. Modelo de análisis factorial
Para predecir la relación entre el rendimiento y el riesgo de un solo portafolio suramericano, partimos del modelo CAPM [Capital Asset Pricing Model], que permite predecir la relación esperada entre el riesgo y el rendimiento esperado de equilibrio en los activos de riesgo, que es una aplicación específica de un modelo factorial. Según el CAPM (Markowitz, 1952), hay una relación directa entre el retorno de un activo y sus factores de riesgo, dada por:
Rt =βRMt+εt (8)
Donde Rt representa el retorno de los activos, β refleja la sensibilidad de los retornos a los riesgos no diversificables y RMt, los excesos de retorno del mercado en su conjunto. Para este estudio y de forma matricial, establecemos la ecuación:
Rt =βR'Mt+εt (9)
Donde Rf es un vector de 1 xn columnas de los excesos de retorno de las acciones de un portafolio latinoamericano en el tiempo t, β es una matriz n x k de coeficientes en los K-factores para cada uno de los n países, R Mf es un vector columna traspuesto de factores comunes en el tiempo t, generados desde el análisis factorial y εt es un vector de n x 1 columna de términos propios relacionados con cada una de las n acciones en el tiempo t. Se asume que los términos son independientes de los factores, cov(RMf,εt)= 0 y distribuidos uniformemente mediante una distribución normal con media cero E(εt)= 0 y matriz de covarianza D en el tiempo, cov(εt, ε')=σ2 I = D y que la matriz de covarianza D que es diagonal y proporcional a la matriz de identidad I.
Para analizar la existencia de factores comunes y su número, utilizamos el método estadístico de análisis factorial, específicamente el análisis de componentes principales que no exige ajuste de distribución de los datos; sin embargo, para poder aplicar el análisis factorial debe tenerse una correlación muy alta entre las variables. La matriz de correlaciones para los rendimientos de los índices accionarios de cada país en el período muestreado se presenta en la tabla 4, con lo cual se puede comprobar que al ser mayores a 0,5, la técnica de análisis factorial es procedente.

Las medidas de adecuación de los datos como la de Kaiser-Meyer-Olkin (KMO) y la prueba de esfericidad de Bartlett permiten confirmar que los coeficientes de correlación parcial son pequeños comparados con los coeficientes de correlación ordinarios, lo que quiere decir que el análisis factorial es viable. Según esta prueba, si el KMO toma un valor entre 1 y 0,90 se dice que es "excelente"; entre 0,90 y 0,80 es "meritorio"; entre 0,80 y 0,70 es "moderado"; entre 0,60 y 0,50 es "mediocre", y por debajo de 0,50 es "inaceptable"; por otro lado, la prueba de esfericidad de Bartlett contrasta la hipótesis nula de que la matriz de correlaciones es una matriz identidad, en cuyo caso no habría correlaciones significativas entre las variables y el modelo factorial no sería pertinente, esta hipótesis nula se acepta cuando el nivel de significancia es >0,05 (Harper & Jin, 2012).
La tabla 5 muestra una medida KMO de 0,718, lo que demuestra que los datos consolidados por los países en el MILA son adecuados para el modelo y como la prueba de esfericidad de Bartlett arroja que su nivel de significancia es 0,000, no es posible afirmar que la matriz de correlaciones es una matriz identidad, lo cual es adecuado para el estudio para la validez del modelo.

Mientras que para cada país de forma individual, dos factores explican la totalidad de la varianza, de acuerdo con la tabla 6 para el MILA encontramos solo un factor en común que la explica, es decir, hay al menos un factor que puede explicar el 73,449% de las variabilidades esperadas de los retornos de un portafolio MILA. Comprobamos la existencia de este componente único con la figura 2, que es el gráfico de sedimentación con el cual se analizan los puntos de quiebre.
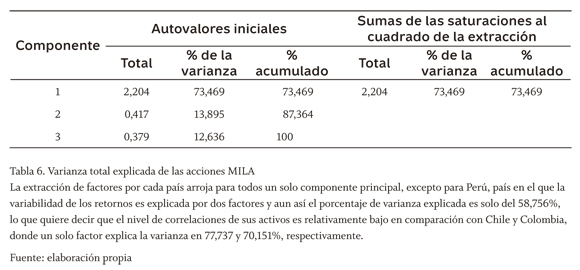
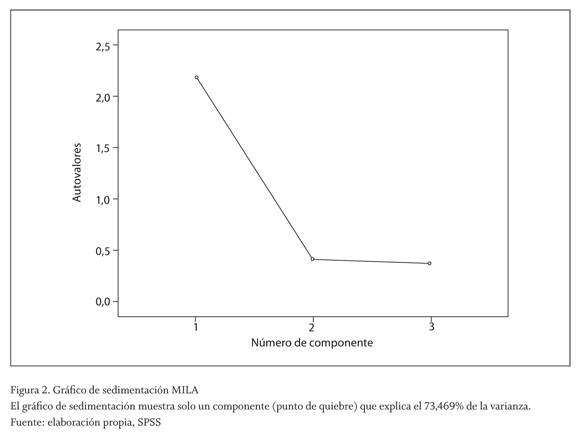
Al analizar el componente extraído de cada país en la matriz de la tabla 7 para el MILA, encontramos que cada uno de los países tiene una alta incidencia en el factor único extraído (>0,8), lo cual indica que hay una alta integración en los mercados de acciones de estos países, ya que son altamente correlacionados e incluirlos en un mismo portafolio permite diversificación pero en una menor medida.
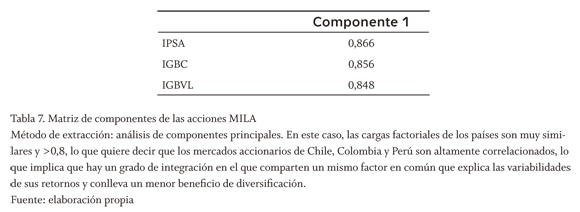
5. Prueba de hipótesis a los resultados
Dados los resultados anteriores, podríamos establecer que aunque hay un alto grado de correlación entre los diferentes países que conforman el MILA, esta no es totalmente cercana a 1, es decir, aunque hay evidencia de integración de acuerdo con los resultados obtenidos, aún hay posibilidades de diversificación para los inversionistas. Estos resultados se analizan estadísticamente mediante una prueba de hipótesis de los betas de cada uno de los países hallados bajo la premisa del CAPM.
Las pruebas de hipótesis consisten en determinar:
Prueba 1: H0: βChile = βMILA cuando la alternativa es Hα: βChile ≠ βMILA
Prueba 2: H0: βColombia = βMILA cuando la alternativa es Hα: βColombia ≠ βMILA
Prueba 1: H0: βPerú = βMILA cuando la alternativa es Hα: βPerú ≠ βMILA
Como en este caso no se puede verificar el supuesto de normalidad, pero la muestra es de 1.298 datos, es decir, grande (>30), para comparar si hay diferencias estadísticamente significativas, se puede utilizar la prueba Z teniendo en cuenta que la distribución de este estadístico es asintóticamente normal y por tanto, la prueba no es exacta sino aproximada (García, 2006), donde:

El beta de cada uno de los países se estima mediante regresiones de los datos de los excesos de retorno de los países, calculados mediante los índices de cada bolsa IPSA, IGBC e IGBVL en dólares, simulando el mercado y los retornos de los activos de cada país calculados con los factores hallados mediante el análisis de componentes principales, los valores tenidos en cuenta para el cálculo de cada beta se señalan en la tabla 8:
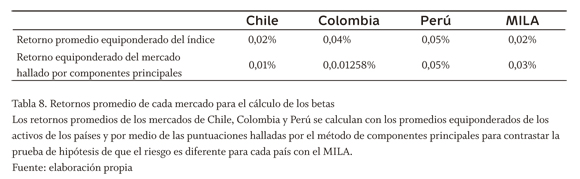
Con una región de rechazo {z/|z|>za/2} y un nivel de confianza del 95%, encontramos los siguientes resultados en la tabla 9 para cada uno de los países comparados con el MILA:

Con lo anterior, podemos entonces establecer que aun a pesar de la evidencia de integración, el entorno de los riesgos de los mercados en cada país es diferente al entorno del MILA, para dar paso a la existencia de una diversificación en las carteras de los inversionistas tanto locales como extranjeros.
Entre los principales beneficios que se esperan de una integración financiera están la diversificación y la ampliación de los activos que se pueden negociar en cada uno de los mercados locales, esto obviamente los hace más atractivos y promueve su desarrollo en conjunto, ya que contribuye a que todos los espacios hablen un mismo lenguaje en cuanto a productos, tecnología, políticas y regulaciones propias del mercado bursátil.
En este estudio se quiso establecer el efecto de la integración en los países que inicialmente conforman el MILA, ya que al existir, es decir, al eliminar las barreras para hacer transacciones internacionales en otros países se pudo establecer que sí es posible lograr una mayor diversificación de portafolios, como en Colombia y Perú, países en los que los inversionistas pueden optimizar sus portafolios aumentando la rentabilidad a la que tienen acceso actualmente en el mercado local y disminuyendo en gran medida su riesgo. Sin embargo, la integración también hace que los mercados tiendan a "parecerse", es decir, a estar sometidos a las mismas condiciones de riesgo, lo cual con el tiempo llevará a una disminución de la diversificación como en el caso de Chile, a cuyos inversionistas no les ofrece mayor ventaja invertir en activos pertenecientes al MILA, ya que las condiciones son muy similares a las que están sometidos en el mercado local.
Esta variabilidad común que pueden tener los países se midió con el análisis de componentes principales, con el cual encontramos que hay un factor común en un 73,449% para los tres países.
Los anteriores resultados no quieren decir que la integración financiera sea negativa; todo lo contrario, se busca establecer su efecto en los portafolios. Pero aparte de este análisis, también se deben tener en cuenta otros aspectos fundamentales como la disminución de los costos transaccionales y la facilidad de inversión en sectores diferentes a los predominantes en cada país, como el hecho de que un inversionista local puede invertir en el sector minero en Chile, o en el de construcción en Perú, y todo esto sin recurrir a intermediarios externos sino a comisionistas de bolsa autorizados presentes en el país y en moneda local. Debido a que las economías son diferentes, la integración financiera no es perfecta, es decir, el nivel de riesgo compartido no es absolutamente el mismo, lo cual fue demostrado con la prueba de hipótesis de los betas de cada país y del MILA, con lo que se establece que el nivel de variabilidad compartido no es del 100% y que se pueden obtener beneficios de diversificación para los diferentes inversionistas.
Conclusiones
Un portafolio diversificado conformado con Chile, Colombia y Perú, países integrantes del Mercado Integrado Latinoamericano, MILA, permite una diversificación eficiente en cuanto brinda acceso a los inversionistas tanto locales como extranjeros a una mayor rentabilidad y a un menor riesgo que en los portafolios de acciones de cada país individual. El MILA le permite a un inversionista chileno pasar de acceder a invertir en un portafolio óptimo con una rentabilidad de 6,74% y un riesgo de 20,83% (tabla 3) a una rentabilidad de 13,54% bajo un riesgo de 22,15%, pero para los colombianos y peruanos no pasa lo mismo. Este estudio encontró que estadísticamente cuando hay integración financiera, se disminuyen los beneficios de diversificación, ya que estos países presentan un binomio de riesgo-rentabilidad de 15,68 y 25,94%, y 50,42 y 28,54%, respectivamente, pues aunque el riesgo del MILA es menor, las rentabilidades también lo son.
Aunque se presencia la diversificación de acuerdo con la teoría moderna de portafolios, los resultados no son tan contundentes como se esperaba: la rentabilidad individual y el riesgo esperado de una cartera MILA no son significativamente mayores; esto demuestra que estos países tienen cierto grado de integración financiera pero no total o perfecta, lo cual comprobamos también con el análisis de los factores en común y contrastamos con la prueba de hipótesis de los betas.
Al aplicar las técnicas de componentes principales a un portafolio MILA, encontramos que la variabilidad de los retornos estaría explicada por una carga factorial en un solo componente principal en 73,449% (tabla 6), lo cual indica una alta correlación entre los retornos de los activos de los países, con ello y basándonos en la teoría moderna de portafolio establecida por Harry Markowitz, podemos decir que hay integración financiera y desfavorece la diversificación para los inversionistas. En contraste, bajo diferentes criterios, ambos métodos señalan la existencia de una integración financiera entre los países pertenecientes al MILA: Chile, Colombia y Perú.
Aun así, el modelo factorial analizado arroja como resultado un único componente principal, del cual se pueden hacer análisis para determinar específicamente cuál factor de riesgo comparten estos tres países. Aún mejor, se espera entonces que en futuras investigaciones se determinen más modelos de medición de integración financiera que permitan proyectar los factores de riesgo más específicos que comparten los activos de los países, ya sea por sectores de la industria o por su comportamiento frente a otros factores macroeconómicos.
Discusión
El tema de la integración financiera ha sido muy estudiado, mediante diversas técnicas económicas y estadísticas, partiendo de técnicas cuantitativas relacionadas con el riesgo, la rentabilidad, los costos, los tipos de cambio y muchos otros aspectos financieros cuyas cifras pueden ayudar a interpretar el comportamiento de los mercados accionarios en su conjunto.
Sin embargo, llega incluso a ser contradictorio el hecho de que los países deseen integrar sus mercados para desarrollarse y ofrecer mayores oportunidades de inversión a los interesados en conformar carteras con activos financieros extranjeros y, a la vez, disminuir los costos y las restricciones de las inversiones transfronterizas, pero tal y cómo se definió en la introducción, la integración puede llevar a una correlación cercana a 1 entre los diferentes países, es decir, que se vayan eliminando las posibilidades de diversificar los portafolios, lo que afecta las carteras óptimas en su riesgo y en su rentabilidad.
El análisis de este estudio se quiso hacer de una forma netamente estadística, teniendo en cuenta solo aspectos cuantitativos de riesgo y rentabilidad de los portafolios, para hacer aplicación de una técnica estadística no utilizada hasta el momento y dejando por el momento de lado aspectos de análisis fundamental como los movimientos de las acciones por diferentes sectores de la economía y la paridad de las tasas de cambio.
Sin embargo, dadas las características de este tema de investigación, sería interesante poder definir con mayor precisión y exactitud los diferentes parámetros o componentes específicos que comparten los diferentes países, como inflación, PIB, tasa de cambio contra una misma moneda, etc. Esto puede llevar a predecir el comportamiento de esos mercados bajo escenarios específicos de riesgos y por sectores específicos de la economía. De igual forma, cuando se habla de integración financiera, también cabe analizar el comportamiento de los costos y la creación de potenciales riesgos de contagio, ya sea de forma general o por mercados específicos o analizar desde el punto de vista de riesgos tanto sistémicos como no sistémicos y demás parámetros relacionados o compartidos por los diferentes países y que afecten la rentabilidad esperada de los portafolios.
Uno de los limitantes del trabajo es la falta de datos históricos de algunos activos de cada país de alta bursatilidad pero que llevan poco tiempo en el mercado.
Referencias
Aragão, José María (1993). La integración en América Latina: objetivos, obstáculos y oportunidades. Integración Latinoamericana, 45-56. Disponible en: http://www.iadb.org/intal/intalcdi/integracion_latinoamericana/ documentos/196-Estudios_3.pdf [ Links ]
Asness, Clifford S.; Israelov, Roni & Liew, John M. (2011). International Diversification Works (Eventually). Financial Analysts Journal, 67 (3), 1-23. [ Links ]
Ayuso, Juan & Blanco, Roberto (2001). Has financial market integration increased during the nineties? Journal of International Financial Markets, Institutions and Money, 11 (3), 265-287. [ Links ]
Bekaert, Geert & Harvey, Campbell R. (2003). Emerging markets finance. Journal of Empirical Finance, 10 (1-2), 3-55. [ Links ]
Best, Ronald W.; Hodges, Charles W. & Yoder, James A. (2007). The Sharpe Ratio and Long-Run Investment Decisions. The Journal of Investment, 16 (2), 70-76. [ Links ]
Bodie, Zvi; Kane, Alex & Marcus, Alan J. (2011). Investments. 9 ed. New York: Mc-Graw Hill. [ Links ]
Buenaventura-Vera, Guillermo & Cuevas-Ulloa, Andrés Felipe (2005). Una propuesta metodológica para la optimización de portafolios de inversión y su aplicación al caso colombiano. Estudios gerenciales, 95, 13-36. [ Links ]
Caicedo-Llano, Juliana & Dionysopoulos, Thomas (2008). Market integration: A risk-budgeting guide for pure Alpha investors. Journal of Multinational Financing Management, 18 (4), 313-327. [ Links ]
Carrieri, Francesca; Errunza, Vihang & Hogan, Ked (2007). Characterizing world market integration through time. Journal of Financial and Quantitative Analysis, 42 (04), 915-940. [ Links ]
Chambet, Anthony & Gibson, Rajna (2008). Financial integration, economic instability and trade structure in emerging markets. Journal of International Money and Finance, 27 (4), 654-675. [ Links ]
Chen, Gong-meng; Firth, Michael & Meng Rui, Oliver (2002). Stock market linkages: Evidence from Latin America. Journal of Banking & Finance, 1113-1141. [ Links ]
Diamandis, Panayiotis F. (2009). International stock market linkages: evidence from Latin America. Global Finance Journal, 20 (1), 13-30. [ Links ]
Driessen, Joost & Laeven, Luc (2007). International portfolio diversification benefits: Cross-country evidence from a local perspective. Journal of Banking & Finance 31 (6), 1693-1712. [ Links ]
Federico, Giovanni (2007). Market integration and market efficiency: The case of 19th century Italy. Explorations in Economic History, 44 (2), 293-316. [ Links ]
Fernández-Izquierdo, María Ángeles & Ma-tallín-Sáez, Juan Carlos (2000). Gestión óptima de carteras internacionales ante la integración de los mercados europeos. Investigaciones Europeas de Dirección y Economía de la Empresa, 6 (3), 87-100. Disponible en: http://www.aedem-virtual.com/articulos/iedee/v06/063087.pdf [ Links ]
García-Ben, Marta (2006). Test con nivel asintótico para hipótesis sobre la media de una población sin suponer normalidad. Facultad de Ciencias Exactas y Naturales, FCEyN, Estadística para Química, 88-112. Disponible en: http://www.dm.uba.ar/materias/estadistica_Q/2008/1/EstadQuimTH2.pdf [ Links ]
Harper, Alan & Jin, Zhenhu (2012). Comove-ments and stock market integration between India and its top trading partners: a multi-variate analysis of international portfolio diversification. International Journal of Business and Social Science, 3 (3), 50-56. Disponible en: http://www.ijbssnet.com/journals/Vol_3_No_3_February_2012/5.pdf [ Links ]
Heston, Steven L.; Wessels, Roberto E. & Rouwenhorst, K. Geert (1995). The structure of international stock returns and the integration of capital. Journal of Empirical Finance, 2 (3), 173-197. [ Links ]
Jin, Zhenhu (2005). The integration of capital markets: Correlation analysis of the market indexes in greater China economies. Academy of Accounting and Financial Studies Journal, 9 (1), 43-53. [ Links ]
Jong, Frank de & Roon, Frans A. de (2005). Time-varying market integration and expected returns in emerging markets. Journal of Financial Economics, 78 (3), 583-613. [ Links ]
Jorion, Philippe (1985). International portfolio diversification with estimation risk. Journal of Business, 58, 259-278. [ Links ]
Jorion, Philippe (1992). Portfolio optimization in practice. Financial Analysts Journal, 48 (1), 68-74. [ Links ]
Kristjanpoller, Werner & Morales, Mauricio (2011). Teoría de la asignación del precio por arbitraje aplicada al mercado accionario chileno. Lecturas de Economía, 74, 37-59. Disponible en: http://www.scielo.org.co/scielo.php?pid=S012025962011000100002 & script=sci_arttext [ Links ]
Lahrech, Abdelmounaim & Sylwester, Kevin (2011). US and Latin American stock market linkages. Journal of International Money and Finance, 30 (7), 1341-1357. [ Links ]
Lence, Sergio H. & Falk, Barry (2005). Cointegration, market integration, and market eficiency. Journal of International Money and Finance, 24 (6), 873-890. [ Links ]
Liow, Kim Hiang & Webb, James R. (2009). Common factors in international securitized real estate markets. Review of Financial Economics, 18 (2), 80-89. [ Links ]
Markowitz, Harry (1952). Portfolio Selection. The Journal of Finance, 7 (1), 77-91. [ Links ]
Meric, Ilhan; Prober, Larry; Eichhorn, Benjamin & Meric, Gulser (2009). A principal components analysis of the portfolio diversification benefits of investing in emerging stock markets. Middle Eastern Finance and Economics, 4, 110-116. [ Links ]
Meric, Ilhan; Kim, Joe H.; Gong, Linguo & Meric, Gulser (2012). Co-movements of and linkages between Asian stock markets. Business and Economics Research Journal, 3 (1) 1-15. [ Links ]
Mittoo, Usha R. & Rakhmayil, Sergiy (2009). Estimating time-varying capital market integration in the EMU [France, Germany, Netherlands]. International Business & Economics Research Journal, 8 (11), 73-88. Disponible en: http://journals.cluteonline.com/index.php/IBER/article/view/3187/3235 [ Links ]
Morelli, David (2010). European capital market integration: an empirical study based on a European asset pricing model. Journal of International Financial Markets, Institutions & Money, 20 (4), 363-375. [ Links ]
Naranjo, Andy & Protopapadakis, Aris (1997). Financial market integration tests: an investigation using US equity markets. Journal of International Financial Markets, Institutions & Money, 7 (2), 93-135. [ Links ]
Opdyke, John Douglas (2007). Comparing Sharpe ratios: so where are the p-values? Journal of Asset Management, 8, 308-336. [ Links ]
Savva, Christos S. & Aslanidis, Nektarios (2010). Stock market integration between new EU member states and the Euro-zone. Empirical Economics, 39 (2), 337-351. [ Links ]
Shackman, Joshua D. (2006). The equity premium and market integration: evidence from international data. Journal of International Financial Markets, Institutions & Money, 16, 155-179. Disponible en: http://ejournal.narotama.ac.id/files/The equity premium and market integration.pdf [ Links ]
Solnik, Bruno H. (1974). Why not diversify internationally rather than domestically? Financial Analysts Journal, 30 (4), 48-54. [ Links ]
Thapa, Chandra & Poshakwale, Sunil S. (2010). International equity portfolio allocations and transaction costs. Journal of Banking & Finance, 34 (11), 2627-2638. [ Links ]
Yu, Ip Wing; Fung, Kang Por & Tam, Chi-Sang (2010). Assessing financial market integration in Asia - Equity markets. Journal of Banking & Finance, 34 (12), 2874-2885. [ Links ]
Bibliografía consultada
Li, Kai; Sarkar, Asani & Wang, Zhenyu (2003). Diversification benefits of emerging markets subject to portfolio constraints. Journal of Empirical Finance, 10, 57-80. Disponible en: http://finance.sauder.ubc.ca/~kaili/shortJEF.pdf [ Links ]













