Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Cuadernos de Contabilidad
versión impresa ISSN 0123-1472
Cuad. Contab. vol.17 no.43 Bogotá ene.-jun. 2016
https://doi.org/10.n144/Javeriana.cc17-43.mmca
El modelamiento matemático y la contabilidad analítica matricial, mecanismos de medición, representación e interpretación contable: ¿un reto aún no asumido por la contametría en el desarrollo científico de contabilidad?, ¿ni tampoco por la praxis de la profesión?*
Mathematical Modeling and Matrix Analytic Accounting, Accounting Measuring, Representation, and Interpretation Tools: Are these a challenge yet to be assumed by 'contametria' (account metrics) in the scientific development of accounting? Is it assumed by the praxis of the profession?
A modelagem matemática e a contabilidade analítica matricial, mecanismos de aferição, representação e interpretação contábil: desafio ainda não assumido pela contametria no desenvolvimento científico de contabilidade, nem mesmo pela práxis da profissão?
José Joaquín Ortiz-Bojacá
Investigador, Universidad Libre. Economista, Universidad Jorge Tadeo-Lozano. Especialista en diseño de sistemas de auditoría, Universidad Nacional de Colombia, Magíster en ciencias financieras y de sistemas, Universidad Central. PhD (c) en administración, Universidad de Celaya, México. Docente investigador, posgrado y pregrado Universidad Libre. Director científico, Revista Criterio Libre. Conferencista y ponente internacional. Docente de posgrados en universidades colombianas. Correo electrónico: Josej.ortizb@unilibrebog.edu.co
*Artículo producto de la investigación Construcción de la teoría general contable, financiado por la Universidad Libre.
Fecha de recepción: 15 de septiembre de 2015 Fecha de aceptación: 15 de mayo de 2016 Disponible en línea: 30 de junio de 2016
Para citar este artículo
Ortiz-Bojacá, José Joaquín (2016). El modelamiento matemático y la contabilidad analítica matricial, mecanismos de medición, representación e interpretación contable: ¿un reto aún no asumido por la Contametría en el desarrollo científico de contabilidad?, ¿ni tampoco por la praxis de la profesión? Cuadernos de Contabilidad, 17(43), 127-155. http://dx.doi.org/10.n144/Javeriana.cc17-43.mmca
Resumen
Este artículo busca establecer las relaciones entre la teoría, la praxis contable y el uso de las matemáticas, tanto en su fundamentación como en su aplicación para la solución de problemáticas de la contabilidad como ciencia y como ejercicio profesional. Ello conlleva afrontar la indagación de los principales aportes en su recorrido tanto de axiomatización como del desarrollo de aplicaciones mediante la utilización de las herramientas matemáticas y sus carencias en la integración en una teoría general, que está por estructurarse, desde un enfoque sistémico e interdisciplinario y bajo el paradigma de la complejidad. Se utilizó una metodología cualitativa basada en el análisis de contenidos de documentos, y la triangulación de fuentes teóricas de información, para determinar un muestreo teórico representativo de esos desarrollos y se seleccionaron dos esquemas de matematización contable considerados fundamentales en este proceso: el enfoque del modelamiento matemático aplicado a las dinámicas patrimoniales y el desarrollo del modelo de la contabilidad analítica matricial, que recurre al análisis de casos ilustrativos por su gran potencial de soporte metodológico en la consolidación de la estructura científica de la contabilidad y por su alto impacto social en la solución de problemas como la justa distribución de la riqueza y el logro del bienestar social, desde una perspectiva de responsabilidad social, sustentada en valores humanos, que deben orientar las decisiones económicas y no a la inversa, como ha venido ocurriendo en la actual fase de financiarización de la economía, con las consecuencias de un resquebrajamiento social profundo, en el cual todas las ciencias enfrentan un reto insoslayable de aportar a su solución desde lo más profundamente humano y en el que la contabilidad como ciencia social, se proyecta como una de las grandes aportantes en el concierto científico universal, siguiendo un programa de investigación centrado en la matematización contable desde lo socioeconómico y desde el bien común.
Palabras clave: Contametría; matematización contable; contabilidad social; modelamiento matemático contable; contabilidad analítica matricial; partida múltiple; algebra matricial
Códigos JEL A10, C02, C61, G10, I31, L21, M41
Abstract
This article aims to establish the relationships between accounting theory, practice, and the use of mathematics, both in their foundation as well as in their application, for the solution of problems of accounting, both as a science and as a professional exercise. This involves facing the search for the main contributions on this path, both regarding axiomatization and the development of applications by means of the use of mathematical tools, as well as its shortcomings regarding the integration into a general theory. This theory is on its way towards structuration, from a systemic and interdisciplinary approach, and under the complexity paradigm. We used a qualitative methodology based on the analysis of the contents of documents, and the triangulation of sources of theoretical information as to create a representative theoretical sample of these developments. Afterwards, we selected two schemas of accounting mathematization considered as fundamental for this process: the mathematical modeling approach applied to equity dynamics and the development of the matrix analytic accounting model, which resorts to the analysis of illustrative cases, due to its huge potential for methodological support in the consolidation of a scientific structure of accounting, and due to its high social impact on problem resolution. An example of which is the fair distribution of wealth and the attainment of social welfare, from a social responsibility perspective, based on human values, which should guide economic decisions, and not the other way around, as it has been happening in the current stage of financialization of economy. The consequences are a deep social fracturing, where all sciences face the unavoidable challenge of contributing from the most human and where accounting, as a social science, projects as one of the greatest contributors of the universal scientific concert, following a research program focused on the accounting mathematization from a socioeconomic and common welfare standpoint.
Keywords: 'Contametria'; accounting mathematization; social accounting; accounting mathematical modeling; matrix analytic accounting; multiple entry; matrix algebra
Resumo
Este artigo visa estabelecer as relações entre teoria, práxis contábil e uso das matemáticas, tanto na fundamentação quanto na aplicação na solução de problemáticas da contabilidade como ciência e como exercício profissional. Trata-se de enfrentar a investigação das principais contribuições no seu percurso tanto de axiomatização quanto do desenvolvimento de aplicações mediante a utilização de ferramentas matemáticas e suas carências na integração em uma teoria geral, a ser estruturada, desde um enfoque sistémico e interdisciplinar e sob o paradigma da complexidade. Uma metodologia qualitativa baseada na análise de conteúdo de documentos foi utilizada e a triangulação de fontes teóricas de informação, para determinar uma amostragem teórica representativa de tais desenvolvimentos, mesmo foram selecionados dois esquemas de matematização contábil considerados essenciais nesse processo: o enfoque de modelagem matemática aplicada às dinâmicas patrimoniais e o desenvolvimento do modelo de contabilidade analítica matricial, que recorre à análise de casos ilustrativos pelo grande potencial de suporte metodológico na consolidação da estrutura científica da contabilidade e pelo alto impacto social na solução de problemas como a distribuição justa de riqueza e a consecução de bem-estar social, desde uma perspectiva de responsabilidade social, baseada em valores humanos, que devem orientar as decisões económicas, mas não o contrário, como já aconteceu na atual fase de financeirização da economia, com as consequências de uma ruptura social profunda, na que todas as ciências enfrentam um desafio incontornável para contribuir na solução desde o mais profundamente humano e em que a contabilidade como ciência social é projetada como uma das grandes contribuidoras no concerto científico universal, seguindo um programa de pesquisa centrado na matematização contábil desde o socioeconómico e desde o bem comum.
Palavras-chave: Contametria; matematização contábil; contabilidade social; modelagem matemática contábil; contabilidade analítica matricial; partida múltipla; álgebra matricial
Introducción
La matematización de los hechos contables (Cano-Morales, 2008) es un fenómeno que no ha logrado el desarrollo necesario para aportar al elevamiento del estatus científico de la contabilidad, pues como lo reconoce Henri Poincaré (2013): "toda ciencia tiene de ciencia lo que tiene de Matemática". Esta verdad es reconocida por la disciplina contable al punto de que dos de sus grandes teóricos Richard Mattessich (2002, 2004, 2005) y Yuji Ijiri (1967) se dedicaron a formalizar la ciencia contable bajo el enfoque axiomático y matemático, y también la han estudiado otros autores que han demostrado la correlación entre el origen de las matemáticas que se entronca íntimamente con el surgimiento de la contabilidad (Cano-Morales, 2008; Springer, Herlihy, Mall & Beggs, 1972). Sin embargo, esta línea de investigación no ha sido de las mejor adoptadas por los académicos de la investigación contable por razones que se tratarán de dilucidar en este artículo. Se entiende por Contametría (Avellaneda & Ortiz, 2012; Franco-Ruiz, 2014; Ortiz-Bojacá, 2012) el enfoque tecnológico de la disciplina, expresado en la matematización de la ciencia contable bajo un enfoque integral, es decir, recogiendo los aspectos económicos y sociales en el análisis de los fenómenos contables. Ello exige reconocer que se hace prioritario seguir trabajando en esa línea de investigación, si se pretende que la ciencia contable se siga consolidando.
Este artículo busca profundizar en los enfoques y soluciones frente a la problemática de la matematización y formalización de la ciencia contable y hace énfasis en la modelización matemática y específicamente en el modelo de la contabilidad analítica matricial, como caminos no explorados suficientemente y que pueden ofrecer valiosas herramientas desde el cálculo y la matemática matricial, que junto con otros enfoques matemáticos pueden contribuir a formalizar muchos de los problemas que aún no ha resuelto la contabilidad como ciencia y que están en el marco de su objeto de estudio: el análisis de la distribución de la riqueza (Franco-Ruiz, 2010) o la representación de los aspectos sociales de los hechos económicos, entre muchos otros que están sobre el tapete.
Para lograr ese objetivo, este artículo se propone desarrollar la investigación en torno a tan importante temática con los siguientes tópicos, que contribuyen a profundizar tanto en las problemáticas, como en las soluciones y sus impactos en el nivel social y económico:
- La formalización y axiomatización de la ciencia contable
- La modelación matemática y su utilización en la fundamentación científica de la contabilidad
- Los métodos matriciales en contabilidad
- La matematización de lo socioeconómico desde el objeto de estudio de la ciencia contable
A continuación, desarrollaremos cada uno de estos tópicos siguiendo una metodología cualitativa y fundamentada en el análisis de textos, para configurar categorías de análisis que permitan la mejor comprensión tanto de las problemáticas como de las soluciones planteadas:
1. La formalización y axiomatización de la ciencia contable
En este apartado, nos proponemos efectuar un sucinto recorrido por los principales aportes y esfuerzos desarrollados en la línea de formalización de la construcción teórica de la contabilidad, para deducir de allí el papel que han jugado las matemáticas en ese proceso, y la forma como se ha extendido el uso de las matemáticas en la comprensión del fenómeno de las dinámicas patrimoniales y sus potenciales avances en el desarrollo de la teoría contable.
Esta línea de los principales esfuerzos de formalización de la teoría contable debe incluir autores como Enrique Ballestero (1979), Leandro Cañibano-Calvo, Jorge Tua-Pereda y José Luis López (1985), Moisés García-García (1974), Yuji Ijiri (1967), Ananias Charles Littleton (1937), Richard Mattessich (2002), Maurice Moonitz (1961), William Andrew Paton y Ananias Charles Littleton (1940), José María Requena-Rodríguez (1977), John K. Shank (1972), Robert T. Sprouse (1976), Stephen A. Zeff (2010). El uso de las matemáticas y los constructos para la formalización de la teoría han ido de la mano en el proceso de construcción teórica de la contabilidad como ciencia.
A continuación, se presenta una síntesis de los avances de la ciencia contable en esa dirección:
Richard Mattessich sentó las bases de una axiomatización de la ciencia contable para plantear de esa manera la necesidad de desarrollar una teoría general de la contabilidad, en su artículo Towards a General and Axiomatic Foundation of Accountancy: with An Introduction to the Matrix Formulation of Accounting Systems (1957) y en su libro Accounting and Analytical Methods. Measurement and Projection of Income and Wealth in the Micro- and Macro- Economy (1964). Fue uno de los primeros en determinar la necesidad de formalizar el conjunto de los flujos de la economía y establecer una teoría que cubriera los fenómenos microeconómicos y los macroeconómicos, pero solo lo logró parcialmente pues su contribución está más orientada hacia la contabilidad de los entes que hacia la macrocontabilidad (Pinilla-Monclus, 1976), que se asimilaba con la contabilidad social, lo cual —de alguna manera— falla al identificar lo uno con lo otro, pues aunque la información económica agregada rebase el análisis de las entidades económicas individuales, no avanza en incluir aspectos relacionados con la responsabilidad social y los fenómenos de la integración social humana, que tienen varias facetas distintas a la económica (Ortiz-Bojacá, 2009, 2010).
Otros autores como el profesor Enrique Ballestero en sus dos libros, uno aparecido en 1975 y el otro en 1979, desarrolló elementos fundantes de la teorización contable como la teoría de las cuentas, la contabilidad multidimensional, la teoría de grafos, entre otros muchos aportes a la estructuración de una teoría contable, incluyendo los aportes de la contabilidad matricial, al igual que Richard Mattessich y otros autores que delinearon esta temática como fundamental en la matematización de la contabilidad, como analizaremos más adelante. En esa misma línea, el profesor John K. Shank (1972), con su texto Matrix Methods in Accounting, elaboró los fundamentos del álgebra de matrices aplicada a la contabilidad.
El libro Costs: Accounting, Analysis, and Control, de A. Wayne Corcoran (1978), es otro aporte interesante por la profusa utilización de diferentes herramientas matemáticas, pues aplica la teoría de las cadenas de [Andrei] Markov para evaluar elementos de contabilidad por áreas de responsabilidad y la presupuestación; el prorrateo de costos indirectos usando el cálculo matricial y el desarrollo de costos estándar con el cálculo infinitesimal, otras aplicaciones con el análisis combinatorio, el muestreo estadístico, las líneas de espera, la programación lineal, el análisis insumo-producto y la programación dinámica (Arenas-Herrera, 2015, p. 3).
Del anterior sucinto muestreo teórico, se puede observar que las matemáticas han jugado un rol muy importante, tanto en la formalización de las relaciones entre las variables intervinientes en las hipótesis científicas en el campo social y en la aplicación del método lógico deductivo, partiendo de unos postulados fundamentales que se pueden expresar en términos matemáticos, y de allí deducir las hipótesis, las cuales no alcanzan la generabilidad, que sí han logrado las ciencias físicas para poder hablar de leyes, proceso que se conoce como la axiomatización y en el que Richard Mattessich ha hecho los mejores aportes para la ciencia contable; pero también se han dado pasos importantes en el proceso de aplicación de las matemáticas al desarrollo de la solución de problemas concretos, el camino que han seguido las disciplinas sociales en su proceso de formalización. A continuación, reseñaremos otros casos en que se comprueba cómo se ha venido ganando terreno en la aplicación de herramientas matemáticas a la Contabilidad, para profundizar finalmente en dos temas que consideramos de gran relevancia en esos procesos de formalización de la contabilidad como ciencia: el uso de modelos matemáticos en la contabilidad y el desarrollo de la contabilidad analítica matricial.
Empezamos por el concepto de flujos monetarios que abre el camino para investigar de dónde proviene la riqueza que, según Richard Mattessich, es el resultado de los ingresos que él define como el "flujo de bienes y servicios durante un período determinado entre el extremo de la producción y el extremo del consumo de un ente" (Mattessich, 2002, p. 19), que genera como contrapartida un equivalente en flujo monetario, lo cual puede ser representado matemáticamente con herramientas como funciones o ecuaciones, que admiten todo el tratamiento matemático y del cálculo que ha sido objeto de estudio en el campo de los números reales, por parte de la ciencia formal matemática. De igual manera, se puede determinar hacia dónde se distribuye ese ingreso, con lo cual queda representado todo el movimiento patrimonial, que de esa manera comprendido y formalizado se puede utilizar en la toma de decisiones para optimizar la generación de ingresos y su distribución, bajo parámetros sociales.
En ese proceso de apoyar la toma de decisiones, se han desarrollado muchos algoritmos matemáticos (algunos reconocidos como investigación de operaciones, programación lineal, matemática financiera, cálculo diferencial, etc.), que se han considerado como independientes de la contabilidad, pero que en nuestro concepto hacen parte del herramental requerido en el análisis de su objeto de estudio, considerado bajo un enfoque interdisciplinario y transdisciplinario, pues todos ellos son elementos determinantes en la optimización de la gestión del patrimonio, en su acepción más amplia.
Desde la perspectiva de la teorización contable, aún no se ha integrado el proceso de formalización de la generación y registro de la información contable sobre el patrimonio (contabilidad tradicional), con los procesos de análisis y estudios sobre esa información para la administración patrimonial, que utiliza gran cantidad de la información financiera de los estados contables y otra información que también se debe revelar en informes más integrales, para dar lugar a estados contables integrales (Franco-Ruiz, 2003), que están por diseñarse y formalizarse. Como lo trataremos más adelante, el modelo matemático que permitiría en forma explícita esa integración, incorporada desde la misma metodología de captación de la información y su análisis, es lo que se ha denominado contabilidad analítica matricial, que se soporta en el método de la partida múltiple. A partir de su implementación, se hace factible integrar las notas a los estados financieros en forma orgánica y sistémica generadas por subsistemas de informes desarrollados y soportados en algoritmos matemáticos diseñados para apoyar decisiones sobre las cuentas implicadas y que afectarán el desempeño de todo el sistema (la empresa), lo que hace más transparentes los informes, pero además más dinámicos y explicativos del fenómeno patrimonial, lo que permite un equilibrio de la información ofrecida para todos sus usuarios o stakeholders (Carbonell, 2011; Escudero & García-Lama, 2014; Guibert-Ucín, 2009; Sriramesh & Ver cic, 2012).
En este punto, debemos reseñar algunas de esas herramientas matemáticas, utilizadas para apoyar la gestión patrimonial. Uno de los elementos básicos en los procesos de toma de decisiones patrimoniales es lo que en términos generales se conoce como matemática financiera (Navarro & Nave, 2001; Vidaurri-Aguirre, 2012), que ha desarrollado variados esquemas para actualizar flujos futuros, utilizando tasas de descuento que tienen su origen en la famosa tasa de interés. Lo interesante es que esos flujos son diseñados siguiendo la metodología contable, para configurar los estados financieros proyectados y el tratamiento que se hace sobre ellos se fundamenta en los conceptos de flujos financieros que reflejan las dinámicas patrimoniales.
Los modelos de producción (Cánovas, Huertas-Navarro & Sempere-Orts, 2011; Cuatrecasas-Arbós, 2012) tienen la misma característica de utilizar información financiera y no financiera, para optimizar el proceso productivo, que es uno de los ejes de las dinámicas patrimoniales y que finalmente se reflejará en los estados financieros de la compañía. El problema que vuelve a salir a flote es que los dos modelos (producción y financiero contable) no se integran debidamente, bajo la convicción de que la información que produce el modelo de producción, solo les interesa a los dueños del capital o a sus delegados que son los administradores y que en una economía de competencia feroz, no se debe divulgar pues puede perjudicar la organización. Sin embargo, la teoría de juegos aplicada por todos los participantes podría conducir a un sistema global, mucho más racional, en términos del conjunto de la sociedad, lo cual lograría la eficiencia, eficacia y productividad de las unidades productivas, lo cual beneficia a consumidores, empleados, clientes, proveedores y a la sociedad en general. Desde luego, el problema es que no se ha reconocido que la información debe ser abierta, bajo el paradigma del bien común (Felber, 2012) pues el modelo de información financiera está diseñado para una sola parte de los interesados. Sería muy conveniente que nuestros profesionales de la contaduría aprendieran a manejar y operacionalizar el concepto de rendimientos de funciones homogéneas de producción y discriminar entre rendimientos constantes, decrecientes a escala o crecientes a escala, para comprender y aportar mucho más al manejo integral del patrimonio en una organización empresarial, para colaborar con el gerente de producción desde una perspectiva integral, lo cual exige una visión científica de la contabilidad como la ciencia del patrimonio, sobre todo desde la perspectiva de la explicación de la "productividad global de los factores" (Cequea-Null, Rodríguez-Monroy & Núñez-Bottini, 2011; Coloma, 1991; Lanteri, 1998).
Si quisiéramos extender el anterior análisis a diferentes áreas de la dinámica patrimonial, deberíamos conectarnos con los problemas de optimización (Cánovas, Huertas-Navarro & Sempere-Orts, 2011) que implican maximizar o minimizar rentabilidades o costos medidos en unidades monetarias o en otro tipo de unidades, lo cual implicaría temáticas como el manejo de los inventarios, el uso de recursos físicos o la programación de la combinación de diferentes materias primas, o diferentes tipos de transporte, o la combinación de diferentes fuentes de financiación, entre otras, todas las cuales se podrían representar por medio de una función objetivo, sujetas a varias restricciones, que en conjunto estructuran un sistema de ecuaciones lineales, así se genera una solución posible desde la programación lineal, todo lo cual es parte del análisis y explicación de las dinámicas patrimoniales. El problema que se plantea es: ¿por qué la ciencia que está llamada a producir conocimiento sobre el fenómeno de las dinámicas patrimoniales, no integra todas esas soluciones en una teoría general contable?
Esta respuesta está por desarrollarse en el amplio objeto de la contabilidad como ciencia social e implicará superar el obstáculo epistemológico de incorporar una visión de compromiso con los diferentes interesados en la información financiera, que hoy se conocen como los stakeholders, lo cual hace parte de la responsabilidad social. También exige un cambio sustancial de la mentalidad del profesional de la contaduría y de los académicos dedicados a la investigación, para dar un paso trascendental en la formalización y matematización de sus conocimientos. En ese proceso, queremos puntualizar y profundizar por dos caminos viables y de alto impacto en el desarrollo de constructos teóricos y de desarrollo de aplicaciones apoyadas en el uso de herramientas matemáticas en el campo contable: la modelación matemática y su utilización en la fundamentación científica de la contabilidad y los métodos matriciales en contabilidad.
A continuación, desarrollaremos cada uno de esos dos caminos, en busca de concientizar sobre la necesidad de profundizar en el uso de las matemáticas en el campo contable:
2. La modelación matemática y su utilización en la fundamentación científica de la contabilidad
Debemos empezar por reconocer que con el liderazgo de Richard Mattessich (2002), la ciencia contable ha seguido el camino de desarrollar su propia formalización, lo cual ha sido acompañado por otros investigadores como Enrique Ballestero (1979), Salvador Cruz-Rambaud, José García-Pérez, Robert A. Nehmer y Derek J. S. Robinson (2010), Richard Michael Cyert y H. Justin Davidson (1962), Yuji Ijiri (1967), Wayne E. Leininger (1980), Alan John Richardson (1996), John K. Shank (1972), Malcolm Smith (2014), Bernard C. Williams y Barry J. Spaul (1992), entre otros. Ellos han hecho un esfuerzo importante en formalizar o axiomatizar la teoría contable, lo cual no es otra cosa que establecer la metodología que permite estructurar la teoría e iniciar por los postulados fundamentales, hasta derivar las explicaciones fundamentales sobre el comportamiento de las dinámicas patrimoniales (Lopes de Sá, 2008, 2009, 2010). Extender la aplicación de las herramientas matemáticas a la interpretación de los fenómenos inherentes a las dinámicas patrimoniales es la tarea que ha continuado esa línea, pero es necesario reconocer que estudiosos de otras disciplinas han venido haciéndola, sin que siquiera sea asimilada dentro del ejercicio profesional de la contaduría, ni que se le dé la importancia suficiente en la formación de los profesionales contables, por lo menos en Colombia (Quijano-Valencia, 2002; Valencia-Valencia, 2011; Valero-Zapata, Patiño-Jacinto & Duque-Cruz, 2013).
Por ello, nos proponemos explorar el camino que ha trazado esta práctica en el desarrollo de la disciplina contable. En este aspecto se puede puntualizar que el uso de las matemáticas en contabilidad ha seguido dos caminos importantes: el uso de modelos matemático contables y la utilización del álgebra matricial.
A continuación, nos adentraremos en cada uno de ellos:
El uso de modelos matemáticos contablesUn modelo matemático contable es la representación en lenguaje matemático de un fenómeno cuyo eje son las dinámicas patrimoniales, con el fin de solucionar problemas teóricos o prácticos, inherentes a la contabilidad, para comprender y explicar el fenómeno implicado (Arenas-Herrera, 2015). Es decir, así como en las ciencias físicas se establecen leyes, que regularmente toman la forma de una fórmula, una ecuación o una función algebraica, que tiene la característica de ser aplicable en forma universal y general, en las ciencias sociales el nivel de generalización es más limitado por lo que los parámetros que asume la función matemática son válidos en un espacio y un tiempo específicos, para lo cual se utilizan los modelos en vez de formalizar leyes universales. Esto es por la misma característica del ser humano que está socialmente sujeto a la incertidumbre y la subjetividad (Castiblanco-Ruiz, 2014).
En ese sentido, un modelo es la representación de un sistema (Menárguez-Tortosa, 2013), sobre el cual se pueden aplicar técnicas analíticas estadísticas y/o matemáticas, entre las cuales se incluye la definición de funciones que correlacionan variables, o esquemas que conectan las variables de entrada con las de salida, para determinar los valores que explican y pronostican el comportamiento futuro y así controlar el desempeño del sistema, que representa el fenómeno objeto de estudio. Para el caso concreto de la ciencia contable, este objeto está conformado por las dinámicas patrimoniales, que tienen que ser explicadas y no solamente representadas o descritas, para controlar todo el sistema y adecuarlo a los objetivos socialmente establecidos.
Para comprender la importancia del uso de los modelos matemáticos en el desarrollo de la ciencia contable y en el ejercicio de la profesión, es necesario hacer conciencia de que ellos son herramientas que permiten procesar, diseñar, integrar, analizar, sintetizar, interpretar y proyectar información para apoyar la comprensión de la multicausalidad de los fenómenos y la toma de decisiones confiables, no solo económicas sino fundamentalmente sociales (Rueda-Delgado, 2011), lo que posibilita efectuar juicios críticos conducentes al logro de los objetivos propuestos por la dirección de la empresa en interacción con todos sus participantes y con diferentes tipos de organizaciones. Se han desarrollado modelos que se han caracterizado como pertenecientes a otras disciplinas como la financiera o la investigación de operaciones, lo cual es un tema de discusión que puede ser superado bajo el paradigma de la complejidad de la ciencia, con su enfoque de la interdisciplinariedad y la transdisciplinariedad (Ortiz-Bojacá, 2009), por lo que entraremos a analizar sus interrelaciones desde lo contable.
El modelamiento matemático contableLos modelos que representan sistemas de eventos discretos, se orientan a determinar las relaciones entre las variables de entrada y las variables de salida para —de esa manera— poder aplicar esa especificación para resolver situaciones problemáticas que involucren las variables modeladas bajo el sistema que se está estudiando. La característica importante de los eventos discretos es que se generan en momentos específicos y no de forma continua en el tiempo.
Para ejemplificar este tipo de modelos se ha seleccionado el modelo de Análisis Envolvente de Datos (Data Envelopment Analysis, DEA) (Rescala, Devincenzi, Rohde, Bonaffini, Giraudo, Bernaola & Pavón, 2012), pues toma como base la información de los estados contables, lo cual no es casual. Para determinar e interpretar la eficiencia en la gestión de administración en una empresa, es necesario recurrir a las matemáticas del modelamiento, lo cual encaja en forma natural con la matematización contable, que debe extender su esquema descriptivo expresado en los estados reflejados en el Balance, al análisis de las relaciones que se dan entre los componentes del fenómeno patrimonial, que tiene como finalidad lograr la eficacia social (Suárez-Pineda, 2014). Hacia allá debe seguir avanzando la ciencia contable, lo cual le exige desarrollar modelos explicativos de las dinámicas patrimoniales.
Así, para explicar las dinámicas patrimoniales, se requiere comprender muy bien e interpretar las finalidades de la organización y las mejores formas de lograrlas, lo cual implica diseñar modelos matemáticos que permitan representar las relaciones entre fines y medios, lo cual supera la técnica tradicional del análisis financiero (Ortiz-Anaya, 2011), que también toma como base los estados contables y busca su interpretación por medio de los indicadores financieros, desde la perspectiva de los objetivos financieros de liquidez, rentabilidad, estabilidad y actividad, pero que no se integran estructuralmente, sino que se dejan a la intuición y experiencia del analista contable. Aquí empiezan los dolores de cabeza para introducir a los contadores en formación que no encuentran asidero para "comprender" e interpretar los estados financieros, sobre bases que no han venido desarrollando en sus procesos educativos, por el afán de aprender (y de los maestros de enseñar) la técnica del registro y generación de los estados financieros, pero sin ir más allá. Esto se les delega a otras profesiones o a los que tienen el privilegio de ascender en la cúpula organizacional.
En esa línea, sin salirse de lo básicamente financiero, el modelo DEA es una aproximación a un modelo discreto, que sin profundizar en las relaciones entre las variables de entrada y salida (o en la terminología matemática variables dependientes e independientes) mide la eficiencia mediante la obtención de una frontera de eficiencia a partir de un conjunto de observaciones tomadas de los estados contables (Rescala, Devincenzi, Rohde, Bonaffini, Giraudo, Bernaola & Pavón, 2012). Se considera que una unidad productiva es eficiente, cuando produce más de algún producto sin demeritar la producción de otros y sin recurrir a más materia prima, mano de obra o bien; también cuando puede disminuir alguna cantidad de materia prima, de mano de obra o de bienes, sin afectar la otra y al mismo tiempo, generar la misma cantidad de productos terminados. Si una unidad productiva logra ser eficiente según las anteriores consideraciones, se puede afirmar que pertenece a la frontera de producción de eficiencia.
Sin embargo, el modelo no explica cómo evaluar las unidades empresariales que no formen parte de la frontera eficiente. Se debe proceder a confrontar una unidad no eficiente con otra que sí lo sea y que tenga un modelo productivo similar. En este sentido, se puede considerar este método matemático como no paramétrico (por no desarrollar una función que relacione variables de entrada y salida) ni tampoco como estadístico pues no se fundamenta en una distribución de probabilidad. De cualquier manera, los resultados arrojados por estos modelos matemáticos sirven para mejorar la toma de decisiones, optimizar el uso de los factores determinantes de la eficacia organizacional, lo que logra elevar la productividad y la eficiencia, mejorar la determinación de precios, optimizar el manejo de inventarios y de cartera, asignar en forma racional los recursos de inversión, etc. Con ello, estamos reconociendo que las mediciones contables no se pueden limitar a retratar los componentes del balance o del estado de resultados, por medio de las diferentes cuentas que los conforman sino que implica generar operaciones "contamétricas" (Avellaneda-Bautista & Ortiz-Bojacá, 2012), para evaluar lo que representan las cifras de esas diferentes cuentas frente a las finalidades de la organización, no solo desde la perspectiva de los propietarios sino de todos los interesados o stakeholders, bajo el enfoque de la responsabilidad social (D'Onofrio, 2006; Jiménez-Aguirre, 2012; Rueda-Delgado, 2011), lo cual implica desarrollar nuevas dimensiones y escalas de medición, como lo trataremos más adelante.
Otros tipos de modelos reflejan situaciones dinámicas y cuya característica es mostrar el desarrollo de diferentes y sucesivos estados en el tiempo que, por tal motivo, reciben el nombre de sistemas dinámicos (Lacomba, 2000). También se pueden tipificar como sistemas continuos cuando el comportamiento analizado es permanente y continuado en el tiempo que, a diferencia de los sistemas discretos, solo se reflejan periódicamente y en momentos específicos. Para el primer caso se utilizan las ecuaciones diferenciales (Fernández-Pérez, Vázquez-Hernández & Vegas-Montaner, 2003); y para algunos fenómenos que se comportan como sistemas dinámicos, pero que tienen la característica de ser discretos, se pueden utilizar las ecuaciones en diferencia, que permiten determinar cómo cambian estas dinámicas, al variar algunos parámetros, como en el caso del crecimiento poblacional. Para la contabilidad, una posible aplicación es estudiar cómo cambian las dinámicas patrimoniales, frente al cambio de parámetros alrededor del comportamiento del PIB, el incremento de la productividad o la eficiencia en el uso de los factores, etc.
Los anteriores modelos matemáticos se consideran deterministas si a cada valor de la variable independiente le corresponde un único valor de la variable dependiente, considerando que no hay más posibilidades de ocurrencia. Al contrario, se consideran modelos probabilísticos, cuando se contemplan múltiples posibilidades de ocurrencia, cada una con diferentes probabilidades, por lo que el análisis cambia. También podemos hablar de modelos discretos matriciales (Blanco, 2013), cuando la situación que se va a estudiar se puede construir como un sistema dividido en clases, o estados, que se pueden representar por vectores o matrices que muestran diferentes etapas del fenómeno. El análisis permite establecer el paso de una etapa a otra hasta llegar a una situación final esperada, a partir de una situación inicial y conociendo las posibilidades de ocurrencia en cada etapa. Por eso se conocen como matrices de transición. Una de las aplicaciones en el campo contable son las cadenas de Markov (Sinclair, 2012), para determinar las tendencias de la cartera al final de un período bajo análisis. Estudiaremos este tipo de modelos en la siguiente sección. Pero antes se estudiará la forma de construir un modelo, mirando su aplicación en el campo contable.
Elaboración de modelos matemáticosEn este punto es interesante introducir algunos elementos que nos permiten orientar el enfoque metodológico que se debe seguir en el proceso de construir un modelo matemático:
Los modelos y la realidad están relacionados a través de dos procesos: la abstracción y la interpretación. El primero de ellos nos obliga a encontrar cuáles son los elementos más importantes del problema y cuáles son los accesorios. Para saber si un elemento es o no importante, tendremos que ver su efecto relativo en la evolución del sistema. En cuanto a la interpretación, debemos de entenderla como la manera en que las componentes del modelo (parámetros, variables) y su comportamiento pueden estar relacionadas con las componentes, características y comportamiento del sistema real que queremos modelar (Navas-Ureña, Esteban & Quesada-Teruel, 2009, p. 2).
Con base en tales fundamentos, nos proponemos seguir el esquema establecido por profesores del Departamento de Matemáticas de la Universidad de Jaén, en el proceso de elaboración de un modelo matemático, tratando de aplicarlo conceptualmente, en lo que podría ser un modelo del crecimiento patrimonial de alguna organización productiva. Los pasos en esta construcción serían los siguientes:
- Descripción del fenómeno real y objetivos del modelo: este primer aspecto formula las preguntas pertinentes para comprender el fenómeno objeto de estudio. En el caso de la dinámica patrimonial de una empresa en particular, las preguntas clave podrían ser: ¿Cuáles son los factores que afectan el crecimiento patrimonial? ¿Cuál ha sido el crecimiento en los últimos años? ¿Cómo se puede tipificar ese crecimiento?
- Elección de variables: este paso es crucial para determinar cuáles son las variables que más impactan en el crecimiento del patrimonio. Podríamos identificar variables internas y variables externas. Tomamos de la teoría de la firma y de la teoría financiera (García-Serna, 2011), podemos proponer dos variables internas: la tasa de rentabilidad sobre ventas y el nivel de endeudamiento y de la teoría de Michael E. Porter (2013), podríamos tomar como variable externa el crecimiento del sector. Aclaramos que el ejemplo es más con carácter didáctico que real, pero se asemeja a lo que se podría diseñar en la práctica contable.
- Relaciones cualitativas entre las variables: una vez definidas las variables para incluir en el modelo, el paso siguiente es establecer la forma como se relacionan las variables con el resultado final, que en este caso es el crecimiento del patrimonio.
- Recopilación de datos: se toman los datos de las tres variables implicadas, para un período definido, que representan el fenómeno bajo estudio, en un período determinado.
- Sobre los datos recopilados, se deduce una función que muestre las relaciones teóricas y generales sobre los cuales se deben aplicar herramientas matemáticas y estadísticas, utilizando la función que se diseñó para mostrar el tipo de relaciones supuestas.
- La comprobación de que el modelo se ajusta efectivamente a la realidad, no es automática, sino que es un proceso recurrente, pues después de cada ajuste, se va aproximando al mejor modelo, sobre el cual se pueden efectuar proyecciones o conclusiones prácticas, para ejercer un control sobre todo el sistema representado.
Finalmente, mostraremos a manera de ejemplo un posible modelo que represente la dinámica del patrimonio, sin pretensiones de reflejar un modelo real, sino a manera pedagógica, para reafirmar la importancia de esta herramienta en la estructuración de esquemas explicativos e interpretativos de las realidades patrimoniales. A continuación, se muestra el hipotético modelo: Incremento del patrimonio de un período a otro = IP
Rentabilidad de las ventas de año anterior = RV(a)
Crecimiento del sector = IS
Nivel de endeudamiento del período anterior = E (a)
α = Parámetro que ajusta el impacto de la variable RV (a)
β = Parámetro que ajusta el impacto de la variable E (a)
σ = Parámetro que ajusta el impacto de la variable IS
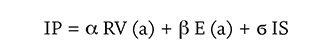
Con este sencillo modelo se pueden hacer inferencias sobre el comportamiento futuro del crecimiento del patrimonio, conociendo las condiciones del desenvolvimiento de las tres variables incluidas en el modelo. Ello permite tomar decisiones con vistas al futuro, sobre las dinámicas patrimoniales, en busca del bienestar de los diferentes interesados en la organización empresarial. Este es un paso fundamental para que la contabilidad dé un salto vital en su función científica de comprender, interpretar y explicar los fenómenos contables, siendo la construcción de modelos matemáticos una herramienta poderosa al servicio del enfoque científico de la contabilidad.
Ahora, desarrollaremos otro caso que refuerza el anterior análisis, sin que se pretenda agotar tan importante temática, sobre la que hay que trabajar en forma sistemática desde la investigación contable. A continuación, se presenta este segundo caso, referente a los métodos analíticos matriciales de la contabilidad:
3. Los métodos matriciales en contabilidad
Desde el invento de la partida doble por Luca Pacioli, se ha reconocido el gran aporte de la contabilidad a la consolidación del capitalismo, que el profesor Carlos Mallo-Rodríguez expresa así: "La contabilidad ha tenido un papel protagonista para medir la diversa evolución del patrimonio afecto a una propiedad, así como el resultado periódico obtenido, por lo que, como veremos más adelante, algunos destacables autores han adscrito un papel esencial a la contabilidad en el desarrollo del capitalismo" (Mallo-Rodríguez, 1995, p. 14).
Sin embargo, es importante señalar que la función científica de la contabilidad debe asumir componentes fundamentales como la comprensión, interpretación y explicación de los fenómenos objeto de estudio, para lo cual se debe apoyar en métodos analíticos y de síntesis, que le permitan lograr tan importantes funciones. Así, el "análisis contable" debe sobrepasar la exposición descriptiva de los fenómenos contables, reflejada en los estados financieros como se conciben en la contabilidad tradicional, para encontrar las causas y explicaciones o interpretaciones de los fenómenos atinentes a las dinámicas patrimoniales, que tienen implicaciones tanto para los intereses de los stakeholders internos de la organización —propietarios y empleados—, como también para los de los stakeholders externos —proveedores, clientes, comunidad y Estado—.
En ese sentido, se debe reconocer cómo la contabilidad puede desarrollar esas funciones científicas y de qué herramientas se debe valer para incorporarlas en la teoría como componentes esenciales de su estructura. Ello ha inquietado a los estudiosos de los temas contables, quienes han buscado la forma de incorporar tales componentes que en su conjunto se han rotulado como "análisis contable", como lo hemos demostrado en apartados anteriores. En ese sentido, Vicente Montesinos-Julve (1976, 1978, 1990) expresa que el análisis contable "recoge la información proporcionada por el modelo contable convencional, la manipula y combina de acuerdo con un modelo formal—que podemos denominar metamodelo, en tanto en cuanto no toma como referente la realidad sino su subrogado contable mostrado en los estados financieros— y procura efectuar a partir de los outputs obtenidos predicciones útiles para la adopción de las decisiones económicas de los usuarios de los estados financieros" (Montesinos-Julve, 1990, p. 3).
Con ello, se está reconociendo que los fines de la contabilidad como ciencia se deben incorporar en su estructura teórica, incorporando herramientas para la toma de decisiones, que para el caso de la apreciación de Montesinos hasta ahora solo se enfocan en los intereses de los propietarios, lo cual también se debe volver válido para la toma de decisiones de los demás stakeholders: empleados, proveedores, clientes, comunidad en general, el Estado, etc. Se podría deducir que esa incorporación se ha venido formalizando bajo la concepción de nuevas ramas de la contabilidad: contabilidad administrativa o gerencial, contabilidad social, contabilidad ambiental, contabilidad del conocimiento, etc. En términos generales, este nuevo enfoque se podría denominar "Contabilidad analítica", que encaja en el concepto de "análisis contable", como lo plantea Montesinos en el párrafo anteriormente transcrito. En concepto de Samuel Leonidas Pérez-Grau "La Contabilidad Analítica es aquella en la que utilizamos fórmulas o expresiones matemáticas para encontrar los resultados buscados. Según el estudioso austro americano Richard Mattesich [sic] (1964), el padre fundador de la contabilidad analítica lo es Gabriel Preinreich (1933) por sus trabajos basados en interés compuesto, anualidades y cálculos de valor presente para el cálculo de la depreciación, amortización e inversión" (Pérez-Grau, 2015, p. 1).
Se torna muy interesante comprender que ese desarrollo se ha venido soportando y apoyando con el paso del concepto de partida doble al concepto de partida múltiple, según palabras de Carlos Mallo-Rodríguez: "La metodología contable que inicia su desarrollo en el principio de dualidad incluido en la partida doble, consistente según Mattessich en una propiedad bidimensional que permite una doble clasificación dentro de un conjunto de clases, ha evolucionado, en base a los desarrollo [sic] matemáticos e informáticos modernos, hacia la partida múltiple, que establece relaciones multidimensionales entre los objetos y sucesos económicos, dando lugar a la creación de las modernas bases de datos multirrelacionales" (Mallo-Rodríguez, 1995, p. 18).
Este proceso se ha visto reforzado por el auge que ha adquirido el álgebra lineal o de matrices, que permite generalizaciones y análisis en la mayoría de los campos del conocimiento. La representación por matrices permitió el diseño de la matriz insumo-producto (entradas-salidas), que desarrolló Wassily W. Leontief (1986), una de las primeras aplicaciones de la contabilidad matricial. Pero mediante la for-malización de la contabilidad, Mattessich logró implementar las hojas de cálculo sistematizadas, que han alcanzado un desarrollo impresionante en la aplicación de soluciones financieras. El problema es que la contabilidad como disciplina científica no ha aprovechado todo el potencial matemático que ofrece el álgebra lineal ni tampoco el potencial para la captación y representación de la información, que le aportaría muchos elementos para soportar su utilización mediante el método matricial que considera las filas como las cuentas a debitar y las columnas como cuentas a acreditar, lo que de entrada es una facilidad para simplificar el doble registro en uno solo, asumiendo que el valor que intersecta una fila y una columna es el correspondiente a un asiento (Ruiz-Palomo, 2014). Ello permite además analizar, proyectar, simular y programar el comportamiento contable de las empresas (Hillier & Hillier, 2010), mediante el uso del álgebra en la ciencia contable.
Al introducirse el manejo matemático sobre los esquemas de representación contable tradicional, nos estamos adentrando en el concepto de "contabilidad analítica", como lo ejemplificaremos siguiendo al profesor Esteban Churruca-Arrizabalaga (1981), quien expone un caso concreto de aplicación de la contabilidad analítica matricial para un sistema de fabricación intermitente, lo cual permite tener una aproximación práctica de estos conceptos, que como lo decíamos anteriormente, no se han sabido aprovechar suficientemente en el ejercicio de la profesión contable ni en el desarrollo de las bases científicas de la contabilidad. Su propuesta inicia analizando la naturaleza de los medios de producción, de los productos a fabricar y de los procesos básicos de fabricación utilizados, y el conocimiento de la organización y sus objetivos. De igual manera, el proceso continúa estableciendo los puntos de referencia o estándares, que permiten evaluar la información de los costos recogidos, cumpliendo uno de los requisitos fundamentales del análisis matemático comparativo sobre funciones objetivo, que de esa manera incorporan un marco propio de las ciencias sociales al introducir los fines perseguidos por el sistema objeto de análisis. También se debe definir el tipo de información analítica de salida que para este caso pueden ser: informes sobre los costes de las áreas económicas (divisiones) y de los productos; informes sobre producción y productividad; informes acerca de la eficacia de la sección comercial e informes analíticos de resultados, entre otros.
Todo lo anterior debe estar concebido para lograr objetivos claramente establecidos sobre la rentabilidad de los productos, para así decidir sobre su continuidad en el mercado, establecer las principales desviaciones con respecto a los estándares y rediseñar la política de comercialización y ventas, etc. El primer paso a este respecto es construir una matriz "Plan de Cuentas", como se ilustra a continuación.
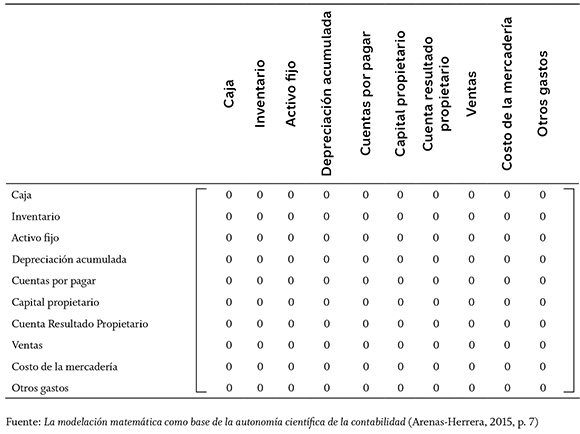
Sobre este tipo de matriz mayor se asientan todas las transacciones de un período bajo análisis, que luego se sumarizan en forma de un balance de comprobación, que genera un efecto neto débito si la diferencia entre los valores de una columna i y una fila i (que representan todos los débitos y todos los créditos a la cuenta i) es positiva, o crédito si es negativa. Esto lo estructura en términos del álgebra matricial el profesor Esteban Churruca-Arrizabalaga (1982, p. 528), de la siguiente manera:
- Saldo de una cuenta Sci. Se obtiene operando como sigue:

Donde
C; = el vector correspondiente a la fila i de la matriz final
Cf = el vector formado por la columna i de la matriz final
f = un vector fila unidad
De la misma manera, mediante un conjunto de fórmulas algebraicas se pueden calcular las diferencias de costos por medio del cálculo matricial, como lo muestra el profesor Esteban Churruca-Arrizabalaga tomando como ejemplo la variable cantidades y calculando sus desviaciones mediante una matriz de desviaciones, de la siguiente manera:

Este mismo procedimiento se aplica a los precios, lo cual se puede hacer extensivo a todos los centros de costos, generando un análisis que tiene efectos múltiples en el discernimiento de las causas de las variaciones, o también en otros requerimientos analíticos como en la distribución de los costos indirectos. Si quisiéramos extender su utilización y aprovechar su potencial analítico, este cálculo matricial enriquecería la integración entre diferentes subsistemas del sistema contable empresarial, por ejemplo, estableciendo relaciones combinatorias de análisis sobre la información del subsistema de producción (como el anteriormente planteado) y el subsistema comercial o el subsistema de investigación y desarrollo, para ligar variables como rentabilidades operativas y comerciales por tipo de productos, y la utilización de otro tipo de variables que permitan el cálculo de indicadores sobre la productividad global de los factores, o el cálculo del valor agregado por procesos orientados al cliente y otros profundos análisis que se verían ampliamente favorecidos por el potencial del cálculo matricial. En síntesis, el método de la contabilidad analítica matricial abre un camino muy amplio y a la vez profundo para desarrollar los esquemas propugnados por Richard Mattessich y el profesor Moisés García-García (1974), para comprender y explicar el flujo de la riqueza o las dinámicas patrimoniales, como lo señala el profesor Lópes de Sá (2010) sobre las dinámicas patrimoniales, y como muy significativamente lo señala el profesor Esteban Churruca-Arrizabalaga: "hay que señalar que el empleo del aparato matricial proporciona a estos modelos una gran coherencia a la hora de efectuar el reparto de los flujos económicos contables" (1982, p. 536).
Pero lo más interesante es que ese potencial analítico permite el manejo de variables expresadas en diferentes escalas de medición, lo que ensancha la capacidad explicativa de la contabilidad como ciencia; el paso del método de captación y registro de la partida doble hacia el método de la partida múltiple facilita el tratamiento de variables diferentes a las económicas (que se miden en términos monetarios), para integrar los factores sociales al estudio de las dinámicas patrimoniales, que hasta ahora se han visto excluidos, o se han diseccionado de manera artificiosa lo que menoscaba la visión integral de la ciencia contable, como analizaremos a continuación.
4. La matematización de lo socioeconómico desde el objeto de estudio de la ciencia contable
Para analizar el impacto de la matematización contable en el campo socioeconómico, es necesario cuestionarse si realmente en la estructura científica de la contabilidad se contempla en forma orgánica lo social y de qué manera se integra con lo económico y lo financiero. Aquí donde se debe reconocer que la corriente de pensamiento contable tradicional, el dominante, le ha dado prioridad a lo financiero y ha excluido lo social, por razones de poder y de conveniencia política. Esta corriente se ampara en la teoría económica de los neoclásicos que le atribuye al mercado la capacidad de optimizar el bienestar social, vía mecanismo de los precios, al asignar de manera correcta los recursos, que así alcanzan el pleno empleo y esto es lo que asegura el mayor bienestar social.
En ese marco conceptual, aparece como irrelevante el concepto de responsabilidad social, pues como lo señaló Adam Smith, el comportamiento egoísta, en forma natural y bajo la sabia mano invisible del mercado, permite que los valores sociales de la solidaridad, la cooperación y la búsqueda del bien común no se exijan en el esfuerzo consciente del ser humano por lograr una sana convivencia con sus congéneres, pues desplegando la avidez para maximizar su propio beneficio sin mayores límites, se logrará el máximo bienestar social. Esta posición no es compartida por otras corrientes de pensamiento como el paradigma interpretativo social (D'Onofrio, 2006), que considera que al contrario es necesario reconocer que la primacía del interés del dueño del capital o del inversionista cuando excluye los demás actores sociales, conduce a una inequitativa distribución de la riqueza, por lo que restablecer el verdadero equilibrio y la justicia social debe pasar por implementar la responsabilidad social, como criterio asegurador de estas condiciones.
De igual manera, la corriente crítica radical (D'Onofrio, 2006) propugna por replantear los mismos objetivos de la información en busca de la solución de los grandes problemas sociales caracterizados por situaciones de pobreza, degradación del medio ambiente, desintegración moral de la sociedad, inseguridad, concentración de riqueza y su injusta distribución en perjuicio de una gran mayoría de la población, ingobernabilidad y condiciones antidemocráticas en el ejercicio del poder, predominio de miseria en una gran mayoría de la población mundial, atraso científico y tecnológico, violencia y corrupción que son encubiertos por modelos y sistemas de información sesgados y que no reflejan la realidad económica y social de los pueblos y todas las organizaciones sociales que le dan estructura (Valencia, 2013).
Si en el tratamiento de la información contable se ha priorizado lo económico financiero, no es difícil deducir que lo social ha quedado excluido en forma sistemática del diseño de los sistemas contables, por lo que se puede concluir que las mediciones de lo social en el marco del objeto de estudio de la ciencia contable, o sea, de las dinámicas patrimoniales concebidas en una visión amplia que incluye diferentes tipos de patrimonios como el cultural, el patrimonio social propiamente dicho, y otros que reflejan la responsabilidad social que asumen todos los actores sociales, no hace parte de los enfoques de medición, valoración y representación contable y consecuentemente de su matematización. Ello exige reconocer que integrar el concepto de responsabilidad social y un conjunto de valores que se expresan desde lo más profundo del ser humano, es requisito para lograr la integración de lo económico y lo social. Por ejemplo, está lo suficientemente estudiado que el sentido de pertenencia de los empleados a la organización tiene un efecto positivo sobre la productividad, lo cual es una típica característica social que debe ser medida de alguna manera, pues tiene un alto impacto en las dinámicas patrimoniales. Igual sucede con otros conceptos como la cultura empresarial, el bienestar de los empleados, la lealtad de los clientes, las relaciones con los proveedores, el aporte al desarrollo humano tanto en la empresa como en la comunidad en que se inserta la organización, etc.
Lo problemático es que el tipo de medición de ese conjunto de factores sociales implica dimensiones diferentes a las tradicionales económicas y que, por ese motivo, se expresan en unidades de medición no necesariamente monetarias y en escalas que se pueden determinar como cualitativas (nominales y ordinales) y no alcanzan el rango de cuantitativas (de proporciones y razones), como sí lo han hecho las mediciones económicas que utilizan la unidad monetaria y sobre las cuales se han efectuado los mayores avances de la matematización en la ciencia contable, como se reseñó en apartados anteriores. Ello no significa que las variables cualitativas no puedan ser objeto de tratamiento matemático, sino que su enfoque es diferente. La pregunta que surge es: ¿cómo integrar mediciones cualitativas y mediciones cuantitativas de tal forma que se puedan tratar conjuntamente y cuya representación se logre diseñar e interpretar bajo el modelamiento matemático para dar una explicación científica de las dinámicas patrimoniales?
Una interesante respuesta se ha dado desde el modelo de la contabilidad matricial, que se apoya en la metodología de la partida múltiple y cuyas características permiten el tratamiento multidimensional y multiescalar. Su fundamento se ha venido desarrollando desde Richard Mattessich y Yuji Ijiri, quienes han sentado las bases epistemológicas de la axiomatización de la teoría contable, con el enfoque bidimensional (partida doble) en el caso del primero, y el enfoque de la partida múltiple para el segundo. Precisamente, este último posibilita la integración de diferentes subsistemas, pues las relaciones que se establecen no implican necesariamente dos conjuntos, sino múltiples conjuntos, cada uno representado en diferentes tipos de unidades (cualitativas o cuantitativas) como expresión de las diferentes dimensiones que conforman el complejo mundo de lo socioeconómico.
La potencialidad de interrelacionar diferentes tipos de subsistemas como expresión de diferentes facetas de la realidad económica social, posibilita su tratamiento integral y no aislacionista como sucede con los informes financieros, que se tratan de complementar a través de profusas notas a los estados financieros, pero que no logran representar en su mejor enfoque explicativo, pues se parte de la base de que lo relevante es lo económico financiero, debiendo lo social ser asumido en forma independiente sin nexos de causalidad o correlación con lo económico o viceversa (característica de algunos modelos de contabilidad social que se han venido desarrollando en forma fragmentada y desasociada de una teoría general), frenando así el desarrollo científico de la contabilidad como ciencia social que debe explicar las dinámicas patrimoniales desde una perspectiva socioeconómica.
La ventaja de la ampliación del esquema de la partida doble a la partida múltiple y la representación matricial es que ensancha el espectro de respuesta a las necesidades de los diferentes tipos de usuarios, lo que permite el estudio de la productividad global de los factores y al explicar su origen, permite una mejor negociación de su reparto entre los diferentes actores, logrando el equilibrio y la transparencia de la información requerida para sentar las bases de una más equitativa distribución de la riqueza y volviendo a un ordenamiento desde lo social, en el cual los valores son los que direccionan las decisiones económicas y no a la inversa, que es lo que se ha venido dando bajo el modelo de financiarización de la economía (Aglietta & Rebérioux, 2009; Amin, Altvater, Morin & Gowan, 2010; Dembinski, 2010; Giraldo, 2005; Orléan, 2006; Pérez, 2010), con las deplorables consecuencias de deterioro social, algunas de cuyas expresiones dramáticas son la corrupción y la desvalorización de lo humano, caldo de cultivo de las crisis económicas, financieras y de valores que caracterizan nuestra actual sociedad posmodernista.
El profesor Carlos Mallo-Rodríguez (1995) y otros tratadistas del enfoque de la contabilidad matricial y de la partida múltiple evalúan las ventajas de estos esquemas que se pueden resumir de la siguiente manera:
- La integración de la información es más sencilla al tener ordenados los datos en forma de matrices.
- Mejor uso de los principios contables en el arte de la ordenación.
- La anotación de la cantidad que corresponde a un asiento se ha de efectuar una sola vez.
- Garantiza que el conjunto de cuentas esté siempre en equilibrio sin necesidad de acudir a balance de comprobación alguno...
- Idoneidad del lenguaje matemático utilizado frente al lenguaje teórico del contador.
- Facilita las interrelaciones entre diferentes sistemas contables.
- Admite una gran flexibilidad en la presentación de los informes finales.
- Permite relacionar con gran precisión los resultados finales con las causas que las han originado.
- Permite que cada vez se amplíe más la conexión de las técnicas matemáticas con la contabilidad.
- Ofrece amplias posibilidades de cara a la contabilidad prospectiva.
- El empleo de las técnicas matriciales permite realizar las operaciones contables con gran facilidad (cálculo de saldos, distribución de gastos, determinación de desviaciones, etc.).
En consecuencia, la matematización de los diferentes procesos contables, desde una perspectiva integral socioeconómica y utilizando todo el herramental matemático, que está a disposición de todas la ciencias, se proyecta de forma muy optimista en el campo contable, que así encuentra un camino expedito para su consolidación científica y con un amplio espectro de impacto social.
Conclusiones y recomendaciones
Como se deduce de los anteriores planteamientos, el potencial de las matemáticas aplicadas desde diferentes enfoques especialmente de la modelación y de la contabilidad analítica matricial, permiten mirar con optimismo el desarrollo científico de la contabilidad enfocado a la solución de los grandes problemas socioeconómicos de la humanidad, pero también exige un esfuerzo de la comunidad académica y profesional, por transformar su mentalidad utilizando cada vez más las matemáticas en sus desarrollos.
Los enfoques interdisciplinarios y transdisciplinarios se tornan imprescindibles en todas las ciencias y especialmente en las sociales, entre las cuales la contabilidad, por su proceso de consolidación en que aún está, requiere emplear a fondo esta visión, como lo demostramos en el transcurso de este artículo, que deja una estructura analítica que pretende convocar al desarrollo de un programa de investigación cuyo eje son los procesos de matematización de la contabilidad, que encuentra vetas importantes de exploración.
La unidad de la teoría contable debe pasar por un cedazo argumentativo que recoja todos los subsistemas, sin que ello constituya una colección de diferentes componentes tratados independientemente, sino al contrario, reconocer en el herramental matemático el fundamento que amalgame diferentes facetas de la realidad de las dinámicas patrimoniales, entendidas en una visión amplia e integradora en la cual lo económico y lo social se analicen y comprendan en sus mutuas relaciones, como fenómenos de la complejidad humana.
Es muy importante que los programas académicos de contaduría pública en Colombia intensifiquen el desarrollo de la competencia matemática, pues este es uno de los obstáculos que afronta la profesión tanto en el ejercicio de la praxis, como en el mismo desarrollo disciplinar desde la investigación científica, pues hay pocos estudios sobre tan importante temática. Nuestros profesionales acuden al uso de la matemática elemental en el ejercicio profesional, sin profundizar en otros niveles del uso matemático, problemática que se hace patente frente a la nueva corriente globalizadora de las Normas Internacionales de Información Financiera, mostrando que los contadores se ven abocados a recurrir a consultores financieros, para el desarrollo de los nuevos enfoques de la valoración como el cálculo del valor razonable y otros que están aflorando en el necesario desarrollo científico de la contabilidad.
Referencias
Aglietta, Michel & Rebérioux, Antoine (2009). El capitalismo financiero a la deriva, el debate sobre el gobierno de empresa. Fernando Arbeláez (trad.). Bogotá: Publicaciones de la Universidad Externado de Colombia. [ Links ]
Amin, Samir; Altvater, Elmar; Morin, François & Gowan, Peter (2010). Crisis financiera, económica sistémica. Madrid: Maia Ediciones. [ Links ]
Arenas-Herrera, Jesús (2015). La modelación matemática como base de la autonomía científica de la contabilidad. Disponible en: http://www.alfinal.com/Economia/modelacionmatematica.php [ Links ]
Avellaneda-Bautista, Campo Alcides & Ortiz-Bojacá, José Joaquín (2012). Explicación contamétrica de las dinámicas patrimoniales desde una concepción social. Revista Criterio Libre, 10 (17), 259-286. Disponible en: https://dialnet.unirioja.es/descarga/articulo/4175414.pdf [ Links ]
Ballestero, Enrique (1975). Principios de la economía de la empresa. Madrid: Alianza Universidad. [ Links ]
Ballestero, Enrique (1979). Teoría y estructura de la nueva contabilidad. Madrid: Alianza Editorial. [ Links ]
Blanco, Juan A. (ed.) (2013). Aplicaciones de modelos ecológicos a la gestión de recursos naturales. Pamplona, España: OmniaScience. [ Links ]
Cano-Morales, Abel María (2008). Preludio histórico de la contabilidad y su analogía directa con la modelación matemática. Revista Universo Contábil, 4 (4), 112-125. Disponible en: http://www.redalyc.org/articulo.oa?id=117015194008 [ Links ]
Cánovas, María Josefa; Huertas-Navarro, Víctor & Sempere-Orts, María (2011). Optimización matemática aplicada. Enunciados, ejercicios y aplicaciones del mundo real con MATLAB: Enunciados, ejercicios y aplicaciones del mundo real con MATLAB. San Vicente, Alicante: Editorial Club Universitario. [ Links ]
Cañibano-Calvo, Leandro; Tua-Pereda, Jorge & López, José Luis (1985). Naturaleza y filosofía de los principios contables. Revista Española de Financiación y Contabilidad, REFC, 14 (47), 293-355. Disponible en: http://aeca.es/old/refc_1972-2013/1985/47-1.pdf [ Links ]
Carbonell, Antonio (2011). Relación entre los stakeholders y el valor de las empresas: La teoría del equilibrio volumétrico. Editorial Académica Española, EAE. [ Links ]
Castiblanco-Ruiz, Fabián Alberto (2014). Una mirada al presupuesto anual de ventas de Rautenstrauch & Villers a partir de los números borrosos: el manejo de la incertidumbre y la subjetividad. Revista Criterio Libre, 12 (20) 199-222. Disponible en: http://www.unilibre.edu.co/CriterioLibre/images/revistas/20/12-Revista-Criterio Libre V12-20-Articulo 9.pdf [ Links ]
Cequea-Null, Mirza Marvel; Rodríguez-Monroy, Carlos & Núñez-Bottini, Miguel Ángel (2011). La productividad desde una perspectiva humana: dimensiones y factores. Intangible Capital, IC, 7 (2), 549-584. Disponible en: http://www.intangiblecapital.org/index.php/ic/article/viewFile/194/229 [ Links ]
Churruca-Arrizabalaga, Esteban (1981). Teoría lineal de la contabilidad. Los modelos matricial y de input-output y su aplicación al cálculo de costes. Revista Española de Financiación y Contabilidad, REFC, X (35), 299-358. Disponible en: https://dialnet.unirioja.es/servlet/articulo?codigo=2481893 [ Links ]
Churruca-Arrizabalaga, Esteban (1982). Contabilidad analítica matricial para un sistema de fabricación intermitente. Revista Española de Financiación y Contabilidad, REFC, XI (38-39), 515-554. Disponible en: https://dialnet.unirioja.es/descarga/articulo/2481859.pdf [ Links ]
Coloma, Germán (1991). Productividad global de los factores: teoría y aplicación al caso de una empresa pública argentina. Buenos Aires: Instituto Torcuato Di Tella, Centro de Investigaciones Económicas. [ Links ]
Corcoran, A. Wayne (1978). Costs: Accounting, Analysis, and Control. New York: John Wiley & Sons. [ Links ]
Cruz-Rambaud, Salvador; García-Pérez, José; Nehmer, Robert A. & Robinson, Derek J. S. (2010). Algebraic Models for Accounting Systems. Singapore, Hackensack, London: World Scientific Publishing. [ Links ]
Cuatrecasas-Arbós, Lluís (2012). Gestión de la producción. Modelos. Lean Management. Capítulo Organización de la producción y dirección de operaciones. Madrid: Ediciones Díaz de Santos. [ Links ]
Cyert, Richard Michael & Davidson, H. Justin (1962). Statistical Sampling for Accounting Information. Englewood Cliffs, New Jersey: Prentice-Hall. [ Links ]
Dembinski, Paul H. (2010). ¿Finanzas que sirven o finanzas que engañan? Madrid: Editorial Pirámide. [ Links ]
D'Onofrio, Paula A. (2006). Las teorías de la contabilidad social y su relación con la responsabilidad social empresaria. El trabajo es una versión de la ponencia presentada y defendida en las sesiones del XV Congreso Internacional de la Academia Europea de Dirección y Economía de la Empresa, Buenos Aires, septiembre de 2006. Disponible en: http://bibliotecadigital.econ.uba.ar/download/contsoc/contsoc_v1_n1_02.pdf [ Links ]
Escudero, Manuel & García-Lama, Jessica (2014). La responsabilidad social empresarial y la creación de valor en América Latina. Bilbao: Publicaciones de la Universidad de Deusto. Disponible en: http://www.deusto-publicaciones.es/deusto/pdfs/otraspub/otraspub06.pdf [ Links ]
Felber, Christian (2012). La economía del bien común: un modelo económico que supera la dicotomía entre capitalismo y comunismo para maximizar el bienestar de nuestra sociedad. Barcelona: Deusto. [ Links ]
Fernández-Pérez, Carlos; Vázquez-Hernández, Francisco José & Vegas-Montaner, José Manuel (2003). Ecuaciones diferenciales y en diferencias: sistemas dinámicos. Madrid: Editorial Paraninfo. [ Links ]
Franco-Ruiz, Rafael Antonio (2003). Hacia un modelo de contabilidad integral. Revista Internacional Legis de Contabilidad y Auditoría, 15, 113-155. Disponible en: http://legal.legis.com.co/document?obra=rcontador&document=rcontador_7680752a7d804 04ce0430a010151404c [ Links ]
Franco-Ruiz, Rafael Antonio (2010). Reflexiones contables, teoría, regulación, educación y moral. 3a ed. Bogotá: Universidad Libre de Colombia. [ Links ]
Franco-Ruiz, Rafael Antonio (2014). Fundamentos ontológicos para la construcción del concepto de contametría. Revista Científica General José María Córdova, 12 (13), 165-190. Disponible en: www.scielo.org.co/pdf/recig/v12n13/v12n13a06.pdf [ Links ]
García-García, Moisés (1974). Contabilidad general: (introducción al análisis circulatorio de la realidad económica). Madrid: Escuela Superior de Cajas de Ahorros, Confederación Española de Cajas de Ahorros, CECA. [ Links ]
García-Serna, Óscar León (2011). Administración financiera, Fundamentos y aplicaciones. Cali: Prensa Moderna Impresores. [ Links ]
Giraldo, César (2005). Financiarización: nuevo orden social y político. En Oscar Rodríguez (comp.). Sistemas de protección social: entre la volatilidad económica y la vulnerabilidad social, Tomo 1, capítulo 6, 233-283. Bogotá: Universidad Nacional de Colombia, Facultad de Ciencias Económicas, Oficina de Comunicaciones, Colección Estudios sobre protección social. Disponible en: http://www.cid.unal.edu.co/files/publications/CID20050919rosipr.pdf [ Links ]
Guibert-Ucín, José María (coord.) (2009). Responsabilidad social empresarial: competitividad y casos de buenas prácticas en pymes. San Sebastián: Universidad de Deusto. [ Links ]
Hillier, Frederick S. & Hillier, Mark S. (2010). Métodos cuantitativos para administración. 3a ed. México: McGraw Hill. [ Links ]
Ijiri, Yuji (1967). The Foundations of Accounting Measurement: A Mathematical, Economic, and Behavioral Inquiry. Englewood Cliffs, New Jersey: Prentice-Hall. [ Links ]
Jiménez-Aguirre, Rubiela (enero-diciembre de 2012). Contabilidad: responsabilidad social - gestión humana. Revista Lúmina, 13, 72-87. Disponible en: http://www.utadeo.edu.co/files/collections/documents/field_attached_ file/lumina_13.pdf?width=740&height=780&inline=true [ Links ]
Lacomba, Ernesto A. (2000). Los sistemas dinámicos ¿Qué son y para qué sirven? Miscelánea Matemática, 32, 39-50. Disponible en: http://albertofest.matcuer.unam.mx/Misc32/Lacomba.pdf [ Links ]
Lanteri, Luis N. (1998). Contribución de la productividad total de los factores al crecimiento del producto, en la Argentina y en los países recientemente industrializados del este de Asia: ¿podría pensarse en un milagro del crecimiento económico argentino? Buenos Aires: Banco Central de la República Argentina, Área de Economía y Finanzas. [ Links ]
Leininger, Wayne E. (1980). Quantitative Methods in Accounting. New York: D. Van Nostrand Co. [ Links ]
Leontief, Wassily W. (1986). Input-Output Economics. New York: Oxford University Press. [ Links ]
Littleton, Ananias Charles (1937). Concepts of Income Underlying Accounting. The Accounting Review, 12 (1), 13-22. [ Links ]
Lopes de Sá, Antônio (2008). Consultoria e análise contábil. Curitiba: Juruá [ Links ].
Lopes de Sá, Antônio (2008/2009). Fundamentos da contabilidade geral. 1a reimpressao. Curitiba: Juruá [ Links ].
Lopes de Sá, Antônio (2009). Tecnologia contábil contemporânea - a Contabilidade Pós-moderna. Curitiba: Juruá [ Links ].
Lopes de Sá, Antônio (2010). Teoria da contabilidade. São Paulo: Atlas. [ Links ]
Mallo-Rodríguez, Carlos (1995). De la contabilidad de los propietarios a la contabilidad de los empresarios. Madrid: Publicaciones de la Real Academia de Ciencias Económicas y Financieras, Discurso de ingreso del académico correspondiente, electo para Madrid. Disponible en: https://racef.es/archivos/discursos/140_web.pdf [ Links ]
Mattessich, Richard (1957). Towards a General and Axiomatic Foundation of Accountancy: with An Introduction to the Matrix Formulation of Accounting Systems. Accounting Research, 8, 328-355. [ Links ]
Mattessich, Richard (1958). Mathematical Models in Business Accounting. Accounting Review, 33 (3), 472-481. [ Links ]
Mattessich, Richard (1964). Accounting and Analytical Methods. Measurement and Projection of Income and Wealth in the Micro-and Macro-Economy. Homewood, Illinois: Irwin. [ Links ]
Mattessich, Richard (2002). Contabilidad y métodos analíticos: medición y proyección del ingreso y la riqueza en la microeconomía y en la macroeconomía. Buenos Aires: La Ley. [ Links ]
Mattessich, Richard (2004). The Rise and Significance of Modern Analytical Methods in Accounting. Energeia, 2 (12), 133-144. Disponible en: http://dspace.uces.edu.ar:8180/xmlui/bitstream/handle/123456789/1877/The_Rise_Mattessich.pdf?sequence=1 [ Links ]
Mattessich, Richard (2005). A Concise History of Analytical Accounting. De Computis, Revista Española de Historia de la Contabilidad, 2, 123-153. Disponible en: http://www.decomputis.org/dc/articulos_doctrinales/mattessich2.pdf [ Links ]
Menárguez-Tortosa, Marcos (2013). Modelos de representación de arquetipos en sistemas de información sanitarios. Tesis doctoral, Departamento de Informática y Sistemas, Facultad de Informática, Universidad de Murcia. Disponible en: https://digitum.um.es/xmlui/bitstream/10201/35157/1/Tesis-MarcosMenarguezTortosa.pdf [ Links ]
Montesinos-Julve, Vicente (1976). En torno al problema de la división en Contabilidad. Revista Técnica Contable, 28 (335), 401-422. [ Links ]
Montesinos-Julve, Vicente (1978). Formación histórica, corrientes doctrinales y programas de investigación en Contabilidad. Revista Técnica Contable, 30 (358), 81-385. [ Links ]
Montesinos-Julve, Vicente (1990). Prólogo. En Francisco Gabás-Trigo. Técnicas actuales de análisis contable. Evaluación de la solvencia empresarial. Madrid: Ministerio de Economía y Competitividad, Instituto de Contabilidad y Auditoría de Cuentas, ICAC. [ Links ]
Moonitz, Maurice (1961). The Basic Postulates of Accounting (Accounting Research Study). New York: American Institute of Certified Public Accountants, AICPA. [ Links ]
Navarro, Eliseo & Nave, Juan M. (2001). Fundamentos de matemáticas financieras. Barcelona: Antoni Bosch Editor. [ Links ]
Navas-Ureña, Juan; Esteban, Francisco J. & Quesada-Teruel, José María (2009). Modelos matemáticos en biología. Teoría. Jaén: Universidad de Jaén. Disponible en: http://matema.ujaen.es/jnavas/web_modelos/pdf_mmb08_09/texto completo.pdf [ Links ]
Orléan, André (2006). El poder de las finanzas. Fernando Arbeláez (trad.). Bogotá: Editorial Universidad Externado de Colombia, Centro de Investigaciones y Proyectos Especiales, CIPE. [ Links ]
Ortiz-Anaya, Héctor (2011). Análisis financiero aplicado y principios de administración financiera. Bogotá: Universidad Externado de Colombia. [ Links ]
Ortiz-Bojacá, José Joaquín (2009). Fronteras de la investigación contable, financiera y económica: autonomía e interdisciplinariedad. Revista de la Facultad de Ciencias Económicas de la Universidad Militar Nueva Granada, 17 (1), 179-194. Disponible en: http://www.scielo.org.co/pdf/rfce/v17n1/v17n1a12.pdf [ Links ]
Ortiz-Bojacá, José Joaquín (2010). La complejidad y la teoría contable. Revista Criterio Libre, 8 (13), 231-250. Disponible en: http://www.unilibre.edu.co/CriterioLibre/images/revistas/13/art07.pdf [ Links ]
Ortiz-Bojacá, José Joaquín (2012). La medición contable bajo un enfoque interdisciplinar y sistémico. Ponencia presentada en el Primer Simposio Internacional de Contametría, Universidad Libre, Bogotá, abril 2012. [ Links ]
Paton, William Andrew & Littleton, Ananias Charles (1940). An Introduction to the Corporate Accounting Standards. Chicago: American Accounting Association, AAA. [ Links ]
Pérez, Carlota (abril de 2010). Dinamismo tecnológico e inclusión social en América Latina: una estrategia de desarrollo productivo basada en los recursos naturales. Revista CEPAL, 100, 123-145. Disponible en: http://repositorio.cepal.org/bitstream/handle/11362/11357/100123145_es.pdf [ Links ]
Pérez-Grau, Samuel Leonidas (2015). Contabilidad analítica. Métodos cuantitativos para la ciencia contable. Disponible en: http://www.monografias.com/trabajos96/contabilidad-analitica/contabilidad-analitica4.shtml, http://www.monografias.com/trabajos96/contabilidad-analítica/contabilidad-analitica.shtml [ Links ]
Pinilla-Monclus, Vicente José (1976). Una nueva fundamentación axiomática de la contabilidad. Revista Española de Financiación y Contabilidad, REFC, 5 (15), 149-170. Disponible en: https://dialnet.unirioja.es/descarga/articulo/2482530.pdf [ Links ]
Poincaré, Henri (2013). Science and Method. New York: Cosimo Clasics. [ Links ]
Porter, Michael E. (2013). On Competition. Boston: Harvard Business School Publishing. [ Links ]
Quijano-Valencia, Olver Bolívar (2002). Armonización de la educación superior: el proyecto escolar de los gremios económicos. Revista Cuadernos de Administración, Universidad del Valle, 28, 100-117. Disponible en: http://cuadernosadm.univalle.edu.co/Articulos/28-Cuadernos_de_Administracion_(Diciembre-2002)/28-(05)_Armonizacion_de_la_educacion_contable...(Olver_Quijano_Valencia).pdf [ Links ]
Requena-Rodríguez, José María (1977). La homogenización de magnitudes en la ciencia de la contabilidad. Madrid: Ediciones Instituto de Ciencias de la Educación, ICE. [ Links ]
Rescala, Carmen; Devincenzi, Gustavo H.; Rohde, Gricela; Bonaffini, María Liliana; Giraudo, Marta V.; Bernaola, Gustavo & Pavón, Rita (2012). Dos modelos para determinar la eficiencia de una empresa constructora. TRIM: Revista de Investigación Multidisciplinar, 5, 21-38. Disponible en: http://uvadoc.uva.es/bitstream/10324/11664/1/TRIM-REV-INVESTG-MULTIDISCIPL-2012-5-DosModelosParaDeterminarLaEficienciaDeUnaEmpresaCo.pdf [ Links ]
Richardson, Alan John (1996). Research Methods in Accounting: Issues and Debates. Vancouver: CGA-Canada Research Foundation. [ Links ]
Rueda-Delgado, Gabriel (2011). Contabilidad para la equidad y la inclusión social. Propuestas para una investigación interdisciplinaria a largo plazo. Revista de la Facultad de Ciencias Económicas de la Universidad Militar Nueva Granada, 19 (1), 159-174. Disponible en: http://www.scielo.org.co/pdf/rfce/v19n1/v19n1a10.pdf [ Links ]
Ruiz-Palomo, Daniel (2014). ¿Es el análisis contable una disciplina científica autónoma? Reflexiones en torno a su objeto y método. Facultad de Ciencias Económicas y Empresariales, Universidad de Málaga. Disponible en: http://www.asepuc.org/banco/el_anAlisis_contable_una_disciplina_cientIfica_autOnoma.pdf [ Links ]
Shank, John K. (1972). Matrix Methods in Accounting. Reading, Massachusetts: Addison-Wesley. [ Links ]
Sinclair, Alistair (2012). Algorithms for Random Generation and Counting: A Markov Chain Approach. New York: Springer Science+Business Media. [ Links ]
Smith, Malcolm (2014). Research Methods in Accounting. Thousand Oaks, California: Sage Publications. [ Links ]
Springer, Clifford H.; Herlihy, Robert E.; Mall, Robert T. & Beggs, Robert I. (1972). Inferencia estadística, Tomo III. México: Unión Tipográfica Editorial Hispanoamericana, Serie de Matemáticas para la Dirección de Negocios. [ Links ]
Sprouse, Robert T. (1976). The Effect of the Concept of the Corporation on Accounting. New York: Arno Press. [ Links ]
Sriramesh, Krishnamurthy & Vercic, Dejan (2012). Relaciones públicas globales: teoría, investigación y práctica. Barcelona: Editorial Universitat Oberta de Catalunya, UOC. [ Links ]
Suárez-Pineda, Jesús Alberto (2014). La eficacia social de la representación contable en Lopes de Sá. Criterio Libre, 12 (20), 225-246. Disponible en: http://www.unilibre.edu.co/CriterioLibre/images/revistas/20/13-Revista-Criterio-Libre-V12-20-Articulo 10.pdf [ Links ]
Valencia, María Mónica (2013). Teoría de la contabilidad social. Disponible en: http://www.gestiopolis.com/teoria-contabilidad-social/ [ Links ]
Valencia-Valencia, Gabriel Ernesto (2011). Mínimos conocimientos en matemáticas que debe adquirir un estudiante en el primer semestre para emprender la carrera de contaduría pública en la Universidad Autónoma Latinoamericana. Tesis de maestría en enseñanza de las ciencias exactas y naturales, Universidad Nacional de Colombia, Sede Medellín. Disponible en: https://core.ac.uk/download/files/334/11055596.pdf [ Links ]
Valero-Zapata, Gloria Milena; Patiño-Jacinto, Ruth Alejandra & Duque-Cruz, Óscar Yamith (2013). Competencias para el programa de Contaduría Pública: una aproximación conceptual. Contaduría Universidad de Antioquia, 62, 11-36. Disponible en: http://revinut.udea.edu.co/index.php/cont/article/download/18910/16147 [ Links ]
Vidaurri-Aguirre, Héctor Manuel (2012). Matemáticas financieras. 5a ed. México: Cengage Learning Editores. [ Links ]
Williams, Bernard C. & Spaul, Barry J. (1992). IT and Accounting: the Impact of Information Technology. London: Chapman & Hall. [ Links ]
Zeff, Stephen A. (2010). Insights from Accounting History: Selected Writings of Stephen Zeff. New York: Routledge. [ Links ]














