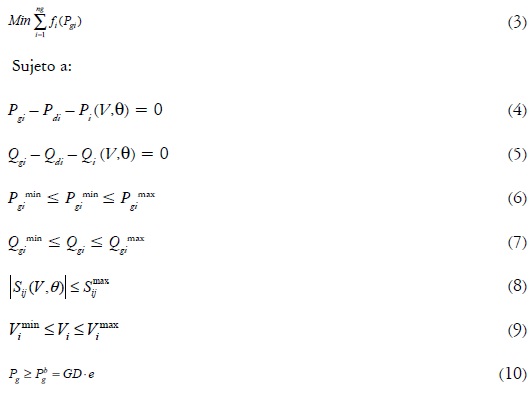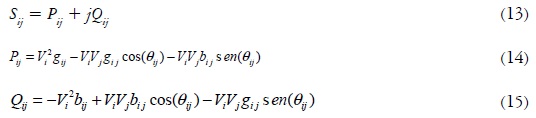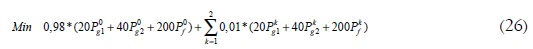Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Universidad
Print version ISSN 0123-2126
Ing. Univ. vol.13 no.2 Bogotá July/Dec. 2009
Modelo AC para el despacho combinado de contratos bilaterales y bolsa de energía considerando restricciones de seguridad*
AC Model for the Combined Dispatch of Bilateral Contracts and Energy Pool Considering Security Constraints**
Modelo AC para o despacho combinado de contratos bilaterais e bolsa de energia considerando restrições de segurança***
Mauricio Granada-Echeverri*****
Luis Alfonso Gallego-Pareja******
* Este artículo se deriva del proyecto de investigación denominado Estudio de redes de distribución de energía eléctrica y desarrollo de herramientas informáticas, con registro de Colciencias COL0041992.
** This articles results from the research project called Study of Electricity Distribution Networks and Development of Computing Tools, registration COL0041992 from Colciencias.
*** Este artigo deriva do projeto de pesquisa denominado Estudo de redes de distribuição de energia elétrica e desenvolvimento de ferramentas informáticas, com registro em Colciencias COL0041992.
**** Ingeniero electricista. Magíster en Ingeniería Eléctrica, Universidad Nacional de Colombia, sede Manizales, Colombia. Profesor de la Universidad de Antioquia, Medellín, Colombia. Correo electrónico: lezama@udea.edu.co.
***** Ingeniero electricista. Magíster en Ingeniería Eléctrica, Universidad Tecnológica de Pereira, Pereira, Colombia. Profesor de la Universidad Tecnológica de Pereira. Correo electrónico: magra@utp.edu.co.
****** Ingeniero electricista. Magíster en Ingeniería Eléctrica, Universidad Tecnológica de Pereira, Pereira, Colombia. Profesor de la Universidade Estadual Paulista Julio de Mesquita Filho Campus de Ilha Solteira, Sao Paulo, Brasil. Correo electrónico: gallegopareja@gmail.co.
Fecha de recepción: 15 de abril de 2009. Fecha de aceptación para publicación: 18 de agosto de 2009.
Submitted on April 15, 2009. Accepted on August 18, 2009.
Data de recepção: 15 de abril de 2009. Data de aceitação para publicação: 18 de agosto de 2009.
Resumen
La confiabilidad es un aspecto fundamental en el diseño y planeamiento de los sistemas de potencia; por ello velar por un sistema confiable es fundamental. Bajo el nuevo esquema de competitividad del sector eléctrico, los sistemas de transporte se ven cada vez más forzados a operar cerca de sus límites, de ahí que sea de vital importancia para el operador de la red utilizar herramientas para un despacho que minimice los posibles racionamientos de energía. En este artículo se presenta un modelo matemático para calcular el despacho, que considera restricciones de seguridad (contingencias simples en líneas de transmisión o transformadores). El modelo contempla los mercados pool y de contratos bilaterales firmes. Las metodologías tradicionales que involucran restricciones de seguridad se basan normalmente en procesos multietapa; en este caso, se propone un modelo de una sola etapa que evita ineficiencias económicas que resultan de aplicar metodologías convencionales de despacho multietapa. También incluye una representación AC del sistema de transporte y permite calcular el sobrecosto debido a las restricciones de confiabilidad. Se encontró que el cumplimiento de contratos bilaterales firmes, cuando estos están por encima de ciertos niveles, puede ocasionar problemas de congestión en las líneas de transmisión.
Palabras clave: Protección de sistemas de energía eléctrica, mercados de energía.
Abstract
Reliability is a key aspect in power system design and planning. Maintaining a reliable power system is a very important issue for their design and operation. Under the new competitive framework of the electricity sector, power systems find ever more and more strained to operate near their limits. Under this new scenario, it is crucial for the system operator to use tools that facilitate an energy dispatch that minimizes possible power cuts. This paper presents a mathematical model to calculate an energy dispatch that considers security constraints (single contingencies in transmission lines and transformers). The model involves pool markets and fixed bilateral contracts. Traditional methodologies that include security constraints are usually based in multistage dispatch processes. In this case, we propose a single-stage model that avoids the economic inefficiencies which result when conventional multi-stage dispatch approaches are applied. The proposed model includes an AC representation of the transport system and allows calculating the cost overruns incurred in due to reliability restrictions. We found that complying with fixed bilateral contracts, when they go above certain levels, might lead to congestion problems in transmission lines.
Key words: Electric power systems-protection, energy markets.
Resumo
A confiabilidade é um aspecto fundamental no desenho e planejamento dos sistemas de potência; por isso trabalhar por um sistema confiável é fundamental. Sob o novo esquema de competitividade do setor elétrico, os sistemas de transporte estão sendo cada vez mais forçados a operar próximo dos seus limites, por isso é de vital importância para o operador da rede utilizar ferramentas para um despacho que minimize os possíveis racionamentos de energia. Neste artigo apresenta-se um modelo matemático para calcular o despacho, que considera restrições de segurança (contingências simples em linhas de transmissão ou transformadores). O modelo contempla os mercados pool e de contratos bilaterais firmes. As metodologias tradicionais que envolvem restrições de segurança baseiam-se normalmente em processos de etapa múltipla; neste caso, propõe-se um modelo de uma só etapa que evita ineficiências econômicas decorrentes da aplicação de metodologias convencionais de despacho em etapa múltipla. Também inclui uma representação AC do sistema de transporte e permite calcular o custo extra devido às restrições de confiabilidade. Encontrou-se que o cumprimento de contratos bilaterais firmes, quando estes estão acima de certos níveis, pode ocasionar problemas de congestionamento nas linhas de transmissão.
Palavras chave: Proteção de sistemas de energia elétrica, Mercados de energia.
Introducción
En los últimos años, el sector eléctrico ha experimentado cambios fundamentales, de los cuales el principal ha sido la liberación de los mercados eléctricos y la introducción de la competencia. Una de las características de los nuevos mercados eléctricos es que los grandes consumidores pueden elegir entre comprar su energía directamente en la bolsa o adquirirla mediante contratos bilaterales.
Un contrato bilateral es un instrumento financiero que establece una cantidad y un precio fijo entre un generador y un consumidor, sin intervención del operador del sistema (Shahidehpour y Yamin, 2002). Estos contratos son normalmente de largo plazo, ofrecen estabilidad en los precios y sirven como protección frente a la volatilidad de los precios de la bolsa; sin embargo, la tendencia a aumentar la cantidad de energía negociada en contratos bilaterales sin la coordinación apropiada del operador del sistema puede llevar a problemas de congestión y al aumento de los precios nodales.
En la mayoría de los mercados, los generadores y grandes consumidores hacen sus ofertas al operador del sistema, el cual establece el esquema de despacho y el precio de cierre del mercado mediante un proceso de optimización. En esta primera etapa prima el criterio económico sobre el criterio técnico. En la mayoría de los casos, los criterios de seguridad (factibilidad ante contingencias) son incluidos en una etapa posterior, por medio de correcciones al despacho previamente calculado.
La introducción de estas correcciones en una etapa posterior del proceso de optimización lleva a ineficiencias económicas en el cálculo del despacho. Para evitar esto, el despacho con restricciones de seguridad se debe calcular en un proceso de una sola etapa. En (Uehara et al., 2008) se presenta un primer intento de incluir restricciones de seguridad en un modelo combinado de despacho en bolsa y contratos bilaterales; no obstante, la metodología está basada en la consideración de factibilidad ante contingencias simples desarrollada por Alsac y Stott (1974), la cual consiste en un proceso iterativo que no garantiza obtener una solución matemática óptima.
Por ello, para obtener un despacho seguro de menor costo es necesario considerar todas las contingencias simultáneamente, lo cual es posible usando flujos poscontingencia acoplados en la formulación del problema. El concepto de flujos poscontingencia se ha utilizado también en el contexto de los mercados de reserva (Cheng et al., 2005) y flujo óptimo seguro (Condren y Gedra, 2006).
El modelo de despacho en bolsa y contratos bilaterales fue propuesto por primera vez por (Galiana et al., 2002). En este artículo se plantea una extensión de este modelo, que incluye restricciones de seguridad (contingencias simples en líneas de transmisión o transformadores). Las restricciones de seguridad se han modelado como se sugiere en (López-Lezama et al., 2006). El resultado es un modelo que muestra la interacción entre los contratos bilaterales, el mercado pool y el efecto sobre estos que pueden tener las contingencias.
Además de presentar el modelo matemático del problema de despacho propuesto, en este artículo se considera un modelo de flujo de carga AC. Gran parte de los modelos de confiabilidad reportados en la literatura (Abdullah et al., 2008; Madrigal y Quintana, 2000; Ashwani y Srivastava, 2005) utilizan modelos simplificados de la red de transmisión. La principal desventaja de este tipo de modelos es que subestiman el efecto de las contingencias en la red, ya que consideran un perfil plano de tensiones y no involucran el efecto de la potencia reactiva en el sistema de transmisión (Menezes y Silva, 2004).
El resto del documento está organizado como sigue: en la sección 1 se describe el modelo tradicional de despacho en bolsa y contratos bilaterales. En la sección 2 se presenta el modelo propuesto, que incluye restricciones de seguridad. En la sección 3 se muestran dos ejemplos de aplicación y se discuten los resultados. Finalmente, en la sección 4 se concluye.
1. Modelo tradicional de despacho en bolsa y contratos bilaterales
En el nuevo contexto de los mercados eléctricos, los agentes tienen la opción de negociar energía directamente en la bolsa o mediante contratos bilaterales. Por lo tanto, los vectores de potencia activa generada y demandada pueden ser divididos en los componentes negociados en bolsa y en contratos bilaterales, como se muestra en la ecuación (1).
En este caso, los subíndices g y d indican generación y demanda, respectivamente, y los superíndices p y b indican los componentes de la potencia negociados en la bolsa y mediante contratos bilaterales, respectivamente.
Siguiendo la notación introducida en (Galiana e Ilic, 1998), la matriz GD representa la matriz de contratos bilaterales. En este caso, cada elemento GD(i, j) indica la potencia negociada entre el generador localizado en la barra i y la demanda localizada en la barra j. Usando esta matriz y un vector columna de unos e, los componentes de los vectores de potencia y demanda activa presentados en la ecuación (1) pueden expresarse como se muestra en la ecuación (2).
El modelo combinado de contratos bilaterales y despacho en bolsa fue propuesto en una serie de artículos (Galiana et al., 2002; Kockar y Galiana, 2002; Cuervo et al., 2002). La formulación básica que incluye demanda inelástica y contratos bilaterales firmes está dada por las ecuaciones (3) a (10).
En este caso, las potencias activas y reactivas inyectadas en la i-ésima barra del sistema están dadas por las ecuaciones (11) y (12).
Así mismo, el flujo de potencia aparente en las líneas está dado por su componente en potencia activa y reactiva, como se muestra en las ecuaciones (13) a (15).
Como se puede observar en la ecuación (3), la función objetivo consiste en minimizar el costo de la potencia generada. Esta minimización está sujeta a las ecuaciones de balance de potencia activa y reactiva, dadas por las ecuaciones (4) y (5); los límites de generación de potencia activa y reactiva, por las ecuaciones (6) y (7); los límites de flujo en las líneas, por la ecuación (8); los límites de tensión en las barras, por la ecuación (9), y, finalmente, las restricciones impuestas por los contratos bilaterales expresados, mediante la ecuación (10).
Nótese que la única diferencia del modelo presentado en las ecuaciones (3) a (10) con un modelo tradicional de flujo de potencia óptimo es el conjunto de restricciones introducido por los contratos bilaterales.
2. Modelo propuesto con restricciones de seguridad
A continuación se presenta un modelo de despacho de contratos bilaterales y bolsa de energía que considera restricciones de seguridad. El modelo propuesto está descrito por las ecuaciones (16) a (24):
Donde el superíndice k se refiere a la k-ésima contingencia, donde k=0 es el caso base. Rk es la probabilidad de operar bajo la contingencia k (en este caso es la probabilidad de falla única de una línea o transformador), nc es el número de contingencias consideradas y Δ representa un vector de restricciones de velocidad de toma de carga. La probabilidad de operar en el caso base es igual a la unidad menos la sumatoria de probabilidades de falla única de los demás elementos, como se indica en la ecuación (25).
En este caso sólo se han considerado contingencias simples, es decir, solamente una línea o transformador está fuera de servicio a la vez (criterio n-1). Sin embargo, el modelo se puede adaptar fácilmente para contemplar contingencias múltiples. Además, se puede observar en la ecuación (23) que el cumplimiento de los contratos bilaterales solamente se considera cuando el sistema no está bajo contingencias, esto es, porque la seguridad del sistema prevalece sobre el cumplimiento de los contratos.
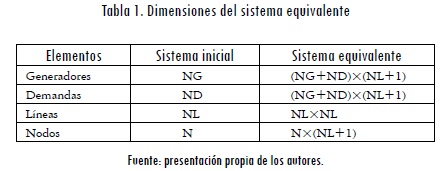
Para resolver el modelo planteado por las ecuaciones (16) a (24) se debe construir un sistema equivalente compuesto por islas, como se sugiere en (López-Lezama et al., 2006). En este caso, cada isla representa un estado del sistema. El sistema equivalente está acoplado mediante las restricciones de velocidad de toma de carga de la ecuación (24), que relaciona cada una de las contingencias con el caso base. En la Tabla 1 se muestran las dimensiones del sistema equivalente.
Para garantizar la factibilidad del modelo propuesto se utilizaron generadores y demandas ficticias. A continuación se ilustra un ejemplo para aclarar estos conceptos. En la Figura 1 se muestra un sistema de potencia de dos nodos con dos generadores y dos líneas de transmisión. Los generadores presentan ofertas de 20 y 40 $/MWh, respectivamente, y deben suplir una demanda de 90 MW, ubicada en el nodo 2.
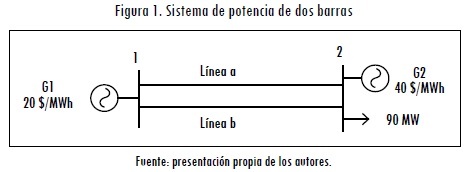
Se supone que los generadores tienen una potencia mínima de 10 MW y una velocidad de toma de carga de 20 MW. Es decir, dada una contingencia, los generadores pueden aumentar o disminuir su potencia entregada en máximo 20 MW. Inicialmente se supone que los dos generadores tienen capacidad suficiente para suplir toda la demanda y que las líneas tienen un límite de transporte de 50 MW. Se supone, además, que no existen pérdidas y que las impedancias en las líneas son iguales.
Por simplicidad se considera inicialmente que no existen contratos bilaterales entre la demanda y los generadores. Al resolver un flujo óptimo tradicional (sin restricciones de seguridad), pasando por alto las pérdidas y considerando un perfil plano de tensiones, se obtiene el resultado ilustrado en la Figura 2.
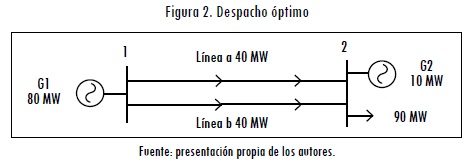
En la Figura 2 se puede observar que el generador más económico (generador 1) suple la mayor parte de la demanda (80 MW); en contraste, el generador 1 es despachado en su mínimo técnico. El costo de operación del sistema es de 20$/ MWhx80MW + 40$/MWhx10MW = 2000$/h. Debido a que las impedancias de las líneas son iguales, los flujos se reparten de forma igual entre ellas. Se puede observar, además, que los flujos en las líneas se conservan dentro de su límite máximo de 50 MW.
Ahora bien, supóngase que ocurre un fallo en la línea b. En este caso, el flujo en la línea a se incrementará hasta llegar a su límite de 50 MW, el generador 2 intentará cubrir los 40 MW restantes necesarios para suplir toda la demanda; sin embargo, sólo podrá generar 20 MW adicionales, debido a su restricción de velocidad de toma de carga. Por lo tanto, habrá un racionamiento de 10 MW. Para que se cumpla la ecuación de balance de potencias en el nodo 2 es necesario poner un generador ficticio que entregue estos 10 MW. El precio de oferta de dicho generador es igual al costo de racionamiento.
Por otro lado, el generador del nodo 1 estaba entregando 80 MW y sólo puede disminuir su producción en 20 MW, debido a su restricción de velocidad de toma de carga. Por lo tanto, pasará a entregar 60 MW. Para que se cumpla la ecuación de balance de potencias en este nodo es necesario introducir una demanda ficticia que consuma 10 MW, puesto que la línea de transmisión sólo puede exportar 50 MW. El uso de generadores y demandas ficticias se muestra en la Figura 3, donde Gf y Df indican generación y demanda ficticia, respectivamente. En este caso, la demanda ficticia no tiene costo y se utiliza únicamente para garantizar la factibilidad del problema de optimización.
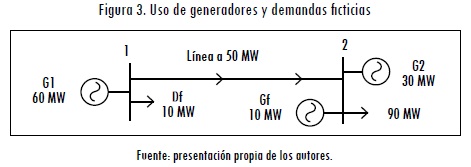
Una forma de evitar el racionamiento cuando ocurre una contingencia es aumentar el despacho del generador 2 de 10 a 20 MW; de este modo, cuando las líneas a o b sufran una contingencia, el generador 2 podrá generar los 40 MW necesarios para cubrir toda la demanda y evitar deslastrar la carga (estos 40 MW corresponden a los 20 MW del despacho inicial más el incremento de 20 MW que le permite su límite de velocidad de toma de carga).
El costo de este nuevo esquema de despacho está dado por: 20$/MWhx70MW + 40$/MWhx20MW = 2200$/h. En este caso se presenta un sobrecosto de 200 $/h para garantizar que no haya racionamiento ante cualquier contingencia simple. Estos 200 $/h representan el coto de la seguridad del sistema. Ahora bien, supóngase que el generador 2 es muy costoso y que la probabilidad de que las líneas a o b fallen sea muy baja; en este caso, no sería económicamente viable aumentar el despacho del generador 2 e incurrir en altos sobrecostos de operación. Por lo tanto, se deben tener en cuenta las probabilidades de falla a la hora de calcular el despacho con restricciones de seguridad. Suponiendo que la probabilidad de falla única de las líneas es del 1% y que el costo de racionamiento es de 200 $/MWh, la función objetivo (ecuación [26]) estaría dada por:
Una de las particularidades de los contratos bilaterales firmes es que estos pueden congestionar la red. Supóngase que la demanda ha firmado un contrato bilateral de 100 MW con el generador 1. En este caso, las líneas a y b alcanzarían su límite de transmisión de 50 MW cada una. Si los nodos 1 y 2 pertenecen a un sistema mayor, cualquier otra transacción que involucre un flujo de potencia en el sentido 1-2 no podrá ser realizada, debido a que las líneas de transmisión han alcanzado su límite.
3. Pruebas y resultados
Para probar el modelo propuesto se utilizó un sistema didáctico de cinco barras y el sistema de prueba del Instituto de Ingenieros Eléctricos y Electrónicos (IEEE, por su sigla en inglés) de 14 barras. Los resultados de las pruebas efectuadas se muestran a continuación.
3.1 Sistema de cinco barras
Con el fin de probar el modelo propuesto y compararlo con el modelo tradicional, sin contingencias, se utilizó el sistema de potencia de cinco barras, mostrado en la Figura 4. Este sistema consta de tres generadores, tres demandas y ocho líneas de transmisión. Para los generadores se asume una función de costo cuadrática, como se indica en la ecuación (27).
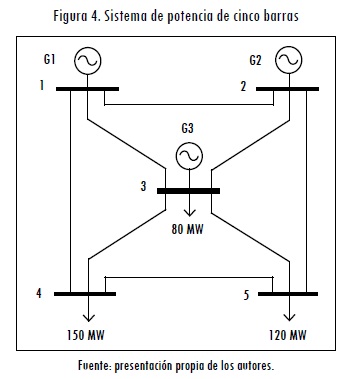
La matriz de contratos bilaterales GD se muestra en la ecuación (28). Se puede observar que la suma de las columnas de GD corresponde a la potencia total demandada en cada una de las barras. Por ejemplo, la columna 3 indica que la demanda ubicada en el nodo 3 tiene un contrato bilateral de 50 MW con el generador 1, y un contrato de 30 MW con el generador 2. Estos dos contratos cubren la demanda total, que es 80 MW.
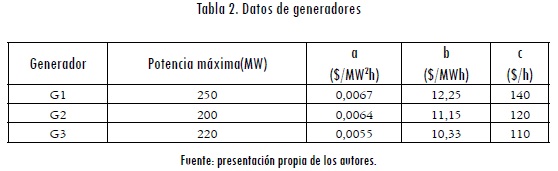
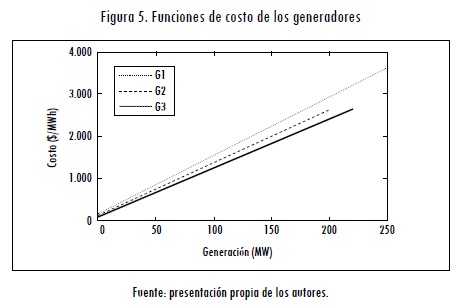
En la Tabla 2 se muestran los datos de los generadores. En este caso, se asume para todos los generadores una potencia mínima de 10 MW y una velocidad de toma de carga de 30 MW. Esto indica que ninguno de los generadores puede aumentar o disminuir la potencia entregada en más de 30 MW cuando ocurre una contingencia. En la Figura 5 se presenta una gráfica de las funciones de costo de los generadores. Se puede observar que el generador más económico es el generador 3; le sigue en costo el generador 2, y, finalmente, el generador 1. En este caso se asume un costo de racionamiento de 300 $/MWh.
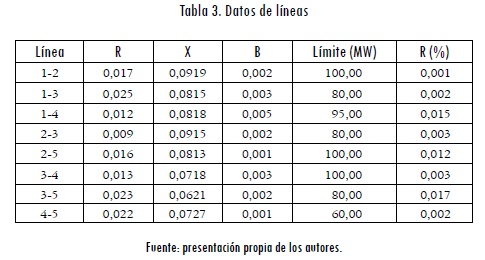
En la Tabla 3 se muestran los datos de las líneas, donde R es la probabilidad de falla única. Se puede observar que las líneas que presentan una mayor probabilidad de falla son las líneas 1-3, 2-5 y 3-5.
3.1.1 Resultados con el modelo de despacho tradicional
Para evaluar el impacto de los contratos bilaterales en el despacho de generación se parametrizó la matriz GD de la siguiente forma: GD(ρ)=ρ.GD; 0≤ρ≤1. Por lo tanto, cuando ρ=1, toda la demanda es suplida por contratos bilaterales, y para ρ=0 toda la demanda es negociada en bolsa. En la Tabla 4 se muestran los resultados del despacho para diferentes valores de ρ. Donde CO corresponde al costo de operación del sistema. Cuando ρ=0,0, el problema de optimización dado por las ecuaciones (3) a (10) se convierte en un flujo de potencia óptimo tradicional. En la Tabla 3 se puede observar que para ρ=0,0 el generador 1 es el que menos potencia entrega (32,33 MW). Esto ocurre, porque este generador es el que presenta mayor costo de operación (Figura 1); por el contrario, el generador 3 sale despachado cerca de su máximo técnico, ya que es el generador con menor costo de operación.
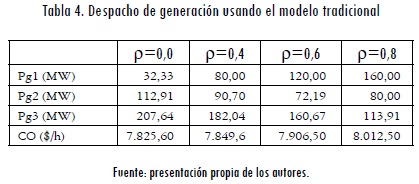
A medida que el parámetro ρ aumenta, se puede observar que el costo de operación del sistema también aumenta. Esto se debe a que los contratos bilaterales celebrados entre la demanda y los generadores (relacionados en la matriz GD) se han dado en cantidades que no son óptimas desde el punto de vista del despacho centralizado. A media que ρ aumenta, la participación en el despacho de los generadores más costosos también aumenta para cumplir las restricciones impuestas por los contratos bilaterales.
La Tabla 5 relaciona los precios nodales en las barras del sistema para diferentes valores de ρ. Estos precios nodales se definen como los multiplicadores de Lagrange, asociados a las restricciones de igualdad de potencia activa (ecuaciones [4] y [17] en los modelos con restricciones de seguridad y sin estas, respectivamente). Se puede observar que para 0≤ρ≤0,6 la diferencia entre los precios nodales es pequeña y se debe solamente a las pérdidas del sistema. Por otro lado, cuando ρ=0,8 se presenta congestión en la línea 1-4, lo que ocasiona que los precios nodales varíen significativamente.
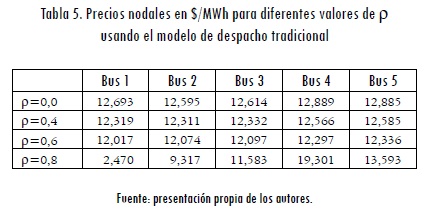
3.1.2 Resultados con el modelo con restricciones de seguridad
Para aplicar el modelo con restricciones de seguridad es necesario construir un sistema equivalente compuesto por islas. Estas islas representan el caso base y cada una de las posibles contingencias. El modelo se ha diseñado para considerar todas las contingencias simples al mismo tiempo. Sin embargo, por simplicidad sólo se han considerado en este caso las contingencias de las líneas 1-3, 2-5 y 3-5, que son las que presentan mayor probabilidad de falla (Tabla 3). El sistema equivalente resultante de aplicar el modelo se muestra en la Figura 6.
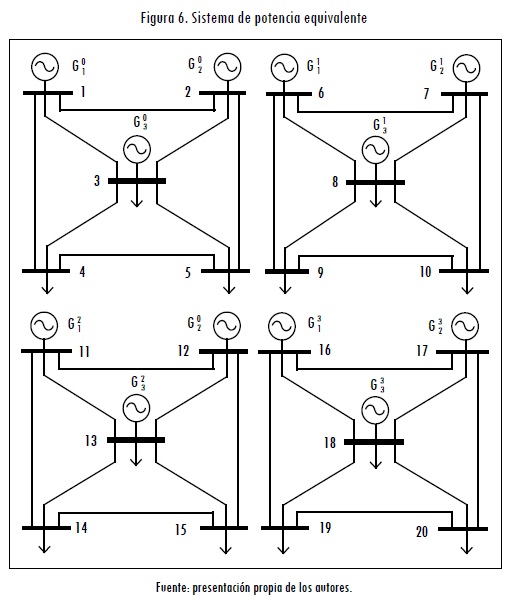
En la Tabla 6 se muestran los resultados correspondientes al despacho de generación con restricciones de seguridad para diferentes valores del parámetro ρ. Se puede observar que el costo de operación en los primeros tres casos (0≤ρ≤0,6) es ligeramente superior al presentado en la Tabla 3. Esto se debe a que la energía se debe distribuir de manera tal que dada una contingencia el racionamiento sea mínimo. Si bien las diferencias en el costo total de operación no son significativas (para este caso en particular), sí lo son en el despacho de los generadores. Para el caso ρ=0,0 el generador 1 debe entregar 56,20 MW en el despacho con contingencias; pero sólo debe entregar 32,33 MW en el despacho sin contingencias.
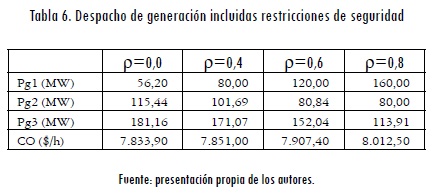
Cuando ρ=0,8, los despachos obtenidos usando ambos modelos son iguales. Esto ocurre porque los contratos bilaterales obligan a los generadores 1 y 2 a entregar 160 y 80 MW, respectivamente; por lo tanto, el resto de la demanda debe ser atendida por el generador 3. La Tabla 7 muestra los precios marginales en cada una de las barras para diferentes valores de ρ. Al igual que en el despacho sin contingencias, los precios marginales se mantienen en valores similares para 0≤ρ≤0,6.
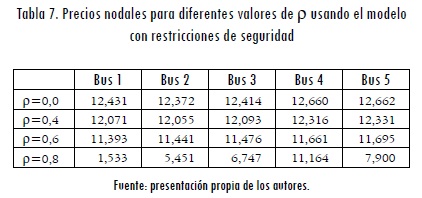
En ambos modelos se presenta congestión en la línea 1-4 cuando ρ=0,8, lo cual provoca que los precios marginales varíen significativamente. A pesar de obtenerse el mismo esquema de despacho para ambos modelos con ρ=0,8, se puede observar que los precios marginales son diferentes. Esto se debe a las diferencias en las funciones objetivo para ambos problemas (véanse ecuaciones 3 y 16).
3.2 Sistema IEEE de 14 barras
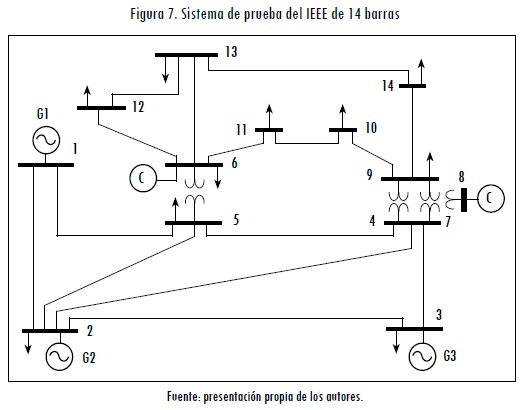
En la Figura 7 se ilustra el sistema de prueba del IEEE de 14 barras. Los datos de este sistema están disponibles en http://www.ee.washington.edu/research/pstca/. Los generadores ubicados en las barras 6 y 8 actúan como condensadores síncronos; por lo tanto, sólo se utilizarán para el despacho los generadores ubicados en los nodos 1, 2 y 3. En este caso se han modificado los datos de los generadores, como se muestra en la Tabla 8.
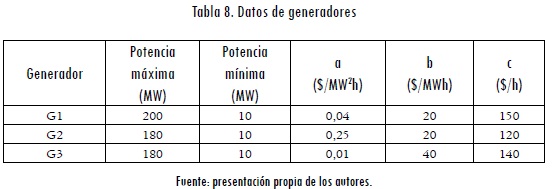
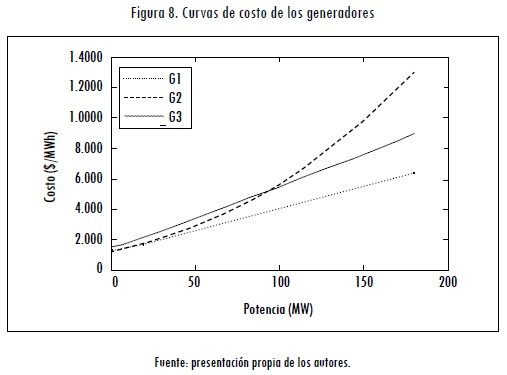
En la Figura 8 se muestran las funciones de costo de estos generadores. El análisis para este sistema se centra en las diferencias entre los modelos con restricciones de seguridad y sin estas, y posteriormente en el efecto de los contratos bilaterales firmes en los precios nodales y en el costo de operación total del sistema.
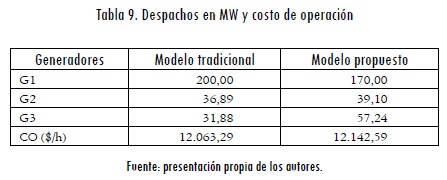
En la Tabla 9 se muestran los resultados cuando se utiliza el modelo con restricciones de seguridad y sin estas (inicialmente no se consideran contratos bilaterales). En este caso, se ha utilizado un costo de racionamiento de 300 $/ MWh y se ha supuesto una velocidad de toma de carga de 40 MW para todos los generadores. Adicionalmente se considera una probabilidad de falla de 1% para cada una de las líneas y transformadores del sistema. Se puede observar que cuando no se consideran contingencias, el generador 1 es despachado en su máximo, dado que es el generador más económico (Figura 8); sin embargo, cuando se consideran restricciones de seguridad, este generador entrega menos potencia y es necesario utilizar recursos más costosos. Las restricciones de seguridad en este caso implican un sobrecosto de 79,3 $/h.
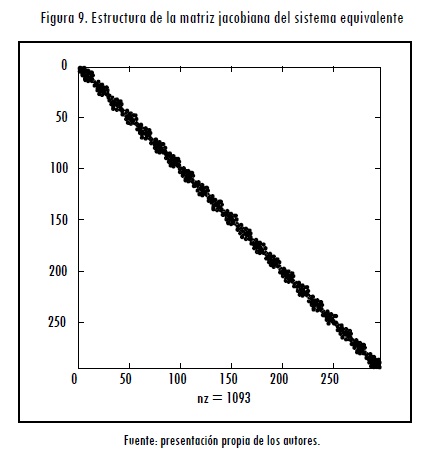
Como se mencionó, es necesario construir un sistema equivalente para resolver el modelo propuesto de despacho óptimo seguro. En este caso el sistema equivalente consta de 294 nodos, 315 generadores y 400 líneas. La estructura de la matriz jacobiana del sistema equivalente se muestra en la Figura 9. En esta se puede observar que tal matriz es altamente dispersa, lo cual facilita el uso de técnicas de descomposición para solucionar el problema. Para resolver el problema de optimización se ha elaborado un programa en Matlab® usando como base el software Matpower (Zimmerman y Murillo-Sánchez, 2007). Este software es un paquete de archivos de uso libre que permite calcular flujos de potencia óptimos y que hace una manipulación adecuada de matrices dispersas.
Para cuantificar el efecto de los contratos bilaterales en la red de transporte se consideraron varios casos con diferentes niveles de contratos para el generador 2. Adicionalmente, se introdujo un límite de transporte de 45 MW en la línea de transmisión que une los nodos 2 y 4. En la Tabla 10 se muestran los despachos para los diferentes casos propuestos. En el caso base no se consideran contratos bilaterales. En los casos 1, 2 y 3 se considera que el generador 2 ha firmado contratos bilaterales con la demanda para atender un total de 40, 60 y 80 MW, respectivamente.
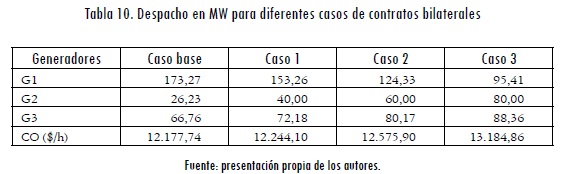
Se puede observar que a pesar de que el generador 3 no tiene contratos bilaterales este aumenta su generación en cada caso. En contraste, el generador 1 disminuye la potencia entregada. Esto ocurre porque se presenta congestión en la línea 2-4, lo cual hace que cada vez que el generador 2 aumente su potencia para cumplir los contratos bilaterales, el generador 1 reduzca su potencia para no saturar la línea 2-4. La potencia que deja de entregar el generador 1 es suministrada por el generador 3. Dado que el generador 3 es más costoso que el generador 1, el costo total de operación del sistema aumenta.
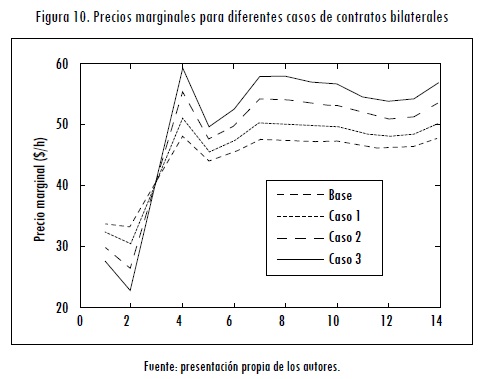
En la Figura 10 se muestran los precios nodales para los diferentes casos estudiados. Se puede observar que la mayoría de los precios nodales aumentan cuando aumenta la cantidad de contratos bilaterales del generador 2. Sin embargo, el precio nodal en el nodo 2 disminuye. Esto se debe a que cualquier incremento de la demanda en el nodo 2 puede ser atendido por el generador 1, sin utilizar la línea congestionada. Por otro lado, cualquier incremento de la demanda en los otros nodos deberá ser atendido por los generadores 2 o 3.
4. Conclusiones
En este artículo se presentó un modelo AC para el despacho combinado de contratos bilaterales y bolsa de energía, que considera restricciones de confiabilidad. Se pudo verificar que la tendencia a aumentar la cantidad de energía negociada en contratos bilaterales, por encima de ciertos niveles, puede llevar a problemas de congestión y al aumento de los precios nodales. Por otro lado, la inclusión de restricciones de confiabilidad puede resultar en un esquema de despacho más costoso, lo cual puede significar una diferencia importante en los ingresos de los generadores.
El principal aporte de este artículo es un modelo de optimización que permite calcular un despacho óptimo seguro en un proceso de una sola etapa. Además, se ha incluido un modelo en AC de la red de transmisión, lo cual hace que los resultados sean más cercanos a la realidad, que los obtenidos con los modelos tradicionales en DC.
En un trabajo posterior se pretende desarrollar un modelo que considere un esquema de despacho de 24 horas, donde se incluyan restricciones intertemporales, como los tiempos mínimos de encendido y apagado de las unidades de generación y la variabilidad de la demanda.
Referencias
ABDULLAH, M. P.; HASSAN, M. Y. y HUSSIN, F. Security cost allocation under combined bilateral-pool market dispatch. 4th IASTED International Conference Power and Energy Systems, Langkawi, Malaysia, 2-4 de abril de 2008, pp. 129-134. [ Links ]
ALSAC, O. y STOTT, B. Optimal load flow with steady-state security. IEEE Transactions on Power Apparatus and Systems, 1974, vol. 93, núm. 1, pp. 745-751. [ Links ]
ASHWANI KUMAR, S. C. y SRIVASTAVA, S. N. Congestion management in competitive power market: a bibliographical survey. Electric Power Systems Research, 2005, vol. 76, núms. 1-3, pp. 153-164. [ Links ]
CHEN, J. et al. Locational-based scheduling and pricing for energy and reserve: a responsive reserve market proposal. Decision Support Systems, 2005, vol. 40, núm. 3, pp. 563-577. [ Links ]
CONDREN, J. y GEDRA, T. W. Optimal power flow with expected security costs. IEEE Transactions on Power Systems, 2006, vol. 21, núm. 2, pp. 541-547. [ Links ]
CUERVO, P. C.; KOCKAR, I. y GALIANA, F.D. Combined pool/bilateral dispatch: part IIIUnbundling costs of trading services. IEEE Transactions on Power Systems, 2002, vol. 17, núm. 1, pp. 1191-1198. [ Links ]
GALIANA, F. D. e ILIC, M. A Mathematical framework for the analysis and management of power transactions under open access. IEEE Transactions on Power Systems, 1998, vol. 13, núm. 1, pp. 681-687. [ Links ]
GALIANA, F. D.; KOCKAR, I. y FRANCO, P. C. Combined pool/bilateral dispatch: part I-Performance of trading strategies. IEEE Transactions on Power Systems, 2002, vol. 17, núm. 1, pp. 92-99. [ Links ]
KOCKAR, I. y GALIANA, F. D. Combined pool/bilateral dispatch: part II-Curtailment of firm and nonfirm contracts. IEEE Transactions on Power Systems, 2002, vol. 17, núm. 1, pp. 1184-1190. [ Links ]
KUMAR, A; SRIVASTAVA, S. y SINGH, S. Congestion management in competitive power market: A bibliographical survey. Electric Power Systems Research, 2005, vol. 76, núms. 1-3, pp. 153-164. [ Links ]
LÓPEZ LEZAMA, J. M. et al. Contingency-based security-constrained optimal power flow model for revealing the marginal cost of a blackout risk-equalizing policy in the Colombian electricity market. Transmission and Distribution Conference and Exposition: Latin America. Caracas, Venezuela, 15 al 18 de agosto, 2006, pp. 1-6. [ Links ]
MADRIGAL, M. y QUINTANA, V. H. A security-constrained energy and spinning reserve markets clearing system using an interior-point method. IEEE Transactions on Power Systems, 2000, vol. 15, pp. 1410-1416. [ Links ]
MENEZES, T. V. y SILVA, L. C. P. An investigation on the accuracy of DC methods for losses allocation in electricity power markets. 4th IASTED International Conference on Power and Energy Systems, 2004. [ Links ]
SHAHIDEPOUR, M; YAMIN, Z. y LI, H. Market operations in electric power systems: forecasting, scheduling, and risk management. 2nd ed. New York: John Wiley & Sons, 2002. [ Links ]
UEHARA, S. K.; NEPOMUCENO, L. y OHISHI, T. A combined pool/bilateral model including post-contingency security constraints. Congreso Brasilero de Automatica (CBA), Juiz de Fora, Brasil, 14 a 17 de septiembre, 2008, pp. 1-8. [ Links ]
ZIMMERMAN, R. y MURILLO-SÁNCHEZ, C. E. MATPOWER 3.2 power systems simulation package: users manual [web en línea], 2007. <http://www.pserc.cornell.edu/matpower/> [Consulta: 01-10-2009]. [ Links ]