* Este artículo se deriva del proyecto de investigación denominado Desarrollo de una herramienta para el diseño de controladores robustos, registrado con el número P 08-80, I 08-40 de la Universidad Autónoma de Colombia.
** This article results from the research project called Developing a Tool for Designing Robust Controllers, registered with the number P 08-80, I 08-40 of the Universidad Autónoma de Colombia.
*** Este artigo deriva do projeto de pesquisa denominado Desenvolvimento de uma ferramenta para o desenho de controladores robustos, registrado com o número P 08-80, I 08-40 da Universidade Autônoma da Colômbia.
**** Ingeniero electrónico. Magíster en Ingeniería, Universidad de los Andes, Bogotá, Colombia. Profesor de la Universidad Autónoma de Colombia, Bogotá, Colombia. Correo electrónico: franklin.pineda@fuac.edu.co.
***** Ingeniero mecánico. Magíster en Ingeniería, Universidad Nacional de Colombia, Bogotá, Colombia. Profesor de la Universidad Distrital Francisco José de Caldas y de la Universidad Autónoma de Colombia, Bogotá, Colombia. Correo electrónico: luini@madrid.com.
****** Ingeniero electrónico. Magíster en Ingeniería Electrónica y de Computadores, Universidad de los Andes, Bogotá, Colombia. Profesor de la Universidad Autónoma de Colombia, Bogotá, Colombia. Correo electrónico: alonso_chica@yahoo.es.

Fecha de recepción: 16 de julio de 2009. Fecha de aceptación para publicación: 19 de agosto de 2009.
Submitted on July 16, 2009. Accepted on August 19, 2009.
Data de recepção: 16 de julho de 2009. Data de aceitação para publicação: 19 de agosto de 2009.

Resumen

En este artículo se presenta una extensión del algoritmo del método de Gauthier, que soluciona la búsqueda de realización mínima multivariable partiendo de matrices de transferencia cuadradas. El algoritmo incorpora previamente la teoría de fracciones coprimas, desarrolladas con matrices de Silvester y factorización qr. Debido a que las fracciones coprimas tienen una especial relación con las matrices en fracción polinomial, se muestran sus diferencias, analizándolas independientemente. Se plantean las características generales y se nombran las funciones desarrolladas para hacer hincapié en los caminos de búsqueda de la fracción coprima que no son únicos, así como tampoco su representación en espacio de estado. Para la demostración se utilizó un sistema dinámico multivariable, donde se comprueban la eficiencia y las limitaciones del algoritmo elaborado, con base en funciones realizadas con la Toolbox de control de Matlab®.

Palabras clave: Algoritmos, matrices, análisis multivariante.

Abstract

This paper presents an extension of Gauthier's algorithm, which solves the problem of searching for the multivariable minimal realization starting from square transference matrices. Previously, the algorithm incorporates the coprime fractions developed with Silvester matrices and qr factorization. Since the coprime fractions have a special relation with matrices in polynomial fraction, they show their differences by analyzing them independently. The general features are set out, and the developed functions named, in order to emphasize the different search paths and their representation in state space (neither of which are not unique) for the coprime fraction. For demonstration we used a multivariable dynamic system, where the efficiency and limitations of the developed algorithm are checked based on the functions performed with the Matlab® Control Toolbox.

Key words: Algorithms, matrix, multivariate analysis.

Resumo

Neste artigo apresenta-se uma extensão do algoritmo do método de Gauthier, que soluciona a busca de realização mínima multi-variável partindo de matrizes de transferência quadradas. O algoritmo incorpora previamente a teoria de frações coprimas, desenvolvidas com matrizes de Silvester e factorização qr. Devido a que as frações co-primas têm uma relação especial com as matrizes em fração polinomial, mostram-se suas diferenças, analisando-as independentemente. Explicam-se as características gerais e nomeiam-se as funções desenvolvidas para fazer insistir nos caminhos da busca da fração co-prima que não são únicos, assim como sua representação em espaço de estado. Para a demonstração utilizou-se um sistema dinâmico multi-variável, onde se comprovam a eficiência e as limitações do algoritmo elaborado, com base em funções realizadas com a caixa de ferramentas de controle de Matlab®.

Palavras chave: Algoritmos, matrizes, análise multivariante.

Introducción

El modelamiento matemático de sistemas es quizá el primer aspecto necesario para formular un sistema de control automático. El ingeniero de control, a partir de una o varias plantas, intenta describirlas de la manera más acorde con un comportamiento inherente, algunas veces por medio de subsistemas, a fin de establecer la mejor aproximación del estado dinámico en cualquier tiempo. Los sistemas, en la mayoría de los casos, son de tipo multivariable, es decir, tienen ya sea más de una entrada, más de una salida o ambas (Chen, 2009).

El modelamiento y la descripción de estos sistemas se pueden representar por medio de matrices de transferencia, sistemas de ecuaciones diferenciales y ecuaciones dinámicas de estado. Estas últimas son más conocidas con el nombre de representación en el espacio de estado y tienen un interés particular, porque permiten un manejo matricial del problema. Generalmente, para trabajos computacionales y de implementación electrónica siempre se recurre al modelo en espacio de estado.

Algunas veces, la descripción en matrices de transferencia no es suficiente para caracterizar un sistema completamente (Chen, 2009); esto se debe a que muchas veces el sistema posee condiciones iniciales que no se pueden reflejar muy bien dentro de una descripción entrada-salida, en especial los estados que pueden tener variables en cualquier tiempo. De igual manera, tampoco se refleja de manera inmediata cuáles polos son controlables, observables y cuáles de ellos no lo son.

No obstante, el desarrollo de las matrices de transferencia se ha convertido en un mecanismo útil para encontrar rápidamente las características esenciales de los sistemas multivariables; entre los más importantes, su orden, sus polos y sus ceros, algo que no se puede saber a priori en una representación de modelo diferencial ni en un modelo de representación de estado. Los mayores trabajos siguen en proceso, intentando minimizar o reducir los modelos para no ver la representación de estado con muchas ecuaciones.

El problema de encontrar una realización mínima para sistemas LTI viene desde los años treinta, para sistemas monovariables, y desde los años sesenta, para sistemas multivariables (De Schutter, 2000). Una matriz de transferencia (MTF), definida como una matriz que posee funciones de transferencia g_ij, se puede descomponer en fracciones polinomiales matriciales así:

Chen (2009) y Basilio y Kauvaritakis (1997) han planteado teóricamente un algoritmo que partiendo de una fracción polinomial matricial izquierda (2), llega a una fracción coprima derecha (3)¹:

Igualmente, es posible llegar a una fracción coprima izquierda (5), partiendo de una fracción polinomial matricial (MPF) derecha (4):

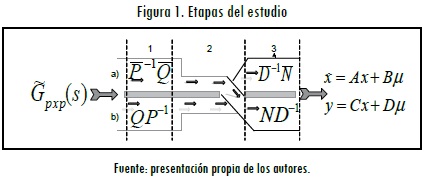
En el procedimiento para la descomposición de la MTF 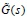a una MPF, sea izquierda o derecha, es inmediato y es posible representarlo de diversas formas; contrario de llegar a una fracción coprima de una MTF, cuyo procedimiento requiere técnicas especiales y cuya representación es única. Cabe mencionar que existe un desarrollo para encontrar fracciones coprimas derechas partiendo de una MPF derecha, buscando el greatest common right divisor (GCRD) (Sinha, 2007) o el caso dual greatest common left divisor (GCLD) (Rough, 1996), pero debido a su complejidad sólo se maneja de forma teórica y dentro de este artículo no será tratado. El diagrama general se puede observar en la Figura 1, donde existen dos caminos a y b para llegar a un sistema descrito por la cantidad mínima de variables de estado con las matrices A, B, C y D.

1. Descripción en fracción polinomial

La descripción en fracción polinomial es una representación matemática de una matriz de funciones de transferencia. Si se aplica esta representación a un sistema de múltiples entradas y múltiples salidas (MIMO), puede revelar características internas, como la cantidad de estados y polos que posee el sistema (Rough, 1996). Aunque este tipo de representación no es única, la forma más fácil de conseguir una descripción polinomial es descomponer la MTF haciendo que la matriz P, la cual siempre será cuadrada, posea siempre en su diagonal principal los denominadores de 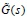, y la matriz Q, los residuos que complementan a P por fila o por columna.

Al tomar una p x q matriz de funciones de transferencia 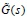de un sistema, es posible descomponerlo hacia la derecha o hacia la izquierda, donde el grado u orden del sistema lo establece el mínimo común múltiplo de todos los denominadores de 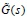, así:

1.1 Fracción polinomial derecha

Al tomar de la MTF los denominadores comunes por columna, se crea la matriz de fracciones polinomiales hacia la derecha (rmpf) (4). Dónde P(s) ϵ R[s]]^pxq, Q(s) ϵ R[s]^pxq.

1.2 Fracción polinomial izquierda

Al tomar de la MTF los comunes denominadores por fila, se crea la matriz de fracciones polinomiales hacia la izquierda (lmpf) (Sinha, 2007). Donde 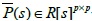, 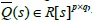. De esta representación podemos generar un sistema en el espaciode estado, pero generalmente no es mínimo. Se define el grado de la descripción polinomial como el grado del polinomio resultante del determinante de 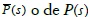. Si este grado es igual a n en (6), entonces es una fracción coprima 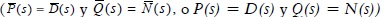y no es necesario hacer los pasos 2 y 3 (Figura 1).

El procedimiento que sigue encuentra fracciones coprimas de las matrices polinomiales no mínimas, por medio de matrices de Silvester. Se debe tener cuidado con los cambios de derecha a izquierda e izquierda a derecha (Figura 1) que tiene el método, pues se presta a confusiones.

2. Fracciones coprimas

El modelo de una fracción coprima es un caso especial de la descripción en matrices en fracción polinomial. En efecto, se cumplen (7) y (8).

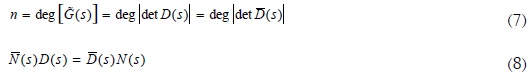
2.1 Fracción coprima izquierda

Debido a que las matrices polinomiales P(s) y Q(s) se pueden expandir como en (9) y (10), las matrices coprimas 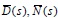, que son de menor grado, se pueden representar en (11), (12):

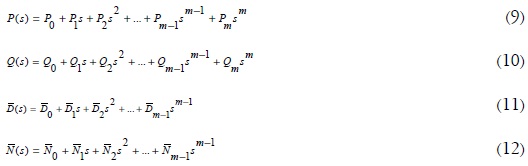
Obsérvese que el grado de 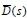debe ser n (6), esto es, m - 1= n; además, para matrices de transferencia cuadradas, todas las matrices implicadas 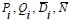son cuadradas q x q. Solucionando M en (13), que se encuentra formada por las submatrices en (14), encontramos la fracción coprima izquierda. T (15) se forma de los coeficientes de P y Q organizados en forma de matriz de Silvester² generalizada (Chen, 2009). Esta matriz debe tener m grupos P, Q formados de arriba hacia abajo, es decir, T debe ser cuadrada de tamaño m (2q).

³

El Teorema 1 implica que T debe ser singular para continuar el algoritmo. Debido a que las P filas deben ser linealmente independientes⁴. Al buscar de arriba hacia abajo, si una Q_i fila dentro del bloque de Q_i por fila llega a ser linealmente dependiente de sus filas superiores tomadas de arriba hacia abajo (up hand side), quiere decir que las subsecuentes Q_i filas también serán linealmente dependientes LI, porque T es de estructura repetitiva; entonces el número de filas linealmente independientes (denotado por v_i) de las Q_i filas es denominado los índices de la fila de 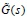y cumplen:

La fracción coprima izquierda (lcf) puede ser obtenida al calcular q vectores nulos de las matrices formadas de cada primer Q_i fila linealmente dependiente y todas sus precedentes linealmente independientes.

2.2 Fracción coprima derecha

De forma dual, las matrices polinomiales 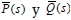se pueden expandir como en (17), (18); entre tanto, las matrices coprimas D(s), N(s), que son de menor grado, se pueden representar en (19) y (20).

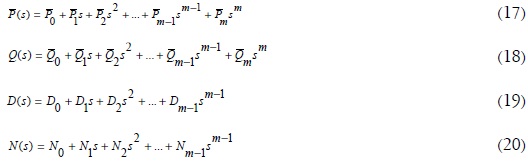
Para este caso, las fracciones coprimas (21) se deben solucionar por medio de la matriz generalizada de Silvester S (23). No obstante, la formación de S difiere notoriamente de la matriz T en estructura, mas no en propiedades, por lo cual cumple el Teorema 1, expresado en términos de S. Si encontramos las columnas linealmente independientes de la matriz generalizada, buscando de izquierda a derecha LHS, debidas a Q_i, entonces los índices por columnas deben cumplir la ecuación (24).

Al calcular los p vectores nulos de las matrices formadas por cada primer Q_i (polinomial izquierda para este caso) columna linealmente dependiente, encontraremos la fracción coprima hacia la derecha (rcf).

2.3 Factorización qr

Una forma sencilla, no única, de encontrar las filas o columnas linealmente independientes dentro de las matrices T (15) o S (23) es aplicar una descomposición qr (Chen, 2009) definida por:

Donde es una matriz triangular superior, de la misma dimensión que 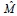, y la existencia de ceros en su diagonal permite identificar rápidamente la existencia de columnas linealmente independientes en 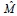(por ejemplo, véase la matriz en la ecuación (26), la cual tendría dos columnas LI). 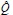es una matriz ortogonal, ignorada para nuestro fin. Con Matlab®, la función descrita como >>{q r}=qr(m) soluciona la descomposición. Es necesario, para el caso de búsqueda de filas linealmente independientes, trasponer la matriz T, para luego aplicar la factorización. Esto optimiza para ambos casos (rcf, lcf) el algoritmo.

El rango y la dimensión de la matriz generalizada de Silvester pueden darnos el valor exacto de las filas o columnas LI; sin embargo, no proporciona ni los índices por fila (16), ni los índices por columna (24); es inconveniente hacerlo por este método.

3. Metodología

3.1 Realización de la fracción coprima

Luego de encontrar las fracciones coprimas es necesario convertir el sistema a espacio de estado. Aunque se presentarán los dos algoritmos, uno para la derecha y otro para la izquierda, ambos son muy semejantes, y se diferencian entre sí por posiciones en las premultiplicaciones matriciales. La idea es llegar a un sistema del tipo (27), donde 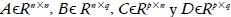, son matrices de valores constantes.

⁵

Definidas las matrices coprimas, sin importar si son hacia la derecha o hacia la izquierda, a partir de sus polinomios en (29) y (30), se plantean metódicamente los dos tipos de realizaciones siguientes:

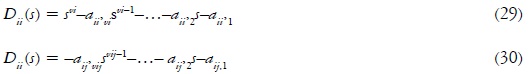
3.2 Realización de la fracción coprima derecha (rcf)

Se escribe K (31) a partir de los coeficientes de s^vi en D(s):

Para obtener directamente los coeficientes de la matriz B, ubicados en la estructura canónica 12 de controlabilidad, se calcula K^-1 (Gauthier, 2008) para este estudio. Aún así, puede quedar en otro tipo de forma canónica controlable. Para el cálculo de la matriz C (35) es necesario previamente obtener N* (33) y expandir cada polinomio como en (34).

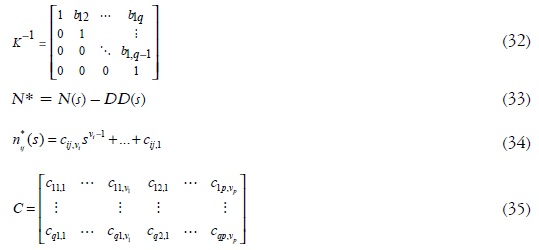
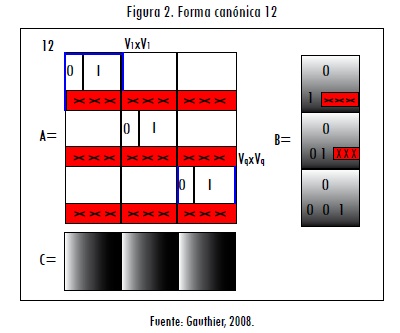
Se escribe A (39) y (40) a partir de los coeficientes del resultado de (36), cuando se expande la matriz D*. Los bloques resultantes de A se posicionan dentro de la forma canónica (véase Figura 2).

3.3 Realización de la fracción coprima izquierda (lcf)

Para este tipo de realización se utiliza el método de Gauthier (2008). Así, por ejemplo, la matriz K debe ser calculada con (41), K^-1 entregará los coeficientes de la matriz C (véase Figura 3, cada columna de la matriz de K^-1 se debe ubicar en los cuadros marcados con x). Para el cálculo de la matriz B, con los coeficientes del resultado (42), se cambian las posiciones de la matriz polinomial D(s) con la matriz de coeficientes constantes D, respecto a la realización anterior (33). Lo mismo sucede para los coeficientes de la matriz A, que se encuentran con base en (43). Los bloques resultantes al expandir los polinomios se deben ubicar en la forma canónica 4 (Figura 3).

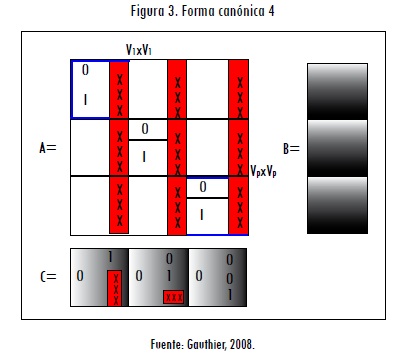
4. Ejemplo

El ejemplo que se muestra a continuación inicia con la búsqueda de una fracción matricial polinomial hacia la izquierda lmpf; luego, por medio de la matriz de Silvester generalizada se hallará la rcf para terminar con una realización mínima en forma canónica 12 (véase Figura 2), que es el camino denominado a de la Figura 1. Para ello se toma un sistema dinámico multivariable modelado como en (Polak, 1966), cuya matriz de transferencia (45) de dos entradas y dos salidas es de grado 4.

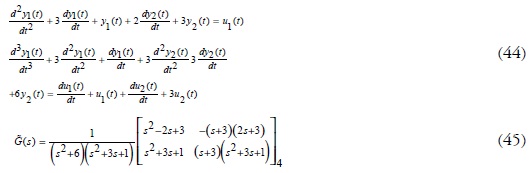
De la matriz de transferencia (45) se obtienen las matrices polinomiales en (46). Obsérvese que el determinante de es de grado 6; por lo tanto, no es mínimo el sistema. Se presenta la matriz de Silvester generalizada S_16x16 en (49) -los demás elementos de la matriz son cero, no se ubican estos, para observar que se forman tres grupos debido al grado más alto en la expansión que posee la matriz 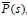; nunca puede suceder que 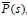sea de menor grado que 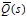, lo cual implica un sistema impropio-, cuyo determinante es cero, por lo tanto, no son coprimos.

Las columnas 11, 15 (debido a n₁), 12 y 16 (debido a n₂) de la matriz (49) son linealmente dependientes (realizar factorización qr), esto quiere decir que existen dos columnas LI, debido a n₁ y dos columnas LI debido a n₂, esto es, μ₁=2 y μ₂=2 de (24). Por lo tanto, el sistema es de orden 4. Calculando y normalizando los vectores nulos asociados a las columnas 11 y 12 de la matriz S (es fácil su cálculo con la función null de Matlab®), obtenemos la matriz M. De (22) se determinan las fracciones coprimas en (52).

A partir de (45), (53), (54) y (55), la realización mínima es (56), debido a la plantilla de forma canónica 12 (Figura 2). El lector podrá probar que su respuesta de paso es similar a la obtenida en la realización (>>figure, step(G); >>figure, step(A,B,C,D)).

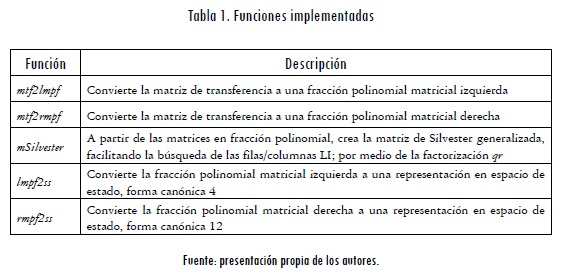
Todos los procesos se han optimizado haciendo uso de Matlab® para conseguir la realización mínima. Estas funciones se describen en la Tabla 1 y pueden ser descargadas de htpp://www.fept.co.nr/myfun.zip, donde el usuario podrá apreciar el desarrollo algorítmico.

5. Conclusiones

En este trabajo se han unido dos técnicas para obtener una realización mínima multivariable. La primera es la obtención de fracciones coprimas a partir de representaciones en fracción de matriz polinomial con matrices de Silvester generalizadas, y en la segunda interviene el método de Gauthier, lo cual en principio es aplicable solamente a fracciones coprimas hacia la izquierda. La extensión que se hace para fracciones coprimas hacia la derecha es una buena alternativa por su sencillez y facilidad en los manejos matriciales y porque la búsqueda de las fracciones coprimas no es sencilla y se debe hacer con ayuda computacional. La creación de las funciones de la Tabla 1 facilita considerablemente este proceso, con las restricciones impuestas para matrices de transferencia cuadradas.

A pesar de que las formas canónicas impuestas como 12 y 4 dentro de los estilos de realización no son las únicas, sí son las que más se utilizan como realizaciones controlables y observables. Estas, a su vez, aportan bastantes ceros, cuyo resultado para cualquier implementación es deseable, ya que requerirá un menor número de componentes.

---

Pie de Página

¹ Una fracción coprima es similar a una fracción polinomial matricial mínima, que define un número mínimo de estados para su representación en espacio de estados. Esto es, .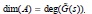
² Existen otras formas de representar la matriz de Silvester, cuyo resultado para el cálculo de M es similar (Chen, 2009).
³ Para la demostración se remite a los lectores a (Rough, 1996, p. 542).
⁴ En la mayoría de los casos se encuentra que las filas de P son linealmente independientes, debido a los corrimientos que poseen las filas de P, y aun así se encontraron casos especiales donde existe la dependencia. Esta es quizás la dificultad para encontrar fracciones coprimas para matrices de transferencia no cuadradas. El autor descarta el problema dentro del algoritmo y centra su atención en matrices de transferencia cuadradas.
⁵ No confundir esta matriz constante con la matriz de fracción coprima, la cual consta de polinomios elementales y cuya sintaxis, de aquí en adelante, será D(s).

---

Referencias

BASILIO, J. C. y KOUVARITAKIS, B. An algorithm for coprime matrix fraction description using silvester Matrices. Linear Algebra and its Applications, 1997, vol. 266, núm. 15, pp. 107-125.        [ Links ]

CHEN, C. T. Linear system theory and design. 3th. ed. Oxford: Oxford University Press, 2009.        [ Links ]

DE SCHUTTER, B. Minimal state-space realization in linear system theory: an overview. Journal of Computational and Applied Mathematics, Special Issue on Numerical Analysis in the 20th Century, 2000, vol. 121, núms. 1-2, pp. 331-354.        [ Links ]

GAUTHIER, A. Formas canónicas: curso de sistemas lineales de múltiples variables [notas de clase]. Bogotá: Universidad de los Andes, 2008.        [ Links ]

—. Identification recurrente des systemes multi-entrees, multi-sorties [These de doctorat]. Grenoble: Institut National Polytechnique de Grenoble, 1977.        [ Links ]

PANOS, J. A. y ANTHONY, N. M. Polynomial matrix description and matrix fractional description of system. En: Linear systems. Boston: Birkhäuser, 2005.        [ Links ]

POLAK, E. An algorithm for reducing a linear. time-invariant differential system to state form. IEEE Transactions on Automatic Control, 1966, vol. 11, núm. 3, pp. 577-579.        [ Links ]

ROUGH, J. W. Linear system theory. New York: Prentice Hall, 1996.        [ Links ]

SINHA, A. Linear systems optimal and robust control. Boca Ratón: CRC Press, 2007.        [ Links ]