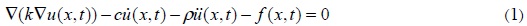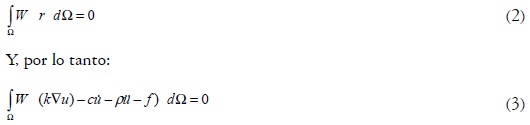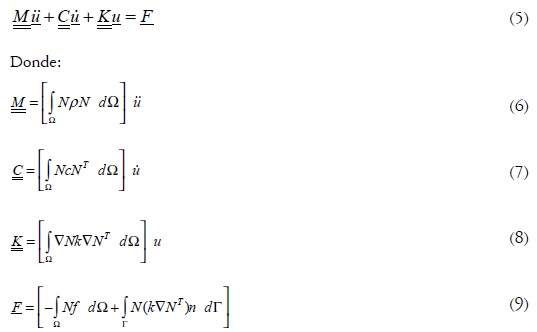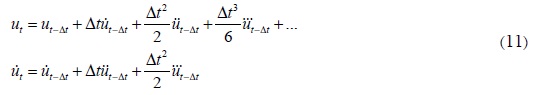Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Universidad
Print version ISSN 0123-2126
Ing. Univ. vol.13 no.2 Bogotá July/Dec. 2009
Diego Alexander Garzón-Alvarado*****
* El artículo es el resultado de un proyecto de investigación denominado Modelado matemático de procesos en ingeniería mecánica y biomédica, financiado por la Universidad Nacional de Colombia, sede Bogotá.
** This article is the result of a research project called Mathematical Processes Modeling in Mechanical and Biomedical Engineering, financed by the Universidad Nacional de Colombia, sede Bogotá.
*** O artigo é o resultado de um projeto de pesquisa denominado Modelagem matemática de processos em engenharia mecânica e biomédica, financiado pela Universidade Nacional da Colômbia, sede Bogotá.
**** Ingeniero mecatrónico. Máster en Ingeniería Mecánica, Universidad Nacional de Colombia, Bogotá, Colombia. Correo electrónico: jpinerosc@bt.unal.edu.co.
***** Ingeniero mecánico, Universidad Nacional de Colombia, Bogotá, Colombia. Máster en Ingeniería Mecánica, Universidad de los Andes, Bogotá, Colombia. Doctor en Mecánica Computacional, Universidad de Zaragoza, España. Profesor asociado del Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Correo electrónico: dagarzona@bt.unal.edu.co.
Fecha de recepción: 1 de abril de 2009. Fecha de aceptación para publicación: 8 de septiembre de 2009.
Submitted on April 1, 2009. Accepted on September 8, 2009.
Data de recepção: 1 de abril de 2009. Data de aceitação para publicação: 8 de setembro de 2009.
Resumen
La solución numérica de ecuaciones diferenciales parciales que evolucionan en el tiempo es un área de trabajo en constante desarrollo. En este trabajo se aborda la solución computacional de la ecuación de onda bajo dos métodos para problemas que involucran el tiempo: el de Newmark y el de diferencias finitas (DF). El método de Newmark tiene una alta precisión y una excelente tasa de convergencia, comparado con el de DF. Por su parte, el método de DF es de fácil implementación. Con el ánimo de comparar estos dos métodos se han puesto en funcionamiento dos problemas típicos-test en FORTRAN: el de una membrana cuadrada totalmente fija en sus bordes con una velocidad inicial en el centro y una viga simplemente empotrada con una velocidad inicial en uno de sus extremos. Cada uno de estos problemas son implementados, espacialmente, con el método de los elementos finitos y, temporalmente, con Newmark y DF. Los resultados muestran que Newmark permite utilizar pasos de tiempo mayores que DF, pero presentan mayor oscilación numérica. Con estos resultados se espera obtener datos iniciales para comparar con otros métodos que serán implementados posteriormente.
Palabras clave: Ecuaciones ondulatorias, ecuaciones diferenciales, convergencia (telecomunicación).
Abstract
The numerical solution of partial differential equations that evolve over time is a research field in constant development. In this paper on the computational solution to the wave equation, two algorithms of time integration are used: the Newmark method and the finite difference method (FDM). The Newmark method has a high precision and excellent convergence rate compared to the FDM. The FDM can be easily implemented. In an effort to compare these two methods, two typical problems using FORTRAN were implemented: first, a square membrane completely fixed at its edges with an initial velocity in the center, and second, a simply supported beam with an initial velocity at one of its ends. These test problems are discretized in the space domain through the finite element method, and in the time domain through the Newmark method and the FDM. The results show that the Newmark method allows using time steps that are greater than those of the FDM, but present a higher numerical oscillation. These results are expected to be the source of initial data for a subsequent comparison with other methods.
Key words: Wave equations, differential equations, telecommunication.
Resumo
A solução numérica de equações diferenciais parciais que evoluíram no tempo é uma área de trabalho em constante desenvolvimento. Neste trabalho aborda-se a solução computacional da equação de onda sob dois métodos para problemas que envolvam o tempo: o de Newmark e o de diferenças finitas (DF). O método de Newmark tem uma alta precisão e uma excelente taxa de convergência, comparado com o de DF. Por sua parte, o método de DF é de fácil implementação. Com o objetivo de comparar estes dois métodos forma colocados em funcionamento dois problemas típicos em FORTRAN: o de uma membrana quadrada totalmente fixa em suas bordas com uma velocidade inicial no centro e uma viga simplesmente embutida com uma velocidade inicial num de seus extremos. Cada um destes problemas são implementados, espacialmente, com o método dos elementos finitos e, temporalmente, com Newmark e DF. Os resultados mostram que Newmark permite utilizar passos de tempo maiores que DF, mas apresentam maior oscilação numérica. Com estes resultados espera-se obter dados iniciais para comparar com outros métodos que serão implementados posteriormente.
Palavras chave: Equações ondulatórias, equações diferenciais, convergência (telecomunicação).
Introducción
Las ecuaciones diferenciales parciales que dependen del tiempo tienen numerosas aplicaciones en diversas ramas de la ciencia y la ingeniería (Gershenfeld, 1998; Mansur et al., 2007). Generalmente, para este tipo de ecuaciones es difícil obtener respuestas transitorias de una manera analítica; por esto se deben utilizar técnicas numéricas para encontrar soluciones aproximadas (Mansur et al., 2008; Loureiro, 2007). La manera más fácil de verificar si estas técnicas numéricas presentan un grado de precisión y fiabilidad es solucionando un problema del cual se conozca su solución analítica, y de esta manera comparar los resultados obtenidos frente a los resultados reales del fenómeno físico (Gershenfeld, 1998; Mansur et al., 2008).
A pesar de la gran cantidad de técnicas numéricas desarrolladas, todos los métodos de integración pueden ser clasificados como explícitos e implícitos. La literatura reporta muchos algoritmos clásicos explícitos (Souza et al., 2004; Tamma et al., 1990) e implícitos (Chung y Hulbert, 1993; Newmark, 1959) para resolver problemas en los que se requiere avance en el tiempo o integración temporal.
Los métodos explícitos no implican solucionar un grupo de ecuaciones lineales para cada paso de tiempo; usan, en cambio, la ecuación diferencial en el tiempo t para predecir la solución en el tiempo t + Δt. La mayoría de problemas requiere un paso de tiempo muy pequeño que cumpla con ciertas condiciones, a fin de obtener una solución estable. Por lo tanto, todos los métodos explícitos son condicionalmente estables respecto a la medida del paso de tiempo (Chapra y Canale, 1998; Akai, 1999).
Por su parte, los métodos implícitos intentan satisfacer la ecuación diferencial en un tiempo t, después de que la solución en el tiempo t-Δt es encontrada. Estos métodos requieren solucionar un grupo de ecuaciones lineales para cada paso de tiempo; pero, en contraprestación, se pueden utilizar pasos de tiempo de mayor tamaño. Los métodos implícitos pueden ser condicional o incondicionalmente estables (Chapra y Canale, 1998; Akai, 1999).
Desde esta perspectiva, en este artículo se estudia el comportamiento de dos familias de métodos de discretización temporal, para integrar la ecuación dinámica de movimiento. Con este propósito se analiza el método de las finitas (Chapra y Canale, 1998) y el de Newmark (Hughes, 2000).
Se solucionaron dos problemas: el primero trata de una membrana elástica cuadrada totalmente fija en sus extremos a la que se le aplica una velocidad inicial en un área central. El segundo problema es el de una viga que se encuentra simplemente empotrada, a la que se le aplica una velocidad inicial en el extremo libre. Para la discretización se trata una formulación compuesta; las variables espaciales se discretizaron por medio de elementos finitos y para el avance en el tiempo se utilizaron los algoritmos que se van a evaluar.
Los resultados demuestran que el método de Newmark permite pasos de tiempo más grandes que los de diferencias finitas, aunque este último es de menor complejidad computacional, por ser tomado en una configuración explícita. Además, el método de DF tiene mayor suavidad en su respuesta transitoria. La organización del artículo es como sigue: en la primera sección se indica la forma de realizar la semidiscretización de la ecuación de movimiento en la dimensión espacial, por medio del método de los elementos finitos; en la segunda se describen cada uno de los métodos que se van a utilizar, sus características y principales aplicaciones; en la tercera se presentan casos de simulación; en la cuarta se describen los resultados, y en la última se concluye.
1. Semidiscretización de la ecuación de movimiento
La ecuación de equilibrio dinámico para problemas escalares de ρgación de onda se puede escribir como (Mansur et al., 2007; Loureiro, 2007; Carrer y Mansur, 1997):
Donde k, c y ρ son los parámetros físicos del problema, los cuales son considerados independientes del tiempo. Si ü = 0 la ecuación (1) es de reacción-difusión, si 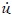 = 0 es una ecuación de onda. Además, Si ü = 0 y
= 0 es una ecuación de onda. Además, Si ü = 0 y 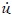 = 0 es una ecuación de Poisson, y finalmente, si
= 0 es una ecuación de Poisson, y finalmente, si 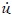 = 0,
= 0, 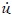 = 0 y f = 0 es una ecuación de Laplace.
= 0 y f = 0 es una ecuación de Laplace.
Para discretizar de forma espacial la ecuación (1) utiliza el método de los elementos finitos. Si (1) es el residuo, se puede multiplicar por la función W de ponderación e integrar a lo largo del dominio para obtener (Zienkiewicz y Taylor, 2000):
Para discretizar el problema es necesario bajar el orden de la segunda derivada, con el ánimo de disminuir la exigencia (debilitación) del polinomio de aproximación (reducción del orden). Con este fin se aplica el teorema de Green (Hughes, 2000; Zienkiewicz y Taylor, 2000), de donde se obtiene:
Donde û es la aproximación de la variable en cualquier parte del dominio, u es el vector solución en los puntos nodales del elemento y N son las funciones de forma del elemento cuadrado bilinear que se utiliza como función base para resolver el problema (Hughes, 2000). La forma de las funciones se puede ver en la Figura 1.
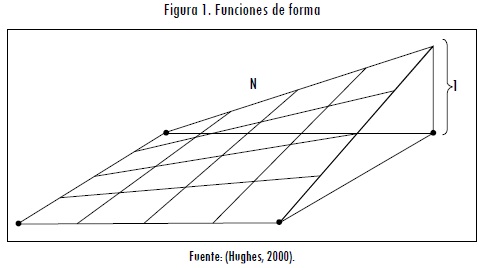
Finalmente, aplicando el método de Bubnov-Galerkin (o Galerkin estándar) en dos dimensiones (Zienkiewicz y Taylor, 2000) -para lo cual la función de ponderación es igual a la función de forma W=N-, se obtiene:
Si se está considerando un sistema estructural, M, C y K denotan matrices de masa, amortiguamiento y rigidez, respectivamente. F es el vector de carga equivalente nodal y 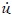 ,
, 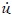 y u son, respectivamente, los vectores desconocidos de aceleración, velocidad y desplazamiento. La solución de la ecuación (5) puede obtenerse mediante un procedimiento numérico de integración temporal con condiciones iniciales en el tiempo t = 0 dadas por
y u son, respectivamente, los vectores desconocidos de aceleración, velocidad y desplazamiento. La solución de la ecuación (5) puede obtenerse mediante un procedimiento numérico de integración temporal con condiciones iniciales en el tiempo t = 0 dadas por 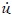 (0) y u(0).
(0) y u(0).
De esta manera, la gran mayoría de problemas dependientes del tiempo se pueden reducir a un sistema de ecuaciones diferenciales ordinarias (EDO) (Zienkiewicz y Morgan, 1982). Por lo tanto, la solución de estas EDO se puede llevar a cabo a través de los métodos de integración temporal, específicamente se utilizan el método de diferencias finitas y el método de Newmark, que se describen a continuación.
2. Métodos de integración temporal
2.1 Familia de métodos de Newmark
En 1959, Newmark presentó una familia de métodos de integración de un paso, para la solución de problemas dinámicos estructurales (Newmark, 1959). Desde ese entonces, este método se ha empleado para el análisis dinámico de una gran cantidad de problemas estructurales en ingeniería y se ha modificado, e incluso mejorado, en muchas investigaciones al respecto (Daniel, 1997; Wood et al., 1981). Para ilustrar el uso de esta familia de métodos de integración numérica se considera la solución de la ecuación lineal de equilibrio dinámico:
El uso directo de la serie de Taylor provee una aproximación de la variable u y su primera derivada:
Para completar el método, Newmark truncó estas ecuaciones y las expresó en función de dos parámetros:
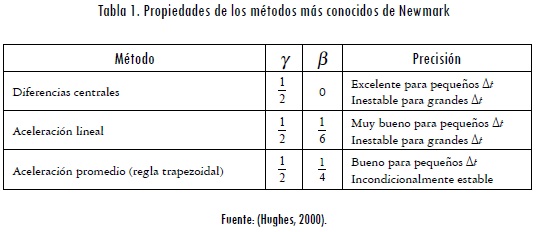
Donde β y γ son los parámetros que definen un tipo de familia particular (véase Tabla 1) (Hughes, 2000). Si se supone que la aceleración será lineal en cada paso de tiempo, la tercera derivada temporal puede ser aproximada mediante:
La sustitución de la ecuación (13) en la ecuación (12) produce las ecuaciones de Newmark en su forma habitual (14):
El término ut es obtenido a partir de las ecuaciones (10) y (14). Con base en las ecuaciones (14) se definen los predictores (Hughes, 2000; Zienkiewicz y Taylor, 2000) como:
La ecuación (17) debe ser resuelta para üt. Newmark utilizó las ecuaciones (14) y (17) iterativamente, en cada paso de tiempo, para evaluar los desplazamientos y las velocidades de cada uno de los grados de libertad del sistema de ecuaciones. Para comenzar a utilizar el método es necesario conocer 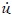 0,
0, 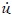 y u0. El término ü0 se puede introducir directamente o se puede calcular de la siguiente expresión:
y u0. El término ü0 se puede introducir directamente o se puede calcular de la siguiente expresión:
Se debe hacer hincapié en que el método de Newmark depende de la elección de los parámetros β y γ (ecuaciones 14 y 17); por lo tanto, es necesario conocer en qué región de estabilidad se está trabajando. En cuanto a la estabilidad para problemas donde C = 0 (amortiguamiento cero), el método de Newmark es condicionalmente estable si (Hughes, 2000):
La familia de Newmark se compone de un gran número de métodos de integración diferentes, lo cual es posible debido al rango de valores distintos que pueden tomar sus parámetros β y γ. Sin embargo, existen casos especiales, muy conocidos, estudiados y frecuentemente usados (Goudreau y Taylor, 1972). Estos métodos se resumen en la Tabla 1.
2.2 El método de diferencias finitas
El método de las diferencias finitas es un método numérico clásico ampliamente utilizado en la solución de problemas en ingeniería y ciencias (Chapra y Canale, 1998). Por su sencillez, rapidez y bajo costo computacional, con frecuencia, es usado en la mayoría de los problemas de onda (Mansur et al., 2007). El método se usa para la discretización espacial o temporal; en este caso, la discretización espacial se realizó por el método de los elementos finitos y se recurre al método de diferencias finitas para realizar la discretización temporal.
Para la discretización temporal se utilizarán aproximaciones en diferencias finitas hacia adelante. Por lo tanto, el término de velocidad tiene la forma (21a):
Donde c es la velocidad de propagación de la onda en el medio, L es una me dida lineal del elemento como el ancho de la celda o su largo y Δt es el intervalo de tiempo que se va a estimar.
Para evaluar cada uno de los métodos descritos se resuelven problemas test que tienen solución analítica, con el objetivo de compararla con la respuesta numérica. Los casos de simulación se presentan en la siguiente sección.
3. Casos de simulación
Luego de haber conocido cada uno de los métodos numéricos de integración temporal utilizados, se describen dos de los problemas físicos típicos empleados para evaluar distintas técnicas numéricas. El primer problema es el de una membrana elástica cuadrada, fija en todos sus cuatro extremos, sometida a una condición de velocidad inicial en una región cuadrada de su centro, que se deja oscilar libremente, tal como se describe en (Mansur et al., 2007). El segundo problema es el de una viga simplemente empotrada, sometida a una condición de velocidad inicial en su extremo libre, tal como se describe en (Zienkiewicz y Taylor, 2000).
3.1 Membrana elástica
La ecuación de onda escalar puede ser escrita como (Zienkiewicz, et al., 1982; Hughes, 2000):
Al realizar la semidiscretización de la ecuación (27) por medio del método de los elementos finitos, y basándonos en el procedimiento seguido para llegar a la expresión (5), se obtiene el sistema de ecuaciones diferenciales ordinarias del problema de onda escalar:
Para el problema test se diseñó una membrana cuadrada, fija a lo largo de todo su contorno y sometida a una condición de velocidad inicial v0(x,y) = c, aplicada en la región sombreada que se muestra en la Figura 2. Para este problema los parámetros del modelo son: a = 1 y c = 1 (Mansur et al., 2007).
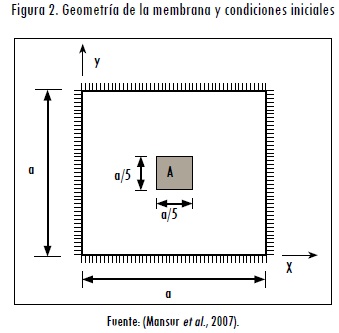
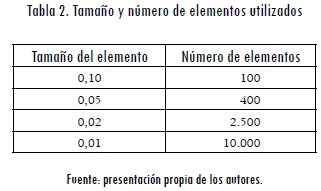
El dominio espacial se discretizó por medio del método de los elementos finitos, tal como se describió en la primera sección, empleando mallas estructuradas con elementos cuadrados bilineales de diferente tamaño, tal como se resume en la Tabla 2.
3.2 Elasticidad plana en una viga
En el segundo caso de test se analiza el comportamiento elástico bidimensional de una viga simplemente empotrada, sometida a una condición de velocidad inicial en su extremo libre. Como nos referimos a un estado de tensión plana, el vector de deformaciones significativas de un punto se define como (Oñate, 1995):
Donde σ son las componentes del esfuerzo, ρ es la densidad de masa y b son las fuerzas del cuerpo. A la anterior expresión se le aplica el proceso descrito (semidiscretización) con el fin de llegar a un sistema matricial de ecuaciones diferenciales ordinarias de la forma:
El término P(σ) depende de los esfuerzos; por ello para llevarlo a una expresión que dependa únicamente de las deformaciones utilizamos la ecuación (32), que transforma la última expresión en:
De manera que cada uno de los términos de la expresión (36) quedan definidos de la siguiente forma:
Para el segundo problema de test se diseñó una viga rectangular, empotrada en uno de sus extremos. En su extremo libre fue sometida a una condición de velocidad inicial υ0 = 0,1. El dominio espacial se discretizó por medio del método de los elementos finitos, tal como se describió, empleando una malla estructurada con elementos cuadrados bilineares de tamaño 0,005, lo que dio como resultado para la viga de acero simulada (Figura 3) un total de 4.000 elementos.

4. Resultados
4.1 Membrana elástica
En el conjunto de imágenes que constituyen la Figura 4 se muestran los resultados obtenidos para la membrana hasta el primer segundo, en diferentes instantes de tiempo (10.000 elementos, dt=0,001).
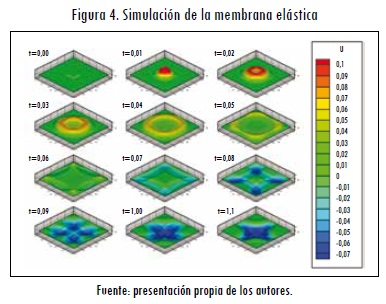
En las figuras 5, 6 y 7 se pueden ver los resultados numéricos obtenidos para el punto central de la membrana (x = 0,5 m; y = 0,5 m), con cada una de las técnicas numéricas de integración descritas, tomando diferentes pasos de discretización para el dominio espacial y para el dominio temporal. Con el fin de evaluar cualitativamente y cuantitativamente la precisión de las soluciones numéricas, se pone en cada una de las gráficas la solución analítica del problema para este punto. Las primeras simulaciones se realizan con un paso de discretización de 0,1 segundos, con cada una de las mallas estructuradas descritas en la Tabla 2.
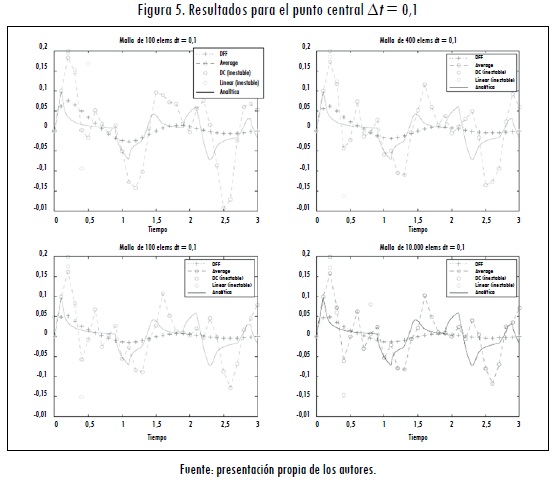
En la Figura 5 se observa la respuesta de las diferentes técnicas de integración con Δt = 0,1 segundos. Para este paso de tiempo los métodos de Newmark de diferencias centrales y de aceleración lineal son inestables. El método de Newmark de aceleración promedio intenta converger presentando oscilaciones. Cabe anotar que la única solución por diferencias finitas que cumple con el criterio de Courant es la primera simulación realizada con una malla de 100 elementos (L=0,1 m); a pesar de ello, en las simulaciones anteriores no existe divergencia.
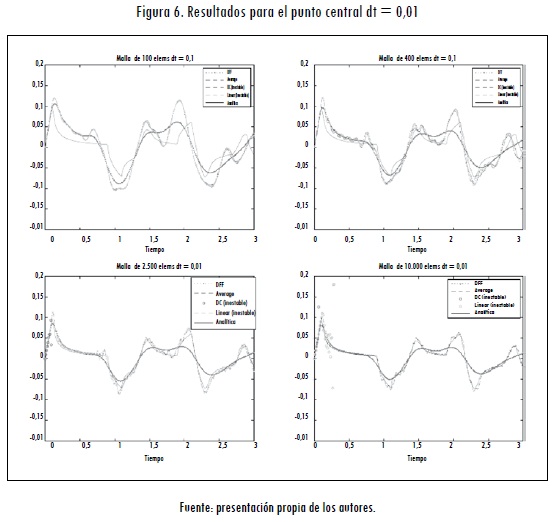
Cuando se disminuye el paso de tiempo empleado de 0,1 a 0,01 segundos, se ve que los métodos de Newmark condicionalmente estables (diferencias centrales y aceleración lineal) convergen para los casos de simulación con 100 y 400 elementos, al igual que el método condicional de aceleración lineal para el caso de 2.500 elementos (Figura 6).
Los métodos de la familia de Newmark que convergen evidencian el mismo comportamiento en sus respuestas. Tanto el método de diferencias finitas como el de Newmark presentan una disminución en el error respecto a la gráfica de la solución analítica. Se observa una tendencia de estabilización en la convergencia de cada uno de los métodos para las mallas de 2.500 y 10.000 elementos.
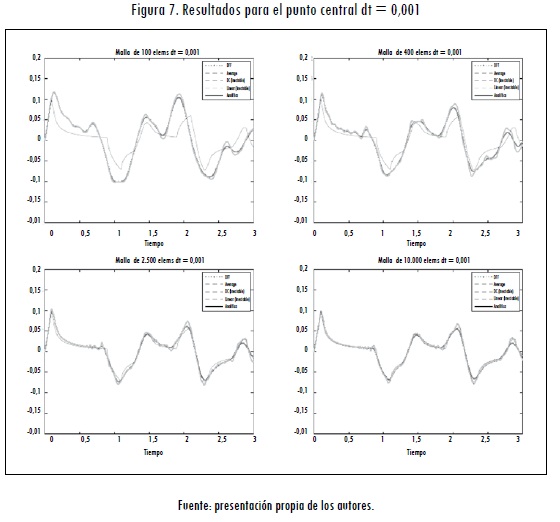
Cuando se utiliza en las simulaciones el paso de tiempo más pequeño (0,001 segundos), todos los métodos de Newmark condicionalmente estables convergen para las mallas estructuradas tomadas. Al igual que en el caso anterior (0,01), las respuestas de toda la familia de Newmark presentan el mismo comportamiento. A medida que aumentan los elementos, se observa en cada uno de los métodos una disminución en la cantidad del error, comparando con la solución analítica (Figura 7).
Para determinar la convergencia de cada uno de los métodos, se calculó el error relativo, en el espacio L2 (Hughes, 2000), utilizando la siguiente expresión:
Y con ayuda de estos valores se determinó la tasa de convergencia (ratio) para cada uno de los algoritmos. Todos los datos obtenidos se pueden observar en las tablas 3 y 4.
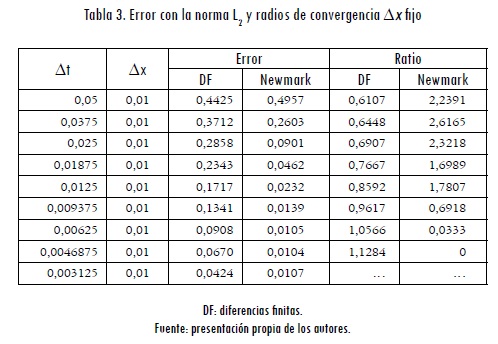
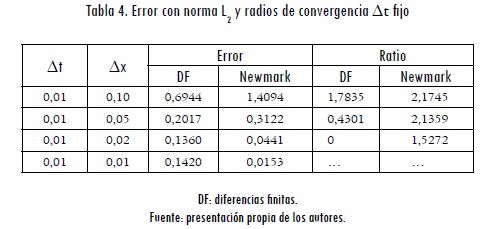
En las tablas se puede ver la diferencia práctica en los órdenes de convergencia de ambos métodos de integración temporal. El método utilizado de las diferencias finitas hacia delante totalmente explícito tiene un orden de conver gencia teórico de 1 (Zienkiewicz y Morgan, 1982) y el método de Newmark (aceleración promedio) tiene un orden de convergencia teórico de 2 (Hughes, 2000).
4.2 Viga en voladizo
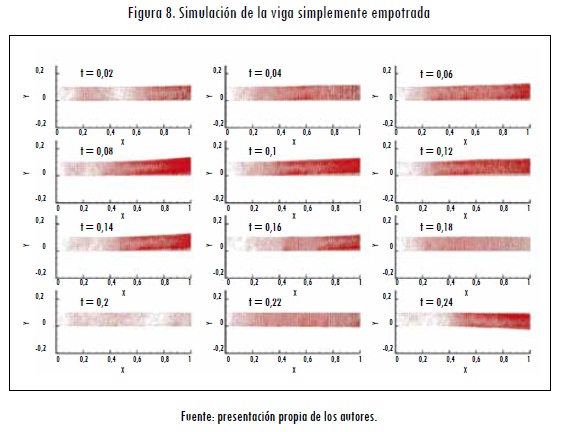
En la Figura 8 se puede observar el desplazamiento total de la viga para los tiempos indicados, con un Δt = 0,001.
La Figura 9 muestra los resultados numéricos obtenidos para la viga en voladizo. Se grafica el desplazamiento del punto central del extremo libre de la viga. La simulaciones se realizaron con los dos algoritmos descritos, utilizando dos pasos temporales distintos (0,0005 y 0,0001).
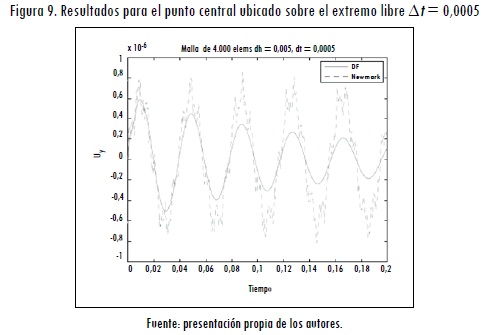
Con el primer paso de tiempo (Δt = 0,0005) se observó que el algoritmo de diferencias finitas presentaba un "amortiguamiento algorítmico", debido a que el problema era de tipo elástico, en el cual no se contemplaba disipación de energía (caso ideal). Se aprecia que el método de Newmark de aceleración promedio converge y da resultados coincidentes con lo esperado.
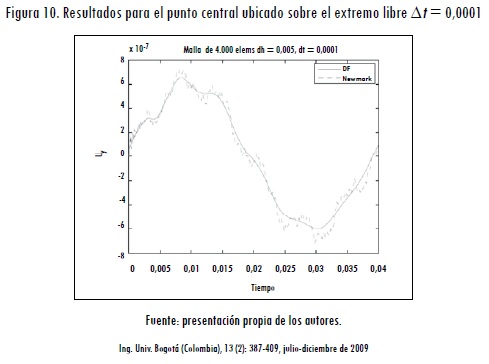
La segunda simulación se realizó con un paso de tiempo más pequeño (Δt = 0,0001). Se muestra de manera ampliada el primer semiciclo de onda que sigue el punto medio del contorno del extremo libre de la viga. Al igual que en las simulaciones de la membrana, el método de las diferencias finitas presenta curvas suaves de solución, diferente al método de Newmark empleado, en el que se presentan oscilaciones debido a los predictores (Figura 10).
5. Conclusiones
- Para las mallas gruesas tomadas de discretización espacial, el método de las diferencias finitas no presenta una buena aproximación, únicamente se ve una tendencia a seguir las concavidades de la curva de solución analítica.
- En cuanto a los métodos de Newmark expuestos, se ve un comportamiento oscilatorio, debido a las correcciones hechas en cada paso por cada uno de los predictores para ajustarse a la curva.
- Al igual que en las diferencias finitas, en el método de Newmark se evidencia que si el paso de tiempo es muy grande, no importa que se refinen las mallas espaciales, pues las respuestas serán similares y estarán alejadas de la solución analítica.
- Para los casos en que convergen, las respuestas obtenidas a través de los distintos métodos de Newmark son iguales y se encuentran sobrepuestas.
- Las respuestas del método de las diferencias finitas para todos los casos son suaves, y presentan dificultad para adaptarse a formas puntiagudas.
- Los radios de convergencia obtenidos en la práctica coinciden con los radios numéricos teóricos consultados.
- Se evidencia que el algoritmo de diferencias finitas para algunos problemas presenta un "amortiguamiento algorítmico", y que los algoritmos de la familia de Newmark, en todos los casos, presentan oscilaciones espurias de alta frecuencia.
Referencias
AKAI, T. Métodos numéricos aplicados a la ingeniería. México: Noriega, 1999. [ Links ]
CARRER, J. A. M. y MANSUR, W. J. Time-domain BEM analysis for the 2D scalar wave equation: initial conditions contributions to space and time derivatives. International Journal for Numerical Methods in Engineering, 1997, vol. 39, núm. 13, pp. 2188-2469. [ Links ]
CHAPRA, S. C. y CANALE, R. P. Numerical methods for engineers. New York: McGraw Hill, 1998. [ Links ]
CHUNG, J. y HULBERT, J. M. A time integration method for structural dynamics with improved numerical dissipation: the generalized-method. Journal of Applied Mechanics, 1993, vol. 30, pp. 371-375. [ Links ]
CHUNG, J. y LEE, J. M. A new family of explicit time integration methods for linear and non-linear structural dynamics. International Journal for Numerical Methods in Engineering, 1994, vol. 37, núm. 23, pp. 3961-3976. [ Links ]
DANIEL, W. J. T. The subcycled Newmark algorithm. Computational Mechanics, 1997, vol. 20, núm. 3, pp. 272-281. [ Links ]
DJOKO, J. K. y REDDY, B. D. An extended Hu-Washizu formulation for elasticity. Computer Methods in Applied Mechanics and Engineering, 2006, vol. 195, núms. 44-47, pp. 6330-6346. [ Links ]
GERSHENFELD, N. The nature of mathematical modeling. Cambridge: Cambridge University Press, 1998. [ Links ]
GOUDREAU, G. L. y TAYLOR, R. L. Evaluation of numerical integration methods in elastodynamics. Computer Methods in Applied Mechanics and Engineering, 1972, vol. 2, pp. 69-97. [ Links ]
HAHN, G. D. A modified Euler method for dynamic analysis. International Journal for Numerical Methods in Engineering, 1991, vol. 32, núm. 5, pp. 943-955. [ Links ]
HOFF, C. y TAYLOR, R. L. Higher derivative explicit one step methods for non-linear dynamic problems. Part I: design and theory. International Journal for Numerical Methods in Engineering, 1990, vol. 29, núm. 2, pp. 275-290. [ Links ]
HUGHES, T. J. R. The finite element method-linear static and dynamic finite element analysis. New York: Dover Publishers, 2000. [ Links ]
HULBERT, G. M. y CHUNG, J. Explicit time integration algorithms for structural dynamics with optimal numerical dissipation. Computer Methods in Applied Mechanics and Engineering, 1996, vol. 137, núm. 2, pp. 175-188. [ Links ]
LINIGER, W. Global accuracy and a stability of one and two steps integration formulas for stiff ordinary differential equations. Conference on the Numerical Solution of Differential Equations, Dundee University, 1969, vol. 109, pp. 188-193. [ Links ]
LOUREIRO, F. S. Métodos de integracão temporal baseados no cálculo numérico de funcões de Green a través do método dos elementos finitos. [MSc Thesis]. Rio de Janeiro: Universidade Federal do Rio de Janeiro-COPPE, 2007. [ Links ]
MANSUR, W. J. et al. Explicit time-domain approaches based on numerical Green's functions computed by finite differences-The ExGA family. Journal of Computational Physics, 2007, vol. 227, núm. 1, pp. 851-870. [ Links ]
—. Numerical solution for the linear transient heat conduction equation using an Explicit Green's Approach. Journal of Heat and Mass Transfer, 2008, vol. 52, núms. 3-4, pp. 694-701. [ Links ]
NEWMARK, N. M. A method of computation for structural dynamics. Journal Engineering Mechanics Division, 1959, vol. 85, pp. 67-94. [ Links ]
OÑATE, E. Cálculo de estructuras por el método de elementos finitos: análisis estático lineal. 2a ed. Barcelona: CIMNE, 1995. [ Links ]
SOUZA, L. A.; CARRER, J. A. M. y MARTINS, C. J. A fourth order finite difference method applied to elastodynamics: finite element and boundary element formulations. Structural Engineering and Mechanics, 2004, vol. 17, núm. 6, pp. 735-749. [ Links ]
TAMMA, K. K. y NAMBURU, R. R. A robust self-starting explicit computational methodology for structural dynamic applications: architecture and representations. International Journal for Numerical Methods in Engineering, 1990, vol. 29, núm. 7, pp. 1441-1454. [ Links ]
TIMOSHENKO, S. y GOODIER, J. N. Theory of elasticity. New York: McGraw-Hill, 1951. [ Links ]
WOOD, W. L; BOSSAK, M. y ZIENKIEWICZ, O. C. An alpha modification of Newmark's methods. International Journal for Numerical Methods in Engineering, 1981, vol.15, núm. 10, pp. 1562-1566. [ Links ]
ZIENKIEWICZ, O. C. y TAYLOR, R. L. El método de los elementos finitos: las bases. Barcelona: CIMNE, 2000. [ Links ]
ZIENKIEWICZ, O. C. y MORGAN, K. Finite element and approximation. New York: Wiley, 1982. [ Links ]