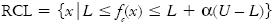Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Universidad
Print version ISSN 0123-2126
Ing. Univ. vol.14 no.1 Bogotá Jan./June 2010
Uso combinado de GRASP y Path-Relinking en la programación de producción para minimizar la tardanza total ponderada en una máquina*
Combined Use of GRASP and Path-Relinking during Production Scheduling in order to Minimize Total Weighted Tardiness in a Machine**
Uso combinado de GRASP e Path-Relinking na programação de produção para minimizar a demora total ponderada numa máquina***
Juan Pablo Caballero-Villalobos*****
* Este artículo se deriva del trabajo desarrollado en programación de la producción, en la Maestría en Ingeniería Industrial del primer autor.
** This article results from the work on production scheduling of the first author in the Industrial Engineering Master Programm.
*** Este artigo deriva-se do trabalho desenvolvido em programação da produção no Mestrado em Engenharia Industrial do primeiro autor.
**** Ingeniero de Sistemas, Universidad Nacional de Colombia, Bogotá, Colombia. Estudiante de Maestría en Ingeniería Industrial, Pontificia Universidad Javeriana, Bogotá, Colombia. Correo electrónico: vega.carlos@javeriana.edu.co.
**** Ingeniero Industrial, Pontificia Universidad Javeriana, Bogotá, Colombia. Magíster en Ingeniería Industrial, Universidad de los Andes, Bogotá, Colombia. Profesor asistente, Departamento de Ingeniería Industrial, Pontificia Universidad Javeriana. Correo electrónico: juan.caballero@javeriana.edu.co.
Fecha de recepción: 19 de agosto de 2009. Fecha de aceptación para publicación: 4 de noviembre de 2009.
Submitted on August 19, 2009. Accepted on November 4, 2009.
Data de recepção: 19 de agosto de 2009. Data de aceitação para publicação: 4 de novembro de 2009.
Resumen
Este trabajo presenta el resultado de integrar dos técnicas metaheurísticas (GRASP y Path Relinking), las cuales, a pesar de la eficiencia reportada en otros problemas, no se han utilizado ampliamente para solucionar problemas de programación de la producción. Estas técnicas se emplearon de manera conjunta para resolver el problema de minimización de la tardanza total ponderada en una máquina, 1  Σ WjTj, a fin de obtener soluciones de calidad en tiempos aceptables. Los resultados experimentales muestran mejoras sustanciales que evidencian estadísticamente la importancia de utilizar Path-Relinking como técnica de postoptimización complementaria de GRASP. Para usar GRASP en la solución del problema mencionado se propone una función de utilidad dinámica para los trabajos por procesar, considerando sus parámetros descriptivos. De este modo, se proporciona una idea clara de su implementación, de modo que empresas de diverso tamaño que enfrentan ese tipo de problema puedan realizarla contando sólo con la disponibilidad de MS Excel, sin tener que recurrir a software especializado.
Σ WjTj, a fin de obtener soluciones de calidad en tiempos aceptables. Los resultados experimentales muestran mejoras sustanciales que evidencian estadísticamente la importancia de utilizar Path-Relinking como técnica de postoptimización complementaria de GRASP. Para usar GRASP en la solución del problema mencionado se propone una función de utilidad dinámica para los trabajos por procesar, considerando sus parámetros descriptivos. De este modo, se proporciona una idea clara de su implementación, de modo que empresas de diverso tamaño que enfrentan ese tipo de problema puedan realizarla contando sólo con la disponibilidad de MS Excel, sin tener que recurrir a software especializado.
Palabras clave: Programación de la producción, GRASP (programa para computador), tiempos y movimientos.
Abstract
This paper shows the results of integrating two meta-heuristic techniques, GRASP and Path-Relinking, which have not been widely used to solve production-scheduling problems despite of their proved efficiency. These techniques were used to solve the problem of minimizing total weighted tardiness problem in a machine, 1  Σ WjTj, and good results in short time were obtained. Experiment outcomes show that the use of Path-Relinking as a final step for GRASP can result in qualitysequence improvements. In order to use GRASP in the solution to this problem, a dynamic utility function for the jobs to process, bearing in mind its descriptive parameters, is proposed. Additionally, this work offers a clear implementation proposal for ventures of different sizes, so they are able to overcome this problem by using MS Excel, instead of specialized scheduling software.
Σ WjTj, and good results in short time were obtained. Experiment outcomes show that the use of Path-Relinking as a final step for GRASP can result in qualitysequence improvements. In order to use GRASP in the solution to this problem, a dynamic utility function for the jobs to process, bearing in mind its descriptive parameters, is proposed. Additionally, this work offers a clear implementation proposal for ventures of different sizes, so they are able to overcome this problem by using MS Excel, instead of specialized scheduling software.
Key words: Production scheduling, GRASP (computer file), times and movements.
Resumo
Este trabalho apresenta o resultado de integrar duas técnicas metaheurísticas (GRASP e Path Relinking), que apesar da eficiência relatada em outros problemas, não tem sido amplamente utilizadas para solucionar problemas de programação da produção. Estas técnicas foram empregadas de maneira conjunta para resolver o problema de minimização da demora total ponderada numa máquina, 1  Σ WjTj, com o objetivo de obter soluções de qualidade em tempos aceitáveis. Os resultados experimentais mostram melhoras substanciais que evidenciam estatisticamente a importância de utilizar Path-Relinking como técnica de pós-otimização complementar de GRASP. Para usar GRASP na solução do problema mencionado propõe-se uma função de utilidade dinâmica para os trabalhos a processar, considerando seus parâmetros descritivos. Deste modo, proporciona-se uma ideia clara de sua implementação, de modo que empresas de diferentes tamanhos que enfrentem esse tipo de problema possam realizá-la contando somente com a disponibilidade de MS Excel, sem ter que utilizar um software especializado.
Σ WjTj, com o objetivo de obter soluções de qualidade em tempos aceitáveis. Os resultados experimentais mostram melhoras substanciais que evidenciam estatisticamente a importância de utilizar Path-Relinking como técnica de pós-otimização complementar de GRASP. Para usar GRASP na solução do problema mencionado propõe-se uma função de utilidade dinâmica para os trabalhos a processar, considerando seus parâmetros descritivos. Deste modo, proporciona-se uma ideia clara de sua implementação, de modo que empresas de diferentes tamanhos que enfrentem esse tipo de problema possam realizá-la contando somente com a disponibilidade de MS Excel, sem ter que utilizar um software especializado.
Palavras-Chave: Programação da produção, GRASP (programa para computador), tempos e movimentos.
Introducción
En la actualidad es fundamental para las empresas del sector productivo lograr un grado de competitividad que garantice su supervivencia en un mercado mundial cambiante. En este contexto, las empresas se ven en la necesidad de contar con una programación de la producción efectiva, a fin de cumplir con los tiempos de entrega a sus clientes, ya que incumplirlos puede resultar en una pérdida significativa de confianza (Pinedo, 2008).
Dado lo anterior, en este artículo se estudia uno de los problemas comunes de la programación de la producción: la tardanza total ponderada para una máquina (Sen, Sulek y Dileepan, 2003), el cual indica una medida de servicio al cliente de acuerdo con su importancia para la empresa, que se conoce como 1  Σ WjTj, en el esquema de clasificación introducido por Graham et al. (1979). Para dar una definición más clara del problema se utiliza la dada por (Sen, Sulek y Dileepan, 2003), que tiene los siguientes supuestos:
Σ WjTj, en el esquema de clasificación introducido por Graham et al. (1979). Para dar una definición más clara del problema se utiliza la dada por (Sen, Sulek y Dileepan, 2003), que tiene los siguientes supuestos:
- n trabajos (1,2, ..., n).
- Todos los trabajos están listos para ser procesados en el instante de tiempo 0, es decir, rj = 0∀j = 1,2, ..., n.
- No se permite el desmonte trabajos.
- Un trabajo está definido por su pj (tiempo de procesamiento), wj (importancia dentro del problema) y dj (tiempo límite de terminación).
El problema consiste en minimizar:
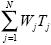
Donde:
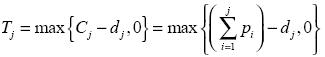
Este problema se clasifica como NP-Hard (Sen, Sulek y Dileepan, 2003), razón por la cual se dificulta su solución óptima a través de métodos exactos para problemas de más de 50 trabajos (Bozejko, Grabowski y Wodecki, 2006), y representa un reto para el estudio de diferentes enfoques metaheurísticos (Wang y Tang, 2009).
Dos factores motivaron la realización de este trabajo: el primero es el reporte de un amplio número de autores sobre las bondades de la implementación y la calidad de los resultados obtenidos en diversos problemas mediante el uso de la metaheurística Greedy Randomized Adaptive Search Procedures (GRASP) y de las mejoras obtenidas a buenas soluciones encontradas mediante la técnica de postoptimización Path-Relinking. El segundo factor fue el resultado de la revisión bibliográfica realizada, en la cual se encontró un escaso número de trabajos que empleen esta combinación de técnicas en la solución de problemas en el campo de programación de la producción, hecho que se amplía en la siguiente sección.
Por lo tanto, este artículo busca establecer la aplicabilidad de la metaheurística GRASP para abordar uno de los problemas clásicos en el campo de la programación de la producción, 1  Σ WjTj, y posteriormente evaluar si existe evidencia estadística de mejoras obtenidas en la calidad de las soluciones, a través de la aplicación de Path-Relinking como medio de postoptimización.
Σ WjTj, y posteriormente evaluar si existe evidencia estadística de mejoras obtenidas en la calidad de las soluciones, a través de la aplicación de Path-Relinking como medio de postoptimización.
Entre las bondades mencionadas para estas dos técnicas se mencionan particularmente: la habilidad del GRASP para construir soluciones factibles y continuar con esta característica a través de su uso (Glover y Kochenberger, 2003), al igual que la característica del Path-Relinking tanto para integrar estrategias de diversificación e intensificación en búsquedas en vecindarios (Glover y Kochenberger, 2003) como para mostrar la pertinencia de implementar Path-Relinking como técnica de postoptimización, a fin de buscar mejorar la calidad de las soluciones de una heurística.
La organización del presente artículo es la siguiente: revisión de algunas de las técnicas utilizadas hasta ahora para resolver el problema en cuestión; explicación de la metodología utilizada, haciendo hincapié en los algoritmos desarrollados; análisis de los resultados computacionales obtenidos, y presentación de conclusiones y recomendaciones.
1. Antecedentes
El problema de la tardanza total ponderada para una máquina ha sido abordado en un gran número de estudios. Y, según la revisión de (Bozejko, Grabowski y Wodecki, 2006), a través de las últimas tres décadas se han usado métodos enumerativos, métodos de construcción y métodos de intercambio, como enfoques de solución.
Los métodos enumerativos combinan la programación dinámica y el Branch and Bound, y han mostrado mejoras sustanciales en las búsquedas exhaustivas, pero son aplicables únicamente a problemas relativamente pequeños, no más de 50 trabajos, debido a su costo computacional (Bozejko, Grabowski y Wodecki, 2006; Wang y Tang, 2009).
Los métodos de construcción usan reglas de despacho para generar una solución acomodando un trabajo en cada paso del algoritmo, y aunque se han realizado una gran cantidad de heurísticas constructivas con excelentes tiempos de respuesta, la calidad de las soluciones no ha sido muy buena (Bozejko, Grabowski y Wodecki, 2006).
Por último, los métodos de intercambio parten de una solución inicial e iterativamente intentan mejorar la solución actual mediante cambios locales. Los intercambios son realizados hasta que no hay una mejora de la solución actual, lo que indicaría un mínimo local. A efectos de mejorar el desempeño de los algoritmos de búsqueda local se han combinado con metaheurísticas, como la búsqueda tabú, el recocido simulado, los algoritmos genéticos y la optimización de colonia de hormigas (Bozejko, Grabowski y Wodecki, 2006).
Bozejko, Grabowski y Wodecki (2006), basándose en estos enfoques, propusieron una búsqueda tabú enfocada en bloques, donde se toman conjuntos o bloques de trabajos y se realizan movimientos compuestos. Tales movimientos consisten en realizar varios movimientos simultáneamente, lo que permite una aceleración en la ejecución del algoritmo.
La revisión hecha por (Liao y Cheng, 2007) centra su análisis en las metaheurísticas usadas para solucionar el problema, dentro de las cuales encuentran: búsqueda evolutiva, búsqueda evolutiva con fase de desestabilización, recocido simulado, aceptación de umbral, aceptación de umbral con paso hacia atrás, todas trabajadas por Feldman y Biskup (2003), y un híbrido de algoritmos genéticos con búsqueda tabú trabajado por Hino, Ronconi y Mendes (2005).
Liao y Cheng (2007), basándose en su revisión, propusieron un híbrido entre búsqueda en vecindario variable (VNS) y búsqueda tabú. Afirman que la VNS ha probado ser una heurística simple y efectiva, y ha sido combinada con otras metaheurísticas como GRASP.
Adicionalmente, en la revisión realizada por (Wang y Tang, 2009) se ve un enfoque hacia programación dinámica, que pone el relieve en el método Iterated Dynasearch, trabajado por (Congram, Potts y Van de Velde, 2002), y VNS, trabajado por (Mladenovic y Hansen, 1997; Hansen y Mladenovic, 2001; Hansen, Mladenovic y Moreno, 2008; Fleszar, Osman e Hindi, 2008). La revisión les permitió plantear el método de búsqueda en vecindad variable basada en la población (PVNS). Este método itera varias veces la heurística VNS para obtener una población de soluciones. A esta población se le aplica una combinación de Path-Relinking, búsqueda de profundidad variable y búsqueda tabú como método de búsqueda local.
2. Aspectos teóricos
A continuación se describen las técnicas utilizadas para resolver el problema de la tardanza total ponderada para una máquina. Dentro de estas se incluyen el algoritmo de búsqueda local 2-optimal y las metaheurísticas GRASP y Path-Relinking.
2.1 Búsqueda local 2-optimal
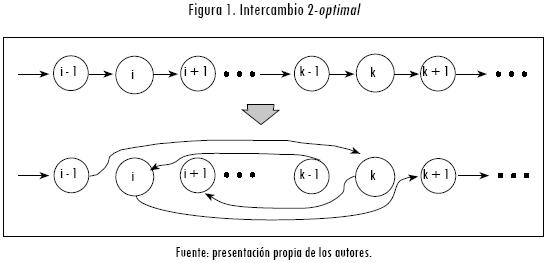
El algoritmo 2-optimal es una de las búsquedas locales más conocidas, junto con 3-optimal y Lin-Kernighan, y se basan en intercambios k-Opt. Básicamente, consiste en eliminar dos arcos de un grafo dirigido, cambiar la dirección de una de las "porciones" resultantes y luego reconectar el grafo (Glover y Kochenberger, 2003) (Figura 1).
2.2 Metaheurística GRASP
La metaheurística GRASP consiste de un proceso iterativo de dos fases: constructiva y búsqueda local. En la primera se genera una solución factible, cuya vecindad es examinada mediante una búsqueda local hasta que se encuentra un mínimo local. Al final, la mejor solución encontrada se deja como el resultado al problema (Glover y Kochenberger, 2003).
Para realizar la fase constructiva es necesario definir una función de costo acorde al problema que se esté tratando, que permitirá evaluar cada elemento que puede conformar la solución factible inicial. Cuando se han evaluado todos los elementos se construye una lista de los candidatos que van a integrar la solución inicial (RCL) con aquellos elementos que obtienen el mejor valor de la función de costo definida. Es decir:
Donde:
ƒc(x) es la función de costo del elemento x.α es un número entre 0 y 1.
En caso de tener un problema de minimización, L es el menor valor de la función de costo encontrado.
En caso de tener un problema de minimización, U es el mayor valor de la función de costo encontrado.
Luego se escoge un candidato al azar de la RCL para adicionar a la solución inicial y se vacía la RCL. El proceso de llenado y limpieza de la RCL se realiza hasta que se tiene construida la solución inicial. La mayor ventaja de este proceso es que la solución inicial se va construyendo, paso a paso, sin afectar la factibilidad del resultado (Glover y Kochenberger, 2003). El seudocódigo es el presentado en la Figura 2.

La segunda fase de GRASP utiliza un método de búsqueda local que intente, por medio de intercambios sencillos de los elementos de la solución inicial, mejorar el valor de la función objetivo de la solución encontrada con la fase constructiva. Estos intercambios son análogos a realizar búsquedas en una vecindad cercana a la solución inicial dentro del espacio de solución del problema (Glover y Kochenberger, 2003). Utilizando intercambios 2-optimal (sección 2.1) el seudocódigo es el presentado en la Figura 3.

Finalmente, el seudocódigo de la metaheurística GRASP resultaría en lo mostrado en la Figura 4.

2.3 Path-Relinking
El Path-Relinking es un enfoque que integra las estrategias de diversificación e intensificación en un esquema de búsqueda. Funciona generando nuevas soluciones mediante la exploración de trayectorias que conectan soluciones de alta calidad. Se toman dos de estas soluciones, una solución inicial y una solución guía, y se genera un camino en la vecindad que conecta a las dos. Esto se hace con movimientos que integren componentes de la solución guía en la solución inicial (Glover y Kochenberger, 2003).
Básicamente, se maneja una lista de soluciones "élite" que comienza vacía. Cada solución encontrada con el método que se esté trabajando es añadida siempre a la lista élite. Si la lista se encuentra llena y una nueva solución es mejor que la peor de la lista, se añade la primera y se remueve la segunda. Por último, cuando se termine el proceso de búsqueda de soluciones y el llenado de la lista élite, se toma la mejor solución de la lista élite (solución guía) con otra solución élite (solución inicial) y se intenta construir el camino que las conecte, en busca de una solución intermedia que sea mejor que alguna de las dos.
3. Desarrollo
Aquí se describe la integración de las técnicas descritas en los párrafos anteriores y la forma en que se implementaron para resolver el problema de la tardanza total ponderada para una máquina. Todos los algoritmos que componen la solución fueron implementados en una macro de MS Excel 2007 en lenguaje Visual Basic para aplicaciones.
3.1 Parámetros
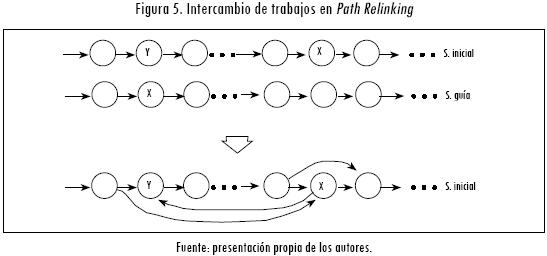
La solución propuesta requiere el parámetro α necesario para la metaheurística GRASP, que indica el porcentaje de elementos que deben adicionarse a la RCL, y es un valor entre 0 y 1; el número de veces que se ejecutarán la fase constructiva y la búsqueda local de GRASP; el tamaño de la lista élite para Path-Relinking, y la información de cada trabajo —tiempo de proceso (pj), importancia (wj) y fecha límite de terminación (dj)—. La aplicación también puede recibir el valor de la mejor solución del problema que se esté procesando, aunque no es obligatorio. Cada trabajo se identifica con un número entero 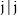 ∈{1, 2, ..., n}, donde n es la cantidad de trabajos del problema. Con esta notación cada programa o solución generada será una permutación de los primeros n números enteros.
∈{1, 2, ..., n}, donde n es la cantidad de trabajos del problema. Con esta notación cada programa o solución generada será una permutación de los primeros n números enteros.
3.2 Implementación del GRASP
Como se mencionó en la sección 2.2, es necesario definir una función de costo para la metaheurística GRASP en su fase de construcción. Para el problema en cuestión se definió la siguiente función de acuerdo con la importancia y tardanza de un trabajo en el instante de tiempo t:

Como el objetivo consiste en minimizar la tardanza ponderada, los elementos que se adicionan a la RCL son aquellos que tienen valores pequeños de ƒc. La implementación de esta función corresponde a las líneas 5 y 14 de la Figura 2.
La fase de búsqueda local se implementó basándose en el algoritmo 2-optimal descrito en la sección 2.1 con la estrategia Best Improvement (Glover y Kochenberger, 2003), donde se examinan todos los posibles intercambios de pares de elementos y se escoge el mejor. En cada intercambio se genera una solución candidata, pero si el valor de la función objetivo de esta es menor que el valor que se obtiene de la solución actual, esta se debe actualizar. Este proceso se repite hasta revisar todos los intercambios de pares de trabajos. Cabe anotar que utilizar esta técnica no destruye la factibilidad de la solución inicial de la primera fase de GRASP, debido a que es un intercambio entre pares de trabajos y no hay restricciones de precedencia entre ellos.
3.3 Implementación de Path-Relinking
Luego de cada iteración de GRASP, la solución obtenida (solución candidata) se analiza para añadirla al conjunto de soluciones élite (sección 2.3). Como primera medida se compara el valor de la función objetivo de la solución candidata; si no existe una solución con el mismo valor de función objetivo, la solución candidata se almacena en la lista élite. Si existe un valor de función objetivo igual, se debe garantizar que la solución candidata es lo suficientemente diferente de las demás de la lista élite de acuerdo con un valor p, que representa un porcentaje de trabajos que deben ser diferentes entre la solución candidata y cada una de las soluciones élites. Si alguna de estas condiciones no se cumple, la solución candidata se descarta.
Adicionalmente, si no se han terminado las iteraciones de GRASP y la lista élite llega a su máximo de elementos, el valor de la función objetivo de la solución candidata se compara con el valor de la función objetivo de la peor solución élite. Si el valor de la función objetivo de la solución candidata es menor, se validan las condiciones expuestas en el párrafo anterior. Si las condiciones se cumplen, la peor solución élite se retira del conjunto de soluciones élite y se añade la solución candidata.
Una vez las iteraciones de GRASP han terminado, se toma la mejor solución élite como solución guía y se compara con cada una de las demás soluciones élites (solución inicial). Si el trabajo en la i-ésima posición de la solución inicial es diferente del trabajo en la i-ésima posición en la solución guía, se ubica el trabajo correspondiente dentro de la solución inicial y se ubica en la posición sugerida por la solución guía (Figura 5).
Nuevamente, se realizan las validaciones descritas anteriormente para esta nueva solución guía y se examina si debe ser añadida a la lista de soluciones élite. Si la nueva solución guía se adiciona al conjunto de mejores soluciones, el proceso de comparación vuelve a comenzar. El proceso finaliza cuando no se encuentran nuevas soluciones para insertar en la lista élite. El seudocódigo de Path-Relinking se presenta en la Figura 6.

4. Resultados computacionales
La solución propuesta fue probada con instancias de problemas de 40, 50 y 100 trabajos, para los que se conoce el mejor valor de la función objetivo encontrado a la fecha. Estas instancias fueron tomadas de las librerías de datos de la OR-Library (http://people.brunel.ac.uk/~mastjjb/jeb/info.html). La solución fue ejecutada 30 veces para cada problema y cada ejecución realizaba 10 iteraciones de GRASP. En todos los casos el tamaño máximo de la lista élite fue de 30 elementos. El parámetro α se trabajó con valores de 0,05; 0,10; 0,15 y 0,20 para GRASP, y el porcentaje de elementos diferentes para poder ingresar a la lista élite en Path-Relinking fue del 20% del número de trabajos del problema.
Los resultados que se presentan a continuación representan la diferencia porcentual del valor de la función objetivo hallado con la solución propuesta respecto a los valores de función objetivo que se conocen de cada instancia. La Figura 7 muestra el resumen de resultados de las 30 ejecuciones de GRASP y las respectivas soluciones élite de Path-Relinking para cada valor del parámetro α de cada instancia.
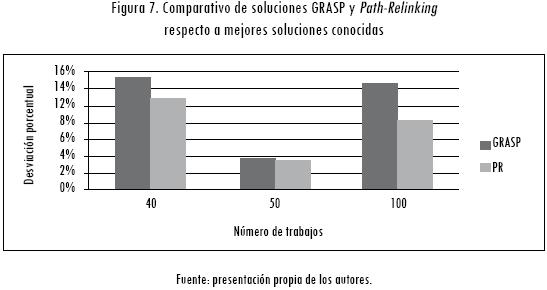
El resumen de los resultados de las 30 ejecuciones de GRASP y las respectivas soluciones élite de Path-Relinking, para todas las instancias y cada valor del parámetro α, se presentan en las figuras 8, 9 y 10.
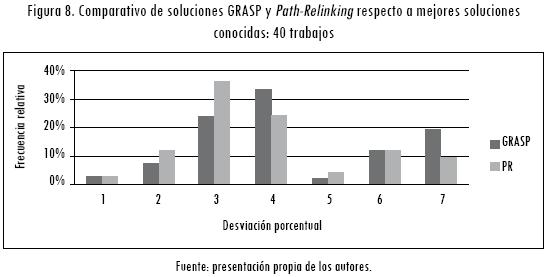
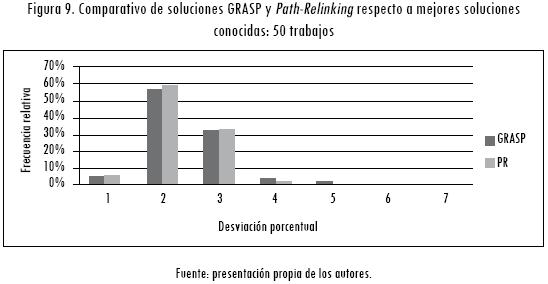
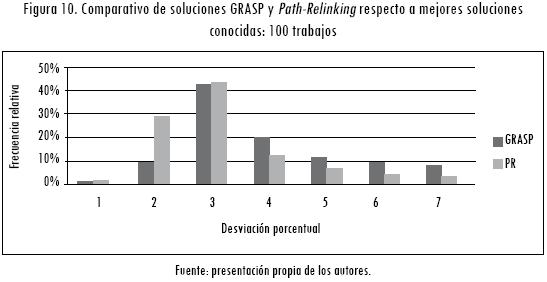
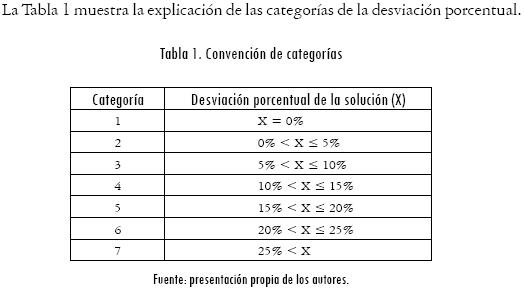
La Tabla 1 muestra la explicación de las categorías de la desviación porcentual.
De lo anterior se podría decir que la técnica de postoptimización Path-Relinking mejora la calidad de las soluciones generadas por la metaheurística GRASP. Esto se evidencia en la Figura 11, que presenta la diferencia de medias para comparar la calidad de las soluciones entre los dos métodos para todos los valores obtenidos, independiente de la instancia del problema, con una confianza del 90%.
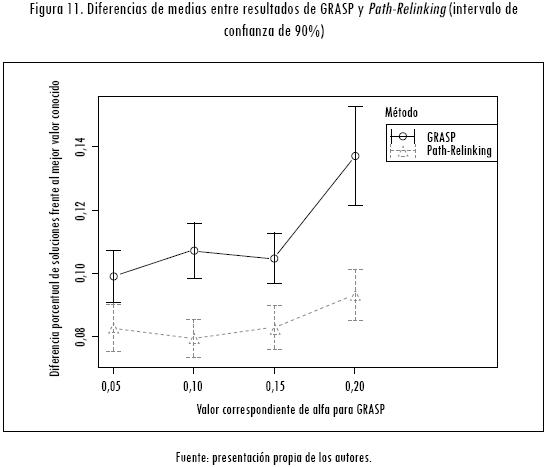
Al analizar la Figura 11 se puede observar que la dispersión de los resultados de Path-Relinking es menor que la dispersión de los resultados de la metaheurística GRASP y hay evidencia estadística con una confianza del 90%, en cuanto a que Path-Relinking mejora la calidad de las soluciones de la metaheurística GRASP para cada uno de los valores de α escogidos (0,05; 0,10; 0,15 y 0,20), y se confirma la relevancia de implementarla como técnica de mejoramiento de las soluciones halladas por una heurística.
De la misma forma, se puede apreciar que no hay diferencia significativa entre los resultados obtenidos con la metaheurística GRASP con valores de α de 0,05; 0,10 y 0,15. Sin embargo, hay indicios para decir que son mejores que los resultados obtenidos con un α de 0,20.
5. Conclusiones y recomendaciones
Se ha propuesto una solución basada en la integración de GRASP y Path-Relinking para el problema 1  Σ WjTj, que obtiene diferencias pequeñas frente a los mejores valores conocidos de las diferentes instancias de los problemas probados y da los mejores resultados en los problemas de 50 trabajos. Adicionalmente, Path-Relinking muestra mejoramientos significativos de las soluciones encontradas por la metaheurística GRASP para todos los valores de α escogidos y se muestra la pertinencia de su implementación como técnica de postoptimización. Además, se da la posibilidad a empresas de diferente tamaño de implementar esta técnica para apoyar la solución de problemas de programación de la producción.
Σ WjTj, que obtiene diferencias pequeñas frente a los mejores valores conocidos de las diferentes instancias de los problemas probados y da los mejores resultados en los problemas de 50 trabajos. Adicionalmente, Path-Relinking muestra mejoramientos significativos de las soluciones encontradas por la metaheurística GRASP para todos los valores de α escogidos y se muestra la pertinencia de su implementación como técnica de postoptimización. Además, se da la posibilidad a empresas de diferente tamaño de implementar esta técnica para apoyar la solución de problemas de programación de la producción.
Aunque la diferencia porcentual entre las soluciones encontradas y las mejores soluciones es de aproximadamente el 8% para Path-Relinking y de alrededor del 12% para GRASP, se recomienda su uso por la facilidad de implementar una sencilla hoja de cálculo, como el caso de Excel de Microsoft Office, Calc de Open Office o KSpread de KOffice, sin que se tenga que incurrir en altos costos por la compra de software de programación de la producción o, en el mejor de los casos, la codificación de técnicas, que aunque reportan resultados de alta calidad, implican un mayor esfuerzo en la programación y requieren, en muchos casos, contar con conocimientos de optimización avanzada, los cuales no siempre se encuentran al alcance de los usuarios de las empresas en nuestro medio. También es importante resaltar que a pesar de que los tiempos de cómputo no son reportados en este estudio, oscilan entre unos pocos segundos hasta diez minutos; tiempos que resultan prácticos para obtener soluciones a problemas grandes con la calidad ya mencionada.
Para futuros estudios se recomienda cambiar la estrategia del método Path-Relinking, de tomar como solución guía la mejor solución élite y, en cambio, tomarla como solución inicial; probar más instancias de problemas, y cambiar la función de utilidad de la fase constructiva de GRASP para estudiar si Path-Relinking también muestra mejoramiento significativo de las soluciones encontradas, con el fin de comparar los resultados contra los resultados del método propuesto en este trabajo.
Referencias
BOZEJKO, W.; GRABOWSKI, J. y WODECKI, M. Block approach-tabu search algorithm for single machine total weighted tardiness problem. Computers & Industrial Engineering, 2006, vol. 50, núms. 1-2, pp. 1-14. [ Links ]
BRUCKER, P. Scheduling algorithms. 5th ed. New York: Springer, 2007. [ Links ]
CONGRAM, R. K.; POTTS, C. N. y VAN DE VELDE, S. L. An iterated dynasearch algorithm for the single-machine total weighted tardiness scheduling problem. INFORMS Journal on Computing, 2002, vol. 14, núm. 1, pp. 52-67. [ Links ]
FELDMANN, M. y BISKUP, D. Single-machine scheduling for minimizing earliness and tardiness penalties by meta-heuristic approaches. Computers and Industrial Engineering, 2003, vol. 44, núm. 2, pp. 307-323. [ Links ]
FLESZAR, K.; OSMAN, I. H. e HINDI, K. S. A variable neighborhood search algorithm for the open vehicle routing problem. European Journal of Operational Research, 2008, vol. 195, núm. 3, pp. 803-809. [ Links ]
GLOVER, F. y KOCHENBERGER, G. A. Handbook of metaheuristics. Dordrecht: Kluwer Academic Publishers, 2003. [ Links ]
GRAHAM, R. L. et al. Optimization and approximation in deterministic sequencing and scheduling: a survey. Annals of Discrete Mathematics, 1979, vol. 5, pp. 287-326. [ Links ]
HANSEN, P. y MLADENOVIC, N. Variable neighborhood search: principles and applications. European Journal of Operational Research, 2001, vol. 130, núm. 3, pp. 449-467. [ Links ]
HANSEN, P.; MLADENOVIC, N. y MORENO PÉREZ, J. A. Variable neighborhood search. European Journal of Operational Research, 2008, vol. 191, núm. 3, pp. 593-595. [ Links ]
HINO, C. M.; RONCONI, D. P. y MENDES A. B. Minimizing earliness and tardiness penalties in a single-machine problem with a common due date. European Journal of Operational Research, 2005, vol. 160, núm. 1, pp. 190-201. [ Links ]
LIAO, C.-J. y CHENG, C.-C. A variable neighborhood search for minimizing single machine weighted earliness and tardiness with common due date. Computers & Industrial Engineering, 2007, vol. 52, núm. 4, pp. 404-413. [ Links ]
MLADENOVIC, N. y HANSEN, P. Variable neighborhood search. Computers & Operations Research, 1997, vol. 24, núm. 11, pp. 1097-1100. [ Links ]
PINEDO, M. L. Scheduling, theory, algorithms, and systems. 3rd ed. New York: Springer, 2008. [ Links ]
SEN, T.; SULEK, J. M. y DILEEPAN, P. Static scheduling research to minimize weighted and unweighted tardiness: A state-of-the-art survey. International Journal of Production Economics, 2003, vol. 83, núm. 1, pp. 1-12. [ Links ]
WANG. y YEN, B. P. C. Single machine scheduling to minimize total weighted earliness subject to minimal number of tardy jobs. European Journal of Operational Research, 2009, vol. 195, núm. 1, pp. 89-97. [ Links ]
WANG, X. y TANG, L. A population-based variable neighborhood search for the single machine total weighted tardiness problem. Computers & Operations Research, 2009, vol, 36, núm. 6, pp. 2105-2110. [ Links ]