Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Universidad
Print version ISSN 0123-2126
Ing. Univ. vol.14 no.2 Bogotá July/Dec. 2010
Ensayos numéricos sobre la formación de patrones de Turing bajo la acción de campos convectivos incompresibles: un acercamiento desde el problema de la cavidad1
Numerical Essays on the Development of Turing Patterns under the Effect of Incompressible Convective Fields: An Approach from the Cavity Problem2
Ensaios numéricos sobre a formação de padrões de Turing sob a ação de campos convectivos incompressíveis: uma aproximação desde o problema da cavidade3
Carlos Humberto Galeano-Urueña5
Juan Miguel Mantilla-González6
1 Este artículo se deriva de un proyecto de investigación denominado Simulación computacional en ingeniería mecánica y biomédica (fase II), financiado por la División de Investigación de la sede Bogotá (DIB) de la Universidad Nacional de Colombia.
2 Submitted on: March 8, 2010. Accepted on: April 8, 2010. This article results from the research project called Computer Simulation in Mechanical and Biomedical Engineering (phase II), funded by the Research Division, Bogota (DIB), Universidad Nacional de Colombia.
3 Data de recepção: 8 de março de 2010. Data de aceitação para publicação: 8 de abril de 2010. Este artigo deriva-se de um projeto de pesquisa denominado Simulação computacional em engenharia mecânica e biomédica (fase II), financiado pela Divisão de Pesquisa da Sede Bogotá (DIB) da Universidade Nacional da Colômbia.
4 Ingeniero mecánico, Universidad Nacional de Colombia, Bogotá, Colombia. Máster en Ingeniería Mecánica, Universidad de los Andes, Bogotá, Colombia. Doctor en Mecánica Computacional, Universidad de Zaragoza, España. Profesor asociado del Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Correo electrónico: dagarzona@bt.unal.edu.co.
5 Ingeniero mecánico, Universidad Nacional de Colombia, Bogotá, Colombia. Magíster en Ingeniería Mecánica, Universidad de Cienfuegos, Cienfuegos, Cuba. Magíster en Matemática Aplicada, Universidad Nacional de Colombia, Bogotá. Profesor asistente del Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Correo electrónico: chgaleanou@unal.edu.co.
6 Ingeniero mecánico, Universidad Industrial de Santander, Bucaramanga, Colombia. Magíster en Ingeniería Mecánica, Universidad de los Andes, Bogotá, Colombia. Profesor asistente del Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Correo electrónico: jmmantillag@unal.edu.co.
Fecha de recepción: 8 de marzo de 2010. Fecha de aceptación para publicación: 8 de abril de 2010
Resumen
En este artículo se presentan varios ensayos numéricos sobre las ecuaciones de reacción-difusión en el espacio de Turing afectadas por campos convectivos presentes en flujos incompresibles, bajo el mecanismo de reacción de Schnakenberg. Los ensayos se realizan en 2D sobre cuadrados unitarios, a los cuales se les impone un campo advectivo proveniente de la solución del problema de flujo en una cavidad. El modelo desarrollado consiste en un sistema desacoplado de ecuaciones de reacción-advección-difusión, junto con las ecuaciones de Navier-Stokes de flujo incompresible, el cual se soluciona de forma simultánea mediante el método de los elementos finitos. Los resultados muestran patrones complejos que mezclan bandas y puntos que llegan al estado estable. Además, se muestran resultados en los que el patrón generado por las concentraciones del sistema reactivo varía tanto en el tiempo como en el espacio, debido al efecto ejercido por el campo advectivo. Los ensayos numéricos muestran que los patrones obtenidos son independientes de las condiciones iniciales y de la malla empleada para la solución.
Palabras clave: Reacción-advección-difusión, inestabilidades de Turing, problema de la cavidad.
Abstract
This work presents a number of numerical examples of reaction-difussion equations in Turing space, modified by convective fields in incompressible flows, using a Schnakenberg reaction mechanism. Examples were made in 2D using quad elements, which have an imposed advective field derived from the cavity problem solution. The developed model consists of an uncoupled system of equations including the reaction-advection-diffusion equations and the Navier-Stokes equations for incompressible flow. This system is solved simultaneously using the finite element method. Results illustrate that complex patterns are formed, mixing dots and stripes which reach a stable state. Changes in pattern concentration in both space and time are also shown due to the effect of the advective field. Numerical examples confirm that pattern formation is independent of initial conditions and mesh.
Key words: Reaction-advection-diffusion, Turing instabilities, cavity problem.
Resumo
Neste artigo apresentam-se vários ensaios numéricos sobre as equações de reação-difusão no espaço de Turing afetadas por campos convectivos presentes em fluxos incompreensíveis, sob o mecanismo de reação de Schnakenberg. Os ensaios realizam-se em 2D sobre quadrados unitários, aos quais se impõem um campo advectivo proveniente da solução do problema de fluxo em uma cavidade. O modelo desenvolvido consiste em um sistema desacoplado de equações de reação-advecção-difusão, junto com as equações de Navier-Stokes de fluxo incompreensível, que se soluciona de forma simultânea mediante o método de os elementos finitos. Os resultados mostram padrões complexos que misturam bandas e pontos que chegam ao estado estável. Além disso, mostramse resultados em que o padrão gerado pelas concentrações do sistema reativo varia tanto no tempo como no espaço, devido ao efeito exercido pelo campo advectivo. Os ensaios numéricos mostram que os padrões obtidos são independentes das condições iniciais e da malha empregada para a solução.
Palavras-Chave: Reação-advecção-difusão, instabilidades do Turing, problema da cavidade.
Introducción
Diversos problemas físicos pueden modelarse mediante el balance de tres fenómenos: la difusión, la convección y la reacción (Garzón, 2007). La primera se define como la dispersión de las especies involucradas en el proceso a lo largo del dominio físico del problema; la convección, como el movimiento de las especies, gracias al transporte por el fluido del medio, y la reacción, como el proceso de interacción mediante la cual se generan o se consumen las especies involucradas en el fenómeno. Matemáticamente, el problema de reacción-advección- difusión (RAD) se expresa a partir de la ecuación diferencial (1), junto con las condiciones de borde (2).
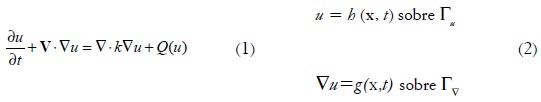
Donde u es la concentración de la especie estudiada; V, la velocidad del medio; k, la constante de difusión; Q(u), la función que define el proceso de reacción; h(x,t), la función que define los valores de u en dirección normal al borde Γu, y g(x,t), la función que define el valor del gradiente de u a lo largo del borde Γ∇. La velocidad V se puede imponer a priori, como en (Madzvamuse, Wathen y Maini, 2003; Madzvamuse, 2000), o puede ser hallada, por ejemplo, mediante la solución del sistema de ecuaciones de Navier-Stokes (Franca y Frey, 1992; Acheson, 1990) para flujo incompresible planteado en (3):

Donde ρ es la densidad del fluido, p es la presión, µ es la viscosidad y ƒ es el vector de fuerzas de cuerpo.
Estas ecuaciones de RAD (1) y otros modelos más complejos, donde intervienen más especies o reactantes, poseen la habilidad para crear ciertos patrones espacio-temporales. Un caso particular son las inestabilidades de Turing (Garzón, 2007; Madzvamuse, Wathen y Maini, 2003), caracterizadas por la aparición de distribuciones de especies (patrones) estables en el tiempo e inestables en el espacio. Dada su especial respuesta, este tipo de modelos matemáticos han inspirado modelos para el estudio de problemas en muy diversos campos, como dinámica de fluidos (White, 1988), transferencia de calor (Hirayama y Takaki, 1988; Ardes, Busse y Wicht, 1997; Lir y Lin, 2001), física de semiconductores (Balkarei et al., 1988), ingeniería de materiales (Krinsky, 1984), química (Zhang y Liu, 2009), biología (Madzvamuse, Wathen y Maini, 2003; Crauste, Lhassan y Kacha, 2008; Rossi y Ristori, 2008; Frederik y Maini, 2003), dinámica de poblaciones (Yi, Wei y Shi, 2009; Baurmanna, Gross y Feudel, 2007; Rothschild y Ault, 1996), astrofísica (Nozakura y Ikeuchi, 1984), ingeniería biomédica (Madzvamuse, 2002; García-Aznar et al., 2007; Ferreira, Martins y Vilela, 2002) y matemáticas financieras.
El análisis de estos sistemas de reacción-difusión (RD), que presentan inestabilidad de Turing, se ha desarrollado tradicionalmente desde dos marcos de trabajo: análisis matemático (Mei, 2000) y simulación numérica (Garzón, 2007; Madzvamuse, 2000). A partir del punto de vista analítico, los esfuerzos por entender el comportamiento de los sistemas de RD se han centrado en el estudio de la relación entre las bifurcaciones del espacio de parámetros y la formación de patrones.
Desde esta perspectiva, se han estudiado los sistemas de RD mediante comparaciones de sub y supersoluciones, teoría de grado, índice de Conley, teoría de puntos críticos y perturbaciones singulares para varios tipos de máximos principales (Mei, 2000). Estos métodos han sido efectivos para el análisis de soluciones estacionarias y ondas viajeras (Rüdiger et al., 2007; Sagués et al., 2004). También se han estudiado escenarios de bifurcaciones complejas en sistemas de RD aplicando métodos de teoría de grupo para problemas con simetrías (Allgower y Georg, 1997; Painter, Othmer y Maini, 1999). Los esfuerzos en esta área del análisis matemático y, específicamente, de la dinámica de sistemas han permitido construir un gran conocimiento, el cual se ha comprobado y ampliado con el uso de la simulación numérica.
La simulación numérica de sistemas de RD ha permitido corroborar el conocimiento obtenido analíticamente sobre la formación de patrones, como en (Madzvamuse, Wathen y Maini, 2003; Madzvamuse, 2000; Painter, Othmer y Maini, 1999; Painter, Maini y Othmer, 2000), donde se han desarrollado ejemplos numéricos sobre la formación de patrones en dominios bidimensionales bajo consideraciones de dominio creciente.
Particularmente en (Madvamuse, 2000) se desarrollan simulaciones numéricas usando un esquema lagrangiano con movimiento de malla, que muestra una gran diferencia entre el estado estacionario para dominios fijos y la continua formación de nuevos patrones para dominios crecientes. En (Madvamuse, 2000) se reporta la aparición de diferentes estructuras que pueden variar entre sistemas de bandas, puntos y combinaciones de estos patrones en dominios con decrecimiento exponencial.
Así mismo, en (Madvamuse, 2009) se reporta la formación de patrones en presencia de campos convectivos con divergencia nula. Por otro lado, otros trabajos numéricos han mostrado los efectos de los campos convectivos en la formación de patrones, al igual que la obtención de patrones de Turing y la transición de estos a ondas viajeras en presencia de campos de velocidad toroidal que modifican la dinámica del sistema.
Siguiendo el estudio de la variación de patrones por la acción de campos convectivos desde la perspectiva numérica, el objetivo de este artículo es solucionar computacionalmente, y de forma simultánea, las ecuaciones de RAD y Navier- Stokes en 2D, para el sistema de reacción de Schnakenberg, con parámetros cinéticos y difusivos en el espacio de Turing. Para ello se soluciona el sistema de ecuaciones de RAD mediante un planteamiento conjunto del método de los elementos finitos y el método de Newton-Raphson (Hoffman, 1992). Respecto a la solución de las ecuaciones de Navier-Stokes, se utiliza un enfoque de Petrov- Galerkin, como el mostrado en (Hughes, Franca y Balestra, 1986).
El trabajo está organizado como sigue: en primer lugar se muestra el modelo matemático del sistema de RAD, incorporando las expresiones de reacción de Schnakenberg. Posteriormente, se muestra la formulación por elementos finitos para la solución numérica del sistema de RAD. En la tercera se describen los ejemplos que se van a resolver, las condiciones de contorno, el tipo de dominio y parámetros computacionales. Posteriormente, se muestran los resultados de algunas de las simulaciones corridas y se finaliza con la discusión y conclusiones de los patrones obtenidos.
1. El modelo de reacción-advección-difusión
1.1 Condiciones de inestabilidad de Turing
Siguiendo el modelo reactivo de Schnakenberg (Garzón, 2007; Madvamuse, 2000; Madvamuse, 2009), el sistema de ecuaciones diferenciales de RD en (1), puede escribirse como (4):
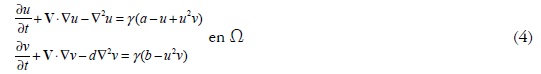
Donde u y v son las especies químicas,∇2u y d∇2v son los términos difusivos, d es la relación entre los coeficientes difusivos de cada especie, γ es una constante adimensional, a y b son parámetros constantes del modelo, V es la velocidad del medio, en tanto que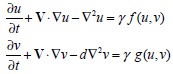 son las funciones de reacción de Schnakenberg.
son las funciones de reacción de Schnakenberg.
La solución de este sistema de ecuaciones conducirá a una distribución de concentraciones espacialmente inestables o patrones de Turing, si se cumplen unas determinadas condiciones, las cuales para el caso de un modelo de RD, sin convección, están dadas por las desigualdades descritas en (5).

Donde 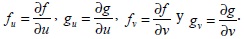
Usando el análisis de estabilidad lineal (Madvamuse, 2000), se pueden calcular los valores de los parámetros adimensionales d y γ, requeridos para la formación de patrones de Turing bajo el modelo de RD. Estos patrones pueden ser identificados por los correspondientes nómeros de onda, tal como los que se mencionan en la Tabla 1.
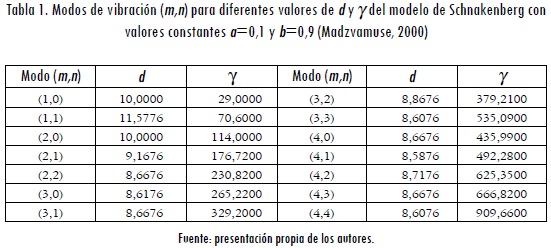
1.2 Solución por elementos finitos del sistema de ecuaciones de RAD
1.2.1 Consideraciones generales
Para solucionar numéricamente el sistema de ecuaciones (4) se optó por una aproximación a través del método de elementos finitos, empleando elementos bilineales de cuatro nodos (Hughes, 2000). Dada las características matemáticas del problema, se implementó una solución con las siguientes consideraciones adicionales:
- Debido a la no linealidad de los términos reactivos incorporados en el modelo, se utilizó el método de Newton-Raphson para solucionar el problema de la evolución temporal de las especies u y v.
- El valor del término de velocidad V empleado en la iteración n dentro de la aproximación de la ecuación de RAD fue el valor calculado en el tiempo n - 1 en la solución de las ecuaciones de Navier-Stokes.
- La integración temporal se ha realizado mediante la regla trapezoidal y una formulación totalmente implícita.
1.2.2 Formulación de la ecuación de residuos ponderados y forma débil
Planteando inicialmente la ecuación de residuos ponderados para el sistema de ecuaciones diferenciales (4), se obtiene la expresión (6):
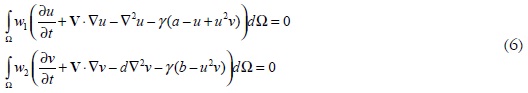
Donde Ω hace referencia al dominio del problema, el cual está limitado por la frontera Γ, mientras w1 y w2 son funciones de peso. Empleando el teorema de Green para el debilitamiento de las ecuaciones (6), se llega a (7).
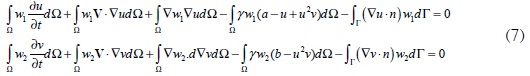
A partir de las ecuaciones de residuos ponderados en su forma débil (7), se pueden plantear los residuos del problema, tal como se muestra a continuación:
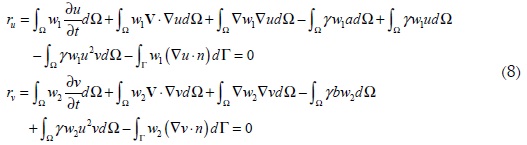
Al definir condiciones de flujo cero, o condiciones de Neumann homogéneas, sobre los contornos del problema, los términos relacionados con la integral de borde de las ecuaciones (8) se cancelan y los residuos se expresan como:
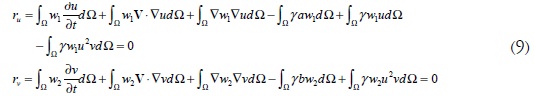
Para plantear la solución discreta se emplean aproximaciones escritas como la combinación lineal de funciones ortogonales, tal como se plantea en (10) (Hughes, 2000; Zienkiewicz y Taylor, 2000), donde estas funciones de aproximación tendrán la misma forma de las funciones de peso w. Así, las variables u y v son escritas en términos de los valores nodales usando las funciones de aproximación N, así:

Donde Nu(x, y), Nv(x, y) y NV(x, y) son las funciones de forma, que dependen ónicamente del espacio empleado para formulación, u y v son los valores de u y v en los puntos nodales, en tanto que el superíndice h indica la discretización de la variable en elementos finitos.
Nótese que el empleo de funciones de peso w con la misma forma que las funciones de aproximación N indica el empleo de una formulación Bubnov-Galerkin, en lugar de una formulación SUPG, capaz de estabilizar los problemas numéricos derivados de la inclusión de los términos advectivos. Esta selección se sustenta en el tamaño de malla empleado en todos los problemas simulados, el cual asegura la obtención de nómeros de Peclet inferiores a la unidad, lo cual garantiza que aón con la formulación Bubnov-Galerkin convencional pueden obtenerse soluciones numéricamente estables (Zienkiewicz y Taylor, 2000).
Mediante la sustitución de (10) en (9) se obtienen los vectores de residuo en su forma discreta (11), donde  y
y  son los vectores de residuo para cada ecuación y ∇N es el vector gradiente de las funciones de aproximación.
son los vectores de residuo para cada ecuación y ∇N es el vector gradiente de las funciones de aproximación.
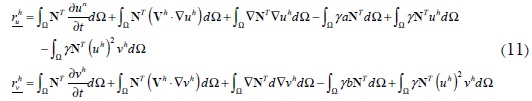
Al emplear una discretización temporal basándose en la ecuación de Crank- Nicolson (Zienkiewicz y Taylor, 2000), la ecuación (11) se convierte en (12). En esta óltima expresión  y
y  son los valores nodales uh y vh evaluados en el tiempo t + Δt, en tanto que &#alpha; es un parámetro característico del método de integración temporal (Hughes, 2000; Zienkiewicz y Taylor, 2000).
son los valores nodales uh y vh evaluados en el tiempo t + Δt, en tanto que &#alpha; es un parámetro característico del método de integración temporal (Hughes, 2000; Zienkiewicz y Taylor, 2000).
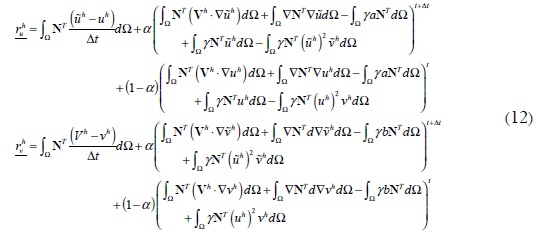
Utilizando las expresiones (12) se pueden calcular cada uno de los términos de la matriz de rigidez tangente, mostrada en (13).
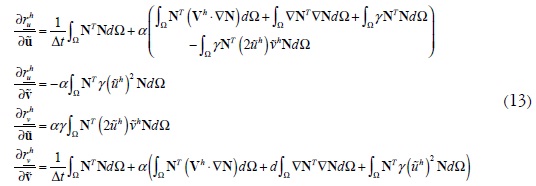
Debe notarse que, a efectos de simplicidad en la solución simultánea de las ecuaciones de RAD y de Navier-Stokes, los términos de velocidad nodal Vh empleados en la ecuación (14) corresponden al paso de tiempo t y no al t + Δt. No obstante, esta simplificación no implica ninguna pérdida de exactitud, pues los dos sistemas de ecuaciones, aunque se resuelven de forma simultánea, se encuentran desacoplados.
Así, los valores nodales uh y vh en el tiempo t + Δt se pueden aproximar mediante un algoritmo iterativo Newton-Raphson, tal como se describe en la ecuación (14), donde Δuh y Δvh representan la diferencia de los valores nodales en dos iteraciones consecutivas.

1.3 Solución de las ecuaciones de Navier-Stokes
La solución de las ecuaciones de Navier-Stokes para la obtención del campo de velocidades que define el término de transporte en el sistema de RAD se realizó empleando una formulación estabilizada de elementos finitos SUPG (de sus siglas en inglés Streamline Upwind Petrov Galerkin), siguiendo un enfoque similar al utilizado en (Hughes, Franca y Balestra, 1986).
De acuerdo con este planteamiento, para cumplir con el criterio de incompresibilidad, sin acudir a formulaciones con términos de estabilización adicionales, se necesita acudir a una solución mixta de elementos cuadriláteros, la cual involucra nueve nodos para el cálculo de las velocidades y cuatro para el cálculo de las presiones (Yi y Wei, 2009; Hughes, Franca y Balestra, 1986).
1.4 Solución computacional
Se plantea analizar la formación de patrones de Turing dentro del dominio de un cuadrado de longitud unitaria, considerando un proceso reactivo caracterizado por la ecuación de Schnakenberg y un campo advectivo asociado al flujo dentro de la cavidad (Hughes, Franca y Balestra, 1986; Chung, 2002; Tu y Yeoh, 2007), problema definido por las ecuaciones (1) y (3). Para terminar de definir el problema, se consideraron como condiciones de borde para las ecuaciones de RAD unas condiciones de flujo nulo (condiciones de Neumann homogéneas). Por su parte, en el caso de las ecuaciones de Navier-Stokes, se consideraron condiciones de velocidad cero en todos los bordes de la cavidad, a excepción de la parte de arriba, donde se ha impuesto una velocidad horizontal VX = c(t).
En la Figura 1 se resume cada una de estas condiciones.
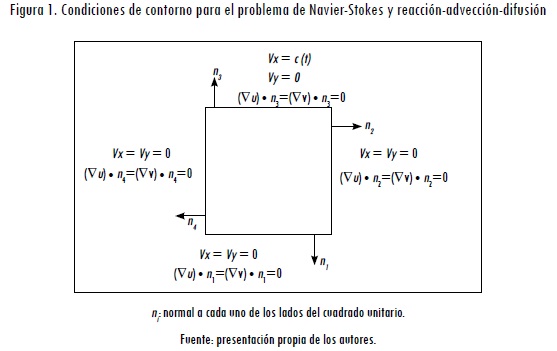
En cuanto a las condiciones iniciales, se realizaron pruebas con dos tipos de condiciones iniciales diferentes. El primer tipo consistió en el estado estable del problema reactivo-difusivo, mientras que el segundo tipo se basó en una perturbación del estado estable homogéneo de cada uno de los términos reactivos, tal como se describe en (15).

Donde ƒ(us,vs) = 0 y g(us,vs) = 0 son los estados estables de los términos reactivos y ε es un parámetro de perturbación aleatorio.
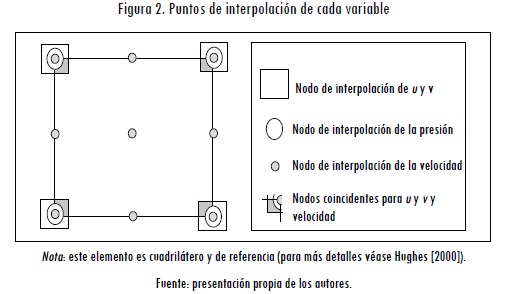
Como ya se mencionó, la discretización empleada consistió en elementos cuadriláteros bilineales de cuatro nodos para el problema de RAD y una formulación mixta para el problema de Navier-Stokes, la cual consistió en elementos de nueve nodos —elemento cuadrilátero cuadrático (Hughes, 2000)— para la interpolación de la velocidad y de cuatro nodos —cuadrilátero bilineal (Hughes, 2000)— para la interpolación de la presión (Figura 2).
Para llevar a cabo la implementación numérica se programó el conjunto de ecuaciones en lenguaje FORTRAN y se solucionaron todos los ejemplos que se ilustran más adelante en un computador portátil de 4.096 MB en RAM y 800 MHz de velocidad de procesador.
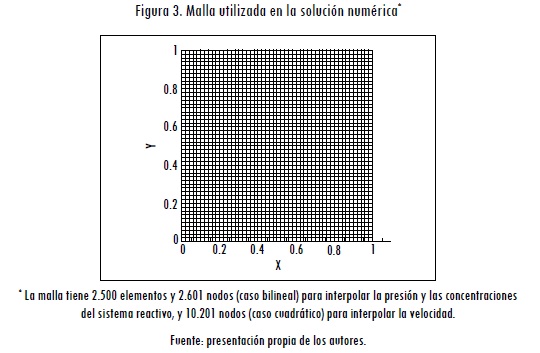
La malla utilizada es igual para todos los ejemplos (Figura 3), la cual consiste en 2.500 elementos cuadriláteros de cuatro nodos para la interpolación de la presión y las concentraciones u y v (para un total de 2.601 nodos), y la misma cantidad de elementos pero de nueve nodos para la interpolación de las componentes de velocidad (para un total de 10.201 nodos).
En la integración temporal se utilizó un paso Δt = 0,01 y como criterio de convergencia del problema no lineal (Newton-Raphson); además, se utilizó un control de error relativo de convergencia 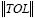 ≤10-14 (Hoffman, 1992).
≤10-14 (Hoffman, 1992).
2. Resultados
Por medio de la formulación numérica por elementos finitos planteada se tuvieron los siguientes resultados. En primera instancia, los relacionados con el campo advectivo de velocidades y, en segunda instancia, los del sistema de RAD, considerando un término convectivo impuesto por la evolución temporal del campo de velocidades calculado. Por brevedad, en los resultados sólo se señala el nivel de concentración de u para el sistema reactivo. La variable v presenta un comportamiento similar, pero con los colores de los patrones invertidos.
2.1 Resultados del campo de velocidades en el problema de flujo en la cavidad
En la Figura 4 se muestran los resultados alcanzados para el problema de la cavidad, el cual es ampliamente referenciado en diferentes trabajos (como Hughes, Franca y Balestra, 1986; Chung, 2002; Tu y Yeoh, 2007). En cada fila se muestra el campo de velocidades obtenido en estado estable, expresado en cada una de sus componentes (Vx, Vy), así como en términos de la resultante, a través de las líneas de corriente. Cada fila corresponde a la solución del problema de la cavidad con una velocidad adimensional en el borde superior diferente: c=0,5, c=5 y c=50 (Figura 4). Estos valores en el contorno son equivalentes a un nómero de Reynolds de 0,5, 5 y 50, respectivamente.
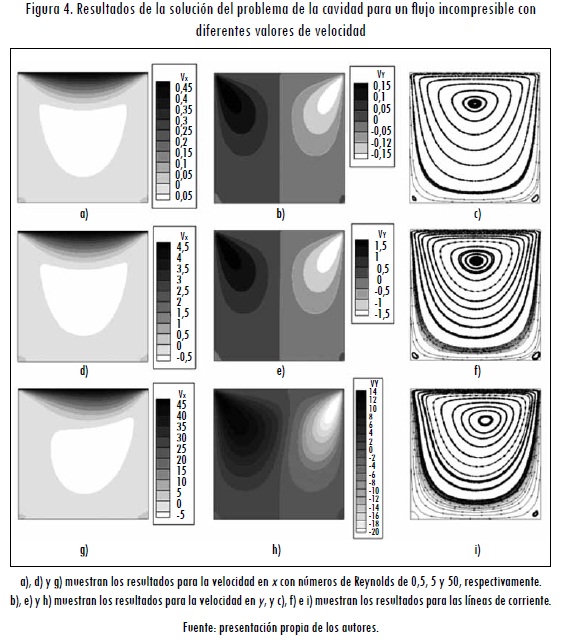
Los resultados muestran la formación de un vórtice en la parte central superior para las dos velocidades más bajas, y de un vórtice en la parte superior derecha para la velocidad más alta (c=50). Los resultados de la magnitud de la velocidad en cada dirección y el patrón resultante concuerdan con los resultados reportados por otros autores como (Hughes, Franca y Balestra, 1986; Chung, 2002; Tu y Yeoh, 2007). Por brevedad en el reporte, en la Figura 4 no se presentan los resultados alcanzados para la presión, ni la evolución temporal de las variables de velocidad y presión.
Estos resultados, y más específicamente, el campo de velocidades en evolución temporal fue impuesto al sistema reactivo a través del termino convectivo para observar el comportamiento de los patrones de Turing ante estos campos de velocidad. En la siguiente sección se muestran los resultados de estas pruebas numéricas.
2.2 Resultados para un modo inicial (1,0)
Tal como se mencionó y se listó en la Tabla 1, para condiciones de RD, diferentes valores en los coeficientes d y γ pueden generar distintos patrones de Turing, que se identifican mediante su nómero de onda. Así, por ejemplo, un patrón de Turing con un nómero de onda (1,0) puede obtenerse a partir un valor d = 10 y γ = 29 (para mayores detalles [Madzvamuse, 2000]).
De esta forma, el primer caso simulado consistió en evaluar la influencia del campo advectivo derivado del problema de flujo en la cavidad, dentro de un caso de RD con d=10 y γ = 29. La simulación consistió en partir de un problema de RD simple, que permite su estabilización temporal (este estado se tomó como t=0), y adicionando posteriormente los efectos advectivos mencionados.
En la Figura 5 se presentan los resultados de la evolución del patrón obtenido para el problema descrito, donde se emplearon tres campos de velocidad definidos por tres nómeros de Reynolds diferentes: 0,5 (columna a Figura 5), 5 (columna b Figura 5) y 50 (columna c Figura 5).

En el experimento numérico de la columna a en la Figura 5 se muestra la formación de un patrón de Turing que gira en el mismo sentido del campo de velocidad. El nuevo patrón generado queda en constante giro y no llega a estabilizarse en ningón tiempo posterior. Se debe notar que el frente de cambio de densidad pasa de ser recto a tener una curvatura, como se muestra en tiempos posteriores.
En la Figura 5b se observa un patrón simétrico que, al igual que en el caso a, queda en constante rotación en el sentido de giro del fluido. En la Figura 5c se observa que a una alta velocidad el sistema llega a un estado estable que tiene una forma senoidal después de haber girado en el sentido del flujo. El tiempo adimensional de estabilización es t = 0,008.
2.3 Resultados para un modo inicial (4,0)
La Figura 6 muestra los resultados para un patrón en estado estable obtenido con los parámetros de la Tabla 1, correspondientes a un nómero de onda (4,0) y tres magnitudes de campo advectivo. En la columna a de la Figura 6 se muestra la evolución del patrón para un campo convectivo con velocidad en el borde de 0,5. En este caso, se observa que el patrón original (formado por los efectos de reaccióndifusión) se distorsiona levemente al incorporar el campo advectivo y alcanza una estabilidad temporal en t=0,04.

En la columna b de la Figura 6 se observa que el campo advectivo (es mayor que en el caso a) rompe las bandas originales y genera puntos aislados en el dominio, que se estabiliza después de t=0,067. El aumento del término convectivo (Figura 6c) lleva a la formación de un patrón estable temporalmente y de forma similar a la del caso b, pero una mayor definición en las manchas alcanzadas. El tiempo de estabilización en este óltimo caso es t=0,032.
2.4 Resultados para un modo inicial (2,1)
En este experimento numérico se utilizaron los parámetros que corresponden al modo (2,1) de la Tabla 1 y los mismos tres campos de velocidad empleados en las pruebas numéricas anteriores. En la Figura 7a se observa que el campo de velocidades impuesto (nómero de Reynolds igual a 0,5) no altera de forma significativa el patrón de Turing original (formado por el efecto reactivo-difusivo); sólo se observa una leve distorsión, que se estabiliza en t=0,02.

En la columna b de la Figura 7 se muestra una distorsión significativa, donde el patrón original rota un ángulo de 90° en dirección del flujo. Se observa, además, la formación de un punto cuyo centro coincide con la posición del vórtice formado en el fluido (Figura 4f). El tiempo de estabilización para este caso es t=0,020.
En la columna c de la Figura 7 se observa que bajo el efecto de un campo advectivo mayor (nómero de Reynolds igual a 50) el patrón se ha perdido por completo; se encuentran dos semibandas bien establecidas en la parte superior e inferior.
3. Conclusiones
En este artículo se han realizado varios ensayos numéricos para el análisis de la formación de patrones de Turing bajo el efecto de un campo advectivo asociado con el problema de flujo en una cavidad (Hughes, Franca y Balestra, 1986; Chung, 2002; Tu y Yeoh, 2007).
Las pruebas realizadas con diferentes parámetros de nómero de onda evidencian que la adición de un término advectivo a la ecuación de RD permite generar inestabilidades de Turing complejas. En dos dimensiones se observa la posibilidad de que aparezcan patrones mezclados de puntos y bandas para campos advectivos fuertes. Se encontró que pueden presentar seudomodos de onda complejos, capaces de cambiar la longitud y forma de las bandas y los puntos.
Para el caso de campos advectivos de pequeña magnitud se observó que el patrón original puede, en algunos casos, rotar en la dirección del campo de velocidad, alcanzar una estabilización temporal o permanecer en rotación sin llegar a un estado estable (véanse figuras 5a y 5b).
Referencias
ACHESON, D. J. Elementary fluid dynamics: Oxford Applied Mathematics and Computing Science Series. Oxford: Oxford University Press, 1990. [ Links ]
ALLGOWER, E. y GEORG, K. Numerical path following. Handbook of Numerical Analysis, 1997, vol. 5, pp. 3-207. [ Links ]
ARDES, M.; BUSSE, F. y WICHT, J. Thermal convection in rotating spherical shells. Physics of the Earth and Planetary Interiors, 1997, vol. 99, pp. 55-67. [ Links ]
BALKAREI, Y. et al. Regenerative oscillations, spatial-temporal single pulses and static inhomogeneous structures in optically bistable semiconductors. Optics Communications, 1988, vol. 66, nóms. 1-2, pp. 161-166. [ Links ]
BAURMANNA, M.; GROSS, T. y FEUDEL, U. Instabilities in spatially extended predator-prey systems: Spatio-temporal patterns in the neighborhood of Turing-Hopf bifurcations. Journal of Theoretical Biology, 2007, vol. 245, pp. 220-229. [ Links ]
CHUNG, T. Computational fluid dynamics. Cambridge: Cambridge University Press, 2002. [ Links ]
CRAUSTE, F.; LHASSAN, M. y KACHA, A. A delay reaction-diffusion model of the dynamics of botulinum in fish. Mathematical Biosciences, 2008, vol. 216, pp. 17-29. [ Links ]
FERREIRA, S.; MARTINS, M. y VILELA, M. Reaction-diffusion model for the growth of avascular tumor. Physical Review, 2002, vol. 65, nóm. 2. [ Links ]
FRANCA, L. y FREY, S. Stabilized finite element methods: II. The incompressible Navier-Stokes equations. Computer Methods in Applied Mechanics and Engineering, 1992, vol. 99, pp 209-233. [ Links ]
FREDERIK, H. et al. Pigmentation pattern formation in butterflies: experiments and models. C. R. Biologies, 2003, vol. 326, pp. 717-727. [ Links ]
GARCÍA-AZNAR, J. et al. Computational simulation of fracture healing: Influence of interfragmentary movement on the callus growth. Journal of Biomechanics, 2007, vol. 40, nóm. 7, pp. 1467-1476. [ Links ]
GARZÓN, D. Simulación de procesos de reacción-difusión: aplicación a la morfogénesis del tejido óseo. Tesis de PhD. Zaragoza: Universidad de Zaragoza, 2007. [ Links ]
HIRAYAMA, O. y TAKAKI, R. Thermal convection of a fluid with temperature-dependent viscosity. Fluid Dynamics Research, 1988, vol. 12, nóm. 1, pp. 35-47. [ Links ]
HOFFMAN, J. Numerical methods for engineers and scientists. New York: Mc Graw-Hill, 1992. [ Links ]
HUGHES, T. The finite element method (linear static and dynamic finite element analysis). s. l.: Dover, 2000. [ Links ]
HUGHES, T.; FRANCA, L. y BALESTRA, M. A new finite element formulation for computational and fluid dynamics: V. Circumventing the Babuska-Brezzi condition: a stable Petrov-Galerkin formulation of the Stokes problema accommodating equal-order interpolations. Computer Methods in Applied Mechanics and Engineering, 1986, vol. 59, pp. 85-99. [ Links ]
JAVIERRE, E. et al. Numerical modeling of a mechano-chemical theory for wound contraction analysis. International Journal of Solids and Structures, 2009, vol. 46, nóm. 20, pp. 3597-3606. [ Links ]
KRINSKY, V. I. Self-organisation: Auto-waves and structures far from equilibrium. Philadelphia: Springer, 1984. [ Links ]
LIR, J. y LIN, T. Visualization of roll patterns in Rayleigh-Bénard convection of air in rectangular shallow cavity. International Journal of Heat and Mass Transfer, 2001, vol. 44, pp. 2889-2902. [ Links ]
MADZVAMUSE, A. A numerical approach to the study of spatial pattern formation in the ligaments of arcoid bivalves. Bulletin of Mathematical Biology, 2002, vol. 64, pp. 501-530. [ Links ]
MADZVAMUSE, A. A numerical approach to the study of spatial pattern formation. D. Phil. Thesis. Oxford: Oxford University, 2000. [ Links ]
MADZVAMUSE, A. Turing instability conditions for growing domains with divergence free mesh velocity. Nonlinear Analysis: Theory, Methods & Applications, 2009, vol. 71, nóm. 12, pp. 2250-2257. [ Links ]
MADZVAMUSE, A.; WATHEN, A. y MAINI, P. A moving grid finite element method applied to a model biological pattern generator. Journal of Computational Physics, 2003, vol. 190, pp. 478-500. [ Links ]
MEI, Z. Numerical bifurcation analysis for reaction-diffusion equations. Berlin: Springer-Verlag, 2000. [ Links ]
NOZAKURA, T. e IKEUCHI, S. Formation of dissipative structures in galaxies. Astrophysical Journal, 1984, vol. 279, pp. 40-52. [ Links ]
PAINTER, K; MAINI, P. y OTHMER, H. A chemotactic model for the advance and retreat of the primitive streak in avian development. Bulletin of Mathematical Biology, 2000, vol. 62, pp. 501-525. [ Links ]
PAINTER, K.; OTHMER, H. y MAINI, P. Stripe formation in juvenile Pomacanthus via chemotactic response to a reaction-diffusion mechanism. Proceedings of National Academy Sciences USA, 1999, vol. 96, nóm. 10, pp. 5549-5554. [ Links ]
ROSSI, F. et al. Dynamics of pattern formation in biomimetic systems. Journal of Theoretical Biology, 2008, vol. 255, pp. 404-412. [ Links ]
ROTHSCHILD, B. y AULT, J. Population-dynamic instability as a cause of patch structure. Ecological Modelling, 1996, vol. 93, pp. 237-239. [ Links ]
RÜDIGER, S. et al. Theory of pattern forming systems under traveling-wave forcing. Physics Reports, 2007, vol. 447, nóms. 3-6, pp. 73-111. [ Links ]
SAGUÉS, F. et al. Travelling-stripe forcing of Turing patterns. Physica D: Nonlinear Phenomena, 2004, vol. 199, nóms. 1-2, pp. 235-242. [ Links ]
TU, J.; YEOH, G. H. y LIU, C. Computational fluid dynamics: a practical approach. Oxford: Elsevier, 2008. [ Links ]
WHITE, D. The planforms and onset of convection with a temperature dependent viscosity. Journal of Fluid Mechanics, 1988, vol. 191, pp. 247-286. [ Links ]
YI, F.; WEI, J. y SHI, J. Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system. Journal of Differential Equations, 2009, vol. 246, pp. 1944-1977. [ Links ]
ZHANG, L. y LIU, S. Stability and pattern formation in a coupled arbitrary order of autocatalysis system. Applied Mathematical Modelling, 2009, vol. 33, pp. 884-896. [ Links ]
ZIENKIEWICZ, O. y TAYLOR, R. The finite element method. The Basis, vol. I. Butterworth-Heinemann, Oxford, 2000. [ Links ]
ZIENKIEWICZ, O. y TAYLOR, R. Finite Element Method, vol. 3. Butterworth-Heinemann College, 2000. pp. 5-150. [ Links ]














