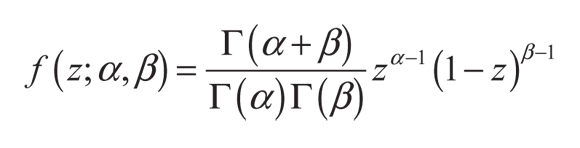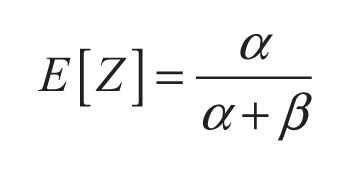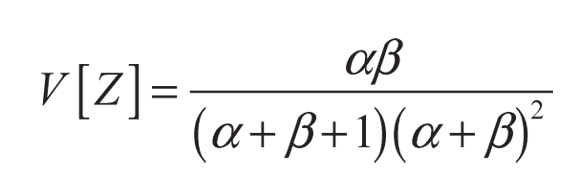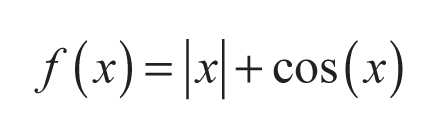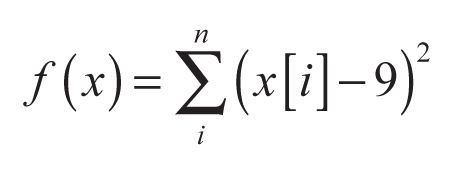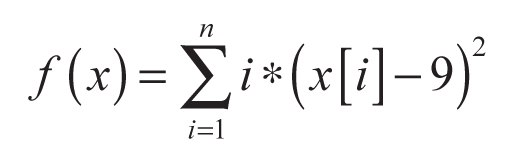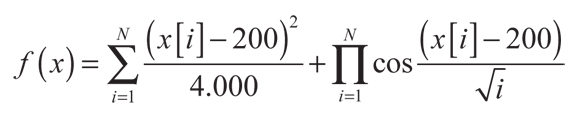Optimización de Monte Carlo usando la distribución beta¹

Monte Carlo Optimization Using Beta Distribution²

Otimização de Monte Carlo utilizando a distribuição beta³

Juan Velásquez-Henao⁴
Yeiny Pulgarín-Agudelo⁵
Eliana Castaño-Arias⁶

¹Este artículo se deriva de un proyecto de investigación denominado Predicción de la demanda mensual de electricidad usando máquinas de vectores de soporte (proyecto de investigación en curso de perfeccionamiento de pregrado), de la Universidad Nacional de Colombia, sede Medellín, Colombia.
²Submitted on September 21, 2010. Accepted on November 18, 2010. This article is derived from the research project Predicting the Monthly Demand of Electrical Supply through Support Vector Machines of the Universidad Nacional de Colombia, Medellin, Colombia.
³Data de recepção: 21 de setembro de 2010. Data de aceitação: 18 de novembro de 2010. Este artigo deriva de um projeto de pesquisa denominado Predição da demanda mensal de eletricidade usando máquinas de vetores de suporte (projeto de pesquisa em aperfeiçoamento), da Universidade Nacional da Colômbia, sede Medellín, Colômbia
⁴Ingeniero civil, Universidad Nacional de Colombia, Magíster en Ingeniería de Sistemas. Doctor en Ingeniería Sistemas Energéticos, Universidad Nacional de Colombia, sede Medellín, Colombia. Profesor de Posgrado en Ingeniería de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, sede Medellín. Correo electrónico: jdvelasq@bt.unal.edu.co.
⁵Estadística, Universidad Nacional de Colombia, sede Medellín, Colombia. Correo electrónico: ylpulgar@unal.edu.co.
⁶Estadística, Universidad Nacional de Colombia, sede Medellín, Colombia. Correo electrónico: eccastan@unal.edu.co.

Fecha de recepción: 21 de septiembre de 2010. Fecha de aceptación: 18 de noviembre de 2010.

Resumen

En este artículo se presenta el novedoso método de Monte Carlo para explorar funciones no lineales n-dimensionales definidas en un dominio compacto que es transformado al hipercubo unitario [0; 1]ⁿ. En esta aproximación se usa la distribución beta para generar muestras aleatorias; entre tanto, los parámetros de la distribución (alfa y beta) son ajustados dinámicamente, tal que en las primeras iteraciones la distribución beta es similar a la distribución uniforme. En las últimas iteraciones, la distribución beta es centrada en el mínimo conocido y la varianza es cercana a cero, tal que únicamente el vecindario alrededor del óptimo es muestreado. El método propuesto es probado usando cuatro funciones bien conocidas.

Palabras clave: Método de Monte Carlo, heurísticas, optimización combinatoria.

Abstract

This paper presents an innovating Monte Carlo method for exploring n-dimensional non-linear functions defined in a compact domain which is transformed to the hypercube [0;1]ⁿ. This approach uses the beta distribution for generating random samples. Te distribution parameters, named alpha and beta, are dynamically adjusted so that, in the first iterations, the beta distribution looks like the uniform distribution. ; in the last iterations, the beta distribution is centered in the known minimum and the variance is near zero, so that only the neighborhood around the optimum is sampled. The method proposed is tested through four well known benchmark functions.

Keywords: Monte Carlo method, heuristics, combinatorial optimization.

Resumo

Neste artigo, apresenta-se um novo método Monte Carlo para explorar funções não lineares n-dimensionais definidas em um domínio compacto que é transformado ao hipercubo unitário [0; 1]ⁿ. Nesta aproximação utiliza-se a distribuição beta para gerar amostras aleatórias; contudo, os parâmetros da distribuição (alfa e beta) são ajustados dinamicamente, de modo que nas primeiras iterações a distribuição seja similar à distribuição uniforme. Nas últimas iterações, a distribuição beta é centrada no mínimo conhecido e a variância é próxima a zero, de modo que somente a vizinhança em torno do ótimo é amostrada. O método proposto é testado com quatro funções de teste bem conhecido.

Palavras chave: Método de Monte Carlo, heurísticas, otimização combinatória.

Introducción

En optimización se desea solucionar el problema formulado como min f(x) sujeto a L ≤ x ≤ U, donde x, L y U son vectores n X 1, y f es una función no lineal, tal que f: Rⁿ → R (Rao, 1996). Este problema se ha abordado exitosamente de diversas maneras, por métodos basados en derivadas y métodos directos (Himmenlblau, 1972; Pierre, 1986; Bazaraa, Sherali y Shetty, 2006). Uno de los principales problemas que enfrentan muchos de los métodos, tanto directos como independientes de las derivadas, es conseguir una exploración a profundidad de las regiones de búsqueda (Törn y Zilinskas, 1989). Cuando no hay una exploración suficiente, por lo general se llega a un mínimo local. La característica estocástica del método de Monte Carlo de optimización permite que se explore la región aleatoriamente y logre una buena exploración con bajo costo computacional (Patel, Smith y Zabinsky, 1988).

El método de Monte Carlo tradicional (Dixon y Szegö, 1978; Rinnooy Kan y Timmer, 1984) se ha aplicado directamente a la solución de problemas reales (Kadri, Gharbi y Trabelsi, 2006; Riabov, Riabov y Tverskoy, 2006) y se ha combinado también con otras metodologías (Lei, 2002; Ren, Ding y Liang, 1988; Dugan y Erkoç, 2009) con el fin de mejorar su desempeño. Por otra parte, la exploración inicial, es decir, la búsqueda de un buen punto de inicio ha sido un problema por resolver para la mayoría de métodos (Himmenlblau, 1972; Pierre, 1986). Dadas las características del método de Monte Carlo, este ha sido escogido por varios métodos para realizar la exploración inicial y potenciar los resultados de la técnica primaria (Beyer y Schwefel, 2002; Bäck, 1996).

El objetivo de este artículo es presentar una modificación del método de Monte Carlo basada en el uso de la distribución beta, y en el cual se utiliza la información recolectada sobre la función objetivo para concentrar el muestreo de la región factible en aquella zona donde se encuentra localizado, posiblemente, el óptimo global.

El resto de este artículo se encuentra organizado como se describe a continuación. En la siguiente sección se describe el método de Monte Carlo tradicional. Posteriormente se presentan brevemente la distribución beta y sus propiedades. Más tarde se expone la metodología propuesta. Seguidamente se ejemplifica y, finalmente, se esbozan las principales conclusiones encontradas.

1. Método de Monte Carlo

La optimización de Monte Carlo está basada en la generación de una secuencia de puntos aleatorios obtenidos de una distribución, usualmente uniforme, con el fin de encontrar el óptimo global (máximo o mínimo) de una función. En la Figura 1 se presenta el algoritmo básico de la optimización de Monte Carlo. En cada iteración se genera un punto candidato aleatorio, x_c, en la región factible (línea 02); en este caso, u es una variable aleatoria uniforme en el intervalo [0, 1].

El punto de mínima, x_l, se actualiza cada vez que se encuentra un punto candidato donde la función objetivo tiene un menor valor que el más bajo conocido (línea 05) hasta ese momento. Se sabe que este algoritmo converge con una probabilidad baja al punto de óptima global en el interior de la región factible; por lo que se usa con más frecuencia para obtener un buen punto de inicio para otros algoritmos estocásticos (Pardalos y Resende, 2002). Una de las causas de este comportamiento es que el algoritmo no aprovecha la información obtenida durante el proceso aleatorio de búsqueda y sigue buscando en toda la región factible, sin concentrarse en la vecindad del óptimo encontrado, tal como lo hacen otros algoritmos estocástico como el recocido simulado (Kirkpatrick, Gelatt y Vecchi, 1983).

2. La distribución beta y sus propiedades

La distribución beta es una función de densidad de probabilidad continua, con dos parámetros α > 0 y β > 0, definida en el intervalo [0; 1] y cuya definición matemática es:

(1)

Donde Γ() es la función gamma. El valor esperado y la varianza de una variable aleatoria Z ∈ [0, 1] que sigue una distribución beta son:

(2)

(3)

Los valores de los parámetros α y β controlan la forma de la distribución.

3. Propuesta metodológica

La metodología propuesta en este artículo se basa en utilizar la distribución beta, definida en la ecuación 1, para muestrear la región factible, en vez de la distribución uniforme (línea 02 en la Figura 1). El objetivo de la modificación es utilizar la información conocida para concentrar la búsqueda en la mejor región encontrada, tal como lo hacen otros algoritmos de optimización estocásticos y aleatorios. La derivación de la metodología se basa en los siguientes aspectos:

• Se requiere que la función de densidad de probabilidad sea unimodal y cóncava hacia abajo. Ello implica que α, β > 1 en la distribución beta.
• El valor esperado de una variable aleatoria que sigue una distribución beta debe coincidir con el óptimo conocido hasta el momento. De esta forma, si z_l es el mejor punto conocido, la ecuación 2 establece la relación que hay entre α y β al reemplazar E[Z] por z_l. Así, se logra investigar la vecindad de z_l.
• La varianza de la variable aleatoria Z debe aumentar a medida que el algoritmo itere, de tal manera que se concentre la probabilidad alrededor de su valor esperado; ello equivale a que la probabilidad de obtener un número aleatorio lejano de z_l se reduzca en cada iteración hasta que se haga prácticamente cero. Para ello se introduce en la ecuación 3 un parámetro C que representa la varianza deseada y a partir del cual se calculan los valores de α y β, que garantizan que α, β > 1. El procedimiento de cálculo se presenta más adelante en esta misma sección.

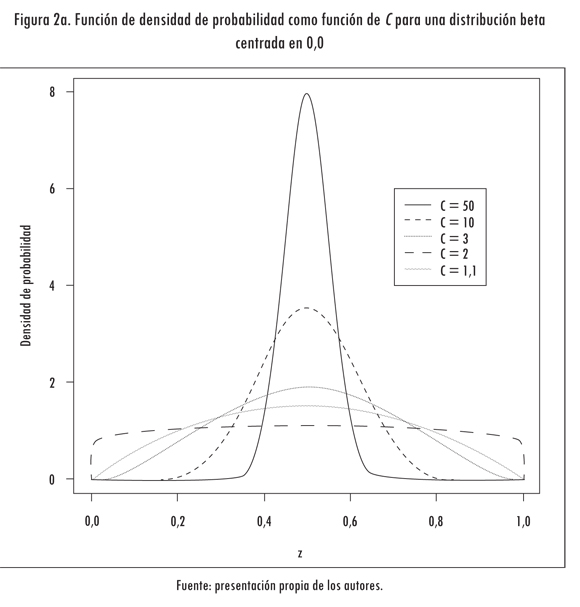
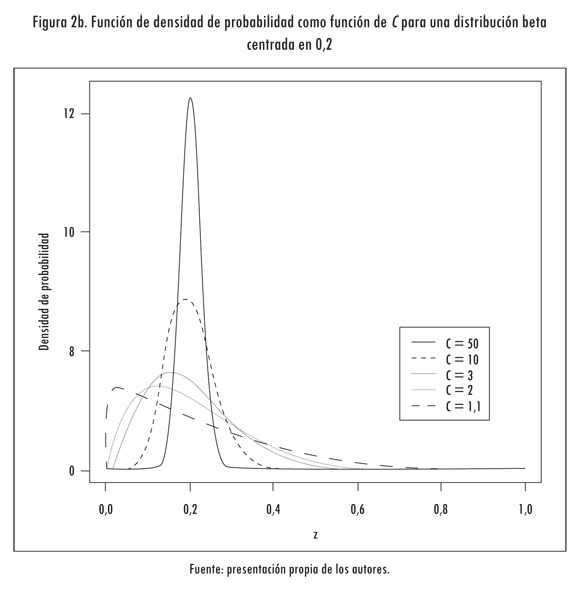
A partir de los tres aspectos anteriores es posible obtener los parámetros α y β de una distribución beta cuyo valor esperado es z_l y cuya varianza deseada es controlada por C. En la Figura 2 se grafica la función de densidad de varias distribuciones beta con valores esperados iguales a 0,5 (Figura 2a) y 0,2 (Figura 2b), y que difieren en el valor de la constante C previamente definida. Para C = 1,1 y z_l = 0,5 (Figura 2a), la distribución obtenida es muy similar a una distribución uniforme; a medida que la varianza aumenta, la función de densidad de probabilidad se concentra alrededor de la media (C = 2, 3, 10 y 50).

En la Figura 3 se presenta el algoritmo de optimización propuesto. En la línea 01 se fijan los valores inicial y final de la constante C, que controla la varianza de la distribución beta; su valor disminuye en cada iteración de acuerdo con la función observada (línea 05). Sea x el punto inicial del algoritmo, que será tomado por defecto como el centro de la región factible o un punto dado (línea 02).

Sea z_l el vector de n dimensiones que contiene el valor esperado. En el caso por defecto es un vector que contiene 0,5 para cada componente (línea 03). Inicialmente se toma una constante C muy cercana a la unidad, por ejemplo, C = 1,1. Esto equivale a iniciar con una distribución muy cercana a la uniforme, que cubre toda la región factible, pues ante la ausencia de información, el óptimo tiene igual probabilidad de estar ubicado en cualquier lugar de la región factible.

En la línea 05 se calcula el valor de C, que controla la varianza de la distribución beta. Este aumenta linealmente en cada iteración desde su valor inicial C_o hasta su valor final C_f , con lo cual la distribución se va haciendo cada vez más delgada, es decir, va desde una distribución platicúrtica a leptocúrtica, al aumentar el número de iteraciones.

En las líneas 06 a 14 se itera sobre cada dimensión, calculando los valores de los parámetros α y β, que definen la forma de la distribución, en función de la variable C. La función rbeta() usada en la línea 15 genera un número aleatorio que sigue dicha distribución de probabilidades.

En la línea 17, el vector de números aleatorios generado, z_c , es transformado del intervalo [0, 1]ⁿ al intervalo [L, U]. Al igual que para el algoritmo de optimización de Monte Carlo, la función objetivo es evaluada en x_c (línea 18), y se actualizan los vectores x_c y z_l cada vez que se encuentra un punto más bajo (líneas 19 a la 22). Es importante resaltar que en el caso n-dimensional se utiliza una distribución beta con un valor esperado diferente para cada dimensión, pero sólo se requiere una única constante C.

4. Ejemplos

4.1 Función unidimensional
En este ejemplo se ilustra el proceso de optimización de la función:

(4)

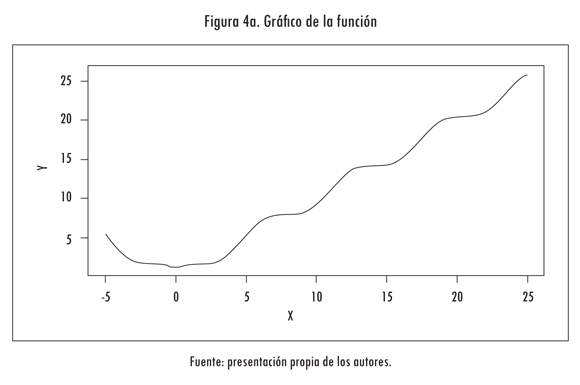
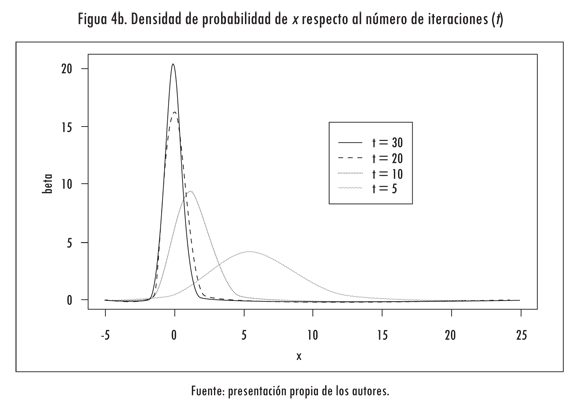
para -5 ≤ x ≤ 25. Esta función tiene un óptimo global en x_opt = 0 y f(X_opt) = 1. La función se presenta en la Figura 4a. Tal como fue indicado en la sección anterior, el punto óptimo inicial es z = 0,5 y C = 1; esto es equivalente, en el sentido estadístico, a tomar una distribución uniforme para z ∈ [0; 1] y x ∈ [-5; 25]. El algoritmo genera números aleatorios z muestreados de la distribución beta y actualiza el valor del mejor punto encontrado. A medida que el algoritmo itera, el valor esperado de la distribución se hace equivalente al mejor punto de mínima encontrado y aumenta progresivamente el valor de C. Este efecto se ilustra en la Figura 4b, en que se muestran las funciones de densidad de probabilidad utilizadas para muestrear z en función de la iteración; en este caso, se graficó la función de densidad de probabilidad para las iteraciones 5, 10, 20 y 30.

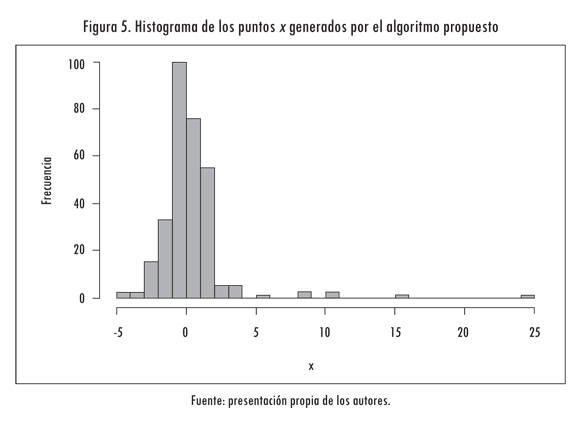
Un efecto del esquema de muestreo utilizado en el algoritmo propuesto es que se explora con mayor frecuencia la vecindad del punto de óptima actual. Ello implica que, al final del proceso, el muestreo se ha concentrado alrededor del punto de óptima global; esto se comprueba al graficar un histograma de los puntos x visitados por el algoritmo de optimización (Figura 5), el cual corrobora que hay una frecuencia de muestreo mucho más alta en la vecindad del mínimo que la apreciada en la totalidad del rango de búsqueda.

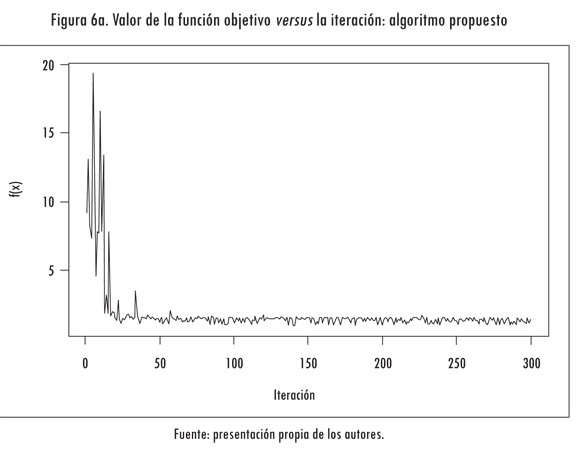
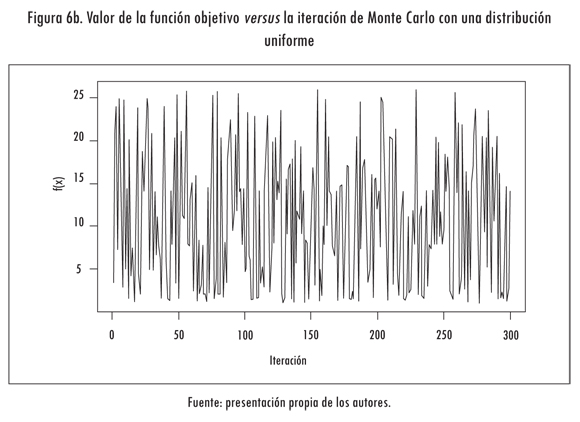
Consecuentemente, el valor de la función optimizada disminuye en función de la cantidad de iteraciones. En la Figura 6a se grafica el valor calculado de la función objetivo en cada iteración (línea continua) y el menor valor encontrado (línea punteada). Para apreciar este efecto se graficó el valor de la función objetivo cuando x es una variable aleatoria que sigue una distribución uniforme en el intervalo -5 ≤ x ≤ 25. Se aprecia que f(x) sigue un valor errático debido a los valores que toma x (Figura 6b).

4.2 Funciones multidimensionales
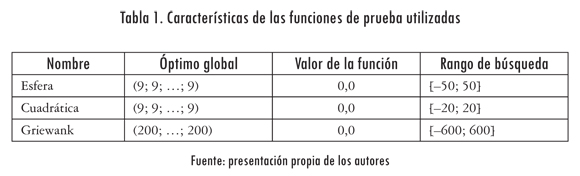
En esta sección se evalúa y se compara el desempeño del algoritmo propuesto para las funciones n-dimensionales definidas a continuación. El óptimo global, el valor de la función en el óptimo y el rango de búsqueda se resumen en la Tabla 1. Para este estudio se usó un número fijo de 30 dimensiones:

• Esfera con centro trasladado:

(5)



• Cuadrática con centro trasladado:

(6)



• Grienwak con centro trasladado:

(7)

Nótese que en la definición original de cada función su óptimo se encuentra exactamente en el centro del rango de búsqueda, por lo que el algoritmo propuesto lo encontraría directamente. Para poder evaluar la potencia del algoritmo propuesto, las funciones usadas se trasladaron. En este estudio se comparó el algoritmo propuesto con la optimización de Monte Carlo, descrito en la Figura 1, usando una distribución uniforme. Para cada función y algoritmo considerado se realizaron 50 corridas independientes; para cada corrida se realizaron 15.000 iteraciones.

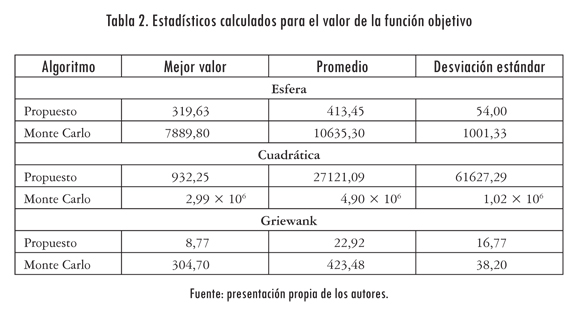
En la Tabla 2 se resumen los resultados obtenidos para las tres funciones de prueba consideradas. "Mejor Valor" es el menor valor encontrado entre todas las 50 corridas; "Promedio" es el valor promedio de menor valor encontrado en cada una de las corridas; "Desviación Estándar" es la desviación estándar calculada sobre la muestra de mejores valores encontrados.

De acuerdo con los resultados presentados en la Tabla 2, el algoritmo propuesto realiza un muestreo mucho más eficiente de la región factible que el método de Monte Carlo tradicional. Para las tres funciones analizadas, el mejor valor encontrado por el algoritmo propuesto está mucho más cercano del mínimo global que el valor hallado usando Monte Carlo con distribución uniforme. Puesto que el valor de la función objetivo es cero en el mínimo global, el mejor valor encontrado es en sí mismo una medida de la lejanía del mejor punto encontrado respecto al óptimo global.

El valor promedio de los mejores valores encontrados en las 50 repeticiones para cada uno de los métodos comparados es siempre menor para el algoritmo presentado en este artículo. Ello indica que el algoritmo propuesto hace una exploración más profunda de la región de búsqueda que el algoritmo de Monte Carlo. Esta conclusión se refuerza al tener en cuenta que la desviación estándar de los mejores valores para las 50 repeticiones del algoritmo es siempre inferior para la metodología propuesta, lo que muestra una mayor robustez.

5. Conclusiones y trabajo futuro

En este artículo se presentó un nuevo algoritmo de optimización de Monte Carlo basado en la distribución beta, el cual se fundamenta en la exploración detallada de la región circundante al óptimo encontrado en cada iteración. Para ello se propuso un esquema iterativo que ajusta dinámicamente los parámetros de la función beta de distribución de probabilidades, de tal forma que su valor esperado coincide con el óptimo encontrado hasta la iteración actual, y su varianza aumenta hasta un valor predeterminado por el usuario. El algoritmo propuesto fue ejemplificado usando cuatro funciones no lineales que han sido ampliamente usadas para la evaluación de algoritmos heurísticos de optimización. Los resultados obtenidos demuestran que el algoritmo propuesto supera ampliamente la optimización de Monte Carlo, que usa una distribución uniforme.

Referencias

BÄCK, T. Evolutionary algorithms in theory and practice. London: Oxford, 1996.         [ Links ]

BAZARAA, M.; SHERALI, H. y SHETTY C.M. Nonlinear optimization. New Jersey: Wiley, 2006.         [ Links ]

BEYER, H. y SCHWEFEL, H. Evolution strategies. Natural Computing. 2002, vol. 1, núm. 1, pp. 3-52.         [ Links ]

DIXON, L. C. W y SZEGÖ, G. P. (eds.). Towards global optimization, parts 1 and 2. Amsterdam: North-Holland, 1978.         [ Links ]

DUGAN, N. y ERKOÇ, S. Genetic algorithm-Monte Carlo hybrid geometry optimization method for atomic clusters. Computational Materials Science. 2009, vol. 45, núm. 1, pp. 127-132.         [ Links ]

HIMMENLBLAU, D. Applied nonlinear optimization. New York: McGraw Hill, 1972.         [ Links ]

KADRI, O.; GHARBI, F. y TRABELSI, A. Monte Carlo optimization of some parameters in gamma irradiation processing. Nuclear Instruments and Methods in Physics Research. 2006, vol. 245, núm. 2, pp. 459-463.         [ Links ]

KIRKPATRICK, S.; GELATT, C.D. y VECCHI, M.P Optimization by simulated annealing. Science. 1983, vol. 220, núm. 4598, pp. 671-680.         [ Links ]

LEI, G. Adaptive random search in Quasi-Monte Carlo methods for global optimization. Computers & Mathematics with Applications. 2002, vol. 43, núms. 6-7, pp. 747-754.         [ Links ]

PARDALOS, P. M. y RESENDE, M. G. C. (eds.). Handbook of applied optimization. New York: Oxford University Press, 2002.         [ Links ]

PATEL, N. R.; SMITH, R. L. y ZABINSKY, Z. B. Pure adaptive search in Monte Carlo optimization. Mathematical Programming. 1988, vol. 43, pp. 317-328.         [ Links ]

PIERRE, D. A. Optimization theory with application. New York: Dover, 1986.         [ Links ]

RAO, S. Engineering optimization, theory and practice. London: Wiley, 1996.         [ Links ]

REN, Y; DING, Y y LIANG, F. Adaptive evolutionary Monte Carlo algorithm for optimization with applications to sensor placement problems. Statistics and Computing. 2008, vol. 18, núm. 4, pp. 375-390.         [ Links ]

RIABOV, G. A.; RIABOV, V G. y TVERSKOY, M. G. Application of Monte-Carlo method for design and optimization of beam lines. Nuclear Instruments and Methods in Physics Research. 2006, vol. 558, núm. 1, pp. 44-46.         [ Links ]

RINNOOY KAN, A. H. G. y TIMMER, G. T. Stochastic methods for global optimization. American Journal of Mathematical and Management Sciences. 1984, vol. 4, pp. 7-39.         [ Links ]

TÖRN, A. y ZILINSKAS, A. Global optimization. Lecture Notes in Computer Science. 1989, vol.350, pp. 1-255.         [ Links ]