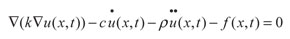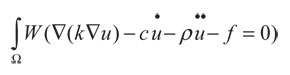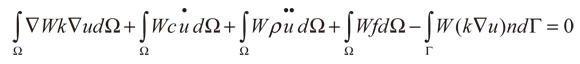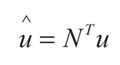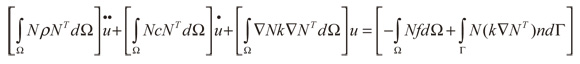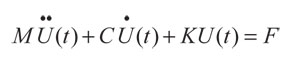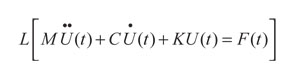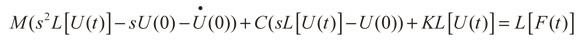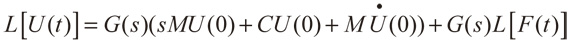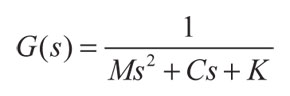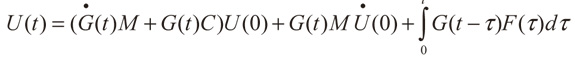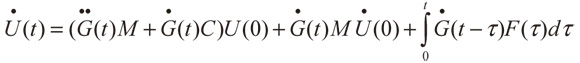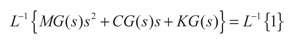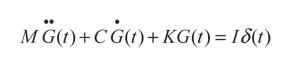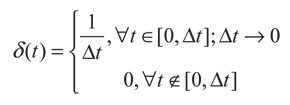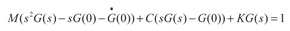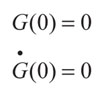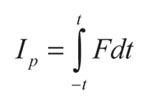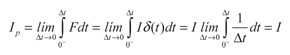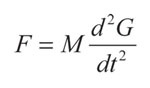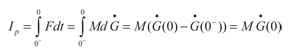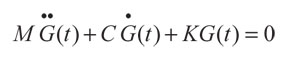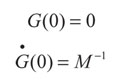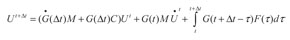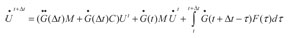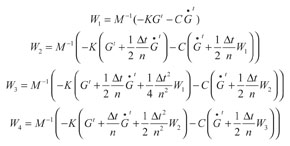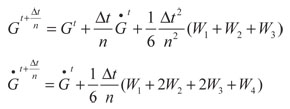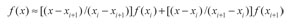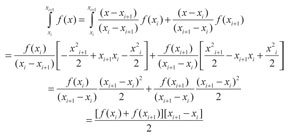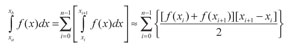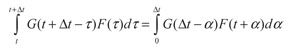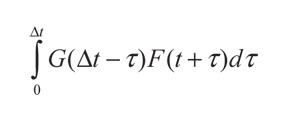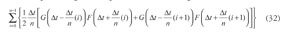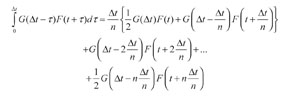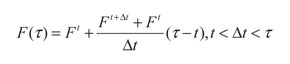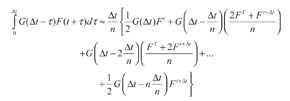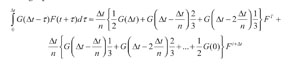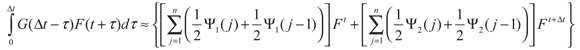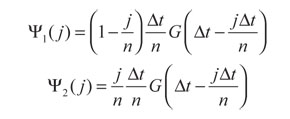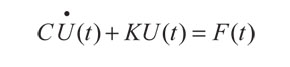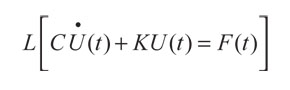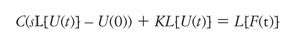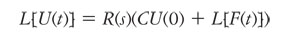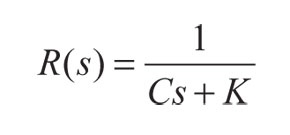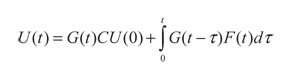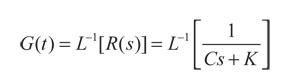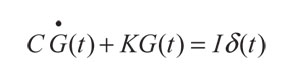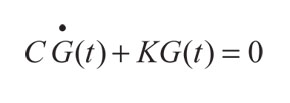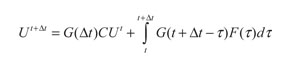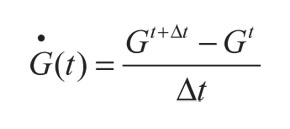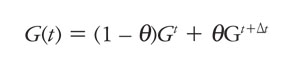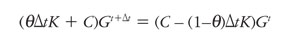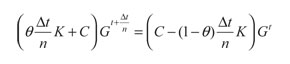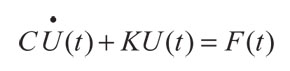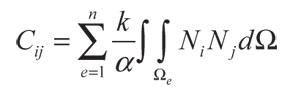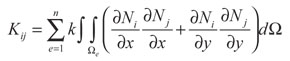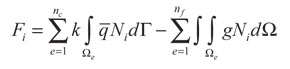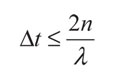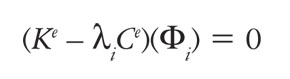Enfoque explícito de Green (ExGA) para la solución de ecuaciones diferenciales parciales en mecánica¹

Explicit Green Approach (ExGA) for Solving Partial Differential Equations in Mechanics²

Enfoque explícito de Green (ExGA) para a solução de equações diferenciais parciais em mecânica³

Diego Garzón-Alvarado⁴
Juan Carlos Piñeros-Cañas⁵

¹Este artículo fue desarrollado por el grupo de investigación en modelado y métodos numéricos en ingeniería (GNUM) y financiado por la Universidad Nacional de Colombia, Bogotá, Colombia.
²Submitted on: Jun 8, 2010. Accepted on: March 24, 2011. This article was developed by the research group on Modelling and Numeric Methods in Engineering (GNUM) and financed by the Universidad Nacional de Colombia, Bogotá, Colombia.
³Data de recepção: 8 de junho de 2010. Data de aceitação: 24 de março de 2011. Este artigo foi desenvolvido pelo grupo de pesquisa em modelado e métodos numéricos em engenharia (GNUM), financiado pela Universidade Nacional da Colômbia, Bogotá, Colombia.
⁴Ingeniero mecánico, Universidad Nacional de Colombia, Bogotá, Colombia. Máster en Ingeniería Mecánica, Universidad de los Andes, Bogotá, Colombia. Doctor en Mecánica Computacional, Universidad de Zaragoza, España. Profesor asociado del Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Correo electrónico: dagarzona@bt.unal.edu.co.
⁵Ingeniero mecatrónico. Máster en Ingeniería Mecánica, Universidad Nacional de Colombia, Bogotá, Colombia. Correo electrónico: jpinerosc@bt.unal.edu.co.

Fecha de recepción: 8 de junio de 2010. Fecha de aceptación: 24 de marzo de 2011.

Resumen

Este artículo presenta la formulación y la implementación de la solución de sistemas de ecuaciones diferenciales parciales mediante el método de Green explícito (ExGA). El método utiliza la transformada de Laplace para obtener la respuesta en el dominio de la frecuencia y, posteriormente, mediante transformada inversa, permite obtener, de forma explícita, la incógnita que soluciona la ecuación diferencial parcial. Se observa la versatilidad del método por la reducción de recursos computacionales para resolver problemas lineales de orden 2 y 1. Se llevan a cabo cuatro ejemplos numéricos para la ecuación de transferencia de calor y elasticidad. Los resultados muestran la exactitud y la precisión del método, el cual puede usar diferenciales de tiempo superiores a los utilizados en algoritmos de integración temporal clásicos con una respuesta cercana a un algoritmo de orden 2.

Palabras clave: Ecuaciones diferenciales, mecánica continua, transmisión del calor, elasticidad.

Abstract

This work presents the formulation and implementation of the solution to partial differential equation systems through the Explicit Green Approach (ExGA). This method uses the Laplace Transform to obtain the solution in the frequency domain and, then, through inverse transform, it makes it possible to explicitly obtain the value that solves the partial differential equation. The versatility of this method in the reduction of computer resources for solving type 2 and 1 linear problems can be observed. Four numerical examples for the heat and elasticity transfer equation are offered. Results show the accuracy of this method, which can use time differentials which are higher to those used in classic time integration algorithms with a solution which is closer to an order algorithm.

Key words: Differential equations,continuum mechanics, heat-transmission, elasticity.

Resumo

Este artigo apresenta a formulação e a implementação da solução de sistemas de equações diferenciais parciais mediante o método de Green explícito (ExGA). O método utiliza a transformada de Laplace para obter a resposta no domínio da frequência e, posteriormente, mediante transformada inversa, permite obter, de forma explícita, a incógnita que soluciona a equação diferencial parcial. Observase a versatilidade do método pela redução de recursos computacionais para resolver problemas lineares de ordem 2 e 1. Foram realizados quatro exemplos numéricos para a equação de transferência de calor e elasticidade. Os resultados mostram a exatidão e a precisão do método, que pode usar diferenciais de tempo superiores aos utilizados em algoritmos de integração temporal clássicos com uma resposta próxima a um algoritmo de ordem 2.

Palavras chave: Equações diferenciais, mecânica contínua, transmissão do calor, elasticidade.

Introducción

Muchas de las ecuaciones diferenciales parciales que describen el comportamiento de fenómenos físicos complejos son dependientes del tiempo (Gershenfeld, 1999; Cebeci, 2004). Típicamente estos problemas se denominan de valor inicial y se presentan frecuentemente en campos como transferencia de calor, propagación de ondas y comportamiento dinámico de estructuras (Akai, 1996). A su vez, estos problemas que evolucionan en el tiempo pueden depender de la posición espacial de las partículas, por lo que se hace necesaria la solución numérica a partir de una discretización de la ecuación diferencial en el dominio espacio-temporal (Zienkiewicz y Morgan, 1982). Por lo tanto, es conveniente aplicar un procedimiento de discretización parcial en el espacio-tiempo, con el cual se reemplazará la ecuación diferencial parcial por un conjunto de ecuaciones diferenciales ordinarias (Zienkiewicz y Taylor, 2000).

Para solucionar este sistema de ecuaciones diferenciales ordinarias, ahora dependientes del tiempo, se han desarrollado numerosas técnicas de integración temporal (Zienkiewicz, Wood y Hine, 1984; Hughes, 2000). La solución de estas ecuaciones diferenciales pueden originar sistemas algebraicos cuya solución son del tipo explícito, semiimplícito o implícito (LeVeque, 2006; Newmark, 1959). Comúnmente en la literatura se encuentran los métodos de la familia de Newmark (1959), Wilson-θ;(Bathe y Wilson, 1973), Hilber-Hughes-Taylor (1977) y Bossak-α (Wood et ál., 1981). Los últimos métodos mejoran la aproximación que se realiza con el métodos de Newmark (Hughes, 2000).

De igual manera, se desarrollaron métodos con un orden de precisión más alto, a fin de disminuir errores numéricos y aumentar el orden de convergencia. Entre los más destacados son los métodos mostrados por Kutta (1901), que son una generalización del método propuesto por Runge (1895), para la obtención de métodos de cualquier orden. Por otro lado, en las décadas de los ochenta y de los noventa, Zienkiewicz, Wood y Hine (1984), utilizando el método de los residuos ponderados en el tiempo, generalizó los métodos de integración temporal a través de su algoritmo single step algorithms (SSpj). En (Zienkiewicz y Taylor, 2000, y Zienkiewicz, Wood y Hine, 1984) se muestra que a partir del métodos SSpj es posible obtener varias familias de solución temporal, incluidas las de Newmark y sus variantes.

Recientemente, Soares y Mansur (2004), a través del métodos Implicit Green Approach (ImGA) establecieron nuevos algoritmos de integración temporal, basados en el cálculo numérico implícito de la función de Green. Posteriormente, Mansur presentó un nuevo algoritmo de integración temporal, el Explicit Green Approach (ExGA), que se diferencia del anterior método por calcular numéricamente, de manera explícita, las funciones de Green. Este método resuelve problemas que involucran ecuaciones de onda, como se observa en (Mansur et ál., 2007). En el 2008, Mansur usó el ExGA para resolver problemas de transferencia de calor (Mansur et ál., 2008).

El objetivo de este trabajo es aplicar el nuevo método de integración temporal ExGA a la solución de problemas de ecuaciones diferenciales parciales con evolución temporal de primer y segundo orden. Específicamente, problemas de elasticidad bidimensional, donde solamente ha sido aplicada la técnica del ImGA, además de revisar los problemas de transferencia de calor, con el fin de validar los resultados obtenidos por Mansur, para realizar un posterior estudio del comportamiento de la técnica en problemas de advección-difusión-reacción.

La discretización espacial se realiza utilizando el método de los elementos finitos (Zienkiewicz y Taylor, 2000; Hughes, 2000). El cálculo numérico de las funciones de Green se realiza explícitamente con los algoritmos de Runge-Kutta cuarto orden y Crank-Nicolson. La implementación del algoritmo se realiza en FORTRAN y las rutinas de solución matricial se apoyan en la librería LAPACK.

1. Discretización parcial de la ecuación de movimiento

La ecuación de equilibrio dinámico se puede escribir como (Mansur et ál., 2007; Loureiro, 2007; Carrer y Mansur, 1997):

(1)

Donde k, c y ρ son los parámetros físicos del problema, los cuales son considerados independientes del tiempo. Si 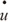= 0, la ecuación (1) es de reacción-difusión; si ü = 0, es una ecuación de onda. Además, si ü = 0 y 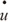= 0, es una ecuación de Poisson. Finalmente, si ü = 0, 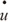= 0 y f = 0, es una ecuación de Laplace (Zienkiewicz y Taylor, 2000). Para discretizar la ecuación (1) se utiliza el método de los elementos finitos. Si (1) es el residuo, se puede multiplicar por cualquier función W de ponderación e integrar a lo largo del dominio para obtener (Zienkiewicz y Taylor, 2000):

(2)

Para solucionar el problema es necesario bajar el orden de la segunda derivada. Con el ánimo de disminuir la exigencia (debilitación) del polinomio de reducción del orden, para esto se aplica el teorema de Green (Hughes, 2000; Zienkiewicz y Taylor, 2000), de donde se obtiene:

(3)

Finalmente, aplicando el método de Bubnov-Galerkin (o Galerkin estándar) en dos dimensiones (Zienkiewicz y Taylor, 2000) (W = N), y la variable se discretiza como:

(4)

Donde û es la aproximación de la variable en cualquier parte del dominio, u es el vector solución en los puntos nodales del elemento, y N son las funciones de forma del elemento utilizado. Por lo tanto, se obtiene:

(5)

Lo que escrito en forma matricial sería:

(6)

Si un sistema estructural es considerado, M, C y K denotan matrices de masa, amortiguamiento y rigidez, respectivamente, F es el vector de carga equivalente nodal y 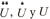son respectivamente los vectores desconocidos de aceleración, velocidad y desplazamiento.

Para solucionar el sistema dado en (6), que evoluciona en el tiempo, se utiliza el método ExGA, que se desarrolla a continuación. Cabe mencionar que existe un buen número de métodos de solución (la mayoría de ellos implícitos): los métodos de la familia de Newmark (1959), Wilson-θ; (Bathe y Wilson, 1973), Hilber-Hughes-Taylor (1977), Bossak-α (Wood et ál., 1981), Runge-Kutta (citado en Akai, 1996), Crank-Nicolson (Hughes, 2000), entre otros.

2. Enfoque explícito de Green (ecuaciones diferenciales de segundo orden)

Para resolver el sistema obtenido a través de la discretización hecha por el método de los elementos finitos (6), se le aplica la transformada de Laplace (Loureiro, 2007):

(7)

Mediante la transformada de Laplace se obtiene un nuevo sistema diferencial, ahora, en el espacio de la frecuencia dado por:

(8)

A partir de la expresión anterior, se puede obtener de forma explícita la incógnita L[U(t)} realizando un despeje algebraico, con lo que se obtiene:

(9)

Donde:

(10)

Aplicando la transformada inversa de Laplace L ^-1 a la ecuación (9), se obtiene:

(11)

A partir de (11) se puede obtener el vector de velocidades del sistema mediante la diferenciación respecto al tiempo; por lo tanto, se obtiene:

(12)

2.1 Cálculo de la matriz de Green

En las expresiones (11) y (12), G(t) representa la función de Green en forma matricial. Para encontrar la matriz de Green G(t), se aplica trasformada inversa de Laplace a la expresión (10) y se obtiene:

(13)

(14)

Donde I representa la matriz identidad y δ(t) es la función delta de Dirac aplicada en un instante τ = 0 expresada como:

0(t )

Si se aplica transformada de Laplace a la anterior expresión se obtiene:

(15)

Para que la anterior expresión sea igual a (10), es necesario que las condiciones iniciales sean:

(16)

El problema descrito por la ecuación (14), con condiciones iniciales (16), involucra en un término la función delta de Dirac, lo cual la hace dependiente, según la definición anterior, del paso de tiempo (Δt) utilizado en el algoritmo. Este comportamiento indeseable se puede remover mediante la transformación del problema impulsivo, a un problema de condiciones iniciales. A partir de la mecánica clásica, se tiene que la definición de impulso está dada por:

(17)

Donde F es el vector de fuerzas aplicado en el instante de tiempo t. De la ecuación (17) se puede calcular el impulso generado por la aplicación de la fuerza en la ecuación (14), es decir:

(18)

También de la teoría clásica de la mecánica se conoce que la segunda ley de Newton puede ser escrita como:

(19)

Donde M es la masa total del sistema y G hace referencia a la matriz de desplazamientos. Por lo tanto, se puede obtener una relación entre el impulso I y la segunda ley de Newton, dado por:

(20)

De esta forma, visto que la expresión (18) es equivalente a (20), en términos del movimiento generado, se concluye que el cálculo de las funciones de Green (G(t)), a través de la ecuación (14), puede ser, alternativamente realizado por la solución de:

(21)

Con condiciones iniciales:

(22)

Con excepción de casos muy simples, en problemas en ingeniería no se cuenta con la matriz de Green analítica; por lo tanto, debe ser calculada numéricamente por algún método de integración temporal utilizando la expresión (21). Si se asume un tiempo t = Δt en las ecuaciones (11) y (12), la solución en cualquier instante de tiempo puede ser calculada recursivamente como:

(23)

Y para velocidad de obtiene:

(24)

Se debe tener en cuenta que para evaluar la anterior expresión recursiva de respuesta en cualquier intervalo de tiempo, es necesario calcular las matrices de Green G(Δt), G (Δt ) y G (Δt) una única vez en un instante de tiempo t = Δt.

2.2 Métodos ExGA y Runge-Kutta

Para utilizar las expresiones explícitas (23) y (24) en la solución del problema de integración temporal de una ecuación diferencial parcial, es necesario resolver de manera previa el sistema de ecuaciones (21). Para ello se utiliza la forma explícita del método clásico de RK⁴:

(25)

Los desplazamientos y las velocidades de las matrices de Green son calculadas mediante:

(26)

Se observa en las ecuaciones anteriores el parámetro n, que define el número de subpasos que se empleara para el cálculo de las matrices G(Δt) y G(Δt ). Cuando se utilizan subpasos (n > 1), el método presenta una mejora en la estabilidad (posibilidad de utilizar pasos de tiempo más grandes) (Mansur, 2007). Si se emplea un número de subpasos adecuado, el tiempo de paso crítico (Δt_max ) que se va a emplear puede extenderse para propósitos prácticos; además, el método de integración temporal explícito utilizado, basado en funciones de Green calculadas explícitamente, puede convertirse en un método de integración temporal incondicionalmente estable (Soares y Mansur, 2004).

2.3 Cálculo de la integral de convolución en el tiempo

La integral de convolución en (23) y (24) tiene en cuenta los efectos de la aplicación de una perturbación externa al sistema físico. Para el cálculo numérico de esta integral se utilizan las formulas de Newton-Cottes, caracterizadas por tomar intervalos de discretización constantes, a diferencia de otras técnicas.

Dentro de las fórmulas de Newton-Cottes más conocidas, se encuentran: la regla del rectángulo, la regla del trapecio y la regla de Simpson. En el presente trabajo se eligió como método de integración la regla del trapecio (Loureiro, 2007; Akai, 1996).

2.3.1 Regla del trapecio

Si se considera una función f(x) cuando x varía desde x_i hasta x_i+1 , se aplica una interpolación de Lagrange con el fin de aproximar la función desde [x_i, f(x_i)} hasta [x_i+1 , f(x_i+l)} por una recta. Así se obtiene (Akai, 1996):

(27)

Esta aproximación se integra analíticamente (Akai, 1996):

(28)

De esta forma se puede aproximar la integral de una función f (x) definida entre x_a y x_b como:

(29)

Donde n representa el número de intervalos (subpasos) en que se divide la función que se va a integrar.

2.3.2 Integral de convolución mediante regla del trapecio

Para desarrollar la integral de convolución numéricamente, se cambia de variable, α = τ - t, y queda la integral y sus límites expresados de la siguiente forma:

(30)

Como α es un parámetro, se expresa la integral de una forma más habitual como se muestra en:

(31)

Si se aplica la regla del trapecio a la anterior integral, se tiene (Akai, 1996):

(32)

Al expandir la sumatoria se obtiene:

(33)

Si se supone que la variación del vector F en el intervalo de tiempo [t, t+Δt} es lineal, entonces:

(34)

Aplicando esta suposición en la expresión (33):

(35)

Agrupando términos comunes:

(36)

De esta forma se puede generalizar la integral de convolución como (Soares y Mansur, 2004; Loureiro, 2007):

(37)

Donde:

Usando la expresión anterior, se realiza la aproximación numérica de la integral de convolución para todo t, que permite su cálculo en n subpasos, con las subsecuentes mejorías que esto conlleva.

3. Enfoque explícito de Green (ecuaciones diferenciales de primer orden)

Para el caso de problemas que involucren diferenciales temporales de primer orden, se aplica la discretización parcial y se obtiene un sistema matricial de la forma (Hughes, 2000):

(38)

Al aplicar la transformada de Laplace se obtiene:

(39)

(40)

Luego de obtener de forma explícita L[F(t)} se tiene la siguiente ecuación de solución:

(41)

Donde:

(42)

Aplicando la transformada inversa de Laplace (L _-1) a la ecuación (41), teniendo en cuenta la ecuación (42), se obtiene:

(43)

3.1 Cálculo de la matriz de Green

En la expresión (43), G(t) representa la función de Green en forma matricial, dada por:

(44)

La función de Green es llamada la respuesta impulsiva del sistema, debido a que puede obtenerse por medio de:

(45)

Con condición inicial: G(0) = 0

Donde I representa la matriz identidad y δ(t) es la función delta de Dirac.

El problema descrito por la ecuación (45) es equivalente a un problema homogéneo de valor inicial con la aplicación de cierta condición inicial (Ozisik, 1993). En (Mansur et ál., 2008) se verifica que la correcta equivalencia para este problema está dada por:

(46)

Con condición inicial: G(0) = C-¹

Si se asume un paso de tiempo t = Δt, la solución para cualquier tiempo de (43) puede evaluarse recursivamente mediante la expresión:

(47)

3.2 Métodos ExGA y Crank-Nicolson

Para utilizar la expresión explícita (47) es necesario resolver antes el sistema de ecuaciones (46), mediante la siguiente aproximación en diferencias finitas para el término de la derivada temporal. Así, se tiene:

(48)

Utilizando el método de la familia θ;-trapezoidal para marcha en el tiempo, se puede escribir la siguiente expresión:

(49)

Al reemplazar las expresiones (48) y (49) en (46), se obtiene el siguiente sistema de ecuaciones lineales:

(50)

Cabe anotar que la matriz de Green se calcula únicamente para el intervalo de tiempo {0,Δt}. Por lo tanto, la expresión anterior se transforma en:

(51)

El parámetro θ; varía en el intervalo {0, 1}. Si 0 = 1, la solución es totalmente implícita. Si θ; = 0, la solución es totalmente explícita. Si 0 = 0,5, la solución es semiimplícita y está dada por el esquema de Crank-Nicolson. Este esquema es el implementado para este trabajo, por ser el único método de la familia θ;-trapezoidal que posee una precisión de segundo orden. Se observa en la ecuación anterior el parámetro n, que define el número de subpasos que se empleará para el cálculo de la matriz G(Δt).

4. Aplicación del algoritmo al problema de transferencia de calor en una placa

A efectos de ilustrar el uso del algoritmo expuesto, se toma el ejemplo de la solución del problema de transferencia de calor en una placa, que involucra diferenciales en el tiempo de primer orden. Es posible utilizar el algoritmo propuesto para validar diferenciales en el tiempo de segundo orden. Con la solución de este problema se busca examinar las principales características del ExGA. Para el ejemplo mostrado se desarrolla un programa en FORTRAN y se grafican los datos utilizando PARAVIEW.

Aquí se toma la placa con condiciones iniciales de temperatura y flujo nulo en todo su contorno (condición Dirichlet). En segundo lugar, la placa es tomada con condiciones iniciales de temperatura y un flujo de entrada en un extremo de su contorno (condición Neumann). Finalmente, se halla la solución de un problema que involucra los dos tipos de condición de contorno (Dirichlet y Neumann).

La discretización espacial de la ecuación parabólica no homogénea de transferencia de calor puede representarse de forma matricial con ayuda del método de los elementos finitos como (Hughes, 2000):

(52)

Con condición inicial T(0) = T⁰, donde C es la matriz de capacitancia, K es la matriz de conductancia térmica y F es el vector de cargas térmicas nodales equivalentes. Estas matrices y el vector pueden ser calculados con las siguientes expresiones:

(53)

(54)

(55)

Donde i, j = 1, ..., n (número de nodos), N_i y N_j son las funciones de forma (Hughes, 2000),n es el número de elementos en el dominio, n_c es el número de elementos con cara en el contorno que tienen prescrito flujo de calor, y n_f es el número de elementos de la región donde la fuente se está aplicando.

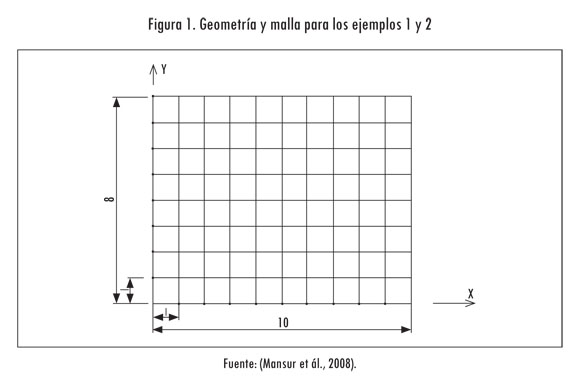
Para la discretización por elementos finitos se han utilizado elementos cuadrados bilineales. La placa para el desarrollo de las simulaciones es de 10m X 8m. Los coeficientes físicos adoptados para la simulación son: α = 1,0m²/s, k = 1,0 W/°Cm.

4.1 Ejemplo 1

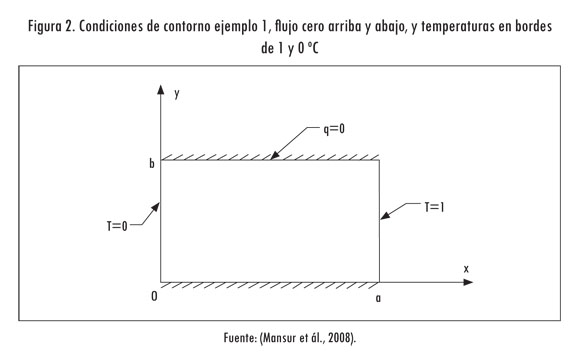
En este ejemplo se considera la placa rectangular de la Figura 1, con condiciones iniciales T (x, y, 0) = 0,0 °C a través de todo el dominio. En el contorno, los lados horizontales de la región rectangular tienen flujo cero, el lado vertical izquierdo tiene temperatura T (0, y, t) = 0,0 °C y el derecho T (a, y, t) = 1,0 °C.

4.2 Ejemplo 2

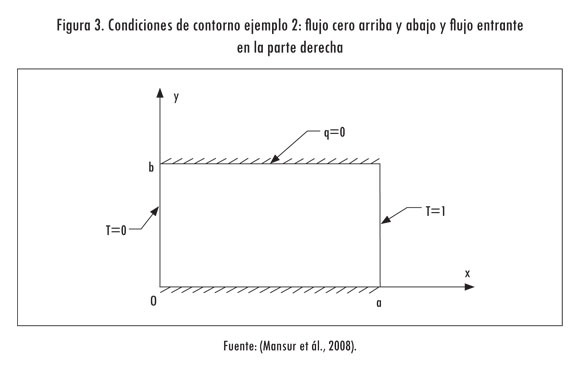
En este ejemplo se considera la placa rectangular de la Figura 1, con condiciones iniciales T (x, y, 0) = 0,0 °C a través de todo el dominio. Las condiciones de contorno son: q(x, 0, t) = q(x, b, t) = 0,0 W/m, T (0, y, t) = 0,0 °C y q(a, y, t) = 0,1 W/m (figuras 2 y 3).

5. Resultados

5.1 ExGA primer orden

El método de Crank-Nicolson utilizado para el cálculo de las matrices de Green, necesarias para solucionar los problemas térmicos descritos, es implícito e incondicionalmente estable. Sin embargo, el método ExGA es explícito y está sujeto a una condición de estabilidad que determina cuál es el mayor tamaño de paso de tiempo (Δt) que se puede utilizar en el método para que exista convergencia. Esta relación se muestra a continuación (Mansur et ál., 2008):

(56)

Donde n es el número de subpasos y λ es el mayor autovalor obtenido de resolver el problema:

(57)

A medida que se toma un número mayor de subpasos, la solución al problema de las matrices de Green es más exacta. Ello se traduce en una mejora en la convergencia del método. Cabe anotar que para este tipo de problema la convergencia aumenta al tomar un número mayor de subpasos y no al disminuir el paso de tiempo (Δt) empleado. Esto significa que las características de estabilidad de Crank-Nicolson son transferidas al método ExGA; por lo tanto, se puede utilizar cualquier paso de tiempo, sin importar lo amplio que sea, y el método tendrá convergencia, siempre y cuando se cumpla con la relación (56).

Para los tres primeros ejemplos el autovalor es igual a λ = 3,8197. Al aplicarlo a la expresión (56), tomando el número de subpasos unitario, se encuentra que el paso de tiempo máximo debe estar por debajo de Δt ≤ 0,5236. Teniendo en cuenta esta restricción se presentan los resultados para cada uno de los ejemplos propuestos, tomando distintos números de subpasos.

5.2 Ejemplo 1 (condición Dirichlet)

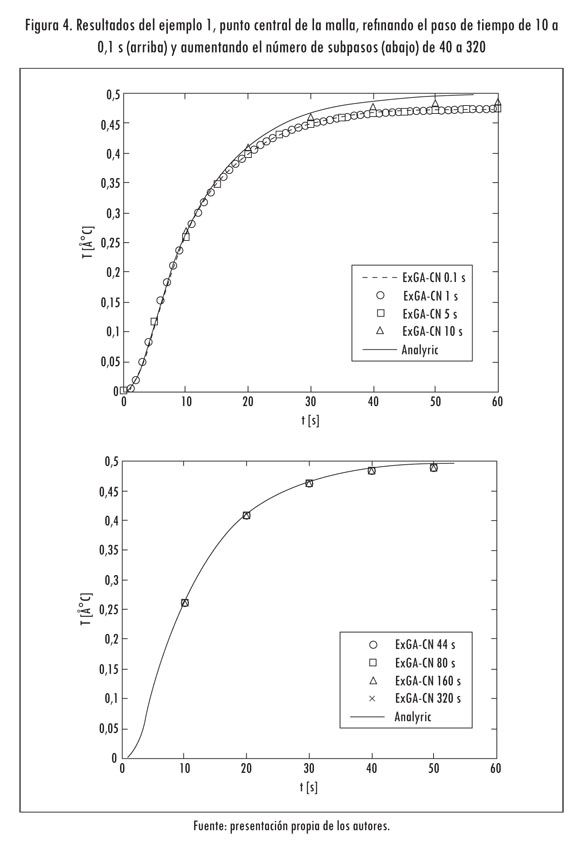
En los resultados presentados en la Figura 4 se realizan cuatro aproximaciones numéricas, utilizando en todas 20 subpasos y pasos de tiempo (Δt) de 0,1; 1; 5 y 10 segundos. Cada una de estas simulaciones se realiza hasta 60 segundos y se compara directamente con la solución analítica.

En la gráfica de la parte superior se muestra que al refinar el paso de tiempo manteniendo el mismo número de subpasos la respuesta del método es la misma. Todos los puntos solución se superponen sobre una misma línea, a excepción del caso en el que se toma Δ = 10 s, lo cual se espera por ser este valor cercano al límite de convergencia del método, para este caso Δ ≤ 10,472 s.

Como los puntos de solución siempre se presentan sobre una misma línea, independiente del Δt que se tome, en la parte de la derecha se muestran los resultados para el problema con un Δt = 10 s, cambiando el número de subpasos a 40, 80, 160 y 320. A medida que aumenta el número de subpasos, mejora de una manera notable la precisión del método. En la Figura 5 se muestran los resultados para toda la placa. Las imágenes se toman cada 12 s. Se ordenan de izquierda a derecha, y de arriba a abajo.

5.3 Ejemplo 2 (condición Neumann)

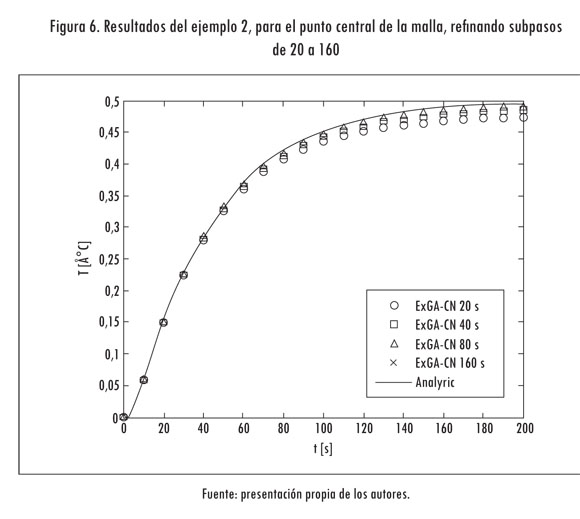
Para este problema se toma un paso de tiempo Δt = 10 s, y 20, 40, 80 y 160 subpasos. Cada una de estas simulaciones se realiza hasta 200 s y se compara directamente con la solución analítica (Figura 6).

Igual que en el caso anterior, el método presenta una mejora en la precisión a medida que aumenta el número de subpasos. También se evidencia la ventaja de poder utilizar pasos de tiempo grandes en problemas que requieren historiales de simulación muy amplios, con la consecuente disminución del costo computacional.

6. Conclusiones

Se presenta en este artículo el estudio de la solución de sistemas de ecuaciones diferenciales parciales mediante el método de Green explícito (ExGA). Se observa que existe una gran ventaja al permitir el uso de pasos de tiempo más amplios, lo que trae como consecuencia una reducción de recursos computacionales para resolver problemas lineales de orden 1 y 2. Esta ventaja puede ser vista directamente, respecto a los métodos clásicos explícitos, en las expresiones que condicionan el paso de tiempo máximo que se va a utilizar, estando para los métodos explícitos convencionales, su condición de estabilidad temporal dada por las mismas expresiones. Cambian únicamente el n por un valor unitario (n = 1).

El método puede usar tiempos superiores a los utilizados en algoritmos de integración temporal explícito con una respuesta cercana a un algoritmo de orden 2. En el cálculo de las matrices de Green se presenta una equivalencia entre las respuestas impulsivas y las condiciones iniciales, dadas estas últimas por matrices inversas de masa, lo cual representa un costo computacional muy alto. Sin embargo, se utilizan algoritmos de condensación como HRZ y Row-Sum, para simplificar el cálculo de estas matrices inversas, a fin de comprobar que su impacto en la precisión del método es mínimo.

Al tomarse un número adecuado de subpasos, el paso de tiempo At puede ser tan grande como se desee, teniendo como única limitación una buena representación gráfica de la respuesta o la necesidad de obtener una respuesta dentro de un margen de tiempo transitorio específico del problema. Otra observación importante extraída del análisis de las aplicaciones es que la precisión del método ExGA es satisfactoria y susceptible a mejora utilizando polinomios de órdenes superiores para el cálculo de la integral de convolución. También se observa que el efecto de aumentar el número de subpasos en problemas de primer orden es el incremento en la precisión del método, diferente a lo que sucede en los problemas de segundo orden, en los cuales este aumento influye únicamente en el tamaño del Δt.

Finalmente, se afirma que el método ExGA es una alternativa interesante en la solución de problemas en los que se necesitan pasos de tiempo muy pequeños, e historiales de simulación extensos, como es el caso de los problemas de elasticidad bidimensional. En estos problemas se puede apreciar, de una mejor manera, la ventaja de los subpasos, lo que permite utilizar pasos de tiempo más grandes que los que se pueden emplear con los métodos tradicionales, sin tener pérdidas en cuanto a precisión.

Referencias

AKAI, T. J. Métodos numéricos aplicados a la ingeniería. México: Noriega, 1996.        [ Links ]

BATHE, K. J. y WILSON, E. L. Stability and accuracy analysis of direct integration methods. Earthquake Engineering and Structural Dynamics. 1973, vol. 1, pp. 283-291.        [ Links ]

CARRER, J. A. M. y MANSUR, W J. Time-domain BEM analysis for the 2D scalar wave equation: initial conditions contributions to space and time derivatives. InternationalJournal for Numerical Methods in Engineering. 1997, núm. 39, pp. 2188-2469.        [ Links ]

CEBECI, T. Analysis of turbulent flows. Amsterdam: Elsevier, 2004.        [ Links ]

GERSHENFELD, N. The nature of mathematical modelling. Cambridge: Cambridge University Press, 1999.        [ Links ]

HILBER, H. M.; HUGHES, T. J. R. y TAYLOR, R. L. Improved numerical dissipation for time integration algorithms in structural dynamics. Earthquake Engineering and Structural Dynamics. 1977, núm. 5, pp. 283-292.        [ Links ]

HUGHES, T. J. R. The finite element method - linear static and dynamic finite element analysis. New York: Dover Publishers, 2000.        [ Links ]

KUTTA, W Beitrag zur Naherungsweisen integration totaler differentialgleichungen. Zeitschrift für Mathematisch Physik. 1901, num. 46, pp. 435-453.        [ Links ]

LEVEQUE, R. J. Finite difference methods for differential equations. Washington: University of Washington; 2006.        [ Links ]

LOUREIRO, F. S. Métodos de integração temporal baseados no cálculo numérico de funções de Green a traves do métodos dos elementos finitos. MSc Thesis, Universidade Federal do Rio de Janeiro, Brasil, 2007.        [ Links ]

MANSUR, W J.; LOUREIRO F. S.; SOARES, D. JR.; DORS, C. Explicit time-domain approaches based on numerical Green's functions computed by finite differences - The ExGA family. Journal of Computational Physics. 2007; núm. 227, pp. 851-870.        [ Links ]

MANSUR, W J. ; VASCONCELLOS, C. A. B.; ZAMBROZUSKI, O. C. ; ROTUNNO FILHO, N. J. M. Numerical solution for the linear transient heat conduction equation using an Explicit Green's Approach. Journal of Heat and Mass Transfer. 2008, vol. 52, núms. 3-4, pp. 694-701.        [ Links ]

NEWMARK, N. M. A method of computation for structural dynamics. Journal Engineering Mechanics Division, ASCE 85. 1959, pp. 67-94.        [ Links ]

OZISIK, M. N. Heat conduction. New York: John Wiley & Sons, 1993.        [ Links ]

RUNGE, C. Uber die numerishe auflosung von differentialgleichungen. Mathematische Annalen. 1895, núm. 46, pp. 167-178.        [ Links ]

SOARES, JR. D. y MANSUR, W. J. A time domain FEM approach based on Implicit Green's functions for non-linear dynamic analysis. International Journal for Numerical Methods in Engineering. 2004, núm. 62, pp. 664-681.        [ Links ]

WOOD, W L.; BOSSAK, M. y ZIENKIEWICZ, O. C. An alpha modification of Newmark's methods. International Journal for Numerical Methods in Engineering. 1981, vol. 15, núm. 10, pp. 1562-1566.        [ Links ]

ZIENKIEWICZ, O. C. y MORGAN K. Finite elements and aproximation. Philadelphia: Dover Publications, 1982.        [ Links ]

ZIENKIEWICZ, O. C. y TAYLOR R. L. El método de los elementos finitos. Las bases. Barcelona: CIMNE, 2000.        [ Links ]

ZIENKIEWICZ, O. C.; WOOD, W L. e HINE, N. W. A unified set of single step algoritms Part 1. General formulation and aplications. International Journal for Numerical Methods in Engineering. 1984, vol. 20, pp. 1529-1552.        [ Links ]