Modelo de maximization de la entropía y costos generalizados intervalares para la distribución de viajes urbanos¹

Maximization Model of entropy and generalized costs for urban travel distribution²

Modelo de maximização da entropia e custos generalizados intervalares para a distribuição de viagens urbanas³

Héctor López-Ospina⁴

¹Fecha de recepción: 15 de febrero de 2012. Fecha de aceptación: 15 de septiembre de 2013. Universidad de Chile, Santiago de Chile, Chile.
²Received: February 15, 2012. Accepted: September 15, 2013. Universidad de Chile, Santiago de Chile, Chile.
³Data de recebimento: 15 de fevereiro de 2012. Data de aceitação: 15 de setembro de 2013. Universidade de Chile, Santiago de Chile, Chile.
⁴Matemático y magíster en Matemática Aplicada, de la Universidad Nacional de Colombia. PhD. en Sistemas de Ingeniería, Universidad de Chile. Especialidad en Transporte, Universidad de Chile, Santiago de Chile, Chile. Correo electrónico: hlopezospina@ing.uchile.cl.

Resumen

En este trabajo se propone la formulación de un modelo de distribución de viajes urbanos doblemente acotado en origen y destino, basado en la maximi-zación de la entropía y minimización de los costos generalizados de viajes, relajando la condición de que dichos costos son un parámetro, extendiendo la formulación bajo el supuesto de que son variables difusas con función de pertenencia intervalar. Adicionalmente, dados dichos supuestos, se obtiene una formulación de un modelo de optimización asociado con elecciones discretas, y se presenta una propuesta de uso del modelo en predicciones. Se desarrolla un ejemplo numérico para explicar la teoría desarrollada.

Palabras clave: Distribución de viajes, maximización de la entropía, optimización difusa, costos intervalares.

Abstract

In this paper we propose the formulation of a model for urban double travel distribution delimited at origin and destination, based on the maximization of entropy and minimization of the generalized travel costs by relaxing the condition that such costs are a parameter, extending the formulation under the assumption that they are fuzzy variables with an intervalar function. In addition, given such assumptions, we propose a formulation of an optimization model associated with discrete choices, and we present a proposal for using the model in predictions. A numerical example is developed for explaining the theory developed.

Keywords: Travel distribution, maximization of entropy, fuzzy optimization, intervalar costs.

Resumo

Neste trabalho propõe-se formulação de um modelo de distribuição de viagens urbanas limitado na dupla origem destino, baseado na maximização da entropia e minimização dos custos generalizados de viagens, relaxando a condição de tais custos serem um parâmetro, estendendo a formulação sob a suposição de que são variáveis difusas com função de pertencia intervalar. Adicionalmente, dados tais supostos, obtém-se formulação de um modelo de otimização associado com eleições discretas, e apresenta-se uma proposta de uso do modelo em predições. Apresenta-se exemplo numérico para explicar a teoria desenvolvida.

Palavras-chave: Distribuição de viagens, maximização da entropia, otimização difusa, custos intervalares.

1. Introducción

En muchos problemas prácticos asociados con la solución de un modelo de optimización matemática como soporte para la toma de decisiones, no se puede considerar el conjunto de parámetros o datos como completamente conocido o determinado, debido a que en diversas aplicaciones dichos datos varían en forma significativa por medio de la experimentación y análisis, o simplemente de acuerdo con la experiencia del tomador de decisiones. Un ejemplo de esto son los costos generalizados de transporte asociados con un viaje entre dos zonas de un sistema urbano, que incluyen los costos asociados con la valoración del tiempo de espera, de acceso y de viaje de cada modo, con la inclusión de la tarifa entre dos zonas de una ciudad (Ortúzar y Willumsen, 2008), que pueden variar de acuerdo con el tipo de viaje, con la persona que realiza el viaje o el horario. Es más, pueden existir variaciones temporales de acuerdo con los cambios en factores exógenos a los individuos, como la frecuencia de los buses, la congestión, el clima, etc.

Para encontrar solución a este tipo de problemas y generar resultados más robustos en diversas áreas de ingeniería y ciencias, se han utilizado varios métodos y técnicas matemáticas y estadísticas. Dentro de los más conocidos se encuentran la optimización estocástica o probabilística, donde se supone que el conjunto de parámetros son aleatorios, pero se tienen distribuciones de probabilidad asociadas. Por otro lado, se tiene la optimización difusa, donde la imprecisión de los datos se puede representar por medio de un grado de pertenencia difusa a un conjunto, ya que los objetos de estudio pueden pertenecer a varias clases (Cadenas y Verdegay, 1999).

Este trabajo se basa en la teoría de los modelos de distribución de viajes urbanos o de un sistema interconectado, donde se supondrá que los costos generalizados tienen como parámetro un intervalo de pertenencia asociado con las posibles variaciones de estos valores, lo que permite generar un análisis de sensibilidad a priori de la solución del modelo e incluye robustez en las soluciones factibles. De esta forma, se propone resolver por medio de una formulación como un problema de optimización de elecciones discretas, para obtener conclusiones válidas sobre las variaciones de los parámetros. La sección 2 explica brevemente el problema de máxima entropía aplicado a la teoría de la probabilidad y desde el punto de vista de la combinatoria. En la sección 3 se desarrolla la formulación del problema y su solución como un problema de elecciones discretas, y por último, en la sección 4, se desarrolla un ejemplo para describir el modelo desarrollado.

2. Maximización de la entropía

Basados en Fang et al. (1997) y Romero (2008) se presentan los principios básicos de la máxima entropía, desde el punto de vista probabilístico, asumiendo distribuciones discretas y finitas. El objetivo de la máxima entropía es generar distribuciones de probabilidad con información dada. De forma más exacta, entre todas las distribuciones de probabilidad que son factibles en un conjunto finito de estados bajo cierto tipo de información, se desea encontrar la que soporte mayor nivel de incertidumbre. Matemáticamente, se define entropía de la siguiente forma:

Definición: Sea X una variable aleatoria discreta, con valores de los estados x , x₂, ..., x_n y con distribución p. = P(X = x_i). Se define la entropía de Shannon para la distribuciónp = (p₁, ..., p_n) como H(p) := — ∑_i.p_i ln (p), (1).

La función H(p) evalúa la cantidad de información que se espera obtener al conocer el valor de X. A su vez, mide el nivel de incertidumbre asociado con próximas realizaciones de X. Como ejemplo, tomemos una variable aleatoria Bernoulli con parámetrop, entonces la entropía se define como: H(p): = — pln(p) — (1 — p) ln (1—p). En el caso en que p tiende a un valor extremo 0 o 1, entonces la solución tenderá a 0, indicando menor estocasticidad en el proceso. Por otro lado, la función de entropía alcanza su valor máximo en p = 0,5, donde se tiene el mayor nivel de incertidumbre posible; es decir, cuando las dos opciones tienen igual probabilidad de ocurrencia. Shannon demuestra que la función H(p) es la única que satisface una cantidad de propiedades que definen la entropía en una distribución (Shannon, 1948). Claramente, en cualquier problema de maximización de la entropía, la solución óptima es la distribución uniforme. Es decir P₁ = P₂ = ... = P_n = 1/n, pero en el caso de tener información adicional del sistema, dicha distribución puede variar de acuerdo con los datos a priori obtenidos. Matemáticamente, si se supone que se tiene g₂(X), ..., g_m(X) m funciones de X con valor esperado conocido notado como α₁, α₂ , ..., α_m , entonces la distribución determinada por el problema de máxima entropía con la información asociada con las funciones g (X) es:

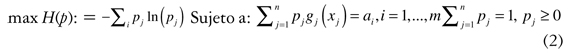
Y a su vez, la solución del problema de optimización (ecuación 2) determina una distribución consistente con las restricciones y que maximiza la incertidum-bre. Este tipo de formulaciones se puede extender a restricciones no lineales, como cuadráticas o de entropía (Fang et al., 1997), pero dado el objetivo del presente trabajo, solo se asumirán restricciones de tipo lineal. Por otro lado, cuando se conocen distribuciones a priori notadas como p° = ( p₁°, ..., p°_n ), es factible variar la formulación de la función objetivo buscando maximizar -∑_i p_j ln (p_j /p°_j).

Existe otro argumento para la derivación de la entropía, usando modelos combinatorios que se asocian con el cálculo de la entropía de una distribución y está formalmente descrito en Romero (2008), y en particular en Ortúzar et al. (2008), aplicado al problema de distribución de viajes, donde se demuestra que la distribución más probable de viajes entre dos zonas i, j T_ij = T * p_ij donde T es el total de viajes generados o atraídos y p_ij es la probabilidad de viajar, entre el par origen destino (i, j) está dado por la maximización de la ecuación de Wilson (1970), Ortúzar etal. (2008):

Por conveniencia, aplicando una transformación monótona creciente a la ecuación 3, por ejemplo el logaritmo natural, se obtiene la misma solución óptima; entonces, la distribución más probable es la solución del siguiente problema: Ln W(T_ij) = ln T! — ∑_{(i, j)} ln(T_ij!). Usando la aproximación de Stirling log X! ≈ X * log X — X, (Romik, 2000), sustituyendo y eliminando los términos que no son optimizables, se obtiene el siguiente problema de programación matemática:

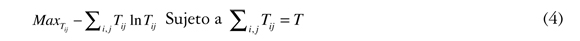
El problema anterior tiene como solución la distribución uniforme de viajes, debido a que esta es la que genera mayor nivel de incertidumbre, pero en el caso de conocer algún tipo de información del sistema, entonces la solución podría ser distinta, por ejemplo, información acerca de los viajes originados o atraídos por zona, o costos, o tiempo de viaje, obteniendo resultados de distribuciones como los mostrados para el problema de probabilidad. Este caso en particular se explicará en la siguiente sección.

3. Planteamiento del problema

En esta sección se realizará una breve introducción al problema de máxima entropía aplicado a la distribución de viajes, suponiendo costos deterministas y extensión a costos intervalares. Esta primera parte está basada en Ortúzar y Willumsen (2008), y Fang et al. (1997). La planeación en los sistemas de transporte urbano se considera un proceso de cuatro etapas o fases, definidas así:

• Etapa 1: generación y atracción de viajes.
• Etapa 2: distribución de viajes.
• Etapa 3: partición modal.
• Etapa 4: asignación en la red.

En estos procesos se considera que la ciudad está dividida en zonas disyuntas, y uno de los objetivos importantes es estimar el número de viajes entre zonas en un periodo determinado (por ejemplo, 24 horas), lo cual es conocido como el sistema de distribución de viajes (etapa 2). Por lo general, el número de viajes que se generan en una zona o el número de viajes que atrae una zona son estimados por modelos de regresión lineal múltiple, por medio de encuestas basadas en las características de los hogares (número de personas, número de trabajadores, ingreso, número de estudiantes, etc.) o el uso del suelo de la zona (cantidad de comercio, centros educativos, empresas, etc.). Estos resultados de generación y atracción por zona son necesarios para estimar su distribución. Uno de los modelos clásicos usados para obtener la distribución de viajes T_ij, donde i es la zona origen y j es la zona de destino, es el de máxima entropía doblemente acotada, que matemáticamente se describe como en la ecuación 5 (Ortúzar y Willumsen, 2008):

Donde la función objetivo del problema (ecuación 5) define la entropía en el sistema o el grado de incertidumbre del sistema urbano asociado, O_i son los viajes generados por la zona i, D_. es la cantidad de viajes atraídos por la zona j, c_i. es el costo generalizado de un viaje por unidad entre el par origen destino y C es el costo total del sistema de transporte que asumen todos los usuarios. Tanto c_ij y C se explican de forma más detallada en la siguiente subsección. Además, si se transforma cada variable como p_ij = T_ij/T, donde T es el total de viajes generados o atraídos en el sistema, entonces se obtiene una formulación equivalente a la descrita en la sección anterior, donde p_i. es la probabilidad de realizar un viaje entre la zona i y la zona j.

3.1. Costos generalizados

En esta sección se describe el concepto de costo generalizado de viaje entre un par origen destino en un sistema de transporte urbano y la razón para analizar dicho parámetro como un intervalo. Basándose en Ortúzar y Willumsen (2008), se pueden definir los costos generalizados en un sistema de transporte como una medida o valor que representa la combinación de los atributos más importantes o relevantes asociados con la desutilidad de realizar un viaje entre un par origen destino El costo generalizado de viaje entre un par origen destino se puede representar como una función lineal de los atributos propios del viaje ponderados con valores que representan la importancia o valoración de cada uno de estos atributos o características, y que son percibidos por el agente que realiza el viaje. Esas valoraciones se obtienen a través de la teoría de elecciones discretas y se pueden suponer difusas o intervalares por los cambios en la valoración de los agentes o variaciones del sistema, tal como se hace en Momeni y Nazemi (2010) para un problema de elección de vehículo o en Dell'Orco y Kikuchi (2004), que, basados en la teoría de la posibilidad para la comparación de utilidades, plantean un modelo de elección de ruta.

Se puede suponer que el costo generalizado intervalar asociado con un modo de viaje k en el par origen destino se escribe como en la ecuación 6:

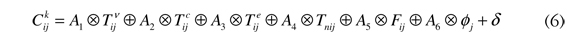
Cada componente de dichos costos se explica a continuación:

• ⊗⊕ son las notaciones usadas para el producto y suma de intervalos cerrados y acotados.
• T_ij^v = [t_ij^v,min, t_ij^v,max] es el intervalo asociado con el tiempo de viaje factible a bordo del vehículo para ir de i a j, donde t_ij^v,min es el tiempo mínimo y t_ij^v,max es el tiempo máximo.
• T_ij^c = [t_ij^c,min, t_ij^c,max] es el intervalo asociado con el tiempo de caminata posible para acceder al modo y llegar al destino.

• T_ij^c = [t_ij^e,min, t_ij^e,max] es el intervalo asociado con el tiempo de espera viable.
• T_nij^c = [t_nij^min, t_nij^max] es el intervalo asociado con el tiempo de transbordo.
• φ es un costo terminal que se supondrá determinista, asociado con estacionamiento en el destino.
• F_ij = [f_ij^min, f_ij^max] es el intervalo que recoge el costo del viaje.
• A₁, A₂, A₃, ..., A₆ son los intervalos donde se encuentran las valoraciones asociadas con cada uno de los elementos del viaje.

Vale la pena anotar que en este caso, el intervalo c^k asociado con un costo generalizado de viaje es obtenido por medio de la aritmética intervalar. De esta forma, es importante tener en cuenta las siguientes propiedades de la lógica difusa.

Definición: Dados dos intervalos cerrados y acotados X = [X₁, X₂] y Y = [Y₁, Y₂], entonces la suma y el producto entre X y Y se definen como: X ⊕ Y = [X + Y₁, X₂ + Y₂], y si se toman X₁, X₂, Y₁, Y₂ positivos no nulos, X ⊗ Y = [X₁ * Y₁, X₂ * Y₂].

Determinar el costo generalizado en términos intervalares permite analizar la sensibilidad de variaciones en los atributos y su implicancia en los resultados en los modelos de distribución de viajes. Además, no es necesario tener un consolidado de los datos asociados con los costos y tiempo de viaje, sino estimaciones de las valoraciones extremas.

3.2 Solución del problema como un problema de elecciones discretas

Teniendo en cuenta el supuesto de que el costo generalizado de viajar entre el par origen destino es un intervalo C_ij=[C_ij^min, C_ij^max], entonces el costo total del sistema C también varía en un rango de posibilidades que se notará en forma de intervalo como C = [C^min, C^max]. De esta forma, el problema de optimización con entropía con costos intervalares se escribe de la forma:

max_tij - ∑^k_i=1∑^l_j=1 T_ij ln T_ij

Para resolver el problema anterior se usará una aproximación basada en la discretización del valor de λ, dado que asumirla como una variable continua implicaría una complejidad bastante alta en la solución, debido a la no linealidad que se generaría en la restricción de costos. Es decir se resolverán n + 1 problemas de entropía asumiendo los siguientes valores para λ = [0, 1/n, 2/n, ..., 1] donde λ = 0 implica que los agentes asumen costos mínimos, λ = 1 indica la consideración que se asumen costos máximos y k/n índica las opciones intermedias. De esta forma, se notará el problema k-ésimo de entropía para la distribución de viajes como:

Por otro lado, se propone el uso de valores intermedios de los costos generalizados como escenarios posibles de optimización, ya que la no linealidad de la función de entropía no garantiza que la solución se encuentre en los extremos del intervalo.

Si se notan α_i, γ_j β_k a los multiplicadores de Lagrange asociados con la ecuación 9, entonces se obtiene por condiciones de primer orden que:

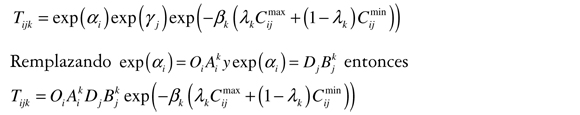
Los valores de A^k_j y A_j^k miden el nivel de beneficios asociado con viajar desde i o a recibir un viaje en j, respectivamente asumiendo costos de viaje (λ_kC_ij^max +(1 -λ_k)C_ij^min). Por lo cual son medidas clave para calcular índices de accesibilidad y atractividad (Martínez, 1995; Martínez y Araya, 2000) en proyectos de transporte y uso de suelo. Por otro lado, β_k es la valoración del costo de viaje de los individuos. Nótese que la variación de λ_k implica la variación de A_l^k, B_j^k y β_k, lo que indica que es factible obtener un intervalo para cada medida. Este resultado es importante en la valoración de proyectos de transporte, pues genera análisis de sensibilidad o rangos factibles de dichas medidas.

La ecuación 9 se puede resolver por medio del sistema de puntos fijos generados por el sistema de ecuaciones, de acuerdo con las condiciones de primer orden. Las técnicas de calibración y estimación de los parámetros del problema de entropía se pueden revisar en Ortuzar y Willumsen (2008). Es importante tener en cuenta que para obtener A_l^k, B_j^k y β_k es necesario conocer la siguiente información de un año base o información de la matriz a priori que se describe a continuación:

Dado que λ_k ∈ [0,1], entonces con la información previa y la solución de los n + 1 problemas de optimización no lineal (ecuación 9) se obtiene un intervalo que asume la variación de la valoración del costo de viaje de los individuos, notada como β ∈ [β^min, β^max]. Este intervalo explica el rango factible de la sensibilidad al costo de viaje. Así como se mencionaron intervalos para las medidas de accesibilidad y los valores óptimos de T_ij*.

Sin embargo, para predicciones se debe usar un solo valor de β, por lo que se propone usar aquel que genere la máxima entropía. Esto es debido a que la información determinística en la ecuación 9 es la cantidad de viajes generados y atraídos por zona (O_i, D_j, ∀_i, j). Pero en los casos aplicados en la práctica, el costo total es una aproximación estimada por la información de la matriz a priori y el uso de los costos generalizados medios (por simplicidad, λ= 0,5). Sin embargo, el promedio es una medida poco robusta, ya que en casos de presencia de datos atípicos dicho valor se puede ver sesgado o mal estimado. Por otro lado, la formulación intervalar añade un componente probabilístico interesante, donde se puede suponer que el costo de viaje es una variable aleatoria uniforme en el intervalo [C_ij^min,C_ij^max ], por lo cual se tiene la misma probabilidad de que un individuo tomado al azar asuma cualquier costo en el intervalo; de esta forma, se propone que la solución del problema de máxima entropía con costos intervalares se obtiene de la forma:

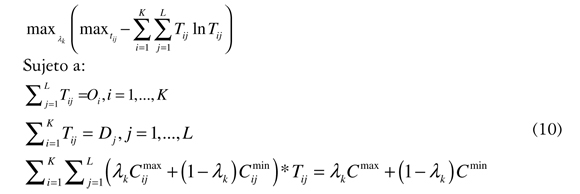
La ecuación 10 se puede analizar como un problema en dos etapas; en la primera se resuelve un problema de optimización no lineal paramétrico en λ_k y en la segunda etapa se encuentra la máxima entropía, dada la variación de dicho valor.

La ecuación 10 podría mejorar las predicciones que se realizan en el sector de transporte en la práctica, donde generalmente se usan costos promedio, ignorando la variabilidad intrínseca de dicha medida o la poca robustez, dada por la presencia de datos atípicos o aglomeraciones por sectores. El hecho de usar la entropía como criterio de selección permite determinar la distribución más probable dada una información conocida como O. y D. y bajo el supuesto de que cada costo en el intervalo de pertenencia tiene la misma probabilidad de ocurrencia.

4. Ejemplo numérico

Para ejemplificar el modelo propuesto con costos intervalares se va a trabajar con una zonificación agregada y basados en datos simulados. En particular, no se describe un cálculo de los costos intervalares, tal como fue descrito en la ecuación 6, debido a que se busca mostrar la bondad del modelo de optimización. En la tabla 1 se presenta la matriz de costos.

Adicionalmente, los vectores orígenes destinos están dados por la información expuesta en la tabla 2.

Basados en esta información, el problema de distribución de viajes (ecuación 10) de la maximización de la entropía y costos paramétricos en λ_k se puede escribir de la siguiente forma extensiva:

Restricciones de balance en el origen:

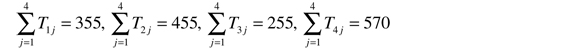
Restricciones de balance en el destino:

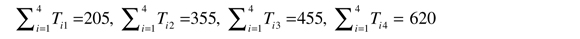
Restricción de costos:

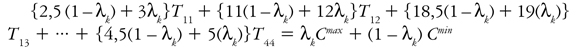
Donde C^min y C^max se obtienen con la información de la matriz de distribución a priori (t⁰) de la forma:

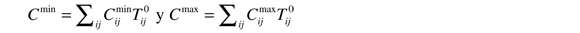
Para mostrar que la máxima entropía se puede alcanzar en cualquier valor del intervalo asociado al costo generalizado, se usarán dos matrices a priori distintas. En el primer caso, la máxima entropía se alcanza en el extremo inferior del intervalo de los costos; en el segundo, la máxima entropía se alcanza cuando se asume el extremo superior de dicho intervalo.

Matriz a priori 1: en la matriz de referencia o a priori (t_ij°) se tiene mayor cantidad de viajes extrazonales que intrazonales (tabla 3).

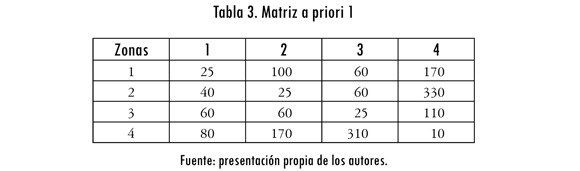
La figura 1 muestra la variación de la máxima entropía para diferentes valores de λ_k ∈ {0, 0,1, 0,2, ..., 1} usando los costos obtenidos por la matriz a priori 1. Los resultados fueron obtenidos usando una versión gratuita del software GAMS (López, 2006).

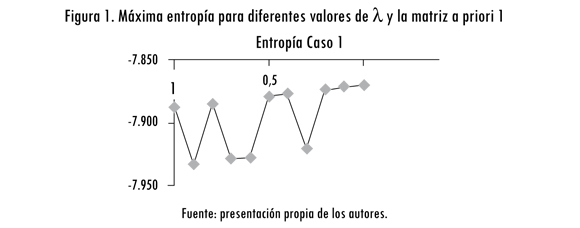
En este caso, la máxima entropía se alcanza en los costos mínimos (λ = 0), pero existen estructuras de costos intermedios (por ejemplo, λ = 0,9 o 0,7) que generan menor entropía que el problema de valor extremo asociado con el máximo del intervalo (λ = 1), lo que implica que dada la información de la matriz a priori, los viajes originados y atraídos por zona se tendría mayor probabilidad de obtener una distribución con la información asociada con los costos máximos que con algunas valoraciones intermedias.

Adicionalmente, la valoración del costo generalizado de viaje b_k varía dentro del siguiente intervalo [—0,6787; —0,07208], donde b_k es el multiplicador de Lagrange de la solución del problema de entropía con λ_k.

Matriz a priori 2: en este caso se realizan más viajes entre las mismas zonas, con lo cual se tiene la matriz a priori (T_ij⁰ ) de la tabla 4.

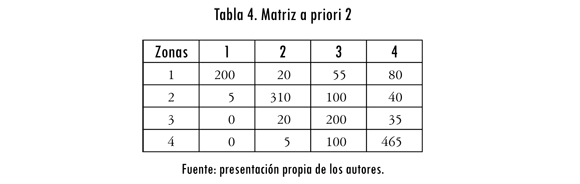
Y se logra la estructura de la solución de entropía analizada en la figura 2.

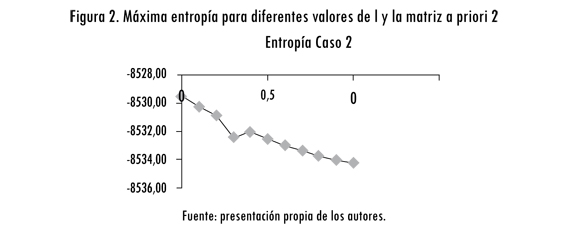
Es decir, la distribución más probable es aquella que asume los costos máximos y la menos probable se obtiene con la información de la matriz de costos mínimos. Este caso es interesante, pues muestra que el buen análisis de los costos generalizados es un factor importante en las predicciones de viajes urbanos.

Es interesante anotar que en ninguno de los dos casos el costo promedio (λ = 0,5) generó la máxima entropía; es más, al hacer pequeñas variaciones de dicho valor (por ejemplo, para el caso 2: (λ = 0,6) se obtienen distribuciones más probables). Por otro lado, dada la no convexidad de las figuras 1 y 2, se puede concluir que entre más fina sea la malla para obtener λ , se conseguirán mejores aproximaciones de la máxima entropía.

5. Conclusiones y trabajos futuros

En este trabajo se propone una formulación extendida del problema clásico de distribución de viajes con el método de máxima entropía, usando costos intervalares. Para lograr dicha formulación se explica brevemente el problema de la máxima entropía en el contexto probabilístico y su formulación como un problema de distribución de viajes. De esta forma, se logra una formulación robusta, debido a que se sensibilizan a priori los parámetros de los costos, lo cual permite generar un conjunto de soluciones intervalares por la formulación como un problema de elecciones discretas análogo a la solución de modelos con variables aleatorias como parámetros de programación estocástica o problemas de teoría de la decisión. Adicional a la formulación se propone una nueva valoración del parámetro de sensibilidad al costo y las medidas de accesibilidad y atractividad por la solución que encuentra la máxima entropía.

Un resultado importante de este tipo de modelaciones es que no es necesario tener la información de los costos de viaje, sino estimar el mínimo costo y el máximo, generando análisis de sensibilidad a priori en las soluciones (Wang y Xiao, 2010). Como trabajo futuro se recomiendan varias líneas claras de investigación, como extender esta formulación a otro tipo de funciones de pertenencia difusa. Por otro lado, incluir parámetros difusos en la generación y atracción de viajes para generar mayor robustez al modelo. Sería interesante aplicar la modelación con datos reales para comparar con los resultados clásicos, y debido a la complejidad del modelo, usar otras técnicas de solución, como metaheurísticas y otras formulaciones de entropía, como los costos cuadráticos. Adicionalmente, se podría comparar la solución del problema intervalar con la solución de un problema asumiendo diferentes distribuciones de probabilidad (programación estocástica) para analizar la robustez del modelo y específicamente de las predicciones. Por otro lado, sería interesante explorar la solución continua de λ resolviendo directamente el problema de optimización de la forma:

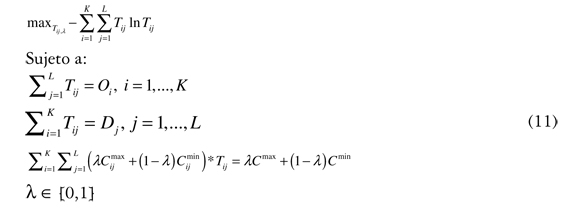
Como conclusión general, se tiene que dado que el problema de la maximiza-ción de entropía es muy usado en la práctica para estimar y realizar predicciones de distribución de viajes, el modelo presentado genera una solución más robusta, incorporando el hecho de que los costos generalizados de viaje pueden variar (en este caso, en un intervalo con la misma probabilidad para un par origen destino), hasta obtener que la formulación propuesta podría mejorar las predicciones que se realizan en el sector de transporte donde generalmente se usan costos promedios ignorando la variabilidad intrínseca de dicha medida o la poca robustez dada por la presencia de datos atípicos o aglomeraciones por sectores.

El hecho de usar la entropía como criterio de selección permite determinar la distribución más probable dada la información conocida o determinística, como los viajes generados y atraídos por zona y bajo el supuesto de que cada costo es no determinista, y se pueden obtener soluciones diferentes al caso promedio. En las simulaciones se muestra que usar costos promedio genera soluciones menos probables que usando costos asimétricos (λ ^ 0,5), por lo cual es necesario en la práctica valorar y obtener con bastante cuidado dicho valor, haciendo pertinente la mejor recolección de datos que capturen la variabilidad de los costos para efectuar predicciones y análisis de políticas urbanas y de transporte; obteniendo así la utilidad en términos reales que puede derivarse de esta investigación.

Referencias

CADENAS, J. y VERDEGAY, J. Modelos de optimización con datos imprecisos. Murcia, España: Universidad de Murcia, servicio de publicaciones, 1999.         [ Links ]

DELL'ORCO, M. y KIKUCHI, S. An alternative approach for choice models in Transportation: use of possibility theory for comparison of utilities. Yugoslav Journal of Operations Research. 2004, vol. 14, num. 1, pp. 1-17        [ Links ]

FANG, S.; RAJASEKERA, J. y TSAO, H. Entropy Optimization and Mathematical Programming. Norwell, MA: Kluwer Academic Publishers, 1997.         [ Links ]

LOPEZ, H. Introducción a GAMS y su aplicación en la solución de modelos matemáticos de optimización. Cuadernillo cursillo XXII Coloquio distrital de Matemáticas y estadística. Bogotá: Universidad Nacional de Colombia, Departamento de Matemáticas, 2006.         [ Links ]

MARTÍNEZ, F. Access, the Economic Link in Transport-Land Use Interaction. Transportation Research B. 1995, vol. 29, num. 6, pp. 457-47.         [ Links ]

MARTÍNEZ, F. y ARAYA, C. Note on Trip Benefits in Spatial Interaction Models. Journal of Regional Science. 2000, vol. 40, num. 4, pp. 789-796.         [ Links ]

MOMENI, H. Y NAZEMI, J. A fuzzy-random Utility Model of Consumer Choice; Uncertainty Effect. World Applied Sciences Journal. 2010, vol. 8, num. 10, pp. 1183-1192.         [ Links ]

ORTÚZAR, J. y WILLUMSEN, L. Modelos de transporte. Santander: Publican, Ediciones de la Universidad de Cantabria, 2008.         [ Links ]

ROMERO, J. Notas sobre Máxima Entropía. Documento de trabajo. México: UNAM Facultad de Ciencias, 2008.         [ Links ]

ROMIK, D. Stirling's Approximation for n!: The Ultimate Short Proof? The American Mathematical Monthly. 2000, vol. 107, num. 6, pp. 556-557.         [ Links ]

SHANNON, C. E. A mathematical theory of communication. Bell System Technical Journal. 1948, vol. 27, pp. 379-423 y 623-656.         [ Links ]

WANG, X. y XIAO, M. Approach of group decision making based on normal distribution interval number with incomplete information. Journal of Control and Decision. 2010, vol. 10. 1494-1498.         [ Links ]

WILSON, A. G. Entropy in urban and regional modeling. London: Pion, 1970.         [ Links ]