Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Universidad
Print version ISSN 0123-2126
Ing. Univ. vol.18 no.1 Bogotá Jan./June 2014
Evaluación de la multiplexación por división de paquetes wavelet1
Performance of Wavelet Packet Division Multiplexing2
Juan Pablo Hoyos-Sánchez3
Pablo Emilio Jojoa-Gómez4
1Fecha de recepción: 19 de septiembre de 2012. Fecha de aceptación: 4 de junio de 2013. Este artículo se deriva de un proyecto de investigación denominado Análisis de subbandas adaptativo al entorno como método de control de acceso, código 3248, desarrollado por el grupo I+D en Nuevas Tecnologías en Telecomunicaciones de la Universidad del Cauca en convenio con el Departamento Administrativo de Ciencias, Tecnología e Innovación Colciencias. Colaboración del grupo GNTT de la Universidad del Cauca, el profesor PhD(c) Óscar Josué Calderón y al MSc. Harold Romo Romero, Universidad del Cauca, Popayán, Colombia.
2Reception date: September 19th, 2012. Data of acceptance: June 4th, 2013. This article derives from a research project títled Análisis de subbandas adaptativo al entorno como método de control de acceso, code 3248. It was developed by the I+D group in New Technologies in Telecommunications in la Universidad del Cauca, in an agreement with the Administrative Department of Science, Technology and Innovetion (Colciencias). In collaboration with the GNTT group of la Universidad del Cauca, especially PhD Óscar Josué Calderón y Msc. Harold Romo Romero, Universidad del Cauca, Popayan, Colombia.
3Ingeniero en electrónica y telecomunicaciones. Estudiante de Doctorado en Ciencias de la Electrónica, Universidad del Cauca, Popayán, Colombia. Correo electrónico: jhoyossanchez@unicauca.edu.co.
4Ingeniero en electrónica, Universidad del Cauca, Popayán, Colombia. Magister en Ingeniería Eléctrica, Universidad de São Paulo, Brasil. Doctor en Ingeniera Eléctrica, Universidad de São Paulo. Profesor de tiempo completo del Departamento de Telecomunicaciones, Universidad del Cauca. Correo electrónico: pjojoa@unicauca.edu.co.
Resumen
Este artículo presenta los resultados de extensas simulaciones acerca de la técnica de transmisión multiusuario llamada multiplexación por división de paquetes wavelet (WPDM). Sus ventajas son la capacidad de transmisión múltiple de señales de una forma robusta y flexible. Las señales de los usuarios son codificadas por funciones base de la familia wavelet packet. La evaluación del desempeño de la multiplexación WPDM fue desarrollada sobre tres condiciones del canal de transmisión: ruido AWGN, desvanecimiento plano Rayleigh y desvanecimiento selectivo en frecuencia.
Palabras clave: Comunicaciones multiusuario, multiplexación, paquetes wavelet, WPDM, AWGN, desvanecimiento, Rayleigh.
Palabras clave descriptores: Multiplexación, paquetes de wavelets, WPDM (Telecomunicaciones), AWGN (Telecomunicaciones), Rayleigh.
Abstract
This article presents the results of extensive simulation about the multiuser transmission technique, named Wavelet Packet Division Multiplexing (WPDM). Its advantages are the capability of multiple signals transmission, in a flexible and robust form. The signals of the multi users are coded by bases functions of the wavelet packet (WP) family. The performance evaluation of the WPDM multiplexing was conducted over three conditions on the transmission channel: AWGN noise, Flat fading Rayleigh and frequency-selective fading.
Keywords: Multiuser communications, multiplexing, Wavelet Packet, WPDM, AWGN, fading, Rayleigh.
Keywords plus: Multiplexing, wavelet packets, WPDM (Telecomunication), AWGN (Telecomunication), Rayleigh.
D0I:10.11144/JAVERIANA.IYU18-1.EMDP
Introducción
Desde sus inicios, los sistemas de comunicaciones multiusuario han buscado el uso eficiente de los recursos, dado que muchos de ellos, como el espectro, son escasos. Diferentes técnicas de multiplexación han recurrido a formas de onda ortogonales como multiplexación por división en el tiempo (TDM) o multiplexación por división en la frecuencia (FDM) y multiplexación ortogonal por división en frecuencia (OFDM) (Proakis, 2008). Sin embargo, la multiplexación por división de paquetes wavelet (WPDM) (Wong et al., 1997 y 2000; Wu, 1998) usa la descomposición wavelet packet discreta, en la cual las formas de onda wavelet packet son auto y mutuamente ortogonales, lo que les permite maximizar el uso del espectro de frecuencias asignado, además de elevar la calidad de transmisión. Por otro lado, la descomposición wavelet packet es fácilmente implementable por su uso de filtros digitales, además de ser muy flexible en su configuración, lo que la hace idónea para los sistemas actuales, como lo son los radios cognitivos. La WPDM ha mostrado grandes ventajas frente a OFDM y TDM, como inmunidad a ruido impulsivo (Wong et al., 2000; Learned et al., 1994; Lindsey, 1997; Ghandi et al., 1997) y a ruido blanco (Marin et al., 2004), por lo cual la WPDM se postula para ser una técnica prometedora de multiplexación de las señales de usuarios frente a técnicas actuales como OFDM.
Este artículo presenta los resultados de simulación de la WPDM en tres distintos canales: ruido blanco auditivo gaussiano (AWGN, por su sigla en inglés), desvanecimiento plano y desvanecimiento selectivo Rayleigh, los cuales son discutidos y comparados con apropiadas fuentes en la literatura.
1. Antecedentes teóricos
El sistema WPDM recurre al uso de la transformada wavelet packet (Daubechies, 1992; Mallat, 2009), la cual parte del uso de dos filtros FIR h{n) y g{n), conocidos como filtros de cuadratura, dado que satisfacen:

A partir de estos filtros, y mediante un algoritmo iterativo, se obtienen las familias de funciones wavelet packet ψ (Daubechies, 1992), que forman un árbol binario en el cual cada nodo está representado por un pareja (j,p), donde j representa el nivel de profundidad en el árbol, y p, el número de nodos a la izquierda de este en ese nivel. En la figura 1 se observan dos ejemplos de las dos posibles estructuras que se pueden obtener: árbol simétrico (todos los nodos finales se encuentran en un mismo nivel de profundidad) y árbol no simétrico o asimétrico (los nodos finales no se encuentran en el mismo nivel de profundidad).
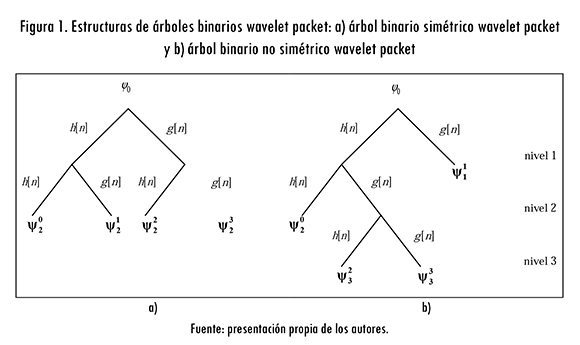
Cada nodo representa un espacio Wjp a partir del cual se obtienen dos nodos hijos, los cuales son 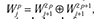 , ortogonales. Las funciones wavelet packet de cada nodo están dadas de forma recursiva por las ecuaciones (2) y (3) (Mallat, 2009):
, ortogonales. Las funciones wavelet packet de cada nodo están dadas de forma recursiva por las ecuaciones (2) y (3) (Mallat, 2009):
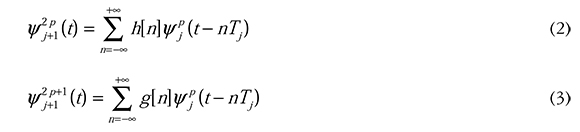
Con Tj = 2jTo, y de forma general:
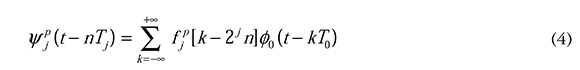
donde (φ0 (t — k) es la función escala que se encuentra en la raíz del árbol y fjp es el filtro equivalente construido de las combinaciones de h{n} y g{n}. En WPDM los mensajes son codificados en amplitud por las funciones ψjp (t- nTj) y son sumadas para conformar la señal s(t) (Wu, 1998). Pero recurriendo a la ecuación de reconstrucción wavelet packet, podemos construir la señal a transmitir como
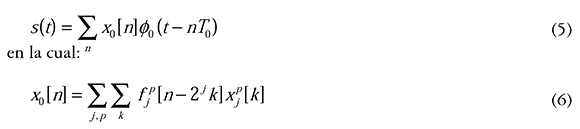
es la secuencia en la raíz del árbol. Así, el sistema WPDM se puede implementar usando un transmultiplexor (Akansu y Haddad, 1992), descrito por la ecuación (6), seguido de un solo modulador en amplitud dado por la ecuación (5), como se ilustra en la Figura 2, donde los coeficientes xjp [k] serían los datos de los mensajes de los usuarios, los cuales toman los valores polares Ebit ∈ {+1, -1}.
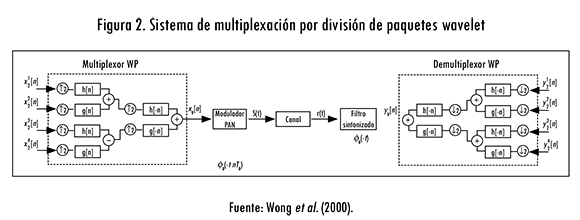
La señal, al ser enviada por el canal de transmisión, se verá afectada por los efectos adversos del canal, que en la simulación serán tratados como ruido blanco aditivo y desvanecimiento Rayleigh. El efecto del ruido blanco aditivo puede resumirse como:

donde n(t) es una secuencia de variables aleatorias con distribución gaussiana de varianza N0 / 2 y media 0, sobre el intervalo [0, T0].
El efecto de la interferencia constructiva y destructiva de las múltiples señales, debida a los múltiples caminos entre el transmisor y el receptor en los cuales no existe línea de vista, se representa como un desvanecimiento tipo Rayleigh. Este desvanecimiento es otra fuente de degradación de la señal, caracterizado como un disturbio no aditivo. Existen varias formas de implementar el desvanecimiento Rayleigh, una de ellas es la establecida por Young y Beaulieu (2000), donde dos secuencias de variables aleatorias idénticamente distribuidas e independientes, con media cero:
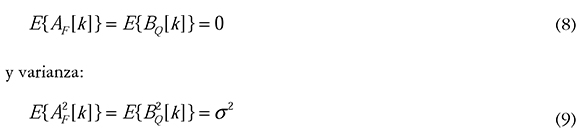
son las componentes en fase y cuadratura del proceso de desvanecimiento X(f) = AF + jBQ (Papoulis, 1991), las cuales pasan por el filtro Doppler, que agrega el efecto de movimiento entre el transmisor y el receptor. Para nuestra simulación la respuesta en frecuencia del filtro Doppler está definido por Jake (Young y Beaulieu, 2000):
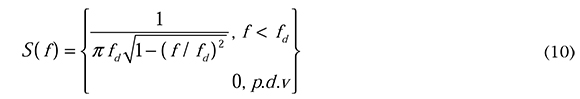
Siendo f la máxima frecuencia Doppler en Hz, dada por fd = υ/λ, υ es la velocidad del vehículo en metros/segundos, y λ es la longitud de onda en metros. La salida es la secuencia compleja del proceso aleatorio de desvanecimiento en el dominio de la frecuencia:
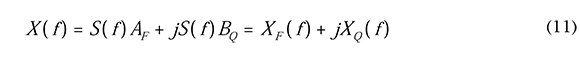
donde se debe realizar la transformada inversa de Fourier para pasar al dominio del tiempo, y luego obtener su magnitud:

ello para generar el desvanecimiento Rayleigh plano en banda base. Dado que el desvanecimiento es un proceso no aditivo, la señal recibida será igual a:

Para el canal selectivo en frecuencia se utilizará el modelo de dos rayos, el cual se genera multiplicando una versión retardada de la señal transmitida con otra instancia de x(t):
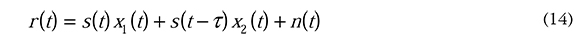
Donde T es el número de muestras atrasadas.
Para obtener los mensajes binarios de los usuarios de la señal recibida r(t) en el receptor, se realiza el proceso de análisis, es decir, primero se pasa dicha señal por el filtro adaptado φ0 (— t) y se muestrea cada T0 segundos para obtener la secuencia en la raíz del árbol:
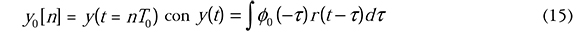
luego esta secuencia pasaría a través del demultiplexor para así obtener los datos de los usuarios

los cuales posteriormente ingresan a un decisor, en el cual la salida será +1 si el valor de entrada es mayor que 0 (valor umbral) y —1 en caso contrario.
2. Resultados
El desempeño del sistema WPDM fue probado sobre diferentes canales de transmisión, en los cuales el análisis se desarrolló variando dos parámetros: la función wavelet madre o función escala y el árbol binario wavelet packet.
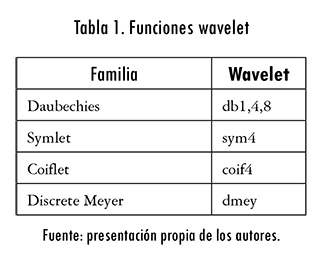
En primera instancia, se limitó el análisis del desempeño a las funciones wavelet listadas en la tabla 1.
2.1. Desempeño de WPDM en un canal AWGN
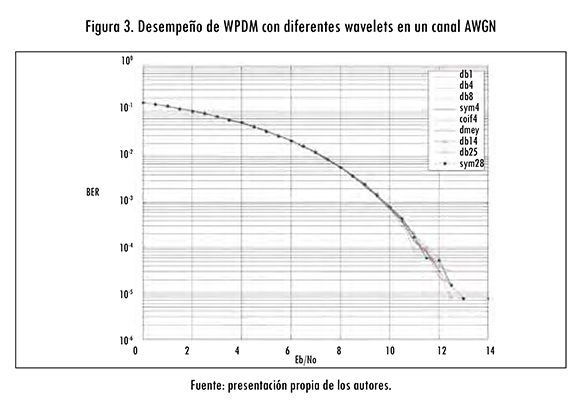
En el canal AWGN, en primer lugar, se varió el tipo de función wavelet a partir de la tabla 1 y las funciones wavelet de orden superior db14, db25 y sym 28, con un árbol binario simétrico de dos niveles (j = 2) y por tanto 2j = 22 = 4 usuarios. Los resultados de la figura 3 muestran que el comportamiento del sistema es muy similar para los diferentes tipos de wavelet utilizadas; por lo tanto, el uso de funciones wavelet de orden superior se hace innecesario. Además, se observa una muy leve diferencia cuando se presentan valores altos de la relación de energía de bit a densidad espectral de ruido.
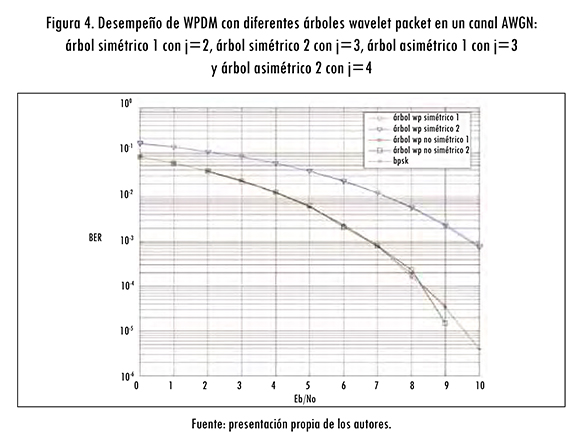
Luego, cuando se deja definida la función db1 como wavelet madre, el comportamiento para un árbol simétrico de 2 niveles con 4 usuarios o de 3 niveles con 8 usuarios es el mismo; pero el desempeño del sistema es muy superior al utilizar arboles binarios no simétricos de 3 y 4 niveles con 4 y 8 usuarios, respectivamente, cuyo desempeño es igual al resultado teórico para la modulación por desplazamiento de fase binaria (BPSK) (Proakis, 2008) como se puede observar en la figura 4. También se aprecia cómo para el mismo número de usuarios al utilizar árboles no simétricos hay un incremento en el nivel de profundidad respecto a los árboles simétricos.
2.2. Desempeño de WPDM en un canal con desvanecimiento plano
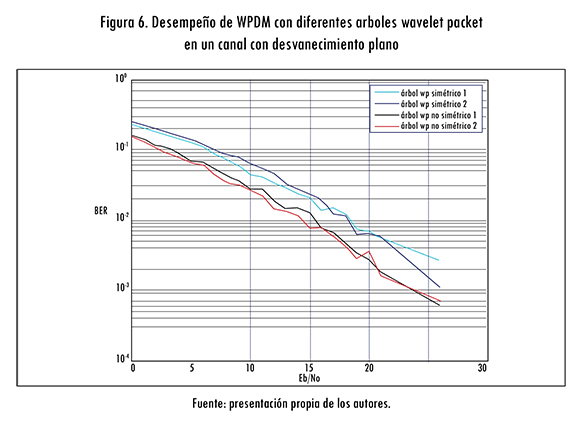
Las figuras 5 y 6 muestran los resultados de las pruebas realizadas del sistema WPDM sobre un canal con desvanecimiento plano y una frecuencia Doppler de 60 Hz, donde la figura 5 se obtuvo de extensas simulaciones con las familias definidas en la tabla 1 y un árbol simétrico de dos niveles.
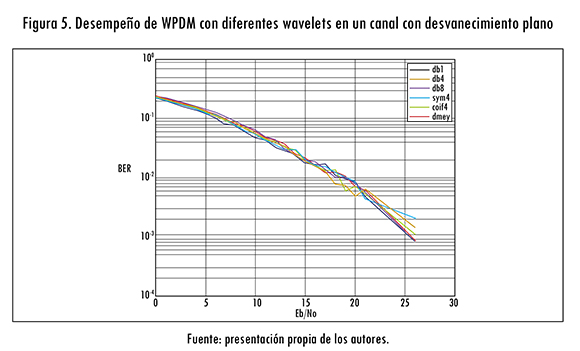
De la figura 5 se aprecia que el comportamiento es muy variable y al igual que en el canal AWGN el desempeño del sistema es muy similar para las distintas funciones wavelet utilizadas.
Cuando se varía el árbol de descomposición wavelet y se deja establecido como wavelet madre la función db1, de la figura 5 se observa que el comportamiento es mejor si el árbol binario utilizado para la implementación de WPDM es no simétrico; esto posiblemente a que su descomposición en subbandas permite combatir los efectos adversos de la interferencia variable en el tiempo.
2.3. Desempeño de WPDM en un canal selectivo en frecuencia
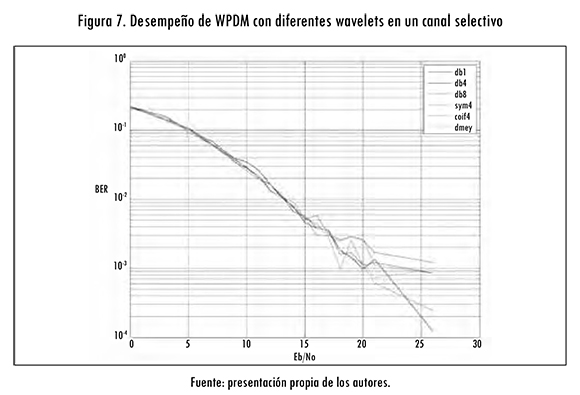
El desempeño del sistema WPDM en un canal selectivo con frecuencia Doppler de 60 Hz es presentado en las figuras 7 y 8, donde se observa un comportamiento muy interesante, dado que, a pesar de que el canal selectivo en frecuencia presenta un nivel de interferencia más alto que el canal plano, su comportamiento es aún mejor. Y como se ha presentado en los anteriores canales, la función wavelet seleccionada no afecta el desempeño del sistema ante un desvanecimiento selectivo como se aprecia en la figura 7.
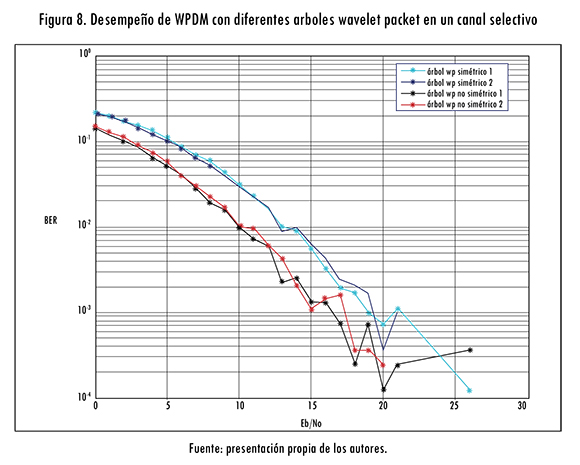
En la figura 8 se puede observar cómo es el desempeño del sistema WPDM, al dejar fija la wavelet madre (db1) y al analizar para diferentes árboles binarios, de la cual se aprecia que el sistema presenta un mejor desempeño cuando se usan árboles binarios no simétricos, al igual que en los canales AWGN y desvanecimiento plano.
Conclusiones
Se encontró que las funciones wavelet no tienen un impacto directo en el comportamiento de WPDM en los diferentes escenarios, mientras que el árbol binario utilizado en el transmultiplexor sí afecta notablemente, a tal punto que permite obtener un desempeño igual al presentado por la modulación BPSK cuando se usan árboles binarios no simétricos en un canal AWGN. También se encontró que el sistema WPDM presenta un gran desempeño frente al desvanecimiento Rayleigh selectivo, lo que ratifica la gran capacidad de eliminación de interferencias banda angosta. A pesar de las grandes ventajas obtenidas al utilizar árboles binarios asimétricos, se observa que su uso ocasiona un incremento en el nivel de profundidad (j) respecto a un árbol simétrico, pues aumenta la complejidad de la multiplexación WPDM.
Adicionalmente, se observó que el comportamiento de familias de orden superior fue muy similar al presentado por las familias de orden inferior; por lo tanto, no amerita su uso, dada la gran complejidad que acarrea implementar filtros de numerosos coeficientes.
Referencias
AKANSU, A. N. y HADDAD, R. A. Multiresolution signal decomposition: transforms, subbands, and wavelets. Boston, MA: Academic, 1992. [ Links ]
DAUBECHIES, I. Ten lectures on wavelets. Philadelphia, PA: SIAM, 1992. [ Links ]
GHANDI, P. P; RAO, S. S. y PAPPU, R. S. Wavelets for waveform coding of digital symbols. IEEE Transactions Signal Processing. 1997, vol. 45, pp. 2387-2390. [ Links ]
LEARNED, R. E.; KRIM. H.; CLAUS, B.; WILLSKY, A. S. y KARL, W C. Wavelet-packet-based multiple access communication. Proceedings SPIE, 1994, vol. 2303, pp. 246-259. [ Links ]
LINDSEY, A. R. Wavelet packet modulation for orthogonally multiplexed communication. IEEE Transactions Signal Processing. 1997, vol. 45, pp. 1336-1339. [ Links ]
MALLAT, S. G. A wavelet tour of signal processing. 3 ed. Burlington, MA: Academic Press, 2009. [ Links ]
MARIN, J. I.; PARRADO, A. L.; CERTUCHE, L. J. y GIRALDO, C. A. Implementación de un sistema de multiplexación por división de paquetes wavelet WPDM. IX Simposio de Tratamiento de Señales y Visión Artificial (STSIVA), Manizales, 2004. [ Links ]
PAPOULIS, A. Probability, random variables, and stochastic processes. 3rd ed. New York: McGraw Hill, 1991. [ Links ]
PROAKIS, J. G. Digital communications. 5th ed. New York: McGraw Hill, 2008. [ Links ]
YOUNG, D. J. y BEAULIEU, N. C. The generation of correlated Rayleigh random variates by inverse discrete Fourier transform. IEEE Transactions on Communications. 2000, vol. 48, pp. 1114-1127. [ Links ]
WONG, K. M.; WU, J.; DAVIDSON, T. N.; Q. JIN y CHING P-C. Performance of wavelet packet-division multiplexing in impulsive and Gaussian noise. IEEE Transactions on Communications. 2000, vol. 48, no. 7, pp. 1083-1086. [ Links ]
WONG, K. M.; WU, J.; DAVIDSON, T. N. y Q. JIN. Wavelet packet division multiplexing and wavelet packet design under timing error effects. IEEE Transactions Signal Processing. 1997, vol. 45, pp. 2877-2890. [ Links ]
WU, J. Wavelet packet division multiplexing. Phd Thesis. McMaster University, Department of Electrical and Computer Engineering, 1998. [ Links ]













