A New Genotype-Phenotype Genetic Vlgorithm for the Two-Dimensional Strip Packing Problem with Rotation of 90^o1

Un nuevo algoritmo genético de genotipo-fenotipo para el problema de Strip Packing de dos dimensiones con rotación de 90^o2

Gustavo Gatica³
Gonzalo Villagran⁴
Carlos Contreras-Bolton⁵
Rodrigo Linfati⁶
John Willmer Escobar⁷

¹This work has been partially supported by Pontificia Universidad Javeriana Cali from Colombia; and by Universidad del Bío-Bío and Universidad Andrés Bello from Chile. In addition, this work has been partially supported by FONDECYT by grant 11150370. This support is gratefully acknowledged. Summitted on: November 11th, 2014. Accepted on: October 19^th, 2015.
²Este trabajo fue parcialmente apoyado por la Pontificia Universidad Javeriana, sede Cali, Colombia, y por la Universidad del Bío-Bío y la Universidad Andrés Bello, de Chile. Así mismo, fue parcialmente apoyado por FONDECYT (acuerdo 11150370). A todos ellos estamos muy agradecidos. Fecha de recepción: 11 de noviembre de 20014. Fecha de aceptación: 19 de octubre de 2015.
³PhD in Engineering at Universidad Santiago de Chile (USACH), Chile. Fulltime profesor at Facultad de Ingeniería, Universidad Andres Bello, Santiago, Chile. E-mail: ggatica@unab.cl y gustavo.gatica@usach.cl
⁴Master in Industrial Engineering (C), Universidad Santiago de Chile (USACH), Chile. Investigator at Universidad Andres Bello y USACH, Santiago, Chile. E-mail: gvillagran@uandresbello.edu
⁵Magister in Engineering, Universidad Santiago de Chile (USACH), Chile. Assistant profesor at Universidad Santiago de Chile (USACH). E-mail: carlos.contrerasb@usach.cl
⁶PhD in Operations Research, University of Bologna, Italy. Fulltime professor at Facultad de Ingeniería, Universidad del Bío-Bío, Concepción, Chile. E-mail: rlinfati@ubiobio.cl
⁷PhD in Operations Research, University of Bologna, Italy. Fulltime professor at Facultad de Ingenieria, Pontificia Universidad Javeriana, Cali, Colombia. E-mail: jwescobar@javerianacali.edu.co

How to cite this article:

G. Gatica, G. Villagrán, C. Contreras-Bolton, R. Linfati, and W. J. Escobar, "A new genotype-phenotype genetic algorithm for the two-dimensional Strip Packing problem with rotation of 90° degrees ", Ing. Univ., vol. 20, no. 1, pp. 119-138, 2016. http://dx.doi.org/10.11144/Javeriana.iyu20-1.ngpg

Abstract

Given a set of rectangular pieces and a fixed width with infinite length, the strip-packing problem (SPP) of two dimensions (2D), with a rotation of pieces in 90° consists of orthogonally placing all the pieces on the strip, without overlapping them, minimizing the height of the strip used. Several algorithms have been proposed to solve this problem, being Genetic Algorithms one of the most popular approach due to it effectiveness solving NP-Hard problems. In this paper, three binary representations, and classic crossover and mutation operators are introduced. A comparison of the three binary representations on a subset of benchmarking instances is performed. The representation R2 outperforms the results obtained by representation R1 and R3. Indeed, some of the best-known results found by previous published approaches are improved.

Keywords : strip packing problem; genotype-phenotype; genetic algorithm; phenotype generation

Resumen

Dado un conjunto de piezas rectangulares con ancho fijo y con longitud infinita, el problema de strip-packing (SPP) de dos dimensiones, con una rotación de las piezas de 90°, consiste en la colocación ortogonal de todas las piezas en la tira, sin sobreponerlas, a fin de minimizar la altura de la tira usada. Se han propuesto varios algoritmos para resolver este problema, pero los genéticos constituyen uno de los enfoques más populares, debido a su eficacia en la solución en problemas NP-hard. En este trabajo se presentan tres representaciones binarias, una operación crossover clásica y operadores de mutación. Las tres representaciones binarias se comparan en un subconjunto de instancias de benchmarking. La representación R2 supera los resultados obtenidos por la representación R1 y R3. De hecho, se mejoran algunos de los mejores resultados encontrados por los trabajos publicados anteriormente.

Palabras clave :  problema de strip packing; genotipo-fenotipo; algoritmo genético; generación fenotipo

Introduction

Strip Packing Problem (SPP) is derived from cut and packing problems, and is considered as NP-Hard due to its combinatorial difficulty [1]. This problem can be found in productive industries, where the optimization of raw materials is converted into economic benefits by reducing production costs [2]. The SPP considers two cases: two-dimensional and three-dimensional. Even though three-dimensional cases are often more attractive for the research community due to their practicality, two-dimensional cases have achieved significant advances in algorithmic approaches and size of the solved instances, increasing high number of elements [3]. In particular, the two dimensional Strip Packing Problem (2D-SPP) is defined as a rectangular region with a width W and infinite height, where all the rectangular pieces i ∈1 = {1,2,..., n} with defined width W and height h_i, must not overlap and could be rotated 90°. The goal of this problem is to minimize the obtained height H of the strip by positioning all the pieces over it [4]. The 2D-SPP has been mathematically formulated in [5]. The 2D-SPP requires that n rectangles must be placed minimizing the height of the strip H. If we consider the Bottom Left corner of the strip as the origin of the region of the plane xy, x should correspond to the width of the direction of the region, and y to the direction of the height. Moreover, the location of every rectangle on the strip would be represented by a coordinate (x, y ) from the bottom left corner. The set of coordinates π = {(x_i, y_i ) V i ∈ 1} is denominated a placement of 1. The 2D-SPP can be formulated as follows:

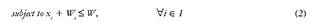
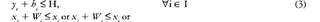
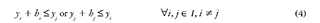
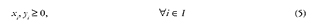
The set of constraints (2), (3), and (5) ensure that all of the rectangles must be placed within the strip with width W and height H. Finally, constraints (4) prevent that rectangles are overlapped.

Several methods for the solution of the 2D-SPP have been proposed. In [6], a Branch-and-Bound algorithm for getting a lower bound by relaxation for the 2D-SPP is proposed. In [7], canonical forms for the SPP, with and without rotation of pieces, are considered. In addition, geometric constraints have been considered in order to reduce the search space. In [8], another exact algorithm to solve subproblems represented by g-staircase placements, without the consideration piece rotation, is proposed.

In order to improve computational times and to solve large size instances, several heuristics have been developed to find good-quality solutions, closer to the optimal ones. In [9], a quasi-human heuristic for the solution of benchmarking sets of instances for the SPP is proposed. In [8], a two-stage intelligent search algorithm, where the second stage is based on a Simulated Annealing approach, is proposed. In [10], a skyline-based heuristic is developed, which corresponds to an approach proposed for indicating the height of the strip supported by a Tabu search procedure to generate different order sequences that indicate the order of placement into the strip.

Two algorithms based on Tabu Search approach have been proposed in [11] and [12]. In [11], a Tabu search procedure is proposed, which considers intensification and diversification procedures to improve the search on the solution space. In [12], a Tabu procedure is proposed, which considers an evaluation function to quantify the empty spaces and the logic of the problem along with an interesting search strategy on the neighborhoods by using a placement heuristic.

Another work using metaheuristics based on trajectory for the SPP is proposed by [13]. In this work, an approach based on Simulated Annealing is developed, using Bottom Left and Best fit placement algorithms. This algorithm proposes a digital coding of the pieces for the addressed problems.

In [2], a greedy algorithm (Reactive GRASP) uses several strategies on the construction of initial solution and improvement stages with different parameters, where they repair infeasible solution without description of procedure of local search. The hybridization of a heuristic (Fast heuristic) with a Simulated Annealing approach, proposed by [8], is also an interesting work. In it, 683 benchmarking instances have been solved, obtaining several best results in comparison with three published algorithms of the literature (SW [14], GRASP [2] and SVC [15]).

The obtained results of [14] have been improved by a randomization proposed by [16]. Genetic Algorithms (GA) has been used widely for solving Strip Packing Problems. These approaches simulate the theory of evolution being part of the Evolutionary Computation [17].

In [18], a Genetic Algorithm is proposed. For this the representation consists of swapping an integer chain that describes the placement order of the pieces into the strip followed by an approach that locates them on the strip by using a Bottom Left algorithm [19]. The evolutionary process requires of crossover operator PMX [19] and an Order-Based mutation [20], [21]. In [22], a Genetic Algorithm that requires specific operators to perform crossover and mutation stages is proposed. Due to the type of representation used by Genetic Algorithms, the operators are forced to repair infeasible solutions that emerge during evolutionary process, altering Darwinian evolution principles [23]. Finally, different algorithms have been proposed for different SPP variants by several authors [24]-[30].

In this paper, a classic Genetic Algorithm with a genotype-phenotype approach [31] is used to solve the 2D-SPP with rotation of 90°. In particular, a binary string and the phenotype of the placement of the pieces into the strip are used. In order to reduce computing times, our algorithm has been parallelized by using an island hybrid model and a master-slave with shared memory [32]. Three binary representations are presented allowing the diversification of the search space [33]. We note that there is a direct relation between the used bits on every representation with respect to the size problem. The obtained results over two benchmarking sets show that the proposed approach is able to obtain 64% of the Best-Known results. However, given the nature of the former algorithm and how close the obtained results are to the lower bounds, it was not possible to find better solutions.

In the following section of this paper, the binary representation used is described; while in the third section, computational results are introduced and discussed. In the last section, conclusions are presented.

1. Materials and Methods

In the following section, we introduce evolutionary process, a description of every representation used, and the placement algorithm.

1.1. Evolutionary Process

This paper proposes a Genetic Algorithm, which operates in a genotype-pheno-type mode. As a genotype, a binary string β is used. The genotype specifies the order of generation of the previous defined phenotype. The phenotype has the responsibility of decoding β. Finally, a placement algorithm allows the location of the pieces on the strip, representing individuals' phenotype for each generation as is shown in Figure 1.

Initially, a starting panmictic population, which is composed of a constant amount of individuals, is proposed. In this population, each individual corresponds to a potential feasible candidate of the problem. The population corresponds to the complete search space. A binary coding that corresponds to the genotype representation of each individual of the population is used. Each individual is evaluated by a fitness function (corresponding to the height of the strip).

Once all the individuals have been evaluated by the fitness function, the proposed algorithm selects and matches them. This process is done by a tournament selecting two individuals. The individuals are combined by a point crossing process generating a new individual. Each new individual is modified by a mutation process changing some elements of its chromosome. Finally, individuals that will be part of the new generation are selected. The pseudocode of the proposed algorithm is shown as follows:

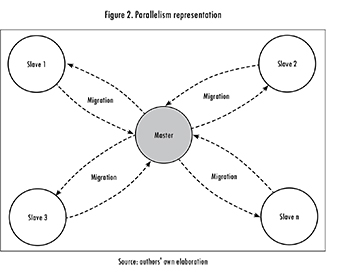
Additionally, a parallelism hybrid model has been applied. This approach allows splitting the population into several individuals, generally corresponding to the number of available units of the used computer, which execute the evolutionary process independently. In addition, every Ngen iterations migrates Y of the best individuals of their population according to the fitness value, i.e. the height of the strip. This process is performed by a Genetic Algorithm operating as coordinator for combining the obtained solutions of each part of the population. The proposed algorithm keeps the same number of individuals in each evolutionary process. The previously described scheme is shown in Figure 2.

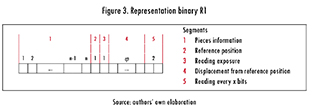
1.2. Representation R1

This paper uses a first binary representation, where each individual's genotype is β and Length L. Let be L the number of n pieces of the problem and φ = [log₂n]- 1 a dimension of set of bits. L could be calculated as follows:

β is divided into 5 segments, as shown in Figure 3. The first segment consists of n bits, which represent the pieces of the problem. The value of 1 indicates if a piece is rotated and the value of 0 indicates otherwise. Segments 2 and 4 are related to the beginning of the interpretation of the order of the pieces. The segment number 2 defines the position of the reference of interpretation. The value of 0 indicates if the interpretation starts at position 1 of segment 1, and 1 if the interpretation begins at position n. The complete conversion of the segment 4 (d) indicates the movement from the reference position to the first position. If the reference position is 0, it is moved d bits to the right, otherwise, it is moved d bits to the left. The segment 3 corresponds to the reading orientation, where 0 indicates if it is read from left to right and 1 otherwise. The last segment of two bits indicates the reading of every x bits by considering the first positions with values 1's and then 0's, where x is the complete conversion of 00, 01, 10, 11, plus one. The expected outcome corresponds to ∧= α ∪α' where α is the set of rotated pieces and α' the not-rotated ones.

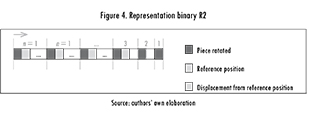
1.3. Representation R2

The second binary representation consists of splitting β into n segments, where each one is numerated as {n, n -1, ...1} and corresponds to the coded piece. Each segment is split in three parts from left to the right. The first part of one bit length indicates that, if the piece has value 1, it is rotated. The second part, of one bit length, corresponds to the reference position indicating the sense of genotype codification. If it has value 1, the piece is positioned at the beginning of J. If it has value 0, the piece is positioned at the end of J. The last part is composed by a set of bits and represents the value of units of displacement in J without the consideration of the θ pieces in the displacement. An example of representation R2 is shown in Figure 4. Note that the size of every segment is given by the number of remaining pieces to be identified. The number of remaining pieces decreases when the reading of the structure continues. The length of each segment i is calculated as |log₂ i| +1 and the length β is expressed by Σⁿ₁₌₁(log₂ i]+1).

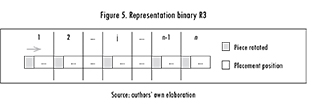
1.4. Representation R3

The third binary representation is given by a set of n segments of dimension [log₂n] + 1 bits, where each one is split, from left to right, into a bit that determines if the piece j is rotated and [log₂n] bits the position to be occupied by θ (Figure 5); according to the obtained value of the complete conversion of the segment [log₂n]. If the value associated to j is 1, the piece must be positioned in θ. If the piece cannot be found, the algorithm uses the following available piece. The length b is calculated as follows L = n • ([log₂n]) + 1.

1.5. Phenotype Generation

We have checked the heuristics Bottom left and Best fit, with and without the consideration of order by area. The algorithm with the best performance and effectiveness was Best-fit, used in [34], where the entrance of the pieces corresponds to Λ . In addition, we have not considered the first placement of every piece in order to preserve the evolutionary process. The pseudocode to evaluate Best-fit is the following:

2. Computational Results

Experiments have been performed on an AMD Opteron(tm) Processor 4386 with 32 GB RAM and GNU/Linux Ubuntu 14.04.2 LTS. The proposed algorithm has been coded in C language. For the parallel population implementation, openMPI was used. Two groups of instances are used, which were proposed by [13] and [33].

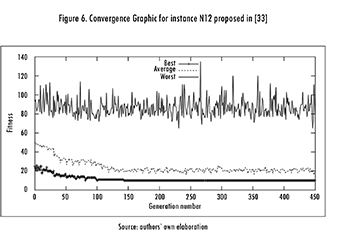
As long as the evolutionary process continues, better individuals are generated until reaching final stages with a convergence to populations that have diverse quality individuals. Most of these individuals have a fitness value (height of the strip) close to the best value population. Figure 6 presents an evolutionary process for a typical case for the N6 problem proposed by [33]. In the axis y, fitness value is presented, while that in the axis x the generation number is shown.

In this case, randomly generated population obtained fitness values between 17 and 100. The fitness value for the best individual becomes close to the Best-Known solutions. From generation 119, the fitness value for the average and the best solution are close to each other (Figure 6). For instance N12, the best individual, was found on generation 101. Note that the curve for the worse individual during the process shows that, for each generation, few groups of individuals with fitness value between 15 and 45 are considered. This process occurs because of the crossover operator that makes the changes out of the first chromosome segment, making these individuals being different in their genotype in comparison with their ancestors. Therefore, it implies that its phenotype is poor with respect to the solution quality.

2.1. Parameters Calibration

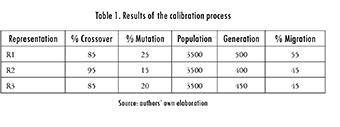
Parameters calibration is a relevant phase for the experiment design of the proposed algorithm [34]-[37]. For the calibration process, some tests were conducted with a subgroup of instances [38] by considering several levels of crossover (65%, 75%, 85%, 95%), mutation (10%, 15%, 20%, 25%, 30%), and population size (500, 1000, 1500, 2000, 2500, 3000, 3500). The amount of generations to evaluate is set by using the methodology described in [38]. The calibration tests were performed individually for each solution representation, in which the obtained results were analyzed for each combination of parameters. The best parameters used for executing all the computational experiments are shown in Table 1.

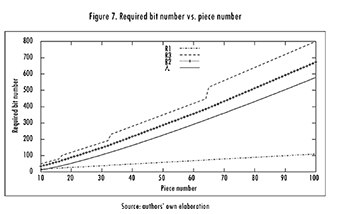
The representation R2 has obtained the best results respect to the Best Known solutions (see section 2.2). In addition, R2 requires less number o generations but needs more bits for representing a solution. A solution could be represented in several ways by R2. Figure 7 shows the ideal value of the difference between number of pieces and bits.

2.2. Analysis of Results

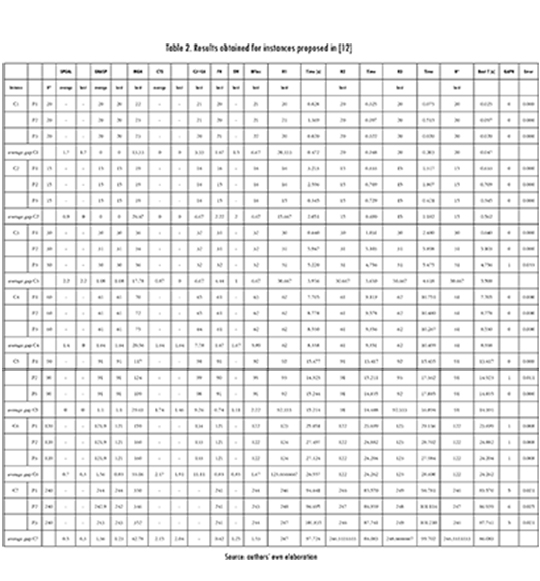
In Table 2, the results obtained on the benchmarking set proposed by [13] are shown. The first compound column of Table 2 corresponds to the problem being considered (instance). The second column corresponds to the Best-known solution (optimal solution H*). Columns 4 to 14 correspond to the results obtained by algorithms SPGAL [22], GRASP [1], MGA [36], CTS [12], CJ+EA [37], FH [8], SW [14], and BFBCC [38]. The following columns show the average and the best results with their corresponding computing times of 10 runs for each instance. Note that we report the obtained results for the three used representations (R1, R2, R3). The value of GAPH is calculated as the difference between best solutions found by all the representations of the proposed approach and the best solution found by SPGAL [22], GRASP [1], MGA [36], CTS [12], CJ+EA [37], FH [8], SW [14], and BFBCC [37]. The value of Error corresponds to the percentage obtained by the value of GAPH over the best solution found by the previous published approaches. Note that the proposed approach is able to obtain the best-known solution for instances C1 to C5 (62% of the complete set). For the remaining instances, the value of Error is less than 3% confirming that the calibration process improves the performance of the proposed approach. Regarding the computing time, the former algorithm obtains values lower than 90 seconds for large size instances. The second representation R2 outperforms the obtained values by R1 and R3 for the subsets of the instances.

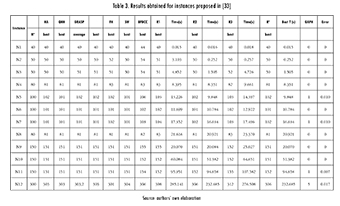
In Table 3, the results obtained for the second set of instances proposed by [33] are shown. The results are compared with algorithms GRASP [1], HA [39], QHH [9], FH [8], SW [14], and BFBCC [37]. The last columns show the best values and the corresponding computing times f of 10 runs for each instance, and the value of GAPH and Error. Representation R2 again obtains the best numerical results achieving a 67% of the Best-Known solutions. The value of the highest deviation obtained respect to the Best Known solutions is only 8%. The numerical results provide a GAPH of only 2.94%, 2.02%, and 1.57% respect to the Best-Known Solutions.

3. Concluding Remarks

This paper proposes three binary representations of genotype-phenotype (R1, R2, R3) within an efficient Genetic Algorithm for the two-dimensional Strip Packing problem with rotation of 90^o. A parallel implementation of the former algorithm is proposed. The essence of Darwinian Evolution has been preserved, without altering the evolutionary process. The obtained results show the effectiveness of the proposed approach. The proposed approach is able to obtain, on average, 67% of the Best-Known solutions. As a further work, it is intended to use another phenotype generation in order to improve the quality of the solution.

References

[1] M. R. Garey and D. S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness. San Francisco, LA: Freeman, 1979.         [ Links ]

[2] R. Álvarez-Valdés, F. Parreño, and J. M. Tmarit, "Reactive grasp for the strip-packing problem," Computers & Operations Research, vol. 35, no. 4, pp. 1065-1083, 2008.         [ Links ]

[3] T. Buchwald and G. Scheithauer, "Upper bounds for heuristic approaches to the strip packing problem," International Transactions in Operational Research, vol. 23, no. 1-2, pp. 93- 119, 2014.         [ Links ]

[4] A. Lodi, S. Martello, and D. Vigo, "Heuristic and metaheuristic approaches for a class of two-dimensional bin packing problems," INFORMS Journal on Computing, vol. 11, no. 4, pp. 345-357, 1999.         [ Links ]

[5] M. Kenmochi, T. Imamichi, K. Nnobe, M. Yagiura, and H. Nagamochi, "Exact algorithms for the 2-dimensional strip packing problem with and without rotations," European Journal of Operational Research, vol. 198, no. 1, pp. 73-83, 2009.         [ Links ]

[6] R. Álvarez-Valdés, F. Parreno, and J. Tmarit, "A branch and bound algorithm for the strip packing problem," OR Spectrum, vol. 31, no. 2, pp. 431-459, 2009.         [ Links ]

[7] Y Arahori, T. Imamichi, and H. Nagamochi, "An exact strip packing algorithm based on canonical forms," Computers & Operations Research, vol. 39, no. 12, pp. 2991-3011, 2012.         [ Links ]

[8] S. C. Leung, D. Zhang, and K. M. Sim, "A two-stage intelligent search algorithm for the two-dimensional strip packing problem," European Journal of Operational Research, vol. 215, no. 1, pp. 57-69, 2011.         [ Links ]

[9] D. Chen, Y Fu, M. Shang, and W Huang, "A quasi-human heuristic algorithm for the 2D rectangular strip packing problem," in Information Science and Engineering, 2008. ISISE'08. International Symposium on, vol. 2, pp. 392-396, IEEE, 2008.         [ Links ]

[10] L. Wei, W.C. Oon, W Zhu, and A. Lim, "A skyline heuristic for the 2D rectangular packing and strip packing problems," European Journal of Operational Research, vol. 215, no. 2, pp. 337-346, 2011.         [ Links ]

[11] R. Álvarez-Valdés, F. Parreño, and J. M. Tamarit, "A Tabu search algorithm for a two-dimensional non-guillotine cutting problem," EuropeanJournal of Operational Research, vol. 183, no. 3, pp. 1167-1182, 2007.         [ Links ]

[12] G. Gómez-Villouta, J.-P Hamiez, and J.-K. Hao, "Tabu search with consistent neighbourhood for strip packing," in Trends in Applied Intelligent Systems. New York: Springer, 2010, pp. 1-10.         [ Links ]

[13] E. Hopper and B. C. Turton, "An empirical investigation of metaheuristic and heuristic algorithms for a 2D packing problem," European Journal of Operational Research, vol. 128, no. 1, pp. 34-57, 2001.         [ Links ]

[14] E. K. Burke, M. R. Hyde, and G. Kendall, "A squeaky wheel optimisation methodology for two-dimensional strip packing," Computers & Operations Research, vol. 38, no. 7, pp. 1035-1044, 2011.         [ Links ]

[15] G. Belov, G. Scheithauer, and E. Mukhacheva, "One-dimensional heuristics adapted for two-dimensional rectangular strip packing," Journal of the Operational Research Society, vol. 59, no. 6, pp. 823- 832, 2008.         [ Links ]

[16] S. Yang, S. Han, and W. Ye, "A simple randomized algorithm for two-dimensional strip packing," Computers & Operations Research, vol. 40, no. 1, pp. 1-8, 2013.         [ Links ]

[17] E. G. Talbi, Metaheuristics: From Design to Implementation, vol. 74. New York: John Wiley & Sons, 2009.         [ Links ]

[18] E. Hopper and B. Turton, "A genetic algorithm for a 2D industrial packing problem," Computers & Industrial Engineering, vol. 37, no. 1, pp. 375-378, 1999.         [ Links ]

[19] S. Jakobs, "On genetic algorithms for the packing of polygons," European Journal of Operational Research, vol. 88, no. 1, pp. 165-181, 1996.         [ Links ]

[20] D. E. Goldberg, Genetic algorithms in search, optimization, and machine learning. Boston: Addison Wesley, 1989.         [ Links ]

[21] G. Syswerda, "Schedule optimization using genetic algorithms," in Handbook of Genetic Algorithms, New York: Van Nostrand Reinhold, 1991.         [ Links ]

[22] A. Bortfeldt, "A genetic algorithm for the two-dimensional strip packing problem with rectangular pieces," European Journal of Operational Research, vol. 172, no. 3, pp. 814-837, 2006.         [ Links ]

[23] M. Affenzeller, S. Wagner, S. Winkler, and A. Beham, Genetic Algorithms and Genetic Programming: Modern Concepts and Practical Applications. Boca Raton: CRC Press, 2009.         [ Links ]

[24] A. Bortfeldt, Ein Genetischer Algorithmus fur das Zweidimensionale Strip-Packing-Problem. Planen, Lernen: Optimieren, 2003.         [ Links ]

[25] R. García-Cáceres, C. Vega-Mejía, and J. Caballero-Villalobos, Integral Optimization of the Container Loading Problem. INTECH Open Access Publisher, 2011.         [ Links ]

[26] K. He, Y. Jin, and W. Huang, "Heuristics for two-dimensional strip packing problem with 90 rotations," Expert Systems with Applications, vol. 40, no. 14, pp. 5542-5550, 2013.         [ Links ]

[27] R. Harren, K. Jansen, L. Pradel, and R. Van Stee, "A (5/3+ E) - approximation for strip packing," Computational Geometry, vol. 47, no. 2, pp. 248-267, 2014.         [ Links ]

[28] J. L. da Silveira, E. C. Xavier, and F. K. Miyazawa, "Two-dimensional strip packing with unloading constraints," Discrete Applied Mathematics, vol. 164, pp. 512-521, 2014.         [ Links ]

[29] J. Thomas and N. S. Chaudhari, "A new metaheuristic genetic-based placement algorithm for 2D strip packing," Journal of Industrial Engineering International, vol. 10, no. 1, pp. 1-16, 2014.         [ Links ]

[30] S. Grandcolas and C. Pinto, "A new search procedure for the two- dimensional orthogonal packing problem," Journal of Mathematical Modelling and Algorithms in Operations Research, pp. 1-19, 2015.         [ Links ]

[31] E. Falkenauer, Genetic Algorithms and Grouping Problems. New York: John Wiley & Sons, 1998.         [ Links ]

[32] E. Alba, ParallelMetaheuristics: A New Class of Algorithms. New Jersey: John Wiley & Sons, 2005.         [ Links ]

[33] F. Rothlauf, "Representations for genetic and evolutionary algorithms," Journal of OperationalResearch Society, vol. 54, no. 10, pp. 1112-1112, 2003.         [ Links ]

[34] E. K. Burke, G. Kendall, and G. Whitwell, "A new placement heuristic for the orthogonal stock-cutting problem," Operations Research, vol. 52, no. 4, pp. 655-671, 2004.         [ Links ]

[35] V. Mancapa, T. Van Niekerk, and T. Hua, "A genetic algorithm for two dimensional strip packing problems," South African Journal of Industrial Engineering, vol. 20, no. 2, pp. 145-162, 2009.         [ Links ]

[36] M. Matayoshi, "The 2D strip packing problem: a new approach with verification by EA," in Systems Man and Cybernetics (SMC), 2010 IEEE International Conference on, pp. 2492-2499, IEEE, 2010.         [ Links ]

[37] V. M. Kotov and D. Cao, "A heuristic algorithm for the non-oriented 2D rectangular strip packing problem," Buletinul Academiei de Stiinte a Republicii Moldova. Matematica, no. 2, pp. 81-88, 2011.         [ Links ]

[38] S. P. Coy, B. L. Golden, G. C. Runger, and E. A. Wasil, "Using experimental design to find effective parameter settings for heuristics," Journal of Heuristics, vol. 7, no. 1, pp. 77-97, 2001.         [ Links ]

[39] W. Huang and D. Chen, "An efficient heuristic algorithm for rectangle - packing problem," Simulation Modelling Practice and Theory, vol. 15, no. 10, pp. 1356-1365, 2007.         [ Links ]