Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería y competitividad
versão impressa ISSN 0123-3033
Ing. compet. vol.15 no.2 Cali jul./dez. 2013
Non-invasive monitoring of transformers using the frequency response from controlled transient signals
Monitoreo no-invasivo de transformadores empleando la respuesta en frecuencia obtenida a partir de señales transitorias controladas
Eduardo Gómez-Luna
Escuela de Ingeniería Eléctrica y Electrónica, Grupo de Investigación GRALTA, Universidad del Valle, Cali, Colombia
E-mail: eduardo.gomez@correounivalle.edu.co
Guillermo Aponte
Escuela de Ingeniería Eléctrica y Electrónica, Grupo de Investigación GRALTA, Universidad del Valle, Cali, Colombia
E-mail: guillermo.aponte@correounivalle.edu.co
Jorge Pleite
Departamento de Tecnología Electrónica, Universidad Carlos III de Madrid, Madrid, España
E-mail: pleite@ing.uc3m.es
Eje temático:Electrical and electronic engineering / Ingeniería eléctrica y electrónica
Recibido: 22 de Abril-2013
Aceptado: 06 de Septiembre de 2013
Abstract
This article presents a novel procedure for applying controlled transient signals analysis with the goal of obtaining the frequency response (FRA) with the transformer in service. For the procedure the method used is IFRA (Impulse Frequency Response Analysis) complemented with the Wavelet Transform. IFRA, has been implemented in previous works to transform transient signals from the time domain to the frequency domain by means of Fast Fourier Transform (FFT); however, Fourier is not the most suitable tool for this type of analysis since by definition, Fourier is useful for processing stationary signals. Taking that into consideration it was used Wavelet Transforms, given their variable time/frequency resolution, which improved the repeatability of the frequency response curves, as observed in experimental results.
The analysis developed was applied in a single-phase distribution transformer of 7620/240 V, 3 kVA, to show the viability of the proposed method, for obtaining the frequency response curve, which could be used for power transformers in service.
Keywords: transformer, on-line FRA, transient signals, signal processing.
Resumen
El siguiente artículo presenta un nuevo procedimiento para emplear señales transitorias controladas con el cual se puede obtener la respuesta en frecuencia (FRA) del transformador en servicio. El procedimiento emplea el método IFRA (análisis de la respuesta en frecuencia ante un impulso) complementado con la Transformada Wavelet. El método IFRA ha sido implementado en trabajos previos, pasando señales temporales al dominio de la frecuencia usando la Transformada de Fourier, sin embargo, Fourier no se considera la herramienta más eficaz para este tipo de análisis dado que fue desarrollada para el procesamiento de señales estacionarias. Teniendo en cuenta lo anterior, en este trabajo se empleó la Transformada Wavelet dado su variabilidad en resolución en el dominio tiempo-frecuencia, con lo cual se mejoró la repetitividad de las curvas de respuesta en frecuencia tal como se observa en los resultados experimentales.
El análisis desarrollado fue aplicado a un transformador de distribución monofásico de 7600/240V, 3 kVA, mostrando la viabilidad del método propuesto, el cual podría también emplearse para la obtención de la curva de repuesta en frecuencia en transformadores de potencia en servicio.
Palabras clave: Transformador, FRA on-line, señales transitorias, procesamiento de señal.
1. Introduction
Power transformers are the most expensive equipment in the power system, and for this reason it is very important to prevent their failure and to detect problems as early as possible. Transformer monitoring based on the operating condition is a tool for early risk situation detection and can be used to make appropriate decisions before a failure occurs. Frequency Response Analysis (FRA) is a technique for assessing the power transformer condition, currently accepted worldwide as a complementary support to other diagnostic techniques, and it is especially valuable for detecting potential mechanical problems, like displacements or deformations in the windings and the core sheets, faults that are very difficult to locate with other methods (Aponte, 2011).
Currently the FRA test is performed with the transformer without loading and de-energized, generating high costs and decreasing supply reliability. This implies that the test is usually not scheduled as frequently as desired, but only when a failure is suspected; for this reason the on-line performance of the frequency-response technique offers substantial benefits for scheduled-based diagnosis in a non-stop service and moreover it could even lead to condition-based maintenance. The on-line FRA method has been implemented through an Impulse Frequency Response Analysis (IFRA). This type of on-line monitoring can be carried out by taking advantage of the transients traveling throughout the system, by measuring them at the input and output of the transformer. Given that those transients might have different causes and characteristics, problems like noise and low repeatability of results (frequency response curve) need further investigation to improve the technique (on-line IFRA) (Gomez-Luna et al, 2013).
Different attempts have been made to carry out the frequency response test with the transformer in service (Gomez-Luna et al, 2013), but most research results still need to ensure measure repeatability and guard against the influence of external factors inherent in the operation of the transformer in the power system.
Consequently, this study presents the analysis of transient signals in Wavelet domain (time-scale) in order to de-noise the signals and compute the frequency response curve (impedance curve) that could allow assessment of the transformer condition. Improved repeatability of the frequency response curves has been observed in experimental results with the proposed method; the transient signals computed by using Continuous Wavelet Transform (CWT) exhibit better repeatability than those computed by using Fourier Transform. Likewise, experiments reveal the convenience of Wavelet-based de-noising strategies.
1.1 Monitoring of transformers based on controlled voltage and current transients
Transient analysis is a signal processing task performed in several power system studies like: fault detection, system protection, power quality disturbances detection and modal analysis, among others. Some non-invasive monitoring techniques include the analysis of current and voltage transients, and recently the analysis of transients has also been proposed as a method for identifying the frequency response with the transformer in service (Malewski et al, 1988; Coffeen, 2003; Wang, 2003). The problem with those proposals is that they use as input uncontrolled signals associated with disturbances inherent in the normal operation of the electrical network: switching pulse (opening and closing switches) or atmospheric events (lightning), where highfrequency components predominate.
Currently the on-line IFRA method uses the disturbances inherent in the normal operation of the electrical network, such as switching-type pulse waves (induced by switches opening and closing) or pulse waves induced for instance by atmospheric events (lightning), where highfrequency components predominate; however, these signals occur in random occurrences. This means that the shape of the disturbance is not controlled; therefore, a sufficient spectral content is not ensured, and for that reason this work was focused on developing a procedure to obtain the on-line frequency response by applying controlled transient signals to the on-line transformer.
The controlled signals are injected into the transformer by means of a generation pulse circuit that permits trigger timing control and ensures an adequate pulse wave shape for a wide frequency content in the input and the output signals (from Hz to MHz).
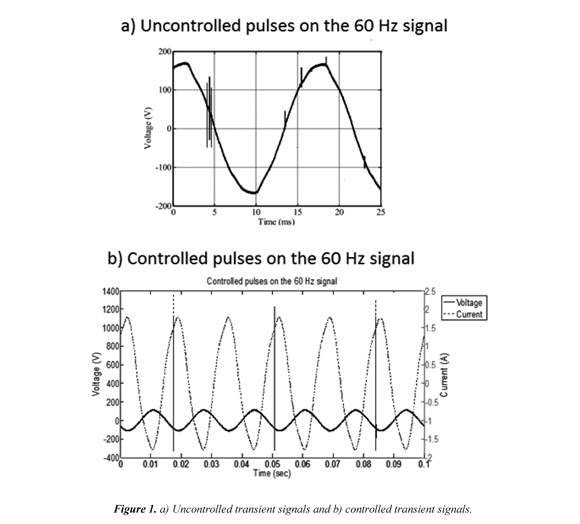
This procedure use a controlled transient signal allowing to change the amplitude, the width, and the phase of the pulse generated on the 60-Hz wave, making sure it had a high spectral content and having a total control over it. Figure 1 shows an example of uncontrolled and controlled signals in the power system.
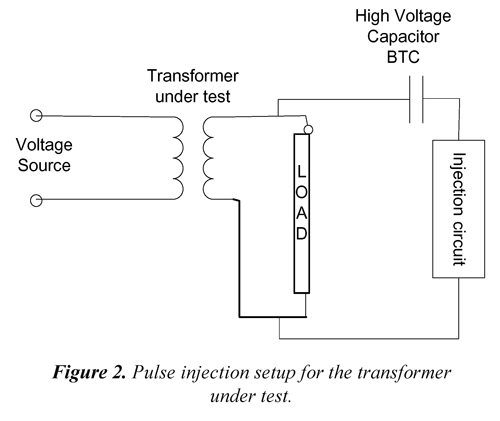
The injection system of controlled pulses used in this work was proposed in (Gomez-Luna et al, 2013), having a zero crossing detector of the 60Hz wave for controlling the injection moment. The injection system diagram is presented in Figure 2.
The voltage and current signals are sampled at a rate of 60 Ms/sec and 12 bits of resolution using the data acquisition recorder PCI-5105 manufactured by National Instruments.
1.2 Mathematical tools for transient signals analysis
Power system transients analysis and signal processing can be carried out by transforming the signal from the time domain to the frequency domain by using, among other tools, the Fourier Transform (FFT) or the Wavelet Transform (WT) (Robertson et al, 1996; Gomez-Luna et al, 2013). One of the tools used for obtaining the on-line frequency response method from transient signals is the Fast Fourier Transform (FFT); however, this tool is more useful for processing stationary signals (Robertson 1996). Even though the Fourier Transform has some improved versions of this application, such as the Short-Time Fourier Transform (STFT), the results still reveal room for improvement. This can be explained by the Heisenberg uncertainty principle which, in terms of signal processing, indicates that it is not possible to find the exact frequency and the exact time when the (sinusoidal) signal components take place. Taking that into consideration, the analysis of transient signals could be hypothetically improved by using Wavelet Transforms, given their variable time/frequency resolution (Leonowicz et al. 2003).
In this work it was used the Continuous Wavelet Transform (CWT) instead of the FFT for transient signals analysis in order to obtain the transformer frequency response curve (impedance curve). An improved repeatability of the frequency response curves was observed in experimental results, showing the convenience of Wavelet-based denoising and filtering strategies.
1.3 Wavelet transform (WT)
The Wavelet Transform, which has received considerable interest in the field of electrical signals, is proposed as a fast and effective means of analyzing voltage and current transients recorded during power system disturbances. Like the familiar Fourier Transform, the Wavelet Transform decomposes a signal into its frequency components.
The basis of the Fourier Transform are sine and cosine functions and, in the case of the Short-Time Fourier Transform (STFT), a window function is added to analyze a determined signal. With the WT the base and window function concepts are naturally conjugated to overcome the problem of solving the analysis with the Fourier approach (Paraskar et al. 2012, Duarte et al, 2012).
Wavelet Transforms have been used for capturing and analyzing power system transients (Mokhtari et al, 2002). The objective is to decompose a signal into different frequency components, so that the decomposition stems from a family of functions that are translations and dilations of a ?(t) function, called wavelets or mother wavelets. These translation and dilation processes are defined in Eq. (1).
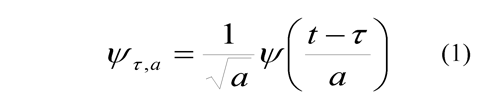
where τ conducts the translation and α provides the dilation (or scaling).The wavelets must have zero average value, finite energy, and fulfill an eligibility condition; these three criteria are formulated in Equations (2), (3) and (4) respectively.
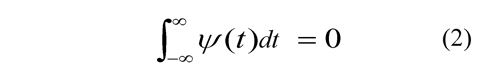
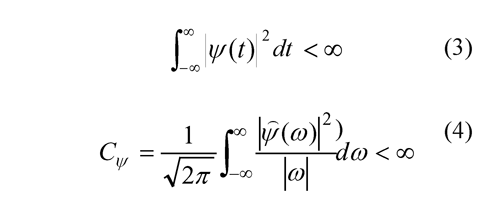
where ψ̂ (ω) is the Fourier Transform of Ψ(t).
For transient signal analysis, the procedure uses the Discrete Wavelet Transform (DWT) and the Continuous Wavelet Transform (CWT).
1.3.1 Discrete wavelet transform (DWT)
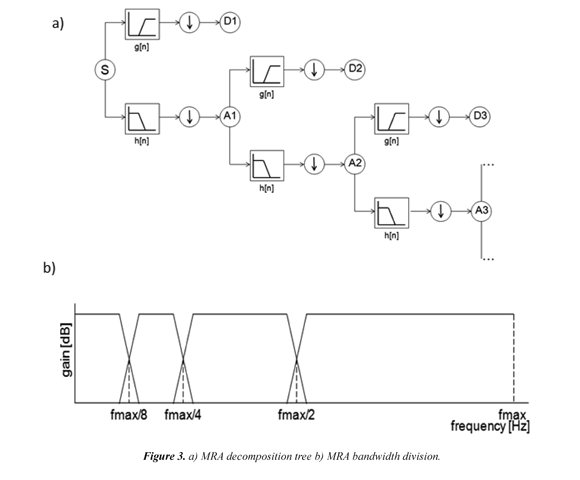
To improve efficiency in terms of computational calculation, the parameters used in Eq. (1) take the values a0=2 and t0=1, which define a practical form of the DWT called Multi-Resolution Analysis (MRA), which can be seen as a signal decomposition by using high-pass filters (HP) and low-pass filters (LP), as shown in Figure 3a.
The low-pass filter output is known as approximation and the high-pass filter output is known as detail.
Figure 3b shows how the bandwidth of the measured signal is divided during the decomposition process.
The MRA analysis decomposes a transient signal from the time domain into low and high frequency information by using high-pass, g[n], and low-pass filters, h[n], to obtain two types of coefficients: the detail coefficients Dn (low frequency) and the approximation coefficients An (high frequency) at decomposition level n, as shown in Figure 3.
Discrete Wavelet Transforms can remove noise from transient signals by using different denoising strategies that allow removal not only of background noise but also low frequency noise like harmonic distortion and other frequencylocalized phenomena.
Filtering and de-noising processes which are possible with the MRA of the Discrete Wavelet Transform (DWT). The mother wavelet Daubechies 4 (db4), which is commonly used for filtering electrical signals (Zheng et al. 2010) was applied to eliminate the electrical system background noise (de-noising) (r(t)) affecting the de-noised voltage and current waveforms.
The power system harmonics were also removed from the signals by modifying the coefficients from a MRA using mother wavelet Daubechies 10 (db10). Then, the voltage and current transient signals were processed to compute the respective frequency spectrum of the transformer.
The de-noised voltage and current waveforms, v(t) and i(t), were processed using Continuous Wavelet Transform (CWT) in order to compute their spectra, V(ω) and I(ω) . For comparison purposes, the spectra based on Fast Fourier Transform (FFT) were also computed. The transformer impedance Z(ω) was computed as the ratio of the voltage spectrum V(ω) to the current spectrum I(ω) for every frequency component.
1.3.2 Continuous wavelet transform (CWT)
The Continuous Wavelet Transform (CWT) is defined in Eq.(5):
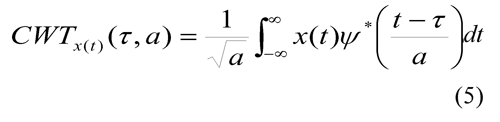
where a is the scaling factor, t is the time shifting factor, ? (t) is the mother wavelet function, and x(t) is the signal to be transformed (Robertson et al, 1996).
In this work it was used the mother wavelet Morlet because it is frequently employed to study signal time-frequency properties (Duarte et al, 2012; Li, 2011) and because it provides control over both central frequency and spectrum bandwidth.
The on-line IFRA technique requires transformation of the signal from the time domain to the frequency domain. Since the Wavelet Transform maps a signal to the time-scale domain, it is necessary to integrate the shifting time domain. (Gomez-Luna et al, 2013) proposed Eq.(6), which was used to compute the transformer frequency response from transient signals.
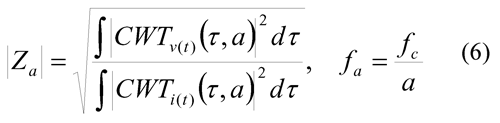
Where Z? is the impedance for a given scale "a". CWTv and CWTi are the CWT of voltage and current signals, respectively.
ƒΑ is the frequency associated with a given scale "a".
ƒc is the central frequency of the mother wavelet spectrum.
Three processes are necessary to obtain on-line FRA: de-noising, filtering and spectrum. With the Wavelet Transform it is possible to do all three.
2. Methodology
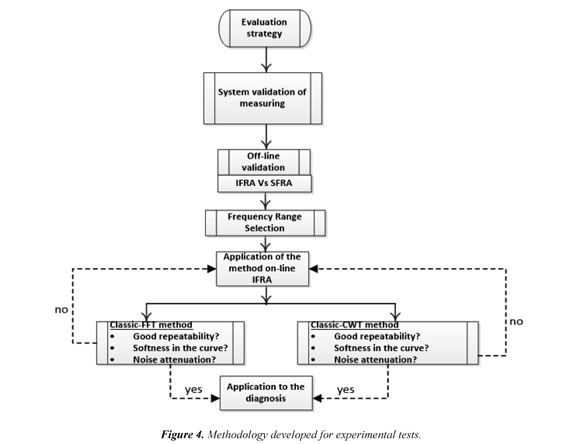
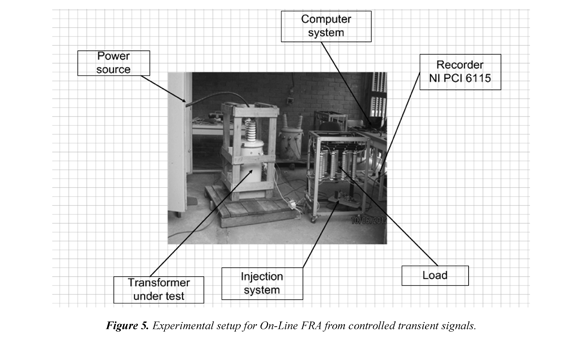
The methodology developed for the experimental tests is shown in Figure 4, on-line frequency response measurements from transient signals were performed on a transformer of 7620/240V, 3 kVA under load and no-load conditions. Figure 5 shows a single-phase transformer under test. The new procedure for applying controlled transient signals analysis was used.
The setup used to measure the transformer voltage and current transient signals is shown in Figure 5, indicating the main components in the on-line test that was employed to obtain the frequency response by injecting controlled pulses.
2.1 On-line FRA tests
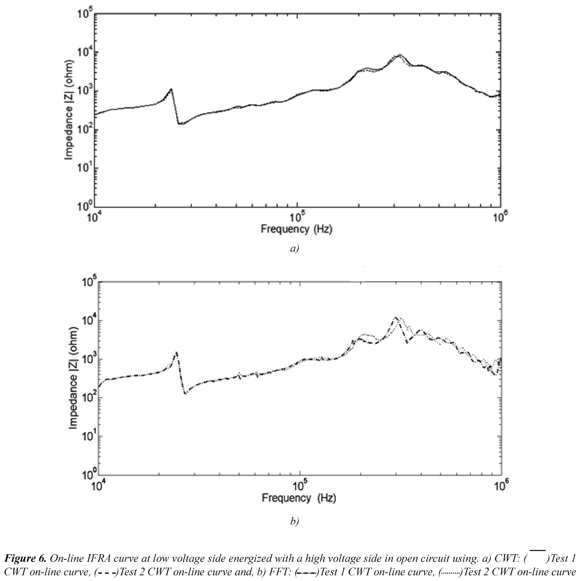
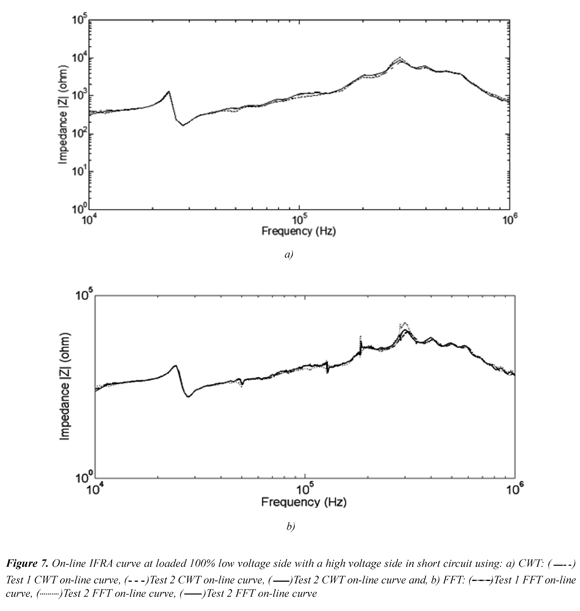
The monitoring of the transformer was based on the continuous tracking of changes in the frequency response curve. Therefore, the repeatability of the curve is the relevant feature to be investigated in a given frequency response analysis technique. In this regard, Figure 6 and Figure 7 present the on-line frequency response curves computed from two and three measurements taken at different times on the transformer, with no variations in its physical structure. It can be observed that the curve computed by using CWT exhibits better repeatability than that computed by using FFT.
3. Results and discussion
Figure 6 and Figure 7 present the frequency response obtained from applying controlled signals and using CWT, in which can be seen the curves repeatability, which is a relevant condition when using the frequency response analysis technique. In this regard, the on-line frequency response curves were computed from two or three measurements (injected pulses called "test #") taken at different times on a single-phase transformer, with no variations in its physical structure.
Table 1 and Table 2 show the qualitative and quantitative results of the curves obtained using Wavelet Transform, according to the results shown in Figure 6 and Figure 7, respectively, for two configurations: the transformer energized (Figure 6) and the transformer loaded (Figure 7). The test label in the figures refers to the number of injected pulses.
4. Conclusions
This paper presents a new procedure to obtaining on-line transformer Frequency Response by applying controlled pulses and using the Wavelet Transform as an improved alternative to the Fourier Transform.
The effectiveness of the Continuous Wavelet Transform (CWT) applied to transient signals in the computation of on-line Frequency Response Analysis curves for transformers has been evidenced in this study, showing that on-line IFRA based on CWT outperformed the correspondent one based on Fast Fourier Transform (FFT) in terms of repeatability, smoothness and signal denoising The computation time, however, was longer for the CWT-based approach.
Although the potential of the on-line IFRA using the Continuous Wavelet Transform has been experimentally demonstrated in this study, further investigation is necessary in order to make the on-line IFRA method as effective and useful as the standard off-line FRA method, for power transformers.
5. Acknowledgments
The authors thank the Colombian Department of Administrative Science, Technology and Innovation (COLCIENCIAS 494-2009) and the Spanish Government (Ministry of Science and Innovation DPI2008-05890) for their support in the development of this work.
6. References
Aponte, G.,(2011). Evaluación de la condición mecánica de los transformadores mediante el análisis de su respuesta en frecuencia. Tesis Doctoral. Escuela de Ingenieria Electrica y Electrónica, Universidad del Valle, Colombia. [ Links ]
Butler-purry, K.L. & Bagriyanik, M. (2003). Characterization of transients in transformers using discrete wavelet transforms. IEEE Transactions on Power Systems , 18 (2), 648-656. [ Links ]
Coffeen, L. (2003). System and method for OnLine Impulse frequency response analysis . US pto., 6369582 B2(12). [ Links ]
Duarte, C., Delmar P., Goossen, K., Barner, K., & Gomez-Luna, E. (2012). Non-Intrusive Load Monitoring Based on Switching Voltage Transients and Wavelet Transforms. Future of Instrumentation International Workshop (FIIW). Oct. 8-9, Gatlinburg (TN). IEEE. [ Links ]
Gomez-Luna, E. Aponte, G., Herrera, W. & Pleite, J. (2013). Experimentally obtaining on-line FRA in transformers by injecting controlled pulses. Ingenieria e investigación , 33 (1), 41-45. [ Links ]
Gomez-Luna, E., Aponte, G., Gonzalez-Garcia, C. & Pleite, J. (2013). Current Status and Future Trends in Frequency-Response Analysis With a Transformer in Service. IEEE Trans. Power Delivery , 28 (2), 1024-1031. [ Links ]
Gomez-Luna, E., Silva, D., Aponte G., Pleite, J. & Hinestroza, D. (2013). Obtaining the Electrical Impedance Using Wavelet Transform From the Time Response. IEEE Trans. Power Delivery , 28 (2), 2012-2014. [ Links ]
Leonowicz, Z., Lobos, T. & Rezmer, J. (2003). Spectrum estimation of non-stationary signals in power systems. In IPST. International Conference on Power System Transients , (pp. 1-6). New Orleans, USA: IPST. [ Links ]
Li, H. (2011). Bearing fault diagnosis based on time scale spectrum of continuous wavelet transform. In IEEE. Eighth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD) (pp.1934-1937). Shanghai: IEEE. [ Links ]
Malewski, R., Douville, J. & Lavallee, L. (1988). Measurement of switching transients in 735 kV substations and assessment of their severity for transformer insulation . IEEE Trans. Power Delivery , 3 (4), 1380-1390. [ Links ]
Mokhtari, H., Karimi-Ghartemani, M. & Iravani, M.R. (2002). Experimental performance evaluation of a wavelet-based on-line voltaje detection method for power quality applications. IEEE Transactions on Power Delivery , 17 (1), 161-172. [ Links ]
Paraskar, S.R., Beg, M.A. & Dhole, G.M. (2012). Continuous Wavelet Transform for Discrimination between Inrush and Fault Current Transients in Transformer. International journal of science, spirituality, business and technology (ijssbt) , 1 (1), 9-14. [ Links ]
Robertson, D., Camps, O., Mayer, J., Gish, .W. (1996). Wavelets and Electromagnetic Power System Transients. Transactions on Power Delivery , 11 (2), 1050-1058. [ Links ]
Wang, M., (2003). Winding movement and condition monitoring of power transformers in service . Doctoral Thesis. Department of Electrical Engineering, University of British Columbia, Canada. [ Links ]
Zheng, E., Liu, Z. & Ma, L. (2010). Study on Harmonic Detection Method Based on FFT and Wavelet Transform. In IEEE. International Conference on Signal processing System (ICSPS) , (pp. 5-8). Dalian, China: IEEE. [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.