Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería y competitividad
versão impressa ISSN 0123-3033
Ing. compet. vol.15 no.2 Cali jul./dez. 2013
Methodology for modeling electricity markets using concurrent constraint programming
Metodología para el modelamiento de mercados de electricidad usando programación concurrente con restricciones
Sandra M. Londoño
Grupo de Investigación en Alta Tensión - GRALTA, Escuela de Ingeniería Eléctrica y Electrónica, Universidad del Valle, Cali, Colombia
E-mail: smlh_78@yahoo.com
Carlos A. Lozano
Grupo de Investigación en Alta Tensión - GRALTA, Escuela de Ingeniería Eléctrica y Electrónica, Universidad del Valle, Cali, Colombia
E-mail: carlos.a.lozano@correounivalle.edu.co
Ferley Castro-Aranda
Grupo de Investigación en Alta Tensión - GRALTA, Escuela de Ingeniería Eléctrica y Electrónica, Universidad del Valle, Cali, Colombia
E-mail: ferley.castro@correounivalle.edu.co
Eje temático: Electrical and electronic engineering / Ingeniería eléctrica y electrónica
Recibido: 03 de Abril de 2013
Aceptado: 14 de Agosto de 2013
Abstract
This article proposes a methodology to model a competitive electricity market using the concurrent constraint programming paradigm (CCP). The market considered is cleared by merit order and based on the game theory equilibrium model, Supply Function Equilibrium (SFE), with asymmetric step functions with multiple blocks. Also, it shows results for a reference case with 3 generation companies (Gencos) to reveal the model behavior.
Keywords: Electricity markets, Constraint programming, Supply Function Equilibrium.
Resumen
Este artículo propone una metodología para modelar un mercado de electricidad competitivo usando el paradigma de programación concurrente con restricciones (CCP). El mercado considerado es despejado por orden de mérito y basado en el modelo de equilibrio de teoría de juegos, Función de Suministro de Equilibrio (SFE), con funciones de paso asimétricas con bloques múltiples. También, se muestran resultados para un caso de referencia con 3 compañías de generación (Gencos) para revelar el comportamiento del modelo.
Palabras clave: Mercados de Electricidad, Programación con Restricciones, Función de Suministro de Equilibrio.
1. Introduction
The problem of determining the possible equilibria reached in a competitive electricity market, with strategic generators influencing the market's clearance price, can be represented as a combinatorial problem or a constraint satisfaction problem (CSP). In this case, concurrent constraint programming (CCP) can be used to solve a CSP. Hence, as shown in(Londoño, 2012), it is possible to use constraint programming to analyze electricity markets, particularly with SFE models using step functions (block form). The SFE model has been widely used (Green & Newbery, 1992), (Von der Fehr & Harbord, 1993), (Berry, et al., 1999), (Anderson & Philpott, 2002), (Rudkevich, 2003), (Correia, et al., 2003), (Li & Shahidehpour, 2005), (Liu, et al., 2006), (Bompard, et al., 2006), (Yuan, et al., 2007), (Holmberg, 2008), (Hasan, et al., 2008), (Hasan & Galiana, 2008), (Gao & Sheblé, 2010), (Bompard, et al., 2010), (Sahraei-Ardakani & Blumsack, 2012) but seldom in block form (Von der Fehr & Harbord, 1993) which is closer to real market condition; besides, it is limited to a few participants. On the other hand, to consider bigger systems and with asymmetric generation companies (Gencos), many approaches have used linear SFE (Baldick, et al., 2004). Recently, a method that allows many asymmetric Gencos with multiple blocks (Hasan, et al., 2008) has been proposed, expressing the problem as a mixed integer linear program (MILP). However, computations times are still high in large systems and it is necessary the linearization of system equations for this kind of market. CCP, which is the proposed solution method in this paper for this kind of market, is a programming paradigm that reduces the search space of a problem using its constraints and makes a controlled search using distribution strategies; then, it is possible to find the market outcomes at low computation times. CCP allows also a much more natural modeling and the linearization of system equations for this kind of market is not necessary. In this way, the proposed solution method makes a contribution to the electricity market modeling problem with several Gencos and multiple blocks each. This article describes the methodology followed to implement this electricity market model using CCP, presenting an example of its application.
This article is organized as follows: in section 2, it offers a general description of what a constraint satisfaction problem is and then, how it is solved through constraint programming. Section 3 presents the methodology for implementing an electricity market model using constraint programming, showing a particular application case. Finally, some conclusions are presented in Section 4.
2. Solving constraint satisfaction problem (CSP) with constraint programming
Constraint satisfaction problems exist when a finite set of variables, each with an associate domain and with a set of constraints on subsets of these variables, are defined. This problem can be represented by (X; D; C), where X is a set of n variables in the problem, so that X:= {X1,..., Xn}.D are associated domains to each of the n variables (D1,...Dn); these domains add domain constraints to the problem in which xi ∈Di, that is, values that can be assigned to xi remain restricted to the values that compose its associated domain Di . The cardinality of each domain is |Di| and a variable x ∈ X is fixed if |D(x)|=1.
Additionally, there is a set of constraints C, each over a subset of X, where values (x, c) are the set of all possible values that x may have given that c is met. Let Xibe a set of k variables, a subset of X (that is, Xi ⊆X), over which constraint ci is applied and having Xi: = {xi1,...,xik}, constraint ci will be a subset of Di1...Dik. Besides, if k = 1, then the constraint applies over only one variable and it will be a unary constraint; if k = 2, two variables will be involved and it will be a binary constraint, and, finally, if the constraint involves three or more variables (k ≥ 3), it will be a n-ary constraint. The solution of a CSP consists of a sequence of values for all its variables for which all of the problem's constraints are met. Considering a CSP (X; D; C), where X := {x1,...,xn} and its associated domains are D1,..., Dn, with xi ∈ Di, and bearing in mind that {di ∈ Di} is a value assigned to variable xi, an n-tuple (d1,...,dn) ∈ D1x...xDn is a solution to (X; D; C) if it satisfies each constraint c ∈ C. To determine if this n-tuple satisfies a constraint ci ∈ C over the set of variables X: = {xi1,...,xik}, where Xi ⊆ X, we must verify if (di1,...,dik) ∈ ci. A CSP is consistent if it has a solution; on the contrary, it is inconsistent.
2.1 Constraint programming
Constraint programming combines traditional search techniques with constraint propagation algorithms for reducing the search space. From the latter, the original problem is transformed into one or more equivalent CSPs, removing values included in the domains of variables that cannot be part of a solution. That is, first a search space pruning is made. This allows, with the proposed method in this paper using CCP, to find a result in a more efficient way than the traditional methods.
The constraint programming paradigm works under the propagation and search approach, which, according to (Van Roy & Haridi, 2004), is based on three main ideas:
-Maintaining partial information
-Using local deduction
-Carrying out controlled search
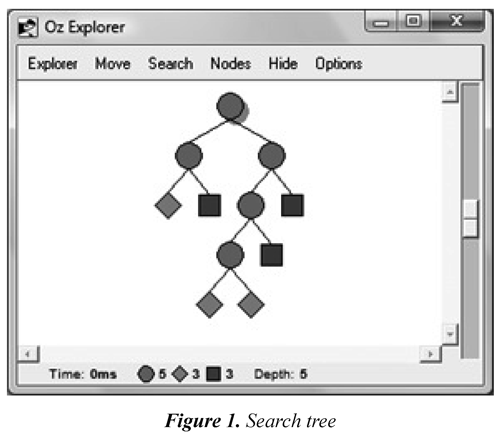
The processes are repeated with each sub-problem created until finding a successful solution or a failed space, in whose case at least one variable exists without values in its domain that comply with the problem's constraints. In the process, a search tree is obtained [Figure 1].
In Figure 1, each circle corresponds to an undefined space and can be the root node or an inner node; the rest are leaf nodes in which have been determined a failed space (square) or a solved space (diamond). More information on concurrent constraint programming and its application can be found in (Van Roy & Haridi, 2004),(Apt, 2003), (Schulte & Smolka, 2000), (Barber & Salido, 2008).
3. Implementation methodology using CCP
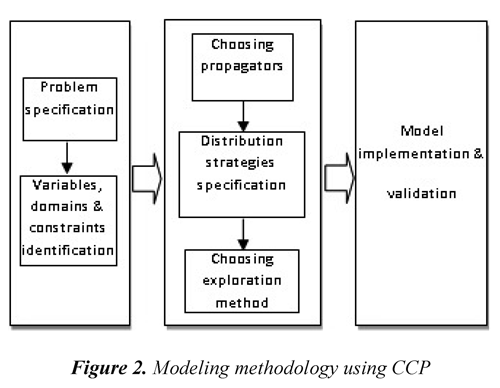
In general terms, to solve a CSP we must: (a) model the problem and (b) find its solution. Figure 2 presents the proposed methodology in this paper to model agent´s strategic behavior within a competitive electricity market.
The first stage in this methodology includes the specification and representation of the problem that, along with the selection of propagators in the second stage, constitute the problem modeling. The other two parts in the second stage establish how the search for the solution will be conducted. Finally, the problem can be implemented in a specific programming language.
3.1 Specification and representation of the problem
The first step to be done is to specify and describe, in detail, the problem to be solved, including all the conditions that must be met, the types of variables of the problem, its characteristics, and what it needs to be determined. From the specification we can identify what the variables are, their domains, and the problem´s constraints.
Specification of the problem
To show the methodology used, we consider the problem of finding the possible equilibriums of a centralized electricity market and dispatched by order of merit. This market has N generating agents that can present their postures or bids to sell energy to a central operator through step functions comprised of NB energy blocks. Block j (j = 1, 2,...,NB) of generator i (i =1, 2,...,N) has a marginal cost (MCij) equal to aij and each of the N generating agents present a function comprised of a set X: = {xi1,...,x}, organized in ii NB ascending manner, and the capacity limits of each of its blocks, Pijmin ≥ Pij ≥ Pijmax. The problem's generating agents are strategic players that can offer a different value of their marginal cost to obtain a greater benefit by trying to manipulate the market´s clearance price (λ) or system's marginal price; additionally, it is considered that they are rational players, hence, xij ≥ aij, ∀ij. However, market rules impose a maximum offer price that permits controlling market power these agents can exert; this price is denominated price ceiling or price cap, then, xij ≤ price_ceiling ∀ij. For their part, market operator seek to cover the system's demand, D, with the lowest cost possible from bids presented from generating agents, considering the following restricted optimization function:
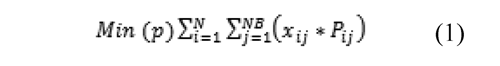
Subject to:
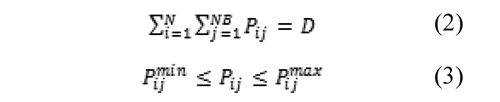
Market equilibria expected as a result will be comprised of the offer prices from each of the N agents that led to that equilibrium, the generation programming determined to minimize system costs, and the clearance price; that is, sets Xi =: } ∀i, Pi =: {pi1,...,pi,NB} ∀i, and the {xi1,...,xi NB market's marginal price (λ) that fulfill the condition that each generator obtains a greater benefit than offering at cost and minimizing system costs is accomplished for the bids presented.
Representation of the problem
The problem described can be represented through the following conditions:
Karush-Kuhn-Tucker conditions (Castillo, et al., 2002) in Eq. (4) - (11), that permit solving the constrained optimization problem presented in Eq. (1) - (3), where λ and µ are the Kuhn-Tucker multipliers. Conditions in Eq. (12) - (14) are also known functions for these types of markets and can be obtained from the problem specification. Condition in Eq. (15) is a known characteristic in these types of markets, which permits eliminating alternatives that will not lead to a solution. Finally, conditions in Eq. (17) - (19) were included for this particular model.
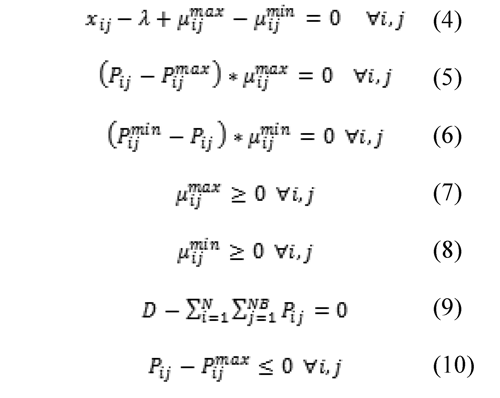

Now, it is necessary to identify the variables, their domains, and the problem's constraints.
Variables and their associated domains
As a result, per equilibrium we expect to obtain the price bids presented by the generators leading to that equilibrium and the power dispatched by the central operator in each case. The domains can be obtained from the problem's specification.
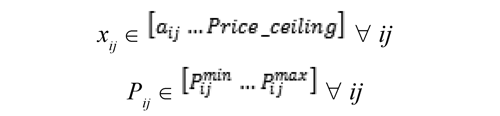
Variable parameters
Other parameters of interest exist like: system's marginal price (λ) and benefit of each generator (Beni); however, both are determined when variables xij and Pij are defined.
3.2 Selection of propagators
To have the complete representation of the CSP as {X; D; C}, where X is the set of n variables in the problem, X: = {x1,...,xn}; D are the domains associated to each of the n variables (D1,...,Dn), and C is a set of constraints, each over a subset of X; it is necessary to select the propagators that will be used to implement the problem's constraints. With the propagators we can, as the name indicates, "propagate" or disseminate information of constraints among the variables involved, reducing the search space of a CSP and transforming it into one or more equivalent CSPs, in which local consistency is accomplished, conserving, in the domains of variables, only those values that can be included in a solution. Considering the search process as a tree, through constraint programming the tree is pruned prior to initiating a search.
The constraints the problem must fulfill correspond to conditions in Eq. (4) - (19) presented in the previous point; to implement them, the following propagators were selected: constraints in Eq. (4) - (9); the last two equations in KKT conditions are not necessaries because they are already considered within the ranges of variables Pij ∀ij. Constraints in Eq. (16) - (19) were also selected as propagators.
The selection criterion in this case was simply based on that the representation of the problem were as natural as possible. However, from the computational point of view, it is possible that other propagators exist that permit implementing these constraints, further reducing the domains of the variables and, thereby, having a more efficient search.
3.3 Distribution strategies
Upon completely defining the representation of the CSP {X; D; C}, it is necessary to determine the strategy that will be used to go over (explore) the search tree and find the solution to the problem. When propagators can no further reduce variable domains, it is said that the space becomes stable. At this point, the space can be failed, solved, or still undetermined; in the first two cases no additional process is needed, given that a response is available from the program - whether an inconsistency among constraints (failed space) or each of the variables with a possible unique value (solved) -.
In the third case, that is, when the space is still not completely determined, it is necessary to conduct a search. This is done by dividing the problem into two or more sub-problems, each of which delivers a new constraint; thus, permitting the return to the propagation process for further reduction of the solution space. Obtaining these sub-problems is accomplished by using "distribution strategies".
To accomplish a distribution of the space, first select one of the still undefined variables, for example x, then select one of the possible values of this variable, for example n; thus, two new constraints x = n and x ≠ n will be available, which together include all the possible solutions. With these two new constraints or propagators, two new problems are created where it is possible to again undergo propagation.
Determination of the new constraint then includes two processes: the first consists of selecting one of the still undetermined variables and the other in distributing over this variable, selecting one of its possible values. The criteria that permit this determination form the distribution strategy, and the search efficiency also depends on this criteria.
In programming systems based on languages that support constraint programming, incorporated distribution strategies exist that can be used in any problem. However, depending on the type of problem, it may be possible that these strategies will not be sufficient to accomplish an exploration that permits reaching a solution; hence, these programming systems also permit including distributors designed by the user, using available standard distribution options or others also designed by the user. In this case, knowledge of the problem may be used to improve search efficiency.
The methodology that must be considered to design the distributor is:
-Variables for distribution
-Filtering
-Selection criterion
-Distribution criterion
-Determination of new constraints
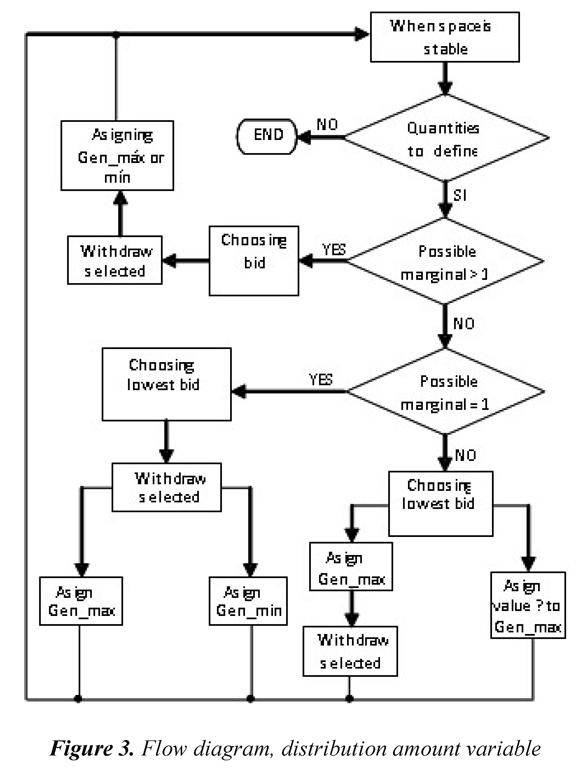
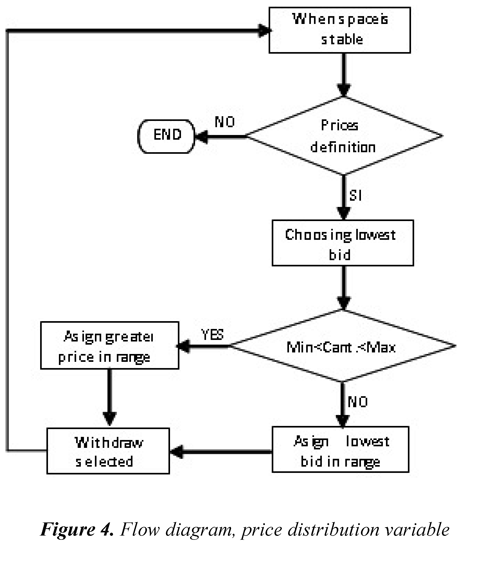
By only using the distribution strategies available in the programming system, it was not possible to reach convergence; hence, for the problem considered it was necessary to design two distribution strategies: one for the amount of generation dispatched and another for the offer price by block. Figure 3 and Figure 4 present the flow diagrams that permit a general view of the strategies designed for the amount and price variables, respectively.
3.4 Selection of exploration metho
In the search or exploration method in this programming paradigm it may be indicated if it is sufficient with one, if all are required, or if we should seek the best of all possible solutions, according to a specific criterion. Hence, different outcomes may be obtained depending on the case we wish to analyze.
The case considered in this article looks to determine all the possible market outcomes in which all the generators obtain greater benefit than offering at cost. To accomplish this, it is first considered that all the generators are pricemakers; we include as an additional input the benefit of offering at cost and the condition that all benefits reached must be greater than such; finally, it is indicated to look for all the possible outcomes.
3.5 Validation and implementation
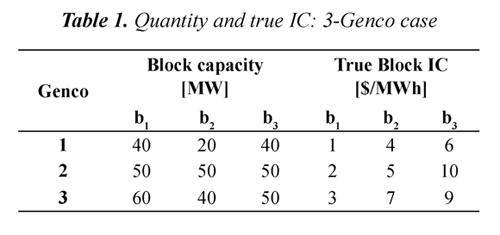
In order to show the implementation of the proposed methodology, results obtained with 3 generation companies (Gencos) with 3 blocks each will be presented. However, we test also with 30 and 60 generation companies. In all cases, the expected results were obtained and were reached at low computing time.In the considered case, there are 3 generation companies (Gencos), each of them owns one generation unit and bids 3 blocks. The data for these blocks from the generators, quantity and incremental cost (IC), are taken from reference (Hasan, et al., 2008) and are included in Table 1. The demand to be met in this case is 145 MW.
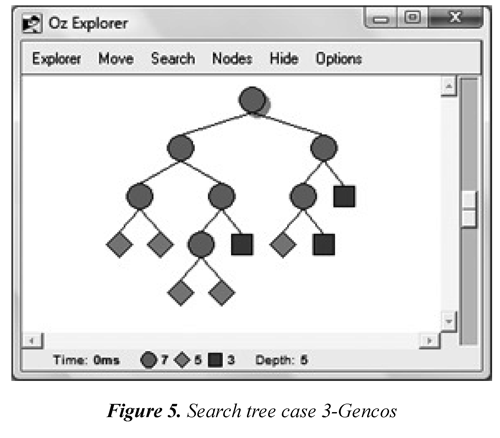
With the set of propagators and distribution strategies specified before, it was possible to implement the reference market using CCP. Figure 5 presents the search tree obtained for this case by using constraint programming when all players are strategic. This tree shows all possible market outcomes, among them, all Nash equilibria. In this figure, circles correspond to the nodes where there is a problem division, i.e., when there are still some variables to define; the squares show a fail state, and diamonds show the found solutions.
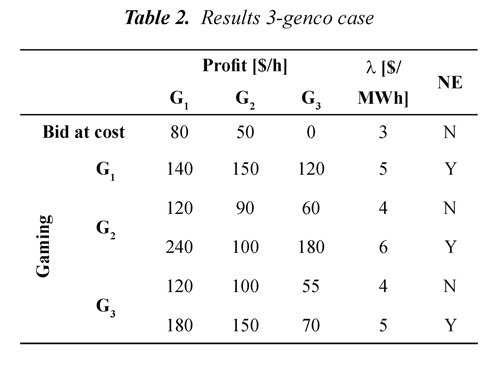
In Table 2, the obtained results when all generators are strategic players are shown. The first row in this table corresponds to all generators bidding at true marginal cost. This table include identification of Genco gaming, profit obtained for each one, and system marginal price (λ); the last column shows whether the solution is a Nash equilibrium. The result when all Gencos bid at cost and the 3 Nash equilibria are the same obtained in reference (Hasan, et al., 2008). The other ones are not Nash equilibria but also meet all constraints of the problem.
4. Conclusions
It has been demonstrated that it is possible to use constraint programming to simulate a competitive electricity market using step functions with multiple blocks to represent bids of competitors, accomplishing adequate computational times that permit considering big systems, which is complicated with traditional methods. This article presents the detail of the methodology used to implement this model.
The methodology posed sought for the implementation of the model to be as natural as possible; however, it is recognized that from the computational point of view there may be considerations like, for example, the selection of propagators, which lead to a much smaller search tree, permitting further increase of efficiency in the search for a solution.
It is important to highlight that although the description of the methodology in this article is accompanied by an example of application for a particular market model, it is possible to include modifications to the model and maintain the methodology posed.
As presented in the methodology, it is necessary to define or design the distribution strategies to conduct a search when the computing space becomes stable. This article presents the diagrams of the two strategies designed for this particular case; however, it is possible to design other strategies for either this problem or for another problem or model considered. In order to design distribution strategies, it is only necessary to follow the general methodology presented and guarantee that with the criteria considered solutions are not lost.
The proposed solution method makes a contribution to the electricity market modeling problem with several Gencos and multiple blocks. From this, it finds the market outcomes at low computation times, allowing a much more natural modeling and the linearization of the equations system it is not necessary.
Until now, the target was to demonstrate that it was possible to use CCP to simulate a competitive electricity market with SFE and leaving a modeling methodology using this programming paradigm. For this purpose, systems with 3, 30 and 60 generation companies were used. In all cases, the expected results were obtained and reached at low computing time. In this first stage, the system was single node; it is recognized that for analysis purposes it is necessary to include the network, which is within the steps to follow.
5. References
Anderson, E., & Philpott, A. (2002). Using supply functions for offering generation into an electricity market. Operatio ns Research , 50 (3), 477-489. [ Links ]
Apt, K. R. (2003). Principles of Constraint Programming . Cambridge: Cambridge University Press. [ Links ]
Baldick, R., Grant, R., & Kahn, E. (2004). Theory and application of linear supply function equilibrium in electricity markets. Journal of regulatory economics , 25 (2), 143-167. [ Links ]
Barber, F. & Salido, M. A. (2008). Problemas de Satisfacción de Restricciones (CSP). In, J. T. Palma Méndez & R. L. Marín-Morales (Comp.). Inteligencia Artificial: Técnicas, métodos y aplicaciones (pp. 385-432). Madrid, España: McGraw-Hill. [ Links ]
Berry, C., Hobbs, B., Meroney, W., O'Neill, R., & Stewart, W. (1999). Understanding how market power can arise in network competition: a game theoretic approach. Utilities Policy , 8 (3), 139-158. [ Links ]
Bompard, E., Lu, W., & Napoli, R. (2006). Network constraint impacts on the competitive electricity markets under supply-side strategic bidding. IEEE Transactions on Power Systems , 21 (1), 160-170. [ Links ]
Bompard, E., Lu, W., Napoli, R., & Jiang, X. (2010). A supply function model for representing the strategic bidding of the producers in constrained electricity markets. International Journal of Electrical Power & Energy Systems , 32 (6), 678-687. [ Links ]
Castillo, E., Conejo, A., Pedregal, P., García, R., & Alguacil, N. (2002). Formulación y resolución de modelos de programación matemática en Ingeniería y Ciencia . Cuenca, España: Universidad de Castilla-La Mancha. [ Links ]
Correia, P., Overbye, T., & Hiskens, I. (2003). Searching for noncooperative equilibria in centralized electricity markets. IEEE Transactions on Power Systems , 18 (4), 1417-1424. [ Links ]
Gao, F., & Sheblé, G. (2010). Electricity market equilibrium model with resource constraint and transmission congestion. Electric Power Systems Research , 80 (1), 9-18. [ Links ]
Green, R., & Newbery, D. (1992). Competition in the British electricity spot market. The Journal of Political Economy , 100 (5), 929-953. [ Links ]
Hasan, E., & Galiana, F. (2008). Electricity markets cleared by merit order - Part II: strategic offers and market power. IEEE Transactions on Power Systems , 23 (2), 372-379. [ Links ]
Hasan, E., Galiana, F., & Conejo, A. (2008). Electricity markets cleared by merit order - Part I: Finding the market outcomes supported by pure strategy Nash equilibria. IEEE Transactions on Power System , 23 (2), 361-371. [ Links ]
Holmberg, P. (2008). Unique supply function equilibrium with capacity constraints. Energy Economics , 30 (1), 148-172. [ Links ]
Li, T., & Shahidehpour, M. (2005). Strategic bidding of transmission-constrained GENCOs with incomplete information. IEEE Transactions on Power Systems , 20 (1), 437-447. [ Links ]
Liu, Y., Ni, Y., & Wu, F. (2006). Impacts of suppliers´learning behaviour on market equilibrium under repeated linear supplyfunction bidding. IEE Proceedings of Generation, Transmission and Distribution , 153 (1), 44-50. [ Links ]
Londoño, S. (2012). Paradigma de programación por restricciones aplicado al modelamiento de mercados de electricidad . Tesis Doctoral, Escuela de Ingeniería Eléctrica y Electrónica, Universidad del Valle, Cali, Colombia. [ Links ]
Rudkevich, A. (2003). Supply function equilibrium: Theory and applications. Proceedings of the 36th Hawaii International Conference on System Sciences . Honolulu, USA, Jan. 6-9. IEEE. [ Links ]
Sahraei-Ardakani, M., & Blumsack, S. (2012). Market equilibrium for dispatchable transmission using FACT devices. In IEEE Power and Energy Society General Meeting (PES GM) . San Diego (CA), July 22-26. IEEE. [ Links ]
Schulte, C., & Smolka, G. (2000/02/04). Finite domain constraint programming in Oz: A tutorial . Berlín, Germany: German Research Center for Artificial Intelligence, Swedish Institute of Computer Science (SICS). [ Links ]
Van-Roy, P., & Haridi, S. (2004). Concepts, Techniques, and Models of Computer Programming . Cambridge (MA), London, UK: MIT Press. [ Links ]
Von der Fehr, N.-H. M., & Harbord, D. (1993). Spot market competition in the UK electricity industry. The Economic Journal , 103 (418), 531-546. [ Links ]
Yuan, Z., Liu, D., & Jiang, C. (2007). Analysis of equilibrium about bidding strategy of suppliers with future contracts. Energy Conversion and Management , 48 (3), 1016-1020. [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.