Modeling and specification of distributed timed systems

Modelamiento y especificación de sistemas distribuidos y temporizados

James J. Ortiz
Computer Science Faculty, University of Namur, Namur, Belgium
Escuela de Ingeniería de Sistemas y computación, Universidad del Valle, Cali, Colombia
E-mail: jor@info.fundp.ac.be

Eje temático: Systems engineering / Ingeniería de sistemas
Recibido: 22 de abril de 2013
Aceptado: 10 de Septiembre de 2013

Abstract

Increasing complexity in distributed and real-time systems makes them very hard to model and specify correctly. Different formal methods are useful for the process of modeling and specification of these kinds of systems. Timed Automata (TA) and Distributed Timed Automata (DTA) are the dominant models of distributed and realtime systems. Unfortunately, their language inclusion and complementation are undecidable. In this paper, we will present logics and automata (Distributed Event Clock Automata (DECA), Memory Event Clock Automata (RMECA), Distributed Event Clock Temporal Logic (DECTL), Memory Event Clock Temporal Logic (RMECTL) fully decidable and they were designed to modeling, specifying and studying the behavior and in particular verifying the correct operation of distributed and real-time systems.

Keywords: Timed Automata, Formal Methods, Temporal Logic, Distributed Timed Systems.

Resumen

El aumento en la complejidad de los sistemas distribuidos y temporizados hace que ellos sean muy difícil de modelar y especificar correctamente. Diferentes métodos formales son útiles para el proceso de modelado y especificación de estos tipos de sistemas. Los Autómatas Temporizados (AT) y los Autómatas Temporizados Distribuidos (ATD) son los modelos formales más utilizados para modelar sistemas de tiempo real y distribuidos. Lamentablemente los algoritmos existentes para calcular la inclusión y complementación de sus lenguajes son indecidible. En este artículo, presentaremos las lógicas (Lógica Temporalizada de Eventos Distribuidos, Lógica Temporizados de Memorización de Eventos) y los autómatas (Autómatas de Eventos Distribuidos, Autómatas de Memorización de Eventos), totalmente decidibles. Estos métodos fueron diseñados para modelar, especificar, estudiar el comportamiento y en especial verificar el buen funcionamiento de los sistemas de tiempo real y distribuidos.

Palabras Clave: Automatas Temporizados, Métodos Formales, Lógica Temporizados, Sistemas Distribuidos.

1. Introduction

The traditional formalisms for reasoning about Real-Time Systems (RTS), are not always adequate for reasoning about Distributed Timed Systems (DTS). The most successful techniques for modeling RTS are Timed Automat (TA) Alur & Dill (1994), Event Clock Automata (ECA) Alur & Henzinger (1998) and Recursive Event Clock Automata (RECA) Henzinger et al. (1998).A TA is a finite automaton augmented with real valued clocks. The model of TA assumes perfect clocks: all clocks have infinite precision and are perfectly synchronized. This causes TA to have an undecidable language inclusion problem Alur & Dill (1994). These negative results for TA spurred a quest for study of expressive but still fully decidable formalisms. To restore decidability, Alur & Henzinger (1998) proposed to restrict the behavior of clocks. Therefore, an Event Clock (EC) Xp is reset when a given atomic proposition N occurs. The event clock values are deterministic and thus ECA are determinizable, making language inclusion decidable. However, the expressiveness of ECA is rather weak. Furthermore, the temporal logic with Event Clocks Raskin & Schobbens (1997) violates the substitution principle: Any proposition should be replaceable by a formula. Hence Henzinger et al. (1998) introduced the notion of "Recursive" Event. In a recursive event model (RECA), the reset of a clock is decided by a lower-level automaton (or formula). This automaton cannot read the clock that is resetting. Clock resets are thus still deterministic, but the concept of "event" is now much more expressive. Also, Henzinger et al. (1998) introduced the temporal logic of recursive event clocks (EventClockTL). In Ortiz et al. (2010), Ortiz et al. (2011), we removed the above limitation of event clocks, inspired by Bengtsson et al. (1998), Krishnan (1999), Akshay et al. (2008), Alur et al. (1994), we introduced : (i) Distributed Event Clocks (DEC) for DRTS: A DEC xq (or y q) records the time since the last (resp. next) reset, measured in the local time of process q and the DEC can advance totally independently if they are in different processes.

However Puri (1998), Wulf et al. (2004) studied the opposite case, where the difference between clocks (drift) is infinitesimally small. (ii) Memory Event Clocks (MEC) for RTS : A MEC x is not really reset, instead, a new clock is created, while the old one is still accessible by indexing. In Ortiz et al. (2010), Ortiz et al. (2011), we proposed formal methods for the modeling and specification of RTS and DRTS based on RECAwith such distributed (a.k.a independent) and memory clocks, yielding the DECA and RMECA. We shown that DECA and RMECA are determinizable, thus closed under complementation; also that their respective language inclusion problems are decidable (more exactly, PSPACE-complete). Additionally, in Ortiz et al. (2010), Ortiz et al. (2011), we proposed extensions of the existing EventClockTL with distributed clocks and memory clocks to allow the specification of distributed and timed properties. RMECTL are PSPACE-complete for the satisfiability and validity problem if the indices of the clocks are encoded in unary and EXPSPACE-complete for the binary case. DECTL are PSPACE-complete for the satisfiability and validity problem. DECA (DECTL) and RMECA (RMECTL) can been used to specify and model systems such as the Controller Area Network (CAN) Monot et al. (2011), WirelessHART Networks De Biasi et al. (2008), and the ARINC-659 protocol Gwaltney & Briscoe (2006). This paper deals with formal methods that can be used to automate the analysis of complex RTS and DRTS and in particular the analysis of the correctness of the system's behavior. Our contribution is to show the applicability of DECA, RMECA, RMECTL and DECTL over a RTS and DRTS.

Structure of the paper. The rest of the paper is organized as follows. In sections 2, we recall preliminary notions. In section 3, we recall the background about of TA, Timed Temporal Logic (TTL) and their several variants. In section 4, we present one example of distributed real-time system modeled on DECA and DECTL.

2. Preliminaries

We first briefly recall the various models of timethat are used in the literature Alur & Henzinger (1994). We present our results in the interval semantics and recall clocks and their constraints.

2.1 Models of time

Models of time can be linear, considering a single future, or branching, considering several alternative futures. We only consider linear time in this paper. Classical automata and Linear Temporal Logic (LTL) also use a linear discrete model of time. The point semantics adds a time stamp to each event of this discrete model. Our goal here is to model real-time reactive systems, and thus we will use the real numbers as our model of time. This avoid a premature commitment to a discretization of time: even if computer systems are often discrete, their discretization grain (e.g. clock speed) should not appear at requirements level.

Let P be a finite set of propositional symbols. A letter is an element of a finite set Σ. In this paper, we choose to define a letter as propositional valuation over P , so we pose Σ = 2P. Let be ℕ the set of natural numbers, ℝ denote the set of real numbers, ℝ≥0 the set of non-negative real numbers. We use the interval semantics. We denote by /_ℝ≥0 the set of real intervals whose bounds are in ℝ≥0. An interval / ∈ / ℝ≥0 is a convex subset of ℝ≥0. Two intervals / and / are said to be adjacent when they are disjoint: / ∩ /' ∅ / ∪ /' and is an interval. An (alternating) interval sequence is a sequence / = /0 /1 /2 ... i.e., of non-empty intervals of ℝ≥0 where: (i) /0={0}; (ii) singular and open intervals alternate; (iii) succesive intervals / j and / j +1 are adjacent for all j ≥ 0 , (iv) if infinite, the sequence of intervals is progressive, i.e., for every t ∈ ℝ≥0, there exists ∈ such that t ∈/ j . An interval state sequence ρ can equivalently be seen as a sequence of elements in 2P x / ℝ≥0. It can also be seen as a signal i.e. a function from ℝ≥0 to states: Let ρ= (σ, /) be an interval state sequence and given t ∈ ℝ≥0, let i ∈ be the interval such that t ∈ / j . We define ρ( t ) as the state σ j . Below, our automata will consider two ISS that define the same signal as equivalent, even if the intervals might be split differently. Given two intervals /1, /2, we define the interval between /1 and /2 by Betwl(/1, /2)={x|/1<x</2}. Given a set S and an interval /, we define S Begins During / by ∃ t ∈ ( S ∩ /), and t ∈ S such that t< /. Symmetrically, we define S Ends During / iff ∃ t , t ∈ ( S ∩ /) and t ∈ S such that t> /.

2.2 Clocks

A clock is a variable that increases with time. Thus, the value of a clock is the time elapsed since its last reset. When we use continuous time, there is not always a "last" reset, e.g. when the reset holds in an open interval. For this case, we will use non-standard clock values of the form υ+, intuitively meaning that the clock was reset just υ units before. The set of non-standard real numbers, noted ℝ ≥0, is the set of {υ, υ+ υ ∈ ℝ≥0} ordered by < ns as following: υ1 < ns υ₂ + iff υ1 ≤ υ2. The addition is commutative, and υ1+υ2= (υ1+υ2)+. ℝ⊥ is ℝ≥0 plus a special value ⊥ for uninitialized clocks. ⊥ is not comparable to other values, and is absorbing for addition. Let X be a finite set of clock names. A clock valuation over X is a mapping υ: X→ ℝ⊥. For a valuation υ and a time value t ∈ ℝ≥0, let υ+ t denote the valuation such that (υ+ t )= υ( x )+ t , for each clock x ∈ X . The set of constraints over X, denoted Φ( X ), is defined by the following grammar where φ ranges over Φ( X ), x ∈ X , c ∈ , and ∼ :{<, ≤, =, ≥, >}:

φ= true |x ∼ c| φ 1 ∧ φ 2

We write ?|=f when the valuation ? satisfies the constraint f. When X has the value ? , we evaluate x~c to false.

2.3 Timed automata

De?nition 1. A Timed Automaton is a tuple A= (S, X, S, s₀, →_ta, Inv, ? , F) such that: (i) S, is a finite alphabet. (ii) X, is a finite set of positive real variables called clocks. (iii) S, is a finite set of locations. (iv) s₀ ∈ S, is the initial location. (v) →_ta ⊆ S x F(X) x 2^x x S, is a finite set of transitions. (vi) Inv:S →F(X) is the function of invariant. (vii) γ:(S?→_ta)→ S, is the fuction than labelling locations and transitions. (viii) F, is an acceptance condition. For instance, for finite acceptance, we have F⊆S, a set of final locations. We also use Büchi (where F⊆S) or parity conditions (where F: S→ N). TA are neither determinizable nor complementable. Their emptiness problem can be solved using the region construction, but their inclusion problem is undecidable Alur & Dill (1994).

2.4 Recursive event clock automata

Recursive Event Clock Automata (RECA) extend Event Clock Automata (ECA). Recursive refers to the fact that the resets of an event clock x_B are controlled by a lower level automaton B: when B passes in a monitored location, it resets x_B. We present here a version of RECA for continuous time, where transitions have all properties of locations.

Definition 2. A RECA A of level / ∈ ℕ is a tuple A=(S, C, S, s0 , →_reca , M, γ, δ, F ) such that: (i) S, is a finite alphabet. (ii) C, is a finite set of clocks, of the form x_B or y_B, with B a lower-level RECA. (iii) S, is a finite set of locations. (iv) s₀ ∈ S, is the initial location. (v) →_reca ⊆ S x S, are the transitions. (vi) M ⊆(S∪ →_reca), is the set of monitored locations or transitions: when the automaton visit such a location, it resets the associated clock. (vii) γ :(S?→_reca)→ S, is a labelling function which labels each location or transition with a symbol. (viii) d:(Sδ→_reca)→F(C), gives the guard or invariant clock constraints. (ix) F, is an acceptance condition, e.g. a set of final locations, or of Büchi accepting locations. Throughout the paper, we assume this uniform naming convention. RECA can be determinized and thus complemented: They are fully decidable Henzinger et al (1998).

2.5 Recursive memory event clocks automata

RMECA increase the expressive power of RECA. In particular, an RMECA of level 0 has no clock, it is a plain finite state automaton. An event-recording clock and an event-predicting clock can be associated with each monitored automaton. The event-recording memory clock x_A^j always records the time that has expired since the i_th last time at which the automaton A could pass through a monitored location, and the event-predicting clock y_A^j always records the amount of time that will expire until the i_th next time at which the automaton A could pass through a monitored location.

Definition 3. A RMECA is a tuple A=(P, S , s0, →_rmeca, C, δ, d, M, F) such that: (i) P, is a set finite of propositional symbols. (ii) S, is a finite set of locations and s0 ⊆ S is the set of starting locations. (iii) →_rmeca ⊆ S x S are the transitions. (iv) A finite set of atomic constraints C, containing clocks x_B j or yB j , with B a lowerlevel RMECA. (v) γ: S→2^Lim(P∪C), is a function which labels each location s⊆S with the set of limits of propositions and constraints that are true in that location. (vi) M ⊆ S, is the set of monitored locations: when the automaton visits such a location, it resets the associated clock (vii) F ⊆ S is a set of Büchi accepting locations.

The clock valuation function over a lowerlevel RMECA at A and time t at ρ, is noted υ^ρ_t: CA→ + ℝ⁺⊥. It assigns a non-standard positive real, or undefined, to each clock variable. The resets are done when A goes in a monitored location. The definition for recording clocks is symmetric.

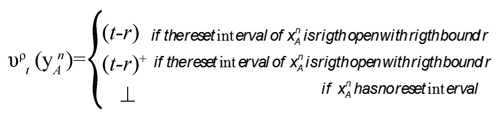
Symmetrically,

If a clock of A is reset by a lower-level B, we say that B is a direct subautomaton of A. For the top-most automaton, we do not care about its monitored states.

2.6 Distributed event clocks automata

To restore full decidability, we use event clocks. For expressiveness, we use RECA with independent clocks Akshay et al. (2008). The event clock xA q (or yA q ) denotes records the time since the last (resp. next time that the automaton A could visit a monitored state, measured in the local time of process q.

Definition 4. A DECA is a pair (A,π) where A is a RECA and π: C →Pr oc maps each clock to a process Proc.

For better readability, we write the owner process in the clock name: π(x^q_A)=q. The clock valuation depends on the ISS ρ, on the reference time of evaluation t, and on the rate t. It assigns a non-standard positive real, or undefined, to each clock variable.

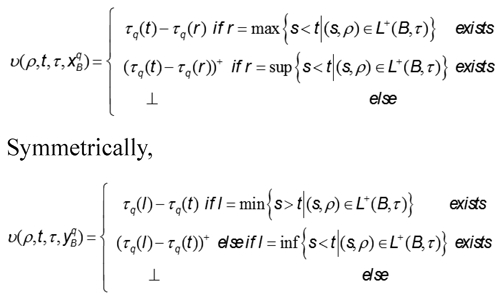
2.7 Recursive memory event clocks temporal logic

RMECTL extends EventClockTL. We generalize its modalities by adding an index k: the recording modality ◄^k_I φ means that the K_th last time that φ was true is in interval t - I, and symmetrically the predicting modality ◄^k_I φ says the next occurrence K_th of φ will occur within I. We count only one occurrence for an interval where φ is continuously true. Such a modality in fact introduces a memory event clock: ◄^k_Iφ means that we reset a memory clock each time φ is true, and we constrain the K_th clock value at the time of evaluation. We denote the temporal logic where k ≤ n by RMECTL_n, for n∈ ℝ. If we allow only index 1, we find back EventClockTL.

Definition 5. The formulas of RMECTL are built from propositional symbols P, boolean connectives, the temporal operators until and since and two symmetric real-time modalities, the recording modality and predicting modality. The formulas φ of RMECTL are defined by the grammar:

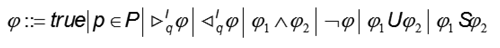
where P is a propositional symbol, / ∈ /  is an interval, and n∈ ℕ⁺. Let φ be a RMECTL formula and let ρ be a signal whose propositional symbols contain all propositions that occur in φ. The semantics of the new modalities are:

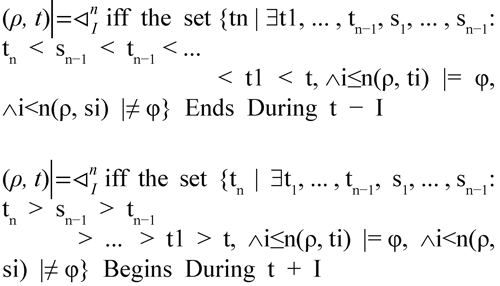
where Begins During and Ends During have been defined in Section 2.1. The intuition is that each ti is a witness of an interval where φ was true, that caused a reset of the clock. They must be distinct intervals, i.e. they must be separated by an interval where φ is false, as witnessed by si. Intuitively, the n-th previous reset is the maximum of the candidates tn, but this maximum might not exist. Hence the indirect definition using Begins During .

2.8 Recursive distributed event clocks temporal logic

DECTL extend the EventClockTL with distributed (independent) clocks. As in subsection 2.6, we assume a set of processes Proc. The clocks of each process will evolve according to its local time by a Rate . DECTL is based on LTL, and adds two local real-time modalities. The recording modality means that was true last time in the interval I according to the local time of q. Symmetrically, the predicting modality qI f says the will occur within I according to the local time of q. If we have only one process, we find back EventClockTL.

De?nition 6. The formulas of DECTL are defined by the grammar:

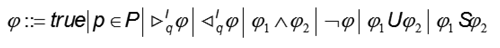
where is a propositional symbol, is an interval and. We can now define how to evaluate the truth value of a DECTL formula along an ISS ρ and a Rate , noted . We omit below.

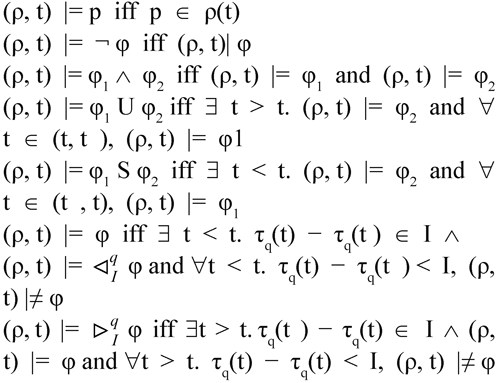
3. Applications of distributed and timed systems

In this section it will be illustrated several examples of distributed and real-time systems which we can model on DECA (RMECTL) and specify on RMECTL (DECTL).

3.1 Complex event detection

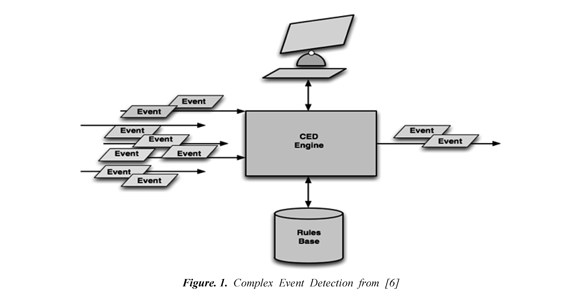
In this subsection we introduce the Complex Event Detection CED Wang et al. (2006) to show how this RTS can be modeled as a RMECA and also we consider the properties of the RTS in RMECTL. Figure 1 shows a CED as a processing concept in order to identify significant events in a cloud of events. CED employs techniques such as complex patterns detection of multiple events: correlation, abstraction, hierarchies between events and relationships between events such as causality, membership, timing and event-driven process. The function of the CED is to discover the information in the events that passing through all layers of an organization and then to analyze its impact at the macro level as complex event and then decide which plan of action in real time. The CED is a technique that reveals the complex events, by inference and correlation of elementary events. There are many commercial applications of CED as securities trading, fraud detection in credit card and business activity monitoring. Here we shown a simplified version of the CED as a RMECA.

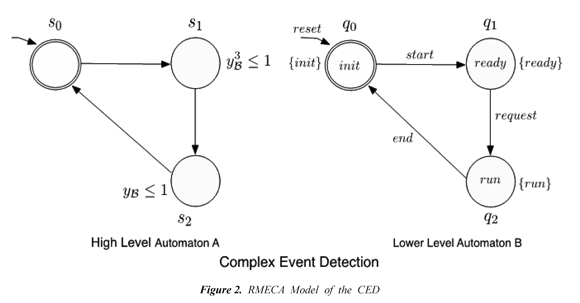
Modeling the CED in RMECA: Figure 2 shows the CED modeled as a RMECA. The high level automaton has the event clock variables and the lower level automaton has the events. The clocks are reset by the initial monitored transition of B. In the location q (lower lever automaton), the automaton receives the event "start". When the automaton receives this event, its control evolves to the monitored location q1 the clock constraint y³_B ≤1 of the high level automaton imposes that the users will send the events"request" 1 time units before crossing the edge to the location q₂. The invariant y³_B ≤1 records the amount of time that will expire until the 1 next time at which the automaton B could pass through a monitored location. The automaton evolves to the monitored location q₂ and the clock constraint y_B ≤1 of the high level automaton and a new clock with value 0 is created. In q₂, the control must wait at least 1 time units and records the amount of time that will expire until the next time at which the automaton B could pass through a monitored location, before crossing the edge to the location q₀.

Properties of CED in RMECTL: The property "asserts that eventually no more that third request per 1 time units will be run and that surely for any attempt to start a request, the request will be run within 1 time units." can be described in RMECTL by the formula:

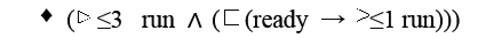
3.3 Communication Protocol

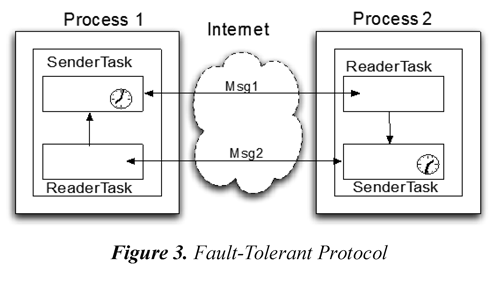
In this subsection we introduce the communication protocol example to show how this DRTS can be modeled as a DECA and also we can consider the properties of the DRTS in DECTL. Let us assume a DRTS consisting of application tasks running under an Operating System while using several processors interconnected via Internet. The crucial problem is to verify both, time properties (e.g. end-to-end response time) and logic properties (e.g. unsafe state avoidance) of the applications incorporating two kinds of shared resources, the processor and the bus. The disadvantage of the traditional models (TA, ECA, RECA, EventClockTL) to specify and verify these systems is that they do not consider the independent clocks of the tasks (e.g. clocks of a task evolve synchronously, but independently of the clocks of the other tasks). The Figure 3 shows the Communication Protocol. The protocol is a simple system consisting of two processes interconnected via Internet. Two Sender and two Reader tasks are running on each process. The clocks on each process are periodically invoked whenever a message must be sent. The clock activates the task SenderTask, which sends a message to Internet. Receiving a message by a process causes an activation of the task SenderTask.

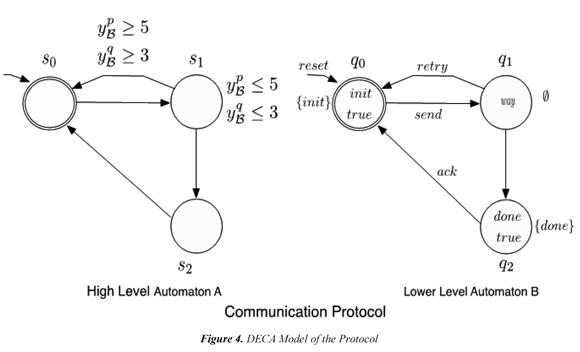
Modeling the Communication Protocol in DECA: Figure 4 shows the communication protocol modeled as a DECA. The high level automaton has the event clock variables and the lower lever automaton has the events. We will call the processes 1 and 2 of the Figure 3 as p and q (Proc = {p, q}, and the set of propositions P = send, retry, ack}) and also the clocks in the processes p and q running to different speeds. The clocks are reset by the initial monitored transition of B. In the location q₀ (lower lever automaton), the process is waiting for the event "send". When the process receives this event, its control evolves to the monitored location q₁ and the clock constraint y_B ^p ≤ 5 of the high level automaton imposes that the message has to be send before 5 time units for the process p, the clock constraint y_B^p ≤ 3 of the high level automaton imposes that the message has to be send before 3 time units for the process q. So this requirement imposes that the message takes less than 5 time units to go "done" for the process p and the message takes less than 3 time units to go "done" for the process q, when they receives the information that a message is sent. In q₁, the control must wait at least 5 time units before crossing the edge to the location q₂ or the control must wait at least 3 time units before crossing the edge to the location q₂. In q₂, the control must wait the "ack" signal before crossing the edge to the location q₃.

Properties of the communication protocol in DECTL: The property "a message is followed by an ack within 5 time units for the process p" can be described in DECTL by the formula:

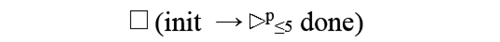
The property "a message is followed by an ack within 3 time units for the process q" can be described in DECTL by the formula:

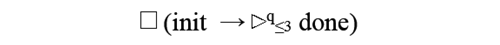
The property "asserts that eventually a message will be done and that surely for any attempt to send a message, the message will be done within 5 time units for the process p." can be described in DECTL by the formula:

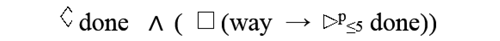
The property "asserts that eventually a message will be done and that surely for any attempt to send a message, the message will be done within 3 time units for the process q." can described in DECTL by the formula:

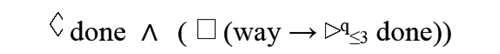
4. Conclusions

We have presented the basis of two framework for analyzing, modeling and specify distributed and real-time systems through of the introduction of independent (or distributed) event clocks, inspired by DECA and the introduction of memory event clocks that are designed to overcome the criticism for being too weak since they only see the time to next event. In contrast to Akshay et al. (2008) and Alur et al. (1994) , we have presented two real-time semantics, and thus we can specify distributed and real-time properties. We have presented DECA and that they are fully decidable, and that their language inclusion problem are PSPACE-complete and EXPSPACE-complete. We presented the logic DECTL and RMECTL to specify distributed real-time properties with distributed observers and allows references to the nth next (nth last) time a formula will be (was) true. The problems of satisfiability, validity and modelchecking of DECTL are PSPACE- complete and RMECTL are EXPSPACE-complete. Finally, we have showed that DECA (DECTL), RMECA (RMECTL) can been used to specify and RTS and DRTS.

5. Acknowledgements

This work was funded by Colciencias (Instituto Colombiano para el Desarrollo de la Ciencia y la Tecnología "Francisco José de Caldas") and to the PReCISE (Research Center in Information Systems Engineering) Université de Namur.

6. References

Akshay, S., Bollig,B., Gastin, P., Mukund, M., & Kumar, K. N. (2008). Distributed Timed Automata with independently evolving clocks. In proceedings of the 19th, International Conference on Concurrency Theory (pp. 19 - 22). Toronto, Canada.         [ Links ]

Alur, R ., & Dill, D.L. (1994). A theory of timed automata. Journal of Theoretical Computer Science , 126 (2), 183 -235.         [ Links ]

Alur, R., Fix, L., Henzinger, T. A. (1994). A determinizable class of timed automata. In proceedings of the conference of Computer Aided Verification (pp. 1-.13). Stanford, California.         [ Links ]

Alur, R., & Henzinger, T. A. (1991). Logics and models of real time: A survey. In REX Workshop (pp. 74-106). The Netherlands.         [ Links ]

Bengtsson, J., Jonsson, B., Lilius, J., & Yi, W. (1998). Partial order reductions for timed systems. In proceedings of the International Conference on Concurrency Theory (pp. 485-500). Nice, France.         [ Links ]

CED protocol. (2009). CED protocol. Recovered 2013/12/15 http://www.thecepblog.com/         [ Links ]

De Biasi, M., Snickars, C., Landernäs, K., & Isaksson, A. (2008). Simulation of process control with wirelesshart networks subject to clock drift. In proceedings of the 32th Annual IEEE International Computer Software and Applications Conference (pp. 1355-1360). Paris, France.         [ Links ]

De Wulf, M., Doyen, L., Markey, N., & Raskin, J-F. (2004). Robustness and implementability of timed automata. In proceedings of the International Conferences on Formal Modeling and Analysis of Timed Systems, Formats (pp. 118-133). Grenoble, France.         [ Links ]

Gwaltney, D. A., & Briscoe, J. M. (2006). Comparison of communication architectures for spacecraft modular avionics systems . Technical report (pp. 36-72). Boston, USA.         [ Links ]

Heitmeyer, C., & Lynch, N., (1994). The generalized railroad crossing: A case study in formal verification of real-time systems . Technical report (pp. 120-131). Cambridge (MA).         [ Links ]

Henzinger, T. A., Raskin, J.-F., & Schobbens, P.-Y. (1998). The regular real-time languages. In The 25th International Colloquium ICALP (pp. 580-591). Aalborg, Denmark.         [ Links ]

Krishnan, P. (1999). Distributed timed automata. Journal of Theoretical Computer Science , 28 (2), 5-21.         [ Links ]

Monot, A., Navet, N., & Bavoux, B. (2011). Impact of clock drifts on CAN frame response time distributions distributions. In 16th IEEE International Conference on Emerging Technologies and Factory Automation (pp. 380-396). Toulouse, France.         [ Links ]

Ortiz, J., Legay, A., & Schobbens, P-Y. (2011). Distributed event clock automata extended abstract. In The 16th International Conference CIAA (pp. 250-263). Blois, France.         [ Links ]

Ortiz, J., Legay, A., & Schobbens. P-Y. (2010). Memory event clocks. In proceedings of the international conferences on Formal Modeling and Anlysis of Timed Systems (pp. 198-212). Klosterneuburg, Austria.         [ Links ]

Puri, A. (1998). Dynamical properties of timed automata. In A. P. Ravn & H. Rischel (Eds.). Formal Techniques in Real-Time and Fault-Tolerant Systems . Lecture Notes in Computer Science (vol. 1486) (pp. 210-227). Berlin: Springer Berlin Heidelberg.         [ Links ]

Raskin, J.-F. & Schobbens, P.-Y. (1997). State clock logic: A decidable real-time logic. In The International Workshop HART (pp. 33-47). Grenoble, France.         [ Links ]

Raskin, J-F. (1999). Logics, Automata and Classical Theories for Deciding Real Time. Ph.D thesis, FUNDP University, Namur, Belgium.         [ Links ]

Wang, F., Liu, S., Liu, P., & Bai, Y. (2006). Bridging physical and virtual worlds: Complex event processing for rfid data streams. In The 10th International Conference on Extending Database Technology (pp. 588-607). Munich, Germany.         [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.