Control predictivo no lineal basado en modelo por modo dual con estabilidad garantizada

Dual mode nonlinear model based predictive control with guaranteed stability

Kelly J. Ramírez
Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia
E-mail: kjramire@gmail.com

Lina M. Gómez
Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia
E-mail: limage@bt.unal.edu.co

Hernán Álvarez
Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia
E-mail: hdalvare@unal.edu.co

Eje temático: Ingeniería eléctrica y electrónica , Ingeniería química / Electrical and electronic engineering , Chemical engineering
Recibido: 8 de noviembre de 2011
Aceptado: 23 de septiembre de 2013

Resumen

En este artículo se propone un Control Predictivo Basado en un Modelo no Lineal (NMPC) pero que opera por modo dual y con estabilidad garantizada. El modo dual se logra usando un controlador PI dentro de la región terminal del NMPC. Para el cálculo de la región terminal (O) y del dominio de atracción se usa la teoría de conjuntos y un algoritmo aleatorizado tipo Montecarlo. En la estrategia de conmutación NMPC al PI se restringen los elementos finales de control suavizando la conmutación. El NMPC por Modo Dual propuesto se implementa en simulación en un Reactor Continuamente Agitado, comparando su desempeño con el de un NMPC multivariable convencional y dos controladores PI. Se concluye que el NMPC por modo dual propuesto es la estrategia de control que además de tener estabilidad garantizada, presenta mejor desempeño.

Palabras Claves: NMPC por modo dual, región terminal, CSTR, controlador PI.

Abstract

This paper proposes a Nonlinear Model based Predictive Control (NMPC), with guaranteed stability using a dual mode Model based Predictive Control approach with a PI controller inside a terminal region. Within the formulation of this control strategy, a terminal region (O) and an attraction domain are calculated using invariant sets theory and a randomized Montecarlo type algorithm. In addition, this proposal is complemented with a commutation strategy to constrain final control elements smoothing controllers commutation. This Dual Mode NMPC multivariable control is implemented by simulation over a Continuous Stirred Reactor Tank and comparing Dual Mode NMPC with a conventional NMPC multivariable and with two PI controllers. Finally, this article concludes that the NMPC for dual mode is the control strategy that in addition to having stability guaranteed, presents a better performance.

Keys Words: CSTR, Dual mode NMPC, PI controller, terminal region.

1. Introduction

Model based Predictive Control was worked for first time in the industry at the end of the XX century with IDCOM (Identification-Command) or MPHC (Model Predictive Heuristic Control), which was proposed in (Richalet, et al., 1978) and (Cutler & Ramaker, 1980). Those strategies needed a dynamic model of the process to predict the effect of the future control action over the output variable. The control actions were determined to minimize the predicted error, restricted to the operational constraints. Those strategies used a dynamic process model to evaluate the response with impulse input signals; it allowed including the restrictions over the input and output variables.

Later, MPC emerges in the academic environment, supported by the adaptable control ideas, which develops strategies to monovariables process, formulated with single input- single output (SISO) models. In those years, Generalized Predictive Control (GPC) is proposed in (Clarke et al., 1987). It use a discrete transfer function CARIMA (Controlled Auto-Regressive Integrated Moving Average) as a model. The discussion about MPC techniques can fill several pages. So the reader is referred to other authors like (Qin & Badwell, 2003).

In most of the MPC reported techniques, the stability is not guaranteed. For that reason, we need a heuristic specific setting for each system even without guaranteed success (Limon, 2002). From the 1980 decade, several MPC formulations have been proposed to overcome the stability problems with MPC schemes that guarantee stability from controller design (Michalska & Mayne, 1993; Alamir & Bornard,1995). There are several academic researches that report MPC designs with guaranteed stability. One of them is dual mode MPC, which is the controller that is studied in this paper (Chen & Allgöwer, 1998). Generally, all the MPC formulations with guaranteed stability use a terminal region which is an invariant of the system. However, there is not a standard methodology to calculate this region. Several authors have resorted to invariant set theory linked to Lyapunov's theory (Limon, 2002; Magni, et al., 2001; Wills, 2003), which formulating stability the region like an ellipse from a level curve of the Lyapunov function. This kind of terminal region is very conservative. Other authors use polyhedral or polytopic representations to terminal region calculation. Although, those regions are bigger than ellipsoidal regions, its calculation has a high computational cost.

Despite of all those effort, nowadays there is not a methodology to calculate the terminal region in an adequate way, with low computational complexity. Then, one of the aims of this work is to use invariant sets and Montecarlo's techniques to calculate the terminal region in a simple way. Other motivation is to propose a nonlinear MPC with stability guaranteed that be simple and useful in industrial environment. For that reason, this work proposes a dual mode MPC with terminal region where a PI controller acts and with a commutation strategy with the purpose of smooth the changes own to dual mode. It is chosen a PI controller for its wide industrial use to looking to increase the chances of implementation of this technique, avoiding change each existing PID controller. Also, it is proposed a methodology to calculate the terminal region of a nonlinear continuous process, based in the invariant set theory and Montecarlo method with randomized algorithms. Finally, the proposed MPC is proved in the continuous stirred tank reactor (CSTR), Benchmark presented in en (Henson & Seborg, 1990).

2. Methodology proposed to design a dual mode MPC (DM-MPC)

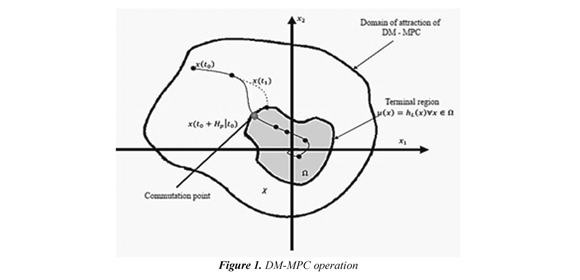
The Dual Mode Model Predictive Control (DM MPC) is a technique that requires the definition of terminal region Ω around of set-point (x_SP). Out of Ω, MPC is responsible to control and to drive the state to the limits of Ω. When the boundary is crossed, the local controller acts with guaranteed stability generated to Ω. In Figure 1, it is showed this operation, where the solid line represents the MPC trajectory that is commutated within of Ω with the linear control law h(x). This function takes the process to a surrounding ϕ, which is sufficiently near of the operation point (ϕ_SP). The region χ, bigger than Ω, corresponds to the domain of attraction of MP.

2.1 Operation of DM-MPC

As it is illustrated in Figure 1, DM-MPC operates with two coupled controllers

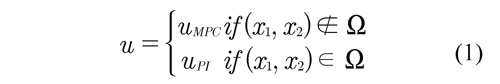
The DM-MPC resolves a typical optimization problem in each sampling time

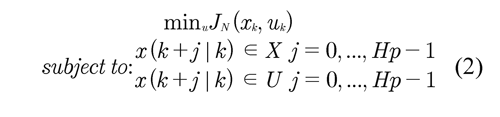
Where the cost-function J_N (x_k,u(k)) is for a two state tow control action process.

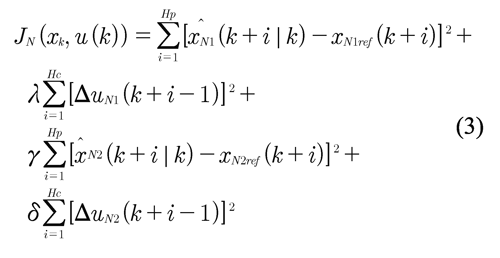
And the subscript N indicates that all states and control actions are normalized in the hypercube [0,1]. The Equations (2) and (3) are typical of a conventional MPC, although here they have a multivariable nature since they are formulated to control two variables. Unlike the MPC, DMMPC has the next restriction in the optimization associated with the invariant region O of the local controller.

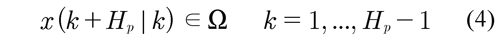
The Equation (4) guarantees that at the end of the prediction horizon Hp, the system is within the terminal region O, where PI controller guarantees stability. The terminal region O of DM-MPC must (Mayne et al., 2000): i) be included in the domain of attraction χ of MPC (Ω ⊆ χ), be closed and with 0 ∈ O; ii) satisfy the control law u = K_Ω (x), u ∈ U, ∀ x ∈ Ω for the local controller; iii) be a positive invariant, guaranteeing the feasibility of the controller in every time instant.

2.2 Methodology to nonlinear DM-MPC

Here it is presented the proposed DM-MPC including the calculation of the terminal region O to the PI linear controller, the computation of the domain of attraction χ of MPC and a strategy of commutation between MPC and PI controllers, for a nonlinear dynamic process, which is modeled as

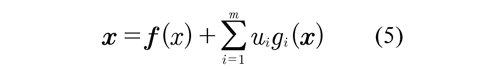
Where x(t)? X is the state of the system, X is the open subset Rⁿ or a differentiable variety M of dimension n, control actions u(t) ? U are measurable and bounded signals in the subset U with dimension R^m, and f,g are real analytic function.

2.1.1 Calculation of the terminal region O

In the terminal region Ω, the local controller (in this case a PI controller) asymptotically stabilizes the system. According with the invariant set theory, Ω groups all stabilized sets in X in π steps to the bounded surrounding Φ_SP around of the setpoint Sp (X,Φ_SP). For each stabilizable set there is a sequence of π admissible control actions that are produced by the local PI controller (Limon, 2002). To calculate S_p (X,Φ_SP) it is made the follow iterative process from π = 1, …, n

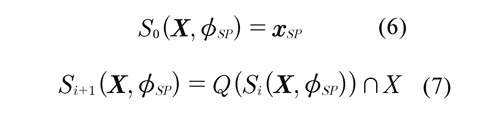
i. Determine the one-step predecessor set Q (Φ_SP) defined as the set of states in ℝⁿ for which exists an admissible input control signal that takes the system to Φ_SP in one step

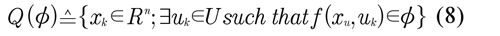
ii. Calculate the interception Q (·) n X

iii. If during this process is found an i such that S_i+1 (X,Φ_sp ) = S_i(X,Φ_sp), then it is found the maximum stabilizable set, and this set is the terminal region or domain of attraction χ of MPC. If not, it must be made the process shown later to find the controllable region ß for the PI controller.

In this work, to calculate Q is used a Montercarlo randomized algorithm with error and fail risk fixed a priori (Gómez, 2009), taking into account the property (Sontag, 1998) R^-T (x) = Q^T (x), that relates the reachable set R (forward) with the predecessor Q (backward). R^-T (x) denotes that reachable set is computed solving the system in inverse time, to obtain the predecessor set. Using equations (6) and (7), and with enough iterations, arrive to the stabilizable set S_π (X,Φ_SP) in π steps.

2.2.2 Calculation of the controllable region ß of PI controller

The controllable region ß is conformed for all points which PI controller visits around of the set-point Φ_SP in a time of 3t. It is considered the region Φ_SP, and not the only point x_SP, because the probability of x = x_SP is zero. Also, the maximum time to the process arrives to the surrounding Φ_SP is taken as 3τ. The reason is that MPC controls the process when it is out of the region Φ_SP. Then, it is just need that PI controller drives the process asymptotically until Φ_SP, taking only the 60% of the total expected time, which is equal to 5τ for first order systems since the controller acts when the disturbance appears. Generally, 3τ time is translated to algorithm steps, according to step size, easing the controller implementation. The controllable region ß is calculated using a Montecarlo's algorithm with error determinated for the Chernoff bound (Fishman, 1996), as it is shown in (Gómez, 2009). Note that intersecting the controllable region ß with the stabilizable set in π steps S_π (X,Φ_SP) it can guarantee that all states that pertain to terminal region reach the bounded surrounding of x_SP (set-point) in π steps. Also, once the state enters in Ω, it never goes out if the disturbance does not change, because Ω is an invariant set of the internal PI controller.

2.2.3 Calculation of domain of attraction χ a commutation proposal for MPC-PI

The MPC of this proposal has a prediction horizon bigger than control horizon (H_p > H_c) and Ω is a invariant set of the system, then, the domain of attraction χ (feasible states set) is the stabilizable states set in Hp steps to Ω, whom contains ΦSP (Mayne et al., 2000):

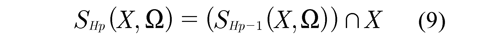
Assuming there are not discrepancies between the model of prediction and the real process, the state reached for the system in Hp steps will be inside Ω. About the commutation strategy, it must avoid instabilities due to switching MPC to PI Therefore, it is proposed to restrict the portion of final element of control available to PI controller in an interval in which the difference between the linear and nonlinear model be settled in a bound of a priori determined error. That is possible because the tuning of the PI controller guarantees the asymptotic stability to the linearized process model, and linear approximation is adequate within Ω.

3. Results and discussion through an example of DM-MPC

To show the properties and advantages of the proposed strategy, the DM-MPC is applied to a reported as nonlinear behavior process: continuous stirred tank reactor (CSTR) with perfect mixing, and taking for the simulation the parameters presented in (Henson & Seborg, 1990), to make a comparison of performance of DM-MPC with a conventional MPC and a PI control.

3.1 Continuous stirred tank reactor model (CSTR)

This CSTR process is modeled with two states using component mass balance and energy balance as they are presented below, where the exothermic irreversible reaction A → B is ocurred:

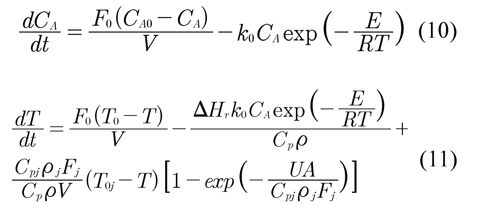
With the parameters: ρ = 1000 g/l, Cp = 1 cal/ g.K., ΔH_r= -2*10⁵ cal/mol, E/R = 9.98*10³ K, k₀ = 7.2*10² min^-1, UA = 7*10⁵ min/K.

And with the nominal conditions: F₀ = 100 l/min, CA0 = 1 mol/l, T0 = 310 K, V = 1000 l, T_0j = 310 K, ?_j = 1000 g/l, C_pj = 1 cal/g.K., F_j = 100 l/min for the steady state point C_A = 0.0753 gmol/l, T = 402.51 K.

3.2 PI Controllers formulation

Two PI control loops are used with the following paired variables: x₁= C_A with u₁= F0 and x₂= T with u₂= F_j. The tuning of PI controllers was made with an optimization technique known as bacterial chemotaxis, inspired in biology and reported first in (Bremermann & Anderson, 1990) but used here with modified proposal by (Alvarez, 2000). Thereby, the proportional gain and integral time (in seconds) for controllers were obtained: [BP_CA tI_CA BP_T tI_T] = [0.100 30 0.5421 28.17] which is heuristically adjusted.

3.3 Conventional MPC controller and DMMPC formulation

For the conventional MPC, Equations (2) and (3) are used, with state normalization at interval [0,1] and with adjustment parameters of the cost function: [α = 12, λ = 6, γ = 12, δ = 6].

For DM-MPC, Equations (1) to (4) are considered. Keeping the previously described procedure, the terminal region Ω and domain of attraction χ, both are calculated below and the strategy of commutation is presented.

3.3.1 Terminal region Ω calculation.

The following steps are made to calculate the terminal region O of local PI controller.

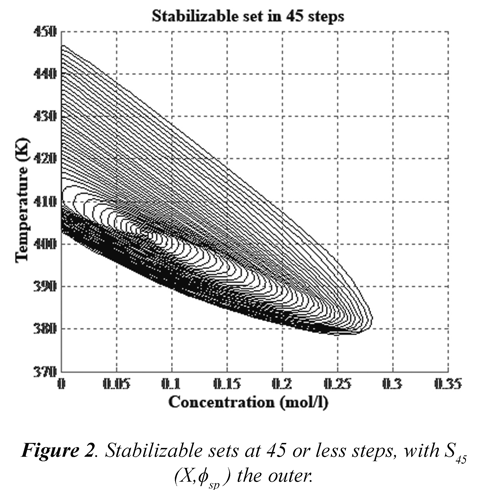
i. Calculate the stabilizable set in 3t = 45 steps: S₄₅ (X, Φ_SP)

Carrying out the described procedure of Equations (6) and (7) with x_SP = [C_A = 0.0753 T = 402.51], and using for Montecarlo method with randomized algorithms with the next adjustments: ε = 0.01, (1-δ) = 0.99 and a sample size of 26400 (according to Chernoff bound), the sets are obtained and shown in Figure 2. It is important to remark that stabilizable sets at least 45 steps (3τ of CSTR stabilization time), are nested, hence they are the invariant sets of the system (Kerrigan & Maciejowski, 2000).

As there is no any i such that S_i+1 (X, Φ_sp) = S_i (X, Φ_sp ), then it is needed to calculate the controllable set ß for PI controller as is shown below.

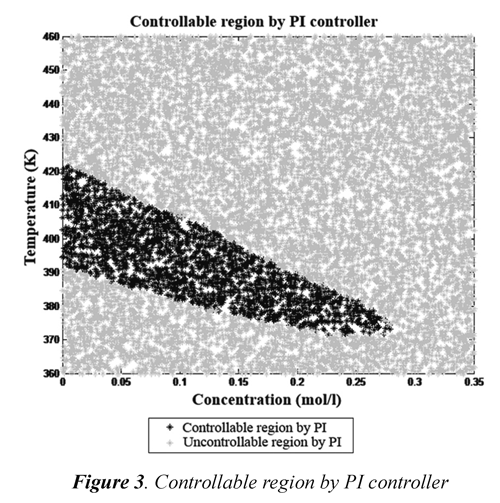
ii. Calculation of the controllable set ß of PI

With the sample size determined (26400 in accordance of Chernoff bound), it is obtained the region shown in Figure 3, with dark grey points denote controllable region ß, that means, all points that reach the region S₄₅ (X, Φ_SP), stabilizable set in 3τ (45 steps), while light grey points indicate the points that do not reach ß.

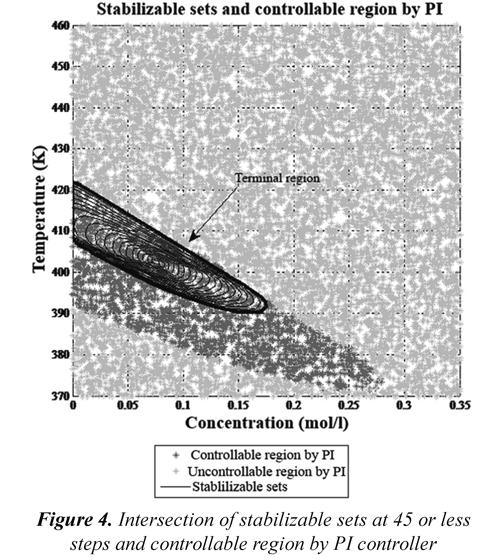
iii. Intersection of stabilizable set in 45 steps S45 (X,Φ_SP) with the ß region.

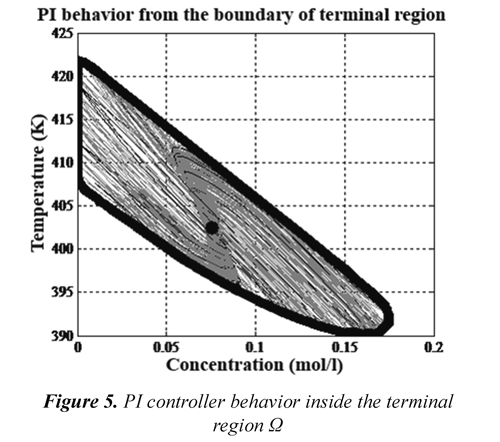
When the ß region is intersected with the other regions obtained from stabilizable set calculation at 45 or less steps, it can guarantee that states of terminal region reach the bounded contour of the set-point Φ_SP, and once they enter to the Ω, they do not leave it, namely, Ω is an invariant set of control system. Figures 4 and 5 illustrate the PI controller behavior inside the terminal region and the intersection of stabilizable sets at 45 or less steps and controllable region by PI controller.

3.3.2 Calculation of the domain of attraction ? of MPC and a commutation proposal

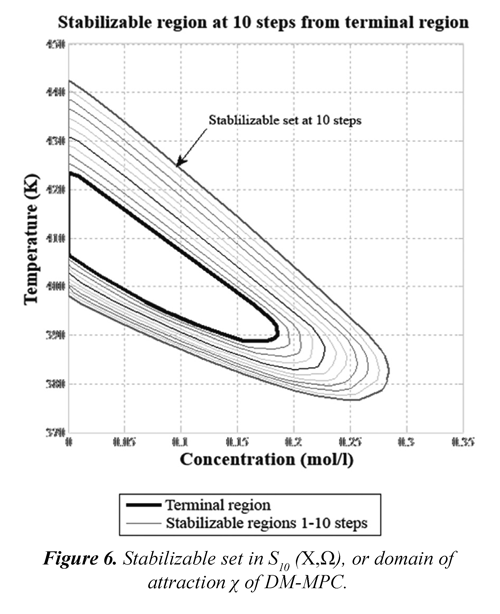
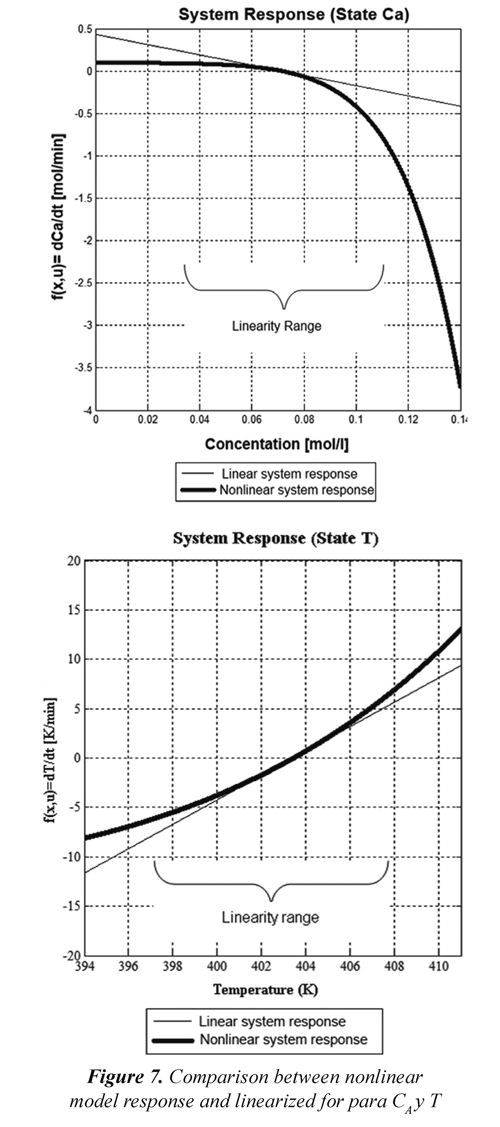
Taking into account that prediction horizon is Hp= 10 steps, an stabilizable set in 10 steps is calculated at Ω: S₁₀ (X, Ω), which is presented in Figure 6. Later, in Figure 7, a comparison between linearized model behavior and nonlinear model behavior is presented, for the two states: reactive concentration and reactor temperature, showing that in surrounding of O, the linearization adjusts accurately with nonlinear behavior of real process.

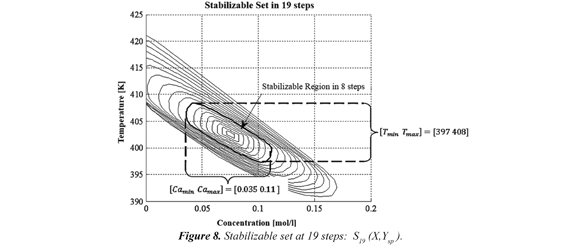
In Figure 7, they are shown the bounds [Ca_min Ca_max] = [0.035 mol/l 0.11 mol/l ] and [T_min T_max] = [397 K 408 K] according to 5% lineal model error, in contrast with nonlinear model. Then, if this bounds are moved to Figure 2, it is possible to detect that with 8 steps the process can be taken to Ω, i. e., the stabilizable set in 8 steps, S₈ (X, Ω), as it is shown in Figure 8.

Therefore, it is required to find the control action intervals that take the system to the discretized boundary of the stabilizable region to 8 steps, they are: [F_0min F_0max] = [56.66 l/min 136.40 l/min] and [F_jmin F_jmax] = [57.88 l/min 132.89 l/min]. Finally, from those limits, it is noted that the valves must operate at interval 60-140 l/min for the PI controllers.

3.4 Simulation results and discussion

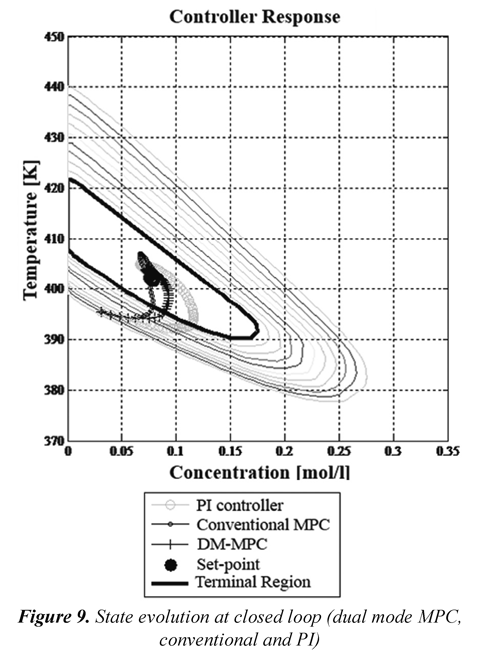
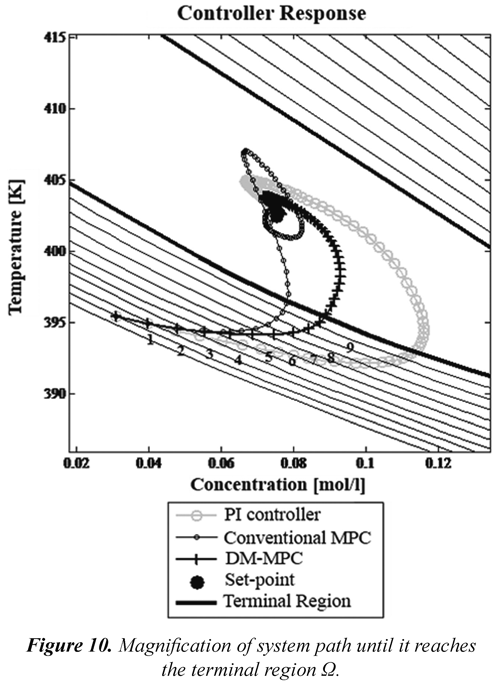
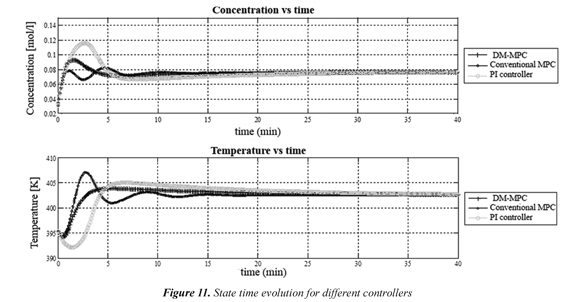
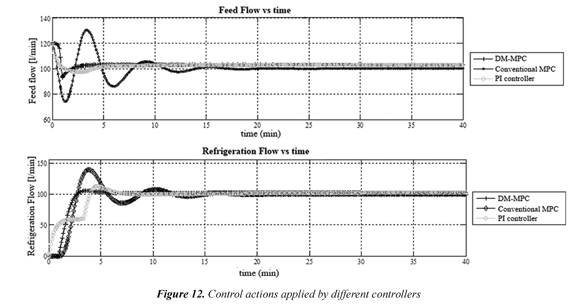
To evaluate the performance of formulated controllers in this work, the initial condition is set in C_A= 0.0311 mol/l and T = 395.39 K, located outside of terminal region and inside attraction domain χ of designed DM-MPC. For this initial condition, the behavior and path until state reaches the set-point is evaluated. In Figures 9 to 12, it can be seen obtained results.

In Figure 10, a clear evidence of adding the constraint (4) to MPC is presented, while DMFigure MPC reaches the terminal region in 10 steps or 1 minute, conventional MPC takes 13 steps to do it. Regarding observed behavior in control action, it can be remarked that conventional MPC creates oscillatory control actions (Figure 12) instead dual mode MPC doesn't generate them.

Generally, in all figures PI controller looks with the poorest performance, instead of the results with PI coupled in DM-MPC. From there, it follows that although PI controller is a linear controller, it only has a proper performance at surroundings of origin (like Ω), therefore it is justified the applied commutation in dual mode MPC.

4. Main findings

In this work a strategy of dual mode MPC is proposed, with guaranteed stability that can be implemented in a local industrial level, with PI controller acting inside a terminal region and while MPC acts outside it.

In the designed MPC strategy, it was proposed a methodology for terminal region calculation and domain of attraction calculation, which is valid for continuous nonlinear processes. In this methodology, invariant set theory and randomized algorithms are used, by means of polyhedral approximation to real set, remarking that this region is bigger than obtained from Lyapunov theory (Limon, 2002) and with a lower computational cost than calculated using actual polyhedral or polytopes procedures, mentioned in introduction.

As a complement of DM-MPC design, it was proposed a commutation strategy, which restricts the control action range, of local PI controllers. For specific case of CSTR, valve movement was restricted to 60 and 140 l/min (PI controller's action), in a region which nonlinear systems behaves like a linear system.

When the obtained performance of DM-MPC is compared with the conventional MPC, it is noted that DM-MPC operates with smoother valve movements than conventional MPC, and reaches the bounded surrounding Φ_SP of set-point in a faster way, leading to conclude that DM-MPC is a satisfactory control strategy, taking into account that besides that it guarantees stability, it has a better performance than obtained from a conventional MPC or PI controller.

Finally, it is remarked that DM-MPC is able to guarantee stability, through the use of MPC and PI controllers, with three novelties, a methodology for terminal region Ω and attraction domain χ calculations, using Montecarlo method with randomized algorithms and a strategy for commutation of controllers.

5. Notation

6. References

Alamir, M. & Bornard, G. (1995). Stability of a truncated infinite constrained receding horizon scheme: The general discrete nonlinear case. Automatica , 31 (9), 1353-1356.         [ Links ]

Alvarez, H. (2000). Control predictivo basado en modelo borroso para el control del pH. Serie Temas de Automática (vol. 10). San Juan, Argentina: Editorial Fundación UNSJ.         [ Links ]

Bravo, J. M., Limon, D., Alamo, T., & Camacho, E.F. (2005). On the computation of invariant sets for constrained nonlinear systems: An interval arithmetic approach. Automatica , 41 (9), 1583­1589.         [ Links ]

Bremermann, H. & Anderson, R. (1990). An alternative to back-propagation: a simple rule of synaptic modification for neural net training and memory . Technical Report PAM-483. Berkeley (CA): University of California, Center for pure and applied mathematics.         [ Links ]

Cannon, M., Deshmukh, V., & Kouvaritakis, B. (2003). Nonlinear model predictive control with polytopic invariant sets. Automatica , 39 (8), 1487 -1494.         [ Links ]

Chen, H. & Allgower, F. (1998). A quasi-infinite horizon nonlinear model predictive control scheme with guaranteed stability. Automatica , 34 (10), 1205-1218.         [ Links ]

Clarke, D. W., Mohtadi, C. & Tuffs, P. S. (1987). Generalized predictive control. Part I: The basic algorithms. Automatica , 23 (2), 137-148.         [ Links ]

Cutler, C. R. & Ramaker, B. L. (1980). Dynamic matrix control- a computer control algorithm. In Proceedings of the joint automatic control conference (vol. 1) (pp. Wp5-B). Piscataway, NJ: American Automatic Control Council.         [ Links ]

De Doná, J.A., Seron, M.M., Mayne, D. Q. & Goodwin, G.C. (2002). Enlarged terminal sets guaranteeing stability of receding horizon control. Systems and Control Letters , 47 (1), 57-63.         [ Links ]

Fishman, G. (1996). Monte Carlo, concepts, algorithms and applications . New York: Springer.         [ Links ]

Gómez, L.M. (2009). Una aproximación al control de procesos por lotes . Tesis de Doctorado en ingeniería de sistemas de control, Instituto de Automática, INAUT, Facultad de Ingeniería, Universidad Nacional de San Juan, Argentina.         [ Links ]

Henson, M.A. & Seborg, D.E. (1990). Output Linearization of General Nonlinear Processes. AIChE , 36 (11), 1753-1757.         [ Links ]

Kerrigan, E.C. & Maciejowski, J.M.(2000). Invariant sets for constrained nonlinear discrete­time systems with application to feasibility in Model Predictive Control. In proceedings of the 41st IEEE Conference on Decision and Control (pp.4951-4956). Australia.         [ Links ]

Kouvaritakis, B., Cannon, M., Karas, A. B., Rohal­Ilkiv,B. & Belavy, C. (2002). Asymmetric constraints with polyhedral sets in MPC with application to coupled tanks system. In Proceedings of the 41st IEEE Conference on Decision and Control (pp. 4107- 4112). Las Vegas.         [ Links ]

Limon, D., Alamo, T. & Camacho, E. F. (2005). Enlarging the domain of attraction of MPC controllers. Automatica , 41 (4), 629-635.         [ Links ]

Limon, D. (2002). Control predictivo de sistemas no lineales con restricciones: estabilidad y robustez . Tesis de doctorado. Escuela Superior de Ingenieros, Universidad de Sevilla, Sevilla.         [ Links ]

Limon, D., Gomes da Silva Jr, J.M., Alamo, T. & Camacho, E. F. (2005). Improved MPC design based on saturating on control laws. European Journal of Control , 11 (2), 112-122.         [ Links ]

Magni, L., De Niicolao, G., Magnani, L. & Scattolini, R. (2001). A stabilizing model based predictive control algorithm for nonlinear systems. Automatica , 37, 1351-1362.         [ Links ]

Mayne, D.Q., Rawlings, J. B., Rao, C. V. & Scokaert, P. O. M. (2000). Constrained model predictive control: stability and optimality. Automatica , 36 (6),789-814.         [ Links ]

Michalska, H. & Mayne, D. Q. (1993). Robust receding horizon control of constrained nonlinear systems. IEEE Transactions on Automatic Control , 38 (11), 1623-1632.         [ Links ]

Qin, S.J. & Badwell, Th. (2003). A survey of industrial model predictive control technology. Control engineering practice , 11 (7), 733-764.         [ Links ]

Richalet, J., Rault, A., Testud, J.L., & Papon, J. (1978). Model predictive heuristic control: Applications to industrial processes. Automatica , 14 (5), 413-428.         [ Links ]

Rohal-Ilkiv, B. (2004). A note to calculation of polytopic invariant and feasible sets for linear continuous-time systems. Annual Reviews in Control , 28 (1), 59-64.         [ Links ]

Sontag, E. (1998). Mathematical Control Theory (2 ed.) New York: Springer.         [ Links ]

Wills, A. G. (2003). Barrier function based model predictive control . Doctoral Thesis, School of Electrical Engineering and Computer Science, University of Newcastle, Australia.         [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.