Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y competitividad
Print version ISSN 0123-3033
Ing. compet. vol.16 no.1 Cali Jan./June 2014
Bioinformática multifractal: Una propuesta hacia la interpretación no-lineal del genoma
Multifractal bioinformatics: A proposal to the nonlinear interpretation of genome
Pedro A. Moreno
Escuela de Ingeniería de Sistemas y Computación, Facultad de Ingeniería, Universidad del Valle, Cali, Colombia
E-mail: pedro.moreno@correounivalle.edu.co
Eje temático: Ingeniería de sistemas / System engineering
Recibido: 19 de septiembre de 2012
Aceptado: 16 de diciembre de 2013
Resumen
El primer borrador de la secuencia completa del genoma humano (GH) se publicó en el año 2001 por parte de dos consorcios competidores. Desde entonces, varias características estructurales y funcionales de la organización del GH han sido reveladas. Hoy en día, más de 2000 genomas humanos han sido secuenciados y todos estos hallazgos están impactando fuertemente en la academia y la salud pública. A pesar de esto, un gran cuello de botella llamado la interpretación del genoma persiste; esto es, la falta de una teoría que integre y explique el complejo rompecabezas de características codificantes y no codificantes que componen el GH como un todo. Diez años después de secuenciado el GH, dos trabajos recientes, abordados dentro del formalismo multifractal permiten proponer una teoría no-lineal que ayuda a interpretar la variación estructural y funcional de la información genética de los genomas. El presente artículo de revisión trata acerca de este novedoso enfoque, denominado: "Bioinformática multifractal".
Palabras clave: Ciencias ómicas, bioinformática, genoma humano, análisis multifractal.
Abstract
The first draft of the human genome (HG) sequence was published in 2001 by two competing consortia. Since then, several structural and functional characteristics for the HG organization have been revealed. Today, more than 2.000 HG have been sequenced and these findings are impacting strongly on the academy and public health. Despite all this, a major bottleneck, called the genome interpretation persists. That is, the lack of a theory that explains the complex puzzles of coding and non-coding features that compose the HG as a whole. Ten years after the HG sequenced, two recent studies, discussed in the multifractal formalism allow proposing a nonlinear theory that helps interpret the structural and functional variation of the genetic information of the genomes. The present review article discusses this new approach, called: "Multifractal bioinformatics".
Keywords: Omics sciences, bioinformatics, human genome, multifractal analysis.
1. Introduction
Omic Sciences and Bioinformatics
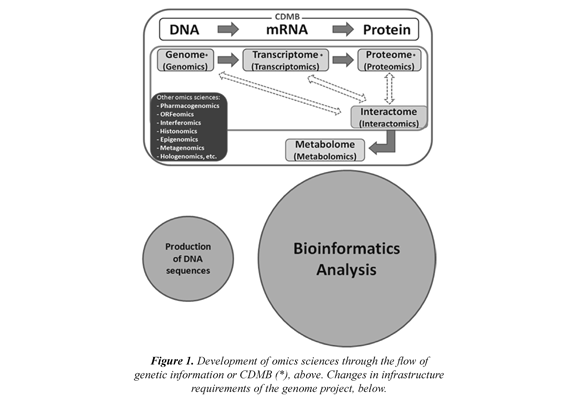
In order to study the genomes, their life properties and the pathological consequences of impairment, the Human Genome Project (HGP) was created in 1990. Since then, about 500 Gpb (EMBL) represented in thousands of prokaryotic genomes and tens of different eukaryotic genomes have been sequenced (NCBI, 1000 Genomes, ENCODE). Today, Genomics is defined as the set of sciences and technologies dedicated to the comprehensive study of the structure, function and origin of genomes. Several types of genomic have arisen as a result of the expansion and implementation of genomics to the study of the Central Dogma of Molecular Biology (CDMB), Figure 1 (above). The catalog of different types of genomics uses the Latin suffix "-omic" meaning "set of" to mean the new massive approaches of the new omics sciences (Moreno et al, 2009). Given the large amount of genomic information available in the databases and the urgency of its actual interpretation, the balance has begun to lean heavily toward the requirements of bioinformatics infrastructure research laboratories Figure 1 (below).
The bioinformatics or Computational Biology is defined as the application of computer and information technology to the analysis of biological data (Mount, 2004). An interdisciplinary science that requires the use of computing, applied mathematics, statistics, computer science, artificial intelligence, biophysical information, biochemistry, genetics, and molecular biology. Bioinformatics was born from the need to understand the sequences of nucleotide or amino acid symbols that make up DNA and proteins, respectively. These analyzes are made possible by the development of powerful algorithms that predict and reveal an infinity of structural and functional features in genomic sequences, as gene location, discovery of homologies between macromolecules databases (Blast), algorithms for phylogenetic analysis, for the regulatory analysis or the prediction of protein folding, among others. This great development has created a multiplicity of approaches giving rise to new types of Bioinformatics, such as Multifractal Bioinformatics (MFB) that is proposed here.
1.1 Multifractal Bioinformatics and Theoretical Background
MFB is a proposal to analyze information content in genomes and their life properties in a non-linear way. This is part of a specialized sub-discipline called "nonlinear Bioinformatics", which uses a number of related techniques for the study of nonlinearity (fractal geometry, Hurts exponents, power laws, wavelets, among others.) and applied to the study of biological problems (http://pharmaceuticalintelligence.com/tag/fractal-geometry/). For its application, we must take into account a detailed knowledge of the structure of the genome to be analyzed and an appropriate knowledge of the multifractal analysis.
1.2 From the Worm Genome toward Human Genome
To explore a complex genome such as the HG it is relevant to implement multifractal analysis (MFA) in a simpler genome in order to show its practical utility. For example, the genome of the small nematode Caenorhabditis elegans is an excellent model to learn many extrapolated lessons of complex organisms. Thus, if the MFA explains some of the structural properties in that genome it is expected that this same analysis reveals some similar properties in the HG.
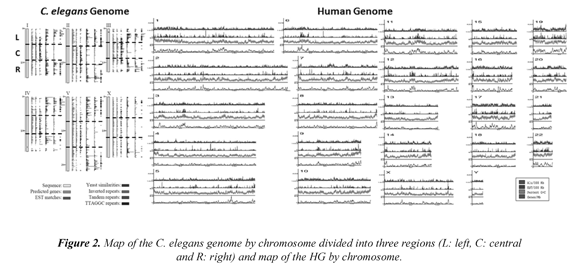
The C. elegans nuclear genome is composed of about 100 Mbp, with six chromosomes distributed into five autosomes and one sex chromosome. The molecular structure of the genome is particularly homogeneous along with the chromosome sequences, due to the presence of several regular features, including large contents of genes and introns of similar sizes. The C. elegans genome has also a regional organization of the chromosomes, mainly because the majority of the repeated sequences are located in the chromosome arms, Figure 2 (left) (C. elegans Sequencing Consortium, 1998). Given these regular and irregular features, the MFA could be an appropriate approach to analyze such distributions.
Meanwhile, the HG sequencing revealed a surprising mosaicism in coding (genes) and noncoding (repetitive DNA) sequences, Figure 2 (right) (Venter et al., 2001). This structure of 6 Gbp is divided into 23 pairs of chromosomes (diploid cells) and these highly regionalized sequences introduce complex patterns of regularity and irregularity to understand the gene structure, the composition of sequences of repetitive DNA and its role in the study and application of life sciences. The coding regions of the genome are estimated at ~25,000 genes which constitute 1.4% of GH. These genes are involved in a giant sea of various types of non-coding sequences which compose 98.6% of HG (misnamed popularly as "junk DNA"). The non-coding regions are characterized by many types of repeated DNA sequences, where 10.6% consists of Alu sequences, a type of SINE (short and dispersed repeated elements) sequence and preferentially located towards the genes. LINES, MIR, MER, LTR, DNA transposons and introns are another type of non-coding sequences which form about 86% of the genome. Some of these sequences overlap with each other; as with CpG islands, which complicates the analysis of genomic landscape. This standard genomic landscape was recently clarified, the last studies show that 80.4% of HG is functional due to the discovery of more than five million "switches" that operate and regulate gene activity, re-evaluating the concept of "junk DNA". (The ENCODE Project Consortium, 2012).
Given that all these genomic variations both in worm and human produce regionalized genomic landscapes it is proposed that Fractal Geometry (FG) would allow measuring how the genetic information content is fragmented. In this paper the methodology and the nonlinear descriptive models for each of these genomes will be reviewed.
1.3 The MFA and its Application to Genome Studies
Most problems in physics are implicitly non-linear in nature, generating phenomena such as chaos theory, a science that deals with certain types of (non-linear) but very sensitive dynamic systems to initial conditions, nonetheless of deterministic rigor, that is that their behavior can be completely determined by knowing initial conditions (Peitgen et al, 1992). In turn, the FG is an appropriate tool to study the chaotic dynamic systems (CDS). In other words, the FG and chaos are closely related because the space region toward which a chaotic orbit tends asymptotically has a fractal structure (strange attractors). Therefore, the FG allows studying the framework on which CDS are defined (Moon, 1992). And this is how it is expected for the genome structure and function to be organized.
The MFA is an extension of the FG and it is related to (Shannon) information theory, disciplines that have been very useful to study the information content over a sequence of symbols. Initially, Mandelbrot established the FG in the 80's, as a geometry capable of measuring the irregularity of nature by calculating the fractal dimension (D), an exponent derived from a power law (Mandelbrot, 1982). The value of the D gives us a measure of the level of fragmentation or the information content for a complex phenomenon. That is because the D measures the scaling degree that the fragmented self-similarity of the system has. Thus, the FG looks for self-similar properties in structures and processes at different scales of resolution and these self-similarities are organized following scaling or power laws.
Sometimes, an exponent is not sufficient to characterize a complex phenomenon; so more exponents are required. The multifractal formalism allows this, and applies when many subgroups of fractals with different scalar properties with a large number of exponents or fractal dimensions coexist simultaneously. As a result, when a spectrum of multifractal singularity measurement is generated, the scaling behavior of the frequency of symbols of a sequence can be quantified (Vélez et al, 2010).
The MFA has been implemented to study the spatial heterogeneity of theoretical and experimental fractal patterns in different disciplines. In post-genomics times, the MFA was used to study multiple biological problems (Vélez et al, 2010). Nonetheless, very little attention has been given to the use of MFA to characterize the content of the structural genetic information of the genomes obtained from the images of the Chaos Representation Game (CRG). First studies at this level were made recently to the analysis of the C. elegans genome (Vélez et al, 2010) and human genomes (Moreno et al, 2011). The MFA methodology applied for the study of these genomes will be developed below.
2. Methodology
The Multifractal Formalism from the CGR
2.1 Data Acquisition and Molecular Parameters
Databases for the C. elegans and the 36.2 Hs_ refseq HG version were downloaded from the NCBI FTP server. Then, several strategies were designed to fragment the genomic DNA sequences of different length ranges. For example, the C. elegans genome was divided into 18 fragments, Figure 2 (left) and the human genome in 9,379 fragments. According to their annotation systems, the contents of molecular parameters of coding sequences (genes, exons and introns), noncoding sequences (repetitive DNA, Alu, LINES, MIR, MER, LTR, promoters, etc.) and coding/ non-coding DNA (TTAGGC, AAAAT, AAATT, TTTTC, TTTTT, CpG islands, etc.) are counted for each sequence.
2.2 Construction of the CGR 2.3 Fractal Measurement by the Box Counting Method
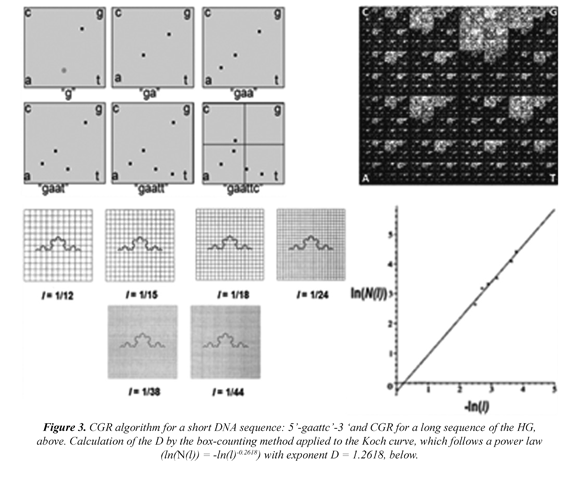
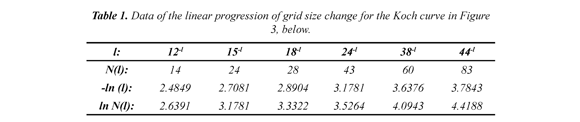
Subsequently, the CGR, a recursive algorithm (Jeffrey, 1990; Restrepo et al, 2009) is applied to each selected DNA sequence, Figure 3 (above, left) and from which an image is obtained, which is quantified by the box-counting algorithm. For example, in Figure 3 (above, left) a CGR image for a human DNA sequence of 80,000 bp in length is shown. Here, dark regions represent sub-quadrants with a high number of points (or nucleotides). Clear regions, sections with a low number of points. The calculation for the D for the Koch curve by the box-counting method is illustrated by a progression of changes in the grid size, and its Cartesian graph, Table 1
The CGR image for a given DNA sequence is quantified by a standard fractal analysis. A fractal is a fragmented geometric figure whose parts are an approximated copy at full scale, that is, the figure has self-similarity. The D is basically a scaling rule that the figure obeys. Generally, a power law is given by the following expression:
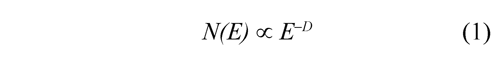
Where N(E) is the number of parts required for covering the figure when a scaling factor E is applied. The power law permits to calculate the fractal dimension as:
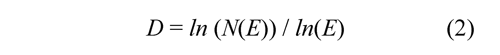
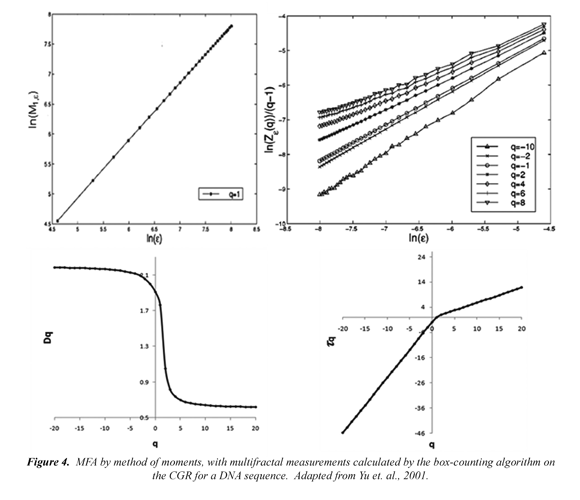
The D obtained by the box-counting algorithm covers the figure with disjoint boxes ɛ = 1/E and counts the number of boxes required. Figure 4 (above, left) shows the multifractal measure at momentum q=1.
2.4 Multifractal Measurement
When generalizing the box-counting algorithm for the multifractal case and according to the method of moments q, we obtain the equation (3) (Gutiérrez et al, 1998; Yu et al, 2001):
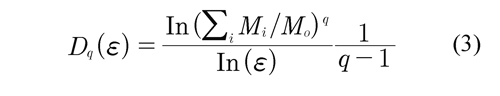
Where the Mi number of points falling in the i-th grid is determined and related to the total number M0 and ɛ to box size. Thus, the MFA is used when multiple scaling rules are applied. Figure 4 (above, right) shows the calculation of the multifractal measures at different momentum q (partition function). Here, linear regressions must have a coefficient of determination equal or close to 1. From each linear regression D are obtained, which generate an spectrum of generalized fractal dimensions Dq for all q integers, Figure 4 (below, left). So, the multifractal spectrum is obtained as the limit:
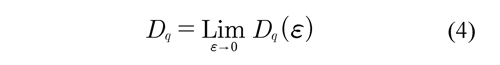
The variation of the q integer allows emphasizing different regions and discriminating their fractal a high Dq is synonymous of the structure's richness and the properties of these regions. Negative q values emphasize the scarce regions; a high Dq indicates a lot of structure and properties in these regions. In real world applications, the limit Dq readily approximated from the data using a linear fitting: the transformation of the equation (3) yields:
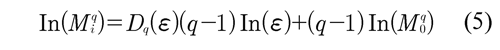
Which shows that ln In(Mi )= for set q is a linear function in the ln(ɛ), Dq can therefore be evaluated as q the slope of a fixed relationship between In(Mi )= and (q-1) ln(ɛ). The methodologies and approaches for the method of box-counting and MFA are detailed in Moreno et al, 2000, Yu et al, 2001; Moreno, 2005. For a rigorous mathematical development of MFA from images consult Multifractal system, wikipedia.
2.5 Measurement of Information Content
Subsequently, from the spectrum of generalized dimensions Dq, the degree of multifractality ΔDq(MD) is calculated as the difference between the maximum and minimum values of D : ΔD qq = Dqmax - Dqmin (Ivanov et al, 1999). When qmaxqmin ΔDq is high, the multifractal spectrum is rich in information and highly aperiodic, when ΔDq is small, the resulting dimension spectrum is poor in information and highly periodic. It is expected then, that the aperiodicity in the genome would be related to highly polymorphic genomic aperiodic structures and those periodic regions with highly repetitive and not very polymorphic genomic structures. The correlation exponent t(q) = (q - 1)Dq, Figure 4 (below, right ) can also be obtained from the multifractal dimension Dq. The generalized dimension also provides significant specific information. D(q = 0) is equal to the Capacity dimension, which in this analysis is the size of the "box count". D(q = 1) is equal to the Information dimension and D(q = 2) to the Correlation dimension. Based on these multifractal parameters, many of the structural genomic properties can be quantified, related, and interpreted.
2.6 Multifractal Parameters and Statistical and Discrimination Analyses
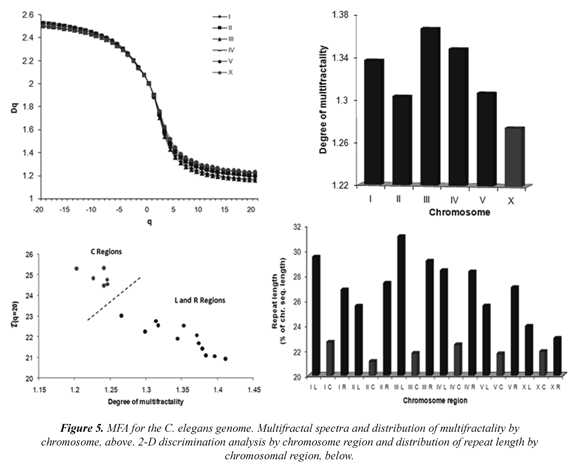
Once the multifractal parameters are calculated (Dq = (-20, 20), ΔDq, πq, etc.), correlations with the molecular parameters are sought. These relations are established by plotting the number of genome molecular parameters versus MD by discriminant analysis with Cartesian graphs in 2-D, Figure 5 (below, left) and 3-D and combining multifractal and molecular parameters. Finally, simple linear regression analysis, multivariate analysis, and analyses by ranges and clusterings are made to establish statistical significance.
3 Results and Discussion
3.1 Non-linear Descriptive Model for the C. elegans Genome
When analyzing the C. elegans genome with the multifractal formalism it revealed what symmetry and asymmetry on the genome nucleotide composition suggested. Thus, the multifractal scaling of the C. elegans genome is of interest because it indicates that the molecular structure of the chromosome may be organized as a system operating far from equilibrium following nonlinear laws (Ivanov et al, 1999; Burgos and Moreno-Tovar, 1996). This can be discussed from two points of view:
1) When comparing C. elegans chromosomes with each other, the X chromosome showed the lowest multifractality, Figure 5 (above). This means that the X chromosome is operating close to equilibrium, which results in an increased genetic instability. Thus, the instability of the X could selectively contribute to the molecular mechanism that determines sex (XX or X0) during meiosis. Thus, the X chromosome would be operating closer to equilibrium in order to maintain their particular sexual dimorphism.
2) When comparing different chromosome regions of the C. elegans genome, changes in multifractality were found in relation to the regional organization (at the center and arms) exhibited by the chromosomes, Figure 5 (below, left). These behaviors are associated with changes in the content of repetitive DNA, Figure 5 (below, right). The results indicated that the chromosome arms are even more complex than previously anticipated. Thus, TTAGGC telomere sequences would be operating far from equilibrium to protect the genetic information encoded by the entire chromosome.
All these biological arguments may explain why C. elegans genome is organized in a nonlinear way. These findings provide insight to quantify and understand the organization of the non-linear structure of the C. elegans genome, which may be extended to other genomes, including the HG (Vélez et al, 2010).
3.2 Nonlinear Descriptive Model for the Human Genome
Once the multifractal approach was validated in C. elegans genome, HG was analyzed exhaustively. This allowed us to propose a nonlinear model for the HG structure which will be discussed under three points of view.
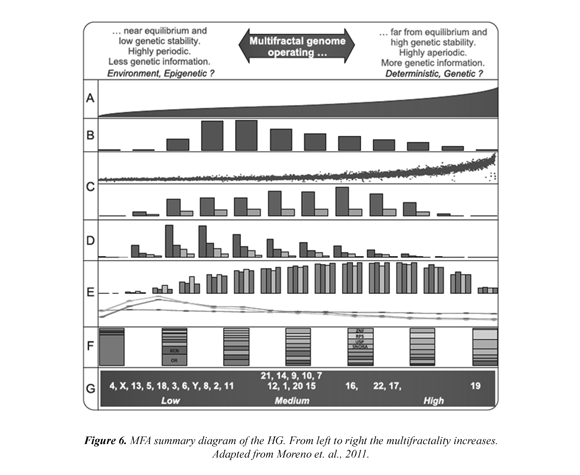
1) It was found that the HG high multifractality depends strongly on the contents of Alu sequences and to a lesser extent on the content of CpG islands. These contents would be located primarily in highly aperiodic regions, thus taking the chromosome far from equilibrium and giving to it greater genetic stability, protection and attraction of mutations, Figure 6 (A-C). Thus, hundreds of regions in the HG may have high genetic stability and the most important genetic information of the HG, the genes, would be safeguarded from environmental fluctuations. Other repeated elements (LINES, MIR, MER, LTRs) showed no significant relationship,
Figure 6 (D). Consequently, the human multifractal map developed in Moreno et al, 2011 constitutes a good tool to identify those regions rich in genetic information and genomic stability. 2) The multifractal context seems to be a significant requirement for the structural and functional organization of thousands of genes and gene families. Thus, a high multifractal context (aperiodic) appears to be a "genomic attractor" for many genes (KOGs, KEEGs), Figure 6 (E) and some gene families, Figure 6 (F) are involved in genetic and deterministic processes, in order to maintain a deterministic regulation control in the genome, although most of HG sequences may be subject to a complex epigenetic control.
3) The classification of human chromosomes and chromosome regions analysis may have some medical implications (Moreno et al, 2002; Moreno et al, 2009). This means that the structure of low nonlinearity exhibited by some chromosomes (or chromosome regions) involve an environmental predisposition, as potential targets to undergo structural or numerical chromosomal alterations in Figure 6 (G). Additionally, sex chromosomes should have low multifractality to maintain sexual dimorphism and probably the X chromosome inactivation.
All these fractals and biological arguments could explain why Alu elements are shaping the HG in a nonlinearly manner (Moreno et al, 2011). Finally, the multifractal modeling of the HG serves as theoretical framework to examine new discoveries made by the ENCODE project and new approaches about human epigenomes. That is, the non-linear organization of HG might help to explain why it is expected that most of the GH is functional.
4. Conclusions
All these results show that the multifractal formalism is appropriate to quantify and evaluate genetic information contents in genomes and to relate it with the known molecular anatomy of the genome and some of the expected properties. Thus, the MFB allows interpreting in a logic manner the structural nature and variation of the genome.
The MFB allows understanding why a number of chromosomal diseases are likely to occur in the genome, thus opening a new perspective toward personalized medicine to study and interpret the GH and its diseases.
The entire genome contains nonlinear information organizing it and supposedly making it function, concluding that virtually 100% of HG is functional. Bioinformatics in general, is enriched with a novel approach (MFB) making it possible to quantify the genetic information content of any DNA sequence and their practical applications to different disciplines in biology, medicine and agriculture. This novel breakthrough in computational genomic analysis and diseases contributes to define Biology as a "hard" science.
MFB opens a door to develop a research program towards the establishment of an integrative discipline that contributes to "break" the code of human life. (http://pharmaceuticalintelligence. com/page/3/).
5. Acknowledgements
Thanks to the directives of the EISC, the Universidad del Valle and the School of Engineering for offering an academic, scientific and administrative space for conducting this research. Likewise, thanks to co authors (professors and students) who participated in the implementation of excerpts from some of the works cited here. Finally, thanks to Colciencias by the biotechnology project grant # 1103-12-16765.
6. References
Blanco, S., & Moreno, P.A. (2007). Representación del juego del caos para el análisis de secuencias de ADN y proteínas mediante el análisis multifractal (método "box-counting"). In The Second International Seminar on Genomics and Proteomics, Bioinformatics and Systems Biology (pp. 17-25). Popayán, Colombia. [ Links ]
Burgos, J.D., & Moreno-Tovar, P. (1996). Zipf scaling behavior in the immune system. BioSystem , 39, 227-232. [ Links ]
C. elegans Sequencing Consortium. (1998). Genome sequence of the nematode C. elegans: a platform for investigating biology. Science , 282, 2012-2018. [ Links ]
Gutiérrez, J.M., Iglesias A., Rodríguez, M.A., Burgos, J.D., & Moreno, P.A. (1998). Analyzing the multifractals structure of DNA nucleotide sequences. In, M. Barbie & S. Chillemi (Eds.) Chaos and Noise in Biology and Medicine (cap. 4). Hackensack (NJ): World Scientific Publishing Co. [ Links ]
Ivanov, P.Ch., Nunes, L.A., Golberger, A.L., Havlin, S., Rosenblum, M.G., Struzikk, Z.R., & Stanley, H.E. (1999). Multifractality in human heartbeat dynamics. Nature , 399, 461-465. [ Links ]
Jeffrey, H.J. (1990). Chaos game representation of gene structure. Nucleic Acids Research , 18, 2163-2175. [ Links ]
Mandelbrot, B. (1982). La geometría fractal de la naturaleza. Barcelona. España: Tusquets editores. [ Links ]
Moon, F.C. (1992). Chaotic and fractal dynamics. New York: John Wiley. [ Links ]
Moreno, P.A. (2005). Large scale and small scale bioinformatics studies on the Caenorhabditis elegans enome. Doctoral thesis. Department of Biology and Biochemistry, University of Houston, Houston, USA. [ Links ]
Moreno, P.A., Burgos, J.D., Vélez, P.E., Gutiérrez, J.M., & et al., (2000). Multifractal analysis of complete genomes. In P roceedings of the 12th International Genome Sequencing and Analysis Conference (pp. 80-81). Miami Beach (FL). [ Links ]
Moreno, P.A., Rodríguez, J.G., Vélez, P.E., Cubillos, J.R., & Del Portillo, P. (2002). La genómica aplicada en salud humana. Colombia Ciencia y Tecnología. Colciencias , 20, 14-21. [ Links ]
Moreno, P.A., Vélez, P.E., & Burgos, J.D. (2009). Biología molecular, genómica y post-genómica. Pioneros, principios y tecnologías. Popayán, Colombia: Editorial Universidad del Cauca. [ Links ]
Moreno, P.A., Vélez, P.E., Martínez, E., Garreta, L., Díaz, D., Amador, S., Gutiérrez, J.M., et. al. (2011). The human genome: a multifractal analysis. BMC Genomics , 12, 506. [ Links ]
Mount, D.W. (2004). Bioinformatics. Sequence and ge nome analysis. New York: Cold Spring Harbor Laboratory Press. [ Links ]
Peitgen, H.O., Jürgen, H., & Saupe D. (1992). Chaos and Fractals. New Frontiers of Science. New York: Springer-Verlag. [ Links ]
Restrepo, S., Pinzón, A., Rodríguez, L.M., Sierra, R., Grajales, A., Bernal, A., Barreto, E. et. al. (2009). Computational biology in Colombia. PLoS Computational Biology, 5 (10), e1000535. [ Links ]
The ENCODE Project Consortium. (2012). An integrated encyclopedia of DNA elements in the human genome. Nature , 489, 57-74. [ Links ]
Vélez, P.E., Garreta, L.E., Martínez, E., Díaz, N., Amador, S., Gutiérrez, J.M., Tischer, I., & Moreno, P.A. (2010). The Caenorhabditis elegans genome: a multifractal analysis. Genet and Mol Res , 9, 949-965. [ Links ]
Venter, J.C., Adams, M.D., Myers, E.W., Li, P.W., & et al. (2001). The sequence of the human genome. Science , 291, 1304-1351. [ Links ]
Yu, Z.G., Anh, V., & Lau, K.S. (2001). Measure representation and multifractal analysis of complete genomes. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics , 64, 031903. [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.