Estudio comparativo del efecto de la dependencia en modelos de riesgos competitivos con tres modos de falla vía estimadores basados en cópulas

Comparative study of the dependence effect on competing risks models with three modes of failure via estimators copula based

María C. Paz-Sabogal
Escuela de Estadística, Facultad de Ciencias, Universidad Nacional de Colombia, Medellín
E-mail: mcpazs@unal.edu.co

Sergio Yáñez-Canal
Escuela de Estadística, Facultad de Ciencias, Universidad Nacional de Colombia, Medellín
E-mail: syanez@unal.edu.co

Carlos M. Lopera-Gómez
Escuela de Estadística, Facultad de Ciencias, Universidad Nacional de Colombia, Medellín
E-mail: cmlopera@unal.edu.co

Eje temático: Estadística / Statistics
Recibido: 21 de octubre de 2012
Aceptado: 10 de diciembre de 2013

Resumen

En un modelo de riesgos competitivos dependientes es imposible determinar las distribuciones marginales a partir solamente de los datos de riesgos competitivos. Esta situación se conoce como el problema de identificabilidad. Zheng y Klein (1995) proponen el estimador cópula gráfico como solución al problema de identificabilidad para dos riesgos competitivos. Para ello asumen una estructura de dependencia usando una cópula para la distribución conjunta entre los tiempos de falla y su parámetro de dependencia conocido. En el caso de un modelo con más de dos riesgos competitivos, Lo y Wilke (2010) proponen el método de combinación de riesgo ("risk pooling method") como una extensión del estimador cópula gráfico cuando la cópula es Arquimediana. En este trabajo para el caso trivariado, se compara la función de sobrevivencia conjunta verdadera, con la función de sobrevivencia conjunta estimada asumiendo independencia entre los tiempos de falla y la función de sobrevivencia estimada mediante el método de combinación de riesgos. Estas comparaciones se realizan vía simulación teniendo en cuenta tiempos de falla asociados a una distribución Weibull y lognormal multivariada y diferentes niveles de dependencia entre los tiempos de falla. Se concluye que el estimador asumiendo independencia es menos eficiente que el estimador de la función de sobrevivencia utilizando el método de combinación de riesgos. Se ilustra la metodología con datos de la confiabilidad de interruptores tipo FL245 en Interconexión Eléctrica S.A. E.S.P. (ISA), que muestran la utilidad de la temática en confiabilidad industrial.

Palabras clave: cópula arquimediana, confiabilidad industrial, identificabilidad, método de combinación de riesgos, riesgos competitivos.

Abstract

In a dependent competing risks model is impossible to determine the marginal distributions from the competing risks data alone. This is known as the identifiability problem. Zheng and Klein (1995) propose the copula graphic estimator as a solution to the identifiability problem for two competing risks. For that, they assume a dependence structure using a copula for the joint distribution of failure times and its dependence parameter known. Lo and Wilke (2010) propose the risk pooling method as an extension of the copula graphic estimator when the copula is Archimedean. This research for the trivariate case, is compared the true joint survival function, with joint survival function estimated assuming independence among failure times and the survival function estimated by the risk pooling method. These comparisons are performed via simulation considering failure times associated with multivariate Weibull and lognormal distributions and different levels of dependence between failure times. We conclude that the estimator assuming independence is less efficient than the estimator of the survival function using the risk pooling method. The methodology is illustrated with reliability data of FL245 switches in Interconexión Eléctrica S.A. E.S.P. (ISA), which show the usefulness of this topic in industrial reliability.

Keywords: archimedean copula, competing risks, identificability, industrial reliability, risk pooling method.

1. Introducción

El tiempo de falla de un sistema con varios modos de falla puede ser modelado como un sistema en serie o un modelo de riesgos competitivos. Cada unidad tiene un tiempo potencial de falla. El tiempo de falla observado es el mínimo de esos tiempos potenciales individuales. En riesgos competitivos bajo el supuesto de independencia entre los tiempos de falla, los datos observados proporcionan información suficiente para determinar de manera única las funciones de sobrevivencia marginal. Sin embargo, el supuesto de independencia no siempre se cumple. Cuando existe dependencia entre los tiempos de falla, queda imposible identificar las distribuciones marginales y la distribución conjunta a partir solamente de los datos de riesgos competitivos, esto es el problema de identificabilidad.

Existen muchas aplicaciones de riesgos competitivos en diversas áreas. En confiabilidad Basu y Klein (1982) obtuvieron algunos resultados en la teoría de riesgos competitivos; Nelson (1990) presenta datos para el tiempo de falla en horas de calentadores industriales, los cuales tienen dos modos de falla; Bedford y Lindqvist (2004) trataron el problema de identificabilidad en sistemas reparables cuando se presentan riesgos competitivos; Bedford (2005) muestra como modelar la confiabilidad en presencia de riesgos competitivos; Manotas et al (2008), estudiaron el efecto en la estimación de la confiabilidad, cuando se asume el supuesto de independencia entre tiempos de falla, que realmente son dependientes; Meeker et al (2009) usaron pruebas de vida aceleradas para predecir la distribución del tiempo de falla de un nuevo producto con dos modos de falla; Yáñez et al (2011) utilizaron el estimador cópula gráfico para dos riesgos competitivos dependientes.

En medicina, los riesgos competitivos son de uso frecuente, ver por ejemplo, Handa et al (2011), Checkley et al (2010) y Cox et al (2007). En economía Lo y Wilke (2010) estudiaron el efecto de los cambios en la compensación por desempleo durante el tiempo del desempleo, este artículo generaliza el estimador cópula gráfico para más de dos riesgos competitivos dependientes, técnica que se estudiará en este trabajo.

En el caso no-paramétrico, la distribución conjunta en un problema con múltiples modos de falla no puede ser completamente identificada en la situación usual cuando sólo se conocen los tiempos mínimos de falla (Tsiatis, 1975). Inclusive en el caso paramétrico, los datos pueden contener poca información sobre el coeficiente de asociación sobre las variables y es necesario hacer algunos supuestos al respecto (Meeker et al., 2009). Para el caso de un modelo con dos riesgos competitivos, Zheng y Klein (1995) proponen el estimador cópula gráfico como una solución al problema de identificabilidad.

Para ello utilizan cópulas como una función no paramétrica que captura la dependencia entre dos variables aleatorias. El problema de identificabilidad es resuelto bajo el supuesto que la cópula y su parámetro de asociación son conocidos y con los datos de riesgos competitivos disponibles.

Manotaset al(2008) estudiaron para tiempos de falla con distribución Weibull y lognormal, el efecto de la estimación de la función de sobrevivencia para el tiempo mínimo asumiendo independencia entre los tiempos de falla que realmente son dependientes. Yáñez et al (2011) estimaron la función de sobrevivencia para el tiempo mínimo asumiendo dependencia entre los tiempos de falla, para un modelo con dos riesgos competitivos, mediante el estimador cópula gráfico propuesto por Zheng y Klein (1995) y realizaron un estudio de simulación para compararlo con el estimador propuesto por Manotas et al (2008). Lo y Wilke (2010) proponen el método de combinación de riesgos ("risk pooling method") como una extensión del estimador cópula gráfico propuesto por Zheng y Klein (1995), cuando la cópula es Arquimediana para un modelo con más de dos riesgos competitivos. La propuesta de Lo y Wilke (2010) es computacionalmente más eficiente que las propuestas por Carriere (1995) y Rivest y Wells (2001). Lo y Wilke (2010) proponen esta metodología basada en cópulas debido a que estos modelos permiten especificar la estructura de dependencia entre los riesgos competitivos con mucha flexibilidad.

En este trabajo se estima la función de sobrevivencia para el tiempo mínimo asumiendo dependencia entre los tiempos de falla, con una estructura de equidependencia para un modelo con tres riesgos competitivos mediante el método de combinación de riesgos. Se compara este estimador con el propuesto por Manotas et al (2008) mediante un estudio de simulación. El método de combinación de riesgos y su comparación con el estimador que asume independencia se ilustra con datos reales de la confiabilidad de interruptores tipo FL245 en Interconexión Eléctrica S.A. E.S.P. (ISA).

Los datos que se usan en la aplicación de la metodología se presentan en la Sección 2. En la Sección 3 se definen algunos conceptos fundamentales de la teoría de riesgos competitivos, el problema de identificabilidad y como se estima la función de sobrevivencia del tiempo mínimo asumiendo independencia entre los tiempos de falla. En la Sección 4 se describen las cópulas Arquimedianas. El método de combinación de riesgos es presentado en la Sección 5. La Sección 6 presenta el estudio comparativo basado en simulación realizado. Los resultados obtenidos se muestran en la Sección 7 y en la Sección 8 se presenta un análisis de sensibilidad. Finalmente, en la Sección 9 se presentan las conclusiones y el trabajo futuro.

2. Datos de interruptores en ISA

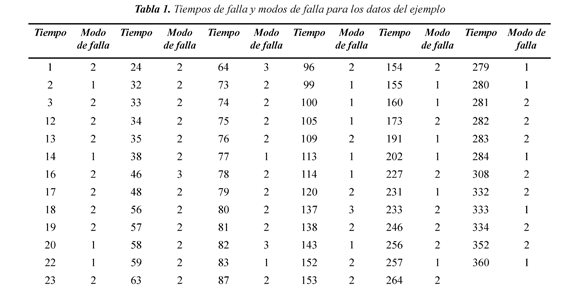
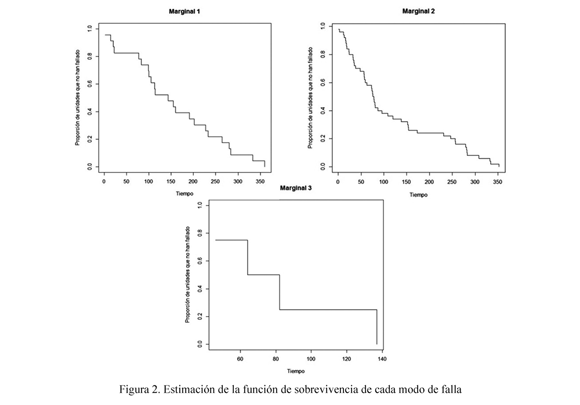
Para ilustrar la metodología presentada en este trabajo se consideran datos de la confiabilidad de interruptores tipo FL245 en Interconexión Eléctrica S.A. E.S.P. (ISA), la cual es una empresa colombiana, cuya actividad principal es el transporte de energía eléctrica. Los interruptores de potencia (ilustrados en la Figura 1) son usados para interrumpir el flujo de corriente y desconectar algún elemento de la subestación, para lo cual se pueden interrumpir tanto corrientes de carga normales como debidas a fallas eléctricas. Los datos consisten de tiempos recurrentes de eventos de mantenimiento correctivo en este tipo de interruptores recolectados entre los años 1985 y 2003 (Lopera & Manotas, 2011). Se hizo un seguimiento a un total de 40 equipos. Los eventos de mantenimiento obedecen a fallas cuyas causas se clasifican principalmente en: 1) fugas de aceite en sistema hidráulico, 2) baja de presión de gas SF6 y 3) deterioro en los instrumentos de calibración. Para llevar a cabo la aplicación se consideró que los procesos de falla asociados a las tres causas antes mencionadas se aproximan a procesos de renovación. Así, de la base de datos completa se seleccionaron 77 datos de falla de tales equipos (tomados de forma que los tiempos de falla previos tuvieran valores similares), de los cuales 4 fueron causados por deterioro en los instrumentos de calibración, 23 por fugas de aceite en sistema hidráulico y 50 por baja de presión de gas SF6. En este conjunto de datos no se presentó ningún tipo de censura. Los datos se presentan en la Tabla 1. En la Figura 2 se muestran los estimadores de Kaplan Meier, suponiendo independencia entre los modos de falla. En este trabajo se considera que los datos de falla pueden ser dependientes, dadas sus características, y de acuerdo a conjeturas planteadas por los especialistas del área.

3. Riesgos competitivos

El tiempo de falla de un sistema con varios modos de falla puede ser modelado como un sistema en serie o un modelo de riesgos competitivos, como se ilustra en la Figura 3. Cada unidad tiene un tiempo potencial de falla. El tiempo de falla observado es el mínimo de esos tiempos potenciales individuales. Así por ejemplo, para un sistema con tres modos de falla, sean T₁, T₂, T₃ , y los respectivos tiempos potenciales, entonces lo que se observa en la práctica son parejas de la forma de la forma (T, δ), donde T es el tiempo mínimo de falla, T = min (T₁, T₂, T₃) y δ es una variable discreta que toma el valor de 0 cuando la observación es censurada, 1 cuando la falla se presenta por el primer modo de falla, 2 cuando la falla se presenta por el segundo modo de falla y 3 cuando la falla se presenta por el tercer modo de falla.

3.1. Problema de identificabilidad

La aproximación tradicional para especificar el modelo de riesgos competitivos es vía tiempos de falla latentes. Se dice que los tiempos de falla son latentes debido a que, por ejemplo, para el caso trivariado se tienen los tiempos de falla potenciales T₁ , T₂ , T₃ , y asociados a los tres modos de falla, de manera que si el primero ocurre, el segundo y el tercero no pueden ser observados. Así T = min (T₁, T₂, T₃) determina el tiempo de falla del sistema completo y una vez que el sistema haya fallado, los demás tiempos de falla no pueden ser observados. El problema de identificabilidad (Tsiatis, 1975) establece que para el caso de modelos de tiempos de falla latentes, dada una función de distribución conjunta con dependencia arbitraria entre las componentes, existe siempre una función de distribución conjunta en la cual las variables son independientes, y la cual reproduce las subdensidades de manera precisa. Así, uno no puede conocer a partir solamente de los datos observados (T, δ), cuál de los dos modelos es correcto, puesto que ambos se ajustan bien a los datos. Crowder (2001) da detalles técnicos sobre este problema que él denomina "El impase de Cox-Tsiatis". En resumen, podemos decir que en la práctica se pueden encontrar las subdistribuciones marginales, asociadas con datos de riesgos competitivos, y ese conjunto es consistente con un número infinito de distribuciones conjuntas de tiempos de falla potenciales. Esto quiere decir que es imposible identificar las distribuciones marginales a partir solamente de los de riesgos competitivos. Zheng y Klein (1995) proponen el estimador cópula gráfico para resolver el problema de identificabilidad, dicho método asume una estructura de dependencia conocida usando una cópula específica para la distribución conjunta de los modos de falla. Este trabajo se hizo para dos riesgos competitivos. Lo y Wilke (2010) extienden el estimador cópula gráfico para más de dos riesgos competitivos con una metodología denominada Método de Combinación de Riesgos, que se utilizará en el desarrollo de este trabajo.

3.2. Estimación de la función de sobrevivencia bajo independencia

Una estructura en serie con componentes funciona sí y sólo sí, todas las componentes funcionan. Para un sistema en serie con tres componentes independientes, la función de distribución para el tiempo mínimo T es:

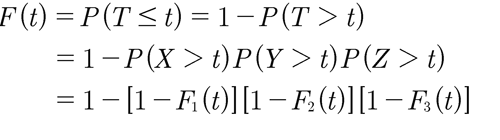
donde (X, Y, Z) son los tiempos de vida asociados a las tres componentes F_i , i = 1, 2, 3 y son respectivamente las funciones de distribución para los componentes y T = min (X, Y, Z) es el tiempo de falla observado del sistema. El estimador de la función de sobrevivencia asumiendo independencia S*(t) se denotará por Ŝ*(t), que es un estimador de la sobrevivencia del tiempo mínimo de falla de un sistema con tres modos de falla que compiten. Este se obtiene como el producto de las funciones de sobrevivencia estimadas bajo una distribución específica, donde para cada función marginal se estiman los parámetros, considerando los tiempos del otro modo de falla como tiempos de censura

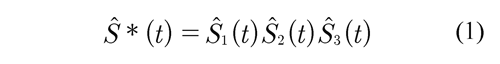
donde Ŝ₁(t), Ŝ₂(t) y Ŝ₃(t) se suponen son las funciones de sobrevivencia marginales estimadas para cada modo de falla.

4. Cópulas Arquimedianas

La cópula Arquimediana está definida por

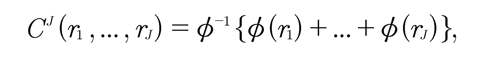
donde ϕ (r): [0,1] → R₊ es el generador de la cópula, una función continua estrictamente decreciente y dos veces diferenciable con ϕ (1) = 0.

La clase de cópulas Arquimedianas cubre un amplio rango de familias; la Tabla 2 muestra las familias más utilizadas para J = 2 , donde 0 es el parámetro de asociación entre las marginales. Además, las cópulas Arquimedianas son fáciles de construir y tienen buenas propiedades como la simetría (C² (r₁ , r₂) = C² (r₂ , r₁) para J = 2) y la propiedad asociativa (C²{(r₁ , r₂), r₃} = C²{r₁ , C²(r₂, r₃)} para J = 2). Otras propiedades se encuentran detalladas en Genest y Mackay (1986).

La metodología a presentar en este trabajo supone cópulas Arquimedianas, cuyas propiedades de simetría y asociatividad son claves en el desarrollo teórico.

5. Método de combinación de riesgos

Lo y Wilke (2010) extienden el estimador cópula gráfico propuesto por Zheng y Klein (1995). Para ello proponen el método de combinación de riesgos para un modelo con más de dos riesgos competitivos cuando la cópula es Arquimediana. A continuación se dan los detalles de este método. Sean (T₁ , ..., T_J) d R+^J tiempos latentes de falla j = 1, ..., J en un modelo de riesgos competitivos J-Dimensional. Se observa solamente Tsi T< Tpara todo i ≠ j. Los jj i T_j, j = 1, ..., J pueden ser dependientes entre sí.

Sea S_j : R₊ → [0,1]la función de sobrevivencia marginal desconocida, continua y estrictamente decreciente de Tj

S_j(t_j) = P(T_j > t_j) = r

donde, r_j se considera como la posición relativa o rango de t_j y es una realización de una variable aleatoria R_j = S_j(T_j) que se distribuye uniforme [0,1]. Se asume que la estructura básica de dependencia de T_j es generada por una cópula conocida, la cual es una distribución conjunta de los rangos de las variables de tiempos de falla. La J-cópula, C^J: [0,1]^J → [0,1] está definida por

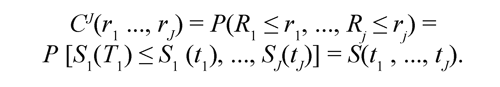
La función de sobrevivencia de T = min (T)_i

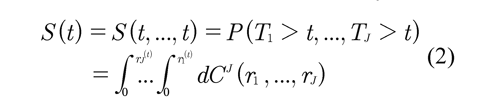
La curva de incidencia acumulada de causa específica Q_J(t_J) está dada por (Crowder, 2001)

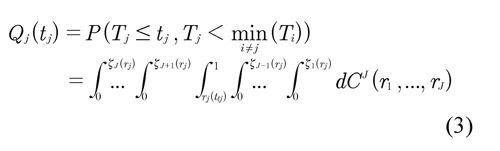
donde ζ_k (r_j) = Sk {S_j }para todo k ≠ j. Note que la inversa existe puesto que S_J es continua y estrictamente decreciente. En aplicaciones, las expresiones (2) y (3) de S(t) y Q_J(t_J) para todo j, se pueden estimar. Para nuestro problema la cópula C^J se debe conocer o se asume conocida para poder determinar las funciones de sobrevivencia marginales {S₁(t₁), ..., S_J(t_J)}. Se asumen cópulas Arquimedianas y se utilizan sus propiedades de simetría y asociatividad. A continuación se ilustra el método de combinación de riesgos para el caso de J = 3 . La idea es combinar las variables T₂ y T₃ para formar una nueva variable T₂₃= min(T₂, T₃). La función de sobrevivencia marginal de Tes definida como S(t) = P(T > t). La cópula de sobrevivencia entre las variables T₁ y T₂₃

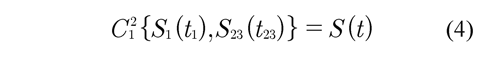
donde, T = min(T₁ , T₂₃) = min(T₁ , T₂ , T₃) , así j es el mínimo de los tiempos de falla.

La aproximación de Zheng y Klein (1995) puede aplicarse directamente para calcular S₁(t₁) y S₂₃). T₂₃ Esto se hace resolviendo las dos ecuaciones

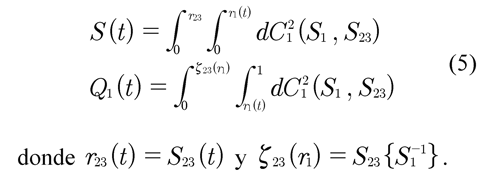
No es necesario crear la variable combinada T₂₃= min(T₂, T₃) para la implementación del método de combinación de riesgos. La razón es que S₁(t₁) y S₂₃(t₂₃) pueden ser identificadas a partir de S(t) y Q₁(t) junto con C₁²{S₁ (t₁ ), 1 S₂₃ (t₂₃)} sin la construcción de Q₂₃(t). Así se estima S₁(t₁), la variable combinada es sólo creada conceptualmente para probar el resultado de identificación. Análogamente, se estiman S₂(t) y S₃(t). Los estimadores se denotan por Ŝ₁(t)_MCRy Ŝ₃(t)_MCR. De aquí se puede1MCR^{, Ŝ}2MCR 3MCRestimar la función de sobrevivencia conjunta denotada por y para J = 3 está dada

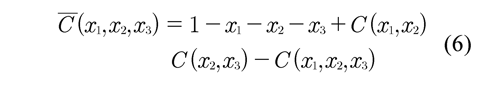
Donde C hace referencia a la cópula y x_i, i = 1,2,3 a las funciones de distribución marginal.

6. Estudio comparativo entre Ŝ*(t) y Ŝ(t)_MCR

Manotas et al (2008) estudiaron para tiempos de falla con distribución Weibull y lognormal, el efecto de la estimación de la función de sobrevivencia para el tiempo mínimo asumiendo independencia entre los tiempos de falla que realmente son dependientes. Yáñez et al (2011) estimaron la función de sobrevivencia para el tiempo mínimo asumiendo dependencia entre los tiempos de falla, para un modelo con dos riesgos competitivos, mediante el estimador cópula gráfico propuesto por Zheng y Klein (1995). En este trabajo se estima la función de sobrevivencia para el tiempo mínimo asumiendo dependencia entre los tiempos de falla, para un modelo con tres riesgos competitivos mediante el método de combinación de riesgos. Se compara este estimador con el propuesto por Manotas et al (2008) mediante un estudio de simulación.

6.1. Esquema de simulación

A continuación se presenta el esquema general para realizar la comparación entre la función de sobrevivencia verdadera del tiempo mínimo de falla S(t) con la función de sobrevivencia estimada asumiendo independencia Ŝ*(t) (ver Ecuación 1) y la función de sobrevivencia del tiempo mínimo de falla utilizando el método de combinación de riesgos, teniendo en cuenta la dependencia entre los modos de falla Ŝ(t)_MCR. Es de anotar que Ŝ*(t) sería el estimador obtenido para la cópula independiente.

1. Se generan distribuciones multivariadas con marginales lognormal y marginales Weibull utilizando la cópula Frank que es una cópula Arquimediana. De aquí, la ecuación general de la función de sobrevivencia verdadera tiene la forma de dicha cópula, esto es

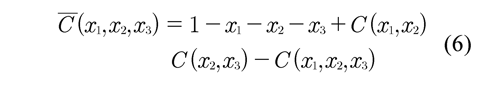
Donde x_i, i = 1, ..., n son las funciones de distribución marginal, las cuales se sustituyen por marginales lognormal o marginales Weibull dependiendo del escenario de simulación considerado y θ es el parámetro de asociación entre las marginales de la cópula. Este parámetro guarda una relación con el coeficiente de correlación τ de Kendall, dada por

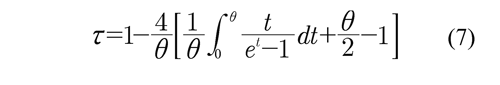
que convierte al parámetro θ de la cópula en una medida de asociación más familiar como el τ de Kendall que tiene una fácil interpretación. La relación en (7) se usará más adelante en el esquema de simulación.

2. A continuación se definen los escenarios

de simulación de acuerdo a las distribuciones multivariadas consideradas.

Los escenarios Weibull a estudiar consideran diferentes formas de la función hazard de los tiempos de falla. Cuando β < 1 , la tasa de falla es decreciente, cuando β > 1, la tasa de falla es creciente y cuando β = 1, la tasa de falla es constante. Los parámetros de escala de la distribución Weibull se fijan en η₁ ,η₂ ,η₃ = 1, ya que el parámetro de dependencia, no depende del parámetro de escala (Lu y Bhattacharyya, 1990). Además, se escogen los modelos Weibull de tal manera que se garantice que existan fallas para cada modo, i = 1, 2, 3. Para ello, se establece que como mínimo haya un 15% de fallas para cada uno de los modos, de tal forma que no se presente un alto porcentaje de censura que dificulta la estimación de las sobrevivencias marginales. Con estas consideraciones los modelos Weibull a estudiar son:

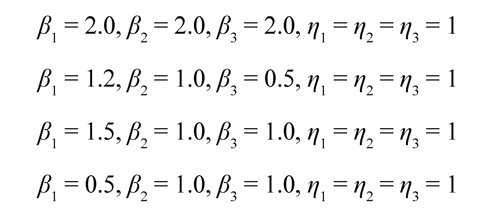
Asociados a cada uno de los casos mencionados anteriormente, se consideran 3 situaciones diferentes asociadas al parámetro de dependencia entre los tiempos de falla, τ = 0.2, 0.5, 0.8, donde τ es el coeficiente de correlación de Kendall. Es decir, para cada uno de los escenarios hay 3 situaciones distintas que abarcan baja, mediana y alta dependencia. De esta manera se consideran 12 casos de simulación para los modelos Weibull.

Los escenarios de los casos lognormal se escogen de tal manera que se garantice que ocurran los tres modos de falla. Cabe resaltar que en la distribución lognormal μ corresponde a un parámetro de escala y σ a un parámetro de forma. En los modelos seleccionados se fija el parámetro de escala μ = 0 y se varía el parámetro de forma σ, ya que éste último permite considerar diferentes pendientes y de esta manera modificar la ocurrencia de cada modo de falla.

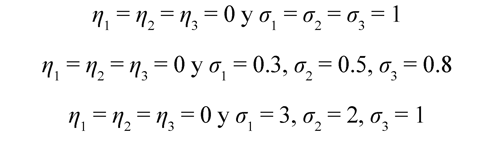
Análogamente, se consideran 3 situaciones diferentes asociadas al parámetro de dependencia entre los tiempos de falla, τ = 0.2, 0.5, 0.8, es decir, se consideran 9 casos de simulación para los modelos lognormal.

3. Para efectos de comparación se utilizan dos criterios, a saber:

i) Se obtienen intervalos de confianza empíricos basados en simulación Monte Carlo para S(t), usando los estimadores Ŝ*(t) y Ŝ(t)_MCR. Se comparan en los percentiles t_p con p = 0.05, 0.25, 0.50, 0.75, 0.95. El procedimiento se resume como sigue:

Para cada uno de los escenarios descritos, se generaron 10000 muestras de tamaño n = 50 de tiempos de falla trivariados, tanto con marginales lognormal como Weibull. Se elige este tamaño de muestra ya que en general en experimentos de confiabilidad se manejan bases de datos no muy grandes, estos estudios son costosos y en algunas ocasiones los datos de falla son difíciles de obtener. Luego en cada escenario se obtienen 10000 estimaciones de S(t_p) usando ambos estimadores Ŝ*(t ) y Ŝ(t ) en cada percentil t con p = 0.05,ppMCRp 0.25, 0.50, 0.75, 0.95. De esta manera se obtiene la distribución empírica de las estimaciones de Ŝ*(t_p) en cada uno de los percentiles considerados. Finalmente, de estas distribuciones se obtienen los límites puntuales de confianza empíricos aproximados del 95%.

Es importante observar que en muchas aplicaciones generalmente se tienen pocas fallas y muchos datos censurados. Bajo estas características, las pruebas formales de bondad de ajuste no son útiles (Meeker et al., 2009).

ii) Se comparan puntualmente los dos estimadores calculando la eficiencia relativa ER _p de Ŝ*(t_p) con relación a Ŝ(t ) en los percentiles t con p =pMCRp 0.05, 0.25, 0.50, 0.75, 0.95.

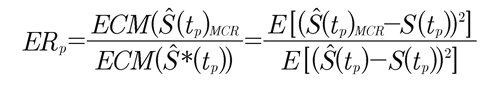
donde, ECM(Ŝ(t )) y ECM(Ŝ*(t )) corresponden pMCRp a los errores cuadráticos medios de los estimadores Ŝ(t )y Ŝ*(t ) respectivamente.

Si ER _p < 1 entonces ECM(Ŝ*(t_p)) > ECM(Ŝ(t_p) _MCR) lo cual indica que Ŝ*(t_p) es menos eficiente frente a Ŝ(t_p)_MCR para la estimación de la función de sobrevivencia verdadera en t.

7. Análisis de resultados

A continuación se presentan los resultados obtenidos para los escenarios con marginales Weibull y marginales lognormal, basados en los dos criterios de comparación descritos en la sección anterior.

7.1. Marginales Weibull

En la Tabla 3 se muestra la eficiencia relativa ER p de la función de sobrevivencia conjunta estimada bajo independencia Ŝ*(t_p) con relación a la función de sobrevivencia conjunta estimada bajo dependencia Ŝ(t en los percentiles p = 0.05, p)_MCR 0.25, 0.50, 0.75, 0.95, para los diferentes niveles de dependencia τ = 0.2, 0.5, 0.8. Se observa también en este caso de estudio que el estimador Ŝ*(t ) es menos eficiente que Ŝ(t para estimarpp⁾_MCRS(t_p), debido a que los valores encontrados de ER_p son todos menores que uno y a medida que aumenta la dependencia el valor de la eficiencia relativa disminuye.

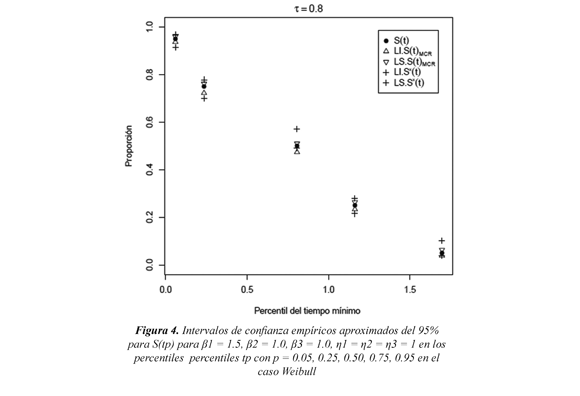
En la Figura 4 se muestra los límites de confianza para el caso Weibull β₁ = 1.5, β₂ = 1.0, β₃ = 1.0, η₁ = η₂ = η₃ = 1, para el nivel de dependencia τ = 0.8. En estas Figura se presenta el valor verdadero de la función de sobrevivencia conjunta denotado en el gráfico por S(t_p), los límites inferior y superior de la función de sobrevivencia estimada bajo dependencia denotados por LI.Ŝ(t)_MCR y LS.Ŝ(t) _MCR respectivamente, y los límites inferior y superior de la función de sobrevivencia estimada bajo independencia denotados por LI.Ŝ*(t) y LS.Ŝ*(t) respectivamente. Estos intervalos de confianza muestran que en los percentiles p = 0.05, 0.25, 0.50, 0.75, 0.95, el estimador asumiendo dependencia contiene el verdadero valor de la sobrevivencia conjunta S(t_p). Los límites para Ŝ*(t_p) son más amplios que los encontrados para Ŝ(t , indicando con ello que p)MCR el estimador Ŝ(t tiene mayor precisión para p)MCR estimar Ŝ*(t_p).

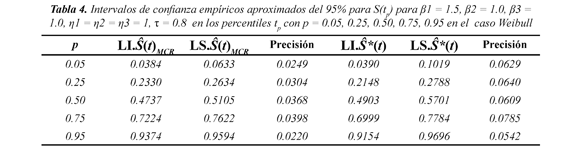
Lo anterior se puede observar en la Tabla 4. Así por ejemplo, observe que para p = 0.75 el límite inferior del intervalo de confianza para dependencia (Ŝ(t_p)_MCR) es LI.Ŝ(t)_MCR = 0.7224 y el límite superior es LS.Ŝ(t)_MCR= 0.7622, con una Presición = 0.7622 - 0.7224 = 0.0398. Para independencia (Ŝ(t_p)) el límite inferior del intervalo de confianza es LI.Ŝ*(t) = 0.6999 y el límite superior es LS.Ŝ*(t) = 0.7784 con una Presición = 0.7784 - 0.6999 = 0.0785, indicando que el intervalo para independencia es más amplio que el intervalo obtenido para dependencia. Gráficamente se puede observar en la Figura 4. Este caso se presenta como una ilustración, los demás casos Weibull estudiados se comportan de manera similar.

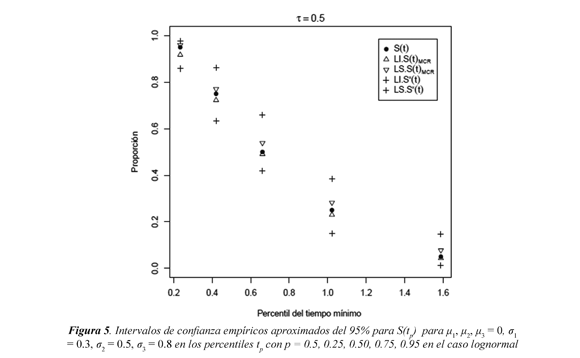
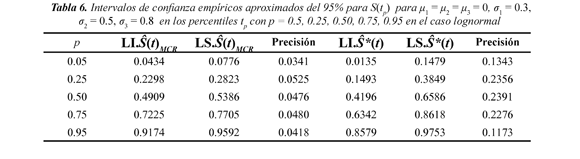
En la Tabla 5 se muestra la eficiencia relativa ER_p de la función de sobrevivencia conjunta estimada bajo independencia S*(t_p) con relación a la función de sobrevivencia conjunta estimada bajo dependencia S(t_p)_MCR en los percentiles p = 0.05, 0.25, 0.50, 0.75, 0.95, para el caso lognormal µ₁, µ₂, µ₃ = 0 y s₁ = 0.3, s₂ = 0.5, s₃ = 0.8, la cual indica que el estimador S*(t_p) es menos eficiente que S(t_p)_MCR para estimar S(t_p), debido a que los valores encontrados de ER_p son todos menores a 1. Se observa además, que a medida que aumenta la dependencia el valor de la eficiencia relativa disminuye. Los límites de confianza se muestran en la Figura 5 para el caso lognormal µ₁, µ₂, µ₃ = 0 y s₁ = 0.3, s₂ = 0.5, s₃ = 0.8 para el nivel de dependencia t = 0.5. Los intervalos de confianza muestran que en los percentiles p = 0.05, 0.25, 0.50, 0.75, 0.95, tanto el estimador que asume independencia S*(t_p) como el que asume dependencia S(t_p)_MCR contienen el verdadero valor de S(t_p). Sin embargo los límites para S*(t_p) son mucho más amplios que los encontrados para S(t_p) MCR, indicando con ello que el estimador S(t_p)_MCR tiene mayor precisión para estimar S(t_p). Lo anterior se puede observar en la Tabla 6. Así por ejemplo, observe que para p = 0.25 el límite inferior del intervalo para dependencia (S(t_p)_MCR) es LI.S*(t) _MCR = 0.2298 y el límite superior es LS.S*(t)_MCR = 0.2823, con una Precisión = 0.2823 - 0.2298 = 0.0525.

7.2. Marginales lognormal

Para independencia (Ŝ*(t_p)) el límite inferior del intervalo de confianza es LI.Ŝ*(t) = 0.1493 y el límite superior es LS.Ŝ*(t) = 0.3849 con una Precisión = 0.3849 - 0.1493 = 0.2356, indicando que el intervalo para independencia es más amplio que el intervalo obtenido para dependencia. Gráficamente se puede observar en la Figura 5. Los demás casos lognormal estudiados se comportan de manera similar.

7.3. Ejemplo utilizando los datos de la Sección 2

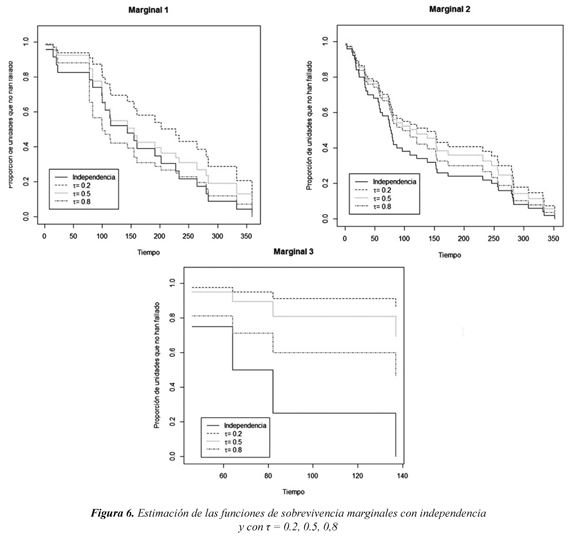
Se ilustra el método de combinación de riesgos con los datos presentados en la Sección 2. La Figura 6, muestra que las distribuciones de sobrevivencia marginales bajo dependencia son diferentes a las obtenidas bajo independencia. Debido a estas diferencias observadas en las funciones de sobrevivencia marginales, es claro que tienen un efecto sobre la función de sobrevivencia conjunta. De acuerdo a lo estudiado en este trabajo se recomienda utilizar Ŝ(t p)_MCR.

8. Análisis de sensibilidad

A manera de chequeo de la validez de los resultados se presentan simulaciones adicionales donde i) se toman marginales combinadas, ii) se verifica la influencia de la escogencia de la cópula.

8.1. Combinación de marginales

En ingeniería de confiabilidad industrial a las distribuciones Weibull y lognormal se les considera como las distribuciones básicas dada su gran aplicabilidad (Meeker y Escobar, 1998; Meeker, 2010); además son representativas de la familia de log-localización-escala. Por ello tomaremos los siguientes escenarios para verificar resultados bajo la cópula Frank y el mismo esquema de simulación descrito en la Sección 6.1.

Los escenarios combinan marginales Weibull y lognormal de tal manera que se garantiza la ocurrencia de los tres modos de falla, es decir, se establece que como mínimo haya un 15% de fallas para cada uno de los modos, de tal forma que no se presente un alto porcentaje de censura que dificulte la estimación de las sobrevivencias marginales. Con estas consideraciones, las combinaciones de marginales Weibull y lognormal a estudiar bajo la cópula Frank son:

• Marginales Weibull: β₁ = 1.5,η₁ = 1; β₁ = 1,η₁= 1 y marginal lognormal: μ₁ = 0, σ₁ = 3
• Marginal Weibull: β₁ = 1.2, η₁ = 1 y marginales lognormal μ₁= 0, σ₁= 0.3, μ₂ = 0, σ₂=

Asociados a cada uno de los casos mencionados anteriormente, se consideran 3 situaciones diferentes asociadas al parámetro de dependencia entre los tiempos de falla, τ = 0.2, 0.5, 0.8, es decir, se consideran 6 casos de simulación para esta combinación de marginales.

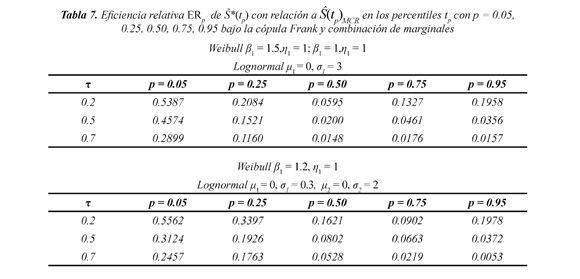
En la Tabla 7 se observa que las eficiencias son menores que uno, confirmando los resultados anteriores.

8.2. Escogencia de la cópula

Primero, observemos que la cópula Frank, siguiendo a Frees y Valdez (1998, pg. 4), tiene una serie de propiedades que la hacen apropiada para aplicaciones empíricas.

Segundo, de acuerdo a Zheng y Klein (1995) y Lo y Wilke (2010), la escogencia de la cópula tiene menor relevancia para los resultados que la escogencia de la medida de asociación entre las variables, lo cual está relacionado con el parámetro de interés de la cópula en este estudio. Específicamente, se ha hecho en este estudio un análisis del comportamiento relativo a tres valores del τ de Kendall como medida de correlación. Sin embargo, a manera de comprobación se chequeó para las cópulas Clayton y Gumbel-Hougaard de la familia Arquimediana y se obtuvieron resultados análogos a los de las Tablas 3 y 5, lo cual sustenta los análisis realizados en este trabajo.

9. Conclusiones

La metodología tradicional en las ciencias e ingeniería para analizar modelos de riesgos competitivos asume independencia entre los modos de falla, lo cual resuelve el problema de identificabilidad. Se ha mostrado en este trabajo que este procedimiento cuando dicho supuesto es incorrecto, genera estimadores ineficientes de la función de confiabilidad. Esta ineficiencia puede generar sobrecostos y mala planeación en diseño, por ejemplo, en mantenimiento preventivo de equipos. Por ello se recomienda utilizar el estimador Ŝ(t , cuando no se tiene certeza que los tiempos p)_MCR de falla son independientes.

Este artículo está enmarcado dentro de una problemática más general que pretende caracterizar la dependencia en modelos de riesgos competitivos con datos de confiabilidad industrial.

10. Agradecimientos

Los autores agradecen a los árbitros y al editor por sus valiosos comentarios que enriquecieron el texto del manuscrito. Este trabajo fue financiado por Colciencias, Colombia. Es parte del proyecto de investigación "Characterization of dependence in competing risks models in industrial reliability", código 110152128913.

11. Referencias Bibligráficas

Basu, A.P. & Klein, J.P. (1982). Some recent results in competing risks theory. Lecture Notes-Monograph Series, Survival Analysis , 2, 216-229.         [ Links ]

Bedford, T. & Lindqvist, B. (2004). The identifiability problema for repairable systems subject to competing risks. Advances in Applied Probability , 36(3), 774-790.         [ Links ]

Bedford, T. (2005). Competing risks modelling in reliability. In, A. G. Wilson. Modern Statistical and Mathematical Methods in Reliability. London: World Scientific Books.         [ Links ]

Carriere, J. F. (1995). Removing cancer when it is correlated with other causes of death. Biometrical , 37(3), 339-350.         [ Links ]

Checkley, W., Brower, R.G. & Muñoz, A. (2010). Inference for mutually exclusive competing events through a mixture of generalized gamma distributions. Epidemiology , 21(4), 557-565.         [ Links ]

Cox, C., Chu, H., Schneider, M.F. & Muñoz, A. (2007). Parametric Survival Analysis and Taxonomy of Hazard Functions for the Generalized Gamma Distribution. Stat Med , 26 (23), 4352-4374.         [ Links ]

Crowder, M. (2001). Classical Competing Risks (1 ed.) London: Chapman & Hall.         [ Links ]

Frees, E.W. & Valdez, E.A. (1998). Understanding Relationships Using Copulas. North American Actuarial Journal , 2 (1), 1-25.         [ Links ]

Genest, C. & Mackay J. (1986). The joy of copulas: Bivariate distributions with uniform marginals. The American Statistician , 40 (4), 280-283.         [ Links ]

Handa, V.L., Blomquist, J.L., McDermott, K.C., Friedman, S. & Muñoz, A. (2011). Pelvic floor disorders after childbirth: effect of Episiotomy, perineal laceration, and operative birth. Obstetrics & Gynecology , 119 (2), 233-239.         [ Links ]

Lo, S. & Wilke, R.A. (2010). A copula model for dependent competing risks. Journal of the Royal Statistical Society , 59(2), 359-376.         [ Links ]

Lopera, C.M. & Manotas, E.C. (2011). Aplicación del análisis de datos recurrentes sobre interruptores FL245 en Interconexión Eléctrica S.A. Revista Colombiana de Estadística , 34 (2), 249-266.         [ Links ]

Lu, J. & Bhattacharyya, G. (1990). Some new constructions of bivariate Weibull models. Annals of the Institute of Statistical Mathematics , 42 (3), 543-559.         [ Links ]

Manotas, E.C., Yáñez, S., Lopera, C.M. & Jaramillo, M.C. (2008). Estudio del efecto de la dependencia en la estimación de la confiabilidad de un sistema con dos modos de falla concurrentes. DYNA , 75 (154), 5- 21.         [ Links ]

Meeker, W. & Escobar, L.A. (1998). Statistical Methods for Reliability Data. London: John Wiley & Sons.         [ Links ]

Meeker, W. (2010). Trends in the Statistical Assesment of Reliability. In, N. Balakrishnan, M. S. Nikulin, N. Limnios, C. Huber-Carol & K. Waltraud. Advances in Degradation Modeling (pp. 3-16). New York: Springer.         [ Links ]

Meeker, W., Escobar, L.A. & Hong, Y. (2009). Using accelerated life tests results to predict product field reliability. Technometrics , 51 (2), 146-161.         [ Links ]

Nelson, W. (1990). Acelerated testing: Statistical models test plans, and data analyses. London: Jhon Wiley & Sons, New York.         [ Links ]

Rivest, L. & Wells, M.T. (2001). A martingale approach to the copula graphic estimator for the survival function under dependent censoring. J. Multiv. Anal , 79 (1), 138-155.         [ Links ]

Tsiatis, A. (1975). A nonidentifiability aspect of the problem of competing risks. Proc. Natl. Acad. Sci. USA , 72 (1), 20-22.         [ Links ]

Yáñez, S., Brango, H.A., Lopera, C.M. & Jaramillo, M.C. (2011). Comparación entre riesgos competitivos vía estimador cópula gráfico. Revista Colombiana de Estadística , 34 (2), 231-248.         [ Links ]

Zheng, M. & Klein, J.P. (1995). Estimates of marginal survival for dependent competing risks based on an assummed copula. Biometrika , 82 (1), 12-38.         [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.