Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería y competitividad
versão impressa ISSN 0123-3033
Ing. compet. vol.16 no.1 Cali jan./jun. 2014
Evaluación del desempeño a tensión por compresión diametral del concreto reforzado con fibras de acero ZP-306
Assessment of the splitting-tensile strength of ZP-306 steel fiber reinforced concrete
Julián Carrillo
Programa de Ingeniería Civil, Universidad Militar Nueva Granada, Bogotá D.C., Colombia
E-mail: wjcarrillo@gmail.com
Angélica P. Barrera-Peñaloza
Programa de Ingeniería Civil, Universidad Militar Nueva Granada, Bogotá D.C., Colombia
E-mail: angelicapbarrerap@gmail.com
Dago A. Acosta
Programa de Ingeniería Civil, Universidad Militar Nueva Granada, Bogotá D.C., Colombia
E-mail: dalejo.a@hotmail.com
Eje temático: Ingenieria civil / Civil engineering
Recibido: 21 de enero de 2013
Aceptado: 13 de septiembre de 2013
Resumen
El concreto reforzado con fibras de acero (CRFA) es un material con gran potencial de uso en viviendas de concreto de baja altura, ya que la capacidad de resistencia de los muros está controlada por la resistencia a tensión diagonal. El artículo presenta los resultados de un estudio experimental para caracterizar la resistencia a tensión por compresión diametral del CRFA que es elaborado con fibra ZP-306 y con concretos locales. El programa experimental incluyó el ensayo de 52 especímenes en forma de cilindros. En el estudio se discuten los modelos de predicción disponibles y se realiza un análisis estadístico para comparar los resultados calculados con los datos medidos. Con base en las tendencias de los resultados experimentales, se proponen ecuaciones para estimar los parámetros que describen la envolvente del comportamiento esfuerzo-deformación del CRFA sometido a esfuerzos de compresión diametral. Las ecuaciones se han desarrollado en un formato versátil para ser incluidas en un reglamento de diseño.
Palabras clave: compresión diametral, concreta reforzada con fibras de acero, contenida de fibras, resistencia a tensión.
Abstract
Steel fibers reinforced concrete (SFRC) is a material with great potential to be used in low-rise concrete housing because the strength capacity of the walls is controlled by diagonal tension strength. The paper shows the results of an experimental study intended to characterize splitting-tensile strength of SFRC made of both ZP-306 fiber and local concrete. The experimental program included the tests of 52 cylindrical-shaped specimens. The study discusses the available predictive models and shows a statistical analysis to compare the predicted results with measured data. Based on trends of the experimental results, equations to estimate the parameters describing the backbone of the stress-strain behavior of SFRC under splitting-tensile strength are proposed. The equations have been developed in a versatile format to be included in a design code.
Keywords: fiber content, splitting, steel fibers reinforced concrete, tensile strength.
1. Introducción
En la industrialización de la vivienda de uno y dos pisos, tanto para vivienda comercial como de interés social, los sistemas constructivos basados en muros monolíticos de concreto constituyen una solución adecuada ante eventos sísmicos, además de ofrecer rapidez de construcción, economía y sostenibilidad (Carrillo, 2010).
La adecuada resistencia a tensión del Concreto Reforzado con Fibras de Acero (CRFA) lo posiciona como un material con gran potencial de uso en este tipo de viviendas, ya que la capacidad de resistencia de los muros está controlada por la resistencia a tensión diagonal. La disponibilidad de información experimental sobre algunas de las propiedades mecánicas del CRFA elaborado con materiales locales, en especial de la resistencia a tensión, es una de las causas principales de la poca utilización de este material en las construcciones de Colombia.
Aunque NSR-10 permite el uso de CRFA, no se indican ecuaciones para estimar las propiedades mecánicas del CRFA. En este artículo se presentan los resultados de un estudio experimental para caracterizar la resistencia a tensión por compresión diametral del CRFA que es elaborado con fibra ZP-306 y con concretos locales. El programa experimental incluyó el ensayo de 52 especímenes en forma de cilindros.
En el estudio se evaluaron características tales como asentamiento, contenido de fibras, masa unitaria, peso específico, contenido de aire, resistencia a compresión, así como la elaboración de la curva esfuerzo-deformación en tensión por compresión diametral. En el artículo se discuten los modelos de predicción disponibles y se realiza un análisis estadístico para comparar los resultados calculados con los datos medidos. Con base en las tendencias de los resultados experimentales, se proponen ecuaciones para estimar los parámetros que definen la envolvente del comportamiento esfuerzo-deformación del CRFA sometido a esfuerzos de tensión por compresión diametral.
2. Concreto reforzado con fibras de acero, CRFA
En la sección C.11.4.6.1 de NSR-10 se indica que las fibras de acero se pueden utilizar para remplazar el refuerzo mínimo por cortante en vigas con altura menor de 600 mm, construidas con concreto de peso normal con resistencia a compresión menor de 40 MPa, y sometidas a un esfuerzo a cortante menor de φ0.17√f' c (donde f'c es resistencia a compresión del concreto y φ es el factor de reducción de resistencia, φ = 0.75). Si se cumplen los parámetros anteriores, se puede utilizar CRFA con una dosificación mayor o igual a 60kg/m3, para remplazar el refuerzo convencional de estribos. Adicionalmente, el CRFA debe cumplir con los límites asociados al desempeño a flexión especificados en la sección C.5.6.6.2 de NSR-10 y, con base en la sección C.3.5.8 de NSR-10, las fibras de acero deben tener relación aspecto no menor a 50 y no mayor a 100. Es importante destacar que NSR-10 no establece requisitos del CRFA para otros elementos estructurales, tales como losas, columnas y muros. Adicionalmente, NSR-10 no propone modelos o ecuaciones para estimar las propiedades mecánicas del CRFA, en especial, las propiedades que gobiernan el desempeño a tensión del CRFA, tal como la resistencia a tensión por compresión diametral.
2.1 Fibras de acero
Las fibras de acero se pueden caracterizar por medio de la relación de esbeltez o de aspecto (lf/ df), la resistencia a tensión del acero o por las características de su desempeño estructural. La relación lf/df se define como el cociente entre longitud y diámetro de la fibra. Por otro lado, la resistencia a tensión de las fibras depende de la calidad del acero; por ejemplo, para contenido bajo o medio de carbono, la resistencia a tensión de las fibras varía entre 400 MPa y 1500 MPa. Al incrementar el contenido de carbono se pueden alcanzar resistencias a tensión cercanas a 2000 MPa; este tipo de fibras son especialmente adecuadas para concretos de alta resistencia (Blanco, 2008; Mármol, 2010). La dosificación, Df, representa la masa de las fibras de acero por unidad de volumen. La fracción de volumen de fibras, Vf, la cual se puede expresar en fracción o en porcentaje, se utiliza para expresar la dosificación de forma adimensional y se calcula como el cociente entre Df y la densidad del acero (γ).
2.2 Resistencia a tensión directa
A diferencia de la resistencia a compresión, la resistencia a tensión del CRFA es significativamente mayor a aquélla de un Concreto Simple, CS, (Ponce, 2008). Para CRFA, la disipación de energía que se desarrollan después de la primera grieta son mayores que los observados en un CS (Blanco, 2008). Sin embargo, es difícil medir la resistencia a tensión pura del concreto, ya que se requieren dispositivos complejos de sujeción para aplicar en los especímenes una carga concéntrica, y los mismos especímenes deben ser elaborados con una geometría especial que requiere el uso de moldes de difícil construcción. Por tanto, se han desarrollado técnicas para evaluar de forma indirecta la resistencia a tensión del concreto, entre las que se destacan las resistencias a tensión por flexión y por compresión diametral.
3. Resistencia a tensión por compresión diametral
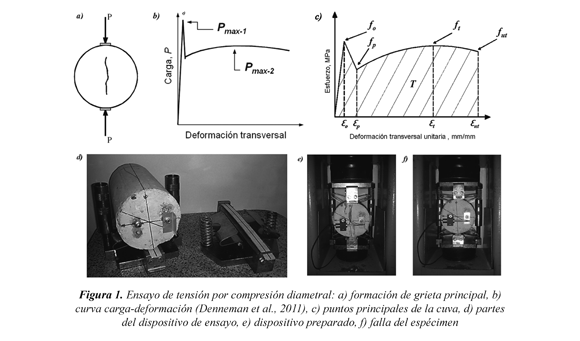
Durante el ensayo de resistencia a tensión por compresión diametral, conocido como ensayo de tensión por hendimiento (NSR-10) o como ensayo brasilero, las cargas se aplican a un cilindro de concreto de 300 mm de altura y 150 mm de diámetro, tal como se muestra en la Figura 1a. Según NTC-722 (2000), la resistencia a tensión por compresión diametral se calcula por medio de la Ec. 1, donde P es la carga máxima aplicada y, l y d son la longitud y el diámetro del cilindro, respectivamente.
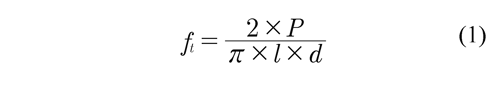
Para evaluar la contribución de las fibras a la capacidad de resistencia a tensión por compresión diametral del concreto, varios autores han propuesto modificaciones al ensayo estandarizado para CS. Por ejemplo, Denneman et al. (2011) adicionaron al ensayo estándar la medición de la deformación transversal perpendicular a la carga aplicada como se muestra en la Figura 1a, para así obtener la curva completa esfuerzo-deformación (Figura 1b). Por medio de una simulación numérica realizada con los datos medidos, Denneman et al. (2011) observaron que la resistencia máxima a tensión por compresión diametral para CRFA, ft (Figura 1c), corresponde al punto máximo (Pmax-2) que se presenta después del primer pico de la curva. Lo anterior, ya que el primer pico de la curva (Pmax-1) representa el límite del estado elástico del CS, a partir del cual inicia la contribución de las fibras.
En la Figura 1c se indican los parámetros principales asociados a la curva envolvente medida durante el ensayo de tensión por compresión diametral; donde, fo es la resistencia a tensión por compresión diametral, ft es la resistencia máxima, fp es la resistencia asociada al inicio de la contribución de las fibras, fut es la resistencia última a tensión por compresión diametral; Ɛ o, Ɛt, Ɛ p y Ɛut son las deformaciones unitarias asociadas a f , f, f y f, respectivamente, y T es la tenacidad otp ut en compresión diametral. Los resultados de la revisión de la literatura revelaron que la mayoría de modelos disponibles sólo propone ecuaciones para estimar ft. A continuación se presentan y discuten los modelos más representativos.
3.1 Modelos de predicción existentes
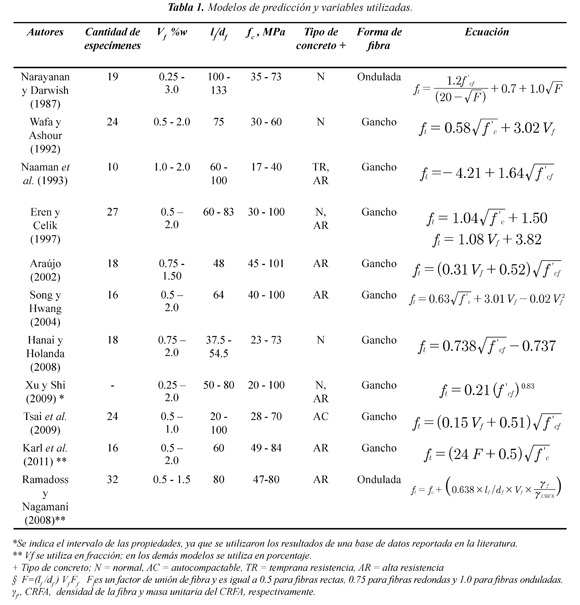
En la Tabla 1 se indican algunos modelos de predicción disponibles en la literatura y las principales variables que se usaron en los experimentos. En cuanto al tipo de muestras, en todos los estudios se utilizaron cilindros con dimensiones estandarizadas (150 mm de diámetro y 300 mm de longitud). Todos los modelos que se indican en la tabla son empíricos; es decir, se obtuvieron a partir de correlaciones con los datos medidos o con bases de datos reportadas en la literatura. En la tabla se observa que los modelos de Naaman et al. (1993), Eren y Celik (1997) y, Xu y Shi (2009), dependen sólo de f'c ó de f'cf.
3.2 Tenacidad
La tenacidad se define como la capacidad del CRFA en seguir resistiendo cargas después de la aparición de la primera grieta, sin llegar al colapso de la estructura. La tenacidad es usualmente cuantificada como el área bajo la curva carga-desplazamiento que se obtiene experimentalmente en ensayos en flexión, tensión o compresión. La principal variable que influye en la tenacidad es la capacidad de adherencia de las fibras (Mármol, 2010). Para el ensayo a flexión, la tenacidad se puede evaluar en términos absolutos, con dos variaciones del método de medición, o en términos relativos. En este último caso, la tenacidad se puede evaluar hasta un determinado desplazamiento y, por tanto, se utilizan índices de tenacidad (It). Estos índices se establecen para diferentes valores de desplazamiento, los cuales se proponen como múltiplos del desplazamiento asociado a la primera fisura. Los índices de tenacidad que se especifican en ASTM-C1609-05 (2005) reflejan principalmente ![]() el incremento de tenacidad debido a la contribución de las fibras, en lugar de reflejar el incremento de resistencia a la primera fisura que se especifica en ACI-544 (1996). Sin embargo, para el ensayo de resistencia a tensión por compresión diametral aún no se han establecido los desplazamientos para obtener los índices de tenacidad.
el incremento de tenacidad debido a la contribución de las fibras, en lugar de reflejar el incremento de resistencia a la primera fisura que se especifica en ACI-544 (1996). Sin embargo, para el ensayo de resistencia a tensión por compresión diametral aún no se han establecido los desplazamientos para obtener los índices de tenacidad.
4. Programa experimental
Para evaluar la resistencia a tensión por compresión diametral del CRFA elaborado con fibras de acero Dramix ZP-306, se utilizó una mezcla de concreto con cuatro dosificaciones de fibras. El programa experimental incluyó el ensayo de 52 especímenes en forma de cilindros. Se utilizaron 12 cilindros para evaluar el contenido de fibras, 28 especímenes para resistencia a compresión y 12 especímenes para resistencia a tensión por compresión diametral y peso específico (en estado endurecido). Adicionalmente, se evaluaron las principales propiedades del concreto en estado fresco.
4.1. Variables de estudio y elaboración de especímenes
El concreto empleado en la elaboración de los especímenes fue premezclado en planta. El tipo de concreto fue de peso normal con resistencia nominal a compresión, f'c = 25 MPa y con tamaño máximo de agregado de 10 mm. De acuerdo con el ancho mínimo de los muros de concreto para vivienda de baja altura (100 mm), así como con los requisitos de NSR-10 y con los resultados de investigaciones previas (Carrillo, 2010; Carrillo et al., 2013), en este estudio se seleccionó la fibra Dramix ZP-306, la cual es una fibra de tramo recto con ganchos en los extremos. La longitud, diámetro y relación lf/ df de la fibra seleccionada es 30 mm, 0.62 mm y 48, respectivamente. El valor proporcionado por el fabricante de la resistencia a tensión de la fibra es 1270 MPa.
Las dosificaciones de fibras se establecieron como porcentaje de la dosificación mínima que se establece en NSR-10 para proporcionar el refuerzo mínimo por cortante en vigas (Df-min = 60 kg/m3). Para estudiar dosificaciones menores que la mínima propuesta para vigas y que pudieran utilizarse en muros de baja altura, en este estudio se utilizaron cuatro dosificaciones: 0, 25, 50 y 100 % de Df-min; es decir, dosificaciones de 0, 15, 30 y 60 kg/m3. La cantidad de fibras asociada a cada dosificación se adicionó y mezcló en el sitio dentro de la mezcladora mecánica del camión transportador. El mezclado de las fibras se realizó siguiendo las recomendaciones del fabricante; es decir, la tasa de adición de fibras al concreto fresco fue aproximadamente igual a 1.7 kg/min y el tiempo de mezclado fue el mayor entre 1 min/m3 ó 5 min. El proceso de curado de todos los especímenes consistió en la aplicación de una membrana de curado tipo emulsión acuosa de parafina, con referencia Antisol blanco.
4.2 Configuración de ensayos mecánicos
Los ensayos de compresión se realizaron siguiendo los lineamientos de NTC-673 (2000). La carga se aplicó a una velocidad de 4.4 kN/min, por medio de una máquina universal marca Controls, referencia MC-66, con capacidad máxima de 2000 kN. En esta máquina, la carga aplicada se mide por medio de un sensor de presión marca Gefran con referencia TPS. Para garantizar la distribución uniforme de la carga, se utilizaron neoprenos en los dos extremos de los cilindros.
Los ensayos de tensión por compresión diametral se realizaron siguiendo los lineamientos de NTC722 (2000), es decir, el esfuerzo se calculó por medio de la Ec. (1). En la Figura 1d se muestra el dispositivo de ensayo, el cual consiste en dos guías para garantizar que la carga se aplique en el centro del diámetro del cilindro. Para aplicar la carga se utilizó la máquina utilizada para los ensayos de compresión. Aunque NTC-722 (2000) no específica la medición del desplazamiento transversal, en este estudio se midió dicho desplazamiento para delinear la curva completa esfuerzo-deformación y así observar la capacidad de desplazamiento después del primer pico de resistencia a tensión por compresión diametral (P, Figura 1b). El desplazamiento transversal max-1 se midió con dos transductores de desplazamiento lineal (uno en cada cara del espécimen), de marca Controls, referencia 82P0331/D y capacidad máxima de 10 mm. Para sujetar los transductores de desplazamiento se realizaron dos anclajes de 4.8 mm (3/16") de diámetro, en cada cara de los cilindros de concreto. Para ello, se utilizó el sistema de anclaje con adhesivo tipo HILTI de referencia HIT-RE-500 SD, el cual se utiliza para fijaciones en concreto de peso normal.
Para la adquisición de los datos durante las pruebas se utilizó una tarjeta marca National Instruments de referencia NI-SCC-68, con módulo de acondicionamiento para sensores de puente completo, de referencia SCC-SG24. El desplazamiento transversal del espécimen se calculó como el promedio de los registros de desplazamiento obtenidos con los dos transductores que se ubicaron en cada cara del espécimen. La deformación unitaria se calculó utilizando la separación medida entre los dos anclajes que sirvieron para sujetar cada transductor. En este estudio, la tenacidad en compresión diametral se calculó como el área bajo la curva carga (kN) - deformación (mm), y por tanto, la unidad de medida es el Joule (J).
5. Resultados y discusión
Para analizar los datos medidos se utilizaron dos parámetros estadísticos: el coeficiente de variación (CV) y el coeficiente de correlación (r). El coeficiente CV representa la relación entre la desviación estándar (S) y el promedio (X) de la muestra, y permite comparar las dispersiones de los datos medidos; es decir, CV es directamente proporcional a la dispersión. El coeficiente r mide el grado de intensidad de una posible relación entre los parámetros medidos y calculados.
5.1 Propiedades del concreto en estado fresco
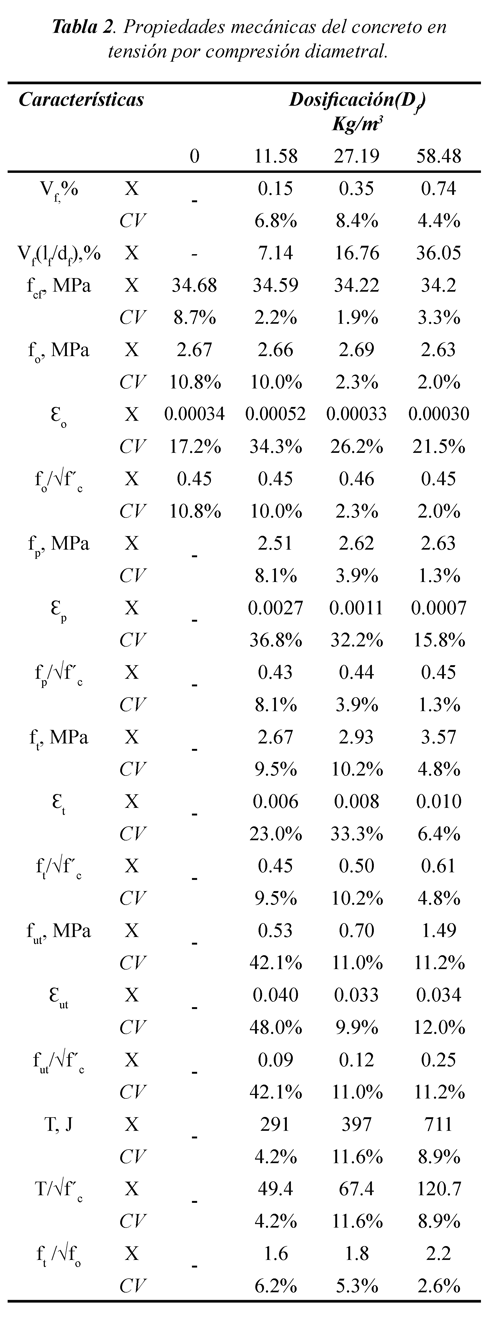
Para medir el valor real de la dosificación de fibras en las tres mezclas de concreto, se siguieron los lineamientos de EN-14488-7 (2007). Se utilizaron tres cilindros de 150 mm de diámetro y 300 de altura para tomar muestras de CRFA en estado fresco. Para inactivar el material cementante, se adicionó suficiente agua a las mezclas. Luego, las fibras se secaron en temperatura ambiente y se extrajeron con un imán. Por último, se determinó el peso de las fibras para así obtener el contenido real de fibras de cada dosificación. Para el análisis de la información medida, en este estudio siempre se utiliza el valor de la dosificación real de fibras que se muestra en la Tabla 2.
En general, la manejabilidad del CS fue mayor a la del CRFA. El asentamiento disminuyó significativamente a medida que la dosificación de fibras aumentó, por ejemplo, disminuyó desde 250 mm para CS hasta 85 mm para CRFA con la mayor dosificación de fibras.
Para medir la masa unitaria y el contenido de aire se siguieron los lineamientos de NTC-1926 (1995). En cuanto a la masa unitaria, el intervalo de los valores medidos (2285 kg/m3 y 2317 kg/m3) se encuentra dentro del límite establecido por NSR-10 (1440 kg/m3 y 2460 kg/m3). Para el peso específico, la tendencia es similar a la de la masa unitaria, pero los valores son aproximadamente 7% menores debido a la evaporación del agua de la mezcla. En cuanto al contenido de aire del CRFA, éste aumentó desde 1.07% para CS hasta 2.23% para CRFA con la mayor dosificación de fibras; es decir, aumentó aproximadamente dos veces en comparación con el contenido de aire del CS.
5.2 Propiedades del CRFA en tensión por compresión diametral
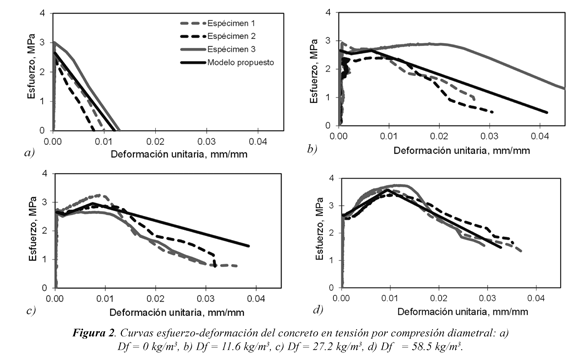
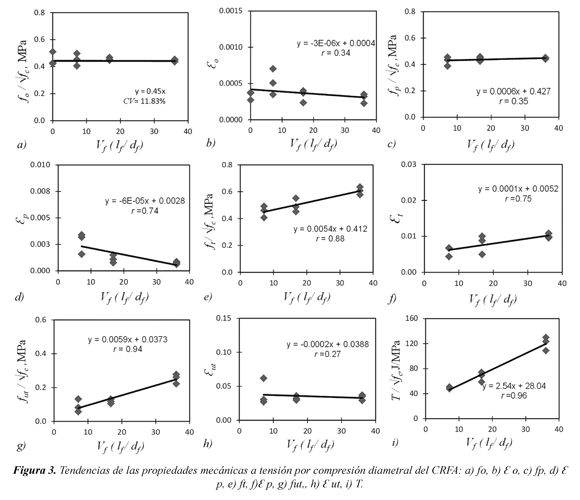
En la Figura 2 se muestran las curvas esfuerzo-deformación medidas durante los ensayos de tensión por compresión diametral para CS y CRFA. En la Tabla 2 se muestra el análisis estadístico de los valores medidos. En la Figura 3 se muestra la variación de las propiedades mecánicas medidas durante los ensayos. Para propósitos de diseño, los valores de resistencia se expresaron en función de la raíz cuadrada de la resistencia a compresión del CS √fc . De forma similar al formato de las ecuaciones propuestas en estudios experimentales previos (Carrillo, 2009; Carrillo, 2012), en la Figura 3 se presenta la relación entre las propiedades del CRFA sometido a esfuerzos de tensión por compresión diametral, y el producto del volumen de fibras y la relación de esbeltez de la fibra [Vf (lf/df)].
En la Figuras 3a se observa que la resistencia a tensión por compresión diametral (fo) permanece casi constante para todas las mezclas. Lo anterior se debe a que este parámetro está asociado a la formación de la primera grieta; es decir, para el punto donde aún no ha iniciado la contribución de las fibras. En la Figura 3b se observa que la deformación Ɛ o disminuye ligeramente con el producto [Vf (lf/df)] y, por tanto, la leve pendiente causa que esta disminución esté asociada a un valor de r significativamente bajo.
En la Figura 3c se observa que el esfuerzo fp incrementa levemente a medida que [Vf (lf/df)] aumenta. Esto se debe a que la degradación de resistencia después de la primera fisura es menor, a medida que aumenta la dosificación de fibras. La disminución de la degradación también se refleja en la deformación Ɛ p asociada a este parámetro (Figura 3d), pues esta deformación disminuye al aumentar el producto [Vf (lf/df)]. En las Figuras 3e y 5f se observa que ft, y Ɛt incrementan a medida que [Vf (lf/df)] aumenta, ya que en este punto, las fibras proporcionan al concreto no sólo la máxima capacidad de resistencia, sino también una capacidad de deformación a tensión mayor que la que se presenta en un concreto sin fibras.
En la Figura 3g se observa que fut aumenta con el manera, la resistencia última es significativamente mayor a la observada en un concreto sin fibras. En cuanto a la deformación Ɛut, en la Figura 3h se observa leve disminución de este parámetro, ya que las fibras logran restringir o mantener la capacidad de deformación máxima de la matriz de concreto. Por último, en la Figura 3i se observa que la tenacidad aumenta en forma lineal con el producto [Vf (lf/df)]. Esto se debe a que la adición de fibras aumenta la energía disipada, la cual está directamente relacionada con el área bajo la curva.
5.3 Modelo de predicción propuesto
A partir de las tendencias de los resultados experimentales, en este estudio se obtuvieron ecuaciones por medio de regresiones lineales. La precisión de las ecuaciones se evalúo por medio del coeficiente de correlación (r) o del coeficiente de variación (CV). En la Tabla 3 se muestran las ecuaciones propuestas, con su respectiva unidad y parámetro estadístico de evaluación.
Para utilizar las ecuaciones que se muestra en la Tabla 3, se deben cumplir las siguientes características producto del CRFA: (i) el tipo de concreto debe ser de peso normal (masa unitaria entre 2250 kg/m3 y 2350 kg/ m3), (ii) la resistencia a compresión del concreto debe variar entre 25 MPa y 35 MPa, (iii) la fibra debe tener extremos en forma de gancho y con resistencia a tensión de 1345 MPa y, (iv) el valor del producto Vf (lf/df) debe variar entre 7 % y 36 %.
5.4 Comparación de modelos de predicción
Para evaluar la precisión de la estimación de la resistencia máxima a tensión por compresión diametral (ft), por medio de los modelos disponibles en la literatura y el modelo propuesto en este estudio, se realizó un análisis estadístico del cociente entre los valores predichos y observados (P/O). Se realizaron dos evaluaciones; una con los modelos que dependen de √fc (o √fcf ) y algunas características de la fibra, y otra con el modelo que depende exclusivamente de ft. Cuando el cociente P/O es igual a uno, significa que, en promedio, el valor predicho es igual al valor medido; si el cociente P/O es menor que uno, el modelo resulta conservador, ya el valor calculado es menor que el valor medido; y si el cociente P/O es mayor que uno, el modelo arroja valores superiores a los medidos, es decir, el modelo resulta inseguro.
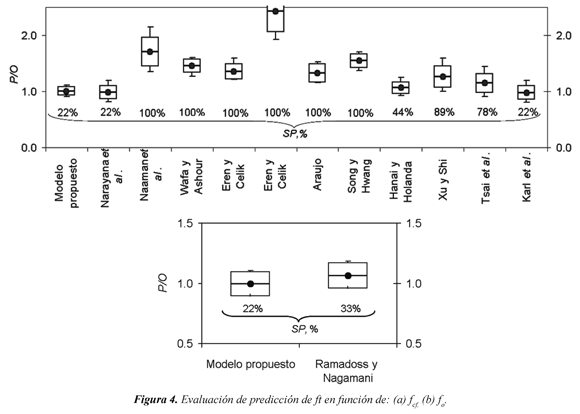
Para facilitar el análisis estadístico de la información, los resultados se presentan en la Figura 4 por medio de un diagrama de cajas y bigotes (box and whisker chart, en inglés). Este diagrama muestra el promedio de los datos de P/O (circulo), la dispersión por medio de la desviación estándar (la altura total del recuadro representa dos veces la desviación estándar) y los valores extremos, máximos y mínimos (línea continua). En la Figura 4 también se muestra la sobre-predicción en porcentaje (Sp%), la cual corresponde al cociente entre el número de datos en los cuales el valor del cociente de resistencias es mayor que 1.05 y el número de datos de la muestra analizada.
En la Figura 4a se observa que los modelos que incluyen sólo el parámetro de resistencia a (de CRFA o de CS) y el volumen de fibras; es decir, los modelos de Xu y Shi (2009), Tasai et al. (2009), y Hanai y Holanda (2008), ya que al incluir un parámetro que representa a las fibras, la ecuación resulta más acertada. Sin embargo, en estos modelos, el valor de P/O es igual a 1.26, 1.14 y 1.06, respectivamente; es decir, los modelos también son inseguros. De esta manera, se obtiene una sobre-predicción de 89%, 78% y 44%, y valores de CV iguales a 0.2%, 0.2% y 0.1%, respectivamente compresión (de CRFA y de CS); es decir, los modelos de Naaman et al. (1993) y Eren y Celik (1997) (Tabla 1), resultan ser los más inseguros, pues se obtienen valores mucho mayores a los medidos. Por ejemplo, el valor de P/O es igual a 1.70 y 2.42 (CV igual a 0.2%), respectivamente y, por tanto, estos modelos sobre-predicen en 100% la resistencia.
La precisión de la predicción es mayor en los modelos que incluyen la resistencia a compresión. Los modelos que además de la resistencia a compresión y el volumen de fibras integran parámetros como la relación de esbeltez y el efecto del tipo de anclaje de las fibras; es decir, los modelos de Narayanan y Darwish, y Karl et al., mejoran aún más la predicción de la resistencia, puesto que el valor promedio de P/O es de 0.98 y un CV de 0.1%, en los dos modelos. Sin embargo, estos modelos sobre-predicen la resistencia en 22%, aproximadamente.
En el modelo aquí propuesto, el valor promedio de P/O es igual a 1.00, el CV es 0.1%, y la sobre-predicción es 22%. La precisión del modelo es mayor que la obtenida con los modelos disponibles en la literatura, ya que el modelo aquí propuesto utiliza el producto [Vf (lf/df)], el cual incluye integralmente las características principales de la fibra, tales como la relación de esbeltez y el volumen de fibras.
En la Figura 4b se muestra la comparación entre los modelos que dependen de fo y diferentes parámetros de las fibras; es decir, se comparó la Ec.6 de la Tabla 3 (este estudio) y el modelo de Ramadoss y Nagamani (2008) (Tabla 6). Se considera que el modelo aquí propuesto es notablemente acertado, ya que el cociente P/O es de 0.99, y la sobre-predicción es 22%. Por otro lado, el modelo de Ramadoss y Nagamani presenta un cociente P/O de 1.06 y una sobre-predicción de 33%; es decir, es inseguro.
6. Conclusiones
En el estudio se observó que la resistencia a tensión por compresión diametral y su deformación unitaria asociada se mantienen casi constantes para el CS y el CRFA, ya que a partir de este punto se inicia la contribución de las fibras de acero. Sin embargo, la resistencia máxima a tensión por compresión diametral y su deformación unitaria asociada incrementan con el producto [Vf (lf/df)], ya que en este punto las fibras proporcionan un efecto de "enganche" en el concreto, lo que genera un incremento en sus capacidades de resistencia y de desplazamiento. En cuanto a la tenacidad, se observó que ésta aumenta de manera lineal cuando incrementa el cociente [Vf (lf/df)]; es decir, se demuestra que la dosificación y la relación de aspecto de las fibras incrementan la energía disipada del concreto.
Los modelos propuestos en la literatura que no incluyen explícitamente las características de la fibra, sobre-predicen en 100% la resistencia máxima a tensión por compresión diametral. Las ecuaciones que incluyen la dosificación, la relación de aspecto y el tipo de gancho de la fibra de acero, incrementan la precisión y disminuyen la variación de la predicción. Por otro lado, la forma funcional de algunos modelos de predicción no es adecuada para ser incluidos en un reglamento de diseño, en donde se requieren ecuaciones no sólo precisas, sino de fácil aplicación. En general, los modelos disponibles en la literatura sólo proponen ecuaciones para evaluar la resistencia máxima a tensión por compresión diametral. En este estudio se han obtenido ecuaciones para estimar los parámetros que caracterizan la envolvente de la curva completa esfuerzo-deformación. Las ecuaciones propuestas buscan simplificar la obtención de diferentes parámetros asociados con la resistencia y con la deformación en tensión por compresión diametral del CRFA. Con el propósito de incrementar la precisión y facilitar su uso por parte de los diseñadores, en las ecuaciones se incluyen explícitamente las características y la dosificación de las fibras.
Las recomendaciones de este estudio pueden ser de fácil implementación en un reglamento de diseño, lo que permitirá incrementar el uso del CRFA en diferentes campos de la ingeniería estructural, particularmente en los muros de concreto para vivienda de interés social, puesto que su comportamiento está controlado por la resistencia en tensión diagonal. En estudios futuros se deben definir los desplazamientos para obtener los índices de tenacidad del CRFA elaborado con materiales locales y sometidos a esfuerzos de tensión por compresión diametral.
7. Agradecimientos
Los autores expresan sus agradecimientos a la Universidad Militar Nueva Granada, UMNG, por el apoyo económico del Proyecto IMPING-1574, y a las Empresas Argos y Proalco (representante de Bekaert en Colombia), en especial a los Ing. Diego Velandia y Liliana Cardona, por la donación del concreto y las fibras, respectivamente. Asimismo, a la Ingeniera Pahola Porras, al Ingeniero Miguel Ospina y al Técnico Oliverio Pinzón, quienes colaboraron en la realización de los ensayos en el Laboratorio de Concretos y Estructuras de la UMNG.
8. Referencias bibliográficas
ACI - Comité 544. (1996). State-of-the-art report on fiber reinforced concrete (ACI 544.1R-96). Farmington Hills (MI): American Concrete Institute. [ Links ]
Araújo, D. (2002). Cisalhamento entre viga e laje pré-moldadas ligadas mediante nichos preenchidos com concreto de alto desempenho. Tesis de doctorado, Universidade de São Paulo, Sao Paulo, Brasil. [ Links ]
Blanco, A. (2008). Durabilidad del hormigón con fibras de acero. Tesis de Maestria. Universidad Politécnica de Cataluña (UPC), Barcelona, España. [ Links ]
Carrillo, J. (2010). Diseño sísmico de VIS construidas con muros de concreto. Revista escuela colombiana de ingeniería , 80, 7-17. [ Links ]
Carrillo, J., González, G., & Aperador, W. (2013). Correlaciones entre las propiedades mecánicas del concreto reforzado con fibras de acero. Revista Ingeniería, Investigación y Tecnología , 14, 435-450. [ Links ]
Denneman, E., Kearsley, E. & Visser, A. (2011). Splitting tensile test for fibre reinforced concrete. Materials and Structures , 44, 1441-1449. [ Links ]
Eren, O., & Celik, T. (1997). Effect of silica fume and steel fibers on some properties of highstrength concrete. Construction and building materials , 11, 373-382. [ Links ]
Hanai, J., & Holanda, K. (2008). Similarities between punching and shear strength of steel fiber reinforced concrete (SFRC) slabs and beams. Ibracon de Estruturas e Materiais , 1, 1-16. [ Links ]
Karl, K., Lee, D., & Hwang, J. (2001). Revision on material strength of steel fiber-reinforced concrete. International Journal of Concrete Structures and Materials , 5, 87-96. [ Links ]
Mármol, P. C. (2010). Hormigones con fibras de acero características mecánicas. Tesis de Maestria, Universidad Politécnica de Madrid, Madrid, España. [ Links ]
Naaman, A., Alkhairi, F., & Hammoud, H. (1993). High Early Strength Fiber Reinforced Concrete. In, Mechanical Behavior of High Performance Concretes, Strategic Highway Research Program. (p. 297). [ Links ]
Narayanan, R., & Darwish, I. (1987). Use of steel fibers as shear reinforcement. Structural Journal , 84 (3), 216-227. [ Links ]
Ponce, D. (2008). Hormigones de altas presentaciones. Proyecto de grado, Universidad Politécnica de Cartagena, Cartagena, Colombia. [ Links ]
Ramadoss, P., & Nagamani, K. (2008). Tensile strength and durability characteristics of high-performance fiber reinforced concrete. The Arabian Journal for science and engineering , 33, 307-319. [ Links ]
Song, P. & Hwang, S. (2004). Mechanical properties of high-strength steel fiber-reinforced Concrete. Construction and Building Materials , 18, 669-673. [ Links ]
Tsai, C., Li, L., Chang, C., & Hwang, C. (2009). Durability design and application of steel. The Arabian Journal for Science and Engineering , 34, 57-79. [ Links ]
Wafa, F., & Ashour, S. (1992). Mechanical properties of high-strength fiber reinforced concrete. ACI Materials Journal , 89, 449-455. [ Links ]
Xu, B., & Shi, H. (2009). Correlations among mechanical properties of steel fiber reinforced concrete. Construction and Building Materials , 23, 3468-3474. [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.