Identificación de parámetros dinámicos de la suspensión de un vehículo

Identification of dynamic parameters in vehicle suspension systems

Luz A. Mejía
Facultad de Ingeniería Mecánica, Universidad Tecnológica de Pereira, Pereira, Colombia
E-mail: adriamec@utp.edu.co

Francisco Valero
Centro de Investigación de Tecnología de Vehículos, Universidad Politécnica de Valencia, Valencia, España
E-mail: fvalero@mcm.upv.es

Vicente Mata
Centro de Investigación de Tecnología de Vehículos, Universidad Politécnica de Valencia, Valencia, España
E-mail: vmata@mcm.upv.es

Eje temático: Ingeniería mecanica / Mechanical engineering
Recibido: 24 de julio de 2013
Aceptado: 17 de enero de 2014

Resumen

En el presente trabajo se aborda la identificación de parámetros dinámicos en vehículos automóviles. Paso previo al desarrollo del problema de identificación, se desarrolla un modelo dinámico para la suspensión delantera de un vehículo de competición. El modelo dinámico se reduce mediante dos metodologías diferentes. La primera se basa en la Descomposición en Valores Singulares y la segunda por dos pasos consecutivos: eliminación de parámetros dinámicamente poco contributivos y Descomposición en Valores Singulares. Finalmente, ambos modelos son analizados y validados mediante el cruce de datos para otras trayectorias diferentes a las de identificación. El modelo obtenido utilizando la eliminación de parámetros poco contributivos reproduce de muy buena manera el comportamiento dinámico del sistema ante la inclusión de errores, por lo que dicha metodología se presenta como la más viable para la obtención del conjunto de parámetros base.

Palabras claves: contribución dinámica, dinámica vehicular, identificación de parámetros dinámicos, sistemas multicuerpo.

Abstract

This work presents the identification of dynamic parameters in automotive vehicles. In order to develop the identification problem, a dynamic model is obtained for the front suspension of a race car. Two new dynamic models are developed, the first of which is based on the Singular Value Decomposition (SVD), while the second comprises two consecutive steps: elimination of less contributive parameters and application of a SVD method. Finally, both models are analyzed and validated by means of data cross-referencing for new trajectories other than those used during the identification process. The model obtained using the elimination reproduces the dynamic behavior with very good approximation even with the inclusion of errors, so it is presented as the most viable methodology for obtaining base parameters.

Keywords: Dynamic contribution, dynamic parameter identification, multibody systems, vehicle dynamics system.

1. Introduction

In the dynamic models used for the simulation and control of systems, the values of certain parameters such as the terms of inertia, masses and the locations of centers of mass are fundamental for obtaining accurate results. The precise values of these dynamic parameters are difficult to obtain because they usually require experimental measurements that have a very high cost. Depending on the size and complexity of the system, it may not be a practical methodology.

Initially, the dynamic parameter identification procedure was developed for serial robots (Khosla and Kanade 1985, Atkenson et al. 1986, Gautier and Khalil 1988), then for closed chain systems such as parallel robots (Bhattacharya et al. 1997, Guegan et al. 2003, Abdellatif et al. 2004 and Grotjahn et al. 2004) and later for vehicle systems (Russo et al. 2000, Chen and Beale 2003, and Venture et al. 2006) and biomechanics (Kraus et al. 2005, Gordon and Hopkins 1997, and Silva et al. 1997). An area such as automotive engineering is not indifferent to the advantages that the identification process contributes to the design and completion of vehicles. Today, there are several commercial software programs for dynamic simulation of vehicles, which allow the real system to be replaced by a virtual one, but the validity of the results depends largely on the accuracy of the dynamic parameters used.

The main objective of this study is to extend the dynamic parameter identification methodology from robotics to vehicle systems. To this end, the results are validated with virtual simulation data collected by the MSC Adams® computational package program. This paper is organized as follows. The second section presents a dynamic model of push-rod front suspension. A dynamic model is then obtained for parameter identification. Comparisons between symbolic and numerical models appear in the fourth section and the most significant conclusions are presented in the fifth section.

2. Identification methodology

2.2 Dynamic model

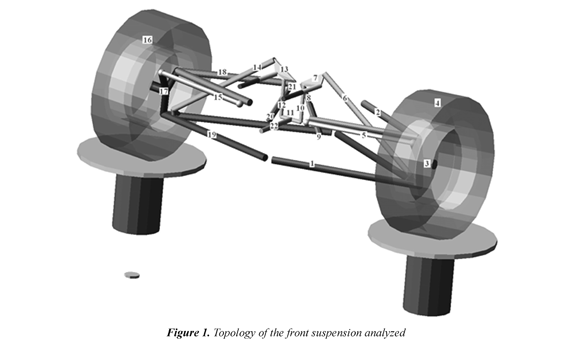
In the suspension that we analyzed, the linkages are considered as rigid bodies, without friction and clearances in the kinematic pairs. The behavior of the damping is considered linear with respect to speed, and the forces and moments applied at the tire contact path are expressed as loads applied at the center of the wheel. The topology (figure 1) corresponds to a double wishbone type front suspension with push-rods, which connects the lower rocker arms to the bell crank and is attached to the chassis with torsion bars instead of coil springs. The antiroll bar allows loads to be transferred from the right to the left side of the suspension. The system has 4 degrees of freedom, vertical movement and the spin of the wheel (Table 1). The generalized coordinates q^→= [x, yl, zl, β0₂₂, ..., β1₂₂,β2₂₂,β3₂₂]^T correspond to the translation and orientation of each local reference frame and Euler parameters are used. These local reference frames are not centroidal. The equation of motion is derived from the Lagrangian formulation,

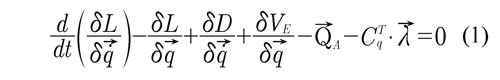
where L is the Lagrangian function, V_E is the elastic potential energy, D is the dissipative energy, τ^→ is the vector of generalized forces, Cq^T is the constraint Jacobian matrix and λ^→ is the vector of Lagrange multipliers. For this particular case, the Lagrangian function is composed only of the kinetic energy and the potential energy is zero because the weight of the components is included as an external gravitational force. The kinetic energy of the element i is given by,

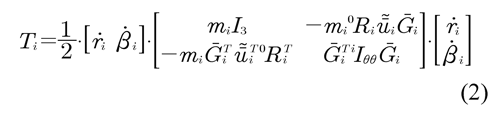
where m_i is the mass of body i. ⁰R_i is the transformation matrix from the body coordinate system i to the global coordinate system. u_i is the screw symmetric matrix of the position vector The first term _dnis n x 1 matrix defined as,

Derivates of the potential and dissipative energies

The spring elements of the suspension are formed by a pair of torsion bars connecting the suspension to the chassis. This system is simplified by replacing the fixed joint for a revolute joint between the bell crank and the chassis and a torque in opposition to its motion as a function of the torsion stiffness of the bar and the turn of the bell crank. Thus, the elastic potential energy is determined as a generalized force. The term corresponding to the derivative of dissipative energy is determined by obtaining the non-conservative forces that depend linearly on the velocity. It is the Raleigh dissipation function of the damper,

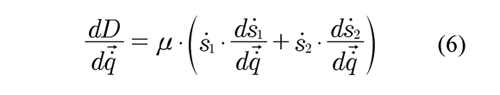
where μ is the damping coefficient and S^.i² is the relative velocity between the upper and lower strut. Although it is known that the damping coefficient is nonlinear, a first approximation is performed, which is considered linear.

Generalized forces

The vector of generalized forces associated with the coordinates of the reference point groups the external and gravitational forces,

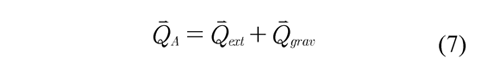
The external forces Fo and Mo applied to the element and 4 and 16 (wheel^→ axles) are^→ equivalent to the forces and moments generated by the ground to the tire at the contact path, which are transferred to the center of mass of the wheel. These actions generate the first generalized force, which is determined by the principle of virtual work as,

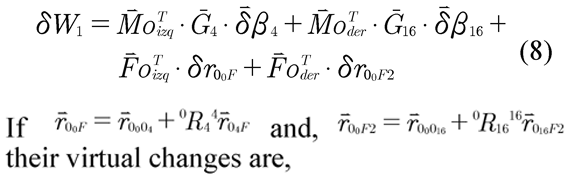
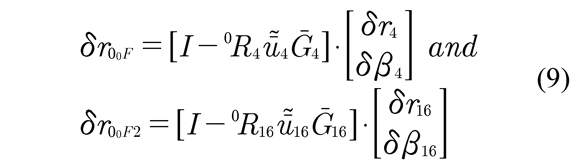
Other generalized forces are those obtained by replacing the action of the torsion bars for a revolution-torque applied to the bell cranks of the suspension system. In this case, the torque generated will be,

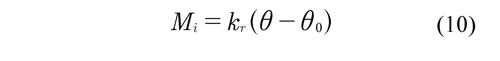
where k_r is the torsion stiffness of the bar, _? is the relative angular displacement between bell crank and chassis and ?₀ is the angle before displacement. For the bell cranks (elements 7 and 13), the definition of these generalized forces is obtained using the virtual work formulation

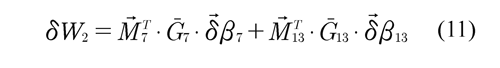
The generalized forces associated with the gravity forces are constituted by the weight of each component of the system. These have not been included in the determination of the potential energy on obtaining the Lagrangian function. The gravitational forces of the element i are obtained as,

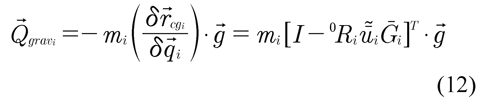
Comparing the equation obtained by adding (8), (11) and (12) with (13),

2.3 Model of identification process

Thanks to the convenient location of the local reference systems of the elements (not centroidal), the dynamic model given by equation (1) is linear with respect to the dynamic parameters; however, it is necessary to regroup as

where K and t^→ are the coefficient matrix that relates the inertial parameters and the vector of generalized forces which include externally applied forces and those due to springs and dampers. The vector of dynamic parameters is made up of inertia terms, the product between the mass and the center of mass and the mass of each element of the mechanical system thus,

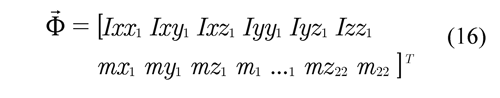
Identifying the dynamic parameters usually also includes the torsion stiffness of the torsion bars and the damping coefficients. However, in this work these parameters are not included because these elements are often modified by engineers to improve the set-up of the vehicle.

K for each element i of the system can also be obtained from the equation of motion determined by Chen and Beale (1999) through of the equation (17),

Regrouping the terms related to the dependent and independent coordinates of equation (15), it can be written as,

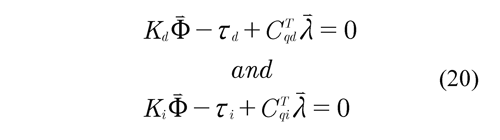
By solving equation (20) for the vector of Lagrange multipliers ?, a linear dynamic model is obtained with respect to the dynamic parameters,

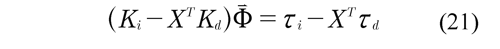
where X = C_qd^-1 . C_qi. It is necessary to consider the inverse of the dependent Jacobian matrix; consequently, the selection of coordinates must guarantee a matrix C_q^dT of full column rank.

The resulting model equation (21) includes a number of equations equal to the degrees of freedom of the system (4 DOF). Since each element includes 10 inertial parameters (220 parameters), this is a system that cannot be solved by the Least Square Method. The way to solve this problem is to include equations corresponding to different positions of the mechanical system to obtain an overdetermined linear system. The matrix obtained is called Observation Matrix of the suspension and a linear dynamic model is obtained with respect to the dynamic parameters,

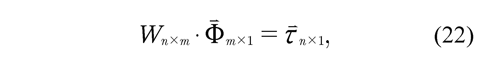
where m is the number of dynamic parameters.

Some of the parameters do not contribute to the dynamics of the system. Additionally, due to the physical nature of the kinematic restrictions, they can only contribute as linear combinations. Therefore, the matrix W is usually rank deficient. However, the solution of the system expressed in equation (22) requires full rank in the observation matrix, which involves reducing the system and obtaining a new set of parameters called base parameters.

2.4 Base parameters

The methodologies used to simplify the system, and consequently to obtain the base parameters in serial and parallel robots (Diaz et al. and Farhat et al.), include the use of methods such as symbolic reduction based on a visualization of possible linear combinations or a numerical procedure such as Singular Value Decomposition or QR Decomposition. However, for moderately large dynamic models, as is the case of the vehicle suspension analyzed here, these methods are not enough. This article presents a reduction procedure involving characterization of the dynamic contribution, since many of the parameters included in the model have a very low influence on dynamic performance but result in an observation matrix with an extremely high condition number. Therefore, before using linear algebra, it is proposed that the model should be simplified according to the contribution of each parameter to the dynamics of the system.

2.4.1 Reduction by characterization of the dynamic contribution

In the field of race car suspension, the location of the elements, packaging issues and the use of lightweight materials causes many of these parameters to have little influence on the dynamics of the system. A consequence of these great differences of contribution is the generation of an ill-conditioned observation matrix, which involves a greater influence of errors from the experimental data and certain inaccuracies of correspondence between the underlying analytical model and the actual system.

To identify these parameters which allow dynamic contribution it is necessary to have an initial estimation of the parameters that can be obtained from the geometry of the elements and the properties of their materials. CAD programs allow us to obtain an initial estimation with a certain degree of approximation. The contribution of the i-th dynamic parameter will be defined as follows,

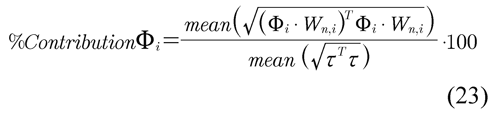
It is worth noting that the contribution defined in equation (9) can be obtained as an average value over a set of different trajectories.

Parameters that contribute little can be eliminated from the vector of parameters F and the corresponding columns of the observation matrix W, thus resulting in a new reduced linear system,

It should be clarified that the dynamic behavior of the system addressed in (24) will not be equal to the original one; therefore, the elimination criterion has to be based on the improvement of the condition number of matrix W, keeping the permissible error between the system (24) and the original one as small as possible. This error can be quantified by means of the absolute relative error defined by the equation,

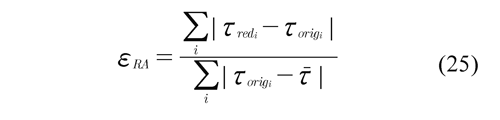
Besides postulating the parameters that contribute most as identifiable parameters, the characterization methodology also makes it possible, when considered for different trajectories, to make an initial estimation of the type of movements that act on a greater number of parameters or movements that excite certain parameters of interest. The trajectories obtained that improve on the identification process will not be evaluated in this study and will form part of future studies.

2.4.2 Reduction by SVD

The purpose of this methodology is to obtain a full rank observation that makes it possible to solve the system using the least squares solution (LSM). Simplifying the system by means of the dynamic characterization of parameters makes it possible to obtain a reduced system using only the parameters that contribute to the dynamics of the suspension; nevertheless, these can have an influence in combination with other parameters, not separately but rather linearly. Subsequently, a full rank observation matrix is achieved by Singular Values Decomposition, obtaining a basic set of parameters W_red • F_red = W_red • F_red. The matrix Wred is decomposed into singular values as,

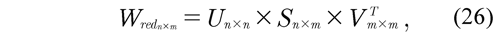
where U and V are orthogonal matrices and S is a diagonal matrix with singular values s₁, s₂, ..., s_r of W_red and r is its rank. The matrix V is divided as

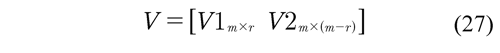
If the system is rank deficient,

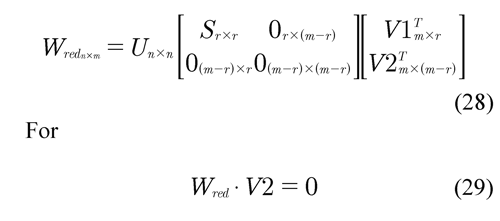
As the previous equation shows, the V2 matrix defines the dependence relationships between the columns of the observation matrix. An independent column in W_red corresponds to a null column in V2. By regrouping V2 and obtaining a submatrix with full rank, it determines the permutation matrix P so that,

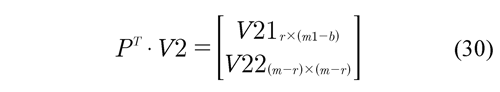
The determination of V22 is not unique and therefore it is also not unique for the permutation matrix. Although for serial and parallel robots they are usually obtained from the first or last row of V2, adding rows whenever these increase the rank of the matrix, for suspensions this type of grouping does not represent an evident natural regrouping of the parameters. By simplification, W_red will be denoted below as W, and F_red as F. The first r columns of the permutation matrix are independent,

For the system mentioned here, it is necessary to emphasize that its solution represents the combination of several parameters, the determination of each individual parameter being impossible. Besides, the values of the vector t^→ differ to some degree of error from the values of the simulated system due to the elimination of noncontributing parameters and to the numerical errors caused by matrix XT from equation (38).

The quality of the parameters is obtained with relative standard deviation for each parameter,

where t^→ and t^→_iden are the forces of the actual system and those obtained from the model using the parameters identified, respectively; and n, m are the dimensions of W1.

3. Discussions and results

The data used in the validation of the dynamic model and subsequent identification of parameters are obtained using MSC Adams in a simulated system, considering the geometry and topology of the real physical system.

3.1 Dynamic characterization

In order to determine the dynamic contribution of each parameter in the suspension dynamics, two excitation trajectories were used for the vertical motion of the wheels at different amplitudes and frequencies. Both trajectories are vertical translations applied to the wheels as variablefrequency harmonic functions, taking into account the limits allowed by the damper displacement and excitation frequencies in a wide range (0-50 Hz) to ensure all the system's operating conditions. The percentage of contribution is obtained by means of equation (23). Only 26 dynamic parameters are more significant than 1% of the total dynamics of the system. However, it is necessary to determine which parameters can be eliminated by virtue of the error obtained between the original system and the reduced one. It has been established that for a reduction of 0.3% - 0.5%, the dynamic error increases from 0.93% to 1.98%.

3.2 Obtaining the base parameters

If SVD is applied, where the rank of the matrix obtained is not given by the number of significant singular values but by the user; that is to say, the rank of the matrix is introduced in decreasing form, analyzing how it influences the condition number of the matrix W1. It is noted that if the rank of the observation matrix is reduced, its condition number improves. Nevertheless, this simplification can eliminate influential parameters from the model, which must be analyzed at the time of deciding how much to decrease the rank by. The absolute relative error e_R between the original and the reduced model is recorded as unsatisfactory if the rank is smaller than 18.

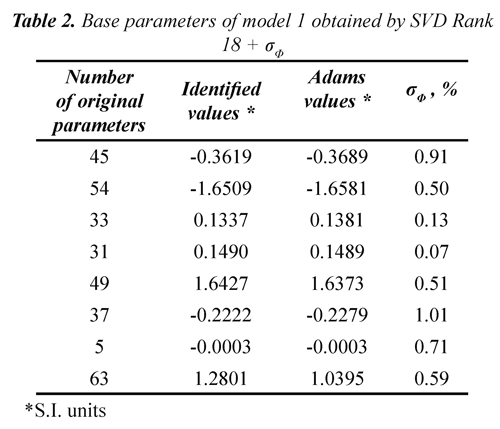
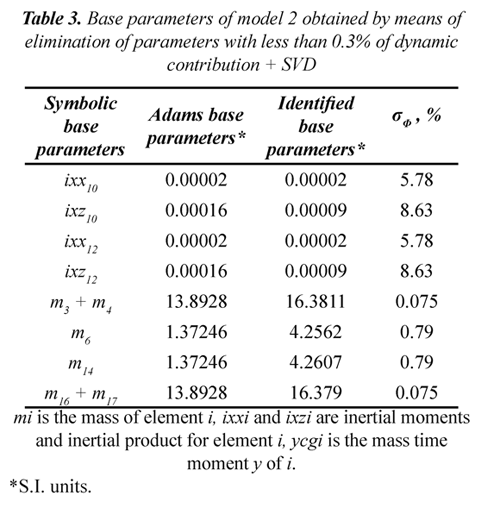
If we make a preliminary reduction before the application of SVD based on the results of the dynamic contribution, we see that the condition number of the matrix decreases by the extent to which we eliminated the less contributing parameters. As is known from the preceding analysis, contributions of less than 0.3% do not modify the original dynamic model significantly, so the criterion for eliminating less contributing parameters is established on the basis of this value. In this case, the removal of a 0.3% contribution has a better condition number. Solving both systems by least squares for the parameter vector base, tables 2 and 3 present the values obtained for the first and second model, respectively, and their values derived from the linear combination with data from MSC Adams. In the first case, the combination of parameters is not presented because of the large size of each term in the vector. As shown in the tables, the two models show good relative standard deviation for each parameter.

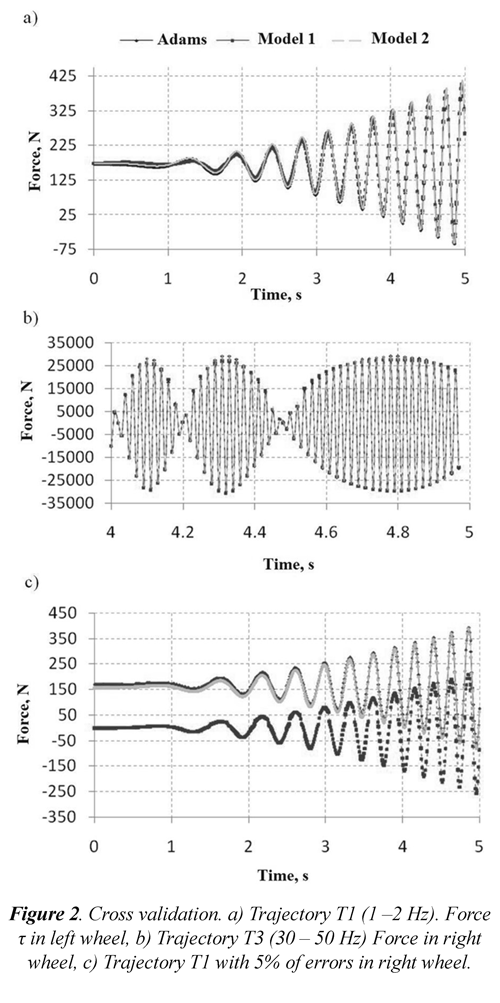
3.3 Cross validation

The sets of base parameters obtained must be validated by verifying these models on different trajectories from the one considered in the identification process for models with and without errors in the 5% of standard deviation in the model included. Even with the inclusion of errors, the models generated by the parameters identified represent a very good approximation to the original model (figure 2), except Model 1 (Singular Values Decomposition and elimination by means of relative standard deviation), which does not present a good approach at low frequencies. This occurs even though it was expected it would not be satisfactory due to the high condition number of matrix W1.

4. Conclusions

Although the first methodology of reduction of the system obtains a better conditioned model, the error it generates in the crossing of data is greater. In addition, this methodology produces highly combined base parameters. On the other hand, the second methodology allows the inclusion of errors in the identification forces and presents a satisfactory behavior for other trajectories.

In the same way, this methodology allows us to develop dynamic models of complex suspension systems based on a reduced number of identified dynamic parameters without significant loss of precision.

For another type of analysis, with lateral and longitudinal forces, where the behavior of the suspension is evaluated as part of the whole vehicle, it is possible to find other dynamic parameters that contribute to the dynamics under new operating conditions.

The proposed methodology for the identification of dynamic parameters has been verified successfully in a simulated system; however, its implementation in a real system requires special attention in reducing the condition number of the observation matrix, which allows for the inclusion of greater system error, as with a real system.

5. References

Chen, K. & Beale, D. (2003). Base Dynamic Parameter Estimation of a MacPaherson Suspension Mechanism. International Journal of Vehicle System Dynamics , 39 (3), 227-244.         [ Links ]

Diaz, M., Mata, V., Farhat, N. & Provenzano, S. (2008). Identifiability of the Dynamic Parameters of a Class of Parallel Robots in the Presence of Measurement Noise and Modeling Discrepancy. Mechanics Based Design of Structures and Machines, 36 (4), 478-498.         [ Links ]

Farhat, N., Mata, V. & Valero, F. (2008). Identification of dynamic parameters of a 3-DOF RPS Parallel Manipulator. Mechanism and Machine Theory , 43, 1-17.         [ Links ]

Jo, S. & Beale, D. (1998). Dynamic parameter Estimation of a MacPherson Strut Suspension. Vehicle Systems Dynamics , 30, 169-184.         [ Links ]         [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.