Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y competitividad
Print version ISSN 0123-3033
Ing. compet. vol.16 no.2 Cali July/Dec. 2014
Una propuesta de clasificación para los índices de estabilidad de tensión
Voltage stability indices - A review and a new classification
Sandra M. Pérez-Londoño*
E-mail: saperez@utp.edu.co
Gerard Olivar-Tost**
E-mail: golivart@unal.edu.co
Juan J. Mora-Flórez*
E-mail: jjmora@utp.edu.co
* Universidad Tecnológica de Pereira, Programa de Ingeniería Eléctrica, Pereira, Colombia.
** Universidad Nacional de Colombia, Depto de Eléctrica, Electrónica y Computación Manizales, Colombia.
Eje temático: INGENIERIA ELECTRICA / ELECTRIC ENGINEERING
Recibido: Marzo 5 de 2013
Aceptado: Octubre 31 de 2013
Resumen
En este artículo se presenta una revisión de las principales metodologías utilizadas para obtener índices de estabilidad de tensión en sistemas eléctricos de potencia. A partir de las clasificaciones propuestas en varias publicaciones, los autores proponen una descripción completa, mediante la inclusión de subcategorías que permiten una determinación rápida de las ventajas y deficiencias de cada propuesta. Como estrategia de presentación de la investigación, se realiza la descripción y clasificación en orden cronológico de algunas de las metodologías más relevantes en el período (1986 - 2012), utilizadas para la obtención de índices de estabilidad de tensión, considerando la información que se requiere para su implementación como criterio de clasificación. Adicionalmente, se realiza un análisis y discusión acerca de la evolución de los índices a partir de la utilización de los sistemas de medición. Finalmente, se presenta un análisis comparativo de las diferentes propuestas de implementación de índices, con el fin de entregar una referencia útil en la discusión relacionada con las metodologías de análisis de estabilidad de tensión en los sistemas eléctricos de potencia.
Palabras claves: clasificación, estabilidad de tensión, índices de estabilidad, revisión.
Abstract
This paper is oriented to present a review of the main approaches commonly used to obtain voltage stability indices in electric power systems. Starting from classifications previously presented, the authors propose a complete review including several subcategories, which help to have a better understanding of these approaches. As strategy to adequately present this research, a chronologically ordered description and a classification of the most relevant characteristics of these proposals, which are aimed to obtain the voltage stability indexes in a time period from 1986 to 2012, is detailed analyzed. The considered classification criterion is related to the information requirements of each one of the reviewed approaches. Additionally, an analysis and a discussion of the evolution of the indexes proposals considering the new available metering equipment are developed. Finally, this review is useful as a reference for discussions related to methodologies associated to voltage stability indexes for electric power systems.
Keywords: classification, review, stability index, voltage stability.
1. Introducción
El monitoreo permanente es indispensable en el sistema eléctrico de potencia (SEP), con el fin de determinar si éste se encuentra funcionando dentro de los estándares y límites de seguridad establecidos para mantener adecuadamente su estabilidad. En relación con la estabilidad de tensión, existen numerosas las metodologías disponibles en las bases bibliográficas para medir, con cierto grado de precisión, el margen de estabilidad del punto de operación del sistema eléctrico. La mayoría de estas mediciones se ha planteado en la forma de índices de estabilidad de tensión (IET), cuyo objetivo es definir una magnitud escalar que pueda ser monitoreada a medida que el sistema presenta cambios ante diferentes contingencias, con el fin de permitir a los operadores y analistas de las redes, realizar las respectivas acciones preventivas y/o correctivas ante un colapso de tensión.
Al realizar una revisión bibliográfica de los índices de estabilidad de tensión, se encuentran diferentes propuestas que proporcionan aproximaciones para determinar la distancia al punto de operación crítico en los SEP, pero existe una gran falencia de información detallada respecto a su organización y clasificación. Existen unas pocas excepciones, como en (Candelo, Caicedo & Castro, 2008) donde se realiza una revisión y comparación de las diferentes metodologías, y se establecen categorías; y también en (Karbalaei, Soleymani & Afsharnia, 2010), donde los autores realizan una clasificación según aquellos índices que se basan en la matriz Jacobiana y los que se basan en las variables y parámetros del sistema. Adicionalmente, teniendo en cuenta que en los últimos años, el monitoreo de los sistemas de potencia ha cambiado sustancialmente, debido a la utilización de unidades de medición fasorial PMU (Phasor measurement Unit, por sus siglas en ingles), en (Phadke & de Moraes, 2008) se presenta una clasificación de las metodologías utilizadas en el monitoreo de la estabilidad de tensión basadas en PMUs: métodos basados en mediciones locales y métodos basados en sistemas de monitoreo área amplia (WAM). Este último concepto ha tomado relevancia en los últimos años debido a la disponibilidad de PMUs con que cuentan los actuales (SEP), además tiene la ventaja de permitir el cálculo de índices con simplicidad y menor esfuerzo computacional (Phadke & de Moraes, 2008; Kamwa et al., 2006; Terzija et al., 2011).
Debido a que la cantidad de índices analizados y clasificados en las referencias (Karbalaei, Soleymani & Afsharnia, 2010; Glavic & Van Cutsem, 2009), es muy bajo y excluyente, el propósito de la revisión realizada en este artículo es entregar una perspectiva más amplia sobre la evolución que han tenido los índices propuestos en la literatura en un amplio periodo de tiempo, pero específicamente sobre aquellos que se han basado en mediciones. A partir de las clasificaciones dadas en (Candelo, Caicedo & Castro, 2008; Glavic & Van Cutsem, 2009), se propone una nueva que permite realizar una mayor cobertura de los índices planteados, para finalmente presentar un panorama organizado de la evolución que han tenido los índices desde los 80's, década en que se presentaron las primeras propuestas, hasta la actualidad. Al final del artículo se presenta una reflexión y discusión sobre las características más importantes de los IET considerados.
2. Clasificación de metodologías de análisis de estabilidad de tensión
Las metodologías utilizadas para analizar la estabilidad de tensión pueden tener innumerables formas de clasificación. Una de estas formas consiste en separarlas en metodologías estáticas y dinámicas, de acuerdo al modelo utilizado del SEP (Kundur, 1994). Es así como, las metodologías estáticas utilizan un modelo de estado estable o un modelo dinámico linealizado, para examinar la viabilidad del punto de equilibrio, representado por una condición específica del SEP. Dentro de esta categoría se encuentran aquellas basadas en análisis de sensitividad utilizando la matriz Jacobiana, tales como dV/dQ, valores propios, valores singulares y flujos de potencia de continuación (Aumuller & Saha, 2002; Flatabo, Ognedal & Carlsen, 1990; Kundur, 1994). Estos generalmente se fundamentan en la solución de las ecuaciones de flujo de potencia ante incrementos específicos en la carga, hasta que se alcanza el punto de colapso de tensión. A partir de allí, se obtiene una medida del grado de estabilidad del SEP para una condición específica de operación, en forma de indicadores de proximidad, márgenes de potencia activa y reactiva, entre otros. En el enfoque estático, no se considera el comportamiento dinámico de los elementos del SEP. Por su parte, las metodologías dinámicas si consideran los aspectos antes mencionados y entregan la respuesta del SEP a una secuencia de eventos discretos en función del tiempo (Balamourgan, Sidhu & Sachdev, 2004; Nizam, Mohamed & Hussain, 2007). Aunque el enfoque dinámico permite obtener resultados más precisos, tiene la desventaja de consumir mayor tiempo computacional debido al requerimiento de modelos más elaborados del SEP, característica que lo hace inapropiado para aplicaciones en tiempo real.
Una de las formas de determinar la estabilidad de tensión de un SEP es a través de IET, los cuales se pueden desarrollar utilizando metodologías estáticas o dinámicas como las mencionadas anteriormente. A continuación se presenta una revisión bibliográfica de algunos de los IET que han sido propuestos y presentados en las bases bibliográficas en los últimos 26 años. Además, se propone una clasificación de estos índices de acuerdo a sus características más relevantes.
3. Clasificación de índices de estabilidad de tensión
Presentar una clasificación de los IET no es tarea fácil, debido a la gran cantidad de propuestas que han sido publicadas en los últimos años, a los diferentes requerimientos que tienen y a que algunos índices pueden pertenecer a más de una categoría, o son susceptibles de redefinirse debido por ejemplo, a la utilización en el sistema de mediciones entregadas directamente por PMUs. Las clasificaciones presentadas en (Candelo, Caicedo & Castro, 2008; Glavic & Van Cutsem, 2009), se amplían en este documento para considerar subcategorías que permiten una mejor comprensión de cada uno de los índices propuestos.
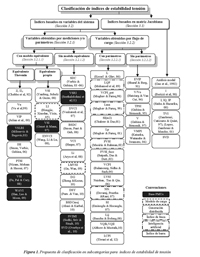
Este articulo esta organizado con referencia a la clasificación propuesta en la figura 1. La clasificación de los IET propuesta está basada en el tipo de información que se requiere para su implementación. De esta forma, los IET pueden inicialmente clasificarse como aquellos basados en las variables del sistema, localizados a la izquierda de la figura 1 ó aquellos basados en la matriz Jacobiana, localizados en la parte derecha de la misma. La figura 1 también indica las secciones en las cuales ha sido dividido el articulo.
El mapa conceptual presentado en la figura 1, permite visualizar rápidamente la forma de clasificación propuesta en este artículo. Allí, cada índice i está representado por la citación que se encuentra al interior de paréntesis. Se utilizan las convenciones para definir cada uno de los índices como: índice de línea, índice de barra, basados en mediciones con PMUs, aquellos que utilizan metodologías de inteligencia artificial, los que son aplicados a sistemas con generación distribuida y aquellos que consideran el modelo de carga para su definición.
A continuación se realiza la descripción de cada una de las categorías presentadas en la figura 1.
3.1 Índices basados en la matriz Jacobiana
Estos índices necesitan los datos completos del SEP como las impedancias o la matriz Jacobiana (en su forma reducida o completa), para determinar el punto de colapso de tensión o el máximo punto de cargabilidad del sistema. Uno de los enfoques estáticos más empleado para el análisis de estabilidad de tensión, es el análisis modal del Jacobiano del flujo de carga presentado en (Gao et al., 1992), donde se emplean los valores propios del sistema para identificar los elementos del sistema de potencia (barras criticas, ramas y generadores) que contribuyen a la inestabilidad de tensión. En (Lof et al., 1993) y (Hong et al, 1997) se proponen índices basados en la descomposición del valor singular SVD (Singular Value Decomposition) de la matriz Jacobiana del flujo de carga, para indicar la proximidad del sistema al limite de estabilidad en estado estable. Esto puede detectarse realizando un seguimiento de la cercanía del valor singular mas cercano a cero. Una de las dificultades de ésta metodología es que para la definición de la matriz Jacobiana del sistema, se requiere de la solución de sistemas de ecuaciones no lineales, la cual puede caer en un punto de singularidad. Por otra parte, en (Overbye et al., 2010), se empleó el algoritmo SVD sobre los datos obtenidos con PMUs, como un indicador de la condición de vulnerabilidad del sistema ante colapsos de tensión. Los autores consideran que la información suministrada por la descomposición del valor singular de la matriz de datos obtenidos por medidores fasoriales, está directamente relacionada con la suministrada por la matriz Jacobiana y esto representa una gran contribución en la definición de índices que no requieren información de parámetros del sistema.
Entre otras de las metodologías que se encuentran en esta categoría, se encuentra el índice i (Berizzi et al., 1998), que utiliza la información del valor singular máximo de la matriz inversa del Jacobiano y su derivada respecto a la carga total del sistema. Por su parte, los índices I, IQ, IP (Sinha & Hazarika, 2000), utilizan en su formulación la información de los elementos de la diagonal del Jacobiano. Un índice que utiliza la información entregada por el vector tangente y que se calcula con el flujo de carga es el TVI (Tangent Vector Based Index), el cual fue presentado inicialmente en (Zambroni, Cañizares & Quintana, 1997) y posteriormente en (Lopes, Zambroni & Mendes, 2001). La principales desventajas de estas metodologías están asociadas con que debido a que están basadas en el modelo del flujo de carga no consideran los componentes dinámicos del sistema, y adicionalmente, no son adecuadas para un esquema de monitoreo en línea.
3.2 Índices basados en variables del sistema
Los índices basados en variables pueden utilizar información de tensiones, corrientes y/o flujos de potencia, que se pueden obtener a través de la solución de flujos de carga o por mediciones (que pueden estar o no basadas en PMUs), además de los parámetros del sistema. De acuerdo a la forma como se obtienen las variables se pueden clasificar en:
3.2.1 Índices basados en variables obtenidas por mediciones y/o parámetros
La principal idea de los índices basados en mediciones es la de utilizar la información fasorial de tensiones y/o corrientes, en el punto donde se realiza el análisis y/o en otros puntos de medición del SEP, los cuales pueden entregar suficiente información en forma directa sobre la inestabilidad de tensión. Algunas implementaciones que utilizan esta metodología, también requieren de parámetros del SEP (resistencias, reactancias, entre otros) dados por los elementos de la matriz admitancia.
En los últimos años, el monitoreo de los sistemas de potencia ha cambiado sustancialmente, debido a la utilización de PMUs, lo cual ha permitido contar con las mediciones de tensión y corriente en magnitud y ángulo sincronizadas vía GPS (Terzija et al., 2011). Esta incursión se ha visto reflejada en el área de la estabilidad de tensión, donde existen varias propuestas relacionadas con la determinación de índices de estabilidad utilizando PMUs. De acuerdo a la clasificación dada en (Glavic & Van Cutsem, 2009), los índices basados en PMUs se clasifican como métodos basados en mediciones locales y métodos basados en mediciones del sistema de monitoreo de área amplia (WAM). Los métodos basados en mediciones locales, utilizan la información entregada por los PMUs de la barra en la cual se está realizando el análisis y en algunos casos se intercambia poca información con otras estaciones de monitoreo. En cambio, los métodos basados en mediciones del sistema de monitoreo de área amplia (WAM), aprovechan la disponibilidad de PMUs en todo el SEP, lo cual permite tener una visión global del comportamiento del sistema. Estos últimos aunque presentan una gran ventaja respecto a los locales, representan un alto requerimiento de medidores con el fin de conseguir que el SEP sea completamente observable. Dentro de los índices que utilizan mediciones y/o parámetros del SEP para su cálculo, se encuentran aquellos que utilizan un modelo equivalente de la red visto desde una barra de carga y aquellos que no lo hacen.
3.2.1.1 Índices que utilizan un modelo equivalente
En los índices que se basan en un modelo equivalente, se considera que el punto de máxima transferencia de potencia en un circuito (en el cual se asume la representación de la carga como potencia constante), coincide con el punto de inicio del colapso de tensión, y esto se puede reflejar en la similitud de las impedancias (línea y carga, para un circuito de dos barras). Por tanto, algunos de los índices que se basan en este criterio, requieren de la estimación de los parámetros de un circuito equivalente de la red visto desde un nodo de carga. Para calcular los parámetros del equivalente se utilizan diferentes algoritmos de identificación, como mínimos cuadrados o su variante mínimos cuadrados recursivos sobre una ventana deslizante de las muestras de datos discretos (Nelles, 2001; Norton, 1986; Raol, Girija & Singh, 2004). Los índices pueden sub-clasificarse de acuerdo al modelo equivalente de la red que emplean en los que utilizan Thevenin y los que definen un equivalente propio.
a. Índices que utilizan un equivalente de Thevenin
Dentro de los que utilizan un equivalente de Thevenin del SEP desde una barra de carga, se encuentra (Chebbo, Irving & Sterling, 1992), que no utiliza algoritmos de estimación ya que obtiene la impedancia equivalente directamente de la matriz Z del sistema. A partir del cálculo de la magnitud de la relación entre la impedancia equivalente de Thevenin vista de la barra de carga y de la impedancia de carga de la barra bajo análisis (Zi/Zii), se define la estabilidad de la barra. En cambio, la metodología dada en (Vu et al., 1999) utiliza la estimación del equivalente de Thevenin, mediante un algoritmo recursivo de mínimos cuadrados, el cual requiere de dos mediciones en el nodo de carga, obtenidas en tiempos diferentes. Por su parte en (Julian et al., 2000), se desarrolló el índice VIP (Voltage Instability Predictor) el cual también utiliza el concepto del equivalente de Thevenin del SEP obtenido mediante mediciones locales, para definir la proximidad al colapso en términos de margen de potencia en lugar de margen de impedancia. Los autores realizan una extensión al considerar los efectos de la dinámica del sistema incluyendo sistemas de excitación y cargas dependientes de tensión y frecuencia. Con el índice VSLBI (Voltage Stability Load Bus Index) definido en (Milosevic & Begovic, 2003), se tienen en cuenta las características de la carga (estáticas o dinámicas) para su formulación, pero esta propuesta requiere conocer con anticipación el modelo y composición de la carga, lo cual en la mayoría de ocasiones es imposible debido a la varianza de la misma. En (Smon, Verbic & Gubina, 2006) y con el fin de simplificar la determinación de los parámetros de Thevenin, se emplea una alternativa al método de mínimos cuadrados, mediante dos mediciones fasoriales consecutivas de tensión y corriente, para formuler el índice ISI (Impedance Stability Index), el cual además utiliza el teorema de Tellegen y los circuitos adjuntos. Algunos indicadores como el índice PTSI (Power Transfer Stability Index) (Nizam, Mohamed & Hussain, 2006) utilizan un híbrido entre el análisis de estabilidad estático y dinámico para su definición. Utilizando el criterio de máxima transferencia de potencia, se determina un índice en cada barra del sistema utilizando la información del flujo de potencia, la tensión e impedancia de Thevenin y la impedancia de la carga. La eficacia de este índice depende directamente del algoritmo de estimación de parámetros utilizado para determinar el equivalente de Thevenin. En (Fu, Pal & Cory, 2008) se encuentra una propuesta definida como VSI (Voltage Stability Index), que utiliza mediciones fasoriales de tensión y corriente obtenidas de PMUs al realizar cambios en el tap del transformador reductor del sistema, con el fin de obtener un modelo equivalente de la red. Por su parte, el índice WAVI (Wide Area Voltage Stability Index) (Han, Lee & Moon, 2009), utiliza el concepto del índice expuesto por Chebbo (1992), pero con la obtención del equivalente de Thevenin con dos unidades fasoriales ubicadas en áreas diferentes. Uno de los problemas que presentan los índices basados en el equivalente de Thevenin, está relacionado con la estimación de sus parámetros, ya que dependen no sólo del algoritmo empleado, sino también de las condiciones dadas en un ambiente real. Así, las mediciones sobre el SEP están condicionadas por el sistema de adquisición y en caso de ruido en las señales, se pueden afectar considerablemente los parámetros estimados y estos a su vez afectan el IET (Genet, Sezi & Maun, 2008).
b. Índices con identificación de equivalente propio
Con respecto a los índices que utilizan un modelo equivalente propio de la red y las mediciones obtenidas directamente del SEP, ya sea en forma local o global, se encuentran: El índice de máxima cargabilidad VSI (Voltage Stability Index) propuesto en (Yanfeng, Schulz & Guzman, 2004), que está basado en el criterio de la máxima transferencia del SEP y utiliza para su definición los valores de las máximas potencias activa, reactiva y compleja. Este índice utiliza las mediciones fasoriales y los parámetros de la red, para simplificar el SEP visto desde una barra con la utilización de un equivalente de red conformado por una fuente, una línea de transmisión y una barra de carga. Dentro del enfoque que utiliza un equivalente propio, también se ha considerado la influencia del modelo de carga en la estabilidad de tensión. Es así como en (Hongjie, Xiaodan & Yixin, 2005) se presentó una mejora al índice L dado por (Kessel & Glavitsch, 1986), a través de un nuevo índice denominado LI, el cual considera la influencia de los modelos de carga ZIP y exponencial. Con el fin de superar las dificultades encontradas al estimar el equivalente de Thevenin mediante mediciones sucesivas, los autores en (Genet & Maun, 2007) asumen que el valor de la caída de tensión entre una barra de carga y el generador más cercano, puede dar una información comparable a la caída de tensión a través de la impedancia de Thevenin. Por tanto, se define el índice VSI para cada barra como la relación entre la tensión en barra de carga sobre caída de tensión en la impedancia de Thevenin. Por su parte, el índice ENVCI (Equivalent Node Voltage Collapse Index) propuesto por (Wang, Li & Lu, 2008), utiliza un modelo equivalente del SEP visto desde la barra bajo estudio, el cual incluye tanto los efectos de la red local como del sistema externo a ésta.
3.2.1.2 Índices que utilizan mediciones y no equivalentes
En esta categoría se encuentran índices a partir del año 2003, donde se presentan alternativas a los índices que utilizan equivalentes (ya sea de Thevenin o propios), utilizando las ventajas de los sistemas de medición modernos. Como ya se había mencionado, las mediciones pueden obtenerse por sistemas convencionales (SCADA, por ejemplo) o sistemas de monitoreo de área amplia. Entre las metodologías de monitoreo de estabilidad de tensión que utilizan mediciones globales entregadas por PMUs se encuentran las descritas en (Glavic & Van Cutsem, 2009; Milosevic & Begovic, 2003; Verbic & Gubina, 2004). Estas metodologías requieren que el número de PMUs instalados entreguen una completa observabilidad del sistema, lo cual puede ser un problema si se tiene en cuenta el costo de dichas unidades; por lo tanto, algunos investigadores prefieren el uso de mediciones locales sobre el sistema. A continuación se citan algunos índices que se encuentran en esta categoría. En (Verbic & Gubina, 2003) y posteriormente presentado de nuevo en (Verbic & Gubina, 2004) y (Verbic, Pantos & Gubina, 2006), los autores proponen el SDC (S difference criterion) un algoritmo de protección contra la inestabilidad de tensión, que puede ser implementado en relés numéricos utilizando mediciones fasoriales de tensión y corriente en los terminales de línea. El principal problema de este índice es que requiere la verificación de que la línea está cargada por debajo de su carga nominal. En (Smon, Pantos & Gubina, 2008) se realiza una mejora al anterior índice ya que no necesita tal verificación y se denomina BSDC (Bus apparent-power difference criterion). Este índice está basado en la medición de la potencia aparente entregada a la barra, en lugar de aquella que esta fluyendo por la línea. En (Abasi & Karbalaei, 2011), se presenta una estrategia de mejoramiento de este índice, considerando los modelos de carga dependientes de la tensión. Otra mejora al índice SDC, se presenta en (Parniani & Vanouni, 2010), donde se propone un índice denominado DSY (Derivate (D) of the load apparent power (S) with respect to its admittance (Y)), utilizando solo los valores RMS de tensión y corriente. Entre las propuestas recientes de índices que utilizan (PMUs), se encuentran el (VSRI, Voltage Stability Risk Index) definido en (Seethalekshmi, Singh & Srivastava, 2011), el cual identifica la vulnerabilidad del SEP ante un colapso de tensión para cada barra del sistema, utilizando series de tiempo de las tensiones en las barras. Otro índice que fue desarrollado posteriormente corresponde al SVIMI (Synchrophasor based voltage instability index) (Sodhi, Srivastava & Singh, 2012), el cual utiliza la magnitud de la tensión en una barra y las consecutivas desviaciones de la tensión en ella. Con el auge de las energías alternativas, en (Venkatesh, Rost & Chang, 2007) se definió el índice denominado DVCI (Dynamic Voltage Collapse Indicator), definido para tiempo real, el cual cuantifica el máximo margen de flujo de MVA del alimentador que conecta al generador eólico con el sistema de distribución, utilizando mediciones locales de potencia y tensión. También, en (Zheng & Kezunovic, 2010) se propone un índice adaptado para sistemas de distribución que incluye diferentes tipos de turbinas eólicas, utilizando sólo las mediciones locales en la subestación para definir el índice en tiempo real. Por su parte el índice VCI (Voltage Collapse Index) propuesto en (Haque, 2007) entrega información de las barras de carga afectadas por problemas de estabilidad del SEP y requiere solamente mediciones locales de tensión y corriente. El índice Li (Line voltaje stability index) (Arya et al., 2008) fue planteado para relés tipo 21 para detectar cuándo, ante un incremento de carga, la impedancia "vista" iguala a la de la línea. Dentro de la categoría de índices que consideran mediciones, se cuenta también con aquellos que consideran las características de las cargas dinámicas, tal es el caso del LMVSI (Linearized Motor Voltage Stability Index) propuesto en (Gu, Wan & Jiang, 2009; Gu & Wan, 2010). Para la implementación de este índice se requiere de un sistema de monitoreo de área amplia y además del conocimiento previo de los parámetros del motor.
3.2.2 Índices basados en variables obtenidas por solución de flujos de carga
Estos índices corresponden a aquellos que se calculan una vez se hayan obtenido los resultados de las variables de un flujo de carga (tensiones y flujos de potencia). Algunos índices necesitan además de estos resultados, algunos parámetros como las impedancias de líneas, entre otros. De acuerdo con lo anterior, la clasificación se realiza en índices basados en flujos de carga y parámetros del SEP e índices basados sólo en la solución de flujos de carga.
3.2.2.1 Índices basados en flujos de carga y parámetros del SEP
Dentro de esta categoría se encuentran la mayoría de los índices propuestos para analizar la estabilidad de tensión de las líneas del sistema. En (Kessel & Glavitsch, 1986), se desarrolló el índice L basado en la solución entregada por un flujo de carga, con el fin de determinar las barras más críticas. En (Moghavvemi & Faruque, 1998b), se utilizan dos indicadores (Voltage Collapse Proximity Indicator) VCPI (potencia) y VCPI (pérdidas) sobre cada línea del sistema, con el fin de identificar aquellas que son críticas. Cuando ambos índices se igualan a uno, se alcanza el punto de colapso de tensión. Posteriormente, en (Mohamed et al., 1989) se presenta el LQP, basado en el concepto del flujo de potencia en la línea. A través del índice Lmn (Moghavvemi & Faruque, 1998a; 1999), los autores detectan aquellas zonas próximas al colapso de tensión, por medio de la observación de líneas que se encuentran bajo condiciones de mayor estrés. El desempeño de los índices Lmn (Moghavvemi & Omar, 1998a) y posteriormente Lp (Moghavvemi & Faruque, 2001), esta influenciado en gran medida por el factor de potencia del sistema, debido a que fueron desarrollados sólo para la potencia activa o reactiva transferidos por la línea. Otro de los índices propuestos para determinar la estabilidad de líneas es el definido como FVSI (Fast Voltage Collapse Index) en (Musirin & Rahman, 2002), que esta directamente relacionado con la potencia reactiva e indirectamente con la potencia activa a través de la línea. Con el fin de evitar la dependencia de los anteriores índices con el factor de carga, en (Eminoglu & Hocaoglu, 2007), se propuso el índice SI (Stability Index), el cual está basado en la ecuación de potencia activa y reactiva transferida a través de una línea de la red de distribución. Otro de los ajustes a algunos problemas relacionados con los índices FVSI, Lmn, LQP y LVSI, se da en (Baozhu & Bolong, 2008), donde se propone el índice Lij el cual no se ve afectado cuando no se considera la resistencia de la línea, a diferencia del LVSI (Naishan, Tao & Qinghua 2006), que ante dicha consideración se anula. Otra de las problemáticas relacionadas con los índices Lmn, LQP y FVSI, radica en que en la presentación de su fundamentación, se ignoran las admitancias paralelas del modelo de la línea. Para solventar esta falencia, se presentó el índice LCPI (Line Collapse Proximity Index) definido en (Tiwari et al., 2012), el cual representa la línea de transmisión por el modelo más exacto (parámetros ABCD del sistema). Entre algunos de los indicadores dinámicos de colapso de tensión para barras, se encuentra el índice VCPI (Voltage Collapse Prediction Index) (Balamourgan, Sidhu & Sachdev, 2004), que requiere la información del fasor de tensión y la topología del sistema. Por su parte, en (Althowibi & Mustafa, 2010a; 2010b), se presentaron los índices para barra VQIBus (Voltage Reactive Power Index at Bus) y para línea VQILINE (Voltage Reactive Power Index at Line), los cuales se basan en la potencia reactiva en la barra de recibo, la impedancia de línea, la tensión en la barra de envío y el ángulo de admitancia de la línea.
La utilización de metodologías de inteligencia artificial no ha sido ajena a la determinación del margen de estabilidad. Tal es el caso de (Devaraj, Preetha & Rani, 2007; Kamalasadan, Thukaram & Srivastava, 2009), donde se utilizan las redes neuronales (RN) para estimar el máximo valor del índice (L) ante condiciones de contingencia. De igual forma (Jayasankar, Kamaraj & Vanaja, 2010), identifican la línea más crítica del sistema mediante el índice Lmn calculado con RN. En la mayoría de las aplicaciones donde se utilizan RN, se aprovechan sus ventajas como clasificador para determinar listas de contingencias, desde las más críticas a las menos severas (Schmidt, 1997; Wan & Ekwue, 2000). En la revisión de la literatura, no se encontraron muchas metodologías para IET donde se utilice la lógica difusa. Entre las pocas está el índice FVSI (Fuzzy Voltage Stability Index) (Satpathy, Das & Dutta Gupta, 2002), donde se calcula el porcentaje de caída de tensión para cada barra, para las condiciones de caso base y caso crítico utilizando el flujo de continuación difuso. Por último, utilizando la ecuación bi-cuadrática que relaciona las magnitudes de las tensiones de envío y recibo y la potencia en el terminal de recibo de una línea, (Chakravorty & Das, 2001) proponen el SI(m2), para medir el nivel de estabilidad de redes de distribución radiales.
3.2.2.2 Índices basados sólo en solución de flujos de carga
Dentro de las propuestas dadas para los IET, también se encuentra la utilización de técnicas probabilísticas. Es así como en (Sharaf & Berg, 1991) el EVIP (Expected Voltage Instability Proximity) analiza el impacto que tiene el comportamiento estocástico de la disponibilidad de los elementos del SEP (centros de generación y líneas) sobre la estabilidad de tensión. La expectativa de la proximidad a un colapso de tensión para cada barra de carga del sistema se evalúa ante la salida forzada de dichos elementos del sistema. El índice V/Vo propuesto en (Hatziargyriou & Van Cutsem, 1994) utiliza la relación entre los valores de la tensión con carga que se obtiene del flujo de carga y sin carga en una barra, para analizar la estabilidad de tensión en cada barra del SEP. Este índice presenta un problema relacionado con la tendencia no lineal que presenta ante cambios en los parámetros del SEP, lo cual no permite realizar una adecuada definición de la proximidad al colapso. También existen índices que utilizan un equivalente del SEP pero utilizan las variables obtenidas con el flujo de carga. El modelo equivalente de dos barras puede utilizarse para cambios pequeños de carga alrededor del punto de operación para el cual se obtuvo, pero ante variaciones de carga en varias barras se pueden ver notablemente afectados los parámetros del equivalente. Por esta razón las barras críticas deben ser actualizadas para cada estado del SEP, lo cual introduce un esfuerzo computacional adicional. Entre las referencias que utilizan dicha aproximación, se encuentran (Jasmon & Lee, 1991) y (Gubina & Strmcnik, 1997), donde se analiza la estabilidad de tensión de redes con topología radial, mediante la obtención de un modelo equivalente que representa a toda la red. Este modelo es válido solo para el punto de operación para el cual fue obtenido. La referencia (Gubina & Strmcnik, 1995) es uno de los primeros artículos que propone la utilización de la información del fasor de tensión de las barras para identificar la ruta de transmisión crítica para los flujos de P y Q, a través del índice denominado TPSI (Transmission Path Stability Index). Este índice extiende el concepto que cuando el punto de inestabilidad de tensión coincide con el punto de máxima transferencia de potencia, se produce la relación que la proyección del fasor de tensión de la carga sobre el fasor de tensión del generador es igual a la mitad de la tensión de este fasor, para sistemas radiales y enmallados. En la definición de VMPI (Voltage Margin Proximity Index) (Kataoka, Watanabe & Iwamoto, 2006), los autores tienen en cuenta los límites de tensión definidos por los operadores de la red, especialmente el límite bajo de tensión. Finalmente, como una de las aplicaciones de la función de energía para determinar la proximidad al colapso, se encuentra (Demarco & Overbye, 1990; 1991), pero esta metodología es costosa desde el punto de vista computacional.
4. Comparación de los enfoques utilizados mediante marcadores de relevancia
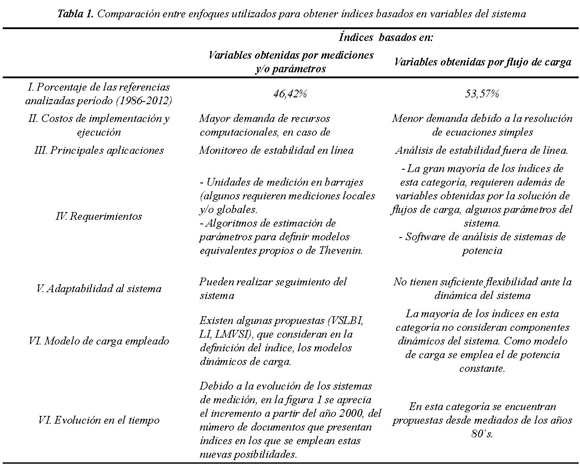
Con el fin de asegurar una mejor comprensión de las características de los índices citados (específicamente de aquellos que utilizan variables del SEP para su definición), se realiza un análisis comparativo de los diferentes enfoques utilizados para su obtención. La tabla 1 muestra la comparación de los enfoques comúnmente utilizados en la obtención de IET, por medio de criterios que evalúan diversos aspectos, como su aplicabilidad, requerimientos y adaptabilidad, entre otros. En la selección de los criterios que definen cada marcador de relevancia se consideran las características más importantes que permiten agrupar los índices analizados y referenciados en los últimos 26 años. El marcador I corresponde a la cantidad de referencias encontradas en el período de observación y permite analizar junto con el marcador VII, las tendencias que se han presentado en la temática de estudio. El marcador II evalúa los diferentes índices, considerando el tiempo requerido para su implementación y ejecución, así como el consumo de recursos computacionales. El marcador III ilustra las aplicaciones en línea o fuera de línea para las cuales se han utilizado los índices que se encuentran en cada categoría. El marcador IV evalúa los requerimientos, respecto a equipo de medición y algoritmos de estimación de parámetros y/o análisis de sistemas de potencia. El marcador V permite analizar la adaptabilidad del índice ante el comportamiento dinámico del sistema. Adicionalmente, el marcador VI está definido para analizar el modelo de carga empleado en la formulación de los índices. Por último, el marcador VII permite realizar un análisis de la evolución de las metodologías utilizadas para la obtención de los índices en el intervalo de tiempo analizado.
Como conclusiones a partir de la tabla 1, se observa que algunas de las ventajas de los enfoques que utilizan variables del SEP obtenidas por mediciones, están asociadas con la adquisición de datos que permiten analizar en forma directa la estabilidad de tensión ante diferentes condiciones de operación y contingencias; con lo cual se posibilita el monitoreo en línea de los sistemas eléctricos de potencia. Uno de los desafíos que presenta el enfoque basado en mediciones para obtener índices, es el gran tamaño de los actuales sistemas de potencia y por tanto la necesidad de disponer de unidades de medición en barras estratégicamente localizadas para lograr la completa observabilidad del sistema. Aunque algunos de los actuales sistemas de potencia a nivel mundial (Noruega, China, India, Estados Unidos, Colombia, Brasil, por mencionar algunos) ya cuentan con sistemas de monitoreo de área amplia, se esperaba encontrar en la revisión bibliográfica realizada, un porcentaje mayor de aplicaciones que utilizaran estas herramientas. Otra de las características relevantes de este enfoque basado en mediciones, es la definición de índices que involucran las características dinámicas de las cargas, que aunque son pocas, permiten realizar análisis cada vez mas cercanos a las condiciones reales de los SEP. Lo anterior demuestra que aún queda mucho por investigar en esta área, y se constituye en uno de los aportes de esta revisión del estado del arte, al visibilizar estas falencias.
Por su parte, los índices basados en las variables obtenidas por la solución de flujos de carga, presentan una menor demanda de tiempo computacional, debido a que se basan en la solución de ecuaciones simples y esto los hace adecuados para aplicarlos en sistemas de potencia de mayor tamaño. Esta ventaja se ve reflejada en que más del 50% de los índices analizados, se encuentran ubicados en esta categoría, con propuestas realizadas desde hace mas de 20 años. Por ejemplo el índice L fue definido a mediados de los 80's y aún se sigue aplicando sobre los sistemas de potencia (Reis & Barbosa, 2006; Suganyadevia & Babulal, 2009). Una de las desventajas de estas metodologías, es la dependencia de algunos parámetros del sistema para su cálculo (por ejemplo, resistencias y/o reactancias de las líneas de transmisión), lo cual las hace poco confiables y precisos, si no se dispone de datos reales del sistema. Por otra parte, se encuentra que el criterio de la máxima transferencia de potencia de una red eléctrica a cargas del tipo constante es el más empleado en la formulación de los índices basados en flujos de carga. Lo anterior, en algunas circunstancias conlleva a que el análisis realizado a través de estos índices sea inexacto, por el gran impacto que tienen las cargas dinámicas en la estabilidad de tensión de un sistema.
Con respecto a la evolución en el tiempo, resulta interesante observar como las metodologías basadas en la inteligencia artificial, especialmente redes neuronales, se han aplicado en los índices basados en variables obtenidas por flujos de carga y no en los basados en mediciones, debido a que se han utilizado para esquemas de entrenamiento supervisado. Esto permite potenciar su aplicación en esquemas de monitoreo en línea. Por su parte, para la estimación de los índices basados en mediciones actualmente se cuenta con mas y mejor calidad de información, por la inclusión de PMUs en los sistemas de potencia. Estos elementos suministran mediciones sincronizadas vía GPS, que adicionalmente permiten optimizar el tiempo computacional requerido.
5. Conclusiones
Con el propósito de analizar la evolución en el tiempo que han tenido algunas de las diferentes propuestas de índices de proximidad al colapso de tensión, se presentó en este artículo una clasificación que utiliza subcategorías para una mejor comprensión de las principales enfoques o alternativas de formulación, principales características, debilidades y potencialidades de aplicación en los sistemas de potencia. Como aporte adicional, en este articulo se presento una comparación entre las distintas alternativas para la formulación de índices de estabilidad de tensión, utilizando marcadores de relevancia, los cuales sirven al ingeniero de potencia, como criterios para la utilización de una u otra metodología, de acuerdo a las necesidades específicas de la investigación y/o recursos de información disponibles para su implementación.
Como aspectos más importantes en la revisión del estado del arte, se determinó que la temática relacionada con los índices que utilizan las mediciones del SEP, es un área de mucho potencial por desarrollar debido a los sistemas de medición actuales, basados fundamentalmente en PMUs, lo que ofrece una nueva forma de operar, monitorear y controlar los sistemas eléctricos de potencia.
Adicionalmente y debido a la alta influencia que tiene la selección del modelo de carga empleado en la evaluación de la estabilidad de tensión, existe un creciente interés por definir índices basados en mediciones que contemplen las características dinámicas del sistema. Debido que aún son pocas las referencias que consideren la dinámica del sistema, ésta es un área promisoria de trabajo y desarrollo actual. De otra parte, aunque las metodologías estáticas basadas en variables obtenidas por flujo de carga no consideran la dinámica del sistema, han sido las mas empleadas desde hace más de dos décadas y existen muchas referencias que reportan mejores implementaciones a través de propuestas recientes.
Finalmente, el estado del arte aquí presentado permite una visión de las principales propuestas de índices, útil en el inicio de cualquier investigación especialmente relacionada con la estabilidad de tensión de los sistemas eléctricos de potencia.
6. Referencias
Abasi, S. & Karbalaei, F. (2011). Diagnosis of Voltage Instability Using BSDC Index in the Presence of Voltage Dependent Loads. Power and Energy Engineering Conference (APPEEC), Asia-Pacific, Wuhan (pp. 1-6). [ Links ]
Althowibi, F. & Mustafa, M. (2010a). On-line Voltage Collapse Indicator for Power Systems. IEEE International Conference on Power and Energy (PECon2010) (pp. 408 - 413). Kuala Lumpur, Malaysia. [ Links ]
Althowibi, F. & Mustafa, M. (2010b). Voltage Stability Calculations in Power Transmission Lines: Indications and Allocations. IEEE Int. Conference on Power & Energy (PECon2010) (pp. 390-395). Malaysia. [ Links ]
Arya, L., Choube, S. & Shrivastava, M. (2008). Technique for voltage stability assessment using newly developed line voltage stability index. Energy Conversion & Management, 49 (2), 267-275. [ Links ]
Aumuller, C. & Saha, T. (2002). Analysis and assessment of large scale power system voltage stability by a novel sensitivity based method. IEEE PES Summer Meeting: 3 (pp. 16-21). Chicago (IL), USA. [ Links ]
Balamourgan, V., Sidhu, T. & Sachdev, M. (2004). Technique For Online Prediction of Voltage Collapse. IEE Proceedings Generation, Transmission, Distribution, 151 (4), 453-460. [ Links ]
Baozhu, L. & Bolong, L. (2008). A Novel Static Voltage Stability Index based on Equilibrium Solution Region of Branch Power Flow. DRPT2008 (pp. 809-814). Nanjing, China. [ Links ]
Berizzi, A., Finazzi, P., Dosi, D., Marannino, P. & Corsi, S. (1998). First and second order methods for voltage collapse assessment and security enhancement. IEEE Trans. On Power Systems, 13 (2), 543-551. [ Links ]
Candelo, J., Caicedo, G. & Castro, F. (2008). Métodos para el estudio de la estabilidad de voltaje en Sistemas de Potencia. Información Tecnológica, 19 (5), 97-110. [ Links ]
Chakravorty, M., & Das, D. (2001). Voltage stability analysis of radial distribution networks. Electric Power and Energy System, 23, 129-135. [ Links ]
Chebbo, A. M., Irving, M. R., & Sterling, M. J. H. (1992, May). Voltage collapse proximity indicator: behaviour and implications. IEE Proceedings C (Generation, Transmission and Distribution), 19 (3), 241-252. [ Links ]
Demarco, C. & Overbye, T. (1990). An energy based security measure for assessing vulnerability to voltage collapse. IEEE Transactions on Power Systems, 5 (2), 419-427. [ Links ]
Demarco, C. & Overbye, T. (1991). Improved techniques for power system voltage stability assessment using energy methods. IEEE Transactions on Power Systems, 6 (4), 1446-1452. [ Links ]
Devaraj, D., Preetha, J. & Rani, R. (2007). Artificial neural network model for voltage security based contingency ranking. Applied Soft Computing 7 (3), 722-727. [ Links ]
Eminoglu, U. & Hocaoglu, M. (2007). Voltage Stability Index for Radial Distribution Networks. In Proceedings of 42nd International Universities Power Engineering Conference (UPEC) (pp. 408-413). Brighton. [ Links ]
Flatabo, N., Ognedal, R. & Carlsen, T. (1990). Voltage stability condition in a power transmission system calculated by sensitivity methods. IEEE Transactions on Power Systems, 5 (4), 1286-1293. [ Links ]
Fu, L., Pal, B. & Cory, B. (2008). Phasor measurement application for power system voltage stability monitoring. IEEE Power and Energy Society General Meeting (pp. 1-8). Pittsburgh, UK. [ Links ]
Gao, B., Morison, G. K. & Kundur, P. (1992). Voltage Stability Evaluation using Modal analysis. IEEE Trans. PWRS, 7 (4), 1529-1542. [ Links ]
Genet, B. & Maun, J. (2007). Voltage Stability Monitoring Using Wide Area Measurement Systems. In, Proceedings of the PowerTech Conferencen (pp. 1712-1717). Lausanne, Switzerland. [ Links ]
Genet, B., Sezi, T. & Maun, J. (2008). Comparison of Thevenin's Equivalent based Methods to Monitor Voltage Stability. In, Proceedings of PSCC. Glasgow, Scotland. [ Links ]
Glavic, M. & Van Cutsem, T. (2009). Wide-area detection of voltage instability from synchronized phasor measurements. Part I: Principle. IEEE Trans. On Power Systems, 24 (3), 1408-1416. [ Links ]
Gu, W., Wan, Q. & Jiang, P. (2009). Linearized Local Voltage Stability Index Considering Induction Motor Load. IEEE Power and Energy Society General Meeting, PES '09 (pp. 1-5). Canada. [ Links ]
Gu, W. & Wan, Q. (2010). Linearized voltage stability index for wide-area voltage monitoring and control. International Journal of Electrical Power and Energy Systems, 32 (4), 333-336. [ Links ]
Gubina, F. & Strmcnik, B. (1995). Voltage Collapse Proximity Index Determination using Voltage Phasors Approach. IEEE Transactions on Power Systems, 10 (2), 788-794. [ Links ]
Gubina, F. & Strmcnik, B. (1997). A simple approach to voltage stability assessment in radial networks, IEEE Trans. On Power Systems, 12 (3), 1121-1128. [ Links ]
Han, S., Lee, B. & Moon, Y. (2009). Development of Voltage Stability Index using Synchro-phasor based Data. Proceedings IEEE T&D Asia & Pacific (pp. 1-4). Seoul, South Korea. [ Links ]
Haque, M. H. (2007). Use of Local Information to Determine the Distance to Voltage Collapse. In, Proceedings of International Power Engineering Conference IPEC (pp. 407-412). [ Links ]
Hatziargyriou, N. & Van Cutsem, T. (1994). Indices for predicting voltage collapse including dynamic phenomena. Technical report TF-38-02-11, CIGRE. [ Links ]
Hong, Y., Pan, C. & Lin, W. (1997). Fast calculation of a voltage stability index of power systems. IEEE Trans on Power Systems, 12 (4), 1555-1560. [ Links ]
Hongjie, J., Xiaodan, Y. & Yixin, Y. (2005). An improved voltage stability index and its application. International Journal of Electrical Power & Energy Systems, 27 (8), 567-574. [ Links ]
Jasmon, G. & Lee, L. (1991). Distribution network reduction for voltage stability analysis and load flow calculations. Electric Power and Energy System, 13 (1), 9-13. [ Links ]
Jayasankar, V., Kamaraj, N. & Vanaja, N. (2010). Estimation of voltage stability index for power system employing artificial neural network technique and TCSC placement. Neurocomputing, 73 (16-18), 3005-3011. [ Links ]
Julian, D., Schulz, R., Vu, K., Quaintance, W., Bhatt, B. & Novosel, D. (2000). Quantifying proximity to voltage collapse using the voltage instability predictor (VIP). In, Proc. IEEE Power Eng. Soc. Summer Meeting (pp. 931-936). Seattle (WA), USA. [ Links ]
Kamalasadan, S., Thukaram, D. & Srivastava, A. K. (2009). A new intelligent algorithm for online voltage stability assessment and monitoring. Electrical Power and Energy Systems, 31 (2-3), 100-110. [ Links ]
Kamwa, I., Beland, J., Trudel, G., Grondin, R., Lafond, C. & McNabb, C. (2006). Wide-Area Monitoring and Control at Hydro-Quebec: Past, Present and Future. IEEE PES General Meeting (pp. 1 -12). Montreal, Canada. [ Links ]
Karbalaei, F., Soleymani, F. & Afsharnia, S. (2010). A comparison of voltage collapse proximity indicators. In, Proceedings of IPEC 2010 (pp. 429-432). Singapore, Singapore. [ Links ]
Kataoka, Y., Watanabe, M. & Iwamoto, S. (2006). A New Voltage Stability Index Considering oltage Limits. IEEE PES PSCE '06 (pp. 1878-1883). Atlanta (GA), USA. [ Links ]
Kessel, P. & Glavitsch, H. (1986). Estimating the Voltage Stability of a Power System. IEEE Transactions on Power Delivery, 1 (3), 346-354. [ Links ]
Kundur, P. (1994). Power System Stability and Control. New York, USA: McGraw-Hills, Inc. [ Links ]
Lof, P.A., Andersson, G., & Hill, D. J. (1993). Voltage Stability Indices for stressed power systems. IEEE Trans. On Power Systems, 8 (1), 326-335. [ Links ]
Lopes, I., Zambron,i A. & Mendes, A. (2001). Tangent Vector as a tool for voltage collapse analysis considering a dynamic system model. In, Proceedings of IEEE Porto Power Tech Conference 2 (pp. 1-5). [ Links ]
Milosevic, B. & Begovic', M. (2003). Voltage-Stability Protection and Control Using a Wide-Area Network of Phasor Measurements. IEEE Transactions on Power Systems, 18 (1), 121-127. [ Links ]
Moghavvemi, M. & Faruque, M. (1998a). Technique for contingency monitoring and voltage collapse prediction. IEE Proc Gen Transm Distrib, 145 (6), 634-40. [ Links ]
Moghavvemi, M. & Faruque, M. (1998b). Real-time contingency evaluation and ranking technique. IEE Proc.-Gener. Transm. Distrib, 145 (5), 517-524. [ Links ]
Moghavvemi, M. & Faruque, M. (1999). Power system security and voltage collapse: a line outage based indicator for prediction. Int. Journal of Electric Power and Energy System, 21 (6), 455-461. [ Links ]
Moghavvemi, M. & Faruque, M. (2001). Technique for assessment of voltage stability in ill-conditioned radial distribution network. IEEE Power Eng. Review, 21 (1), 58-60. [ Links ]
Mohamed, A., Jasmon, G. & Yusoff, S. (1989). A Static Voltage Collapse Indicator using Line Stability Factors. Journal of Industrial Technology, 7 (1), 73-85. [ Links ]
Musirin, I. & Rahman, T. (2002). Novel Fast Voltage Stability Index (FVSI) for Voltage Stability Analysis in Power Transmission System. In, Proceedings of Student Conference on Research and Development SCOReD (pp. 265-268) Kuala Lumpur, Malaysia. [ Links ]
Naishan, H., Xu, T. & Qinghua, L. (2006). The analysis of abundance index of voltage stability based circuit theory. Guangxi Electric Power, 12-14. [ Links ]
Nelles, O. (2001). Nonlinear system identification. Berlin, Heidelberg, Germany: Springer-Verlag. [ Links ]
Nizam, M., Mohamed, A. & Hussain, A. (2007). Dynamic Voltage Collapse Prediction on a Practical Power System Using Power Transfer Stability Index. In Proceedings SCOReD 2007 (pp.1-6). [ Links ]
Norton, J. (1986). An introduction to identification. London, UK: Academic Press. [ Links ]
Overbye, T., Sauer, P., DeMarco, C., Lesieutre, B. & Venkatasubramani, M. (2010). Using PMU data to increase situational awareness. (2010). PSERC Report 10-16. [ Links ]
Parniani, M. & Vanouni, M. (2010). A Fast Local Index for Online Estimation of Closeness to Loadability Limit. IEEE Transactions on Power Systems, 25 (1), 584-585. [ Links ]
Phadke, A. & de Moraes, R. (2008). The Wide World of Wide-Area Measurement. IEEE Power and Energy Magazine, 6 (5), 52-65. [ Links ]
Raol, J., Girija, G. & Singh, J. (2004). Modelling and Parameter Estimation of Dynamic Systems, Institution of Engineering and Technology. London, UK. [ Links ]
Reis, C. & Barbosa, F. (2006). A Comparison of Voltage Stability Indices. In, Proceedings of IEEE Melecon 2006 (pp. 1007-1010). Malaga, España. [ Links ]
Satpathy, P. K., Das, D. & Dutta Gupta, P.B. (2002). A novel fuzzy index for steady state voltage stability analysis and identification of critical busbars. Electric Power Systems Research, 63 (2), 127-140. [ Links ]
Schmidt, H. (1997). Application of artificial neural networks to the dynamic analysis of the voltage stability problem. IEE Proc-Gener. Transm. Distrib. 144 (4), 371-376. [ Links ]
Seethalekshmi, K., Singh, S. & Srivastava, S. (2011). A Synchrophasor Assisted Frequency and and Voltage Stability Based Load Shedding Scheme for Self-Healing of Power System. IEEE Transactions on Smart Grid, 2 (2), 221-230. [ Links ]
Sharaf, T. A. & Berg, G. (1991). Probabilistic voltage stability indexes. IEE Proceedings-C, 138 (6), 499-504. [ Links ]
Sinha, A. & Hazarika, D. (2000). A Comparative study of voltage stability indices in a power system. Electrical Power and Energy System, 22 (8), 589-596. [ Links ]
Smon, I., Verbic, G. & Gubina, F. (2006). Local voltage-stability index using Tellegen's theorem. IEEE Transactions on Power Systems, 21 (3), 1267-1275. [ Links ]
Smon, I., Pantos, M. & Gubina, F. (2008). An improved voltage-collapse protection algorithm based on local phasors. Electric Power Systems Research 78 (3), 434-440. [ Links ]
Sodhi, R., Srivastava, S. & Singh, S. (2012). A Simple Scheme for Wide Area Detection of Impending Voltage Instability. IEEE Transactions on Smart Grid, 3 (2), 818 - 827. [ Links ]
Suganyadevia, M. & Babulal, C. (2009). Estimating of Loadability Margin of a Power System by comparing Voltage Stability Indices. In, Proceedings of INCACEC 2009 (pp. 1-4). Tamilnadu, India. [ Links ]
Terzija, V., Valverde, G., Deyu, C., Regulski, P., Madani, V., Fitch, J. et. al. (2011). Wide-Area Monitoring, Protection, and Control of Future Electric Power Networks. IEEE Proceedings, 99 (1), 80-93. [ Links ]
Tiwari, R., Niazi, K. & Gupta, V. (2012). Line collapse proximity index for prediction of voltage collapse in power systems. Int. Journal of Electrical Power and Energy Systems, 41 (1), 105-111. [ Links ]
Venkatesh, B., Rost, A. & Chang, L. (2007). Dynamic Voltage Collapse Index-Wind Generator Application. IEEE Transactions on Power Delivery, 22 (1), 90-94. [ Links ]
Verbic, G. & Gubina, F. (2003). Fast voltage-collapse line protection algorithm based on local phasors. IEE Proceedings on Generation, Transmission and Distribution, 150 (4), 482-486. [ Links ]
Verbic, G. & Gubina, F. (2004). A new concept of voltage-collapse protection based on local phasors. IEEE Trans. Power Syst., 19 (2), 576-571. [ Links ]
Verbic, G., Pantos, M. & Gubina, F. (2006). On voltage collapse and apparent power losses. Electric Power System Research, 76 (9-10), 760-767. [ Links ]
Vu, K., Begovic, M., Novosel, D. & Saha, M. (1999). Use of local measurements to estimate voltage-stability margin. IEEE Transactions on Power Systems, 14 (3), 1029-1035. [ Links ]
Wan, H. & Ekwue, A. (2000). Artificial Neural Network based contingency ranking method for voltage collapse. Int. Journal of Electr. Power & Energy Syst., 22 (5), 349-354. [ Links ]
Wang, Y., Li, W. & Lu, J. (2008). A new node voltage stability index based on local voltage phasors. Electric Power Systems Research, 79 (1), 265-271. [ Links ]
Yanfeng, N., Schulz, G. & Guzman, A. (2004). Synchrophasor-Based Real Time Voltage Stability Index. In, IEEE PES, Mississippi State Univ. (pp. 1029-1036). [ Links ]
Zambroni, A., Cañizares, C. & Quintana, V. (1997). New techniques to speed up voltaje collapse computations using tangent vectors. IEEE Trans. On Power Systems, 12 (3), 1380-1387. [ Links ]
Zheng, C. & Kezunovic, M. (2010). Distribution System Voltage Stability Analysis with wind farms integration. Proceedings North American Power Symposium (NAPS 2010) (pp. 1-6). Arlington (TX), USA. [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.