Metodología híbrida basada en el regresor knn y el clasificador boosting para localizar fallas en sistemas de distribución

Hybrid methodology based on knn regression and boosting classification techniques for locating faults in distribution systems

Andrés Zapata-Tapasco*
E-mail: jjmora@utp.edu.co

Juan Mora-Flórez*
E-mail: anfezapata@utp.edu.co

Sandra Pérez-Londoño*
E-mail: saperez@utp.edu.co

* Grupo de Investigación en Calidad de Energía Eléctrica y Estabilidad (ICE3). Programa de Ingeniería eléctrica de la Universidad Tecnológica de Pereira (UTP), Pereiera, Colombia

Eje temático: INGENIERíA ELéCTRICA Y ELECTRóNICA / ELECTRICAL AND ELECTRONIC ENGINEERING
Recibido: 03 de Mayo de 2013
Aceptado: 29 de Abril de 2014

Resumen

En este artículo se presenta una metodología híbrida de localización de fallas en sistemas de distribución, a partir de una técnica de regresión basada en el método de los k vecinos más cercanos y una técnica de clasificación en la cual se utilizan múltiples clasificadores básicos en una estrategia denominada 'Boosting'. En la metodología propuesta, inicialmente el sistema se divide por zonas para entrenar la máquina de clasificación. Después se parametriza y entrena la máquina de regresión basada en knn y la máquina de clasificación. Finalmente, para un dato nuevo, la técnica de regresión permite estimar la distancia a la cual ocurrió la falla, y el método de clasificación permite ubicar la falla en una de las zonas predefinidas, eliminando el problema de múltiple estimación. El localizador propuesto se prueba en el sistema de distribución IEEE 34 nodos, donde presenta un buen desempeño tanto para clasificación (precisión mínima de 95.7 %), como para regresión (error máximo absoluto de 8.05%). Esta propuesta es de fácil implementación, rápida y de bajo costo computacional.

Palabras Clave: Boosting, clasificación, k vecinos más cercanos, localización de fallas, regresión.

Abstract

This paper presents a hybrid methodology for fault location in power distribution systems, by using a regression technique based on k nearest neighbors and a classification technique which uses multiple simple classifiers in a Boosting strategy. The proposed methodology first subdivides the power system into zones to train the classification technique. Then the parameters of the regression technique are adjusted and the classification technique is trained. Finally, for an unknown case, the regression technique estimates the fault distance, and the classification technique locates the fault in one of the predefined zones, solving the multiple estimation problem. The IEEE34 node test feeder is used to test the proposed fault locator, where a good performance is obtained either in the classification task (minimal precision of 95.7 %) and the regression task (highest absolute error of 8.05%). The proposed method can be easily implemented in a power system, is fast and has low computational effort.

Keywords: Boosting, classification, k nearest neighbors, fault location, regression.

1. Introducción

La calidad de la energía eléctrica es un tema de gran importancia, debido al modelo actual de mercado. En los sistemas de distribución, la calidad se mide de acuerdo a la continuidad del servicio mediante índices fijados por entidades regulatorias. Uno de los aspectos que más afectan la continuidad es la ocurrencia de fallas paralelas en el sistema de distribución de energía eléctrica; por lo que es necesaria la localización rápida de fallas en sistemas de distribución.

El problema de localización de fallas se resuelve generalmente con métodos basados en el modelo eléctrico del sistema de distribución. Estos métodos estiman la distancia a la falla a partir de las medidas de tensión y corriente en estado de falla y prefalla en la subestación, y de los parámetros del circuito. Sin embargo, el resultado es una distancia que puede coincidir en muchos puntos del sistema de distribución debido a la existencia de múltiples laterales en el sistema, lo que se denomina como problema de múltiple estimación, Mora (2006). Adicionalmente, estos métodos son severamente afectados por variaciones en el modelo del sistema eléctrico.

Recientemente se han implementado técnicas de clasificación que, a partir de bases de datos de eventos registrados en la subestación, permiten ubicar una falla según unas zonas predefinidas en el sistema de distribución. Estas técnicas de clasificación hacen parte del descubrimiento del conocimiento a partir de bases de datos (knowledge discovery database - KDD), área cuyo principal reto es procesar gran cantidad de datos automáticamente, identificar los patrones más significativos y presentar este conocimiento en una forma apropiada, Hu (1995). El KDD involucra otros campos tales como la estadística, el aprendizaje de máquina, inteligencia artificial, entre otros. La minería de datos es un paso en el proceso de KDD, que consiste en aplicar análisis de datos y algoritmos de descubrimiento que producen una particular enumeración de patrones (o modelos) sobre los datos, Fayyad et al. (1996).

La minería de datos ha sido aplicada exitosamente a problemas de investigación en muchos campos de la industria. En el área de ingeniería eléctrica, se ha utilizado para el diagnóstico de fallas en sistemas de distribución, Chien et al. (2002), Peng et al. (2004), Liu & Schulz (2002), Huang (2002), para determinar la posible causa de falla del sistema (elemento fallado). En Hsu et al. (1991) se utiliza la información de llamadas de los usuarios y la dirección de éstos para estimar la región de falla.

El método propuesto en este artículo tiene como entradas a los atributos obtenidos de las señales de tensión y corriente en la subestación. Dentro de los trabajos existentes que también utilizan estas entradas se pueden mencionar el propuesto en Mahanty & Gupta (2004), en el cual se estima la distancia a la cual ocurrió la falla en una línea de transmisión usando redes neuronales de base radial. En Thukaram et al. (2006) se utilizan redes neuronales artificiales (ANN) para estimar la distancia de falla en sistemas de distribución, sin embargo todavía no se soluciona el problema de múltiple estimación. En Mora et al. (2009) se realiza una comparación entre las máquinas de soporte vectorial y el método de los k vecinos más cercanos (knn) para clasificación en el problema de localización de la zona en falla en sistemas de distribución. Finalmente, en Morales (2010), se plantea una estrategia híbrida de localización, utilizando el método knn tanto para clasificación como para regresión, para el caso de fallas simuladas a condición nominal.

En este artículo se propone una estrategia para resolver el problema de múltiple estimación en la localización de fallas de baja impedancia utilizando técnicas basadas en minería de datos. La metodología híbrida propuesta integra un método de clasificación y uno de regresión; la respuesta de la zona de falla complementa la distancia estimada de falla y permite la solución del problema de múltiple estimación. Se seleccionan los métodos basados en minería de datos sobre los métodos basados en el modelo por la sensibilidad que estos últimos presentan respecto a cambios en el modelo eléctrico de la red, lo cual se evita considerando todos los posibles escenarios de operación en el entrenamiento de las técnicas de minería de datos. Adicionalmente, se realiza un análisis teniendo en cuenta diferentes condiciones de operación del circuito para verificar la robustez y precisión de los dos métodos.

Este artículo está dividido en 5 secciones. En la sección 2 se presenta los aspectos teóricos del método basado en los k vecinos más cercanos y del método Boosting. En la sección 3 se presenta la metodología de aplicación de la estrategia híbrida de localización de fallas. En la sección 4 se presentan los resultados obtenidos y finalmente, en la sección 5 se presentan las conclusiones de la investigación.

2. Aspectos teóricos básicos

La minería de datos se ha aplicado satisfactoriamente a diferentes problemas. Dentro de las técnicas más utilizadas se encuentra el método Boosting, el cual es una estrategia que combina la respuesta de múltiples máquinas de aprendizaje, lo cual incrementa el rendimiento del método, Bishop (2006), y mejora su habilidad de generalización respecto a la respuesta de una máquina sencilla, Wu et al. (2007).

Adicionalmente, se utiliza el método de regresión basado en los k vecinos más cercanos, de fácil implementación. La respuesta de estos dos métodos se combina como un híbrido para solucionar el problema de múltiple estimación.

2.1 Método de los k vecinos más cercanos para regresión

El método de los k vecinos más cercanos (knn) es un método de aproximación no paramétrica, que permite resolver problemas de clasificación y regresión y se fundamenta en el supuesto que la clase a la cual corresponde un objeto es la misma a la que pertenecen sus vecinos más cercanos, Moujahid (2008).

En este artículo, el método de los knn se utiliza para estimar la distancia a la cual ocurrió la falla. Para implementar este método cada caso se representa por un vector tal como se presenta en (1), donde x_ij son los atributos del dato i y y_i es la variable que se quiere estimar.

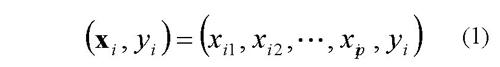
Cuando se tiene un dato desconocido, el algoritmo calcula la distancia de éste con los demás casos en la base de dato; el valor de y_q del dato desconocido x_q se calcula como el promedio del valor de y de los k casos más cercanos a éste. La forma de calcular el valor de y del nuevo dato también se puede modificar para considerar un mayor peso a los datos más cercanos al dato desconocido.

La asignación se realiza según la similitud de los casos en la base con el nuevo dato, sin embargo existen diferentes medidas de similitud, las cuales se presentan a continuación.

2.1.1 Distancia entre dos puntos

Las normas utilizadas para el cálculo de la distancia se presentan en las ecuaciones (2) a (5), Kecman (2001).

La distancia de Mahalanobis se expresa como la norma en la ecuación (4), en la cual W es la matriz de covarianza del conjunto de datos.

2.1.2 Asignación de la variable objetivo

La asignación de la variable objetivo y se realiza de una de las siguientes formas:

a. Promedio aritmético de los k casos más cercanos a x_q según la ecuación (6).

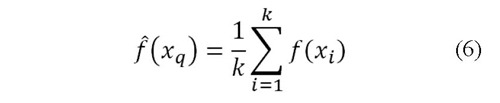
b. Promedio ponderado de los k casos más cercanos a x_q según la ecuación (7).

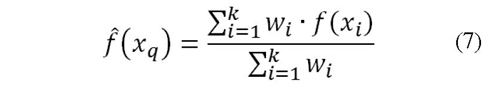
El peso w_i en (7) varía inversamente con la distancia, lo cual indica que los datos más cercanos a x_q tendrán más peso en la estimación de f (x_q), España (2008). Tres funciones de se proponen para probar el algoritmo, utilizando el inverso de la distancia (8), el cuadrado del inverso de la distancia (9) y un kernel Gaussiano (10).

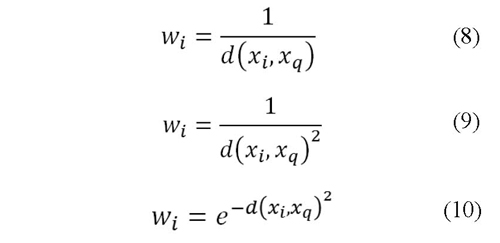
2.1.3 Precisión del método de regresión

La precisión del método se calcula según el error absoluto como se presenta en la ecuación (11).

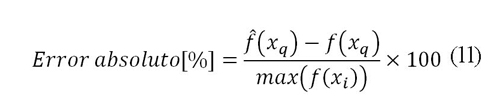
2.2 Método Boosting para clasificación

Para la solución del problema de localización de fallas en sistemas de distribución se implementa la técnica de clasificación Boosting, la cual hace parte de las técnicas de minería de datos más influyentes, según recientes investigaciones, Wu et al. (2007). Para esta investigación se utiliza como técnica base a los biclasificadores lineales, por lo tanto, es necesario implementar un esquema de descomposición y votación para manejar el problema de multi-clasificación, los cuales se explican en Mora (2006).

La técnica de clasificación Boosting se basa en entrenar varios clasificadores básicos de forma secuencial, de forma que para entrenar el clasificador actual se utiliza una función de error, la cual se modifica según el rendimiento del clasificador anterior. La forma más utilizada se denomina Adaboost y fue propuesta por Freund & Schapire (1996). En este artículo se utiliza el Adaboost.M1, el cual es un método que permite modificar los pesos del conjunto de datos.

2.2.1 Adaboost M1

El método asume que todos los ejemplos corresponden a puntos en un espacio p-dimensional, los cuales tienen establecida una clase C. Los datos de entrenamiento son de la forma presentada en (12).

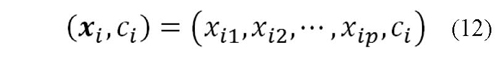
En la ecuación (11), xij son los atributos que representan al dato y ci es la clase asociada al dato xi. En la primera iteración se inicializan los pesos de los datos iguales. Con este conjunto de datos se entrena una técnica de clasificación básica denominada clasificador 'débil' con objetivo de minimizar el error de clasificación, el cual está dado por los pesos de los datos como se muestra en la ecuación (12).

Para la siguiente iteración se modifican los pesos de los datos, aumentando el peso de los datos mal clasificados para que tengan más relevancia en el nuevo cálculo del error. De esta manera, el algoritmo concentra el esfuerzo de los clasificadores débiles en los datos más difíciles.

El método continúa hasta que se hayan entrenado m clasificadores débiles. Al final se combina la respuesta de todos los clasificadores débiles para obtener una hipótesis de clasificación definitiva.

El algoritmo Adaboost.M1 se presenta a continuación, tal como se muestra en Bishop (2006).

1. Inicializar el coeficiente de pesos de los datos w_n = 1/N , donde N es el número de datos.

2. Para cada uno de los m biclasificadores débiles, se debe:

a.) Entrenar un clasificador y_m (x_m) para los datos de entrenamiento que minimice la función de error ponderada (13).

En cada iteración se debe garantizar que la suma de los pesos sea igual a 1.

3. El modelo o hipótesis de clasificación final se obtiene de las respuestas de todos los clasificadores débiles como se muestra en (17)

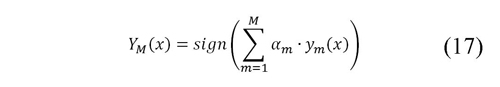
El proceso descrito anteriormente se modifica para incluir otro criterio de parada según la precisión para los datos de parametrización. En cada iteración de m se determina la clase asignada por el método para los casos de parametrización según la ecuación (17); después se calcula la precisión mediante la ecuación (18). Si la precisión es mayor a 0.98 el algoritmo termina.

2.2.2 Biclasificador lineal

Este clasificador es una forma de árbol de decisión, el cual asigna la clase a un nuevo dato tal como se muestra en (19). Por lo tanto, este tipo de clasificador simplemente divide el espacio en dos regiones separadas por una superficie de decisión lineal paralela a uno de los ejes, Bishop (2006).

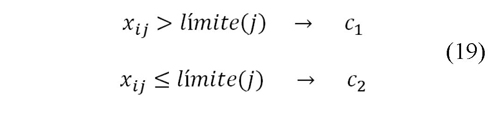
3. Metodología híbrida propuesta

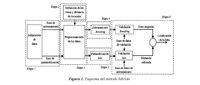
El esquema híbrido de localización de fallas sigue la estructura mostrada en la figura 1. Las etapas mencionadas se explican a continuación.

3.1 Adquisición de datos

Debido a que los eventos de falla no son frecuentes en el sistema y que éstos generalmente no son registrados de forma correcta, las bases de datos de falla en sistemas de distribución no son lo suficientemente grandes para utilizarlas en el entrenamiento de los métodos de clasificación. Por esta razón, la base de datos de fallas se obtiene mediante simulación del circuito bajo estudio, utilizando una herramienta computacional que simula automáticamente fallas mediante un proceso conjunto entre ATP y Matlab, Villar & Jaimes (2006). Cada registro de fallas se representa por una serie de atributos obtenidos de las señales medidas de tensión y corriente.

3.2 Definición de las zonas y distancia de los nodos

Para el problema de clasificación, a cada nodo del sistema de distribución se le asigna una zona, la cual se define previamente según criterios como la longitud del tramo de línea, la topología del circuito, ubicación de elementos de protección, disponibilidad de suficientes datos de fallas en cada zona y criterios de mantenimiento. Si es posible, cada zona debe tener sólo un lateral para evitar el problema de múltiple estimación, Mora (2006).

Para el problema de regresión, la variable objetivo corresponde a la distancia desde la subestación hasta el nodo en falla. Esta información se obtiene de la topología del circuito.

3.3 Preprocesamiento de los datos

Para el problema de clasificación, el preprocesamiento de los datos consiste en asignar la etiqueta de la zona correspondiente a cada caso de falla en la base de datos. Para el problema de regresión, se asigna a cada caso la distancia a la cual ocurrió la falla. Adicionalmente, se seleccionan los atributos que se utilizan para el entrenamiento del método. Otros problemas requieren la detección de datos anómalos, manejo del ruido y estrategias para resolver el problema de los datos faltantes. Sin embargo, ninguna de estas tareas se realiza en este problema, debido a que las bases de datos obtenidas por simulación están completas.

3.4 Entrenamiento del método Boosting

Con la zonificación definida en la etapa 2 y la base de datos de entrenamiento, se entrena el método de clasificación siguiendo la estrategia Adaboost.M1 explicada anteriormente para cada tipo de falla. Para el entrenamiento, todos los atributos disponibles son utilizados.

3.5 Parametrización del método knn

Esta etapa consiste en encontrar los parámetros que tengan una mejor estimación de la distancia para datos nuevos o desconocidos mediante la técnica de la validación cruzada, Gutiérrez et al. (2010). Ésta técnica consiste en dividir el conjunto de datos en n subconjuntos, después se entrena la máquina de regresión con n-1 de ellos y se prueba con el faltante, esto se repite para todos los subconjuntos. Posteriormente, se obtiene la estimación de la distancia ̂ de cada dato en la base de parametrización. El error de validación cruzada, para una combinación de parámetros, se obtiene mediante la ecuación (20).

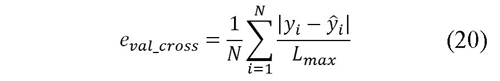
El error de validación cruzada se obtiene para cada combinación de parámetros y se escoge la combinación con menor error.

La estrategia descrita anteriormente se realiza para cada combinación de atributos, ya que no se utilizan todos a la vez debido a que algunos de estos no proporcionan buena información y pueden empeorar la respuesta del método. La selección de los mejores atributos se realiza mediante la evaluación del error obtenido ante datos desconocidos y para esto se prueba un conjunto de datos no utilizados en la parametrización, y se obtiene el error mediante la ecuación (20). Las mejores combinaciones de atributos son aquellas con menor error.

En esta etapa es posible utilizar una base de datos reducida debido a que mientras más grande es la base de datos, más se incrementa el esfuerzo computacional.

3.6 Validación de los métodos ante datos desconocidos

Finalmente, se realiza una prueba para calcular la precisión de los métodos ante datos desconocidos (datos que no fueron considerados en la etapa de parametrización). Para cada dato desconocido se determina el tipo de falla siguiendo la metodología propuesta en Das (1998). La precisión para el método de clasificación se calcula como se muestra en (18), con el archivo de entrenamiento obtenido. Por otro lado, se tiene que entrenar un regresor para cada uno de los tipos de falla. Este regresor se activa, según el tipo de falla determinado.

Para la validación del método knn se complementa la base de datos de entrenamiento con los datos disponibles. Con los parámetros óptimos obtenidos en la etapa 5 se prueban las mejores combinaciones de descriptores. El error en la estimación para el método de regresión se calcula como se presenta en (21).

El resultado de distancia estimada y zona de falla se combina para eliminar el problema de múltiple estimación.

4. Resultados y discusión

4.1 Sistema de prueba

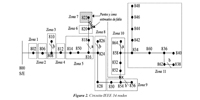
La metodología propuesta se prueba en el sistema IEEE 34 nodos presentado en IEEE (2000), que corresponde a un circuito de distribución real ubicado en Arizona, operado a 26.7 kV. El sistema presenta cargas desbalanceadas, laterales monofásicos y múltiples calibres de conductor. El sistema se subdivide o zonifica en 11 zonas tal como se muestra en la figura 2. La zona 11 contiene 9 nodos debido a que la longitud del tramo de línea entre ellos es muy corta.

4.2 Escenarios de prueba

Los escenarios utilizados para probar el algoritmo, incluyen fallas en todos los nodos del sistema excepto en la subestación. Se simularon cuatro condiciones diferentes de carga además de la promedio, con variaciones de carga entre 30 - 60%, 60 - 85%, 85 - 105% y 30 - 105%. Se simularon además 4 escenarios de variación de la tensión en la subestación entre los valores de 95 - 98%, 98 - 102%, 102 - 105% y 95 - 105% y 4 escenarios de variación de la longitud de las líneas en intervalos de 95 - 98%, 98 - 102%, 102 - 105% y 95 - 105%.

Para cada escenario propuesto se utilizan diferentes resistencias de falla, las cuales toman valores entre 0.05 Ω y 40 Ω, comúnmente utilizados en este tipo de pruebas, Dagenhart (2000). Se obtuvieron en total 126,854 datos para parametrización y prueba.

4.3 Selección de atributos

Los atributos seleccionados corresponden a la variación en magnitud y ángulo entre los estados estacionarios de prefalla y falla de la componente fundamental de tensión y corriente medidos desde la subestación, los cuales presentaron buenos resultados en trabajos anteriores, Gil (2013). Se tiene en cuenta medidas de línea y de fase. Cada registro de falla tiene 24 atributos.

4.4 Prueba a condición nominal

a. Parametrización knn

En esta prueba se utilizan fallas simuladas a condición nominal en la parametrización y entrenamiento, la base de datos está compuesta por casos con resistencia de falla entre 0.05 a 40 Ω en pasos de 4Ω. La base de datos contiene 2,618 casos para todos los tipos de fallas.

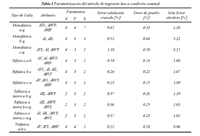
Los resultados de parametrización para el método de regresión knn se presentan en la Tabla 1. Para la parametrización se utilizan 1,118 datos y se dejan 1,500 datos de prueba. En la Tabla 1, el parámetro d representa la norma utilizada para el cálculo de la distancia, el cual puede tomar uno de los siguientes valores:

• d = 1 → Norma 2 o distancia Euclídea

• d = 2 → Norma 1 o distancia Manhattan

• d = 3 → Norma L∞ o norma Chebyshev

• d = 4 → Distancia de Mahalanobis

P representa el método de asignación de la variable objetivo (ver sección 2.1.2), el cual puede tomar los siguientes valores:

• P = 1 → selección de la clase con mayor frecuencia

• P = 2 → selección de la clase con menor distancia media

• P = 3 → selección con ponderación de casos seleccionados (1 ⁄ d)

• P = 4 → selección con ponderación de datos (1 ⁄ d2)

• P = 5 → selección con ponderación de datos usando kernel Gaussiano (e-d)

Finalmente, k representa el número de vecinos.

b. Entrenamiento del método Boosting

El entrenamiento se realiza con la misma base de datos utilizada anteriormente para parametrizar el método knn, la cual contiene 2,618 casos de falla.

c. Validación de los métodos knn y Boosting

La base de datos de validación está conformada por 7,140 casos simulados con resistencia de falla entre 1 a 39 Ω en pasos de 1 Ω (sin incluir los casos ya utilizados en la parametrización y entrenamiento). Los resultados de la validación para el método de regresión knn y el método Boosting se muestran en la Tabla 2 para todos los tipos de falla.

4.5 Prueba considerando fallas a diferentes condiciones de operación

a. Parametrización knn

Se utilizan los mejores parámetros encontrados a condición nominal presentados en la Tabla 1.

b. Entrenamiento del método Boosting

En esta prueba se incluyen en el entrenamiento todas las condiciones de operación del circuito mencionadas en la sección 4.2. Con esto se consideran las variaciones en la carga, variaciones en la tensión de la subestación, incertidumbre en la longitud de la línea y operación a condición nominal. Se obtiene una base de datos completa para el entrenamiento de 34,034 casos considerando resistencias de falla de 0.05 a 40Ω en pasos de 4Ω. El tiempo requerido en la etapa de entrenamiento del método Boosting usando un PC Core2Quad @2.66 GHz, 4GB RAM es cerca de 395 segundos.

c. Validación de los métodos knn y Boosting

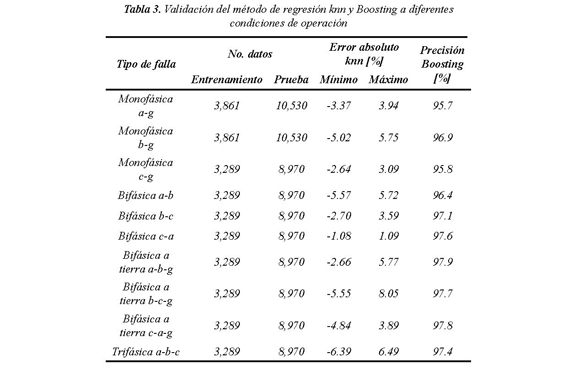
La base de datos de prueba contiene 92,820 casos con resistencia de falla entre 1 a 39 Ω en pasos de 1 Ω, sin incluir los casos utilizados en la parametrización. Para validación se utiliza una base de datos de entrenamiento con 34,034 casos de falla. Los resultados de validación del método de regresión y clasificación se presentan en la Tabla 3; se obtiene un buen desempeño en la estimación, el error absoluto máximo es de 8.05%, lo que representa un error de 4.74 km en la estimación de la distancia y un buen desempeño del método Boosting, superior a 95.7 % para todos los tipos de falla.

En la Tabla 4 se presenta el resultado de la matriz de confusión para la falla monofásica a-g, la cual obtuvo la menor precisión en la prueba. La matriz de confusión muestra una mala clasificación principalmente entre las zonas 1 y 2, y entre las zonas 10 y 11. En otras zonas la confusión fue menor. Esta dificultad en la clasificación puede ser resuelta mediante un cambio en la definición de las zonas. Los datos mal clasificados fueron asignados a una de las zonas adyacentes.

d. Localización con la metodología híbrida

A manera de ejemplo específico, para una falla monofásica en la fase a, simulada a 48.12 km desde la subestación, en el tramo entre los nodos 820 y 822 (que incluye las zonas 6 y 7), se obtiene una distancia de falla estimada mediante el método de regresión knn de 46.92 km. La distancia estimada coincide en dos diferentes puntos del sistema, uno entre los nodos 820 y 822 y otro entre los nodos 854 y 852. La zona que obtiene el método Boosting como la más probable de falla es la 7 (la cual incluye al nodo 822). Por lo tanto, uniendo las dos respuestas se puede concluir que la falla ocurre entre los nodos 820 y 822.

La distancia estimada ofrece una aproximación a la ubicación de falla, sin embargo esta distancia se cumple para otros sitios del sistema, entonces se utiliza la respuesta de la zona asignada para determinar el lateral en el cual se espera que haya ocurrido la falla. A partir de las dos respuestas se puede localizar rápidamente la falla y se puede disminuir el tiempo de restauración del servicio. La respuesta de la metodología híbrida se muestra en la figura 2.

5. Conclusiones

En este artículo se soluciona el problema de localización de fallas en sistemas de distribución mediante una metodología híbrida que combina la respuesta de un método de clasificación y uno de regresión. La metodología híbrida presentada es una alternativa de fácil implementación y exigencia computacional baja, la cual puede ser de gran ayuda en la solución del problema de localización de fallas en redes de distribución de energía eléctrica.

Como se muestra en las pruebas realizadas, las dos metodologías presentan una buena precisión para todos los tipos de fallas y la unión de sus respuestas permite eliminar el problema de múltiple estimación y dar una localización de falla más adecuada. La precisión del método de clasificación es mínimo 95.7 % y el error máximo absoluto es de 8.05% para regresión.

Finalmente, los resultados muestran la eficiencia del método y demuestran que su aplicación permite resolver el problema de localización de fallas en sistemas de distribución.

6. Agradecimientos

Este artículo fue apoyado por el programa de Jóvenes Investigadores "Virginia Gutiérrez de Pineda" del Departamento Administrativo de Ciencia, Tecnología e Innovación (COLCIENCIAS) y la Universidad Tecnológica de Pereira, Colombia.

7. Referencias

Bishop, C.M. (2007). Pattern Recognition and Machine Learning. New York, USA: Springer-Verlag.         [ Links ]

Chien, C., Chen, C., & Lin, Y. (2002). Using Bayesian network for fault location on distribution feeder. IEEE Transactions on Power Delivery, 17 (3), 785- 793.         [ Links ]

Dagenhart, J. (2000). The 40-O ground-fault phenomenon. IEEE Transactions on Industry Applications, 36 (1), 30-32.         [ Links ]

Das, R. (1998). Determining the locations of faults in distribution systems. Ph.D. dissertation. University of Saskatchewan. Saskatoon, Canada.         [ Links ]

España, G., Mora, J., & Torres, H. (2008). Estrategia de regresión basada en el método de los k vecinos más cercanos para la estimación de la distancia de falla en sistemas radiales. Rev. Fac. Ing. Univ. De Antioquia, 45, 100-108.         [ Links ]

Fayyad, U., Piatetsky-Shapiro, G., & Smyth, P. (1996). From Data Mining to Knowledge Discovery in Databases. AI Magazine, 17 (3), 37-54.         [ Links ]

Freund, Y., & Schapire, R. E. (1996). Experiments with a new boosting algorithm. Thirteenth International conference on Machine Learning (ICML) (pp. 148-156). Bari, Italy.         [ Links ]

Gil, W., Mora, J., y Pérez, S. (2013). Análisis comparativo de metaheurísticas para calibración de localizadores de fallas en sistemas de distribución. Ingeniería y Competitividad, 15 (1), 103-115.         [ Links ]

Gutiérrez, J., Mora, J., & Pérez, S. (2010). Strategy based on genetic algorithms for an optimal adjust of a support vector machine used for locating faults in power distribution systems. Rev.fac.ing.univ. Antioquia, 53, 174-184.         [ Links ]

Hsu, Y., Lu, F., Chien, Y., Liu, J., Lin, J., Yu, P., & Kuo, R. (1991). An expert system for locating distribution system faults. IEEE Transactions on Power Delivery, 6 (1), 366-372.         [ Links ]

Hu, X. (1995). Knowledge Discovery in Databases: an Attribute Oriented Rough Set Approach. Doctoral Thesis, Department of Computer Science, University of Regina, Canada.         [ Links ]

Huang, S. (2002). Application of immune-based optimization method for fault-section estimation in a distribution system. IEEE Transactions on Power Delivery, 17 (3), 779-784.         [ Links ]

IEEE. (2000). IEEE Distribution System Analysis Subcommittee. Radial test Feeders. Recovered 15/03/2015 http://www.ewh.ieee.org/soc/pes/dsacom/testfeeders/index.html        [ Links ]

Kecman, V. (2001). Learning and soft computing. Cambridge-London, UK: The M.I.T. Press.         [ Links ]

Liu, Y., & Schulz, N. (2002). Knowledge-based system for distribution system outage locating using comprehensive information. IEEE Transactions on Power Systems, 17 (2), 451-456.         [ Links ]

Mahanty, R., & Gupta, P. (2004). Application of RBF neural network to fault classification and location in transmission lines. IEE Proceedings Generation, Transmission and Distribution, 151 (2), 201-212.         [ Links ]

Mora, J. (2006). Localización de Faltas en Sistemas de Distribución de Energía Eléctrica usando Métodos basados en el Modelo y Métodos de Clasificación Basados en el Conocimiento. Tesis Doctoral, Departamento Tecnologías de la Informática, Universidad de Girona, Girona, España.         [ Links ]

Mora, J., Morales, G., & Perez, S. (2009). Learning-based strategy for reducing the multiple estimation problem of fault zone location in radial power systems. IET Generation, Transmission & Distribution, 3 (4), 346-356.         [ Links ]

Morales-España, G., Mora-Flórez, J., & Carrillo-Caicedo, G. (2010, Nov). A complete fault location formulation for distribution systems using the k-Nearest Neighbors for regression and classification. In, Transmission and Distribution Conference and Exposition: Latin America (T&D-LA), 2010 IEEE/PES (pp. 810-815). IEEE.         [ Links ]

Moujahid, A., Inza, I., Larrañaga, P. (2008). Clasificadores k-NN. Departamento de Ciencias de la Computación e Inteligencia Artificial. Universidad del País Vasco-Euscal Erriko Unibertsitatea. Recuperado 15/03/2015 http:// www.sc.ehu.es/ccwbayes/docencia/mmcc/docs/t9knn.pdf        [ Links ]

Peng, J., Chien, C., & Tseng, T. (2004). Rough set theory for data mining for fault diagnosis on distribution feeder. IEE Proceedings - Generation, Transmission and Distribution, 151 (6), 689-697.         [ Links ]

Thukaram, D., Shenoy, J. U., & Ashageetha, H. (2006). Neural network approach for fault location in unbalanced distribution networks with limited measurements. In, Power India Conference, 2006 IEEE (pp. 8-pp). IEEE.         [ Links ]

Villar, R., & Jaimes, F. (2006). Caracterización de circuitos de distribución para estudios de calidad en sistemas de energía eléctrica. Tesis de grado, Escuela de Ingenierías Eléctrica, Electrónica y Telecomunicaciones, Universidad Industrial de Santander, Colombia.         [ Links ]

Wu, X., Kumar, V., Quinlan, J., Ghosh, J., Yang, Q., Motoda, H. et. al. (2007). Top 10 algorithms in data mining. Knowledge and Information Systems, 14 (1), 1-37.         [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.