Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y competitividad
Print version ISSN 0123-3033
Ing. compet. vol.17 no.1 Cali Jan./June 2015
A literature review of bounding volumes hierarchy focused on collision detection
Revisión de literatura de jerarquía volúmenes acotantes enfocados en detección de colisiones
Simena Dinas
E-mail: simena.dinas@correounivalle.edu.co
José M. Bañón
E-mail: jose.banon@correounivalle.edu.co
* Escuela de Ingeniería de Sistemas y Computación, Universidad del Valle, Cali, Colombia
Eje temático: SYSTEMS ENGINEERING / INGENIERíA DE SISTEMAS
Recibido: Febrero 18 de 2014
Aceptado: Febrero 3 de 2015
Abstract
A bounding volume is a common method to simplify object representation by using the composition of geometrical shapes that enclose the object; it encapsulates complex objects by means of simple volumes and it is widely useful in collision detection applications and ray tracing for rendering algorithms. They are popular in computer graphics and computational geometry. Most popular bounding volumes are spheres, Oriented-Bounding Boxes (OBB's), Axis-Aligned Bounding Boxes (AABB's); moreover, the literature review includes ellipsoids, cylinders, sphere packing, sphere shells, k-DOP's, convex hulls, cloud of points, and minimal bounding boxes, among others. A Bounding Volume Hierarchy is usually a tree in which the complete object is represented tighter fitting every level of the hierarchy. Additionally, each bounding volume has a cost associated to construction, update, and interference tests. For instance, spheres are invariant to rotation and translations, then they do not require being updated; their constructions and interference tests are more straightforward then OBB's; however, their tightness is lower than other bounding volumes. Finally, three comparisons between two polyhedra; seven different algorithms were used, of which five are public libraries for collision detection.
Keywords: Axis-aligned bounding box (AABB), bounding volumes hierarchies, convex objects, oriented bounding box (OBB), spheres.
Resumen
Un volumen acotante es un método común para simplificar la representación de los objetos por medio de composición de formas geométricas que encierran el objeto; estos encapsulan objetos complejos por medio de volúmenes simples y son ampliamente usados en aplicaciones de detección de colisiones y trazador de rayos para algoritmos de renderización. Los volúmenes acotantes son populares en computación gráfica y en geometría computacional; los más populares son las esferas, las cajas acotantes orientadas (OBB's) y las cajas acotantes alineadas a los ejes (AABB's); no obstante, la literatura incluye elipses, cilindros empaquetamiento de esferas, conchas de esferas, k-DOP's, convex hulls, nubes de puntos y cajas acotantes mínimas, entre otras. Una jerarquía de volúmenes acotantes es usualmente un árbol, en el cual la representación de los objetos es más ajustada en cada uno de los niveles de la jerarquía. Adicionalmente, cada volumen acotante tiene asociado costos de construcción, actualización, pruebas de interferencia. Por ejemplo, las esferas so invariantes a rotación y translación, por lo tanto no requieren ser actualizadas en comparación con los AABB no son invariantes a la rotación. Por otro lado la construcción y las pruebas de solapamiento de las esferas son más simples que los OBB's; sin embargo, el ajuste de las esferas es menor que otros volúmenes acotantes. Finalmente, se comparan dos poliedros con siete algoritmos diferentes de los cuales cinco son librerías públicas para detección de colisiones.
Palabras Clave: Cajas acotantes orientadas (CAO), cajas acotantes alineadas a los ejes (CAAE), esferas, jerarquía de volúmenes limitantes, objetos convexos.
1. Introduction
Collision detection concerns the problem of determining if, when, and where a pair of objects are intersecting (Ericson, 2005). A pair of objects intersecting together is a Boolean question that must answer whether or not they are intersecting, whereas temporal information about the instant time of the intersection should be numerically answered. Finally, the position of the intersection between the objects should be answered with spatial information. The if question has to be answered before the others and it determines the validity of the other questions, but the order of when, and where questions depends on the applications. Some applications of collision detection can be found in robotics and computer graphics areas. However, specific areas of application include, but are not limited to: molecular modeling, physical-based simulation, computer animation, dynamic simulation, surgical simulation, virtual environments, motion planning, obstacle avoidance, and virtual prototyping among others (Lin et al., 1996; Ericson, 2005). Collision detection is a bottleneck for several applications because of the computational complexity. Moreover, it remains a challenge even though, recently, several authors have developed new algorithms and methods to accelerate the process (Zhigang et al., 2010; Avril et al., 2011).
Most collision detection methods are divided into two phases: i) broad-phase methods are related to determining the pair of objects involved in potential collision, and ii) narrow-phase methods are focused on checking the exact collision for every pair identified in broad phase (Mirtich, 1997). Moreover, potential collisions identified in broad-phase are not always real collisions; the existence of collisions is checked in narrow phase. The main reason of narrow-phase is related to checking each pair for intersection. Convex objects, spatial partitioning, and bounding volumes hierarchies are the most important narrow-phase techniques. Bounding volume hierarchies are widely used in the literature. They have three requirements i) each level in the hierarchy represent a tighter fit than its parents, ii) a set of child nodes in the hierarchy depict the same part of the object covered by its parent node, and iii) the bounding volume should fit the original node as tight as possible with a high degree of accuracy for the original model. However, two opposite criteria guide the selection of the bounding volume: it should be as tight as possible and the intersection test for a pair should be as efficient as possible (LaValle, 2006).
The most widely used bounding volumes are Axis-Aligned Bounding Box (AABB) (Xiao-Rong et al., 2009); spheres (Hubbard, 1996; Pitt-Francis and Featherstone, 1998; Arcila, 2009); Oriented Bounding Box (OBB) (Gottschalk et al., 1996). Moreover, (Arcila, 2011) included in his work a double bounding volume hierarchy (for spheres, AABB's, and OBB's): an outer and an inner representation. The outer bounding volume is widely used; it is focused on determining the collision, and accelerates the process in broad phase. The inner bounding volume is used to accelerate the collision acceptance process.
This document is organized as follows: Collision Detection is described in Section 2 and Bounding Volume Hierarchies are developed in Section 3. Sections 4 and 5 describe Bounding Volume Requirements and Bounding Volume Performance, respectively, whereas Previous Work and Conclusions are depicted in Sections 6 and 7, severally. Finally, references are listed in the last part of the document.
2. Collision detection
The collision problem has been solved by means of different techniques. Analytical methods, geometric methods, accurate techniques, hierarchical representations, and optimization methods are frequently used (Lin & Gottschalk, 1998). Collision detection is an important topic in areas like robotics, physics modeling, animation, geometric modeling, and video games among others (Bing et al., 2009; Xiao-Rong et al., 2009; Zhigang et al., 2010). Searching for and finding collisions between objects are critical problems based on solving an intersection point or area between objects. An accurate technique compares the faces of the objects; however, it is computationally expensive. Other accurate techniques involve mesh, for instance, level of details and triangulation to compare polyhedral by using a face-face test. Several approximations to the solution can be found in the literature; nevertheless, most of them can be classified into three categories: i) geometrics, ii) bounding volume hierarchies, and iii) spatial subdivision (Xiao-Rong et al., 2009). Geometric approaches are based on analyzing the shape of each model, tracking and capturing the closest features between two or more models; for more details, see (Mirtich, 1998). Bounding volume hierarchies construct a tree by subdividing the model into small pieces, which should be tighter for lower levels; for more details see (Bradshaw, 2002). Finally, spatial subdivision divides the space into cells; every object falls into a cell; for more details, see (Castro et al., 2008).
The most common implementations are based on hierarchical bounding volumes. A bounding volume is usually the simplest geometric primitive that encloses one or more objects and leads to cheaper overlapping tests (Ericson, 2005). The bounding volumes most frequently used are spheres, cylinders, ellipsoids, and boxes. Each object in the scene is represented by a bounding volume. An object is divided hierarchically, usually by a recursive subdivision. Each part of the object is represented as bounding volume hierarchies. The most common hierarchical object representation is a tree. The problem of detecting a collision between two or more objects can be reduced to detect collisions between their bounding volume hierarchies. Some approaches have been implemented by means of outer bounding volumes to quickly reject an intersection, and inner bounding volumes to quickly accept a collision (Huber, 1998; Arcila, 2008; Weller and Zachmann, 2008; Arcila, 2011).
Partitioning the space and partitioning the object are commonly used techniques. The former, a well-known technique is based on dividing the space, for instance, into eight subspaces known as Octrees (Joseph, 2003) by means of subdividing the main planes. The latter, is focused on divided the object into portions, and the division depends on the implementation. Spatial partitioning techniques include (Glass, 2005): i) Uniform or Regular Grid in which the space is split into equal cells by using axis-aligned cells (Teschner, et al., 2003); ii) Quadtree/Octree, which refine the space subdivision in populated zones by means of axis-aligned cells. Quadtree and Octree are terms used for two-dimensional and three-dimensional trees, respectively (Samet, 1988; Frisken & Perry, 2005); iii) K-Tree, which is a generalization of Quadtrees and Octrees to k dimensions (Bentley, 1975); and vi) Binary Space Partitioning Tree (BSP tree), which subdivides the space by means of arbitrarily oriented planes (Luque et al., 2005). On the other hand, analytic techniques combine potential field-based algorithms and bounding volumes. The object is represented by a bounding volume and a repulsive vector field is used to detect the collision. Recursive subdivision and interval arithmetic are popular techniques.
3. Bounding volumes hierarchies
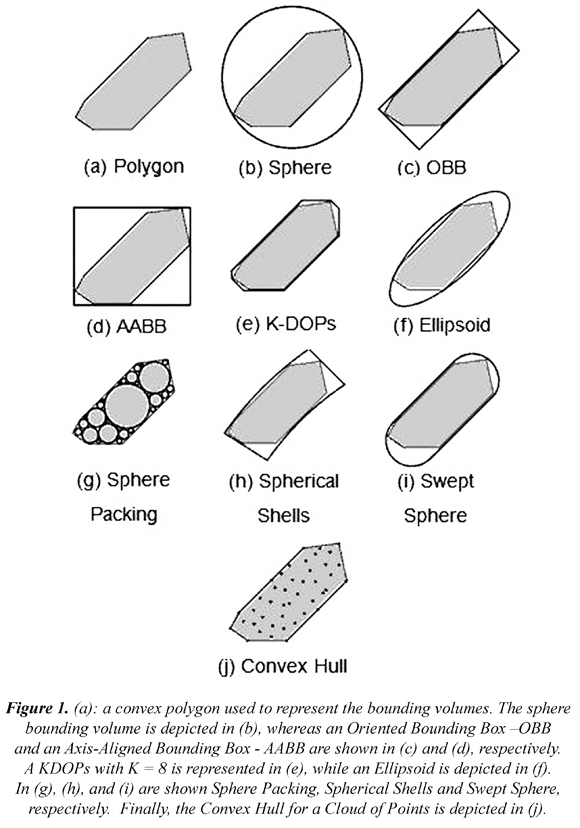
A list of the most important bounding volumes and a graphical representation are shown in Figure 1; all of they are based on the polygon depicted in figure 1(a).
3.1 Spheres
This is based on enclosing a convex polyhedron in a sphere; it is usually called the outer sphere (Hubbard, 1996; Pitt-Francis, 1998; James & Pai, 2004). However, inner spheres have been explored (Arcila et al., 2009). The outer sphere allows binding the polyhedron; it is used to quickly determine non-intersection between the polyhedron. In contrast, the inner sphere is used to determine intersection between polyhedral. An advantage of sphere bounding volumes is its efficiency to calculate intersections and distances. Although spheres are invariant to translation and rotations, they are not good bounding volume for elongated polyhedron (Figure 1 (b)).
An intersecting approach showed the hierarchical sphere construction for non-convex objects (Quinlan, 1994). Moreover, (Palmer & Grimsdale, 1995) took advantage of object-oriented techniques to create a collision detector for moving objects. Hubbard (1995a) executed an exhaustive comparison between Octrees subdivision and sphere-tree, obtaining as result a better adjustment of spheres than Octrees. The sphere-tree was constructed by using a medial-axis surface as skeletal representation of the objects to optimize the technique (Hubbard, 1995a; Hubbard, 1995b; Hubbard, 1996). O'Sullivan and Dingliana (1999) worked on the approximation of the surface of the objects by using spheres-tree. James and Pai (2004) introduced the Bounded Deformation Tree, or BD-Tree, developed for deformable models of rigid bodies. Moreover, OBB and spheres were combined in (Chang et al., 2008) to take advantage of the best of each. A set of works have been developed around collision detection; however, the main results were the Doctoral Thesis by Arcila (2008).
Initially, (Muñoz et al., 2001a; Muñoz et al., 2001b; Muñoz et al., 2002) developed a set of heuristics for the circular representation of polygons. This work was the basis for double representation of spheres developed by Arcila (2008) and Arcila (2011). This representation was compounded by inner spheres, which accelerate the collision detection and outer spheres to accelerate the non-intersection tests. Finally, based on previous work, a dynamic collision detector was developed (Dinas, 2009; Dinas et al., 2010).
3.2 Oriented bounding box (OBB)
Using the polyhedron orientation, a rectangle is calculated to cover it. Advantages of these volumes are the invariance to translation and rotations. Accordingly, it is possible to move and rotate the object and the bounding volume together; however, the collision test is computationally more expensive than the AABB test (Figure 1 (c)).
A work was focused on the construction of a data structure and efficient and exact algorithm to general polygonal models. Additionally, they compared hierarchical representation based on sphere trees, AABB trees, and OBB tree. The comparison demonstrated that OBB's are asymptotically faster (Gottschalk et al., 1996; Gottschalk, 2000). The dynamics of OBB's was studied in (Eberly, 2007; Eberly, 2008). Several authors have worked on improving fitting and overlapping tests for OBB's, for instance, Jian-Hong et al., (2008) The double representation constructed by (Arcila, 2008; Arcila et al., 2008; Arcila, 2011). Finally, double bounding volumes were used; Zhigang et al., (2010) combined the best of AABB's and OBB's, whereas Chang et al., (2008) exploit the compactness of OBB's and the simplicity of spheres.
3.3 Axis-Aligned bounding box (AABB)
An AABB is an enclosing axis-aligned rectangle that covers the polyhedron. Its main advantages are: i) it is easy to find the rectangle, ii) OBB's are invariant to translations, and iii) the test between OBB's is straightforward; nevertheless, it is not invariant to rotation, as a result, changes in the objects' directions require changes in the bounding box (Figure 1 (d)).
A proposal was developed to accelerate the overlapping test between AABB's. Complex models were explored by van den Bergen (1997) and van den Bergen (1998) for rigid motion and deformation. To provide better understanding of running time from AABB, Weller et al., (2006) analyzed the average time for AABB under different assumptions. In contrast, a double representation composed by inner and outer AABB was proposed by Arcila (2005), and extended in Arcila (2008), and Arcila (2011). A hybrid technique was proposed by combining OBB and AABB. It takes advantage of the compactness of OBB's and the efficient overlapping test of AABB's (Zhigang et al., 2010). Finally, a method was proposed, which decreases storage space; consequently, reduce the detection time (Xiao-Rong et al., 2009).
3.4 K-Discrete orientation polytopes (K-DOP's) or fixed-direction hull (FDH)
A DOP is a generalized AABB. A DOP is a convex polytope containing the object, constructed by taking a number k of appropriately oriented planes at infinity and bringing it closer to the object until they collide. The most popular DOP's are calculated by 6 axis-aligned planes (axis-aligned bounding box), 10 axis-aligned planes (beveled bounding box on vertical edges), 18 axis-aligned planes (beveled on all edges), or 26 axis-aligned planes (beveled on all edges and corners) (Klosowski, 1998) (Figure 1 (e)).
Zachmann (1998) showed improvements by using a re-aligned k-DOP (only one). In contrast, Kimmerle (2004) combined a stochastic collision detection and k-DOP's. A parameterized k-DOP was introduced by Sobottka and Weber (2005), who worked on optimal values of k based on empirical data. The application on collision detection was focused on hair simulation taking into account the natural aspects of the hair and geometrical properties.
3.5 Ellipsoids
Ellipsoids are tighter fitting than spheres for elongated objects, chiefly arms and legs in humanoid modeling; they are not invariant to rotations; however, their calculation and the test between ellipsoids is more complex than spheres volumes (Arcila & Bañón, 2005; Bing et al., 2009) (Figure 1 (f)).
The smallest volume closing ball or ellipsoid was proposed by Welzl (1991). In contrast, (Wang et al., 2001; Wang et al., 2002; Wang et al., 2004) introduced an algorithm for moving ellipsoids. The work by (Choi et al., 2006a; Choi et al., 2006b; Choi, 2008; Choi et al., 2009) was based on continuous collision detection for two moving ellipsoids; however, this approach obtained similar results to those reported by Wang et al., (2001).
3.6 Sphere packing
Sphere packing is an arrangement of non-overlapping spheres enclosing a space. The size of spheres can be equal (regular) or different (irregular). A special kind of sphere packing is the Apollonian sphere packing (Figure 1 (g)). The works by Weller et al. (2006), focused on constructing a data structure for proximity queries and penetration volumes called inner sphere tree. The inner sphere tree was constructed by using a heuristic approach, voxelization and batch neural gas clustering algorithm (BNG), known from artificial intelligence (Weller & Zachmann, 2008; Weller & Zachmann, 2009a; Weller & Zachmann, 2009b; Weller & Zachmann, 2011). In Weller and Zachmann (2010) a prototype for sphere packing algorithm was constructed by using a GPU assistant.
3.7 Spherical shells
A pair of concentric spheres is computed; the polyhedron falls into the separation between the inner and outer spheres. Consequently, the outer sphere should enclose the entire geometry and then all vertices fall into the sphere. In contrast, the entire geometry should lie outside the inner sphere (See Figure 1 (h)). Krishnan et al., (1998a) and Krishnan et al., (1998b) focused on exploring both: tight fitting shells and fast overlap between both.
3.8 Swept sphere volume
The representation is straightforward: a radius and a swept volume. The most important swept sphere volumes are Point Swept Spheres (PSS); Line Swept Spheres (LSS); Rectangle Swept Sphere (RSS). The advantages of these volumes correspond to the sphere advantages. PSS, LSS, and RSS are invariant to translation; however, only PSS is invariant to rotation (See Line Swept Spheres, Figure 1 (i)). The authors introduced a new bounding volume called core primitive shape, whose growth includes point, linear, and rectangular shapes (Larsen et al., 1999). RSS were widely explored in (Larsen et al., 2000). In contrast, the LSS was explored to represent safe human-robot interaction, where the spheres encapsulate the link motions and the distance by using the size of each sphere (Corrales et al., 2011).
3.9 Cloud of points and convex hull (CPCH)
It is based on constructing a convex hull for a cloud of point; it is the smallest convex volume containing the object and, hence, a hull is a tight bounding volume (Tang et al., 2008) (Figure 1 (j)). Clouds of points are mostly focused on surface reconstruction and they are important for animated three-dimensional graphics. For instance, (Klein & Zachmann, 2004) used the cloud of point to reconstruct a surface. In Figueiredo et al. (2010), the authors combined voxelization and Overlapping AABB (OAABB) construction. The work of Pan et al. (2011) was focused on cloud of noisy points. Finally, convex hulls were used in (Liu et al., 2008) by using convex decomposition of the scene, convex polyhedral or convex objects. The application of the work developed by Lui et al. (2008) focused on real-world video games.
3.10 Minimum volume bounding box (MVBB)
Given a set of N points in an m-dimensional space, it is the minimum box where they all fall. The box has the minimum area and volume. Barequet and Har-Peled (1999) proposed an efficient algorithm to calculate MVBBs in three dimensions, whereas, Huebner et al., (2008) worked on shape approximations by means of MVBB decomposition to robot grasping.
3.11 Cylindrical
It is based on the radius of bounding circumference of the shape and a swept line. Finding the smallest enclosing cylinder for any object is checked in (Chan & Tan, 2004); the authors proposed an iterative approach to determine if an object can be enclosed in a cylindrical shape. In contrast, (Ketchel & Larochelle, 2006) explored a line-based cylindrical bounding volume.
3.12 Oriented convex polyhedral
It is the tightest convex polyhedral possible called R(S); (Bade et al., 2006a; Bade et al., 2006b) constructed an R(S) by using intersections of half spaces. This bounding volume is more accurate than an Oriented Bounding Box and more flexible than k-DOPs; however, the result of an Oriented Convex Polyhedral can be a k-DOP.
3.13 Spheres with uniform radius
Objects are represented by spheres with uniform radius by means of space subdivision approaches; its approach detects collisions between moving spheres by using three operations: collision, entering, and leaving. The first is used to detect collision, whereas second and third are used to detect changes in the spaces. A sphere is entering to a new space while, it is leaving the old one (Kim et al., 1998).
3.14 Zonotopes
Zonotopes are the generalization of a polytope in any dimension. They are usually studied by means of Voronoi diagrams, Minkowski sums, or Vectors. Zonotopes are symmetric convex polyhedral, invariant to 180° rotation. They were proposed as bounding volumes, not only because of their efficiency for collision tests but also because of their optimal constructions (Guibas et al., 2003).
3.15 QuOSPO
Quantized Orientation Slabs with Primary Orientations. Its bounding data structure combines and extends the advantages of OBB and k-DOPs (He, 1999).
4. Bounding volumes requirements
Several authors have written about the bounding volumes, including the importance, minimal requirements, construction cost, test cost, and evaluation, among others. Because of their importance, several authors have studied their impact and cost of computing, and have developed strategies to decrease the cost (Terdiman, 2001; Yoon & Manocha, 2006). Comparisons, techniques and most significant bounding volumes can be found in the literature (Mu & Oslejšek, 2000; Andersen & Bay, 2006; Koziara & Bićanić, 2005). Requirements for bounding volumes should include:
Tight fitting to approximated objects: Tighter fitting bounding volumes are computationally more expensive.
Efficient creation: The complexity of the bounding volume is related to the complexity of its creation; however, more complex volumes should be tighter fitting.
Efficient updating: Bounding volumes invariant to rotation and translation do not require updates.
Efficient overlap tests: Smaller computational costs are associated to simpler bounding volumes (as spheres and boxes).
Low memory usage: Simpler bounding volumes are lower memory use and smaller computational costs; nevertheless, they are less tight fitting.
Suitable for hierarchy construction: A bounding volumes tree helps to decrease the number of overlapping tests.
All requirements are important; however, there is not a bounding volume that fall into everyone and they depend on the application. Nevertheless, efficiency in bounding volumes is equally important to the following requirements of bounding volumes hierarchies (Bradshaw, 2002):
Volume Approximation: children nodes representing a tighter fit than its parent,
Covered Area: children nodes should cover the same parts of the object covered by the parent node,
Automatic Creation: hierarchy construction does not use human interaction, and
High Degree of Accuracy: the bounding volumes should fit the original model as tightly as possible.
5. Bounding volumes performance
Performance of bounding volumes can be evaluated using equation (1) (Gottschalk et al., 1996; van den Bergen, 1997; Klosowski et al., 1998).
T = Nu * Cu + Nv * Cv (1)
Where T is the total cost function for detecting interference between a pair of objects depicted by a bounding volume hierarchy; Nu is the number of primitives, i.e. bounding volumes, that are updated during the traversal of the hierarchies; Cu is the cost of updating a primitive due to motion; Nv is the number of overlapping tests performed, and Cv is the cost of performing an overlapping test between a pair of primitives nodes from the hierarchy.
However, (Krishnan et al. 1998; Larsson & Akenine-Möller, 2008) used an extended version of equation (1). It separate bounding volumes and primitives (see equation 2).
T = Nu * Cu + Nv * Cv + Np * Cp (2)
Where Nu is the number bounding volumes updated due to motion; Cu is the cost of updating the bounding volume; Np is the number primitives tested for interference, and Cp is the cost of testing the primitives for interference.
If the bounding volume is not enough to detecting a collision, the faces of the objects have to be compared by a face-face test or a triangle-triangles test (Arcila, 2008). Because of the comparison is computationally expensive, they cannot be considered in real-time collision detection. For instance, equation (1) ignores the difference between primitives and bounding volumes, while equation (2) establishes the difference by using Cp for primitives and Cu for bounding volumes.
6. Results and discussion
To develop the experiment we use the next set of recognized libraries for collision detection: PQP and RAPID use hierarchical OBB trees (Larsen et al., 1999; Gottschalk et al., 1996), whereas SOLID uses hierarchical AABB trees (Van den Bergen, 1997). QUICKCD and I-COLLIDE use hierarchical k-DOPs (Klosowski, 1998) and convex polyhedral (Cohen et al., 1995), respectively.
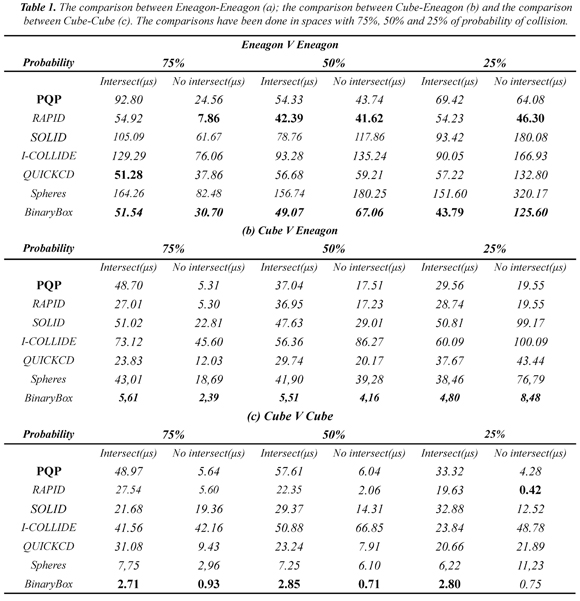
We compare results obtained by Arcila (2011) by using bounding and containing volumes for Spheres and binary boxes. Conditions were: boolean proximity query, 10.000 iterations per experiment, polygonal objects and spherical volume for simulations with 75%, 50% and 25% of probability of collision. Objects were Eneagon (18 vertices, 36 edges and 20 faces) and Cube (8 vertices, 12 edges and 6 faces).
Table 1 shows three experiments: Eneagon-Eneagon, Cube-Eneagon and Cube-Cube. The comparison between a pair of Eneagons shows that RAPID reports four of the lowest times algorithm whereas QUICKCD and BinaryBox record only one. RAPID is superior in this test because it uses OBB, which has a perfect adjustment for flatten and elongated polyhedron; on the other hand, the adjustment for Binary boxes and K-DOPs is good enough. In contrast, BinaryBox is the winner in the comparison between Cube-Eneagon, which has the lowest times for all and Cube-Cube with five. The reason of the results for Cube-Eneagon and Cube-Cube is because there are similarities between the representation and the objects; thus, the proposed algorithm and the representation take advantage of that.
Sphere algorithm has the higher values for Eneagon-Eneagon whereas, it take the second place in the comparison between cubes; which is uncommon because of the representation; however, it is important to highlight the contribution of containing spheres to the result; the comparison between internal spheres makes the algorithm faster (Arcila, 2011). It happens because the spheres perfectly enclose in the cube, while Eneagons produces different kind of elongated polyhedral on borders. Finally, results of SOLID depend on the orientation of the polyhedral; because they work with AABB.
7. Conclusions
Firstly, we have contextualized the bounding volumes on Collision Detection. Although bounding volumes are not limited to collision detection, they are widely used in this field; it is widely used to determine the interference between objects. Secondly, we have explored 15 bounding volume hierarchies; for each, we discussed some important features and showed applications and improvements. Spheres and Bounding Boxes are popular, the former due to simplicity and invariance to rotations and translations; however, they are a poor representation for elongated objects. The latter are invariant to rotation (OBB) or not (AABB); however, their calculation is straightforward. Finally, we explored the most important requirements and the most common methods to evaluate bounding volumes. Requirements are important to selecting the best bounding volume for applications; in contrast, evaluations and comparisons are important to understand the complexity of applications and make implementations improvements.
8. Acknowledgement
The authors thank to COLCIENCIAS and Universidad del Valle for economical and academic support.
9. References
Andersen, K. A., & Bay, C. (2006). A survey of algorithms for construction of optimal heterogeneous bounding volume hierarchies. Technical Report. Copenhague, Denmark: Department of Computer Science, University of Copenhagen. [ Links ]
Arcila, O. (2008). Nuevas Representaciones Dobles (Externas e Internas) en Detectores de Colisiones Jerárquicos. Tesis Doctoral. Facultad de Ingeniería, Universidad del Valle, Cali, Colombia. [ Links ]
Arcila, O. (2011). Nuevas Representaciones Dobles: Estudio e Implementación. Linköping Studies in Science and Technology. Doctoral Thesis. Editorial Académica Española, Madrid, España. [ Links ]
Arcila, O., Dinas, S., & Banon, J. M. (2012). Collision detection model based on Bounding and containing Boxes. In Proceedings of the XXXVIII Conferencia Latinoamericana En Informática -CLEI 2012 (pp. 1-10). Medellín, Colombia: CLEI. [ Links ]
Avril, Q., Gouranton, V., & Arnaldi, B. (2011, March). Dynamic adaptation of broad phase collision detection algorithms. In, IEEE. VR Innovation (ISVRI), 2011 IEEE International Symposium on (pp. 41-47). Singapore, Singapore: IEEE. [ Links ]
Bade, A., Suaib, N. M., Zin, A. M., & Sembok, T. M. T. (2006a). New Bounding Volume Approach for Detecting Collision in Computer Animation. Malaysian Journal of Computer, Science 19 (2), 127-140. [ Links ]
Bade, A., Suaib, N. M., Zin, A. M., & Sembok, T. M. T. (2006b). Oriented Convex Polyhedra for Collision Detection in 3D Computer Animation. In, Proceedings of the 4th international conference on Computer graphics and interactive techniques in Australasia and Southeast Asia, GRAPHITE '06. (pp. 127-193). New York, USA. [ Links ]
Barequet, G., & Har-Peled, S. (1999). Efficiently Approximating the Minimum-Volume Bounding Box of a Point Set in Three Dimensions. In, Proceedings of the tenth annual ACM-SIAM (Society for Industrial and Applied Mathematics) symposium on Discrete algorithms, SODA '99 (pp. 82-91). Philadelphia (PA), USA: SODA. [ Links ]
Bentley, J. L. (1975). Multidimensional Binary Search Trees Used for Associative Searching. Communications of the ACM, 18 (9), 509-517. [ Links ]
Bing, H., Yangzihao, W., & Jia, Z. (2009). An Improved Method of Continuous Collision Detection Using Ellipsoids. In, IEEE. IEEE 10th International Conference on Computer-Aided Industrial Design Conceptual Design, 2009 - CAID CD 2009 (pp. 2280-2286). Wenzhou, China: IEEE. [ Links ]
Bradshaw, G. (2002). Bounding Volume Hierarchies for Level-of-Detail Collision Handling. Doctoral Thesis, Trinity College Dublin, Dublin, Ireland. [ Links ]
Castro, R., Lewiner, T., Lopes, H., Tavares, G., & Bordignon, A. (2008). Statistical Optimization of Octree Searches. Computer Graphics Forum, 27 (6), 1557-1566. [ Links ]
Chan, C., & Tan, S. (2004). Putting Objects into a Cylindrical/Rectangular Bounded Volume. Computer-Aided Design, 36 (12), 1189 - 1204. [ Links ]
Chang, J.-W., Wang, W., & Kim, M.-S. (2008). Efficient Collision Detection Using a Dual Bounding Volume Hierarchy. In Proceedings of the 5th international conference on Advances in geometric modeling and processing, GMP'08. (pp. 143-154). Berlin, Heidelberg, Germany. [ Links ]
Choi, Y.-K. (2008). Collision Detection for Ellipsoids and other Quadrics. Doctoral Thesis, University of Hong Kong, China. [ Links ]
Choi, Y.-K., Chang, J.-W., Wang, W., Kim, M.-S., & Elber, G. (2006a). Real-time Continuous Collision Detection for Moving Ellipsoids Under Affine Deformation. Technical report. Hong Kong, China: University of Hong Kong. [ Links ]
Choi, Y.-K., Wang, W., Liu, Y., & Kim, M.-S. (2006b). Continuous Collision Detection for Two Moving Elliptic Disks. IEEE Trans. Robotics, 22 (2), 213-224. [ Links ]
Choi, Y.-K., Chang, J.-W., Wang, W., Kim, M.-S., & Elber, G. (2009). Continuous Collision Detection for Ellipsoids. IEEE Transactions on Visualization and Computer Graphics, 15 (2), 311-325. [ Links ]
Cohen, J. D., Lin, M. Ch., Manocha, D., & Ponamgi, M. K. (1995). I-COLLIDE: An interactive and exact collision detection system for large-scale environments. In, Proceedings of the 1995 Symposium on Interactive 3D Graphics (pp. 189-218). Monterey (CA), United States. [ Links ]
Corrales-Ramón, J. A., Candelas-Herías, F. A., & Torres-Medina, F. (2011). Safe Human-Robot Interaction Based on Dynamic Sphere-Swept Line Bounding Volumes. Robotics and Computer-Integrated Manufacturing, 27 (1), 177-185. [ Links ]
Dinas, S. (2009). Detector de Colisiones Dinámico Basado en Esferas Exteriores e Interiores. Tesis de Maestría, Facultad de Ingeniería, Universidad del Valle, Cali, Colombia. [ Links ]
Eberly, D. (2007). Intersection of Objects with Linear and Angular Velocities Using Oriented Bounding Boxes. Geometric Tools, LLC. Recovered 15/05/2015 http://www.geometrictools.com/Documentation/IntersectionRotatingBoxes.pdf [ Links ]
Eberly, D. (2008). Dynamic Collision Detection Using Oriented Bounding Boxes. Geometric Tools, LLC. Recovered 15/05/2015 http://www.geometrictools.com/Documentation/DynamicCollisionDetection.pdf [ Links ]
Ericson, C. (2005). Real-Time Collision Detection (The Morgan Kaufmann Series in Interactive 3-D Technology). Morgan Kaufmann. [ Links ]
Figueiredo, M., Oliveira, J., de Araújo, B. R., & Pereira, J. A. M. (2010). An Efficient Collision Detection Algorithm for Point Models. In, Proceedings of the International Conference on Computer Graphics and Vision, Graphicon 2010 (pp. 30-37). St. Petersburg, Russia. [ Links ]
Frisken, S. F., & Perry, R. N. (2005). Simple and Efficient Traversal Methods for Quadtrees and Octrees. Graphics tools The JGT editor's choice, 7 (3), 1-12. [ Links ]
Glass, K. (2005). Analysis of Broad-Phase Spatial Partitioning Optimizations in Collision Detection. Technical Report. Grahamstown, South Africa: Rhodes University. [ Links ]
Gottschalk, S. A. (2000). Collision Queries Using Oriented Bounding Boxes. Doctoral Thesis. The University of North Carolina, Chapel Hill, USA. [ Links ]
Gottschalk, S. A., Lin, M. C., & Manocha, D. (1996). Obbtree: A Hierarchical Structure for Rapid Interference Detection. Computer Graphics, 30 (Annual Conference Series), 171-180. [ Links ]
Guibas, L. J., Nguyen, A., & Zhang, L. (2003). Zonotopes as Bounding Volumes. In, Proceedings of the fourteenth annual ACM-SIAM (Society for Industrial and Applied Mathematics) Symposium on Discrete Algorithms, SODA '03 (pp. 803-812). Philadelphia (PA), USA. [ Links ]
He, T. (1999). Fast Collision Detection Using QuOSPO Trees. In, Proceedings of the 1999 Symposium on Interactive 3D Graphics, I3D '99 (pp. 55-62). New York, USA. [ Links ]
Hubbard, P. M. (1995a). Collision Detection for Interactive Graphics Applications. IEEE Transactions on Visualization and Computer Graphics, 1 (3), 218-23. [ Links ]
Hubbard, P. M. (1995b). Collision Detection for Interactive Graphics Applications. Doctoral Thesis, Brown University, Providence (RI), USA. [ Links ]
Hubbard, P. M. (1996). Approximating Polyhedra with Spheres for Time-Critical Collision Detection. ACM Trans. Graph, 15 (3), 179-210. [ Links ]
Huber, E. H. (1998). Intersecting General Parametric Surfaces Using Bounding Volumes. In, Proceedings of the Tenth Canadian Conference on Computational Geometry -CCCG'98 (pp. 52-53). Montréal, Québec, Canada: McGill University. [ Links ]
Huebner, K., Ruthotto, S., & Kragic, D. (2008). Minimum Volume Bounding Box Decomposition for Shape Approximation in Robot Grasping. In, Proceedings of the International Conference on Robotics and Automation - ICRA 2008 (pp. 1628-1633). Pasadena (CA), USA. [ Links ]
James, D. L., & Pai, D. K. (2004). Bd-Tree: Output-Sensitive Collision Detection for Reduced Deformable Models. ACM Trans. Graph, 23 (3), 393-398. [ Links ]
Jian-Hong, G., Peng, Q., & Chen, J. X. (2008). Improved Strategies for OBB Fitting and Overlap Test for OBB. In, Proceedings of the International Conference on Computer Science and Software Engineering 2008 -CSSE (2), IEEE Computer Society (pp. 996-999). Wuhan, Hubei. [ Links ]
Joseph, J. S. (2003). Dynamic Spatial Partitioning for Real-Time Visibility Determination. Master thesis. Department of Computer Science, New Mexico State University, New Mexico, Mexico. [ Links ]
Ketchel, J. S., & Larochelle, P. M. (2006). Collision Detection of Cylindrical Rigid Bodies for Motion Planning. In, Proceeding of the IEEE International Conference on Robotic and Animation 2006 -ICRA'06 (pp. 1530-1535). Orlando (FL), USA. [ Links ]
Kim, D.-J., Guibas, L. J., & Shin, S. Y. (1998). Fast Collision Detection Among Multiple Moving Spheres. IEEE Transactions on Visualization and Computer Graphics, 4 (3), 230-242. [ Links ]
Kimmerle, S., Nesme, M., & Faure, F. (2004). Hierarchy Accelerated Stochastic Collision Detection. In, Proceedings of the 9th International Workshop on Vision, Modeling, and Visualization, VMV, (pp. 307-314). Stanford (CA), USA. [ Links ]
Klein, J., & Zachmann, G. (2004). Point Cloud Collision Detection. Computer Graphics Forum, 23 (3), 567-576. [ Links ]
Klosowski, J. T., Held, M., Mitchell, J. S. B., Sowizral, H., & Zikan, K. (1998). Efficient Collision Detection Using Bounding Volume Hierarchies of k-DOPs. IEEE Transactions on Visualization and Computer Graphics, 4 (1), 21-36. [ Links ]
Koziara, T., & Bicanic, N. (2005). Bounding box collision detection. In, Proceedings of the 13th Association of Computational Mechanics in Engineering Conference - ACME (pp. 33-37). Sheffield, UK: University of Sheffield. [ Links ]
Krishnan, S., Gopi, M., Lin, M. C., Manocha, D., & Pattekar, A. (1998a). Rapid and Accurate Contact Determination Between Spline Models Using Shell-Trees. Computer Graphics Forum, 17 (3), 315-326. [ Links ]
Krishnan, S., Pattekar, A., Lin, M. C., & Manocha, D. (1998b). Spherical Shell: a Higher Order Bounding Volume for Fast Proximity Queries. In, Proceedings of the 3rd Workshop on the Algorithmic Foundations of Robotics on Robotics: The Algorithmic Perspective, WAFR '98, (pp. 177-190). Natick (MA), USA. [ Links ]
Larsen, E., Gottschalk, S. A., Lin, M. C., & Manocha, D. (1999). Fast Proximity Queries with Swept Sphere Volumes. Technical Report. Chapel Hill, USA: Department of Computer Science, University of North Carolina. [ Links ]
Larsen, E., Gottschalk, S. A., Lin, M. C., & Manocha, D. (2000). Fast Distance Queries with Rectangular Swept Sphere Volumes. In Proceedings of the IEEE International Conference on Robotics and Automation, 2000. ICRA '00 (pp. 3719-3726). San Francisco (CA), USA. [ Links ]
Larsson, T. & Akenine-Möller, T. (2003). Strategies for bounding volume hierarchy updates for ray tracing of deformable models. Technical Report, ISSN 1404-3041 ISRN MDH-MRTC-92/2003-1-SE, Västerås, Sweden: Mälardalen University. [ Links ]
LaValle, S. M. (2006). Planning Algorithms. Cambridge, U.K.: Cambridge University Press. Recovered 15/05/2015 at http://planning.cs.uiuc.edu/ [ Links ]
Lin, M. C., & Gottschalk, S. A. (1998). Collision detection between geometric models: A survey. In Proceedings of the 8th IMA Conference on mathematics of surfaces (pp. 37-56). Birmingham, England. [ Links ]
Lin, M. C., Manocha, D., & Cohen, J. (1996). Collision Detection: Algorithms and Applications. Technical Report. Chapel Hill, USA: University of North Carolina. [ Links ]
Liu, R., Zhang, H., & Busby, J. (2008). Convex Hull Covering of Polygonal Scenes for Accurate Collision Detection in Games. In Proceedings of graphics interface 2008, GI '08, (pp. 203-210). Toronto, Canada. [ Links ]
Luque, R. G., Comba, J. L. D., & Freitas, C. M. D. S. (2005). Broad Phase Collision Detection Using Semi-Adjusting BSP-Trees. In, Proceedings of the 2005 symposium on Interactive 3D graphics and games, I3D'05 (pp. 179-186). New York, USA. [ Links ]
Mirtich, B. V. (1997). Efficient Algorithms for Two-Phase Collision Detection. Technical Report. Cambridge (MA), USA: MERL - A MITSUBISHI Electric Research Laboratory. [ Links ]
Mirtich, B. V. (1998). V-Clip: Fast and Robust Polyhedral Collision Detection. ACM Trans. Graph. 17 (3), 177-208. [ Links ]
Mu, F. & Oslejsek, R. (2000). Bounding volume hierarchy analysis (case study). Technical Report. Brno, Czech Republic: Faculty of Informatics, Masaryk University. [ Links ]
Muñoz, C. A., Arcila, O., & Bañón, J. M. (2001). Un modelo de representación circular para polígono. Energía y Computación, 11 (2), 6-13. [ Links ]
Muñoz, C. A., Arcila, O., & Bañón, J. M. (2002). Una Nueva Representación Jerárquica Basada en Esferas Sencilla, Rápida y Eficiente. Información Tecnológica, 13 (4), 141-147. [ Links ]
O'Sullivan, C., & Dingliana, J. (1999). Real-Time Collision Detection and Response Using Sphere-Trees. In Proceedings of the 15th Spring Conference on Computer Graphics (pp. 83-92). Bratislava, Slovakia: Comenius University. [ Links ]
Palmer, I. J., & Grimsdale, R. L. (1995). Collision Detection for Animation Using Sphere-Trees. Computer Graphics Forum, 14 (2), 105-116. [ Links ]
Pan, J., Chitta, S., & Manocha, D. (2011). Probabilistic Collision Detection Between Noisy Point Clouds Using Robust Classification. International Symposium on Robotics Research (ISRR) (pp. 1-16). Flagstaff (AZ), USA. [ Links ]
Pitt-Francis, J., & Featherstone, R. (1998). Automatic Generation of Sphere Hierarchies from CAD Data. Proceeding of the 1998 IEEE International Conference on Robotics and Automation (pp. 324-329). Lueven, Belgium. [ Links ]
Quinlan, S. (1994). Efficient Distance Computation Between Non-Convex Objects. In, Proceedings of the 1994 IEEE International Conference on Robotics and Automation (pp. 3324-3329). San Diego, CA, USA. [ Links ]
Samet, H. (1988). An Overview of Quadtrees, Octrees, and Related Hierarchical Data Structures. In: R. A. Earnshaw (Ed.) Theoretical Foundations of Computer Graphics and CAD, volume 40 of NATO ASI Series F: Computer and System Sciences (pp. 51-68). Berlin, Germany: Springer-Verlag. [ Links ]
Sobottka, G., & Weber, A. (2005). Efficient Bounding Volume Hierarchies for Hair Simulation. In, Proceeding of the 2nd Workshop in Virtual Reality Interactions and Physical Simulations (VRIPHYS '05) (pp. 1-10). Pisa, Italy. [ Links ]
Tang, P., Jiang, L., & Liu, H. (2008). Collision Detection of High Density Point Set Based on Convex Hull. In, Proceedings of the 2008 International Conference on Computer Science and Software Engineering (pp. 1174-1177). [ Links ]
Terdiman, P. (2001, march). Memory-optimized bounding-volume hierarchies. Recovered 15/05/2015 at http://www.codercorner.com/Opcode.pdf [ Links ]
Teschner, M., Heidelberger, B., Mueller, M., Pomeranets, D., & Gross, M. (2003). Optimized Spatial Hashing for Collision Detection of Deformable Objects. In, Proceedings of Vision, Modeling, Visualization VMV'03 (pp. 47-54). Munich, Germany. [ Links ]
van den Bergen, G. (1997). Efficient Collision Detection of Complex Deformable Models Using AABB Trees. Journal of Graphics Tools: JGT, 2 (4), 1-14. [ Links ]
van den Bergen, G. (1998). Efficient Collision Detection of Complex Deformable Models Using AABB Trees. J. Graph. Tools, 2 (4), 1-13. [ Links ]
Wang, W., Choi, Y.-K., Chan, B., Kim, M.-S., & Wang, J. (2002). Efficient Collision Detection for Moving Ellipsoids Based on Simple Algebraic Test and Separating Planes. Technical Report, TR-2002-16. Hong Kong, China: Department of Computer Science and Information Systems, University of Hong Kong. [ Links ]
Wang, W., Choi, Y.-K., Chan, B., Kim, M.-S., & Wang, J. (2004). Efficient Collision Detection for Moving Ellipsoids Using Separating Planes. Computing, 72 (1-2), 235-246. [ Links ]
Wang, W., Wang, J., & Kim, M.-S. (2001). An Algebraic Condition for the Separation of Two Ellipsoids. Comput. Aided Geom. Des., 18 (6), 531-539. [ Links ]
Weller, R., Klein, J., & Zachmann, G. (2006). A Model for the Expected Running Time of Collision Detection Using AABB Trees. In, Prodeeding of the 12th Eurographics Conference on Virtual Environments, EGVE'06 (pp. 11-17). Switzerland, Switzerland. [ Links ]
Weller, R., & Zachmann, G. (2008). Inner Sphere Trees. Technical Report, IfI-08-09. Clausthal-Zellerfeld, Germany: Technische Universität Clausthal, Clausthal University of Technology. [ Links ]
Weller, R., & Zachmann, G. (2009a). Inner Sphere Trees for Proximity and Penetration Queries. In, Proceedings of the 2009 Robotics: Science and Systems Conference (RSS) (pp. 1-7). Seattle (WA), USA. [ Links ]
Weller, R., & Zachmann, G. (2009b). A Unified Approach for Physically-Based Simulations and Haptic Rendering. In, Proceedings of the 2009 ACM SIGGRAPH Symposium on Video Games, Sandbox '09 (pp. 151-159). New York, USA. [ Links ]
Weller, R., & Zachmann, G. (2010). Protosphere: A GPU-Assisted Prototype Guided Sphere Packing Algorithm for Arbitrary Objects. In, Proceeding of the ACM SIGGRAPH ASIA 2010 Sketches (pp. 8:1-8:2). New York, USA. [ Links ]
Weller, R., & Zachmann, G. (2011). Inner Sphere Trees and Their Application to Collision Detection. In, Coquillart, S., Brunnett, G., & Welch, G. (Ed.) Virtual Realities (pp. 181-202). London, UK: Springer. [ Links ]
Welzl, E. (1991). Smallest Enclosing Disks (Balls and Ellipsoids). In, H. Maurer (Ed.) New Results and New Trends in Computer Science (vol. 555) (pp. 359-370). Berlin- Heidelberg, Germany: Springer. [ Links ]
Xiao-Rong, W., Meng, W., & Chun-Gui, L. (2009). Research on Collision Detection Algorithm Based on AABB. In, Proceeding of the 2009 IEEE International Conference on Natural Computation (pp. 422-424). [ Links ]
Yoon, S.-E. & Manocha, D. (2006). Cache-efficient layouts of bounding volume hierarchies. Computer Graphics Forum, 25 (3), 507-516. [ Links ]
Zachmann, G. (1998). Rapid Collision Detection by Dynamically Aligned DOP-Trees. In, Proceedings of the Virtual Reality Annual International Symposium, VRAIS '98 (pp. 90-97). Washington DC, USA. [ Links ]
Zhigang, F., Jianxun, J., Jie, X., & Xiaochi, W. (2010). Efficient Collision Detection Using Bounding Volume Hierarchies of OBB-AABBs and its Application. In, Proceeding of the International Conference on Computer Design and Applications 2010 (ICCDA) (pp. 242-246). [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.