Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y competitividad
Print version ISSN 0123-3033
Ing. compet. vol.17 no.2 Cali July/Dec. 2015
Toys as teaching tools in engineering: the case of Slinky®
Juguetes como instrumentos de enseñanza en ingeniería: el caso del Slinky®
Simón Reif-Acherman
Escuela de Ingeniería Química, Facultad de Ingeniería, Universidad del Valle. Cali, Colombia
E-mail: simon.reif@correounivalle.edu.co
Eje temático: CHEMICAL ENGINEERING / INGENIERíA QUíMICA
Recibido: Abril 28 de 2015
Aceptado: Junio 26 de 2015
Abstract
Though not so much nowadays educationally exploited as it should be, toys are very useful resources in courses in science and engineering. A widely known toy, the Slinky®, is used through this article to explain in a simple way important physical principles and to show how they have been applied for scientific and technological developments.
Keywords: Heat transfer, nanotechnology, toys, waves.
Resumen
Aunque no tan explotados educacionalmente hoy en día como debiera ser, los juguetes resultan recursos muy útiles en cursos de ciencias e ingenierías. Un juguete ampliamente conocido, el Slinky®, es utilizado en el presente artículo para explicar de manera sencilla importantes principios físicos y mostrar como ellos han sido aplicados en desarrollos científicos y tecnológicos.
Palabras clave: Juguetes, nanotecnología, ondas, transferencia de calor.
1. Introduction
The usefulness of including the description of the operation of elements of everyday life as a strategy of pedagogical explanation of some physical principles has increased acceptance. Toys, both due to their wide visibility and availability and their own motivational effect, are a clear example of it. Some of them, originally devised with exclusive entertainment purposes, have motivated further interesting scientific applications through elaborate technological developments. This article illustrates the governing physical principles of the operation of one widely known toy, as well as some of its potential applications in science and engineering.
2. Slinky®
A Slinky® is a simple toy composed of coils of ribbon-like wire with a rectangular cross- section, resembling a helical spring (figure 1), invented by the naval engineer Richard James in the 1940's while he worked in a Philadelphia's shipyard (James, 1947). Made from a flexible 90- turn metal spring with about 7 cm diameter, each Slinky® contains about 20 m of flat steel wire (1/10 inch wide) and weighs approximately 225 g. Compressed, a Slinky® coil is only 5.7 cm, but when stretched into a helix it can become as long as 4.5 m without deforming it permanently. Some geometrical features pointed out in the James's patent are the use of a rectangular cross section with a width-to-thickness ratio of 4:1 for winding the spring, compressed height approximately equal to the diameter, the almost no pre-tensioning although adjacent turns (coils) that touch each with no applied forces, and the toy's ability to remain in an arch shape on a horizontal surface. With only just three changes regarding the original design (crimps added on the end to prevent children from poking the eyes, the use of galvanized steel to make it more durable and the introduction of a more flexible and less deformable plastic version, which allowed the toy to be more easily reversed end- to-end without tangling), Slinky® became from its debut in 1945 a magical toy that mesmerized generations of children and adults.
Originally focusing on the finding of a way to hold delicate instruments steady onboard ships during storms at sea, James accidentally found himself with one of the world's favorite toys along the history. After knocking one of the torsion springs off of his workbench he observed that, instead of tumbling to the ground, the spring 'walked' down a series of steps, coiled itself back up, and standing on its end. James experimented with various types of steel wires, lengths, coil compressions, and weights in an effort to find a spring that would recoil to reform its shape but remain flexible enough to 'walk'. Once he had found the right wire and design, the success was immediate, and the toy's sales went from four hundred units in the first ninety minutes since to have been offered to a North-American department store to more than 350 million units worldwide in so far seven decades of existence (Michelsen, 2009).
What seems like a simple item, is in fact a very complicated toy that appears to defy the laws of nature. Slinky® exhibit some truly startling physics, with curious static and dynamic features. Its hanging configuration (Mak, 1987; Sawicki, 2002), the dispersion of waves propagating along it (Crawford, 1990, 1987; Vandegrift et al., 1989; Blake & Smith, 1979; Young, 1993), its modes of oscillation when suspended vertically and the subsequent behavior when it is dropped (Cross &Wheatland, 2012; French, 1994; Gluck, 2010), as well as its ability to 'walk' down stairs (Longuet-Higgins, 1954; Hu, 2010) have very probably been the more studied topics related with this toy.
3. 'Unusual' behavior
One of the best ways to see the range of forces acting in this toy is to watch a Slinky® as it tumbles down a flight of stairs. When placed on an upper step of a stair the toy has potential or stored energy. Once its free end is lifted, the Slinky® rotates about a diameter and quickly dropped to the next lower step, walking down stairs all by itself. The energy is quickly 'released' and converted to kinetic energy. As the slinky moves down the steps this energy transfers in an extensional wave which propagates back and forth repeatedly along the axis of the spring with a speed given by the square root of the ratio of stiffness to density, in a similar way as a sound wave that travels through a substance by transferring a pulse of energy to the next molecule. As the axis is not a straight line but instead consists of two roughly straight portions joined by a U-shaped semicircle, the propagations don't occur in a simple only one direction, but consider movements down replacing the energy lost in various frictional effects as well as the stretching of the spring to several times its original length with the subsequent possibility of a not- relatively small deflection of the spring.
As the wave travels, successive turns of the spring move by first upward, then along the arc of the spring, and then down onto the second lower step. When several adjacent turns are already in contact and the wave has reached the last coils on the first step, those coils are pulled up with enough speed along the arc that they overshoot the second step and (provided the step dimensions are appropriate) land on the third step, being the entire sequence of events next to be repeated (see figure 2) (Anonymous, 2014).
How quickly the Slinky® moves under the influence of gravity depends of physical properties of the slinky, such as the spring constant and the mass of the metal, as well as some of its geometrical parameters (such as length and diameter). The height of each step is decisive in determining whether the velocity of the free end will be sufficient to sustain the motion, since it is this height which determines the magnitude of the initial disturbance, but not affects the time spent in the whole displacement. Different tests have showed an average time period of about 0.5 s for a variety of steps, independent of their corresponding heights.
The rectangular cross section of the Slinky®s wire becomes a crucial parameter for its success because of the reduction in the ratio of the spring's stiffness to its mass compared to that of a wire with a circular cross section. The smaller ratio results in a slower speed for the wave propagation, being this one the reason why a plastic Slinky®, with different stiffness and density, requires about twice the time of a steel Slinky® to traverse a step.
In summary, the Slinky®, thanks to the gravity and its own momentum, stretches to reach the next step down, reforms itself, then stretches again to reach the next step, and so on for getting 'walk' down a flight of stairs. A slightly restricted simple two- link, two-degree-of-freedom mathematical model for the overall motion of a Slinky® as it walks down stairs, tumbling end over end, including a rotational spring and rotational dashpot at the hinge that connected the massless rigid coil, with equal point masses at both ends of each round, has been recently published and solved numerically (Hu, 2010).
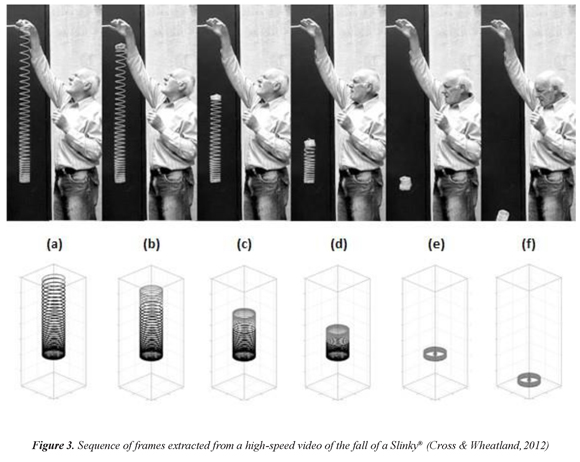
The strange and intriguing features exhibited by the dynamics of an initially stretched falling Slinky® in a gravitational field becomes other sample of the astonishing and confounding behavior of this toy. Common sense tells that when a Slinky® initially suspended from its top is released, all parts of the toys should fall downward under the influence of gravity. However, that is not the case because instead of falling or rising, the Slinky® will remain briefly suspended in air as if it was levitating, as shown in the frames (a) to (d) in the figure 3. After an experimentally estimated suspension time of about 0.3 s, the collapsing top section collides with the bottom -frame (e)- and the whole toy continues its fall -frame (f)-. Several public videos show, both at normal and slow velocities, this seemingly inexplicable behavior (Anonymous, 2012, 2011).
The physical explanation for this behavior is that the tension in the Slinky®, which supports the mass below, relaxes from the top downwards after the release of the top end, as the turns of the Slinky® collapse one by one. Gravity pulling down and tension pulling up are the equal and opposite forces responsible for the lack of movement of the bottom coils. A tension wave runs down the slinky releasing the tension at a speed of about 50-100 loops per second for a typical Slinky (depending on such things as the thickness of the coils), and ahead of a wave front the turns are still stretched. Once the wave front strikes into the bottom, it 'knows' that the top has been released and no longer levitates. The center of mass that all the time shifts but it is always located somewhere in between the top and bottom of the toy, still accelerates according to gravity all the way down to the ground from the moment it's released, thus fulfilling both the Newton's laws and Galileo's observations about falling objects.
4. Science and engineering applications
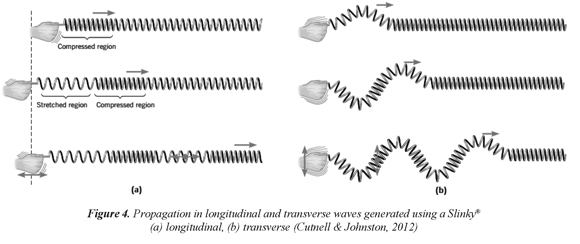
Slinky® not only makes, however, a fun toy. In addition to its playtime functions, Slinky® has many practical applications in physics and engineering activities. Almost all the diagrams of longitudinal waves, to cite the most simple example, given in textbooks or drawn on the board in class are depicted, generally for liquids, especially water, as transverse waves inside a tube. However, this is a problem, for example, when the concept of longitudinal wave motion and propagation must to be explained and understood when the medium is air instead water. Sound travelling in air as a longitudinal wave cannot be so much easily seen, which contributes to exacerbate the students confusion regarding the difference between the two types of waves. The waves in this latter case have, instead of high and low displacements, areas of compression (pushed together) and rarefaction (pulled apart), which correspond to regions of high and low pressure. In this way, the toy is currently used to clearly illustrate difficult concepts encountered in acoustics (Astrom, 2011). Several behaviors of mechanical (and electromagnetic) waves can be easily illustrated by exploring the motions of a Slinky®. Longitudinal, transverse, and standing waves, with different directions of the waves' displacements regarding the toy's movement, can be produced by either vibrating the first coils up and down vertically, or back and forth or side to side horizontally (Figure 4).
Light, that also has properties of a transverse wave, although it is an electromagnetic wave, has likewise benefited from the help of Slinky® for its understanding. The toy was part of a group of inexpensive and sensitive devices devised in 1958 by scientists at M.I.T. to perform experiments in high school physics in order to contribute to demonstrate basic principles. Because of the similarity of their behavior with those of mechanical waves, reflected light and radio waves were easily introduced in physics courses by a moving wave in two directions, on its way out and again coming back on the rebound (figure 5). The returning wave comes back on the opposite side of the Slinky®.
Studies on plasma physics can also be benefited from experiments carried out with the Slinky™. The fact that plasmas and a Slinky® suspended from a ceiling by an array of strings are both systems where their respective wave characteristic equations have been modified to include a linear restoring force, explains the analogy found between the dispersion relation for transverse electromagnetic radiation in the former one and the dispersion relation for transverse waves in the latter one (Crawford, 1968). The analogy makes this toy a useful tool to particularly illustrate the behavior of a dispersive medium with a definite and simple dispersion relation and, from a more general view point, as a possible alternative for quantitative experiments in courses on plasma physics (Scott, 2010).
A Slinky® also makes a handy model of earthquake waves. When stress on large blocks of rock becomes greater than the strength of the rock and they fracture, vast amounts of energy are released. This careening energy sent into surrounding earth in all directions takes the form of several different kinds of seismic waves, usually classified in two main types. The body waves, of higher frequency, which travel through the interior of the earth, and the surface waves, of lower frequency, that travel only through the crust, and that although are not the first to arrive, are the almost entirely responsible for the damage and destruction associated with earthquakes. Slinky® is usually used to effectively demonstrate characteristics of these kind of seismic waves and the wave propagation (Braile, 2010).
The first kind of a body wave and the fastest one to arrive to distant points, a compressional or primary wave, resulted similar to the longitudinal disturbance created by stretching a tout Slinky®, plucking a coil back, and letting it go. The second kind of body wave, the shear or secondary wave, which travels more slowly and only through solid rock, can be compared to the disturbance generated by pulling laterally or vertically part of the toy relative to its length, and letting it again to go, creating in this way the well-known sinuous wave ripple. The slowest seismic wave, a surface type called Rayleigh, which rolls along the ground just like a wave rolls across a lake or an ocean and moves the ground up and down and side-to-side in the same direction that the wave is moving, transmitting energy from the epicenter (the point on the surface that's above the focus) along the earth's surface, can be modeled by a circular- motion wave generated by pushing and pulling the Slinky® simultaneously with a movement up and down. A last wave type that shake things from side to side, so-called Love wave, transverse as the secondary wave but confined to the earth's surface as the Rayleigh one but producing entirely horizontal motion, can be modeled by holding two
Slinky®s one above the other, moving both side to side at the same time, and also moving the top Slinky® further in each direction than the bottom Slinky®. The bottom Slinky® in this last activity illustrates the rapid decrease in the energy of a surface wave with depth.
The toy's behavior has not only tested at earth. Slinky® is one of the more than sixty toys carried by different Space Shuttle missions since 1985 in order to evaluate the dynamics of their structures and demonstrate the behavior and the fulfillment of the laws of elementary physics of familiar objects in the microgravity environment of space. The great variety of toys taken into space showed a pattern. In microgravity, toys that pushed off a surface moved at greater speeds, and those that moved through a fluid (air or water) by themselves were not as efficient in space. Regarding particularly Slinky® and the study of the physical laws that govern the mechanics of springs, the series of experiments developed by the crew members of the STS-54 Mission between January 13 and 19, 1993, showed that in the new environment it behaves like neither a spring nor a toy but as a continuously propagating wave (NASA STI, 2012).
A new space project, also involving Slinky® is carried out by NASA's engineers from few decades ago regarding the possibility that 'solar sails', as they are called, could capture the solar photon flow and use that to propel spacecrafts through the vacuum of space just as boats are powered by wind. The radiation blasted out by the sun that strikes a large, shiny, sail-like structure pushes very gently but constantly on it, much as the wind pushes on a sail. In this way, over time, the spacecraft should get going very fast using no fuel at all. Some early designs developed had shown that the bigger a solar sail is, the better it will work, but, simultaneously will require stiff masts to stretch it out and make it smooth. NASA planned to use very long, strong, and lightweight masts that coil up like Slinky® and in this way to be launched together with the sail into a space on a rocket, and then uncoil to their full length once in space. Although a NASA Space Technology mission (ST8), that would test in 2009 a new type of ultra-light graphite mast 40 meters long and only 1.4 kilograms weight (linear mass density of 34 g/m), called SAILMAST (Scalable Architecture for the Investigation of the Load Managing Attributes of a Slender Truss), was canceled, the developments involving the Slinky®'s concept have continued (Alhorn & Scheierl, 2010). The purpose was provide athoroughinvestigation of the fundamental attributes of the design, subsequently allowing extrapolation to generalized gossamer truss structures that may be different in geometry, loading, or design, observe if SAILMAST stays straight and stiff enough in space to support a solar sail, and conclude about the real possibilities of solar sailcraft's collaboration with near term key NASA roadmap missions (McEachen et al, 2005).
Several other applications involving Slinky® can be mentioned. Ground heat exchangers for heat pump systems are increasingly utilized for heating and cooling buildings by taking advantage of a relative constancy in the ground temperature below a certain depth throughout the year (figure 6). The difference in temperature between the outside air and the ground can be utilized as a preheating means in winter and pre-cooling in summer by operating a ground heat exchanger. Some special models in which the pipe is curled into a Slinky® shape have been gaining acceptance in places where natural temperature recharge of the ground is not vital, and especially in USA, because of the possibility to place more pipes into shorter trenches in order to reduce the amount of land space needed, enhance the heat transfer area within a limited space, increase the thermal performance, and take advantage of their low initial cost (Xiang et al, 2015; Chong et al., 2013; Neuberger et al., 2014). Current investigations in order to get better cooling performance coefficients of some microelectromechanical (MEMS) devices (Çelen, 2012), or to find semiconductor oxide structures with unique and attractive properties with potential uses in spintronics also involved the utilization of slinky structures (Sealy, 2004).
A device whose basic structure is derived from the Slinky®'s concept is currently used for inductive electromagnetic stimulation of neural cells. This design had improved significantly the focal effect of the stimulator, reduced its inductance, and, as a result, improved its efficiency by generating bursts of pulses and expanding the utilization of the system to possible functional activation of certain neuro-muscular structures when peripheral nerves are stimulated (Zimmermann & Simpson, 1996).
Biologists and chemists use Slinky® to illustrate some of the four structural levels of a protein (Baker & Allen, 1979). Although the straight line that forms its primary structure, it means the sequence of amino acids that make up the protein, becomes an impossibility for Slinky®, the other three can be assimilated with some of its movements. The secondary structure, The secondary structure, held together by hydrogen bonding between nearby carboxyl and amino groups within the polypeptide chain, either coils up like a slinky (an alpha-helix) and can also lengthen, contract, and bend much like it, or it is folded into a fan-like configuration (a beta-pleated sheet). Taking a Slinky® and bending it easily allows explaining the tertiary structure, or the way that the coil or fan of the polypeptide is folded up. Two or more Slinkys, both of them tangled up, help to explain the quaternary structure for those proteins that have more than one polypeptide.
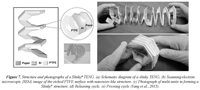
To conclude, imagine regular printed paper. Use glue sticks to paste it on thin sheets of two materials with different polarities, aluminum foil and polytetrafluoroethylene (PTFE or Teflon®) thin film, and fold it into a Slinky® shape. When a Slinky® origami so formed is compressed, the paper and Teflon repeatedly come into contact. When this force is released, they separated, and electrons from the surface of one of these materials have been stolen from the surface of the other, resulting in a triboelectric effect, or a static electricity charging. Nanotechnologists at the Georgia Institute of Technology in Atlanta have developed origamis built on this basic structure that could take advantage of triboelectricity to eventually power electronics in a cheap, lightweight, environmentally friendly way (Yang et al., 2015). The fact that paper is a popular, cheap, and currently available material makes even more eye-catching this energetic alternative because of the possibility to make cheaper, recyclable and widely used triboelectric generators with a broad technological impact in the field of renewable and sustainable energies. Electricity could then flow out the aluminum foil via copper wires. The prototype Slinky® in the first experiments, a triboelectric nanogenerator (TENG) connecting seven units in parallel, provided a voltage of 20 V, a current of 2 micro-amperes, and a peak power density of 0.14 watts per square meter, being enough to light up four commercial LEDs simultaneously (figure 7). Thanks to the multifuntionality showed by the Slinky® TENG at realizing motions such as stretching, lifting, and twisting like a real metal Slinky®, the former can effectively harvest mechanical energy from various directions, in contrast to the conventional TENG. The origami approach so developed can also serve as simple self-powered pressure sensor when connected to a voltage meter.
Because some interesting electrical properties at radio frequencies, North-American troops were able to press Slinky® into service as a mobile radio antenna in the Vietnam war for survivalist situations. Thanks to its resonance of a quarter wave between 7 and 8 MHz when it is stretched to lengths between 5 and 15 feet, it is possible tune a standard Slinky® within that range by only extend the coil to approximate size, then expand or contract it to reach the desired resonance. The toy's configuration is also increasingly harnessed by engineers for scaling down it to the nanoscale for a successful use of its stretching, compressing, bending and twisting characteristics as conducting wires within flexible electronic, photonic, and electromechanical devices (Xu et al., 2011; Sun et al., 2006). Potential usefulness of helical springs on this scale as sensors and actuators in nanoelectromechanical systems has been successful tested with different materials (Kim et al., 2011; Gao et al., 2005; Korgel, 2005; Poggi et al., 2004).
5. Conclusions
Toys are usually miniature replicas of future realities and science and engineering teachers can find many uses for them. Important advances in electricity, radio, and flight involved, for example, the use of kites. Benjamin Franklin (1706-1790) and his son William (1730-1813) tackled the electricity of a lightning bolt in 1752 by using a kite, a key, and a Leyden jar. Guglielmo Marconi used a kite to lift aerials for wireless communication; Orville and Wilbur Wright modified a box kite and proved that humans could fly, and some flight patterns of the Frisbee had influence on military
aerodynamics. Some M.I.T students built in 1975 a non-electronic computer made of tinkertoys, and chemical engineers invented Silly Putty (a toy essentially based on a mixture of silicone oil and borax that has unusual abilities to slowly flow like a liquid, stretch to incredible lengths, bounce like a rubber ball and shatter like glass if struck with a hammer) and the Super Ball (an extremely elastic ball made of synthetic polymer polybutadiene and other ingredients with a very high coefficient of restitution that exhibits unusual models of impacts) as result of a research for developing a synthetic rubber.
As above, there are many other examples showing the close connection between science, technology and toys in both senses. This article shows that even unexpected or seemingly impossible behaviors exhibited by some toys, such as the case of Slinky®, can be favorably used to explain scientific principles in an easy and entertaining way. In an era of high technology, with toys almost always requiring a seemingly endless supply of batteries to keep them operating, Slinky® remains an example of the application of simple physical principles to produce a toy with a surprising performance, providing a common ground for a type of learning that allows applying what it is already know in order to contribute to the understanding of what it is currently seen but can't fathom. It is this type of learning which not only can be applied better to the world around us, but that can inspire more discovery and learning.
6. Acknowledgement
I would like to express my gratitude to the anonymous reviewers on a draft of this paper for their helpful comments and suggestions.
7. Bibliographic references
Anonymous (2014). Slinky walking down the stairs. Recovered 13/09/2014 https://youtu.be/EZeFm-5MCuI [ Links ]
Anonymous (2012). Slow Motion - Slinky Compilation. Recovered 18/08/2014 https://www.youtube.com/watch?v=Tdh_R7po6Dw [ Links ]
Anonymous (2011). Slinky Drop Extended. Recovered 18/08/2014 https://www.youtube.com/watch?v=oKb2tCtpvNU [ Links ]
Alhorn, D. C., & Scheierl, J. M.(2010). FeatherSail - Design, Development and Future Impact. Document prepared for the 57th JANNAF Joint Propulsion Meeting. 3-7 May 2010. Colorado Springs, U.S.A. [ Links ]
Astrom, R. (2011). Advanced acoustic demonstration videos for higher education: Longitudinal wave motion. Journal of the Acoustical Society of America, 129 (4), 26-46. [ Links ]
Baker, J. J. W., & Allen, G. E. (1979). A Course in Biology. Massachusetts, USA: Addison-Wesley. [ Links ]
Blake, J., & Smith, L. N. (1979). The Slinky as a model for transverse waves in a tenuous plasma. American Journal of Physics, 47 (9), 807-808. [ Links ]
Braile, L. W. (2010). Seismic Waves and the Slinky: A Guide for Teachers. Recovered 10/09/2014 http://web.ics.purdue.edu/~braile/edumod/slinky/slinky.pdf [ Links ]
çelen, S. (2012). Laser micro-machined semi- slinky like MEMS structures: Novel interface coolers. Opt. Laser Technol., 44, 2043-2048. [ Links ]
Crawford, F. S., Jr. (1990). Slinky-whistler dispersion relation from 'scaling'. American Journal of Physics, 58 (10), 916-917. [ Links ]
Crawford, F. S., Jr. (1987). Slinky whistlers. American Journal of Physics, 55 (2), 130-134. [ Links ]
Crawford, F. S., Jr. (1968). The Berkeley physics course (v. 3). New York, USA: McGraw Hill. [ Links ]
Cross, R.C., & Wheatland, M.S. (2012). Modeling a falling slinky. American Journal of Physics, 80 (12), 1051-1060. [ Links ]
Cutnell, J. D., & Johnson, K. W. (2012). Physics (9 ed.) Hoboken (NJ), USA: Wiley. [ Links ]
Chong, Ch. S. A., Gan, G., Verhoef, A., Gonzalez- Garcia, R., & Vidale, P.L. (2013). Simulation of thermal performance of horizontal slinky-loop heat exchangers for ground source heat pumps. Applied Energy, 104, 603-610. [ Links ]
French, A.P. (1994). The suspended Slinky - A problem in static equilibrium. The Physics Teacher, 32 (4), 244-245. [ Links ]
Fujii, H., Yamasaki, S., & Maehara, T. (2013). Numerical modeling of Slinky-coil horizontal ground heat exchangers considering snow coverage effects. Document prepared for the 38th Workshop on Geothermal Reservoir Engineering Standford University. 11-13 February, 2013. Standford (CA), USA. [ Links ]
Gao, P. X., Ding, Y., Mai, W., Hughes, W. L., Lao, C., & Wang, Z. L. (2005). Conversion of zinc oxide nanobelts into superlatticestructured nanohelices. Science, 309 (5741), 1700-1704. [ Links ]
Gluck, P. (2010). A project on soft springs and the slinky. Physics Education, 45 (2), 178-185. [ Links ]
Hu, A.-P. (2010). A simple model of a Slinky walking down stairs. American Journal of Physics, 78 (1), 35-39. [ Links ]
James, R. T. (1947). Toys and process of use. U.S. Patent 2.415.012, January 28. [ Links ]
Kim, S., Kim, W., & Cho, M. (2011). Design of nanosprings using Si/SiGe bilayer thin film. Japanese Journal of Applied Physics, 50 (7R), 070208-1 - 070208-3. [ Links ]
Korgel, B. A. (2005). Nanosprings take shape. Science, 309 (5741), 1683-1684. [ Links ]
Longuet-Higgins, M. S. (1954). On Slinky: The dynamics of a loose, heavy spring. Mathematical Proceedings of the Cambridge Philosophical Society, 50 (2), 347-351. [ Links ]
Mak, S. Y. (1987). The static effective mass of a slinkyTM. American Journal of Physics, 55 (11), 994-997. [ Links ]
McEachen, M. E., Trautt, T. A., & Murphy, D. M. (2005). The ST8 SAILMAST Validation Experiment. Proceedings of the 46th AIAA/ ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, April 18- 21, Austin, Texas. Recovered 15/07/2015 http://nmp.nasa.gov/st8/ tech_papers/AIAA%202005-18840-McEachen-SAILMAST.pdf [ Links ]
Michelsen Jr., M. W. (2009). Happy Birthday SlinkyTM! Antiques & Collecting Magazine, 114 (9), 30-34. [ Links ]
NASA STI Program (2012). Toys in space, 2. Recovered 26/10/2014 https://www.youtube.com/watch?v=E9RDlIjgftI [ Links ]
Neuberger, P., Adamovský, R., & ![]() edová, M. (2014). Temperatures and Heat Flows in a Soil Enclosing a Slinky Horizontal Heat Exchanger. Energies, 7 (2), 972-987. [ Links ]
edová, M. (2014). Temperatures and Heat Flows in a Soil Enclosing a Slinky Horizontal Heat Exchanger. Energies, 7 (2), 972-987. [ Links ]
Pedersen, C. (2010). Ground-source heat pumps. Publication No. AE1483. North Dakota State University Energy. [ Links ]
Poggi, M. A., Boyles, J. S., Bottomley, L. A., McFarland, A. W., Colton, J. S., Nguyen, C. V., Stevens, R. M., & Lillehei, P. T. (2004). Measuring the compression of a carbon nanospring. Nano Letters, 4 (6), 1009-1016. [ Links ]
Sawicki, M. (2002). Static elongation of a suspended slinkyTM. The Physics Teacher, 40, 276-278. [ Links ]
Scott, S. M. (2010). Toys and American culture: an encyclopedia. Santa Barbara (CA), USA: Greenwood. [ Links ]
Sealy, C. (2004). A rich family of slinky materials: Nanotechnology. Mater. Today, 7 (4), 7. [ Links ]
Sun, Y., Choi, W. M., Jiang, H., Huang, Y. Y., & Rogers, J. A. (2006). Controlled buckling of semiconductor nanoribbons for stretchable electronics. Nature Nanotechnology, 1, 201-207. [ Links ]
Vandegrift, G., Baker, T., DiGrazio, J., Dohne, A., Flori, A., Loomis, R., Steel, C., & Velat, D. (1989). Wave cutoff on a suspended slinky. American Journal of Physics, 57 (10), 949-951. [ Links ]
Xiong, Z., Fisher, D.E., & Spitler, J.D. (2015). Development and validation of a Slinky® ground heat exchanger model. Appl. Energy, 141, 57-69. [ Links ]
Xu, F., Lu, W., & Zhu, Y. (2011). Controlled 3D Buckling of Silicon Nanowires for Stretchable Electronics. ACS Nano, 5 (1), 672-678. [ Links ]
Yang, P.-K., Lin, Z.-H., Pradel, K. C., Lin, L., Li, X., Wen, X., He, J.-H., & Wang, Z. L. (2015). Paper-based origami triboelectric nanogenerators and self - powered pressure sensors. ACS Nano, 9 (1), 901-907. [ Links ]
Young, R. A. (1993). Longitudinal standing waves on a vertically suspended slinky. American Journal of Physics, 61 (4), 353-359. [ Links ]
Zimmermann, K. P., & Simpson, R. K. (1996). "Slinky" coils for neuromagnetic stimulation. Electroencephalography and clinical Neurophysiology, 101, 145-152. [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento