Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y competitividad
Print version ISSN 0123-3033
Ing. compet. vol.18 no.1 Cali Jan./June 2016
Evaluation of the structural reliability of a grandstand subjected to anthropic loads
Evaluación de la confiabilidad estructural de una tribuna sometida a cargas antrópicas
Diana C. Millán-Yusti
Grupo de Investigación en Ingeniería Sísmica, Eólica, Geotécnica y Estructural G-7, Escuela de Ingeniería Civil y Geomática, Universidad del Valle. Cali, Colombia.
E-mail: diana.c.millan@correounivalle.edu.co
Johannio Marulanda
Grupo de Investigación en Ingeniería Sísmica, Eólica, Geotécnica y Estructural G-7, Escuela de Ingeniería Civil y Geomática, Universidad del Valle. Cali, Colombia.
E-mail: johannio.marulanda@correounivalle.edu.co
Peter Thomson
Grupo de Investigación en Ingeniería Sísmica, Eólica, Geotécnica y Estructural G-7, Escuela de Ingeniería Civil y Geomática, Universidad del Valle. Cali, Colombia.
E-mail: peter.thomson@correounivalle.edu.co
Eje temático: INGENIERÍA CIVIL / CIVIL ENGINEERING
Recibido: Abril 16 de 2015
Aceptado: Septiembre 10 de 2015
Abstract
The presence of crowds in soccer stadia produce dynamic loads which can in turn induce changes to the dynamic properties of the structural system and cause vibrations that exceed admissible comfort levels. The South Grandstand of the Pascual Guerrero Olympic Stadium in Cali, Colombia, has been the traditional stand for the rowdiest groups of fans during the soccer season, making it ideal for studies on human-structure interaction and structural reliability. This paper describes the analysis of the structural reliability of the grandstand using serviceability limit states recommended in international standards,. The methodology included the characterization of the dynamic response of the structure during several soccer matches, the formulation of the load functions for people jumping, simulations of the location of spectators in the stand using fuzzy logic and the incorporation of this information in a finite element model that was updated with experimental results. Structural reliability indexes were obtained for the response of the grandstand to anthropic loads.
Keywords: Anthropic loads, limit states, model updating, structural reliability.
Resumen
Los estadios de fútbol son estructuras donde la actividad del público genera cargas aleatorias de magnitudes considerables que inducen cambios en las propiedades dinámicas del sistema estructural, generando vibraciones que en algunos casos superan los límites admisibles de confort. La Tribuna Sur del Estadio Olímpico Pascual Guerrero de Cali, Colombia, ha sido tradicionalmente el lugar de encuentro de grupos de hinchas durante la temporada de fútbol, convirtiéndola en el escenario perfecto para estudios sobre interacción humano-estructura y confiabilidad estructural. En este artículo se presentan los resultados del análisis de confiabilidad estructural de la Tribuna, tomando como referencia los estados límite de servicio recomendados en normas internacionales. La metodología usada consistió en la caracterización de la respuesta de la estructura durante diferentes partidos de fútbol, la formulación de funciones de carga para personas en movimiento, la simulación de la ubicación de las personas mediante lógica difusa y su posterior aplicación en un modelo en elementos finitos ajustado con resultados experimentales. Se obtuvieron los índices de confiabilidad estructural que representan el comportamiento de la Tribuna ante cargas antrópicas.
Palabras claves: Ajuste de modelos, cargas antrópicas, confiabilidad estructural, estados límite.
1. Introduction
Any civil structure can be susceptible to failures if the loads, structural properties, or service conditions differ considerably from those used in the design phase. These differences are associated with various sources of uncertainty, including over-simplifications for structural models and simulations, variations in geometric parameters and material properties, changes in structural mass due to occupancy, and different uses of the structure during its useful life (Moreno & Thomson, 2011). In general, service and comfort limits are often neglected, as priority is generally given to security criteria during the design process. However, structures such as gyms, pedestrian bridges, arenas, and stadia are vulnerable to vibrations that affect functionality during service conditions and, hence, it is advisable to improve the analyses of these structures and the existing methodologies for their evaluation (Hernandez et al., 2011; Villamizar et al., 2014). This implies the implementation of structural monitoring systems to obtain the structural response, and that live loads and the effects of the human-structure interaction need to be fully characterized.
Traditionally, structural reliability has been defined as the probability that a given state function limit of a structure is exceeded during a given time. It is an appropriate alternative for providing a measure of the safety level of structures built with various materials, technologies and support conditions, and subject to different types of excitations. Freudenthal was one of the pioneers who implemented probabilistic methods for structure reliability analysis for different materials (Almeida & Rodriguez, 1999; Yao & Kawamura, 2001). Methods for structural reliability have been widely accepted for the analyses of existing structures. One example of this is the work done by Nuñez et al. (2011), who carried out the assessment of the seismic vulnerability of Wing B of the San Ignacio University Hospital using structural reliability techniques, based on dynamic spectral analyses of the structural model for various loads. Another example is the work by Lopez et al. (2011) who evaluated the structural reliability of a 10-level building located on soft soils while taking into account the cumulative effect of damage caused by earthquakes over time.
In recent years, detailed consideration has been given to the effects of dynamic loads such as earthquakes, wind loads, and human-structure interaction in structural analysis and design through the use of finite-element software. Structural modeling has evolved with the objective of providing accurate information regarding the actual behavior of the structure due to different load conditions, by incorporating methodologies such as experimental data based model updating, uncertainty modeling and structural reliability analysis (Guerra et al., 2006). This paper describes the results of a reliability analysis of the South Grandstand of the Pascual Guerrero Olympic Stadium in the city of Cali, Colombia, using ambient and forced vibration records and model updating techniques based on anthropic loads.
2. Methodology
A structural reliability analysis seeks to define the probability of a failure in a structure. Hence, the different load conditions to which a building may be exposed need to be identified by performing a structural analysis in which the respective variables are considered together with the expected consequences due to possible loads and structural conditions. The probability of failure of a structural element may be obtained from Equation 1 (Ditlevsen & Madsen, 1996) where Pf is the probability of failure, R is the capacity function of the structure, S is the load demand, and G is the limit state function.
Pf=P(G(R,S)≤0 (1)
In general terms, if the strength capacity is greater that the demand due to loads there is a security margin. In this sense, the security margin can be expressed with the concept of reliability index (β); for which a larger value of β implies a lesser probability of failure and vice versa (Ditlevsen & Madsen, 1996). The reliability index depends on the mean and the variance of the capacity of the structure and the demand, according to the considered limit state (Equation 2),
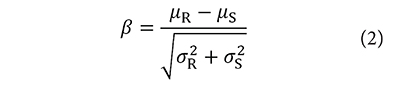
where µR and σR are the respective mean and standard deviation of the strength distribution curve; and µS and σS are the mean and standard deviation of the load distribution curve. The reliability index is expressed in terms of the inverse of the cumulative standard normal function of the failure probability (Equation 3). Due to the inverse proportionality between the reliability index and the probability of failure, a smaller value of the probability of failure implies a larger value of the reliability index, which indicates the structure is safer (Muñoz et al., 2012).
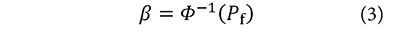
2.1 Description of the structure
The Pascual Guerrero Stadium has four independent stands (West, East, South and North) built with a combination of steel and reinforced concrete structural elements, and isolated from each other with expansion joints. This study focuses on the assessment of the South Grandstand. Thirteen frames, supporting the roof and the seating deck, conform the structure of this stand. The frames are formed by two main reinforced concrete columns in a V shape, two beams of the same material that support the secondary beams of the stands and, on the outer side of the frame, a steel strut adds stiffness to the upper cantilever. The frames are interconnected by secondary reinforced concrete beams, as well as the steel beams that make up the tiers and those that support the concourses.
2.2 Modal identification
The main operational frequencies and mode shapes of the South Grandstand were identified using a portable data acquisition system and ambient and forced vibration tests. The forced vibration tests consisted of sine-sweeps from 1 to 20Hz using an APS 400 mass exciter placed on the lower cantilever. Data was acquired from five seismic accelerometers (Wilcoxon ResearchModel 731A) distributed on the central frame of the stand (Figure 1), and digitized with a 16-bit SC-2345 National Instruments Board.
Figure 1. Experimental setup.
Data processing included the of band-pass filtering of data between 0.5 and 28 Hz to remove noise and disturbances in the signal outside the range of interest. Additionally, power spectrums were calculated for each signal using a 1024 length Hanning window and 50% overlap. Eighth-order transfer functions were fitted to the frequency data, and operational frequencies were identified at 5.0, 8.4, and 9.4 Hz. The first of these frequencies is associated with vertical movements of both the upper and the lower cantilevers, the second with the vertical mode of the lower cantilever, and the third frequency corresponds to the transverse mode of the frame with bending in the upper and lower cantilevers.
2.3 FEM development and updating
The South Grandstand was modeled using the structural analysis software SAP200 based on information gathered from the as-built specifications and drawings of the structure. The FE model has 10419 DOF with 6057 nodes and 9926 beam-type elements corresponding to columns and beams of the main frames, tiers, piles and the roof elements. Figure 2 shows the scheme of the structural model of the stand.
Figure 2. Finite element model of the South Stand of the Pascual Guerrero Stadium.
The model was updated using the information of the three modes identified experimentally. The model was updated by varying parameters such as the Young's modulus of the elements, the constants of elasticity of the foundation springs and the additional dead mass. These parameters were varied using the Application Programming Interface (API) that allows interaction with SAP2000 for bidirectional exchange of information with the mathematical software MATLAB. The API was used to automate the updating process, as it can be used to modify model parameters and extract results of mode shapes corresponding to the modified numerical model. These numerical results were then compared with the experimental data and assessed with an objective function (OF), Equation 4, in order to determine the percentage of difference between compared data.
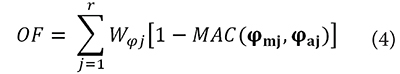
In Equation 4, r is the number of modes to update (in the present case three), φrj is the experimental modal form, φaj the analytical mode shape, and Wφj are weights which, in this case, were assumed to be equal for all three modes.
Initial parameter values were chosen to be those in the construction specifications and information regarding design materials was used to define the ranges of variations in these parameters. Operational frequencies and mode shapes obtained from the dynamic experimental analysis were used in the OF, which was defined in terms of the differences between experimental and numerical frequencies and mode shapes. Differences between mode shapes were quantified using the Modal Assurance Criterion (MAC) (Allemang, 2003). The MAC value (Equation 5) is a coefficient that can have a value between 0 and 1, and it provides a measure of the similarity between two modal vectors in terms of a least squares quotient. A MAC value of 1 corresponds to a perfect correlation or similarity, while a value of 0 means there is no relationship between the vectors.
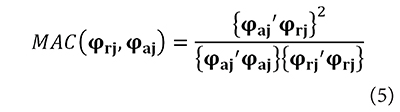
Regarding the foundation model, a pile factor was used as multiplier of an initial stiffness value for each layer of soil in the specific site. The stiffness of the three layers and the stifness at the base of the pile are 981 kN/m, 1962 kN/m, 3924 kN/m, and 4707 kN/m, respectively. Updating the values of stiffness for the footings in translational and rotational directions was accomplished by allowing the variation to range from 40% to 140% of the initial estimate. The initial value of the vertical translational stiffness was taken to be 195219x104 N/m and, after updating, the final value was 191162.35x104 N/m. The initial value for both horizontal directions of translational stiffness was 136359x104N/m and the final value was 133525x104 N/m. As far as the value of the rotational stiffness of the footings with respect to the two horizontal axes, the initial estimate of 4905x105 N/(m.rad) was updated to a final value of 4803.07x105 N/(m.rad). The rotational stiffness with respect to the vertical axis was given an initial value of 19620x105 N/(m.rad) and updated to 19212.30x105 N/(m.rad).
The values of the modulus of elasticity for both beams and columns were also updated. The initial estimate of 191 GPa for the modulus of elasticityof the beams was allowed to vary within a range of 85% and 120% and was updated to a value of 178.48 GPa. The modulus of elasticity of the columns was allowed to vary within the same range, and changed from an initial estimate of 210 GPA to a final value of 227.51 GPa. The additional dead load (the seats), which was allowed to vary in a range from 90% to 110%, was updated to a final value of 1.01 times the initial estimate. The OF reached a sub-optimal value of 0.29 where the level of modal correlation is 92%, 94%, 97% y 89%. These results are considered satisfactory, taking into account the complexity of the structure.
2.4 Load characterization
A series of tests were carried out in order to characterize the loads generated by a person by having individuals with different biodynamic properties jump on a load platform. The experimental loads was classified in five groups according to the jumping frequency (1.50-2.50 Hz). A one DOF model was then used to find a relationship between the load generated by anindividual jumping and an external force acting on the corresponding mass. Each specific load the grandstand according to the criteria specified in the following section. The one DOF system is described by a transfer function (Equation 6) where m, c, and k correspond to biodynamic properties of the human body. Constants a and b are coefficients of the denominator that correspond to poles at very high frequencies added such that the number of poles is greater than the number of zeros, making the system transfer function realizable without affecting the dynamics of the system at lower frequencies. P(s) is the Laplace Transform of the external force applied to the one DOF system and F(s) corresponds to the load produced by the individual on the structure. The experimental data obtained from the load platform was used as input to the system to calculate the respective external forces for different individuals.
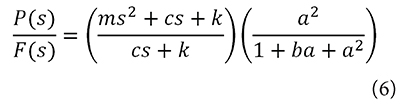
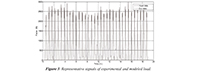
MATLAB was used to generate values of the biodynamic data, corresponding to mass, stiffness and damping, for each of the one DOF human models added to the grandstand FE model. This data was generated to have a normal distribution in the ranges defined by Brownjohn (1999) and Coermann (1962). Care was also taken to generate values independently, such that the value of a parameter at a given moment would not depend on previously generated values. As shown in Figure 3, the loads resulting from these models correspond well with experimental values.
Figure 3. Representative signals of experimental and modeled load.
3. Criteria for the structural reliability analysis
The reliability analysis of the South Grandstand of the Pascual Guerrero Stadium was conducted for anthropic loads considering serviceability limit states. The International Standard ISO 2631-1, which specifies the effects of vibrations on a person's health and comfort, was used to define the service conditions. This standard has been used previously by other researchers to evaluate the effects of vibrations on humans in multiple structures (Caprioli, Reynolds & Vanali, 2007). The ISO 2631-1 provides a basic evaluation method of vibration using weighted root-mean-square acceleration (RMSa) (Equation 7), where aw is the weighed acceleration and T is the duration of the measurement.
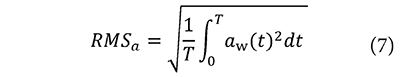
The natural frequency of the structure and the acceleration level are combined to evaluate the serviceability limit states. The human body tends to be more sensitive to vertical vibrations ranging from 2 to 8 Hz. Based on the RMSa level in units of m/s2, the ISO2631-1 establishes six categories of perception: 1) accelerations with an RMSa value less than 0.351 are acceptable for a person in a passive state; 2) RMSa values in the range 0.315-0.630 produce some discomfort; 3) values in the range 0.630-1.000 are considered slightly uncomfortable; 4) RMSa ranging between 1.000-1.250 are classified as uncomfortable; 5) values between 1.250 -2.500 are very uncomfortable, and 6) values of RMSa greater than 2 are considered extremely uncomfortable and will likely cause panic.
3.1 Location criteria
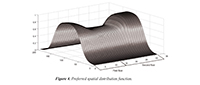
Spatial distribution of spectators is one of the main uncertainties for stadia analyses. As the Pascual Guerrero Stadium was recently refurbished to meet FIFA requirements, with all the grandstands being furnished with new seating, one of the criteria for spectator location was the distribution of the seats. An algorithm was developed to model spectator distribution based on photographs and videos taken during important soccer matches with the stadium at full capacity. Based on this, different areas of the stand were classified according to observed stereotyped behavior, as spectators that arrive early show a preference towards sitting on the upper and lower part of the stand. These spectator trends were described with fuzzy logic theory, with membership functio ns to classify personal spectator preferences. Specifically, S-shaped functions were used to describe the comfort of each spectator, by taking into account factors such as the number and proximity of other people surrounding the particular spectator and available seating nearby. These functions were divided into the four sections as defined in Equation 8, based on the parameters a and b that define the limits of the inclined part of the curve (Figure 4).
Figure 4. Preferred spatial distribution function.
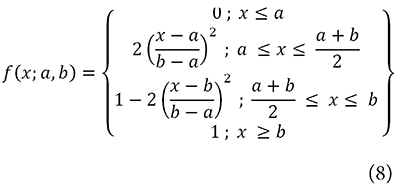
Additionally, a two-dimensional membership function based on sigmoid functions (with coordinates representing location of seats in rows and columns) was used to classify preferred seating areas in the stand, according to observed spectator behavior during matches. One of these maps is shown in Figure 4, where rows 1 to 14 correspond to the first floor and rows 15 to 32 correspond to the second floor of the grandstand. Each of the markers in Figure 5 indicates a spectator position for a 5% capacity of the stadium.
Figure 5. Preferred spectator locations.
Based on the spatial distribution of N spectators, the same number of one DOF models, each with specific biomechanical properties, were added to the grandstand model at the N respective locations. Damping and stiffness were represented by link elements in the SAP2000 FE model. For each of the N masses, a specific external load p(t) was applied to represent the force induced by the corresponding spectator on the structure. Finally, the acceleration response of the stand was calculated using time history analyses. Four hundred simulations were performed using the API of SAP2000, for different percentages of capacity and spatial distributions of the spectators.
3.2 Risk analysis
The effective load produced by a group of people jumping depends largely on the ability of each person to jump rhythmically. As the spectators who normally occupy the South Stand during the soccer season tend to be fans who use percussion instruments to mark the beat of the songs and chants, it is reasonable to assume that most of the spectators will be jumping synchronously and generating a critical load scenario. This hypothesis was tested by acquiring data of the acceleration response of the stand and videos of the spectators during soccer matches that had different levels of attendance. The videos were analyzed to identify the levels of excitement and synchronization of the spectators while jumping and this information was correlated with the response of the structure.
The acceleration response of the lower cantilever of the stand during an important match with an attendance of 95% is shown in Figure 6. Peak accelerations were recorded during instants of synchronous jumping of the public and, specifically, a maximum response acceleration of 2.10 m/s2 was recorded after a goal was scored by the home team. Strong correlations were observed between the load produced by the spectators and the level of excitement, and between the load and the synchronization of the jumping. An operational frequency of the structure at 2.25 Hz and a second frequency at 4.45 Hz, which corresponds to the second harmonic, were identified during synchronized jumping using a time-frequency analysis of the structural response. It was found that during most soccer matches fans jumped at this frequency of 2.25 Hz + 0.1 Hz, which corresponds to the beat of most of their chants. The dynamic loads were modeled with the data from the load platform corresponding to the same jumping frequency. Analyses of the structural response were carried out with following levels of attendance: 5%, 10%, 11%, 20%, 25%, 30%, 35%, 45%, 50%, 60%, 70%, 75%, 80% and 90%.
Figure 6. Measured accelerations during soccer match.
3.3 Results and discussion
Figure 7 (a) shows a histogram of the RMSa accelerations of the structural response measures during soccer matches. As the RMSa are positive with an asymmetric distribution, the histogram is compared to Log-Normal, Extreme Values, Weibull and Exponential probability density functions. The data fits better to a Weibull function according to the Anderson-Darling test, although data from specific matches also fit well to Log-Normal functions. The cumulative distribution function F(x) is shown in Figure 7 (b) and it is the integral of the probability density function f(t) as given in Equation 9. As shown in Figure 7 (a), 0.75% of the RMSa acceleration data fall in the "slightly uncomfortable" category of the serviceability limits. Based on the evaluation of the structural reliability, the probability of exceeding this limit is given in Table 1.
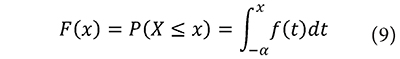
Figura 7. (a) Histogram and probability density functions, (b) Cumulative distribution function.
Table 1. Reliability analysis results.
The lower cantilever of the grandstand was identified as being the most prone to vertical vibrations. Of the different points considered on the structure in the reliability analysis, it has the lowest reliability index with a value of 2.29. These results indicate that the structure is within the range of safety according to the Eurocode that specifies a reliability index greater than 1.5 for serviceability limit states.
4. Conclusions
According to the structural reliability analysis, spectators in the South Stand of the Pascual Guerrero Stadium can produce vibrations that are "slightly uncomfortable" according to serviceability limits for vibrations recommended in ISO 2631-1. The lower cantilever is the point where vertical vibrations tend to have the largest amplitudes. Although this point on the stand has a reliability index of 2.29, the results indicate the structure is within the service range defined in the Eurocode, thus concluding that there is minimal risk. In general terms, the retrofit of the South Stand has greatly improved its serviceability conditions as vibrations in the lower cantilever of the previous structure were critical and caused spectators to feel unsafe.
As grandstand structures are subjected to external loads due to spectators moving about randomly or fans jumping in a synchronous manner, it is recommended that the analysis of this type of structures consider uncertainties and the statistical characterization of each variable. The methodology applied in this work can be extended to analyses of other grandstands to evaluate the structural reliability for anthropic, seismic, wind or any other type of dynamic loads.
5. References
Allemang, R.J. (2003). The modal assurance criterion-twenty years of use and abuse. Sound and vibration, 37, 14-23. [ Links ]
Almeida, P., & Rodrigues, J. (1999). Modal analysis of the structure of a soccer stadium. SPIE proceedings series, 1999. Society of Photo-Optical Instrumentation Engineers (pp. 1417-1422). Sao Paulo (SP), Brazil. [ Links ]
Brownjohn, J.M.W. (1999). Energy dissipation in one-way slabs with human participation. In, Proceedings of the Asia-Pacific Vibration Conference '99, Nanyang Technological University (pp. 11-13) Singapore. [ Links ]
Brownjohn, J.M.W. (2001). Energy dissipation from vibrating floor slabs due to human structure interaction. Shock and Vibration, 8 (6), 315-23. [ Links ]
Caprioli, A., Reynolds, P., & Vanali, M. (2007) Evaluation of serviceability assessment measures for different stadia structures and different live concert events. Proceedings of the 25th international modal analysis conference, Orlando, USA. [ Links ]
Coermann, R.R. (1962) The mechanical impedance of the human body in sitting and standing position at low frequencies. Human factors, 4 (5), 227-53. [ Links ]
Ditlevsen, O. & Madsen, H.O. (1996). Structural reliability methods. New York, USA: Wiley. [ Links ]
Guerra, Á.C., Sanchez, M., y Reyes, J.C. (2006). Análisis probabilístico del comportamiento dinámico de estructuras. Bogotá D.C., Colombia: Universidad de los Andes. [ Links ]
Hernández, D.F., Pizano, D.G., y Thomson, P. (2011). Implementación de un sistema de control activo para disminuir las vibraciones producidas por personas en una tribuna. Revista Facultad de Ingeniería Universidad de Antioquia, (61), 83-92. [ Links ]
Muñoz, E., Núñez, F., y Magallón, A. (2012). Ingeniería de Puentes. En, E. Muñoz (Ed.) Ingeniería de Puentes (Tomo 3) (Capítulo I). Bogotá D.C., Colombia: Pontificia Universidad Javeriana, Editorial Gente Nueva. [ Links ]
NO 2631-1 (1997). Mechanical vibration and shock-Evaluation of human exposure to whole body vibration. Part1: General requirements. London, UK: International Organization for Standardization. [ Links ]
Núñez, F., Muñoz, E., y Prieto, J. (2011). Confiabilidad estructural del edificio del hospital universitario San Ignacio, cuando es sometido a excitación sísmica. Revista Ingeniería de Construcción, 19 (2), 95-100. [ Links ]
Thomson, P., y Moreno, C.P. (2011). Incertidumbre paramétrica en modelos dinámicos de estructuras civiles. Revista Ingeniería y Competitividad, 12 (1), 111-125. [ Links ]
Villamizar, S.X., Gómez, D., y Thomson, P. (2014). Efectos de interacción humano-estructura en losas. DYNA: Revista de la Facultad de Minas, 81 (184), 129-137. [ Links ]
Yao, J.T., & Kawamura, H. (2001). On structural reliability. Journal of Temporal Design in ArchiÂtecture and the Environment, 1 (1), 1-5. [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento