1. Introduction
Hydropower plants are an alternative power source 1. However, these systems could be potential sources of greenhouse gases (GHG) due to flooded organic matter biodegradation after filling stage or entering organic matter through the tributaries 2-8. Tropical reservoirs are estimated to emit 1.300-3.000 g CO2 eq/kWh while boreal reservoirs are estimated to emit 160-250 g CO2 eq/kWh. Other energy sources such as natural gas power plants, oil burning and carbon burning are estimated to emit 400-500 g CO2 eq/kWh, 790-900 g CO2 eq/kWh and 900-1.200 g CO2 eq/kWh respectively 9.
Organic matter biodegradation is carried out by many microorganism groups in presence or absence of oxygen. Biodegradation in absence of oxygen is called anaerobic biodegradation and it is composed by a series of processes with methane (CH4) and carbon dioxide (CO2) as final products 10-11. These gases have a recalcitrant property in the atmosphere 12 but each one contributes with a different heating. For instance, CH4 has a global warming potential (GWP) 34 times more than CO2’s GWP on a 100-year timescale but CO2’s effects in atmosphere can last hundreds of years because carbon cycles through several Earth system reservoirs have vastly different residence times 13-14. For this reason, every nation must implement a GHG inventory which includes hydropower plants inputs in order to establish control measures 15. On a global basis, the GHG emissions from reservoirs are equivalent to 4% and 20% of other anthropogenic emissions of CO2 and CH4 respectively, and 70% and 90% of these emissions (from CO2 and CH4 respectively) proceed from tropical reservoirs 8.
An action taken for GHG studies is the development of mathematical models to predict the formation and behavior of these gases during reservoir’s useful lifetime, for possible goals to decrease atmosphere emissions. Different studies have been developed to appraise predicting GHG formation models 16-19. Considering that GHG formation in reservoirs is given by organic matter biodegradation, most of the models are conceptually conceived according to biodegradation rates, hence it is important to consider the decomposition kinetics 20.
In this contribution, it was studied the GHG formation rate in Topocoro reservoir located in Santander, Colombia, according to kinetic anaerobic biodegradation of organic matter in water and vegetal samples from the reservoir, throughout laboratory tests with batch reactors, in which production of CO2 and CH4 was quantified. It was performed a linear mathematical model to predict CO2 formation and an exponential mathematical model to predict CH4 formation. Finally, the measuring data adjustment to resulting data after implementing mathematical models in Matlab was evaluated.
2. Materials and methods
2.1 Study area
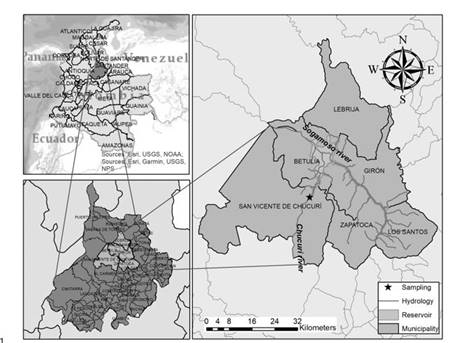
The study of the behavior of GHG generation from the Topocoro reservoir in Sogamoso hydroelectric dam was contemplated in this contribution. It is located in Southamerica, in Northwest Colombia (7° 6' 11.57" N, 73° 24'37.09" O), on Santander department, at the canyon where Sogamoso River crosses the Serranía de la Paz 21, 75 km upstream of its river outlet in Magdalena river and 62 km downstream of the Suarez and Chicamocha rivers confluence. The reservoir uses the Sogamoso river in the generation of electric energy through the construction of a 190 m high dam and an underground powerhouse. It has 820 MW of installed capacity and a mean annual generation of 5.056 GWh/year. The filling volume is 8.5 million m3, its mean flow is 474.6 m3/s and the surface area of the water mirror is 6960 ha. Currently, it is the fourth dam in Colombia with the biggest installed capacity 22. The tributaries of the reservoir are summarized in Table 1.
Table 1 Tributaries of Topocoro reservoir. Adapted from 22
| Tributary | Multiyear discharge (m/s) | Basin area (ha) | Precipitation (mm/d) |
|---|---|---|---|
| Chicamocha | 135.0 | 133,200 | 2.59 |
| Suárez | 195.0 | 982,300 | 6.38 |
| Chucurí | 8.7 | - | 4.97 |
| Aguas blancas | 0.88 | - | 4.46 |
| Sogamoso | 540.0 | 111,944 | 7.90 |
The area of influence of the project is shown in Figure 1. Particularly, this study is focused on GHG generation at the point where Chucurí river enters to the reservoir. This river is one of the most important tributaries in terms of organic matter contribution because it takes all the wastewaters from the municipality of San Vicente de Chucurí, as it does not count with a wastewater treatment plant, and finally that organic matter goes into the reservoir contributing to the total emission of GHG from Topocoro.
2.2 Sampling
The water sampling was made on September 11th, 2015, during the post-filling reservoir stage in the dry-to-wet transition season. It was chosen this seasonality so that rainfalls were not abundant enough to generate aeration processes in water due to flow increase that could affect the strict anaerobic bacteria responsible for CH4 generation, nor organic matter dilution processes as a consequence of water volume increasing. Water samples were collected from the aphotic zone at the point where Chucurí River enters to Topocoro reservoir. For this purpose, it was used a Kemmerer bottle which was submerged at 0.7 m depth. This distance was calculated with the Secchi disk at the point it was no longer visible from the surface. 20 L of water at this depth were collected with the Kemmerer bottle and were transferred to plastic containers, previously purged with the same reservoir water. The sampling process and the subsequent transport to the laboratory were carried out according to GDCON sampling protocol (GE-PR-004-GDCON) based on the 1060 Collection and preservation of samples from the 22nd Edition of Standard methods for the examination of water and wastewater 23.
Additionally, in order to evaluate organic matter biodegradation by microorganisms in the reservoir, a pickup of Puyol grass from Cynodon genus, a representative unit of land cover in the study area 21, was performed in the reservoir surrounding area during the same day of the water sampling. These grass samples were preserved with alcohol and paper during its transport to the laboratory.
2.3 Experimental setup
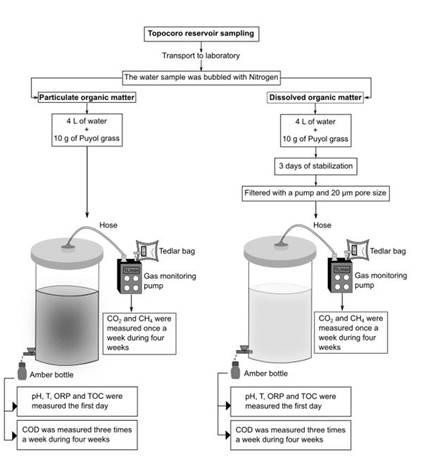
The experimental setup lied in analyzing particulate and dissolved organic matter degradation kinetics by anaerobic microorganisms from the reservoir’s water. According to 21 the water samples were bubbled with Nitrogen gas so the dissolved oxygen in the column was displaced, making sure that water conditions were anaerobic, after moving the samples from the reservoir to the laboratory. Subsequently, the experimental setup was designed as Figure 2 shows. To obtain the GHG contribution by particulate organic matter biodegradation, it was employed a 5 L capacity reactor, with 10 g of Puyol grass which was previously cut into pieces and 4 L of nitrogen-purged water from the reservoir, allowing 1 L of air column so the gases could rise from the water column 22. Similarly, to obtain the GHG contribution by dissolved organic matter biodegradation, it was implemented the same previous setup, and additionally, this mix was stabilized during three days in order to be then homogenate and filtered with a pump and a 20 µm pore size so it contained the dissolved organic matter only. This experimental setup was conducted during a month (30 days) and it was designed in order to measure the parameters recommended to be measured in the determination of GHG emissions from reservoirs according to 15.
For the purpose of evaluating the gas formation, it was necessary to measure the quantity of CO2 and CH4 produced during the organic matter degradation inside both reactors. A plastic hose was disposed on the upper part of the reactors in the 1 L air column, so gas samples could be taken out once a week during the one month the experimental setup lasted.
2.4 Physicochemical analysis
The assays were executed in the GDCON group laboratory, accredited by Instituto de Hidrología, Meteorología y Estudios Ambientales (IDEAM) in the norm 17025:2005 under the resolution 3564/2014. pH and redox potential (ORP) analysis were performed with a WTW pH7110 equipment, Total Organic Carbon (TOC) analysis were performed with a TOC Apollo 9000 analyzer and Chemical Oxygen Demand (COD) analysis were performed with a spectrophotometer. The analyses were made following the methodologies established on the Standard Methods for the Examination of Water and Wastewater 23 (See Table 2).
Table 2 Parameters analyzed
| Parameter | Abbreviation | Units | Reference method |
|---|---|---|---|
| pH | pH | - | 4.500 H+B |
| Redox potential | ORP | mV | 2.580 B |
| Temperature | T | °C | - |
| Total organic carbon | TOC | ppm C | 5.310 B |
| Chemical oxygen demand | COD | mg O2/L | 5.220 D |
| CO2 concentration | [CO2] | mg/L | Internal method |
| CH4 concentration | [CH4] | mg/L | Internal method |
The parameters pH, ORP, TOC and temperature were measured the first day of the experimental setup. The parameter COD was measured three times a week (Monday, Wednesday and Friday) during the one month the experimental setup lasted. All physicochemical analyses were made taking out a small volume of water from both reactors with amber bottles (See Figure 2).
2.5 Methane and Carbon Dioxide measurements
Samples were taken directly from the hoses located on the top of the reactors. The hoses were connected to a gas monitoring pump and this pump was also connected to a 0.5 liters capacity Tedlar bag. After the pumping, the hoses were sealed to prevent the gas exchange with the environment. The pump’s suction flow was 1 L/min and each sample was taken during 5 minutes. The Tedlar bags were sealed and then were taken to the analysis in the Gas chromatography-mass spectrometry (GC-MS) 7890A, with detector 5975C and with a conductivity detector. The samples were manually injected, employing 0.4 mL of sample using a gas syringe 21. Retention times in the cromatograph were 2.4 minutes and 3.6 minutes for methane and carbon dioxide respectively. As mentioned before, these concentration gases were measured once a week during the one month the experimental setup lasted (See Figure 2).
2.6 Linear mathematical model for CO 2
The temporal variation of CO2’s mass
Where the term
Where 𝑀𝐺 is the CO2’s mass exchange rate over time t due to biochemical and physic processes that contribute to mass exchange (mass time-1). The terms 𝑀𝑖𝑛 and 𝑀𝑜𝑢𝑡 are the CO2’s inlet and outlet mass flow over time t respectively (mass time-1), that can be estimated using the following Eq. (3) and Eq. (4):
𝑄𝑖𝑛 and 𝑄 𝑜𝑢𝑡 represent the inlet and outlet flow over time t (volume time-1) respectively. The CO2’s inlet mass flow into the reactor
If Eq. (5) is substituted in Eq. (2), a simple equation of exchange rate of CO2 concentration in the batch reactor over tieme t is obtained by Eq. (6):
The term 𝑀𝐺 can be written using Eq. (7):
Where
Where
V: Water volume in the reactor (volume)
The differentials for Eq. (8) are:
Considering Eq. (7) and Eq. (8) in Eq. (6), and taking into consideration that there is not inflow nor outflow (i.e.
Eq. (9), Eq. (10) and Eq. (11) represent a first order ordinary differential equation system of initial value to determine the CO2 evolution over time into the reactor.
2.7 Exponential mathematical model for CH 4
Authors like Tremblay et al. 20 and Sogari 24, point out that CO2 production rate by decomposition of flooded soil and vegetation can be predicted by Eq. (12) as follows:
Where:
𝑀(𝑡): Gas mass produced over time (mass)
𝑀𝑀𝑎𝑥: Maximum quantity of gas produced under the most favorable conditions (mass)
𝐴: Parameter that depends on environmental variables such as temperature, and the degradation organic matter.
According to 20 and 24 for this model, 𝑀 (60 d) = 0 in the case of methane which indicates that the maximum CH4 production rate doesn’t occur just after filling the reservoir, but it can occur after 60 days. For CH4, as will be seen further, it was implemented this model, because real data exhibited an exponential behavior, unlike CO2 that exhibited a linear behavior. The parameter A used was 0.1497, whose value was the one that minimized the error of the model and data. For the parameter Mmax it was used the following Eq. (13) 16:
Where:
2.8 Computational model
The computational model stage was carried out using the programming language MatLab. The Eq. (9), Eq. (10) and Eq. (11) were developed for the CO2 first order model, and the Eq. (12) and Eq. (13) were developed for the CH4 exponential model. The differential equations were solved by Runge Kutta method with MatLab’s command ode45 which solves ordinary differential equations. The results obtained after running the models were graphed and then were compared with results measured by the chromatographer. R2 parameter was calculated in order to determine how good the model adjustment to reality is.
3. Results and analysis
3.1 Physicochemical parameters
Table 3 shows the initial values of the physicochemical parameters. pH and temperature conditions were appropriate for the growth of the adequate group or archaea in charge of methane production; pH was adjusted very well to microorganisms requirements and temperature was in a value really close to the optimum operating range, taking into account that methanogenic archaeas live in strict environmental conditions, they are considered mesophilic because they operate in an optimum temperature range between 25-35° C, and they are considered neutrophil because their optimum pH range is close to neutral between 6.8-7.4 25-26. The negative values of redox potential measured, allow concluding that reducing conditions were favored, thus, strict anaerobic metabolism of the archaeas.
Table 3 Initial physicochemical parameters
| Sample | pH | Redox potential (mV) | Temperature (°C) | TOC (ppm C) |
|---|---|---|---|---|
| Water + Dissolved organic matter | 6.748 | -50.5 | 24 | 14.314 |
| Water + Particulate organic matter | 7.318 | -164.3 | 24 | 18.347 |
It was found that TOC concentrations in the second reactor were higher (Table 3), because this reactor contained particulate organic matter, while the first reactor contained only dissolved organic matter due to filtering process. This parameter was used as an input for the DOC and POC values in the linear model.
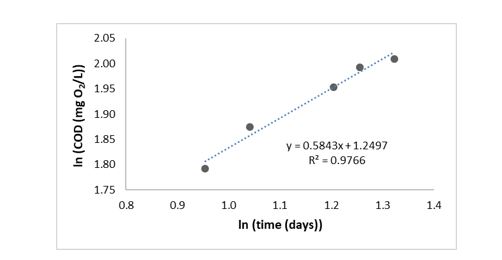
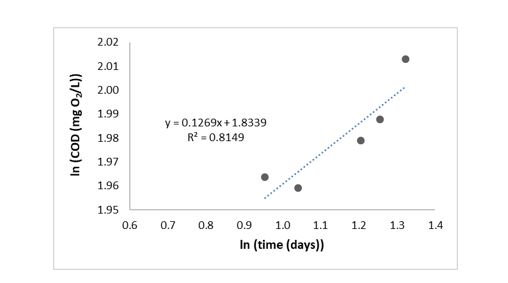
Figure 3 and Figure 4 show the interpolation of COD after data linearization implemented by the methodology contemplated in 27, where the natural logarithm function was employed (to both variables, dependent and independent), for both dissolved and particulate organic matter. Each figure includes the equation of fit to the line and R2 parameter to evaluate the variables correlation.
In both figures, the R2 parameter obtained was close to 1, this indicates a good fit of data to a straight line, and the slope of both equations was used to get the organic matter biodegradation rate for the linear model to predict gases generation.
3.2 Biodegradation rates for linear model
Biodegradation rate for both dissolved and particulate organic matter was 0.5843 mg O2/L.d and 0.1269 mg O2/L.d, respectively (Figure 3 and Figure 4), this indicates that dissolved organic matter biodegradation rate was bigger, what was expected because the dissolved organic matter is the most assailable way for microorganisms.
Linear model required organic matter biodegradation rates as an input data, so that, it was necessary to perform a unit conversion to mg CO2/L.d. For this purpose, it was implemented a 1:1 conversion factor, assuming that 1 mol of consumed O2 produces 1 mol of CO2. Starting from both constants, it was obtained the biodegradation rates as follows:
⏺ For dissolved organic matter:
⏺ For particulate organic matter:
3.3 Gas emissions
The results of gas production in each reactor are shown in Table 4. In both cases, CH4 was produced just after the third week of the experimental setup, and this coincides with the postulation of the exponential mathematical model, which considers that CH4 is not produced since the beginning, unlike CO2 that is produced immediately in both reactors and it has a linear behavior. This is because in time zero the amount of methanogenic archaeas, which are responsible of CH4 production, was not significant yet.
Conversely, CO2 exhibited a linear behavior and its production was greater than CH4’s, because this last gas was produced only during the final step of the anaerobic biodegradation process, whilst CO2 was produced at various stages of the process, since the beginning until the end.
Table 4 Volume of produced gas
| Day | Water + Dissolved organic matter | Water + Particulate organic matter | ||
|---|---|---|---|---|
| CH 4 (mL) | CO 2 (mL) | CH 4 (mL) | CO 2 (mL) | |
| 7 | 0.0000 | 4.8376 | 0.0000 | 10.7294 |
| 14 | 0.0000 | 23.5938 | 0.0000 | 10.9784 |
| 21 | 0.2061 | 33.7351 | 0.5957 | 20.5303 |
| 30 | 0.7167 | 46.2520 | 3.8152 | 35.8673 |
In order to compare the gas production data with the results after the implementation of the models, the gas volume was converted to concentration units using the ideal gas equation (Eq. (16)), following the methodology presented in 21:
Where:
𝑃: Pressure at which the experiment was performed (0.84 atm)
𝑉: Gas volume produced (mL)
n: Gas moles produced (moles)
𝑅: Constant of ideal gas (0.082 atm.L/mol.K)
𝛵: Temperature at which the experiment was performed (297 K)
Finally, the amount of gases produced for both dissolved and particulate organic matter biodegradation were summed up to have the total amount of produced gas by both contributions, and it was divided by the 4 L of water used in each reactor. In Table 5, the final results of produced gases during the 30 days experimentation are shown.
Table 5 Total produced gas concentrations
| Day | CH 4 (mg/L) | CO 2 (mg/L) |
|---|---|---|
| 7 | 0.0000 | 5.9228 |
| 14 | 0.0000 | 13.1539 |
| 21 | 0.1109 | 20.6466 |
| 30 | 0.6269 | 31.2443 |
Results from Table 5 can be also expressed in terms of gas fluxes, knowing the radius of surface water (0.077 m) and the emission gas time in both batch reactors, as shown in Table 6.
3.4 GHG model implementation
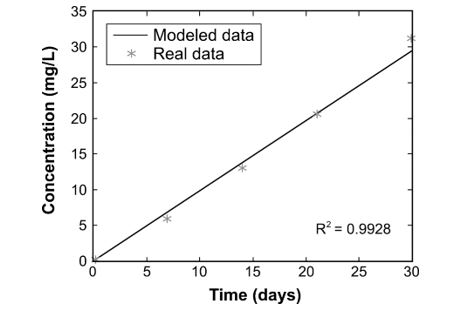
Figure 5 shows the linear model for CO2 and its comparison with real measured data. It can be seen that the model proposed presents a good fit to measured data, because the determination coefficient R2 indicates it is a good correlation being a value close to 1. After this result, we can conclude that CO2 production from organic matter anaerobic biodegradation follows a first order biodegradation kinetics and it can be simulated with the first order differential equation of initial value shown in Eq. (9), Eq. (10) and Eq. (11) because it accomplishes the assumptions.
The variables and parameters contemplated in this model, such as the amount of DOC and POC and its biodegradation rate, can be considered as good estimates of formation of linear behave gases produced by microbial organic matter biodegradation.
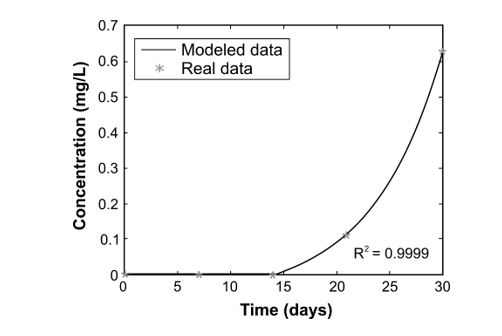
For the case of CH4 and its non-linear behavior during measurements, the exponential model proposed in 20 and 24 was implemented. For the first two weeks it was established in the model a value of zero for the CH4 produced because CH4 was produced just after the day 14. In Figure 6, it can be seen that the adjustment of the model to the behavior of real data was very accurate, because the value of R2 indicated a good fit (value close to 1), considering the adaptation made to the model so during the first 14 days the value of CH4 concentration was zero. According to this result, it can be concluded that the assumptions of the model were satisfied, that is to say, CH4 production in Topocoro reservoir by organic matter anaerobic biodegradation exhibited an exponential behavior and during the first days after starting the biodegradation the CH4 concentration was null. This exponential behavior of CH4 is due to a progressive increase in the number of methanogenic microorganisms, which adapt to environmental conditions following the microorganism’s growth kinetics. Besides, for CH4 production it is necessary that a series of substrate making processes used by methanogenic archaeas during their metabolism - like acetate, hydrogen and carbon dioxide - occur 19. Therefore, its production is slower than CO2’s considered in this study.
4. Conclusions
The flooded organic matter in a reservoir constitutes an important source of GHG emission to the atmosphere. In this contribution, at laboratory scale, it was quantified the emission of CO2 and CH4 using two batch reactors filled with water and Puyol grass from Topocoro reservoir, located in Santander, Colombia. One reactor was employed to analyze the dissolved organic matter biodegradation and the other was employed to analyze the particulate organic matter biodegradation. Negative values of ORP measured in both reactors showed anaerobic environment favoring, strict condition for methanogenic archaes proliferation, which are responsible for CH4 generation as the last product of organic matter anaerobic decomposition. Further, pH was tested to have a value close to 7 and temperature was tested to have a value close to 25° C, since these archaes are neutrophilic and mesophilic, thus, environmental conditions were not a limiting factor for their reproduction.
On the other hand, it was quantified the production of CO2 and CH4 during the experimental setup. CO2 started being emitted from the water column since the first week, whilst CH4 required two weeks to be produced. This was expected because CO2 is produced since the second stage of organic matter anaerobic decomposition (acidogenesis) until the final stage (methanogenesis), whereas CH4 is produced only during the final stage.
It was detected that CO2 and CH4 generation, due to organic matter biodegradation in both reactors, presented different behaviors. CO2 exhibited a linear production while CH4 exhibited an exponential production. So, following the objective of calibrating mathematical models for the generation of these two gases, it was found that CO2 is fitted to a linear model and conversely, CH4 is fitted to an exponential model. This fact allows to conclude that production of these gases can be predicted knowing the organic matter biodegradation rate, independent of the number of microorganisms involved in these reactions. Biodegradation rate is a good estimate to predict the production of these gases because it depends on the physicochemical variables that affect reaction rate and gas production. In this study, mathematical models were implemented to quantify these GHG’s emissions, with the purpose of calibrating them and to have the best parameters that represent this process and that minimize the error. In future research, this calibration can be implemented to quantify gas emissions during a longer time frame than considered in this study, and thus, to comply with the United Nations Framework Convention on Climate Change about inventory of GHG flows in each country.