1. Introducción
El proceso de división celular de cualquier célula puede llevarse a cabo siempre y cuando las condiciones del medio y la disponibilidad de nutrientes prevalezcan, en caso contrario, este proceso se detiene. Sin embargo, cuando hablamos de células cancerosas, pueden suceder eventos muy particulares1. Cuando el tumor es relativamente pequeño, la gran mayoría de células reciben nutrientes por difusión y el crecimiento es aproximadamente exponencial. Una vez el tumor aumenta su tamaño, la difusión de nutrientes deja de ser eficiente, produciendo una caída de la concentración de éstos, rezagando el crecimiento del tumor en dirección opuesta al gradiente de concentración. Cabe destacar también que a medida que el tumor crece, la eliminación de desechos se hace también más difícil 2.
Se podría entonces pensar en que eventualmente el tumor llegue a un punto de equilibrio donde no es posible su viabilidad por falta de nutrientes y por su incapacidad de eliminar los desechos celulares, desafortunadamente, este no es el caso. Al igual que otros tejidos celulares, las células tumorales exhiben el fenómeno denominado angiogénesis, el cual se caracteriza por la transición del tumor desde un estado desvascularizado y localizado a un estado vascularizado con la capacidad de proliferar e invadir tejido cercano.
En este proceso, aunque se sabe que el sistema inmune juega un papel sumamente importante, los mecanismos involucrados aún no son muy bien comprendidos, aunque se supone que la respuesta puede aparecer ante cualquier inflamación, segregando sustancias químicas citotóxicas dentro del tumor para eliminarlo 3. Desafortunadamente, la respuesta inmune puede también tener un efecto negativo, ya que puede incentivar la vascularización del tumor 4,5.
Con estas consideraciones, es de vital importancia conocer el papel que puede jugar estas interacciones sumadas a un tipo de tratamiento específico. Por tal motivo se propone un modelo matemático sencillo, que permita extraer algunas conclusiones del comportamiento dinámico del sistema.
2. Metodología
2.1 Modelo matemático
El presente modelo describe la dinámica de la interacción de células cancerosas, células del sistema inmune y la acción de un tratamiento de degradación fotocatalítica de células de cáncer.
Sean 𝑥(𝑡) y 𝑧(𝑡) la cantidad de células cancerosas y la cantidad de células de la respuesta inmune, el modelo de muerte celular se expresa como:
En trabajos previos se ha supuesto que el crecimiento tumoral puede ser descrito por modelos que consideran la ley de potencia o curvas de Gompertz 6. En este modelo se asume por simplicidad que las células tumorales crecen logísticamente en ausencia de respuesta inmune con razón de crecimiento 𝑎𝑏. Esto con base a trabajos realizados sobre crecimiento tumoral en ratones 7. Aunque no se hace una diferenciación entre células NK (Natural Killers por sus siglas en inglés) y los linfocitos T CD8, se asume que cada una de ellas puede destruir a las células cancerígenas, además que las células tumorales tienen la capacidad de activar características citotóxicas en este tipo de células. Eventualmente, las células tumorales serán destruidas después de un número de encuentros con células del sistema inmune y debido a la acción del tratamiento, que suponemos como primera aproximación de carácter exponencial con tasa de desactivación 𝑑.
Por lo general se supone que el término de interacción entre el sistema inmune y células tumorales tienen la forma de Michaelis-Menten 8 la cual describe la velocidad de reacción de muchas reacciones enzimáticas. El modelo propuesto usa una simplificación de la suposición de Kuznetsov et al. donde se sustituye la función de tipo Michaelis-Menten por una función de Lotka-Volterra. Esta suposición se fundamenta en que se piensa en las células tumorales y las del sistema inmune como dos especies que intentan sobrevivir en el mismo ecosistema permitiendo la característica principal que es lograr un efecto de saturación en el sistema 9) .Adicionalmente se incluye un término de carácter logístico para describir alteraciones o respuestas inmunológicas adicionales a las producidas por las células tumorales, que pudieran generar un nivel basal o de saturación en ausencia de cáncer con una tasa de activación 𝑒𝑓.
En el modelo, 𝑏 representan la capacidad de carga (nivel de equilibrio) del sistema en ausencia de sistema inmune y sin tratamiento, 𝑐 representa la constante de velocidad para la acción del sistema inmune y 𝑑 el efecto del tratamiento sobre las células cancerosas, 𝑓 la capacidad de carga del sistema inmune a nivel basal (ajeno a la respuesta tumoral), 𝑔 representa la constante de proporcionalidad para la activación del sistema inmune debido a la presencia de las células cancerosas y ℎ la capacidad de carga de las células cancerosas involucradas en este proceso de activación. La constante 𝑖 es la tasa de velocidad a la que mueren las células del sistema inmune a medida que luchan contra el cáncer.
A continuación, se presenta un análisis sencillo sobre casos hipotéticos, que pueden ayudar a la comprensión del modelo (1).
2.1.1 Respuesta del sistema en ausencia del sistema inmune
En ausencia de respuesta inmune 𝑧 =0 (respuesta lenta o sistema inmune debilitado):
La cual puede reescribirse como:
Sea
Entonces,
Los puntos críticos de esta ecuación son:
y cuya solución está dada por Boyce et al.10:
En ausencia de respuesta inmune, existe un punto crítico inestable (𝑥 =0) para cualquier condición inicial 𝑥≠0 y punto crítico estable, 𝑥 =𝐾.
Una capacidad de carga 𝐾>0 implica que las células tienden a un punto de equilibrio 𝐾. Si bien 𝑥 es decreciente para 𝑥0 >𝐾, es decreciente para 𝑥0 <𝐾, lo que da un indicio de que se debe buscar 𝐾 lo suficientemente pequeña.
Para que la solución sea positiva invariante, debe ser que 𝐾 >0, y de acuerdo con su definición, 𝐾= (𝑎𝑏-𝑑)/𝑎, se concluye que el único efecto del tratamiento para este caso es la reducción de la cantidad de células cancerosas.
2.1.2 Respuesta del sistema inmune en ausencia de cáncer
Un breve análisis del comportamiento del sistema inmune se puede analizar en la ausencia de células cancerosas, esto es:
Que se puede escribir de la forma (6) con una tasa intrínseca 𝑒𝑓:
En este punto resulta conveniente aclarar que la respuesta del sistema inmune no presenta esta dinámica de forma arbitraria, esta respuesta es debida a una perturbación, de otra forma, la población de células del sistema inmune se asume en cero.
De acuerdo con el modelo, el sistema inmune responde ante una perturbación llegando a una capacidad de carga 𝑓 que es la máxima concentración de células inmunes, concentración a la cual el sistema se satura y no puede responder más allá de este punto.
2.1.3 Análisis interacción cáncer - sistema inmune - tratamiento fotodinámico con nanomaterial
El modelo de la triple interacción está descrito por las ecuaciones (1), como se mostró en la sección anterior, es conveniente el análisis de los casos de respuesta del sistema en ausencia de un factor, esto permite una interpretación más clara del sistema. A partir de esto se puede concluir:
El tumor se puede representar como un sistema coevolutivo el cual tiende a una capacidad de carga 𝐾= (𝑎𝑏-𝑑)/𝑎 que puede desencadenar o no un estado metastásico y el efecto tanto del tratamiento como del sistema inmune es disminuir esta capacidad de carga y eventualmente erradicar el cáncer.
2.1.4 Efecto del sistema inmune sobre e tumor
La dinámica del tumor puede ser reescrita como:
Entonces,
Por lo tanto, aunque la tasa intrínseca de crecimiento tumoral permanece invariante, la tasa global
Se ve disminuida por efecto del sistema inmune. Esto muestra la importancia del fortalecimiento del sistema inmune en el tratamiento.
2.1.5 Efecto del tumor sobre el sistema inmune
La dinámica del sistema inmune está representada por:
Esta ecuación puede ser reescrita como
Como se puede ver en la ecuación anterior, aunque la tasa intrínseca de la respuesta inmune permanece constante, la tasa global
Ahora se ve disminuida por las interacciones de células cancerosas y células del sistema inmune, esto es, algunas células del sistema inmune mueren en el proceso de eliminación del tumor, pero esta respuesta se ve “reforzada” a medida que avanza el tratamiento y el tumor se elimina.
2.2 Análisis de estabilidad
El modelo que describe la degradación fotocatalítica de células cancerosas está dado por:
Donde 𝑥, 𝑦≥0 denotan las poblaciones de células cancerosas y de células del sistema inmune respectivamente y las tasas de crecimiento quedan expresadas por:
Las ceroclinas para este sistema quedan entonces definidas por:
Para el sistema dinámico (10) se pueden hacer las siguientes consideraciones (Hirsch et al. 11):
1. Para el sistema coevolutivo, el crecimiento de una población influye sobre la otra. Para la tasa de crecimiento 𝑀(𝑥,𝑧):
Por lo tanto, siempre que la respuesta inmune aumente, la tasa de crecimiento de células cancerosas se verá disminuida. Ahora, para la tasa de crecimiento de células del sistema inmune:
Por lo tanto, la tasa de crecimiento para la respuesta inmune aumenta para 0 <𝑥 <𝑥 y aumenta para 𝑥>𝐿, donde:
2. Si la población de células del sistema inmune es muy grande, ambas poblaciones decrecen para cierto 𝐾 >0 tal que:
Para el caso particular del modelo, la existencia de 𝐾 implica:
Como se demostrará posteriormente, 𝐾 existe por encima de la separatriz en el punto crítico más positivo tal que 𝑧 >0 determinado por la solución del sistema:
Si en este punto crítico 𝑧 >0, siempre se cumple que 𝑀(𝑥, 𝑧) ∧ 𝑁(𝑥, 𝑧)< 0. En el caso que la concentración de células cancerosas sea muy alta, existe una región tal que:
P existe por debajo de la separatriz anteriormente descrita si y solo si el punto crítico del sistema implica 𝑧 >0.
3. En ausencia de una de las especies, la otra presenta una tasa de crecimiento positiva hasta cierto valor de la población, después de esta a tasa se convierte en negativa. Por lo tanto, existen las constantes 𝛼, 𝛽>0 tal que:
Por lo tanto, para el sistema 1,
2.2.1 Análisis de estabilidad asintótica
El sistema (1) presenta los siguientes puntos fijos:
Para analizar la estabilidad local de los puntos fijos hemos encontrado la matriz jacobiana del sistema:
Se comprobó que 𝑃1 es un punto inestable, 𝑃2 es estable si y sólo si (𝑎𝑏-𝑑)/𝑐, 𝑃3 es estable si y solo si 𝑎𝑏−𝑑>0 y 𝑏(𝑔(ℎ−𝑏) −𝑖) + 𝑓𝑒+ (𝑑(𝑔(2𝑏−ℎ)+𝑖)/𝑎−(𝑑/𝑎)^2𝑔<0, 𝑃4 es estable y 𝑃5 es inestable. En la sección 3 se realizan simulaciones numéricas donde se ilustran los puntos fijos para diferentes condiciones.
3. Resultados
3.1 Análisis de plano fase para el modelo de degradación fotocatalítica de células cancerosas con interacción del sistema inmune
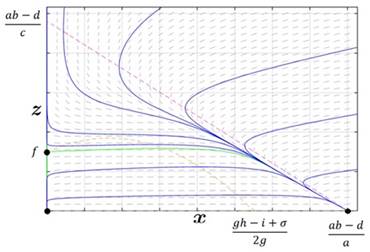
Caso 1. Las ceroclinas no se cruzan y el conjunto de puntos frontera de la ceroclina x siempre es mayor al conjunto de puntos frontera de la ceroclina z.
Este es el caso menos deseable, aunque el tratamiento inhibe el crecimiento de las células cancerosas, al pasar el tiempo, el sistema inmune se deprime hasta el punto de colapsar, el crecimiento de células cancerosas continúa hasta muy posiblemente causar la muerte del paciente tratado, la Figura 1 ilustra este caso donde las curvas azules representan diferentes estados o condiciones iniciales del sistema, la curva verde representa la separatriz del sistema,
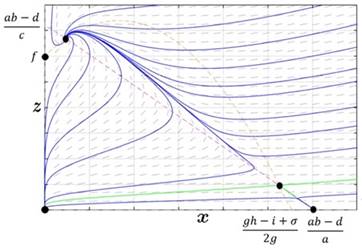
Caso 2. Los conjuntos de puntos frontera de ambas ceroclinas se intersecan en dos puntos.
En este caso, la efectividad del tratamiento depende del punto donde se dé inicio al tratamiento mismo, si el tumor ha alcanzado estados avanzados descritos por la separatriz (curva color verde Figura 2), el sistema inmune colapsa, con la posterior muerte del paciente. En un estado no tan avanzado, el tratamiento causa una mejora significativa del paciente, logrando la recuperación del sistema inmune y dejando al tumor en estado de latencia (tumor controlado).
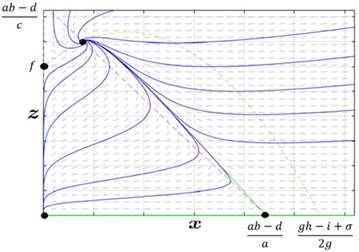
Caso 3. Las ceroclinas se intersecan exactamente en un punto con:
En este caso, el tratamiento tiene el efecto deseado de controlar el tumor, incluso en estados muy avanzados del cáncer, impidiendo el colapso del sistema inmune, aunque el tratamiento no sea capaz de lograr la erradicación completa del tumor (Figura 3).
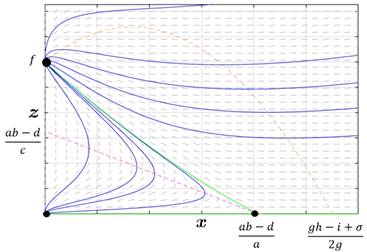
Caso 4. El conjunto de puntos frontera definidos por las ceroclinas no se intersecan, y la ceroclina x está por debajo de la ceroclina z.
Este es el caso más deseable, el tratamiento no sólo será capaz de controlar el tumor, sino que será capaz de eliminarlo en estados avanzados. Por supuesto, este estado se logra aumentando la eficacia del tratamiento, optimizando los tiempos de internalización de nanomaterial y aumentando la absorción de energía radiante. La Figura 4 ilustra este caso.
Como se pudo observar, el análisis de plano fase indica las condiciones más apropiadas para la aplicación del tratamiento. En particular, se busca que la ceroclina 𝑥 esté siempre por debajo de la ceroclina 𝑦 para lograr una erradicación por completo de las células de cáncer, o en su defecto que se toquen en un solo punto con x lo más pequeño posible si (𝑎𝑏−𝑑)/𝑐>𝑓 y con x lo más grande posible en caso contrario para garantizar un punto en el que la población de células cancerosas esté controlada.
4. Conclusiones
El modelo matemático propuesto, aunque sencillo, logra recoger varios aspectos importantes de la interacción del sistema inmune con células cancerosas expuestas a un tratamiento (Se usa como ejemplo una terapia fotodinámica experimental), indicando las posibles direcciones en las que se podría abordar el trabajo Initro e incluso Invivo del tratamiento modelado.
Notemos que, bajo las suposiciones del modelo, la naturaleza o tipo de cáncer no es una característica intrínseca del mismo, lo que da una luz sobre su posible aplicación a diversos tipos de cáncer con la apropiada interpretación de los parámetros. Se podría pensar en la aplicabilidad del modelo a combinación de tratamientos para el cáncer en el que la terapia fotodinámica podría ser un coadyuvante.
Por otro lado, se podría pensar en la aplicabilidad del modelo a enfermedades en donde se entre a competir con el sistema inmune e incluso para enfermedades autoinmunes, incluyendo los diferentes tratamientos para tales enfermedades.
Las conclusiones del modelo son claras, presentando tres escenarios posibles, erradicación de las células cancerosas, control de éstas o el debilitamiento total del sistema inmune. Por supuesto estos tres escenarios dependen de los valores de los parámetros del modelo. En la práctica, es posible que algunos de estos parámetros no sean susceptibles a modificación, pero sin duda, de ser posible la modificación de algunos (como por ejemplo la velocidad de respuesta del sistema inmune) se podría aumentar la eficacia del tratamiento, es decir, el modelo da indicios de cuál sería una posible ruta para mejorar el tratamiento en general, ya sea modificando los parámetros actuales o modificándolos con la ayuda de otros agentes externos como por ejemplo el uso de medicamentos o coadyuvantes.