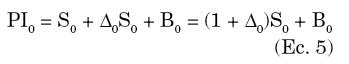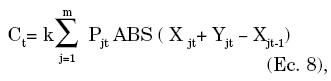Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Estudios Gerenciales
Print version ISSN 0123-5923
estud.gerenc. vol.18 no.85 Cali Oct./Dec. 2002
EVALUACIÓN DE LA APLICACIÓN DE DOS MODELOS DE VALORACIÓN DE OPCIONES A LA ADMINISTRACIÓN DE PORTAFOLIOS
JULIÁN BENAVIDES F.
Director del Departamento de Finanzas Universidad Icesi Ph. D. (C). Tulane University Ph. D. (C). Universidad Icesi
Fecha de recepción: 13-09-2002 Fecha de aceptación: 25-11-2002
SUMARIO
El artículo revisa la teoría de opciones y propone un método para la implementación del "Portfolio Insurance" basado en el modelo binomial, el cual es evaluado en oposición al modelo de Black-Scholes. Usando datos reales y simulados se encuentra que el método de Black-Scholes se desempeñamejor en condiciones "inestables"; el modelo binomial, en cambio, obtiene mejores resultados con tendencias definidas en los precios de las acciones (crecientes, decrecientes o estables durante un período extendido).
PALABRAS CLAVES
Portafolios, "Portfolio Insurance", Opciones, Modelo Binomial, Modelo Black-Scholes, Excel.
Clasificación: A
ABSTRACT
The paper reviews some aspects of the option theory and proposes a method to implement portfolio insurance based on the binomial model, which is evaluated together with a similar method based on the Black-Scholes model. Using real data and simulations, I find that Black-Scholes method does better under "unstable " conditions; the binomial model excels for clear trends in asset prices (stable, decreasing or increasing for a long period).
KEYWORDS
Portfolio insurance, Options, Binominal model, Black-scholes model, Excel.
ESTRUCTURA
- Justificación
- Fundamento teórico
- Ejemplo práctico
- Estática comparativa
- Conclusiones
JUSTIFICACIÓN
La inversión en acciones y portafolios de acciones es una práctica poco extendida entre los inversionistas colombianos. Las razones que se pueden aducir como causas de este comportamiento son las siguientes:
- Poca profundidad y baja liquidez del mercado de acciones.
- Bajos niveles de confianza en la transparencia de la información financiera y en los resultados reportados por las empresas que cotizan en bolsa. Adicionalmente el bajo valor bursátil de las acciones no parece preocupar a los accionistas controladores, por lo que el inversionista minoritario infiere altos beneficios privados de control, lo que resulta en renuencia a la inversión por temor a la expropiación de beneficios.
- Ausencia de mecanismos respaldados institucionalmente para la reducción o cobertura de riesgo financiero.
A este respecto el reporte de octubre de 2002 de la Superintendencia de Valores consigna que solamente 16 acciones (de 59 transadas y 122 inscritas) clasifican como acciones de alta bursatilidad. La acción de mayor bursatilidad (Banco de Bogotá) registra una media de 785 operaciones mensuales con un volumen de COL$ 13.107.413 por operación. El número de operaciones diarias promedio para esta acción fue de 9.24. La acción de menor bursatilidad dentro de este grupo (Cementos Paz del Río) registra menos de una operación promedio diaria. En conjunto durante el período reportado (cuatro meses anteriores al reporte) sólo se realizaron 64.67 operaciones diarias de compraventa de acciones.
Aunque puede discutirse mucho respecto a las causas fundamentales de la renuencia tradicional a la inversión en bolsa, el propósito de este artículo es revisar el concepto de cobertura de riesgo financiero y esbozar una aplicación práctica del mismo a través de una estrategia "home-made" (realizada directamente por el inversionista) que combina posiciones en acciones y posiciones en bonos de bajo riesgo. Esta técnica, conocida como "Portfolio Insurance", fue desarrollada en los años 80 por profesores de la Universidad de Berkeley y ampliamente utilizada antes de la crisis de 1987 donde el comportamiento del mercado desnudó cruelmente sus limitaciones; los conceptos, sin embargo, son esencialmente válidos y se siguen aplicando extensivamente. El artículo utiliza dos tipos de modelos para el cálculo de las posiciones del portafolio: 1). El binomial, desarrollado por Cox, Ross y Rubinstein (1979) y Rendleman & Bartter (1979); y 2). El Black-Scholes (Black, Scholes, 1973) y Merton (1973)). La valoración de opciones Put por medio del modelo binomial es revisada con cierta amplitud, lo mismo que el cálculo de las posiciones asociadas al "Portfolio Insurance" y sus costos de transacción, lo cual puede considerarse el aporte central del artículo. Aunque procedimientos similares se realizan para el modelo de Black-Scholes, éste no se describe con el mismo detalle; el lector interesado puede consultar Benninga (2000), quien desarrolla el "Portfolio Insurance" para la fórmula de Black-Scholes del cual deriva la aplicación aquí descrita para la fórmula binomial, aunque a diferencia del tipo original aquí se consideran los costos de transacción. La evaluación de los modelos se realiza sobre un portafolio de acciones inscritas en la Bolsa de Valores de Colombia e involucra los costos de transacción en los que se incurre al ajustar las posiciones o rebalancear el portafolio. Mientras que el modelo binomial es más agresivo en el ajuste de posiciones (dada su naturaleza aproximada), por lo que incurre en mayores costos de transacción, el Black-Scholes se ajusta más lentamente. Así, el binomial responde más rápido a variaciones en el mercado, por lo que esencialmente se comporta mejor cuando hay tendencias definidas tales como incrementos o decrementos continuados en el valor de las acciones (o activos subyacentes) e incluso estabilidad de los precios. El modelo de Black-Scholes se comporta mejor cuando el proceder de los activos subyacentes es irregular (alta volatilidad durante el período de "Insurance", Rubinstein 1985) y su desempeño se afecta menos cuando los costos de transacción son importantes.
Como activo libre de riesgo se utilizan TES a un año, puesto que maduran al mismo tiempo que el "Portfolio Insurance", los cuales se liquidan a las tasas de mercado. Aquí los modelos se alejan de las condiciones ideales que suponen una tasa libre de riesgo inmutable.
El principio del "Portfolio insurance" no puede ser más sencillo: ante una tendencia alcista el capital debe invertirse en acciones; si la tendencia es a la baja éste debe revertirse en activos insensibles a las condiciones del mercado, como bonos libres de riesgo o, en el peor de los casos, dinero en efectivo. Los diferentes modelos sólo difieren en la proporción en la cual estas dos inversiones deben repartirse y en la celeridad de respuesta a variaciones en el precio de los activos subyacentes.
FUNDAMENTO TEÓRICO
El concepto de cobertura que se implementa en el "Portfolio Insurance" (PI desde este momento en adelante) es una estrategia sencilla de minimización de riesgo financiero que implica la combinación de posiciones largas (lo que quiere decir comprar) en las acciones o portafolio a asegurar y en un tipo de activo derivado conocido como Opción Put; esta estrategia es conocida como Put Protectivo. Este tiene un horizonte que está definido por el tiempo de maduración o vencimiento de la opción Put.
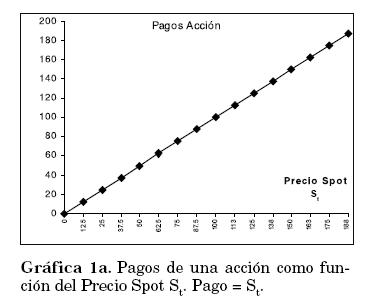
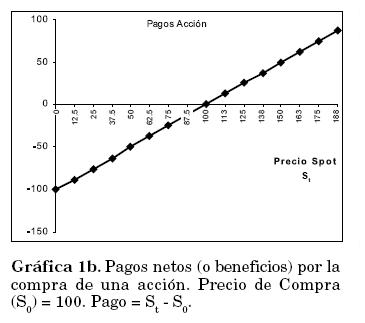
Al comprar una acción S sabemos que el pago final recibido por la acción al momento de venderla (liquidar la posición) corresponde al precio spot St (Pago = St ). La Gráfica 1a nos muestra este comportamiento. Para calcular el pago neto se debe restar el costo inicial de la acción S0. El pago neto se expresa como St - S0. La gráfica 1b representa estos beneficios.
Antes de describir el comportamiento de una Opción Put procedemos a definirla. Una Opción Put es el derecho, mas no la obligación, de venta de un activo (en este caso una acción o portafolio de acciones) a un precio determinado, conocido como precio de ejercicio X, en una fecha futura determinada conocida como fecha de vencimiento o de maduración. El tiempo hasta la expiración (o vencimiento) de la opción se denomina T.
Cuando la opción puede ejercerse en cualquier momento entre su emisión y expiración se conoce como una opción tipo americano, en caso contrario la opción se denomina tipo europeo. Los pagos recibidos al ejercer la opción se observan en la Gráfica 2a.
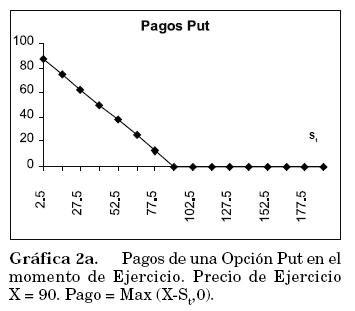
Cuando el precio de ejercicio es superior al precio spot de la acción (X>St), el propietario de la opción la ejerce, pues puede vender la acción S a un valor mayor al del mercado. Su utilidad es entonces St-X. Cuando X < St el propietario no ejerce la opción pues puede vender la acción a un precio mayor que el pactado en la opción; su utilidad en este caso es 0. En ambos casos debe restarse la prima pagada por la compra de la opción si se quieren obtener los pagos netos de la operación (Gráfica 2b).
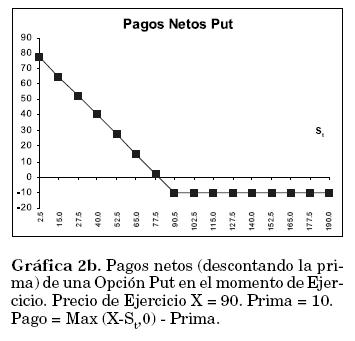
Una función que describe este comportamiento es Máximo (X - St,0).
La racionalidad que justifica la compra de una opción como la descrita anteriormente estriba en que se elimina la posibilidad de pérdidas más allá de un nivel pre-establecido por el precio de ejercicio X.
Un ejemplo sencillo clarifica el concepto. Supóngase que se desea comprar una acción S cuyo precio actual es de COL$ 100. También se quiere eliminar la posibilidad de pérdidas a un 10%, pero se desea conservar la posibilidad de ganancia que implica la valorización de la acción.
La limitación de las pérdidas implica que se desea que en el momento de liquidar posiciones se pueda vender la acción S al menos por COL$ 90. Esto se consigue comprando una Opción Put con precio de ejercicio X = COL$ 90.
El análisis del resultado puede realizarse definiendo dos rangos (1: St < X y 2: St >X):

La combinación de las dos posiciones, la compra de la acción y del put, se muestra en la Gráfica 3.
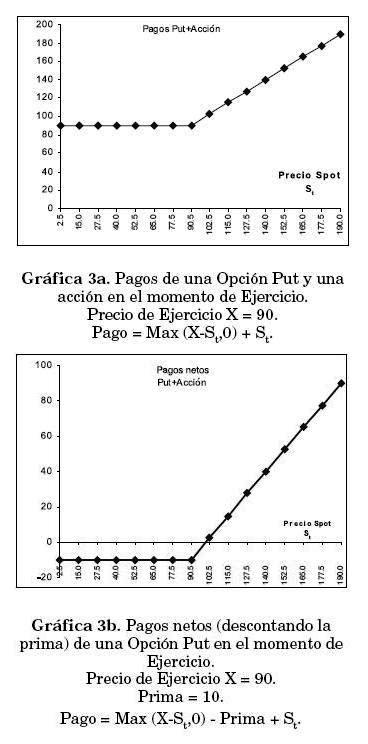
La posición del "Portfolio Insurance" es entonces S+P (Put Protectivo), donde S es la acción y P es un Put sobre una acción S. La erogación inicial es S0 + P0.
VALORACIÓN DE OPCIONES CON LA FÓRMULA DE BLACKSCHOLES
Un método muy utilizado para la valoración de opciones es la aplicación de la fórmula de Black-Scholes (Black y Scholes 1973, Merton 1973). Esta fórmula, cuyo desarrollo le mereció a sus autores un premio Nobel, utiliza el principio de no arbitraje para encontrar el valor de una opción tipo Europeo, con base en cinco parámetros de fácil estimación:
1. S0: El valor de la acción o activo subyacente en el momento de emitir la opción.
2. X: El precio de ejercicio de la opción.
3. T: El tiempo hasta la expiración o madurez de la opción.
4. r: La tasa de interés libre de riesgo.
5. σ: La volatilidad del activo subyacente. La fórmula derivada por Black-Scholes para un Put es:
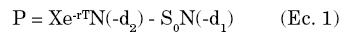
Donde N(.) es la distribución normal acumulada y d1 y d2 vienen dados por los siguientes términos:
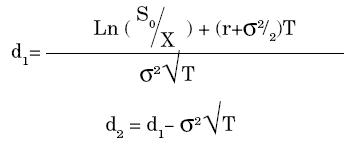
El supuesto fundamental de la fórmula de Black-Scholes es que los precios del activo subyacente están determinados por un proceso continuo tipo lognormal donde
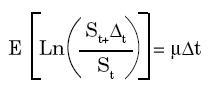
y
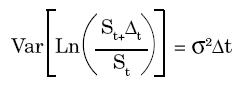
Otra alternativa para calcular el PI es la valoración binomial, mucho más intuitiva y directa. La teoría de la valoración binomial fue desarrollada por Rendleman & Bartter (1979) y Cox, Ross and Rubinstein (1979).
Describiremos este método en detalle puesto que su aplicación es la base de la metodología que aquí se desarrolla.
VALORACIÓN DE UNA OPCIÓN PUT
MÉTODO BINOMIAL (DOS PERÍODOS)
Los supuestos del modelo son:
- Existen dos períodos: el inicial, donde se suscribe la opción, y el final, donde la opción expira.1 El tiempo transcurrido entre estos períodos es T.
- El activo subyacente S, cuyo valor actual es S0, sólo puede tomar dos valores futuros (lo que es equivalente a decir que el futuro sólo tiene dos estados: U y D): SU o SD. Podemos expresar SU1 = S0U y SD1 = S0d. Los factores u y d multiplican al valor anterior S0 ya conocido.
- Se cumple que u > r > d.2
- Existe un bono cero cupón o de descuento puro sin riesgo; la tasa libre de riesgo se denomina r. Esta tasa se compone continuamente, lo que implica que el valor futuro de un bono con valor de B0 en el siguiente período es igual a B0Exp(rT), independiente de si el estado es u o d. La tasa normalmente se expresa en términos anuales, por lo que si el tiempo transcurrido entre el período 0 y el 1 es un año, el valor de T es igual a 1. Si el horizonte es menor, T corresponde a la fracción anual o porcentaje transcurrido. (Si el tiempo hasta la expiración es de cinco meses, T = 5/12).
Con el principio de no arbitraje dos activos que tengan pagos futuros idénticos deben tener el mismo precio hoy. El método replica los pagos de la Opción Put (en realidad el método aplica para cualquier derivativo) en términos de activos cuyo precios, actual y futuro, en cada estado, son conocidos.
Sean VU1 y VD1 los pagos futuros en cada estado de la opción Put, que corresponden (en el caso de un Put) a:
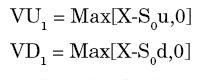
Sean Δ y B el número de unidades del activo subyacente y del bono libre de riesgo que componen el portafolio respectivamente. Es importante notar que el valor actual de cada bono es igual a 1. Para cada estado se debe cumplir que:
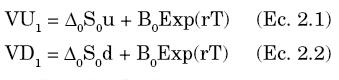
Este es un sistema de dos ecuaciones con dos incógnitas: los valores de Δ0 y B0. Despejamos las incógnitas y encontramos que
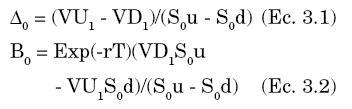
El valor hoy de la Opción Put corresponde al valor de la inversión en el activo subyacente Δ0S0 más el valor de la inversión en el bono libre de riesgo B0 (recuerde que el valor actual del bono libre de riesgo es 1, por lo que B0 corresponde tanto al número de bonos requeridos como al valor de la inversión en bonos).
Sea P0 el valor del Put en el momento 0, según los supuestos previos se tiene que
"PORTFOLIO INSURANCE"
Como se definió previamente la posición del put protectivo es S0 + P0. Si reemplazamos el valor de P0 con la ecuación 4, tenemos:
La ecuación 5 nos permite sintetizar el put protectivo. Pero a diferencia de un put protectivo real, donde se compran acciones y puts en el período 0 y las posiciones no se ajustan en ningún momento (una estrategia estática), el PI es una estrategia dinámica donde las posiciones se ajustan con una frecuencia definida por el inversionista (o su asesor). La razón de este ajuste es la naturaleza sintética del PI, dado que en realidad no se dispone de un put sino de un portafolio réplica que duplica los pagos del put. Esto puede observarse en el momento de expiración de la estrategia. En caso de que St > X, el put protectivo implica que todo el portafolio está representado en acciones (la opción put no se ejerce y las acciones se venden a precio de mercado St o se conservan), ya que el PI replica estos pagos también debe estar representado totalmente en acciones. Si retrocedemos al momento de iniciar el PI normalmente se tienen posiciones en acciones y bonos, por lo que debe disponerse de un medio para ajustar las posiciones. Para que esto sea posible es necesario definir la frecuencia (el número de veces) de ajuste en las posiciones. Tal decisión resulta de sopesar dos factores: 1). La exactitud con la que se quiere replicar el put protectivo, y 2). Los costos de transacción. El primero permite un seguimiento fiel del put protectivo (idealmente las posiciones deberían ajustarse continuamente), mientras que el segundo nos devuelve al mundo real pues reduce el rendimiento cada vez que se compran/venden acciones o bonos. Evaluaremos esta decisión cuando implementemos el PI en condiciones reales.
Una vez definida la frecuencia de ajuste se procede a recalcular Δ y B el número de veces requerido y se transan los activos de tal forma que se dupliquen los pagos del put protectivo.
El procedimiento se delinea a continuación:
Sabemos por la ecuación 5 que los porcentajes de inversión en la acción S (activo subyacente) y en los bonos sin riesgo definidos por el put protectivo son iguales a:
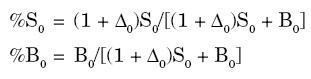
Si K0 representa el presupuesto de inversión disponible, el monto invertido en acciones y en bonos es
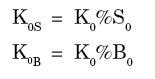
Debemos ahora determinar el número de unidades del activo subyacente S a comprar.3

El número de bonos se define directamente puesto que se supone que el precio de cada bono es 1. Como ya se dijo, el éxito del portafolio réplica estriba en duplicar lo más fidedignamente posible los pagos del put protectivo. Establecer los montos iniciales de la inversión en la acción S o activo subyacente y los bonos no garantiza una proporción adecuada en todo el horizonte de vida (hasta la fecha de expiración o fecha donde el inversionista liquida sus posiciones). Dado el comportamiento aleatorio de los precios del activo subyacente, se requiere ajustar las posiciones con una frecuencia determinada por el inversionista. En la vida real es costoso liquidar posiciones, por lo que un seguimiento perfecto no es posible y el inversionista debe elegir una frecuencia de ajuste que le brinde la seguridad adecuada sin elevar demasiado los costos de transacción.
Por ejemplo: sea la fecha de liquidación 1 año (T=1); supongamos que el inversionista se siente razonablemente seguro si rebalancea su portafolio mensualmente (n = 12).4
Con estas condiciones t = T/N = 1/12. Es claro entonces que los cálculos anteriores deben repetirse once veces para ajustar de manera adecuada las proporciones.
Al momento de realizar el primer rebalanceo el precio del activo subyacente es S1, por lo que lo obtenido al cabo de un mes corresponde a
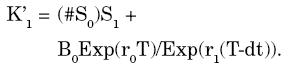
Donde el primer término designa al valor que toma en el período 1 la inversión en acciones al multiplicar el número de acciones que se compró en el período 0 por su precio actual y el segundo término al valor de los bonos habiendo transcurrido un período desde su compra, en el supuesto de cambios en la tasa de interés.
Conocido el valor real del activo subyacente S1 podemos calcular los correspondientes SU2 y SD2, y los valores del Put VU2 y VD2. Valores hipotéticos que permiten calcular el portafolio de réplica.
El ciclo requiere que ahora se calculen Δ1 y B1, lo que permite hallar %S1 y %B1. Multiplicando %S1 por K1 hallamos el monto de la inversión en el activo subyacente, y si dividimos este valor por S1 encontramos #S1 el número de unidades del activo subyacente que componen el portafolio en el período 1.
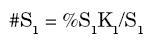
El ciclo se reanuda y se repite hasta que se alcanza el momento de expiración del put. Es necesario en cada período ajustar el tiempo al vencimiento para el bono.5
EJEMPLO PRÁCTICO
Evaluaremos el resultado del PI en un portafolio de acciones correspondiente a acciones de alta bursatilidad de la Bolsa de Valores de Colombia (Tabla 1).
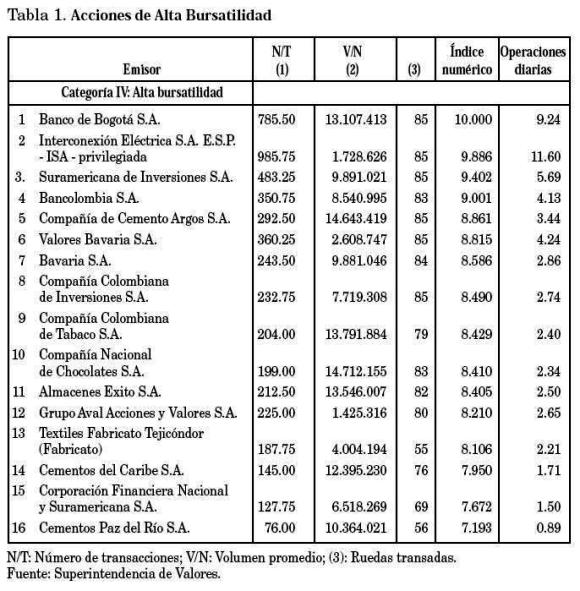
El portafolio está conformado por cinco acciones de alta bursatilidad que se transaron al menos desde el 1o. de enero de 1998: Cia. Nacional de Chocolates, Bavaria, Banco de Bogotá, Cementos Argos y Suramericana.
Es necesario encontrar la volatilidad anual (σP) del portafolio para estimar los valores de u y d (Ver nota de pie de página No. 2).
CÁLCULO VOLATILIDAD DEL PORTAFOLIO
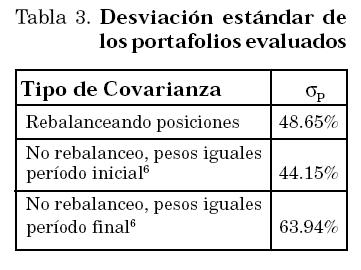
Este es un procedimiento estándar en finanzas que depende de la matriz varianza-covarianza del portafolio (Tabla 2). Sin embargo, los cálculos que se realizan implican implícitamente un rebalanceo del portafolio que mantenga los pesos relativos de las diferentes acciones constantes. Alternativamente podemos hallar σP para un portafolio donde no se rebalanceen las posiciones. Puesto que ambos métodos implican liquidación de posiciones exploraremos empíricamente cuál produce mejores resultados.

La matriz varianza-covarianza anualizada sobre los retornos mensuales entre 1o. de enero de 1998 hasta 1o. de enero 2001 (cuatro años), utiliza las siguientes fórmulas:

La volatilidad de un portafolio compuesto por acciones es igual a

Donde wi y wj son los pesos de las acciones i y j respectivamente y σij es la covarianza entre la acción i y la acción j, cuando i = j el término se refiere a la varianza.
Los resultados se reportan en la Tabla 2, para un peso relativo de 20% para cada acción (Portafolio "Equally weighted"). Los datos corresponden a los precios reportados por la Superintendencia de Valores al inicio de cada mes para las acciones que conforman el portafolio. El año 2002 no se incluye puesto que se utilizará para evaluar los resultados de la aplicación de las dos metodologías empleadas.
ACTIVO Y TASA DE INTERÉS LIBRES DE RIESGO
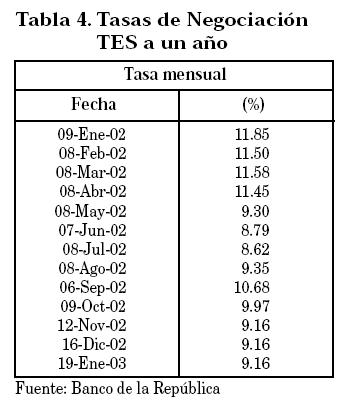
El activo libre de riesgo considerado para la estructuración de las posiciones del PI es el bono de tesorería (TES) con vencimiento a un año. Como ya se mencionó, el modelo de valoración prevé una tasa libre de riesgo constante durante todo el período de vida del PI; este no es el caso cuando se involucran variables reales. Incluso el término "libre de riesgo" es inexacto, como lo demostró la crisis de los TES de mediados de 2001.
En la Tabla 4 se consignan las diferentes tasas a las cuales se negociaron estos títulos, las cuales se requieren para el cálculo de la rentabilidad de la porción del capital invertida en este activo. Se supone que las tasas no varían (un supuesto fuerte) entre las fechas de negociación reportadas y las fechas de ajuste del portafolio.
CONSTRUCCIÓN DEL PORTAFOLIO
Para evaluar el desempeño de ambos modelos se construyeron o simularon diferentes tipos de portafolio, cuyas características se definen a continuación:
- Portafolio "Equally weighted" (EW) con rebalanceo continuo, en el cual la inversión en las diferentes acciones se ajusta mensualmente para mantener el mismo peso relativo.
- Portafolio "Equally weighted" (EW) sin rebalanceo, en el cual la inversión en las diferentes acciones no se ajusta mensualmente y el término "Equally weighted" se refiere al peso relativo en la fecha en que el portafolio se conforma inicialmente.
- Portafolio compuesto por una sola acción.
Para los portafolios EW se utilizaron datos reales del comportamiento de las acciones en el año 2002 (valores de fin de mes) y datos simulados para ilustrar los resultados de los dos modelos en mercados al alza, estables, a la baja y aleatorios (siguiendo una distribución lognormal). Las diferentes construcciones y resultados se ilustran en las gráficas 4 y 5. La Gráfica 4 presenta el comportamiento de las acciones del portafolio durante el período estudiado; la tendencia es claramente alcista, con un rendimiento mayor a 40% para todas las acciones. Cada serie corresponde a 12 datos, que comprenden un año de negociación y la duración de la estrategia.
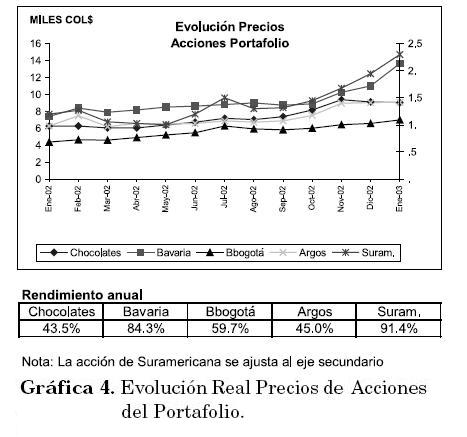
La Gráfica 5 muestra la evolución del valor de cada portafolio (real y simulado), las características de las simulaciones se presentan en la Tabla 5.
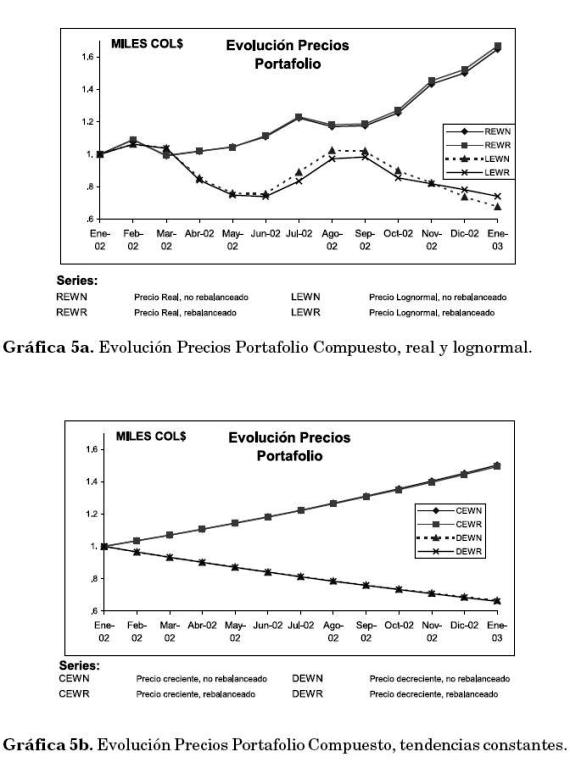
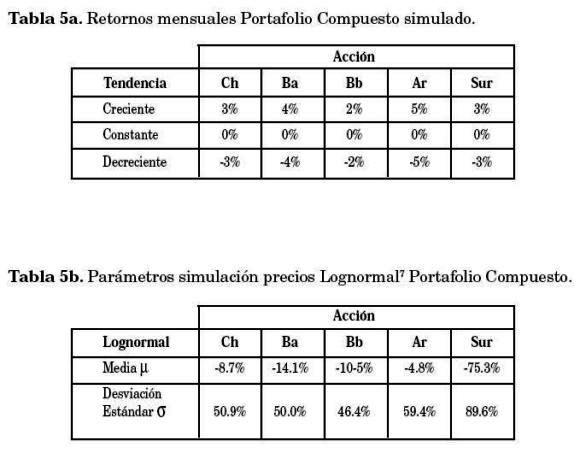
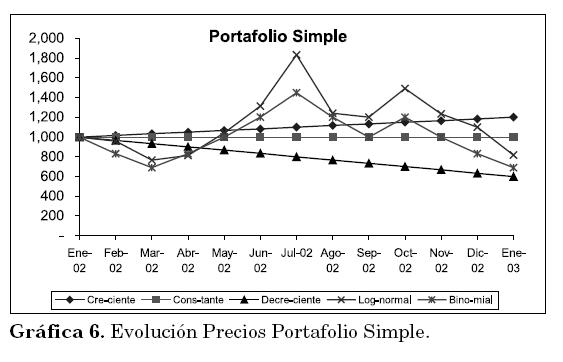
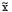 (dt)1/2], donde
(dt)1/2], donde 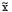 es una variable aleatoria con N[0,1], dt=1/12 (Benninga 2000).
es una variable aleatoria con N[0,1], dt=1/12 (Benninga 2000).Con respecto al comportamiento simulado de los portafolios simples éstos siguen los parámetros establecidos en la Tabla 6, los cuales se visualizan en la Gráfica 6.

EVALUACIÓN ESTRATEGIAS DE "PORTFOLIO INSURANCE"
CONSTRUCCIÓN HOJA DE CÁLCULO
El modelo de evaluación implementado consta básicamente de los cálculos referentes al PI y de los referentes a los costos de transacción, para ambos modelos. Adicionalmente se incluyó un área para la simulación de variaciones de precios de los portafolios.
La Tabla 7 presenta una síntesis del modelo binomial, que incluye las explicaciones pertinentes que clarifican su funcionalidad (El modelo completo puede solicitarse al autor).
La evaluación del desempeño de las dos estrategias se realiza mediante la siguiente fórmula:
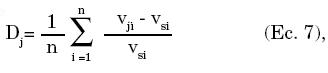
donde j: binomial, black-scholes; vji es el valor del portafolio en el período i con la estrategia j y vsi es el valor del activo subyacente en el período i. Tal medida permite evaluar el desempeño de cada estrategia y compararla con su contraparte.
La principal dificultad de la evaluación de los modelos estriba en el cálculo de los costos de transacción del portafolio EW con rebalanceo. De período a período las posiciones se deben ajustar: (1) por el cambio de los precios relativos entre las acciones; y (2) por las compras o ventas que la estrategia misma recomienda. Luego el costo de transacción por período es:
donde Xjt (Xjt-1)representa el número de acciones que se requieren para mantener el portafolio EW en el período t (t-1) de la empresa j y Yjt el número de acciones requeridas por el ajuste de posiciones del PI. El término entre paréntesis representa el cambio neto en el número de acciones por empresa, y la función ABS significa valor absoluto puesto que este costo se paga ya sea que se vendan o se compren acciones. El costo porcentual de la transacción es k, y Pjt es el precio de la acción j en el período t.
Cuando el portafolio es EW pero no se rebalancea, la ecuación 8 se reduce a

El caso para simulaciones de un solo activo (m=1) se simplifica a Ct = kABS(PtYt) = kABS (ΔSt), donde ΔSt es el cambio en la posición del activo subyacente s para el período t.
Para el ajuste de la posición en el activo libre de riesgo la fórmula en todos los casos es
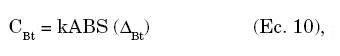
donde ΔBt es el cambio en la posición del activo libre de riesgo B para el período t.
ESTÁTICA COMPARATIVA
En esta sección se consignan los resultados empíricos de los modelos examinados.
El desempeño de cada estrategia puede observarse para diferentes portafolios y tendencias en el precio de las acciones en la Gráfica 6. Los resultados de los diferentes comportamientos mostrados y de resultados para portafolios compuestos de una sola acción se reportan en la Tabla 8.
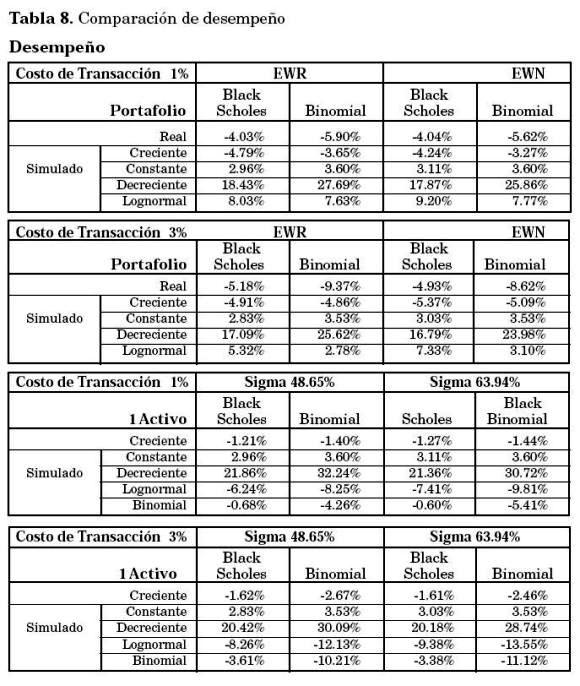
En primer lugar se evalúa la bondad de la estrategia de PI, cualquiera que sea el método empleado para implementarla. Cuando los precios del activo subyacente son estables o decrecen, la estrategia PI reporta mejores resultados que el activo subyacente; este es precisamente el concepto de seguro. Cuando la tendencia es creciente el valor del activo subyacente excede al valor de la estrategia PI (este es también el caso de los datos reales, puesto que los precios de las acciones mostraron un comportamiento creciente durante todo el año 2002), debido a los costos de transacción y a los menores retornos en la inversión en bonos; sin embargo, excepto para costos de transacción muy altos (>3%) la diferencia no excede al 10%. Con precios oscilantes (Simulación Lognormal) la estrategia PI excede el valor del activo subyacente, lo cual es una prueba tangible de la bondad de estos métodos.
Los resultados muestran que en general el modelo de Black-Scholes se desempeña mejor que el binomial en condiciones cambiantes. En particular para el caso de portafolios compuestos el modelo Black-Scholes domina en las condiciones reales del año 2001 y en la simulación lognormal; sin embargo, el modelo binomial lo excede cuando la tendencia de precios es decreciente, lo cual es una característica nada despreciable, estable o definitivamente creciente. Si esto se asocia con las condiciones del mercado se debería escoger el modelo binomial si las perspectivas son muy positivas, muy negativas o si los precios son muy estables. Lo mismo se aplica para cuando el portafolio está compuesto por una sola acción. Es claro que este comportamiento se debe a que el modelo binomial, por ser más impreciso en la valoración del put, es más agresivo en ajustar sus posiciones.
Ninguna de las condiciones cambia si se incrementan los costos de transacción; como sería de esperar, a mayores costos de transacción peor es el desempeño del PI.
En cuanto a los resultados de usar portafolios rebalanceados periódicamente (EWR) o no (EWN), los datos no son concluyentes. Con costos de transacción del 1%, el modelo Black- Scholes reporta mejores resultados para los datos reales (relativamente crecientes) y la simulación decreciente para el portafolio EWR. Al incrementar los costos de transacción al 3% los resultados cambian un poco; en el caso de los datos reales, el costo de rebalancear el portafolio parece ser demasiado alto y el portafolio EWN se comporta mejor. Sin embargo, para la simulación con datos crecientes el resultado es el opuesto, el portafolio EWR es superior al EWN con costos de transacción de 3%.
Para el modelo binario y costos de transacción del 1%, el portafolio EWR se comporta mejor que el EWN solamente en caso de una tendencia decreciente en los precios. Al incrementar los costos al 3%, el portafolio EWR supera al EWN en los casos de las tendencias sostenidas creciente, constante y decreciente.
Solamente dos tipos de datos producen el mismo resultado tanto para el modelo binomial como el de Black- Scholes, en ambos niveles de costos: El portafolio EWR lo hace mejor para la tendencia decreciente y el portafolio EWN lo hace mejor para la simulación lognormal. En el primer caso la razón parece ser la mayor posibilidad de ajuste que brinda el EWR, que se revierte para el segundo caso.
El último elemento de análisis es la volatilidad de la acción, lo cual aplica al portafolio simple. Vale recordar que este es el elemento más problemático al utilizar los modelos aquí descritos, puesto que esta volatilidad cambia en cada momento del tiempo. Con bajos costos de transacción el modelo binomial se comporta mejor cuando la volatilidad histórica es baja. Esto no se generaliza al incrementarse los costos de transacción, aquí los resultados son mejores con tendencias crecientes o constantes. El modelo Black-Scholes tampoco es estable al incrementarse los costos de transacción, aunque los resultados con baja volatilidad dominan en los casos de tendencias creciente y decreciente y simulaciones lognormal; el resultado se revierte para la tendencia creciente al incrementar los costos de transacción al 3%.
CONCLUSIONES
Este artículo revisa parcialmente algunos de los principales resultados de la teoría de opciones y los aplica a la administración de portafolios. Aunque este es un caso frecuente en la literatura, la comparación de los resultados empíricos de dos modelos de "Portfolio Insurance" no lo son. La metodología implementada pretende ser rigurosa al incluir: 1). Los costos de transacción y su efecto en la aplicabilidad de las técnicas descritas; y 2). Tasas de interés variables y de mercado. Aunque la validez de los resultados puede comprometerse por la inclusión de una tasa libre de riesgo variable, este es un riesgo que se acepta para tratar de acercar los resultados a la vida real. Trabajos posteriores pueden incluir un tratamiento más riguroso de la tasa de interés, así como series de datos más extensas y medidas de desempeño mejor elaboradas. Es posible también encontrar formulaciones sobre estos resultados que puedan establecer generalizaciones sobre la bondad de los métodos aquí descritos e implementados.
Finalmente es importante resaltar las limitaciones de esta técnica. El supuesto fundamental para que el PI funcione es la posibilidad de negociar sin limitaciones los activos involucrados, tanto las acciones como el bono libre de riesgo. Esto requiere la existencia permanente de un mercado tanto para la compra como para la venta. En condiciones normales este supuesto es verdadero, pero en condiciones de crisis es posible que muchos vendedores salgan al mercado y no existan compradores, lo que tiende a deprimir los precios e incrementar las pérdidas. Esto fue lo que sucedió en 1987, cuando en EE. UU. esta técnica tuvo su apogeo. A pesar de esto, el concepto sigue siendo válido y una herramienta práctica cuando no existen, como sucede en Colombia, mercados de cobertura de riesgo financiero.
En cualquier caso se espera que esta revisión de métodos computacionales asequibles sea de utilidad a los inversionistas potenciales o reales de portafolio y permita un acercamiento a las técnicas de administración de portafolios.
NOTAS AL PIE DE PÁGINA
1. El modelo puede extenderse a varios períodos. Si T es el tiempo hasta la expiración, cada período t tiene una duración de T/n. Cuando n tiende a infinito, en ciertas condiciones (ver la siguiente nota de pie de página), la fórmula binomial converge a la fórmula de Black-Scholes.
2. Si u = Exp(σt1/2) y d = Exp(-σt1/2), donde σ es la volatilidad del activo subyacente y t el tiempo asignado para cada período, la fórmula binomial converge a la de Black-Scholes.
3. Este cálculo también aplica cuando el activo subyacente es un portafolio.
4. En este caso no extendemos el modelo binomial a varios períodos, lo que estamos haciendo es recalcular el modelo de dos períodos con una frecuencia definida por n.
BIBLIOGRAFÍA
Banco de la República. Estadísticas Títulos de Tesorería. http://www.banrep.gov.co (Enero 2003). [ Links ]
Benninga, Simon. Financial Modeling. Cambridge, MA: The MIT Press (2nd edition, 2000). [ Links ]
Black, Fischer y Myron Scholes. The pricing of Options and Corporate Liabilities. The Journal of Political Economy 81(3), 1973. [ Links ]
John C. Cox, Stephen Ross y Mark Rubinstein. "Option Pricing: A Simplified Approach". Journal of Financial Economics, 7(3), (September 1979). [ Links ]
Merton, Robert C.. "Theory of Rational Option Pricing". Bell Journal of Economics and Management Science 4(1), (Spring, 1973). [ Links ]
Rendleman, Richard J. y Brit J. Bartter. "Two-State Option Pricing". Journal of Finance, 34(5), 1979. [ Links ]
Rubinstein, Mark. "Alternative Paths to Portfolio Insurance". Financial Analysts Journal , 41(4), (1985). [ Links ]
Superintendencia de valores. Información Acciones. http://www.supervalores.gov.co (Enero 2003). [ Links ]