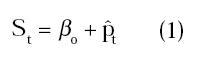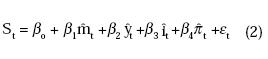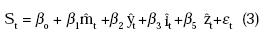Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Estudios Gerenciales
Print version ISSN 0123-5923
estud.gerenc. vol.21 no.96 Cali July/Sept. 2005
EVALUACIÓN DE PRONÓSTICOS PARA LA TASA DE CAMBIO EN COLOMBIA
CARLOS IGNACIO PATIÑO, JULIO CÉSAR ALONSO CIFUENTES1
1Economista, Universidad del Valle. Maestría en Economía, Iowa State University. Ph.D., Iowa State University. Profesor de tiempo completo del Departamento de Economía de la Universidad Icesi. Profesor-Investigador. jcalonso@icesi.edu.co
Fecha de recepción: 08-02-2005 Fecha de aceptación: 15-06-2005
RESUMEN
Este documento analiza la capacidad de predicción dentro de la muestra (in sample) de cuatro modelos de tasa de cambio nominal para Colombia durante el período 1984:I - 2004:I. Se emplean los enfoques monetarios de precios rígidos (Dornbusch (1976) - Frankel (1979)) y el de Balassa - Samuelson, que le da un papel central a los diferenciales de productividad. Adicionalmente se analiza la condición de la paridad del poder adquisitivo (PPP). La capacidad predictiva de dichos modelos es comparada con un camino aleatorio. Las medidas empleadas para evaluar los pronósticos son la raíz cuadrática del error de pronóstico (rms) y el coeficiente de desigualdad de Theil. Se observa que a pesar de tener una gran capacidad de predicción, ningún modelo supera al camino aleatorio. Dicha conclusión corrobora los resultados presentados en la literatura sobre los determinantes de la tasa de cambio nominal.
PALABRAS CLAVE
Tasa de cambio, modelos econométricos, Colombia, pronósticos.
Clasificación: JEL: F310, C220, C530
ABSTRACT
This paper analyses the in sample forecasting performance of four models for the Colombian exchange rate during the period 1984:I - 2004:I. The sticky price monetary (Dornbusch (1976) - Frankel (1979)) and the Balassa - Samuelson (which gives a central role to the productivity differentials) approaches are used. Additionally, the Purchasing Power Parity condition (PPP) is analyzed. The forecasting ability of these models is compared using a random walk as a benchmark model. The measures used to evaluate the forecasts are the root mean square error (rms) and inequality coefficient of Theil. It is found that despite the great ability to predict, no model overcomes the random walk. This conclusion strengthens the previous results in the exchange rate determinants literature.
INTRODUCCIÓN
Los movimientos de la tasa de cambio nominal en Colombia durante los últimos años y en especial durante el 2004, han dejado desconcertados a analistas, hacedores de política y actores del mercado de divisas. La baja capacidad de previsión de los movimientos de la divisa parece revelar una gran necesidad de más investigación en el tema. Pero este resultado no es único de nuestro país, a principios de los años ochenta Meese y Rogoff (Meese y Rogoff (1983a) y Meese y Rogoff (1983b)) demostraron el bajo poder de los modelos teóricos disponibles en la época para explicar de forma sistemática el comportamiento de las principales tasas de cambio nominal, y naturalmente el bajo poder de predicción de los modelos. En primera instancia estos resultados parecieron alocados, pero diferentes investigadores los corroboraron (Frenkel y Roose (1995) presentan una recopilación de los principales intentos, todos fallidos, de desvirtuar los resultados de Meese y Rogoff). Estos resultados frustrantes para los investigadores de la tasa de cambio, provocaron la aparición de diferentes modelos en la década de los años noventa, que aún no proveen un gran adelanto en entender los movimientos de las principales monedas del mundo (Por ejemplo Cheung, Chinn y García (2003)).
Este documento analiza diferentes modelos teóricos para encontrar los determinantes fundamentales de la tasa de cambio nominal en Colombia, al mismo tiempo que examina sus capacidades para predecir el comportamiento de la tasa de cambio (dentro de la muestra) durante el período 1984:I - 2004:I. A lo largo del período analizado se han observado diferentes regímenes cambiarios en Colombia. Hasta 1991 se empleó el sistema de minidevaluaciones (crawling peg) adoptado en 1967. De acuerdo con Cárdenas (1997), desde 1991 hasta enero de 1994 se adoptó un segundo régimen que permitió una mayor flexibilidad del tipo de cambio gracias a una banda implícita. Como lo menciona Cárdenas (1997), a partir del 24 de enero de 1994 se adoptó un sistema de bandas móviles (crawling bands) que estuvo vigente hasta 1999, cuando se adoptó un sistema de libre flotación. Dichas modificaciones al régimen cambiario han originado una mayor volatilidad a la tasa de cambio a partir de 1994 (Ver Gráfico 1).
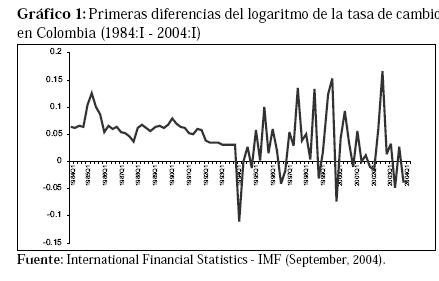
Los recientes movimientos de la tasa de cambio nominal no parecen poder ser explicados por los modelos convencionales adoptados en la década de 1970. En la literatura sobre los determinantes fundamentales de la tasa de cambio nominal se encuentran diversos enfoques y aproximaciones. Por ejemplo, Cárdenas (1997) evalúa la validez empírica de los modelos basados en el enfoque moderno de activos. Según este enfoque, la tasa de cambio nominal fluctúa con el fin de equilibrar la demanda externa de activos nacionales. Para tal propósito, Cárdenas (1997) adopta el modelo monetario simple con precios flexibles, el modelo monetario con precios rígidos y el modelo de balance de portafolio, con el fin de evaluar la consistencia teórica de dichos modelos. En este trabajo, la capacidad predictiva de los modelos empleados no es evaluada. Por otro lado, Meese y Rogoff (1983a) analizan la capacidad predictiva fuera de muestra de varios modelos estructurales de tasa de cambio nominal. Igualmente, analizan los modelos monetarios de precios flexibles y precios rígidos encontrando que dichos modelos estructurales no se desempeñan bien a pesar de basar sus predicciones en los valores actuales de las variables explicativas. Meese y Rogoff (1983a) concluyen que un camino aleatorio (random walk) tiene mayor capacidad predictiva que los modelos estructurales analizados.
Recientemente, Cheung, Chinn y García (2003) argumentan que las variaciones del dólar y del euro no pueden ser explicadas por los modelos tradicionales propuestos durante la década de 1970. Señalan que los recientes movimientos de las tasas de cambio sólo pueden ser explicados por resultados empíricos y teóricos relacionados con la correlación entre variables como las posiciones de los activos externos y la tasa de cambio real, así como los diferenciales de productividad. Cheung et al. (2003) señalan que estos nuevos modelos (propuestos en la década de 1990) no han sido evaluados sistemáticamente en cuanto a su capacidad predictiva fuera de muestra. Teniendo en cuenta lo anterior, los autores evalúan un conjunto de modelos propuestos en la década de 1990. Para efectos de la medición de la capacidad predictiva, varias medidas son empleadas: Error Medio al Cuadrado (MSE), cambio en la dirección y la prueba de consistencia propuesta por Cheung y Chinn (1998). Sus resultados señalan que según la medida del Error Medio al Cuadrado (MSE), ningún modelo logra superar a un camino aleatorio. Sin embargo, teniendo en cuenta el criterio del cambio en la dirección, algunos modelos estructurales lo consiguen. Finalmente, de acuerdo con el criterio de consistencia, encuentran que las predicciones están cointegradas con el valor verdadero de los tipos de cambio.
Basado en lo anterior, este documento analiza tres de las especificaciones propuestas por Cheung et al. (2003), para el caso de la tasa de cambio nominal en Colombia, evaluando sus capacidades de pronóstico. Para esto, se analiza la capacidad predictiva de dichos modelos empleando criterios de evaluación como el error de simulación rms (raíz cuadrática media) y el coeficiente de desigualdad de Theil. Para efectos de la comparación se emplea un camino aleatorio y la condición de paridad del poder adquisitivo (PPP).
cinco secciones, además de esta introducción. En la segunda sección se presentan los modelos teóricos que son evaluados. En la tercera se estudian las propiedades de las series empleadas en el análisis (raíces unitarias). En la cuarta se determina si existe o no una relación de largo plazo (cointegración) entre las variables de cada especificación. En la quinta se presentan los modelos estimados y se analiza su capacidad predictiva. Finalmente, en la sexta se comentan los resultados obtenidos en los pronósticos dentro de la muestra.
MODELOS TEÓRICOS A EVALUAR
Existe un buen número de modelos teóricos que han sido empleados para modelar el comportamiento de la tasa de cambio nominal (Chinn (1997), Dornbusch (1976), Cárdenas (1997), Owen (2001), Rosenberg (2000) y Meese y Rogoff (1983) entre otros). Para analizar el caso colombiano se adoptan los modelos propuestos por Cheung et al (2003). Inicialmente se define el camino aleatorio (random walk) como modelo de referencia. Adicionalmente, como especificación de referencia se emplea la condición de paridad del poder adquisitivo (PPP por sus siglas en inglés). De acuerdo con lo anterior se tiene la siguiente identidad:
donde, St representa el logaritmo de la tasa de cambio nominal (pesos colombianos por dólares), pt es el logaritmo del nivel de precios (IPC base 2000) y "ˆ" denota el diferencial entre países (Colombia - Estados Unidos). Al tratarse de una identidad, la ecuación (1) no es estimada.
En segundo lugar, se encuentra el modelo monetario con precios fijos. En este modelo la condición de paridad de poder adquisitivo (PPP) se omite ya que se supone que los precios en el corto plazo son rígidos. Siguiendo a Dornbusch (1976), un incremento en la oferta monetaria (doméstica) genera una salida de capitales (debido a la caída en la tasa de interés) lo cual genera una depreciación de la tasa de cambio Este modelo puede ser expresado como:
donde mt es el logaritmo de la oferta monetaria (M1), yt es el logaritmo del PIB real (a precios del 2000), it es la tasa de interés y πt es la tasa de inflación. La ecuación (2), puede ser interpretada como una extensión de la ecuación (1) donde las variables macroeconómicas capturan la demanda por dinero y los efectos de sobrepaso (overshooting effects). Aunque Cárdenas (1997) impone restricciones a los coeficientes de la ecuación (2), Cheung et al (2003) sugieren que la teoría no presenta una guía clara para hacerlo. Por lo tanto, se estimará la ecuación (2) sin restricciones.
Los siguientes dos modelos corresponden al enfoque Balassa - Samuelson. En este tipo de modelos, el papel de los diferenciales de productividad toma una mayor importancia para explicar las variaciones de la tasa de cambio nominal; por ejemplo, Clements y Frenkel (1980) y Chinn (1997) emplean diferenciales de productividad para explicar la tasa de cambio nominal. En este orden de ideas, la especificación que incluye el diferencial de productividad será:
donde zt representa una medida de productividad, como por ejemplo la producción por empleado. A diferencia de la ecuación (2), la ecuación (3), basada en la productividad, no asume que la paridad de poder adquisitivo se mantiene en el largo plazo (por esta razón no incluye el diferencial de inflación). En este tipo de modelos, el patrón de la tasa de cambio está determinado por el diferencial de productividades.
Finalmente, el cuarto modelo incorpora el efecto Balassa - Samuelson a través del diferencial de productividades, el efecto balance de portafolio a través de las variables relación deuda- PIB y activos externos netos y el efecto de sobrepaso por medio de la tasa de interés real. La especificación de este modelo «compuesto» es la siguiente:
donde rt es la tasa de interés real, gdebtt es la relación deuda/PIB, tott, es el logaritmo de los términos de intercambio y nfat representa los activos externos netos. A esta ecuación se le impone un coeficiente igual a uno al diferencial del logaritmo del nivel de precios 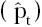 para determinar la tasa de cambio real reexpresando (4).
para determinar la tasa de cambio real reexpresando (4).
SERIES Y ORDEN DE INTEGRACIÓN
Para efectos del análisis propuesto se emplean datos trimestrales para Colombia y Estados Unidos durante el período comprendido entre 1984:I y 2004:I. Las series son obtenidas en su mayoría a través de la base de datos del Fondo Monetario Internacional (International Financial Statistics). Para el análisis se emplean: la tasa de cambio nominal (pesos colombianos por dólares); el IPC base 2000 para Colombia y Estados Unidos; la oferta monetaria (M1) para Colombia (obtenido a través de la base de datos del Banco de la República) y Estados Unidos sin desestacionalizar; las tasas de interés: Prime Rate (Estados Unidos) y la tasa de interés pasiva para Colombia (obtenida a través de las Estadísticas Históricas del DNP) a tres meses; los términos de intercambio para Colombia, calculados a partir de los índices de precios de las exportaciones y las importaciones con base 2000; los activos externos netos y el PIB para Colombia (Estadísticas Históricas DNP - Cuentas Nacionales DANE) y Estados Unidos (Bureau of Economic Analysis - NIPA Tables) a precios del 2000 y sin desestacionalizar.
La serie de productividad se calcula dividiendo el PIB por el número de empleados y convirtiendo a índice (base 2000). El empleo para Colombia es obtenido a través del empalme de la Encuesta Nacional y la Encuesta Continua de Hogares realizado por Lasso (2002). El empleo para Estados Unidos se obtiene por medio del Bureau of Labor Statistics (tanto la serie para Colombia como la serie de empleo para Estados Unidos son sin desestacionalizar). Finalmente, el diferencial de la relación deuda-PIB es calculado empleando un proxy para la deuda. Debido a la insuficiencia de datos, es necesario usar la serie Financiamiento, publicada a través de la base de datos del FMI. Con esta serie se calcula la proporción y se aplica el diferencial.
Para obtener las series de inflación y la tasa de interés real, se efectúa la cuarta diferencia del logaritmo del IPC y se resta el valor rezagado de la inflación a las tasas de interés nominal, respectivamente. Se observa que algunas de las series presentan una fuerte estacionalidad.
Antes de llevar a cabo las pruebas de cointegración y las medidas de predicción para los modelos de tasa de cambio propuestos, es necesario determinar el orden de integración de los procesos generadores de los datos empleados en el análisis. Para lo anterior, inicialmente se analiza la estacionalidad de las series por medio de las pruebas de Dickey - Fuller (1979) aumentada (ADF), Phillips - Perron (1988) y la prueba no paramétrica de Breitung (2002). Adicionalmente, se lleva a cabo la prueba de raíces unitarias de Kwiatkowski, Phillips, Schmidt y Shin (1992) (KPSS) cuya hipótesis nula corresponde a un proceso estacionario (alrededor de una tendencia) versus la hipótesis alterna de la presencia de una raíz unitaria. Los resultados de estas pruebas, tanto para los niveles de las series como para sus primeras diferencias, son reportados en la Tabla 2. Se puede decir que existe alguna evidencia para afirmar que todas las series están integradas de orden uno I(1), excepto las series 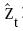 y tott (diferencial de productividad y términos de intercambio) para las cuales la evidencia señala que puede tratarse de series I(0).
y tott (diferencial de productividad y términos de intercambio) para las cuales la evidencia señala que puede tratarse de series I(0).
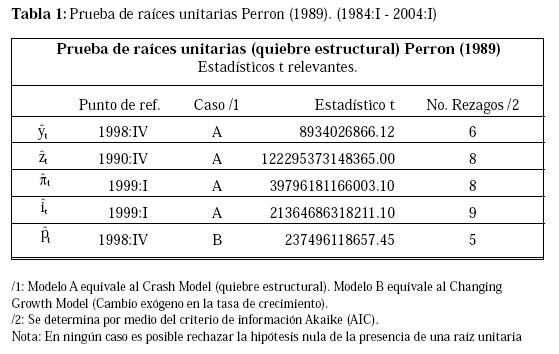
Dado que la evidencia no es robusta, es necesario llevar a cabo otro tipo de pruebas que se ajusten a las características de las series analizadas. Por lo tanto, adicionalmente se lleva a cabo la prueba de raíces unitarias de Perron (1989) que tiene en cuenta cualquier cambio en la función de tendencia de las series. Esta prueba se efectúa a las series que presentan algún tipo de quiebre estructural ya que las pruebas convencionales pierden poder frente a este tipo de casos. Los resultados de esta prueba se reportan en la Tabla 1. Para las series 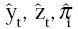 y
y 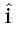 , se emplea el caso A ya que se observa un cambio exógeno en el nivel de las series (los puntos de quiebre son señalados en la Tabla 1), mientras que para la serie
, se emplea el caso A ya que se observa un cambio exógeno en el nivel de las series (los puntos de quiebre son señalados en la Tabla 1), mientras que para la serie 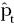 , se emplea el caso B ya que esta serie presenta un cambio exógeno en la tasa de crecimiento. Como se observa, los estadísticos t calculados son bastante grandes y por lo tanto no es posible rechazar la hipótesis nula de una raíz unitaria. Por lo tanto, por medio de esta prueba es posible reafirmar que existe evidencia sobre el orden de integración de las series (I(1)).
, se emplea el caso B ya que esta serie presenta un cambio exógeno en la tasa de crecimiento. Como se observa, los estadísticos t calculados son bastante grandes y por lo tanto no es posible rechazar la hipótesis nula de una raíz unitaria. Por lo tanto, por medio de esta prueba es posible reafirmar que existe evidencia sobre el orden de integración de las series (I(1)).
Adicionalmente se lleva a cabo la prueba de estacionaridad alrededor de una tendencia no lineal de Bierens (1997). La hipótesis nula de esta prueba implica la presencia de una raíz unitaria con «drift». La ventaja de esta prueba frente a la de Perron (1989) radica en que no es necesario determinar el punto de quiebre ya que al incluir el polinomio, los datos se suavizan. Esta prueba se lleva a cabo en las series que aparentemente presentan una tendencia no lineal: 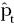 , nfa,y
, nfa,y 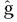 debtt. La Tabla 3 reporta los resultados de la prueba de Bierens (1997) para los diferentes grados del polinomio de Chevishev. De acuerdo con lo reportado se observa que los resultados (estadísticos para cada posibilidad) señalan que la serie
debtt. La Tabla 3 reporta los resultados de la prueba de Bierens (1997) para los diferentes grados del polinomio de Chevishev. De acuerdo con lo reportado se observa que los resultados (estadísticos para cada posibilidad) señalan que la serie 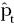 , presenta una raíz unitaria con «drift» ya que no es posible rechazar la hipótesis nula (comparando los cuatro estadísticos). Por otro lado, los resultados no son concluyentes para las serie nfat, lo cual corrobora los resultados obtenidos por medio de las pruebas anteriores con respecto al orden de integración de dicha serie. En cuanto a la serie
, presenta una raíz unitaria con «drift» ya que no es posible rechazar la hipótesis nula (comparando los cuatro estadísticos). Por otro lado, los resultados no son concluyentes para las serie nfat, lo cual corrobora los resultados obtenidos por medio de las pruebas anteriores con respecto al orden de integración de dicha serie. En cuanto a la serie 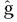 debtt, los resultados señalan que no existe una raíz, pero de nuevo, no son concluyentes para determinar la no linealidad de la tendencia.
debtt, los resultados señalan que no existe una raíz, pero de nuevo, no son concluyentes para determinar la no linealidad de la tendencia.
Resumiendo, de acuerdo con las pruebas convencionales y para los casos especiales como quiebre estructural y tendencia no lineal (Tablas 1 a 3), se puede asegurar que las series empleadas están integradas de orden uno.
RELACIÓN DE LARGO PLAZO DE LAS SERIES
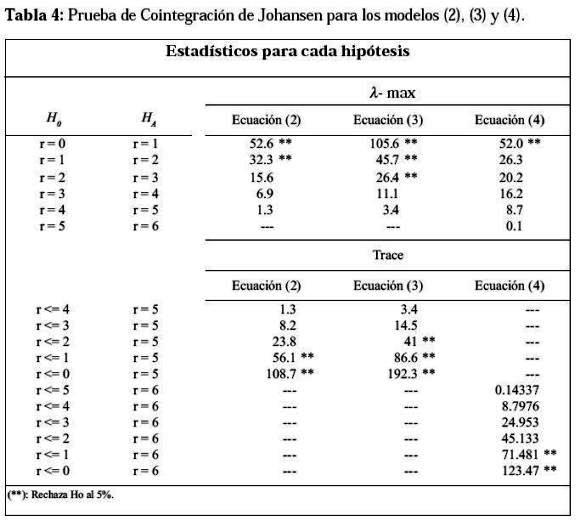
Para determinar la relación de largo plazo entre las variables involucradas en los diferentes modelos y descartar posibles relaciones espurias emplea la prueba de Cointegración de Johansen1 (1988). Los resultados de esta prueba para las tres especificaciones son reportados en la Tabla 4. De acuerdo con los estadísticos reportados, para la ecuación (2) existen dos vectores de cointegración, para la ecuación (3) existen tres vectores de cointegración y para la ecuación (4) existe un vector de cointegración. Es posible entonces estimar las especificaciones propuestas por medio del método de Mínimos Cuadrados Ordinarios (MCO) ya que se comprueba la existencia de una relación a largo plazo entre las variables incluidas en cada especificación.
EVALUACIÓN DE PRONÓSTICOS
Modelos estimados y evaluación de pronósticos
Los resultados de las estimaciones de los modelos (2), (3) y (4) se reportan en la Tabla 5. Los modelos (2) y (3) presentan coeficientes de determinación bastante altos (98% y 97% respectivamente) mientras que el modelo (4) posee un coeficiente de determinación bastante bajo (28%). Por otro lado, las variables explicativas de las dos primeras especificaciones son conjuntamente significativas a un nivel de confianza del 99%. Cabe anotar que dada la restricción impuesta a la ecuación (4), en la Tabla 5, la variable dependiente para esta ecuación es st - 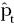
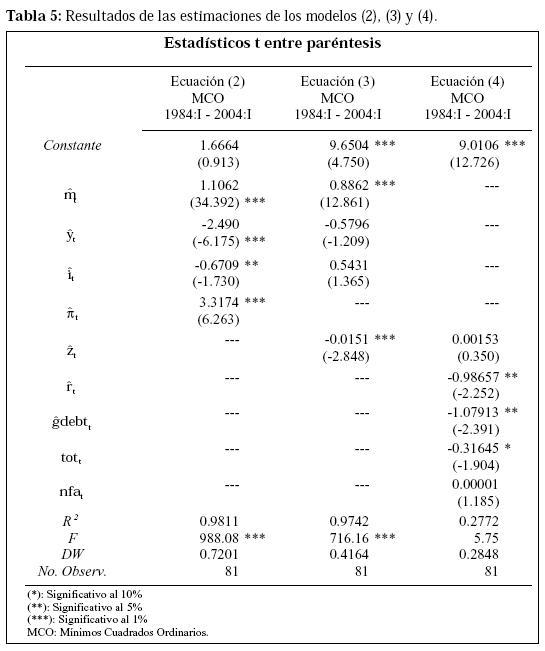
Para evaluar los pronósticos generados dentro de la muestra por cada modelo, se emplean dos tipos de medidas. La primera es la raíz cuadrática media del error de pronóstico (rms). La rms del error es una medida de desviación de la variable simulada de su curso en el tiempo (Pindyck y Rubinfeld (1998)). Esta medida se define como:
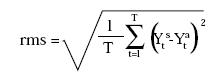
Donde, Ys t - Ya t y T representan el valor pronosticado de la variable dependiente, el valor observado de la variable dependiente y el número de períodos respectivamente.
Cabe anotar que el error de simulación rms debe evaluarse comparándolo con el tamaño promedio de la variable analizada. Por lo tanto es necesario calcular el error porcentual rms, el cual se define como:
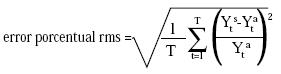
La segunda medida empleada para evaluar la capacidad de pronóstico es el coeficiente de desigualdad de Theil, que emplea la rms del error de pronóstico. Este coeficiente se define como:
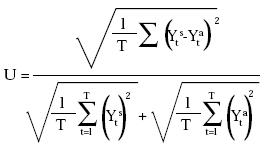
Este coeficiente mide la rms del error en términos relativos. Antes de observar los resultados de dichas medidas para cada ecuación, es necesario analizar gráficamente los pronósticos generados por cada modelo. El Gráfico 2 muestra los valores pronosticados por cada modelo al igual que los pronósticos generados a través de la condición de la paridad del poder adquisitivo (PPP) y el camino aleatorio (modelo de referencia).
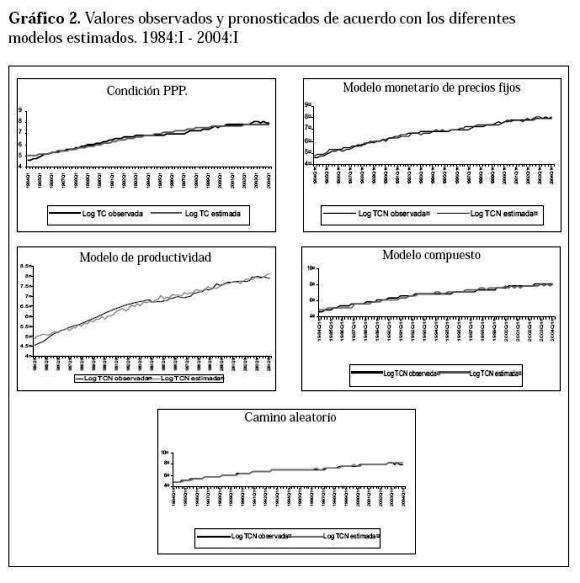
De acuerdo con el Gráfico 2, se puede decir que el modelo que mejor predice la tasa de cambio (mejor ajuste) es el camino aleatorio definido como: Δst = bo+et. A pesar de lo anterior, los demás gráficos muestran una calidad bastante alta en sus pronósticos. Para corroborar el análisis gráfico, la Tabla 6 presenta los cálculos de las medidas de evaluación de pronósticos.
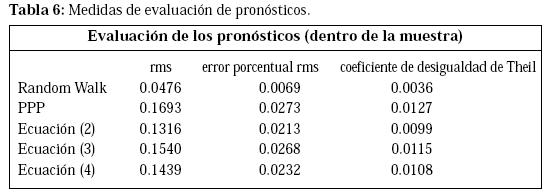
Analizando la raíz cuadrática media (rms) del error de pronóstico para cada modelo, se puede afirmar que el modelo que presenta una variable pronosticada con la menor desviación es el camino aleatorio, seguido por el modelo monetario de precios fijos (estimado como ecuación (2)). De igual manera, el error porcentual rms obtenido para el camino aleatorio señala que este modelo es el que mejor predice la tasa de cambio nominal en Colombia. Finalmente, de acuerdo con el coeficiente de desigualdad de Theil, el camino aleatorio presenta el mejor pronóstico de la tasa de cambio. Cabe anotar que dicho coeficiente siempre está entre cero y uno. Si el valor del coeficiente es igual a cero, el valor observado es igual al valor pronosticado. En este orden de ideas, dado que el coeficiente calculado para el camino aleatorio es bastante cercano a cero (0.0036), se puede decir que los valores pronosticados a partir de dicho modelo son muy cercanos a los valores observados de la tasa de cambio. Finalmente, dejando de lado al camino aleatorio, se observa que el modelo monetario de precios fijos supera al modelo de productividad (ecuación (3)) y al modelo compuesto (ecuación (4)). Sin embargo, el modelo compuesto se comporta mejor que el de productividad, siendo este último el que logra los pronósticos más pobres.
COMENTARIOS FINALES
Este documento analiza la capacidad de los modelos de tasa de cambio nominal propuestos en la década de 1990 para predecir el comportamiento de la tasa de cambio nominal en Colombia durante el período 1984:I - 2004:I. Los modelos empleados corresponden a los enfoques monetario y de diferenciales de productividad (Balassa - Samuelson). También se analiza un modelo compuesto que involucra el diferencial de productividad y el efecto de balance de portafolio. Las tres especificaciones propuestas son comparadas con la capacidad predictiva de un camino aleatorio y la condición de la paridad del poder adquisitivo (PPP). Inicialmente se analizan las propiedades de las series empleadas en las tres especificaciones y se determina que todas las series presentan una raíz unitaria (integradas de orden uno). Para lo anterior, se emplean las pruebas convencionales y otras pruebas adicionales que presentan un mayor poder frente a casos especiales. Posteriormente se determina si existe o no una relación de largo plazo entre las variables por medio de las pruebas de cointegración de Engle y Granger (1987) y de Johansen (1988). De acuerdo con los resultados obtenidos, se determina que existe una relación de largo plazo y por lo tanto es posible estimar las especificaciones propuestas por medio del método de mínimos cuadrados ordinarios.
Finalmente se evalúa por medio de diferentes medidas la capacidad de pronóstico que presentan los modelos estimados determinando que ningún modelo logra superar los pronósticos obtenidos a través del camino aleatorio (random walk). Los resultados señalan que los modelos teóricos desarrollados durante la década de 1990 no superan la habilidad del camino aleatorio para pronosticar la tasa de cambio nominal. Sin embargo, tal como lo señalan Cheung et al (2003), los resultados obtenidos no son un claro indicativo de la pobre capacidad de los modelos analizados para explicar los movimientos de la tasa de cambio. Es decir, aunque los resultados coinciden con los presentados por Cheung et al (2003), el ejercicio llevado a cabo no involucra todas las posibles medidas para evaluar la capacidad predictiva de los modelos estructurales analizados. A partir de estos resultados surge la necesidad de emplear especificaciones no lineales que logren captar las asimetrías presentes en el mercado de divisas.
NOTAS AL PIE DE PÁGINA
1. También se efectuó la prueba de cointegración de Engle y Granger (1987) con resultados poco contundentes (Estos resultados no son reportados).
BIBLIOGRAFÍA
Bierens, H. J. (1997). Testing the Unit Root with Drift Hypothesis Against Nonlinear Trend Stationarity, with an Application to the US Price Level and Interest Rate. Journal of Econometrics 81, 29-64. [ Links ]
Breitung, J. (2002). Nonparametric Tests for Unit Roots and Cointegration. Journal of Econometrics 108, 343-63. [ Links ]
Cárdenas, M. (1997). La tasa de cambio en Colombia. Cuadernos de Fedesarrollo 1, Bogotá: Tercer Mundo Ed. [ Links ]
Cheung, Y., Chinn M. & Garcia, A. (2003). Empirical Exchange Rates of the Nineties: Are Any Fit to Survive?. Santa Cruz Center for International Economics Paper 03(14). [ Links ]
Cheung, Y. & Chinn, M. (1998). Integration, Cointegration, and the Forecast Consistency of Structural Exchange Rate Models. Journal of International Money and Finance. 17, 813-30. [ Links ]
Chinn, M. (1997). Paper Pushers or Paper Money? Empirical Assessment of Fiscal and Monetary Models of Exchange Rate Determination. Journal of Policy Modeling. 19, 51-78. [ Links ]
Clements, K. & Frenkel, J. (1980). Exchange Rates, Money, and Relative Prices: The Dollar-Pound in the 1920´. Journal of International Economics. 10, 249-262. [ Links ]
Dickey, D.A. & Fuller, W.A. (1979). Distribution of the Estimators for Autoregression Time Series with a Unit Root. Journal of the American Statistical Association. 74, 427-31. [ Links ]
Dornbusch, R. (1976). Expectations and Exchange Rate Dynamics. Journal of Political Economy. 84, 1161-1676. [ Links ]
Engle, R.F. & Granger, C.W. (1987). Cointegration and Error Correction: Representation, Estimation, and Testing. Econométrica. 55, 251-76. [ Links ]
Frankel, J. A. (1979). On the Mark: A Theory of Floating Exchange Rates Based on Real Interest Differentials. American Economic Review. 69, 610-22. [ Links ]
Frenkel, J. A. & Rose, A. (1995). Empirical Research on nominal Exchange Rate. en Grossman y Rogoff Handbook of Internacional Economics. 1689-1729 [ Links ]
Hylleberg, S., Engle, R. F., Granger, C. W. J. & B. S. Yoo. (1990). Seasonal Integration and Cointegration. Journal of Econometrics. 44, 215-238. [ Links ]
Johansen, S. (1988). Statistical Analysis of Cointegrating Vectors. Journal of Economic Dynamics and Control. 12, 231-54. [ Links ]
Kwiatkowski, D., P. Phillips, P. Schmidt, and Y. Shin. (1992). «Testing the Null Hypothesis of Stationarity Against the Alternative of a Unit Root: How Sure Are We that Economic Time Series Have a Unit Root?» Journal of Econometrics 54, 159-78. [ Links ]
Lasso, F. J. (2002). «Nueva metodología de la Encuesta de hogares ¿Más o menos desempleados?» DNP, Archivos de Economía, Doc 213. [ Links ]
MacKinnon, J.G. (1991). «Critical Values for Cointegration Tests». In «Long-run Economic Relationships: Readings in Cointegration», (Eds) R.F. Engle and C.W.J. Granger, Oxford University Press, Oxford, pp 267. [ Links ]
Meese, R. A. and K. Rogoff. (1983a): «Empirical Exchange Rate Models of the Seventies: Do They Fit Out of Sample?» Journal of International Economics 14: 3-24. [ Links ]
Meese, R. A. and K. Rogoff. (1983b): «The out-of-sample failure of empirical exchange rate models: sampling error or misspecification?» en Exchange Rates ad International Macroeconomics: NBER y University of Chicago Press: 67-105. [ Links ]
Owen, D. (2001): «Importance of Productivity trends for the euro» European Economics for Investors, March. [ Links ]
Perron, P. (1989): «The Great Crash, the Oil Price Shock, and the Unit Root Hypothesis» Econometrica 57: 1361-401. [ Links ]
Pindyck, R.S y D. L. Rubinfeld. (1998): «Econometría Modelos y Pronósticos» McGraw - Hill Ed., México. Cuarta edición. [ Links ]
Phillips, P. and Perron, P. (1988): «Testing for a Unit Root in Time Series Regression». Biometrika 75: 335-46. [ Links ]
Rosemberg, M. (2000): «The Euro´s Long-Term Struggle» FX Research Special Report Series, No. 2. [ Links ]