Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Estudios Gerenciales
Print version ISSN 0123-5923
estud.gerenc. vol.25 no.112 Cali July/Sept. 2009
¿QUÉ TAN BUENOS SON LOS PATRONES DEL IGBC PARA PREDECIR SU COMPORTAMIENTO?UNA APLICACIÓN CON DATOS DE ALTA FRECUENCIA
JULIO CÉSAR ALONSO*1, JUAN CARLOS GARCÍA2
1Ph.D en Economía, Iowa State University, Estados Unidos. Profesor tiempo completo y Director CIENFI (Centro de Investigaciones en Economía y Finanzas), Universidad Icesi, Colombia. Dirigir correspondencia a: Universidad Icesi, Calle 18 No. 122-135, Cali, Colombia. jcalonso@icesi.edu.co
2Estudiante de Economía y Negocios Internacionales, Universidad Icesi, Colombia. Asistente de Investigación, Semillero de Investigación, Facultad de Ciencia Administrativas y Económicas, Universidad Icesi, Colombia. juangarcil@hotmail.com
* Autor para correspondencia.
Fecha de recepción: 29-09-2008 Fecha de corrección: 24-01-2009 Fecha de aceptación: 27-07-2009
RESUMEN
El objetivo del artículo es evaluar la utilidad de patrones de comportamiento para predecir el comportamiento futuro del Índice General de la Bolsa de Colombia (IGBC). Para tal fin, se emplearon 18 diferentes especificaciones del modelo GARCH-M y datos de alta frecuencia. Los modelos considerados tienen en cuenta el efecto Leverage, el efecto Día de la Semana, el efecto Hora y el efecto Día-Hora. Se evalúan 115 pronósticos para los siguientes 10 minutos para cada uno de los 18 modelos, empleando estadísticas descriptivas y las pruebas de Granger y Newbold (1977) y Diebold y Mariano (1995). Se encuentra que la mejor especificación es la que no tiene en cuenta el efecto día-hora en la media ni en la varianza.
PALABRAS CLAVE
Intraday, Garch-M, efecto Día de la Semana, efecto Hora, efecto Día-Hora.
Clasificación JEL: G17, G14, C53
ABSTRACT
How useful are the IGBC trends for forecasting future performance? An application using high frequency data
The purpose of this article is to evaluate the usefulness of performance trends for forecasting the future performance of the IGBC (Colombian exchange market index). To this end, 18 different specifications of the GARCH-M model and high frequency data were used. The models in review considered the leverage, day-of-the-week, hour-of-the-day, and day-hour effects. 115 different forecasts for the next 10 minutes were assessed for each of the 18 models, using descriptive statistics and the Grangers and Newbold (1977) and Diebolds and Mariano (1995) tests. The best model was found to be the one that does not consider the day-hour effect on the mean or the variance.
KEYWORDS
Intraday, Garch-M, day-of-the-week effect, hour-of-the-day effect, and day-hour effect.
RESUMO
Quanto valem os padrões da IGBC para prever seu comportamento? Uma aplicação com dados de alta frequência
O objetivo do artigo é avaliar a utilidade de padrões de comportamento para prever o comportamento futuro do Índice Geral da Bolsa da Colômbia (IGBC). Para esse fim, se empregaram 18 diferentes especificações do modelo GARCH-M e dados de alta frequência. Os modelos considerados têm em conta o efeito Leverage (Avalancagem), o efeito Dia da Semana, o efeito Hora e o efeito Dia-Hora. São avaliados 115 prognósticos para os 10 minutos seguintes para cada um dos 18 modelos, empregando estatísticas descritivas e as provas de Granger e Newbold (1977) e Diebold e Mariano (1995). Se verifica que a melhor especificação é aquela que não tem em conta o efeito dia-hora na média nem na variação.
PALAVRAS-CHAVE
Intraday, Garch-M, efeito Dia da Semana, efeito Hora, efeito Dia-Hora.
INTRODUCCIÓN
Pronosticar el comportamiento de los mercados accionarios y en últimas determinar patrones de comportamiento en los mercados financieros, ha sido materia de mucho interés tanto para actores del mercado como para académicos.1 Diferentes autores han encontrado patrones de comportamiento en los mercados financieros para diversos activos financieros y países. Trabajos como los de Gibbons y Hess (1981), Jarrett y Kyper (2006), Keef y Roush (2005), Keim y Stambaugh (1984), Lakonishok y Levi (1982) y Rogalski (1984), han analizado el comportamiento de los retornos de diferentes activos durante la semana de negociación y han encontrado diferentes patrones en los retornos dependiendo del día de la semana. Para el caso colombiano, Alonso (2006) empleando una muestra de datos diarios, encontró evidencia a favor de un patrón de comportamiento determinado por el día de la semana en el mercado accionario y en el de la tasa de cambio.
De otro lado, la disponibilidad de grandes bases de datos que recogen el comportamiento del mercado accionario transacción por transacción (tic by tic) y el aumento de la capacidad de cómputo, han permitido la proliferación de trabajos con este tipo de información. Esta literatura se ha concentrado en encontrar patrones de comportamiento dentro del día, como por ejemplo, los trabajos de Amihud y Mendelson (1987, 1991), Baillie y Bollerslev (1991), Cyree y Winters (2001), Grundy y McNichols (1989), Hong y Jiang (2000), Leach y Madhavan (1993), Romer (1993), Stoll y Whaley (1990). Toda esta literatura sugiere que los retornos y la volatilidad exhiben un comportamiento en el que los precios de apertura y cierre presentan mayor ruido que los de horas intermedias, revelándose un comportamiento en forma de U tanto en la varianza como en los retornos, o en otros casos una forma de J invertida explicada por la mayor variabilidad de los precios de apertura que los de cierre.
La finalidad de este trabajo es emplear datos de alta frecuencia para evaluar el poder de predicción fuera de muestra para el mercado de capitales colombiano2 de un grupo de modelos que identifique patrones de comportamiento al interior del día. El artículo busca encontrar un modelo estadístico que permita disminuir el grado de certidumbre sobre el comportamiento del futuro inmediato (próximos 10 minutos) de operadores del mercado accionario colombiano.
Para lograr este objetivo se empleará el modelo GARCH en media (GARCH- M) propuesto por Engle y Bollerslev (1986), al cual se le incluyen los efectos Día de la Semana, Día-Hora, Apalancamiento (leverage) y la aproximación por Rango. El resto del documento se organiza en tres partes: una que discute los modelos que se emplearán, la siguiente sección presenta la metodología seguida y la evaluación de los diferentes modelos de proyecciones, y la última sección expone unos comentarios finales.
1. MODELOS PARA LA IDENTIFICACIÓN DE PATRONES Y CONSIDERACIONES PARA LAS ESTIMACIONES
Para lograr el objetivo de encontrar el mejor modelo para pronosticar la media del comportamiento del mercado accionario colombiano, se emplearán observaciones para cada 10 minutos del Índice General de la Bolsa de Colombia (IGBC) desde el 26 de diciembre de 2006 a las 13:00 horas, hasta el 9 de noviembre de 2007 a las 13:00 horas, para un total de 5.077 observaciones. La serie ha sido obtenida del sistema de información Bloomberg. Igualmente, por cada periodo de 10 minutos se dispone de datos como el máximo y mínimo valor del IGBC.3
Tal vez el modelo más empleado para modelar la media de un activo son los modelos ARIMA o ARIMAX, los cuales dominaban la literatura hasta principios de los años ochenta. Pero, en la década de los años ochenta se presenta un quiebre en el tipo de modelos que se emplean para modelar el comportamiento de los activos, pasando a una mayor importancia de la volatilidad que a la media.
Así, el modelaje del comportamiento de los rendimientos de un activo financiero o índice accionario, sufrió un cambio radical a partir del desarrollo del modelo ARCH (q) por Engle (1982) y el GARCH (p,q) por Bollerslev (1986). Estos modelos han permitido analizar el comportamiento de la varianza no constante de los modelos que se empleaban hasta ese momento. En especial, los modelos ARCH y GARCH permitieron capturar el fenómeno de Volatility Clustering de los rendimientos de los activos; es decir, periodos de volatilidad alta están seguidos de periodos de volatilidad alta, mientras que periodos de volatilidad baja son seguidos por periodos de volatilidad baja. Este modelo ha sido modificado desde su creación con el fin de incorporar otros aspectos que permitan explicar hechos estilizados del comportamiento de los mercados financieros (ver por ejemplo Alonso y Arcos ( 2006)). Un ejemplo de estos modelos es el GJR-GARCH de Glosten, Jagannathan y Runkle (1993), que permite un comportamiento asimétrico en la varianza al incorporar variables que miden el efecto apalancamiento (también conocido como leverage effect por su traducción en inglés).
Por otro lado, Rogers y Satchell (1991) proponen un estimador para la volatilidad (s) a partir del Rango (Range) definido como la diferencia logarítmica entre el precio máximo y el precio mínimo del activo dentro de un intervalo dado que puede ser un minuto, una hora o un día; estos autores han creado un camino diferente en la modelación de la volatilidad del precio de los activos. La intuición del criterio del rango es que periodos de alta volatilidad deben presentar una alta diferencia entre el precio máximo y el mínimo, y en periodos de baja volatilidad, esa diferencia debe ser baja. Este mecanismo de estimación de la volatilidad ha sido denominado por los autores como el Range Based Criteria. Igualmente, el Rango como variable explicativa en modelos de volatilidad ha empezado a usarse comúnmente. Algunos ejemplos son el trabajo hecho por Alizadeh, Brandt y Diebold (2002) quienes incorporaron la variable Rango a un modelo de volatilidad estocástica, o también, el trabajo de Brandt y Jones (2006), al igual que el de Chou (2005), quienes a partir de modelos autorregresivos para la varianza, a los cuales se les incluyó la variable Rango dentro de ellos, explican el comportamiento de la volatilidad.
Finalmente, es importante anotar que sin importar cómo se modele la volatilidad de los activos (o de sus rendimientos), una práctica relativamente común es emplear modelos que incorporan en la media el efecto de la volatilidad. A estos modelos se les conoce como GARCH en media (GARCH-M por su nombre en inglés GARCH in mean).
Sin embargo, es importante mencionar que al momento de modelar la volatilidad de la rentabilidad de alta frecuencia (cada cinco, diez o veinte minutos) con modelos GARCH, aparecen problemas metodológicos mencionados por Andersen y Bollerslev (1997) y Giot (2005). Intuitivamente, Andersen y Bollerslev muestran que a medida que se emplea una frecuencia más baja para la estimación de modelos GARCH, es más probable la existencia de un sesgo en los parámetros GARCH y ARCH y, en especial, la probabilidad de que los coeficientes sumen uno aumenta. En otras palabras, al aumentar la frecuencia en la muestra con que se estiman los modelos GARCH, se corre el riesgo de capturar ruido de la estacionalidad intradía que puede provocar sesgo en la estimación de los parámetros del modelo GARCH.
La literatura sugiere varias opciones para evitar ese sesgo o ruido provocado por la estacionalidad intradía. Por ejemplo, Andersen y Bolerslev (1997) proponen emplear retornos desestacionalizados (Rett). Si se supone que la estacionalidad intradía es determinística y se cuenta con observaciones intradía con espacios regulares (por ejemplo; cada 10 ó 30 minutos), entonces los rendimientos desestacionalizados se pueden calcular de la siguiente manera:
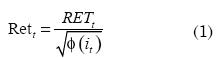
Donde RETt corresponde a los retornos observados y φ(it) representa el componente determinismo de la estacionalidad intradía. Giot (2005) sugiere calcular φ(it) por medio de un promedio de todos los retornos al cuadrado que corresponden a la misma hora y día de la semana del rendimiento observado (RETt). De tal manera que para periodos de 10 minutos, se obtienen para cada uno de los cinco días de la semana tantos φ(it) como periodos de 10 minutos existan en un día de mercado.4 Así, los modelos serán estimados con las series desestacionalizadas y posteriormente será incorporada la estacionalidad intradía para obtener el pronóstico de la media del IGBC.
En el caso de este artículo, se evaluarán nueve especificaciones del modelo GARCH-M a utilizar. La especificación 1 corresponde al modelo GARCH planteado por Engle y Bollerslev (1986). La especificación 2 incluye el rango5, Dt, en la varianza del modelo GARCH planteada por Christoffersen (2003). La especificación 3, propuesta por Berument y Kiymaz (2003), incluye la ecuación de la media y la de la varianza de los retornos variables dummy que recogen el efecto que tiene cada día en los retornos. El efecto día de la semana (DWE por sus siglas en inglés) se expresa de la siguiente forma y se introduce tanto a la ecuación de la media como la varianza:
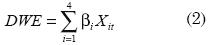
Donde X1t = 1 si el día corresponde a un lunes y X1t = 0 en caso contrario. Así mismo, X2t = 1 cuando el día es un martes y así sucesivamente. No se empleará variable dummy para el día viernes, de tal manera que el intercepto capturará el efecto del viernes.
La especificación 4 es una adaptación de la anterior para medir el efecto de la hora. Conviene aclarar que en Colombia el horario de negociación de la Bolsa de Valores inicia a las nueve de la mañana y termina a la una de la tarde, lo que da un total de cuatro horas de negociación. El efecto hora del día (HDE por sus siglas en inglés) se expresa de la siguiente manera, y se introduce tanto en la ecuación de la media como de la varianza:
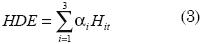
Donde H1t = 1 si se trata de la primera hora de negociación, es decir, de 9:00 A.M. a 10:00 AM, y H1t = 0 en cualquier otro caso. Similarmente, H2t = 1 si el rendimiento corresponde a un momento entre 10:00 A.M. a 11:00 A.M., y así sucesivamente. Para la última hora de negociación no se empleará variable dummy.
Para la especificación 5 se consideran variables dummy que toman el valor de 1 teniendo en cuenta la hora y el día. Dado que el horario de bolsa es de cuatro horas por día y de cinco días a la semana, se tendrá un total de [4(5)-1 = 19] variables dummy. Donde el intercepto en las dos ecuaciones corresponde a la última hora de negociación del viernes.
La especificación 6 corresponde a un TGARCH; es decir, es un modelo GARCH que incluye un umbral (threshold en inglés); el umbral intenta capturar el efecto apalancamiento. Este modelo corresponde al planteado por Glosten et al. (1993). El efecto apalancamiento (THRSH por la abreviación de threshold) se introduce a la ecuación de la varianza de la siguiente manera:
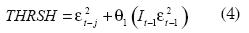
Donde la variable It-1 es una dummy que toma el valor de uno si el exceso de retorno anterior (εt-1) es negativo y cero en caso contrario. Este modelo pondera de manera diferente el efecto de retornos negativos en la varianza que el de los retornos positivos.
La especificación 7 incluye tanto el efecto del día de la semana (DWE) como el umbral (THRSH) en el modelo GARCH. La especificación 8 incluye el efecto hora del día (HDE) y el THRSH. Finalmente, la especificación 9, incluye el DWE, el HDE y el THRSH.
Cada especificación considera dos opciones de modelamiento para la media: el Modelo A, aquel que incluye un proceso ARMA (p,q) en la media, y el Modelo B que no lo incluye; por lo tanto, se tiene un total de 18 modelos a estimar (Tabla 1).
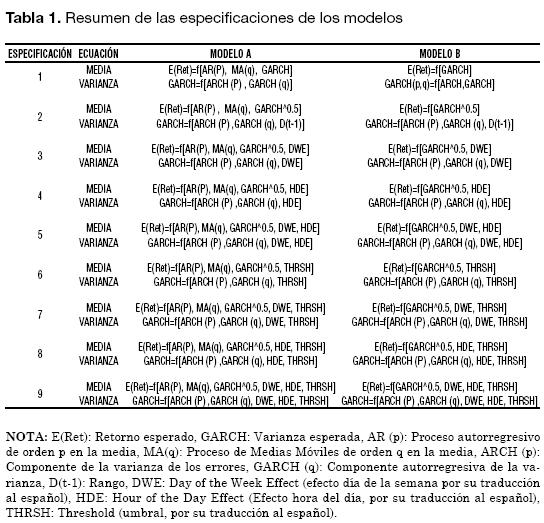
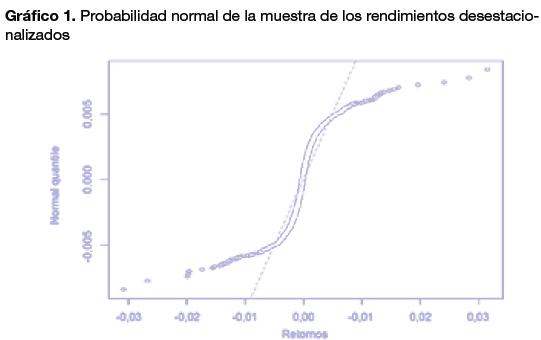
Antes de estimar los nueve modelos referenciados a continuación, es importante notar que la muestra presenta uno de los hechos estilizados identificados por Alonso y Arcos (2006): las colas pesadas. Esta característica se puede observar en el correspondiente gráfico de probabilidad normal presentada en el Gráfico 1. De acuerdo con este resultado, suponer que la distribución de los retornos sigue una distribución normal, pareciera no ser sustentable. Siendo consecuentes con
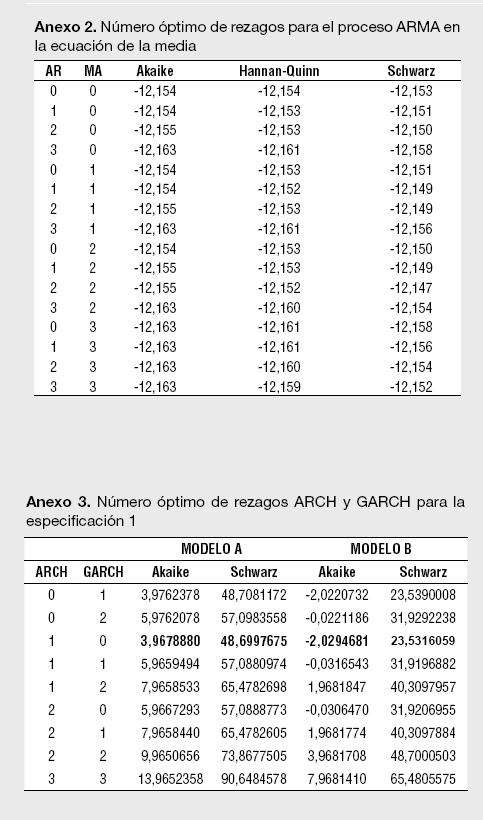
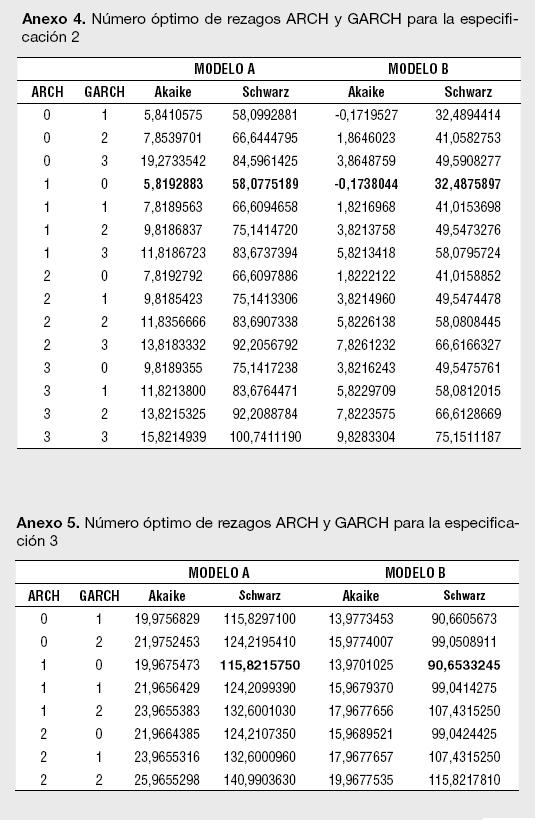
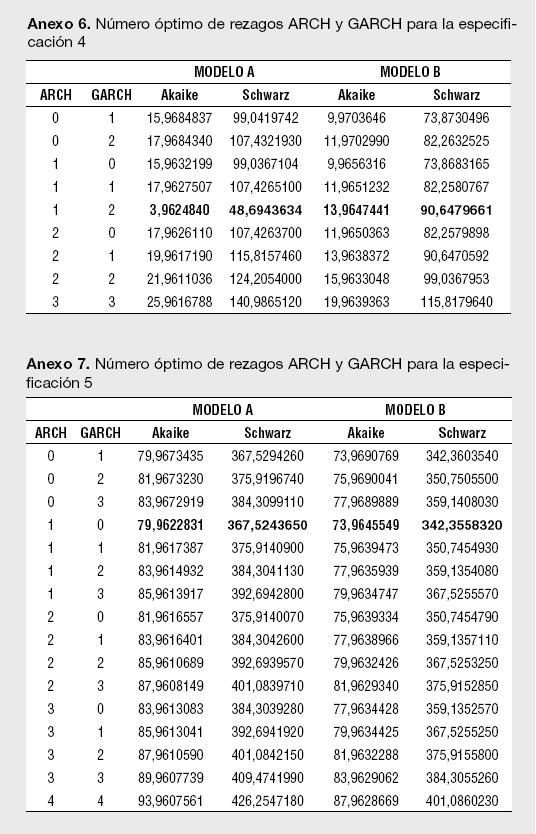
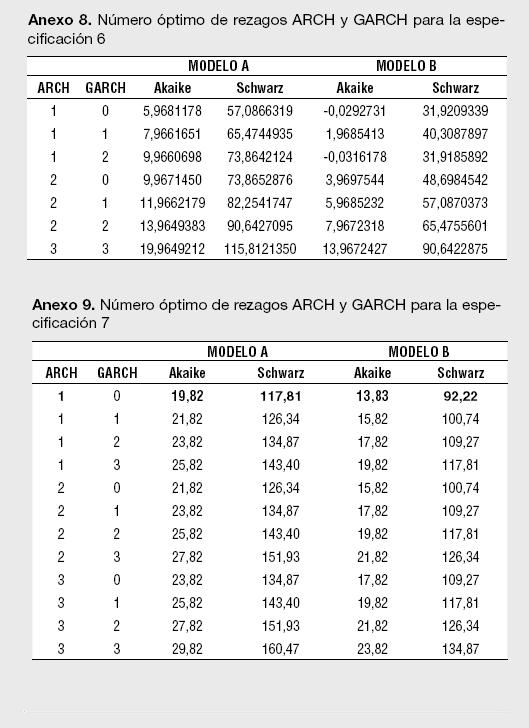
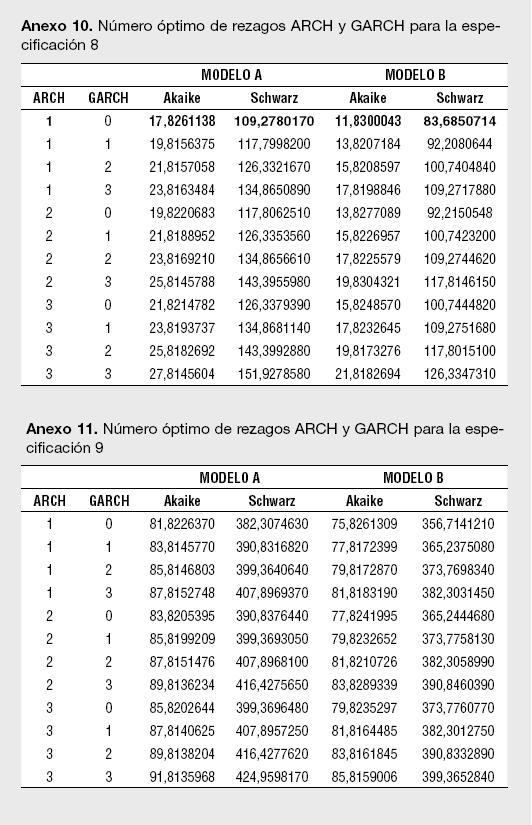
Un segundo paso para la estimación de los modelos reportados en la Tabla 1 es determinar el número óptimo de rezagos para los componentes autorregresivos y media móvil del ARMA. Empleando los criterios de información de Akaike, Hannan-Quinn y Schwarz se encontró que el orden de rezago del modelo ARMA para los retornos esperados corresponde a un ARMA(0,3), o lo que es lo mismo, un MA(3). De esta manera, para cada estimación del Modelo A, siempre se presentará un proceso MA (3) en la ecuación de la media. Un tercer paso necesario para cada especificación es determinar el orden ARCH y GARCH para modelar la varianza; tal y como lo sugiere Enders (2004),7 se emplean los criterios modificados de Akaike y Schwarz en el orden de rezago para la parte ARCH y GARCH en la ecuación de la varianza.
Los resultados para el número óptimo de rezagos para el proceso ARMA en la media, así como el del proceso GARCH (p,q) en la ecuación de la varianza, se presentan en los Anexos 1 a 11. Es importante destacar que las estimaciones de los modelos se han realizado utilizando el algoritmo de Berndt, Hall, Hall y Hausman (1974);8 el cual es usado para la optimización numérica de la función de Máxima Verosimilitud. La ventaja de usar el BHHH es que impide que el proceso iterativo pare al encontrar mínimos locales; dado que funciona en dos etapas, cualquier mínimo local encontrado es tratado como el punto de partida de la segunda etapa.
2. RESULTADOS DE LAS PREDICCIONES DE LOS MODELOS Y SU EVALUACIÓN
Para evaluar el comportamiento de los pronósticos fuera de muestra de cada una de las especificaciones empleadas, se usa una ventana móvil para estimar el correspondiente modelo y se genera un pronóstico de un paso adelante. La primera muestra empleada para obtener el primer pronóstico one step ahead va desde el 27 de diciembre de 2006 a las 9:00 horas, hasta el 31 de agosto de 2007 a las 13:00 horas (3.924 observaciones). En total, esto implica un total de 1.152 ventanas sobre las cuales se evaluará el comportamiento de cada especificación.9
En otras palabras, se construye el pronóstico para el período T + 1 (T+1) a partir del valor esperado de la correspondiente especificación sujeto a la información disponible hasta el período T, esto es: T+1 = ET[RT+1]. El error de predicción será ξT+1= RT+1-T+1. En este caso, T = 3.924,3.925,...,5.076, lo cual implica que al final del ejercicio se dispone de una serie de 1.152 errores de predicción one step ahead que van desde el primer día a la primera hora de trading de septiembre de 2007 hasta la última hora de trading del 9 de noviembre del mismo año. Una vez estimados cada uno de estos modelos para las ventanas móviles, se procede al análisis del vector de errores de predicción por medio de cuatro métricas de error diferentes:
- Raíz cuadrada del error de predicción cuadrático medio (RMSPE por su sigla en inglés), definido como:
- Error de predicción porcentual promedio (MPPE por su sigla en inglés), que se define:
- Error de predicción absoluto promedio (MAPE), definido así:
- Proporción de excepciones de signo (p*), que se define como:
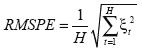
donde H es el número de observaciones de error de predicción, y (ξt) es el error de predicción en el periodo t.
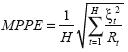
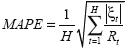
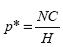
donde NC es el número de no coincidencias de signo entre el dato predicho y el real.
En la Tabla 2 se reportan estos estadísticos para los 18 modelos. Los valores mínimos del RMSPE, MPPE, MAPE y p* corresponden a los modelos 2A, 4A, 5A y 7B, respectivamente. De otro lado, el valor máximo del RMSPE corresponde al modelo 1A, del MPPE y MAPE al 7B y del p* al 1B. De modo que no existe un modelo de los aquí analizados que minimice los cuatro criterios simultáneamente.
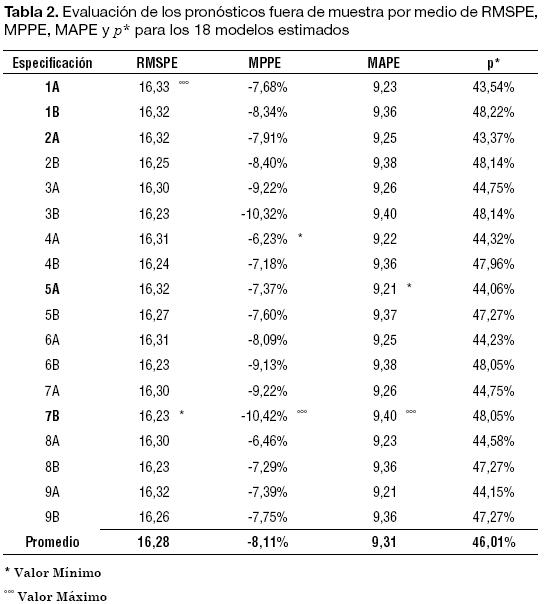
Una forma complementaria de evaluar el comportamiento de los pronósticos es emplear un análisis de corte inferencial, a diferencia del descriptivo realizado anteriormente. Dos pruebas estadísticas utilizadas con relativa frecuencia para evaluar el comportamiento de dos modelos diferentes para pronosticar una serie, son las de Granger y Newbold (1977) y la de Diebold y Mariano (1995). Dichas pruebas implican como hipótesis nula que ambos modelos tienen la misma precisión en el pronóstico.
La prueba de Granger y Newbold (1977) implica construir las series:
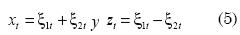
Donde ξit es el error de predicción del modelo i en el periodo t. Si la hipótesis nula es correcta, entonces no debe existir correlación entre xt y zt. Esta hipótesis nula se puede rechazar empleando el estadístico de prueba que sigue una distribución-t con (H-1) grados de libertad, donde rxz es el coeficiente de correlación muestral. Si rxz es estadísticamente diferente de 0 y positivo, entonces el modelo 1 tendrá mayor MSPE; en caso contrario, el modelo 2 tendrá mayor MSPE.
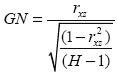
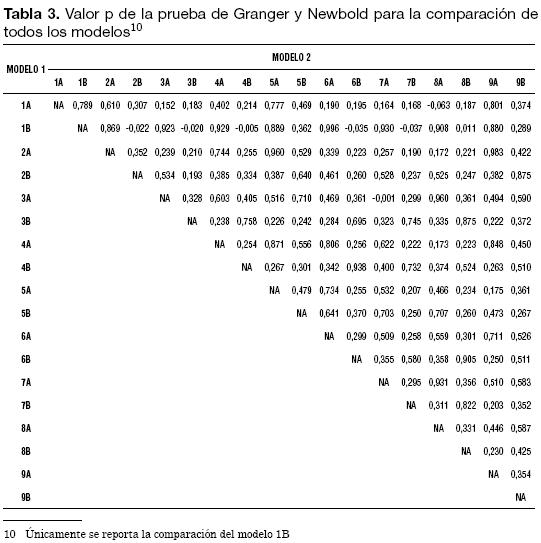
Como se aprecia en la Tabla 3, para el caso de comparar el modelo 1B contra los modelos 2B, 3B, 4B, 6B y 7B, se puede rechazar la hipótesis nula que los modelos producen los mismos pronósticos. El coeficiente rxz es positivo (ver Anexos 12 y 13) y el p valor es menor al 5% para todos los casos. Por lo tanto, según la prueba de Granger y Newbold (1977) con una confianza de al menos el 95%, se puede rechazar la hipótesis nula de igual precisión en la predicción entre el modelo 1B y los modelos 2B, 3B, 4B y 6B, en favor de la alterna de que cualquiera de los últimos predice mejor que la especificación 1B. Igualmente, la especificación 8A tiene mayor precisión en la predicción que la 1A con una confianza del 90%, y la especificación 3A tiene mayor precisión que la 7A con una confianza del 99% (Anexos 12 y 13).
De otro lado, en la Prueba de Diebold y Mariano (1995) es necesario construir la serie dt :
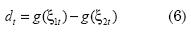
Para el caso de este artículo, 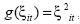 , luego se calcula el estadístico
, luego se calcula el estadístico 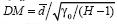 , donde d es el promedio y y0 es la varianza muestral. El estadístico DM sigue una distribución t con H-1 grados de libertad.
, donde d es el promedio y y0 es la varianza muestral. El estadístico DM sigue una distribución t con H-1 grados de libertad.
En el Anexo 14 se presentan los valores asociados a la prueba de Diebold y Mariano (1995) para parejas de modelos. Dado que para todas las comparaciones posibles entre todas las especificaciones tratadas aquí no se rechaza la hipótesis nula de que los modelos tienen el mismo poder de predicción; entonces se concluye por esta prueba que no existe algún modelo entre los planteados que estadísticamente prediga mejor que otro.
3. CONCLUSIONES
En este documento se evalúa el poder de predicción fuera de muestra de 18 modelos para el comportamiento de la media de los rendimientos cada 10 minutos del IGBC. Para cada uno de los modelos se calculan 1.000 pronósticos fuera de muestra para los siguientes 10 minutos de negociación. El procedimiento implica para cada una de las 1.152 ventanas estimar el correspondiente modelo y pronosticar, a partir del modelo estimado, la media del rendimiento para los siguientes 10 minutos. Una vez estimado este pronóstico se incorpora a la muestra una observación más y el procedimiento se repite.
De esta manera se cuenta con 1.152 pronósticos por modelo para evaluar qué tan bueno ha sido cada uno de los 18 modelos al momento de pronosticar. Para evaluar este comportamiento se emplearon dos tipos de aproximaciones. La primera implica el cálculo de métricas descriptivas como RMSPE, MPPE, MAPE y p*. La segunda aproximación implica dos pruebas estadísticas (las de Granger y Newbold (1977) y la de Diebold y Mariano (1995)) que permite rechazar la hipótesis nula de que una pareja de modelos producen pronósticos igualmente buenos.
Al emplear los criterios de RMSPE se encuentra que el modelo con el mejor comportamiento es el modelo TGARCH-M (modelo 7B) que incluye el efecto del día de la semana tanto en la media como en la varianza; es decir, el modelo que más se acerca a los valores reales de acuerdo con este criterio es uno que incluye el patrón del día de la semana en la media, la varianza, la varianza en la media, dos términos de media móvil, y tiene en cuenta el comportamiento asimétrico de la varianza. Pero, por otro lado, este modelo es el que tiene los mayores MPPE y MAPE. Finalmente, este modelo tiene una proporción de signos errados en la predicción de 48,05%; proporción relativamente alta cuando se compara con otros modelos.
Al concentrarse en el modelo que tenga la menor proporción de errores en el signo predicho, el mejor modelo es el 2A, modelo que se diferencia del 7B en tres aspectos: i) no incluye los componentes de media móvil en la media, ii) no incluye el efecto del día de la semana en la media y la varianza, y iii) no incluye el umbral pero sí incluye el rango como medida de dispersión.
Por otro lado, al efectuar las pruebas de Granger y Newbold (1977) y la de Diebold y Mariano (1995), la conclusión es que todos los modelos proveen pronósticos que estadísticamente son iguales. En este orden de ideas, si se desea emplear un modelo para predecir el comportamiento de los rendimientos del IGBC para los próximos 10 minutos, será prácticamente lo mismo emplear cualquiera de las 18 especificaciones consideradas. Así, por ser el modelo más parsimonioso, se recomienda emplear el modelo 1A. Modelo que no incluye efectos de asimetría, ni efectos del día de la semana o la hora.

NOTAS AL PIE DE PÁGINA
1. Por ejemplo, Alonso y Patiño (2005) presentan una revisión bibliográfica y un ejercicio en torno al pronóstico de la tasa de cambio en Colombia.
2. Para ser más precisos se desea pronosticar la media del IGBC y no su volatilidad.
3. Al realizarse las pruebas de raíces unitarias, se concluyó que la serie del Ln (IGBC) es I (1), es decir, que la serie de los retornos (primeras diferencias del Ln (IGBC), es un proceso estacionario. Los resultados de estas pruebas se presentan en el Anexo 1.
4. En el caso del IGBC se tienen cuatro horas de negociación y seis periodos de 10 minutos por día, lo que implica 24 φ(it) diferentes.
5. El Rango, como ya se dijo, puede ser entendido como la diferencia logarítmica entre el valor máximo y el mínimo del índice dentro del periodo t.
6. Los grados de libertad de cada uno de los modelos fueron estimados, y el mejor modelo fue escogido siguiendo los criterios de información modificados de Akaike y Schwarz (Enders, 2004).
7. Akaike modificado: AIC = -1n(L) + 2n, y el Schwartz Modificado: SBC = -1n(L) + n(1n((T)), donde L es el máximo valor de la función de máxima verosimilitud, T es el tamaño de la muestra y n es el número de parámetros estimados.
8. También conocido como el algoritmo BHHH.
9. Por ejemplo, para predecir el valor del retorno esperado en el período 3.925 (primera ventana) se emplean las 3.924 primeras observaciones y se pronostica un paso adelante. Como se conoce el valor real del retorno en t=3.925, se puede construir el error de predicción para t=3.925 para los 18 modelos. Inmediatamente, los modelos se re-estiman usando una observación más; es decir, se emplean las primeras 3.925 observaciones. Finalmente, se realizan las predicciones de los retornos para el periodo 3.926 y se determina el correspondiente error de predicción para ese período. El proceso se continúa hasta agotar la muestra.
REFERENCIAS BIBLIOGRÁFICAS
1. Alizadeh, S., Brandt, M.W. y Diebold, F.X. (2002). Range-Based Estimation of Stochastic Volatility Models. The Journal of Finance, 57(3), 1047-1091. [ Links ]
2. Alonso, J.C. (2006). The Day-of-The-Week effect: the Colombian exchange and stock market case. Presentado en el III Simposio Nacional de docentes de finanzas, Bogotá, Colombia. [ Links ]
3. Alonso, J.C. y Arcos, M.A. (2006). Cuatro hechos estilizados de las series de rendimientos: Una ilustración para Colombia. Estudios Gerenciales, 22(100), 103-123. Disponible en: http://bibliotecadigital.icesi.edu.co/biblioteca_digital/bitstream/item/992/1/ilustracion_colombia.PDF [ Links ]
4. Alonso, J.C. y Patiño, C.I. (2005). Evaluación de pronósticos para la tasa de cambio en Colombia. Estudios Gerenciales, 96, 13-26. Disponible en: http://bibliotecadigital.icesi.edu.co/biblioteca_digital/bitstream/item/361/1/Evaluacion_de_pronosticos_para_tasa_de_cambio.pdf [ Links ]
5. Amihud, Y. y Mendelson, H. (1987). Trading Mechanisms and Stock Returns: An Empirical Investigation. The Journal of Finance, 42(3), 533-553. [ Links ]
6. Amihud, Y. y Mendelson, H. (1991). Volatility, Efficiency, and Trading: Evidence from the Japanese Stock Market. The Journal of Finance, 46(5), 1765-1789. [ Links ]
7. Andersen, T.G. y Bollerslev, T. (1997). Intraday periodicity and volatility persistence in financial markets. Journal of Empirical Finance, 4(2-3), 115-158. [ Links ]
8. Baillie, R.T. y Bollerslev, T. (1991). Intra-Day and Inter-Market Volatility in Foreign Exchange Rates. The Review of Economic Studies, 58(3), 565-585. [ Links ]
9. Berndt, E., Hall, B., Hall, R. y Hausman, J. (1974). Estimation and inference in nonlinear structural models. Annals of Economic and Social Measurement, 3/4, 653-666. [ Links ]
10. Berument, H. y Kiymaz, H. (2003). The day of the week effect on stock market volatility and volume: International evidence. Review of Financial Economics, 12(3), 363-380. [ Links ]
11. Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 31(3), 307-327. [ Links ]
12. Brandt, M.W. y Jones, C.S. (2006). Volatility Forecasting with Range-Based EGARCH Models. Journal of Business y Economic Statistics, 24(4), 470-486. [ Links ]
13. Chou, R.Y. (2005). Forecasting Financial Volatilities with Extreme Values: The Conditional Autoregressive Range (CARR) Model. Journal of Money, Credit y Banking, 37(3), 561-582. [ Links ]
14. Christoffersen, P.F. (2003). Elements of financial risk management. San Diego, CA: Academic Press. [ Links ]
15. Cyree, K.B. y Winters, D.B. (2001). An Intraday Examination of the Federal Funds Market: Implications for the Theories of the Reverse-J Pattern. The Journal of Business, 74(4), 535-556. [ Links ]
16. Diebold, F.X. y Mariano, R.S. (1995). Comparing Predictive Accuracy. Journal of Business and Economic Statistics, 13(3), 253-263. [ Links ]
17. Enders, W. (2004). Applied econometric time series (2nd ed.). Hoboken, NJ: J. Wiley. [ Links ]
18. Engle, R.F. (1982). Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econométrica, 50(4), 987-1007. [ Links ]
19. Engle, R.F. y Bollerslev, T. (1986). Modeling the persistence of conditional variances. Econometric Reviews, 5(1), 1-50. [ Links ]
20. Gibbons, M.R. y Hess, P. (1981). Day of the Week Effects and Asset Returns. The Journal of Business, 54(4), 579-596. [ Links ]
21. Giot, P. (2005). Market risk models for intraday data. European Journal of Finance, 11(4), 309-324. [ Links ]
22. Glosten, L., Jagannathan, R. y Runkle, D. E. (Writer) (1993). On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. Journal of Finance, 48(5), 17798-1801. [ Links ]
23. Granger, C.W.J. y Newbold, P. (1977). Forecasting economic time series. New York, NY: Academic Press. [ Links ]
24. Grundy, B.D. y McNichols, M. (1989). Trade and the Revelation of Information through Prices and Direct Disclosure. The Review of Financial Studies, 2(4), 495-526. [ Links ]
25. Hong, H. y Jiang, W. (2000). Trading and Returns under Periodic Market Closures. Journal of Finance, 55(1), 297-354. [ Links ]
26. Jarrett, J.E. y Kyper, E. (2006). Capital market efficiency and the predictability of daily returns. Applied Economics, 38(6), 631-636. [ Links ]
27. Keef, S.P. y Roush, M.L. (2005). Day-of-the-week effects in the pre-holiday returns of the Standard y Poors 500 stock index. Applied Financial Economics, 15(2), 107-119. [ Links ]
28. Keim, D.B. y Stambaugh, R.F. (1984). A Further Investigation of the Weekend Effect in Stock Returns. The Journal of Finance, 39(3), 819-835. [ Links ]
29. Lakonishok, J. y Levi, M. (1982). Weekend Effects on Stock Returns: A Note. The Journal of Finance, 37(3), 883-889. [ Links ]
30. Leach, J. y Madhavan, A. (1993). Price experimentation and security market structure. Review of Financial Studies, 6(2), 375-404. [ Links ]
31. Rogalski, R.J. (1984). New Findings Regarding Day-of-the-Week Returns over Trading and Non-Trading Periods: A Note. The Journal of Finance, 39(5), 1603-1614. [ Links ]
32. Rogers, L.C.G. y Satchell, S.E. (1991). Estimating Variance From High, Low and Closing Prices. The Annals of Applied Probability, 1(4), 504-512. [ Links ]
33. Romer, D. (1993). Rational Asset-Price Movements Without News. The American Economic Review, 83(5), 1112-1130. [ Links ]
34. Stoll, H. y Whaley, R. (1990). Stock market structure and volatility. Review of Financial Studies, 3(1), 37-71.35. [ Links ]














