Artículo de Investigación/Research Article

Método para el Diagnóstico de Rodamientos Utilizando la Complejidad de Lempel-Ziv

Diego L. Guarín-Lopez¹, Álvaro A. Orozco-Gutierrez², Edilson Delgado-Trejos³

¹Departamento de Ingeniería Eléctrica, Universidad Tecnológica de Pereira, Pereira-Colombia, dlguarin@gmail.com

²Departamento de Ingeniería Eléctrica, Universidad Tecnológica de Pereira, Pereira-Colombia, aaog@utp.edu.co

³Grupo MIRP, Centro de Investigación, INSTITUTO TECNOLÓGICO METROPOLITANO, Medellín-Colombia, edilsondelgado@itm.edu.co

Fecha de recepción: 25 de noviembre de 2010 / Fecha de aceptación: 29 de junio de 2011

Resumen

La presencia de una falla en un rodamiento hace que el sistema mecánico evolucione de una dinámica débilmente no lineal a una dinámica fuertemente no lineal, por lo tanto los métodos lineales comunes en el dominio del tiempo y la frecuencia no son adecuados para el diagnóstico de rodamientos. En el presente artículo se propone una metodología novedosa no lineal para la detección de fallas en rodamientos, que usa la medida de complejidad sugerida por Lempel y Ziv para caracterizar las señales de vibración. La ventaja principal de este método sobre las demás técnicas de análisis no lineal es que no requiere la reconstrucción de un atractor, por lo que es adecuado para realizar análisis en tiempo real. Los resultados obtenidos muestran que la complejidad de Lempel-Ziv es una herramienta efectiva para el diagnóstico de rodamientos.

Palabras clave: Diagnóstico de rodamientos, Complejidad de Lempel-Ziv, Análisis de señales de vibraciones.

Abstract

The presence of a fault in a bearing makes the mechanical system evolve from a weakly nonlinear dynamic to a strong non-linear dynamic; therefore the linear methods in time and frequency are not suitable for bearing diagnosis. This article uses a novel nonlinear method for bearing diagnosis, which uses the complexity measure suggested by Lempel and Ziv to characterize the vibration signals. The main advantage of this method over other nonlinear analysis techniques is that it does not require the reconstruction of an attractor; therefore it is suitable for on-line analysis. The results show that the Lempel-Ziv complexity is an effective tool for bearing diagnosis.

Keywords: Bearings diagnosis, Lemple-Ziv Complexity, vibration signals analysis.

1. Introducción

El análisis basado en las señales de vibración ha sido la técnica más usada para la detección y diagnóstico de defectos en máquinas rotativas, como las fallas en rodamientos, lo cual es de vital importancia en la industria ya que evita las paradas indeseadas, permitiendo ahorrar tiempo y disminuir el desperdicio de materia prima. Tradicionalmente, esta técnica de diagnóstico involucra el análisis de las señales de vibración en los dominios del tiempo y/o la frecuencia. En el dominio del tiempo, parámetros estadísticos tales como la raíz media cuadrática (RMS), kurtosis, el factor de cresta, el sesgo, entre otros, se calculan para detectar la existencia de fallas (Tandon & Choudhury, 1997; Heng & Ñor, 1998; Li & Wu, 1989; Williams et al., 2001).

Estas estadísticas poseen la ventaja que se calculan rápidamente, desafortunadamente, no son efectivas a la hora de detectar fallas incipientes en rodamientos. El análisis en frecuencia, basado en la transformada de Fourier, es quizás el método más usado en la industria para el diagnóstico de fallas (Taylor, 2003). Este análisis requiere la selección inteligente de un ancho de banda, el cual depende de la geometría del rodamiento y las condiciones de operación, esto implica que para cada rodamiento se debe identificar una banda de frecuencia la cual permitirá el posterior análisis, por lo tanto el análisis basado en la transformada de Fourier no es un buen candidato para la detección y diagnóstico automático de fallas.

Otras técnicas en el dominio de la frecuencia tales como el análisis cepstrum (Tandon, 1994), análisis de la señal envolvente (Jones, 1996), cancelación adaptativa del ruido (Ho & Randall, 2000) y de-noising (Bolaers et al., 2004) se han usado para el diagnóstico de fallas, pero la exactitud de estos métodos al igual que el análisis de Fourier, depende en gran medida de las dimensiones del rodamiento y las condiciones de operación. Recientemente métodos basados en análisis tiempo-frecuencia tales como la transformada corta de Fourier (Li & Wu, 1989), la distribución Vigner-Ville (Staszewski et al., 1997) y el análisis wavelet (Li & Ma, 1997) se han usado para la detección de fallas en rodamiento y se ha encontrado que dichos métodos de análisis son más efectivos que los mencionados anteriormente.

Un inconveniente común de las técnicas mencionadas, radica en el supuesto de que se está supervisando un sistema físico que posee una función de transferencia lineal, donde el principio de superposición se aplica. Esto significa que la respuesta de la máquina a múltiples entradas (e.g., falla en diferentes posiciones de la máquina) se obtendrá al observar una entrada a la vez, y posteriormente adhiriendo los resultados individuales. Sin embargo, se ha mostrado en Harsha (2006) que el mejor modelo para un rodamiento está basado en la teoría Hertziana de contacto, en la cual se asigna una relación no lineal entre la fuerza ejercida sobre un resorte y su deformación. Adicionalmente se mostró qué cambios en la holgura, la velocidad de operación, la carga y la fricción pueden hacer que el sistema dinámico se comporte de manera caótica. Por lo tanto, las técnicas que asumen que el sistema dinámico es lineal (i.e., satisface el principio de superposición), no pueden identificar las verdaderas características de falla, ya que estas pertenecen a un sistema dinámico no lineal.

En la actualidad es posible encontrar una vasta cantidad de artículos donde se utilizan técnicas de análisis no lineal para el diagnóstico de rodamientos, siendo la más popular la dimensión de correlación (d2). En los estudios presentados por (Logan & Matew, 1996a; 1996b) se muestra que el valor de d2 es diferenciable entre un rodamiento normal y uno con alguno de los principales defectos en rodamientos (e.g., defecto en elemento rodante, en carril interno y carril externo). Sin embargo, el cálculo de la dimensión de correlación requiere de una gran cantidad de datos, una selección inteligente de la región de escalamiento y un tiempo computacional sustancial (Mekler, 2008). Por lo tanto, este tipo de medidas de complejidad no son adecuadas para el diagnóstico en tiempo real de la condición de rodamientos. Aunque en la literatura reciente se reportan procedimientos para el entrenamiento mediante penalizaciones basadas en complejidad para incrementar la robustez en la detección automática de eventos que pueden ser fisiológicos o mecánicos (Delgado, et al., 2011), las técnicas de dinámica no lineal conllevan esfuerzos computacionales inherentes al proceso que no dependen de los métodos de entrenamiento.

La medida de complejidad de Lempel-Ziv (complejidad LZ)  es una estadística que puede ser utilizada como una herramienta alternativa para el análisis de señales provenientes de un sistema dinámico no lineal. En estudios realizados en el campo de la bioingeniería se ha encontrado que la complejidad es útil para monitorizar el efecto de la anestesia en pacientes (Zhang & Roy, 1999), de este estudio se pudo apreciar que cuando el paciente estaba despierto (mayor actividad cerebral) el valor de la complejidad LZ del EEG era mayor que el calculado cuando el paciente estaba dormido. Un estado entre despierto y dormido tenía un valor de complejidad LZ intermedio. También se ha utilizado para la detección de taquicardia ventricular (Zhang, Zhu, Thakor, & Wang, 1999), en este estudio se mostró que la complejidad LZ posee una marcada ventaja a la hora de detectar la taquicardia ventricular comparado con otros métodos en el dominio del tiempo y la frecuencia.

Recientemente se usó la complejidad LZ para monitorear pacientes con riesgos cardíacos en un periodo de 24 horas (Ferrairo et al., 2004), se pudo concluir que esta medida es sensible a pequeñas variaciones del pulso cardíaco y que es útil para el monitoreo en línea. Qu & Jiang (1998) calcularon el valor de la complejidad para el monitoreo de grandes máquinas rotativas y se encontró que variaciones mínimas en la condición de funcionamiento de la máquina generaban alteraciones en el valor de la complejidad; dichas variaciones no fueron detectadas con otras estadísticas calculadas en el dominio del tiempo.

En Yan & Gao (2004) se presentó uno de los pocos estudios donde se utiliza la complejidad LZ para el diagnóstico de fallas en rodamiento y en este estudio se encontró que la complejidad LZ es útil para diferenciar entre rodamientos sin falla y con falla. También se determinó que el valor de la complejidad es independiente de la carga axial que se le ejerce al rodamiento, pero no de la velocidad de operación. Recientemente, se presentó en Hong & Liang (2009) un nuevo estudio sobre la aplicación de la complejidad LZ para la detección de fallas en máquinas rotativas, donde fueron validados los resultados obtenidos en Yan & Gao (2004).

En comparación con la dimensión de correlación, y en general con la mayoría de estadísticas no lineales, la complejidad LZ tiene bajo costo computacional (Small, 2005), ya que no involucra la reconstrucción del atractor en el espacio de estados a partir de la serie temporal. Esto la hace viable para formar parte de un sistema de diagnóstico de rodamientos en tiempo real. El presente documento está organizado de la siguiente manera: En la sección 2 se muestra el algoritmo para calcular la complejidad LZ de una serie temporal, se introduce la base de datos y se presenta la metodología propuesta para la detección de fallas en rodamientos. Posteriormente en la sección 3 se analiza la viabilidad de la complejidad LZ para la detección de fallas incipientes además se presentan los resultados obtenidos al aplicar la metodología propuesta a la base de datos. Finalmente en la sección 4 se presentan las conclusiones a las que se pudo llegar gracias al presente estudio.

2. Materiales y métodos

2.1 Base de datos

La base de datos utilizada fue tomada del Bearing data center de la universidad de Case Western (C.W.R. University, 2010). Estos registros fueron adquiridos por medio de un acelerómetro adherido a la carcasa de rodamientos normales y defectuosos, en la base de datos se varía la carga del motor y el tamaño de la falla. Todas las fallas tienen una profundidad de 0,2827 mm. Las fallas se pueden diferenciar en tres tipos: Falla en los elementos rodantes, falla en el carril interno y falla en el carril externo. Dichas fallas fueron generadas con un lápiz eléctrico, por lo tanto son fallas localizadas. Los datos se capturaron a 24 kHz; la velocidad del eje υ_eje varía de acuerdo a la carga del motor como se muestra en Tabla 1. Para todas las pruebas se usaron rodamientos SKF 6205-2RS JEM.

Además de la base de matos mencionada se realizaron pruebas con señales simuladas, estas señales se generaron teniendo en consideración que la energía de una señal de vibración de un rodamiento en condiciones normales de funcionamiento de distribuye principalmente entre la frecuencia de paso de la bola (f_pb) y unos cuantos armónicos (Yan & Gao, 2004).

2.2 Complejidad de Lempel-Ziv

La complejidad de Lempel-Ziv es una medida de la regularidad de una secuencia simbólica. Cuando se estima la complejidad de una serie de tiempo es necesario primero emplear algún esquema de codificación para convertir los datos de alta precisión en secuencias de elementos que pertenecen a un conjunto pequeño y finito. La complejidad algorítmica se define como el número de secuencias que se observan en una secuencia simbólica como una fracción del máximo número posible de secuencias. El máximo número de secuencias posible son las que se observan para una secuencia aleatoria de símbolos.

La complejidad LZ es equivalente al radio de compresión ofrecido por el algoritmo de Lempel y Ziv (Ziv & Lempel, 1978). Para una serie temporal, la complejidad LZ es usada como una medida de la estructura subyacente en la serie temporal. Sin embargo, el cálculo de la complejidad para el análisis no lineal de series temporales depende de la elección de un buen esquema de codificación. El esquema de codificación se refiere a una operación g la cual transforma cada dato de la serie temporal {X_n} en un símbolo que pertenece a un alfabeto A. Es decir g(X_n) ∈ A donde A = {a₁, a₂, ..., a_d} es algún alfabeto de d símbolos.

La complejidad algorítmica se calcula de la siguiente manera:

Sea S una secuencia de símbolos de tamaño n la cual está dada por S = (S₁, S₂, ..., S_n) donde cada S_i es uno de los d símbolos, S_i ∈ A = {a₁, a₂, ..., a_d}. Para el caso binario A = {0, 1}, i.e. S está compuesta solo de ceros y unos. Para el caso general, sea A un alfabeto de d (d ≥ 2) símbolos. Sea c(n) un contador de las nuevas sub-secuencias de la secuencia S; P y Q denotan dos secuencias que son sub-cadenas de S; PQ es la concatenación P y Q; PQπ representa una secuencia que es la concatenación de P y Q con el último símbolo borrado. Sea υ(PQπ) todas las sub-cadenas de PQπ. Para calcular la complejidad LZ de la secuencia S = {S_i}_{i = 1, 2, ... n’} donde S_i ∈ A, se procede de la siguiente manera:

a) Se inicializa c(n) = 1, P = S₁ y Q = S₂. Entonces PQπ = S₁. Si Q ∈ υ(PQπ), se deja P sin alterar y se actualiza Q = S₂, S₃; si Q ∉ υ(PQπ) se hace c(n) = c(n) + 1, se actualiza P = S₁, S₂ y Q = S₃; b) Suponga ahora que P = S₁S₂...S_r, Q = S_r+1. Si Q ∈ υ(PQπ), se deja P sin alterar y se actualiza Q = S_r+1 S_r+2, y luego se observa si Q ∈ υ(PQπ). Se repite la comparación anterior hasta que Q ∉ υ(PQπ). Entonces c(n) = c(n) + 1. Suponga que Q = S_r+1 S_r+2 S_r+i en este momento. Entonces P se actualiza a P = S₁S₂...S_rS_r+1S_r+2...S_r+i y se hace Q = S_r+i+1; c) Se repite el paso b) hasta que Q alcance la última cadena de S = {S_i}_{i = 1, 2, ... n}. Así se termina el cálculo de la complejidad c(n) de la secuencia S Para un alfabeto de d símbolos y una secuencia de tamaño n se mostró (Lempel & Ziv, 1976) que

Dado que ε_n → 0 cuando n → ∞, entonces

Por lo tanto es más práctico considerar la complejidad Lempel-Ziv normalizada

2.3 Detección de fallas en rodamientos utilizando la complejidad de Lempel-Ziv

Para la detección de fallas en rodamientos utilizando la complejidad de Lempel-Ziv normalizada, expresada en (4), como característica discriminante y se propone el siguiente procedimiento:

2.3.1 Pre-proceso

El pre-proceso para las señales de vibración de máquinas rotativas fue propuesto por Logan & Matew (1996), este consiste en tipificar la señal (restar la media y dividir por la desviación estándar) y posteriormente aplicar un filtro pasa-bajos a la señal con una frecuencia de corte muy superior a la (f_pb).

2.3.2 Selección del tamaño del segmento

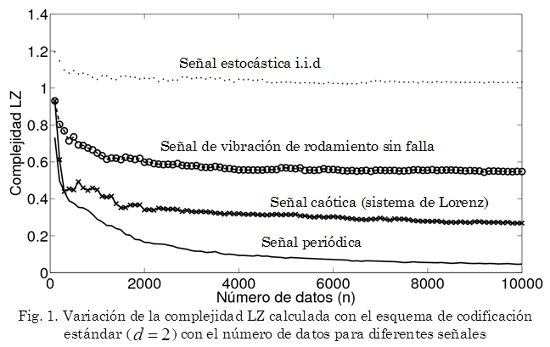
A pesar que el valor de la complejidad LZ se normaliza para hacerla independiente del número de datos, se ha mostrado (Hu & Principe, 2006) que con n < 10³ los cálculos de la complejidad LZ no son estables. Después de algunas observaciones fue posible notar que el número de datos necesario para que el valor de la complejidad LZ se estabilice depende de la dinámica del sistema que generó la señal. En la Fig. 1 se muestran la cantidad de datos necesarios para obtener un valor estable de la complejidad de LZ para señales provenientes de diferentes sistemas dinámicos. En general, se encontró que n ≈ 2¹² es suficiente para las señales de vibración.

2.3.3 Esquema de codificación

En general el valor de la complejidad LZ depende del esquema de codificación elegido (Small, 2005). En la literatura es posible encontrar tres esquemas de codificación, dos de ellos diseñados para mapas y un tercero para flujos, en este caso se analizarán los dos primeros (dado que se están analizando señales discretas). El primer esquema de codificación conocido como esquema de codificación estándar es un esquema de codificación cuantificado. Para realizar la codificación, primero se elige la cantidad de símbolos d del alfabeto A, posteriormente se divide el rango de valores de la señal a convertir en d bins equi-probables y a cada dato de la señal se le asigna un elemento del alfabeto de acuerdo al bin en que se encuentre. Con este esquema de codificación es posible tener alfabetos de d ≥ 2

El segundo esquema de codificación es conocido como esquema de codificación diferencial y es un esquema de codificación no cuantificado, en este solo se permiten alfabetos binarios o ternarios. Para el alfabeto binario se simboliza con 1 si la señal es creciente (X_i+1 > X_i) y con 0 si la señal es decreciente o no cambia (X_i+i ≤ X_i). Para el alfabeto ternario se simboliza con 1 si la señal es creciente (X_i+1 > X_i), con 0 si la señal es decreciente (X_i+1 < X_i) y 2 si la señal no cambia (X_i+1 = X_i)

2.3.4 Calculo de la complejidad de Lempel-Ziv

Una vez la señal ha sido pre-procesada, se ha elegido el segmento de la señal adecuado y se ha transformado dicho segmento por medio del esquema de codificación elegido, es posible obtener la el valor de la complejidad de Lempel-Ziv de dicho segmento por medio de la aplicación del algoritmo descrito anteriormente.

Una vez aplicada la metodología a una señal de vibración se obtiene un único número el cual caracteriza la señal, dicho número puede ser utilizado posteriormente para detectar fallas en rodamiento por medio de algún método de clasificación (e.g. K vecinos más cercanos).

3. Resultados y discusión

3.1 Validación del uso de la complejidad de Lempel-Ziv para la detección temprana de fallas en rodamientos

Para ilustrar la relevancia de la complejidad LZ para la detección temprana de fallas en rodamientos, se comparan los valores obtenidos de la complejidad y otras herramientas de caracterización normalmente usadas para el análisis de señales de vibración (e.g. rms, kurtosis, análisis espectral), para una señal de vibración simulada. Según Yan & Gao (2004) la mayor parte de la energía de una señal de vibración de un rodamiento en buenas condiciones está concentrada en la f_pb (la cual depende de la geometría del rodamiento y de su velocidad de operación) y en unos pocos armónicos. Por lo tanto es posible construir una señal que simule la vibración de un rodamiento en buenas utilizando (5)

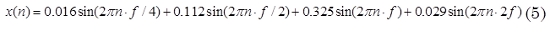
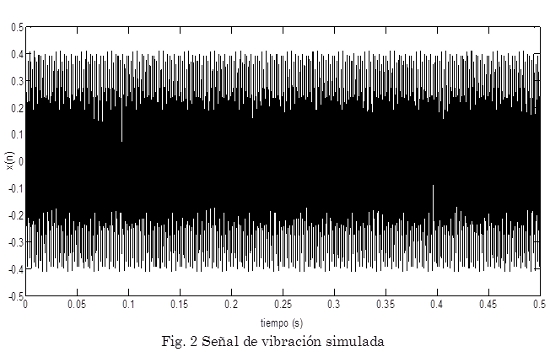
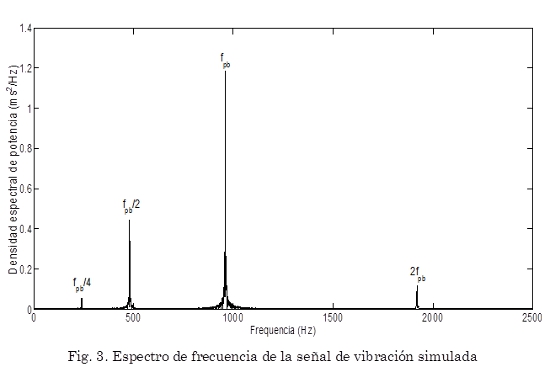
Donde f = 960 Hz. La señal y su espectro de frecuencias se muestran en las Fig. 2 y 3. respectivamente; la señal se muestreo a 5000 Hz y se utilizaron 0,5 s para el análisis. Para las siguientes pruebas se le añadió ruido blanco gaussiano a (5) de la siguiente forma

y la relación entre la señal y el ruido (SNR) medida en decibeles está dada por la ecuación (7):

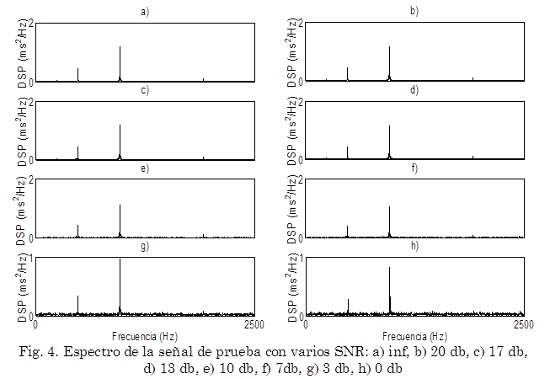
Dónde 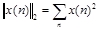. Si e(n) = 0  para todo n entonces SNR = inf. En la 2 se observa como varía el espectro de potencia de la señal de prueba con la SNR.

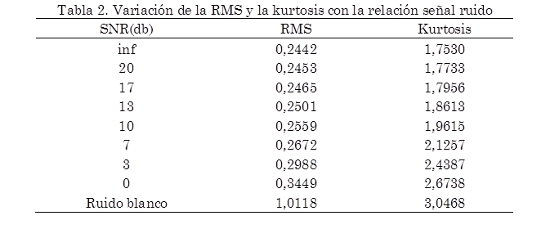
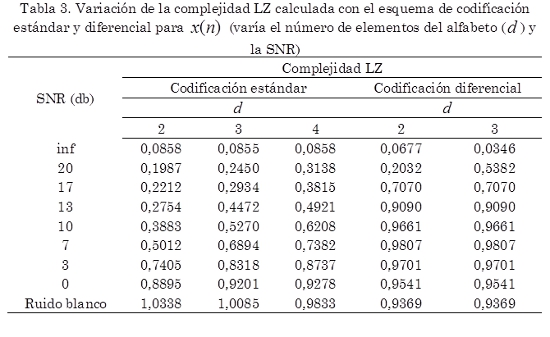
En la Tabla 2 se observa como varía la raíz media cuadrática (RMS) y la kurtosis con la relación señal ruido. En la Tabla 3 se muestra la variación de la complejidad LZ calculada con el esquema de codificación estándar cuando se varía el número de elementos del alfabeto d y la relación señal ruido. En la Tabla 1 se muestra la variación de la complejidad LZ calculada con el esquema de codificación diferencial cuando se varía el número de elementos del alfabeto d y la relación señal ruido.

En la Tabla 2 se puede notar que la RMS varía aproximadamente 0,1 cuando la señal pasa de no tener ruido (SNR = inf) a tener un SNR = 0 db. Esto indica que la RMS es poco sensible a la presencia de ruido aditivo. Lo cual la hace una mala herramienta para la detección de fallas en estado temprano en un rodamiento (esto debido a que la presencia de una falla incipiente en un rodamiento adhiere componentes de baja energía en todo el espectro (Ghafari et al., 2008), lo cual es un fenómeno similar al que se obtiene al adherir ruido blanco a una señal). De la Fig. 4. se observa que la diferencia entre el espectro de frecuencias de la señal simulada sin ruido (Fig. 4a) y los diferentes valores de la relación señal ruido (Fig. 4b y h) es mínima, de hecho se requiere de un experto entrenado para poder detectar las diferencias entonces, utilizando este método se descarta la posibilidad de un sistema automático de detección de fallas incipientes.

En la Tabla 2 se nota que hay una diferencia cercana a la unidad para la kurtosis calculada a la señal sin ruido y a la señal con una SNR = 0 db, esto indica que es una estadística sensible a la presencia de ruido en una señal. Pero cuando SNR > 13 db, la kurtosis cambia muy poco; por lo tanto la kurtosis puede arrojar buenos resultados a la hora de detectar falla en rodamientos, siempre y cuando estas fallas no sean incipientes.

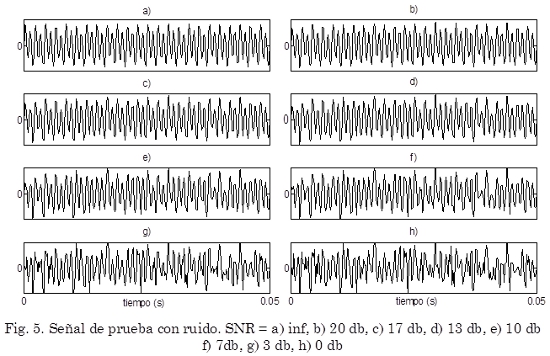
Es importante anotar que en la Tabla 1 se presentan los valores de la complejidad LZ calculada con los dos esquemas de codificación mencionados anteriormente y para varios valores de d. Se nota que la diferencia entre una señal sin ruido y una señal con SNR = 20 db es considerable, por lo tanto se puede concluir que la complejidad LZ es sensible a la presencia de ruido aditivo de muy baja magnitud. En la Fig. 5. se observa que la diferencia entre una señal sin ruido y una señal con SNR = 20 db es muy poca, y de las estadísticas utilizadas únicamente la complejidad LZ es capaz de detectar de manera considerable la diferencia entre ambas señales.

Se observa también en la Tabla 1 que si se aumenta el número de elementos del alfabeto se aumenta la sensibilidad de la complejidad LZ calculada con el esquema de codificación estándar al ruido de baja magnitud, pero al mismo tiempo se obtienen valores de complejidad LZ altos con valores de la relación señal ruido no tan altos. Por ejemplo, para d = 2 la diferencia que se obtiene al calcular la complejidad LZ cuando SNR = 3 db y SNR = 0 db es alrededor de 0,1490, pero cuando d = 4 la diferencia se reduce a 0,0541. Se nota además que la complejidad LZ calculada con el esquema de codificación diferencial es muy sensible al ruido, pero esta misma sensibilidad hace que se sature muy rápido, para esta estadística tener un SNR < 10 db es lo mismo que tener ruido blanco. Se puede observar entonces que no existe diferencia entre los resultados obtenidos con el alfabeto binario y el ternario, esto debido a que la señal varía rápidamente y existen pocos elementos consecutivos idénticos.

A continuación se presentarán resultados donde sólo se considera el esquema de codificación estándar, ya que como se comprobó, la complejidad LZ calculada con el esquema de codificación diferencial es muy sensible al ruido pero a su vez se satura muy rápido, lo cual la hacer una gran herramienta para detectar fallas pero posiblemente sea incapaz de discriminar entre diferentes tamaños y ubicación de la falla.

3.2 Diagnóstico de Rodamiento Utilizando la Complejidad de Lempel-Ziv

Siguiendo el método propuesto en el presente documento, cada señal se tipificó y se le aplicó un filtro pasa-bajo con una frecuencia muy superior a la f_pb, la cual según Hong & Liang (2006) para un rodamiento 6205-2RS JEM SKF sano se puede determinar a partir de la υ_eje de (8)

En este caso se utilizó un filtro Butterworth pasa bajo de orden 10 con una frecuencia de corte de 2,5 kHz. Es necesario mencionar que el filtrado solo se aplica para eliminar las componentes de muy alta frecuencia que no aportan información significativa, así que no es necesario seleccionar un valor de frecuencia de corte específico para cada rodamiento, solo uno lo suficientemente alto. El valor de 2,5 kHz se puede utilizar de forma general.

3.2.1 Dependencia con la carga del motor

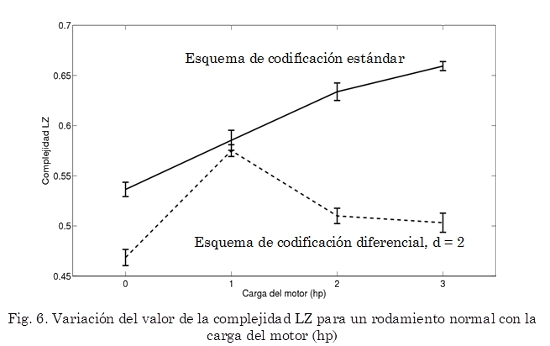
En la Fig. 6. se muestra cómo varía la complejidad LZ calculada a un rodamiento normal cuando varía la carga del motor. Se observa que la complejidad LZ para un rodamiento sin falla depende de la carga del motor, para el esquema de codificación estándar se nota que la complejidad varía casi linealmente con la carga del motor, es decir a mayor carga mayor la complejidad LZ de la señal; este mismo fenómeno no ocurre con el esquema de codificación diferencial, pero como ya se mencionó, con este esquema de codificación la complejidad LZ se satura. De hecho el fenómeno que se presenta en la Fig. 6 también ocurre en la Tabla 1 donde la complejidad LZ para el ruido blanco tiene un valor menor que la señal de prueba con un SNR = 10 db.

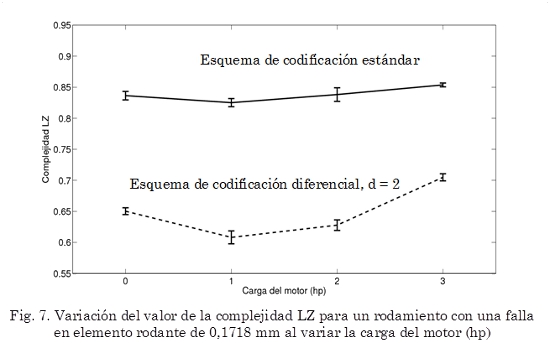
En la Fig. 7 se observa que cuando existe una falla en el rodamiento (en este caso en elemento rodante) la complejidad LZ es casi constante para las diferentes cargas del motor (por lo menos para el esquema de codificación estándar).

3.2.2 Dependencia con el tamaño de la falla

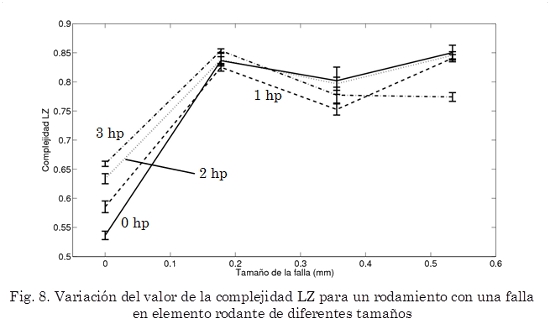
En la Fig. 8 se muestra como varía la complejidad LZ al aparecer una falla en el elemento rodante y al ir aumentando de tamaño. Es posible observar que con la estadística utilizada se obtiene la detección (i.e., diferencia explícita cuando un rodamiento tiene falla y cuando no la tiene), pero no es posible diferenciar entre los diversos tamaños de falla. En la gráfica se incluye el comportamiento cuando se varía la carga del motor, por lo que se nota que a mayor carga es menor la diferencia entre rodamiento sin falla y con falla, por lo tanto a medida que aumente la carga del motor será imposible detectar cuando se presenta una falla. Un fenómeno similar ocurre cuando la falla se encuentra en el carril externo y en el carril interno, si no hay carga o esta es pequeña (≤ 1 hp) siempre es posible diferenciar entre rodamiento con falla y sin falla, pero a medida que aumenta la carga del rodamiento la diferencia se reduce y se hace más complicada la correcta detección de la falla.

3.2.3 Dependencia con la ubicación de la falla

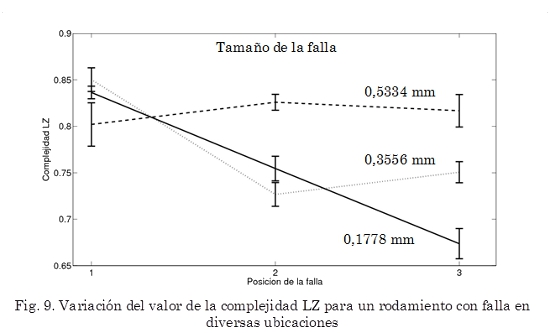
Un sistema de diagnóstico no sólo debe ser capaz de identificar la presencia de una falla en el rodamiento, también debe poseer la capacidad para discriminar en qué zona se produjo la falla. En las siguientes gráficas, la posición de la falla se distribuye de la siguiente manera: (1) Falla en elemento rodante; (2) Falla en carril interno; (3) Falla en carril externo. En la Fig. 9 se observa que para fallas con un tamaño de 0,1778 mm es posible por medio de la complejidad LZ identificar en qué lugar del rodamiento ocurrió la falla pero para fallas de mayor tamaño no se puede identificar su ubicación. Un fenómeno similar ocurre cuando la carga del motor es diferente de cero. Para una carga de 3 hp no es posible identificar la ubicación de la falla con ningún tamaño.

3.2.4 Tiempo de cómputo

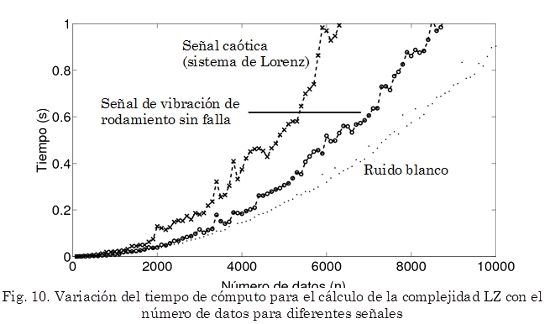
Se realizaron una serie de pruebas en un computador dotado con un procesador Intel Centrino Duo a 1,83 GHz con 2 Gb de RAM. Se tomaron tres señales provenientes de diferentes sistemas dinámicos, los resultados se presentan en la Fig. 10. Es posible notar que para cualquiera de las señales con n ≤ 2¹² el tiempo de cómputo para calcular la complejidad LZ no es superior a 0,4 s (para la señal de vibración este tiempo es cercano a 0,2 s), esto indica que es posible realizar un diagnóstico en línea de rodamiento utilizando la complejidad LZ.

4. Conclusiones

En la actualidad, el diagnóstico de rodamientos usualmente se realiza por medio del análisis de Fourier de la señal de vibración, pero esto implica conocer las propiedades geométricas del rodamiento, las condiciones de operación y contar con una persona entrenada en dicho análisis, lo cual suele llevar largo tiempo. En el presente estudio se propone una metodología por medio de la cual utilizando la complejidad de Lempel-Ziv fue posible diagnosticar el estado de un rodamiento sin necesidad de conocer sus propiedades. También se pudo demostrar que la complejidad LZ es más sensible a la presencia de ruido aditivo de pequeña magnitud que otros métodos como la RMS o la Kurtosis. Debido a esto, es posible asegurar que el método aquí presentado es adecuado para el diagnóstico de rodamientos.

Con las pruebas realizadas sobre señales simuladas se determinó que el número de datos mínimo para que la complejidad LZ sea independiente del tamaño de la señal depende de la dinámica de la señal (i.e., si posee alguna dinámica o no), y de las características de la dinámica. Se encontró que con n ≥ 2¹² se tiene un valor estable para cualquier señal.

Gracias a las pruebas realizadas a la base de datos, se pudo demostrar que cuando no existe falla en el rodamiento, la complejidad LZ depende de la carga del motor, pero cuando se presenta una falla en el rodamiento esta dependencia desaparece. También se pudo determinar que cuando el motor se utiliza en vacío (sin carga) existen diferencias significativas entre la complejidad LZ de la señal de un rodamiento sin falla y uno con falla de diferentes tamaños. Adicionalmente se encontró que cuando no existe carga en el motor la complejidad LZ sirve para localizar el lugar del rodamiento donde se presenta la falla.

Finalmente, gracias al estudio sobre el tiempo de cómputo necesario para calcular la complejidad LZ a señales de diferente índole y diferentes longitudes fue posible verificar que es posible implementar un sistema de diagnóstico de rodamientos en tiempo real. Por lo tanto, se puede concluir que la complejidad de Lempel Ziv es una herramienta adecuada para el diagnóstico de rodamientos y debe ser considerada para su implementación en la industria.

5. Agradecimientos

D. L. Guarín fue patrocinado por el programa jóvenes investigadores e innovadores de Colciencias, año 2011. E. Delgado agradece al Centro de Investigación del Instituto Tecnológico Metropolitano –ITM a través del proyecto P09225.

Referencias

Bolaers, F., Cousinard, O., Marconnet, P., Rasolofondraibe, L., (2004); Advanced detection of rolling bearing spalling from denoising vibratory signals, Control Engineering Practice, 12, 181-190.         [ Links ]

C.W.R., University, (2010); Bearing data center, Obtenido de http://www.eecs.case.edu/laboratory/bearing/download.htm        [ Links ]

Delgado, E., Sepúlveda, F.A., Röthlisberger, S., Castellanos, G., (2011); The rademacher complexity model over acoustic features for improving robustness in hypernasal speech detection. In Book: Computers and Simulation in Modern Science, Volume V, WSEAS Press, University of Cambridge, UK, 130-135.         [ Links ]

Ferrairo, M., Signorini, M., Cerutti, S., (2004); Complexity analysis of 24 hours heart rate variability time series, International Conference of the IEEE EMBS, San Francisco, CA (USA), 3956-3959.         [ Links ]

Ghafari, S., Golnaraghi, F., Ismail, F., (2008); Effect of localized faults on chaotic vibration of rolling element bearings, Nonlinear Dynamics, 53, 287-301.         [ Links ]

Harsha, S., (2006); Nonlinear dynamic analysis of a high-speed rotor supported by ball bearings, Sound and Vibration, 290(1-2), 65-100.         [ Links ]

Heng, R., Ñor, M., (1998); Statistical analysis of sound and vibration signals for monitoring rolling element bearing condition, Applied Acoustics, 53(1), 211-226.         [ Links ]

Ho, D., Randall, R., (2000); Optimization of bearing diagnostic techniques using simulated and actual bearing fault signals, Mechanical Systems and Signal Processing, 14(5), 763-788.         [ Links ]

Hong, H., Liang, M., (2006); De-noising mechanical signals by hybrid thresholding, IEEE International Workshop on Robotic and Sensors Environments, Ottawa, Canada, 65-70.         [ Links ]

Hong, H., Liang, M., (2009); Fault severity assessment for rolling element bearings using the Lempel-Ziv complexity and continuous wavelet transform, Journal of Sound and Vibration, 320, 452-468.         [ Links ]

Jones, R., (1996); Enveloping for bearing analysis, Sound and Vibration, 30, 10-15.         [ Links ]

Lempel, A., Ziv, J., (1976); On the complexity of finite sequences, IEEE Transaction on Information Theory, 22(1), 75-81.         [ Links ]

Li, C., Ma, J.. (1997); Wavelet decomposition of vibrations for detection of bearing localized defects. NDT & E. International, 30, 143-149.         [ Links ]

Li, C., Wu, S.. (1989); On-line detection of localized defects in bearings by pattern recognition analysis. Journal of Engineering for Industry, 111, 331-336.         [ Links ]

Logan, D., Matew, J., (1996a); Using the correlation dimension for vibration fault diagnosis of rolling element bearings. Basic concepts, Mechanical Systems and Signal Processing, 10(3), 241-264.         [ Links ]

Logan, D., Matew, J., (1996b); Using the correlation dimension for vibration fault diagnosis of rolling element bearings. Selection of experimental parameters, Mechanical Systems and Signal Processing, 10(3), 251-264.         [ Links ]

Mekler, A., (2008); Calculation of EEG correlation dimension: Large massifs of experimental data, Computer Methods and Programs in Biomedicine, 92(1), 154-160.         [ Links ]

Qu, L., Jiang, J.D., (1998); The complexity analysis of vibration signals of large rotating machinery, Journal of Xi'an Jiaotong University, 32(6), 31-35.         [ Links ]

Small, M., (2005); Applied nonlinear time series analysis, Applications in physics, physiology and finance, World Scientific.         [ Links ]

Staszewski, W., Worden, K., Tomlinson, G., (1997); Time-frequency analysis in gearbox fault detection using the wigner-ville distribution and pattern recognition, Mechanical Systems and Signal Processing, 11(5), 673-692.         [ Links ]

Tandon, N., (1994); A comparison of some vibration parameters for the condition monitoring of rolling element bearing, Journal of the International Measurement Confederation, 12(3), 285-289.         [ Links ]

Tandon, N., Choudhury, A., (1997); An analytic model for ball bearing vibrations to predict vibration response to distributed defects, Sound and Vibrations, 205(3), 275-292.         [ Links ]

Taylor, J., (2003); The vibration anaylsis handbook, 2 ed., VCI.         [ Links ]

Williams, T., Ribadeneira, X., Billington, S., Kurfess, T., (2001); Rolling element bearing diagnostics in run to failure lifetime testing, Mechanical system and signal processing, 15(5), 979-993.         [ Links ]

Yan, R., Gao, R., (2004); Complexity as a measure for machine health evaluation, IEEE Transaction on Instrumentation and Measurement, 53(4), 1327-1334.         [ Links ]

Zhang, X., Roy, R., (1999); Predicting movement during anaesthesia by complexity analysis of electroencephalograms, Medical and Biological Engineering and Computing, 37(3), 327-334.         [ Links ]

Zhang, X., Zhu, Y., Thakor, N., Wang, Z., (1999); Detecting ventricular tachycardia and fibrillation by complexity measure, IEEE Transaction on Biomedical Engineering, 46(5), 548-555.         [ Links ]

Ziv, J., Lempel, A., (1978); Compression of individual sequences via variable-rate coding, IEEE Transaction on Information theory, 24(5), 530-536.         [ Links ]