Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
TecnoLógicas
versão impressa ISSN 0123-7799versão On-line ISSN 2256-5337
TecnoL. no.27 Medellín jul./dez. 2011
Artículo de Investigación/Research Article
Configuración de Vórtices en Películas Finas: Teoría Ginzburg-Landau No Lineal
José José Barba-Ortega1, Miryam Rincón-Joya2
1Facultad de Ciencias, Departamento de Física, Universidad Nacional de Colombia, Bogotá-Colombia, jjbarbao@unal.edu.co
2Facultad de Ciencias, Departamento de Física, Universidad Nacional de Colombia, Bogotá-Colombia, mrinconj@unal.edu.co
Fecha de recepción: 25 de febrero de 2011 / Fecha de aceptación: 25 de agosto de 2011
Resumen
En este trabajo investigamos teóricamente el estado de Shubnikov en una película superconductora con sección transversal cuadrada con un defecto inserido en su centro. La muestra está inmersa en un campo magnético uniforme y homogéneo aplicado perpendicularmente a su plano. Asumimos que el defecto interno está lleno de un material metálico. La presencia de dicho material se simula mediante las condiciones de contorno de de Gennes, vía la longitud de extrapolación, parámetro b>0. Utilizando la teoría Ginzburg-Landau dependiente del tiempo con el método de variables de unión, estudiamos el número de vórtices, supercorrientes, curvas de magnetización y energía libre en función del campo magnético aplicado. Espontáneamente una interacción de un par vórtice-antivórtice (V-AV) dentro de la muestra puede aparecer. Esta interacción puede ocurrir dentro o fuera del defecto metálico. Podemos apreciar que la aniquilación del par VAV ocurre cada vez más cerca del defecto a medida que b→0 (materiales más metálicos).
Palabras clave: Parámetro de de Gennes, Ginzburg-Landau, mesoscópico, variables de enlace.
Abstract
In this work, we investigated theoretically the Shubnikov state in a superconducting film with square cross section with a defect inserted in the center. The sample is immersed in a uniform and homogeneous magnetic field applied perpendicular to its plane. We assume that the internal defect is filled with a metallic material. The presence of such material is simulated by the boundary conditions of de Gennes, via the extrapolation length, parameter b> 0. Using the time-dependent Ginzburg-Landau theory with the Link variable method, we analyze the vortex number, supercurrents, magnetization curves and free energy as function of the applied magnetic field. Spontaneously a vortex-anti-vortex pair (V-AV) interaction into the sample can appears. This interaction can occur inside or outside the metal defect. We see that the VAV pair annihilation occurs closer the defect when b→0 (more metallic material).
Keywords: De Gennes parameter, Ginzburg-Landau, mesoscopic, link variable.
1. Introducción
El comportamiento de un material superconductor en contacto con un material metálico es uno de los aspectos de la física de la superconductividad que más ha sido estudiado en los últimos años. Un superconductor puede ser utilizado en la creación de altos campos magnéticos y en generadores, los cuales serían embobinados con superconductores, y estos podrían, a su vez, generar la misma cantidad de electricidad con un menor gasto energético. Las aplicaciones actuales de superconductores de altas temperatura incluyen artefactos magnéticos que protegen sistemas médicos de imagen, SQUIDS, sensores de infrarrojo, aceleradores de partículas, transporte de vehículos de levitación etc. El campo de la electrónica ofrece una magnífica gama de aplicaciones de los superconductores. La aplicación de superconductores en medios de transporte se ha desarrollado usando helio líquido como un refrigerante. Otra aplicación puede verse en medicina, la imagen de resonancia magnética (MRI) juega un papel importante en la medicina de diagnóstico. Los campos magnéticos intensos que se necesitan para estos instrumentos son una aplicación perfecta de superconductores. Es sabido que cuando un superconductor está en contacto con un metal, los efectos de proximidad pueden inducir dominios locales donde la nucleación de la superconductividad es favorecida (Lange et al., 2003; Gillijns et al., 2005). El interés entre superconductividad, magnetismo y materiales metálicos se ha extendido al estudio de nanoestructuras superconductor-ferromagneto, superconductor-superconductor a mayor temperatura critica.
Estudios previos han mostrado que los parámetros críticos superconductores como corriente crítica, campo crítico, temperatura crítica pueden ser modificados fuertemente construyendo estas nanoestructuras (Moshchalkov et al., 1995; 1999; Souza et al., 2006). En trabajos recientes, estudiamos la dinámica de vórtices en muestras en contacto con diferentes tipos de materiales usando la teoría Ginzburg-Landau dependiente del tiempo (Cabral et al., 2010; Barba et al., 2010a; 2010b; 2011) y encontramos que para una interface superconductor-metal el sistema presenta una respuesta completamente diamagnética en la curva de magnetización, mientras que para interfaces superconductor-superconductor su efecto es totalmente paramagnético, el cual se debe a la captura de flujo magnético dentro de la muestra debido a la barrera de energía superficial. Por otra parte la existencia de potenciales de ancoraje representa otra característica importante en la dinámica de vórtices en el superconductor. Dependiendo de los potenciales de ancoraje, estos sistemas cuánticos presentan diferentes estructuras de vórtices los cuales pueden modificar los parámetros críticos. Es también de gran interés el estudio del proceso de aniquilación de un par vórtice-antivórtice.
En los últimos años ha habido varios estudios acerca de la configuración vórtice-antivórtice en superconductores mesoscópicos (Chibotaru et al., 2000; Misko et al., 2003; Berdiyorov et al., 2006; Geurts et al., 2006). Por ejemplo, Sardella (2009) encontró que los vórtices y antivórtices coexisten en equilibrio en configuraciones moleculares. La contribución principal de este trabajo es explorar la configuración de vórtices en un prisma superconductor con sección transversal cuadrada con un defecto en su centro. El defecto está hecho de un material metálico y la muestra está inmersa en un campo magnético paralelo al eje del prisma. Analizamos la nucleación de vórtices y antivórtices incrementando el campo magnético desde cero hasta que el primer par de vórtices sea creado. El campo entonces decrece hasta alcanzar valores negativos, y luego es de nuevo incrementado para cerrar el ciclo de histéresis. En este proceso el vórtice viaja acercándose al centro de la muestra, es luego, atrapado por el defecto metálico, y es aniquilado por el antivórtice creado al invertir la polaridad del campo. Calculamos la magnetización, topología del parámetro de orden y la posición y la velocidad de la singularidad vórtice-antivórtice como función del tiempo.
2. Ecuaciones Ginzburg-Landau dependientes del tiempo
Las ecuaciones Ginzburg-Landau dependientes del tiempo (TDGL) (Thinkham 1996; Bolech et al., 2000) las cuales describen el estado superconductor mediante el parámetro de orden Ψ y el potencial vectorial A en el calibre de campo cero están dadas por:
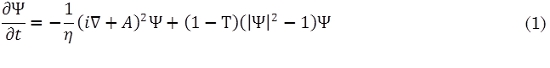
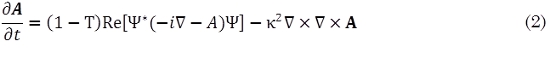
Las ecuaciones (1) y (2) fueron re escaladas de la siguiente forma: el parámetro de orden Ψ en unidades de Ψ∞(0)=(α/β)1/2, donde α y β son dos parámetros fenomenológicos propios del material. Temperaturas en unidades de la temperatura critica Tc, longitudes en unidades de la longitud de coherencia ξ(0) que identifica la caída media de los electrones superconductores dentro del material, tiempo en unidades de t0=πħ / 96KBTc, A en unidades de Hc2(0)Tc(0), donde Hc2(0) es el segundo campo termodinámico, campo en el cual el material pasa del estado superconductor al estado normal. La energía libre de Gibbs en unidades de G0=(αTc)2/β. Las ecuaciones son complementadas por las condiciones de frontera apropiadas para el parámetro de orden. La condición de contorno general para un superconductor, encontrada por de Gennes, está dada por (3):

donde n es el vector unitario, perpendicular a la superficie del superconductor, b es la longitud de extrapolación de de Gennes. Para todas las simulaciones, usamos b>0, cual describe una interface superconductor-metal.
La discretización de las TDGL fue realizada detalladamente por Groop (1996). Usamos el método UΨ para resolver las ecuaciones en una malla discreta, n es el vector unitario perpendicular a la superficie del superconductor, b es la longitud de extrapolación de de Gennes. Para las simulaciones, usamos b>0, cual describe una interface superconductor-metal y b=∞ que describe una interface superconductor-vacío.
3. Resultados y discusión
En nuestra simulación usamos el método de Euler con un espaciamiento de red ax = ay = 0,3 para resolver las ecuaciones en su parte temporal, en una red rectangular de tamaño dy = dx = 30ξ(0) con una temperatura fija T=0, κ=25. El tiempo de relajación fue mantenido fijo en β=1, el parámetro Ginzburg-Landau en κeff = κ2⁄(d2⁄ξ(0)) = 25, correspondiendo, por instancia a una película delgada de Nb con espesor d≈73 nm, asumiendo ξ(0)=40 nm y κ=2,125. La Fig. 1. Muestra la densidad de electrones superconductores mediante el modulo del parámetro de orden superconductor y su fase para una muestra cuadrada de tamaño 30ξ(0)x30ξ(0) a una temperatura T=0, hacia un campo magnético aplicado He=0,21 y He=0,55.
La fase del parámetro de orden superconductor varía desde –π hasta π, así, circulaciones iguales a 2π través de cualquier trayectoria cerrada identifican la presencia de un vórtice en la muestra, así ΔΦ=2πL, donde L indica la vorticidad. En la Fig. 1 (superior), vemos la configuración de vórtices para L=4 en una muestra cuadrada libre de defectos, la variación de fase a través de la muestra es igual a ΔΦ=8π. En la parte inferior de la Fig. 1 la muestra posee dos defectos aislantes, ocho vórtices se acomodan en los defectos, cuatro en cada uno, aunque no son visibles en el diseño de la magnitud del parámetro de orden, existe un cambio de fase igual a ΔΦ= 8π alrededor de cada defecto.
La entrada de los vórtices ocurre a través de los puntos más cercanos en la superficie externa de los huecos. En la Fig. 2 observamos el modulo del parámetro de orden y su fase para una muestra cuadrada con un defecto metálico en su interior caracterizado por (a) b= 0,1 (b) b=1,0 (c) b=10 (d) 1/b=0.
Vemos en la Fig. 2a L=9 vórtices en la muestra, estando todos ellos dentro del defecto, la variación de fase a través de una trayectoria que encierre el defecto es ΔΦ=18π. No obtenemos ninguna información de la vorticidad observando el parámetro de orden en la Fig. 2 (izquierda). La Fig. 2b muestra L=7 vórtices, estando todos ellos ubicados igualmente en el defecto. Las Fig. 2c y 2d, L=6 y L=3 se ubican en el defecto respectivamente y uno de ellos en la parte superconductora. Los vórtices en el defecto metálico repelen los vórtices en la región superconductora, esta repulsión es mayor en cuanto mayor sea el carácter metálico del defecto, a su vez para valores menores de b para un campo magnético constante.
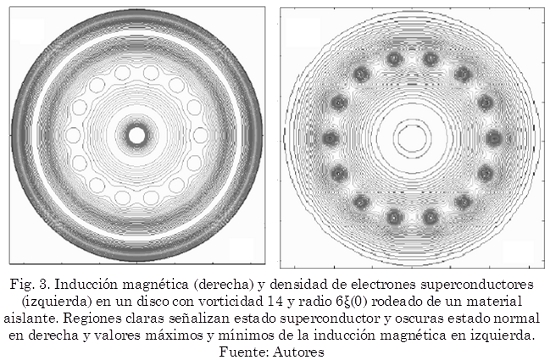
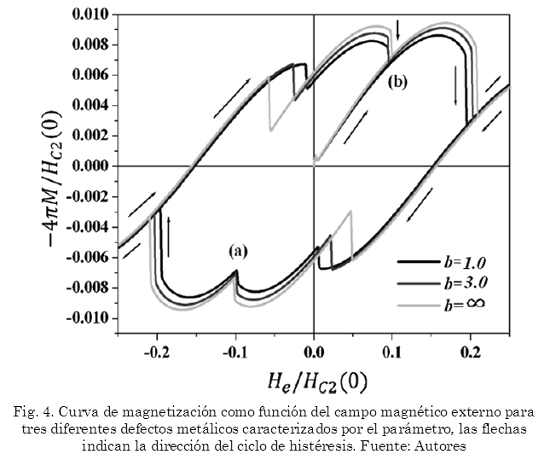
En la Fig. 3 mostramos la inducción magnética y la densidad de electrones superconductores en un estado estacionario para el caso de un disco de radio R=6ξ(0) rodeado de un aislante en un campo magnético He=1,6Hc2(0). En esta interface superconductor vacío o aislante, vemos que la superconductividad es suavemente suprimida en una región cerca a la superficie debido a las corrientes de apantallamiento. La inducción magnética tiene su valor máximo en la superficie de la muestra. La Fig. 4 muestra el ciclo de histéresis para un campo magnético entre +0,3Hc2(0) y -0,3Hc2(0), para varios valores de b. Saltos en la curva de magnetización indican los valores de Ha donde los vórtices o los antivórtices entran en la muestra. El campo magnético es incrementado desde cero hasta un valor en el cual los primeros dos vórtices entran en la muestra, entonces el campo decrece hasta el valor opuesto en el cual dos antivórtices penetran en la muestra.
Los campos magnéticos He/Hc2(0)=0,047; 0,023; 0,005 y He/Hc2(0)=-0,055; -0,025; -0,0088 para b= 3.0,1.0 para campos crecientes y decrecientes en el ciclo de histéresis correspondientes a la salida de un vórtice y entrada de un antivórtice respectivamente, inmediatamente después que un vórtice o antivórtice permanece en el defecto. Los puntos (a) y (b) corresponden a la entrada de un antivórtice y de un vórtice respectivamente, el cual permanecerá atrapado en el defecto metálico. El par vórtice antivórtice se aniquilará dentro o fuera del defecto. Podemos ver que el primer campo crítico termodinámico decrece cuando b decrece. Este resultado es consistente con el hecho que la superconductividad y la barrera superficial de los bordes del defecto son suprimidos o disminuidos facilitando la entrada del campo magnético en el defecto.
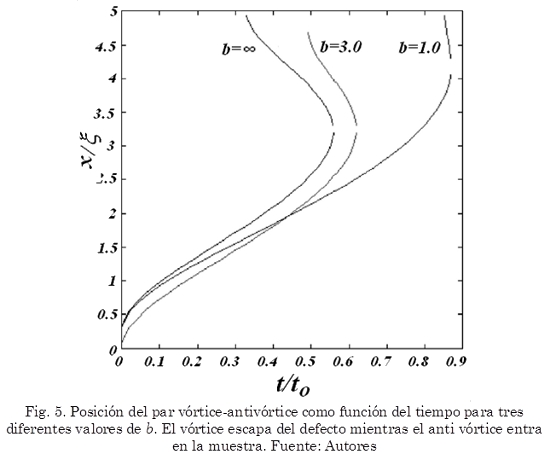
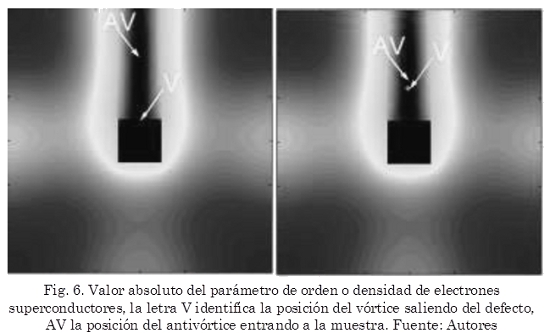
En la Fig. 5 observamos la posición del par vórtice-antivórtice como función del tiempo. Puede notarse que, decreciendo el valor de b el punto de encuentro vórtice antivórtice se localiza más cerca al defecto, en otras palabras, cuando el defecto se vuelve más metálico el ancoraje del mismo se vuelve más eficiente por lo tanto la colisión acontece cada vez más cerca de él. Observando el comportamiento de la curva posición en función del tiempo, podemos ver que la velocidad del antivórtice, en promedio, tiende a decrecer cuando decrece b. Por otra parte la velocidad promedio del vórtice dejando el defecto crece muy rápidamente. Para el caso de b=0,05 (no mostrado en la figura) no observamos la colisión vórtice antivórtice porque los dos vórtices escapan del defecto antes que el campo magnético sea reversado. La Fig. 5 representa la topología del parámetro de orden en el momento en que la colisión acontece.
Sivakov (2003), dedujo que la velocidad de un vórtice es del orden de 103 m/s, usando esta referencia, en nuestro caso, el tiempo en el cual el anti vórtice es visible es Δt=0,5517t0, la distancia que viaja es Δy=2,875ξ(0), tomando Tc=3,72 K y ξ(0)=230nm, los parámetros relevantes para el Sn, la velocidad promedio del antivórtice es υAV = 1,5x105 m/s. Por otra parte en la entrada del vórtice al defecto, encontramos que Δt = 0,2135t0, Δy = 1,625ξ(0), con lo cual obtenemos υV = 2,2x105 m/s, se ha visto experimentalmente que estas grandes velocidades en un proceso de aniquilación vórtice antivórtice son similares a aquellas desarrolladas durante los primeros estadios de avalancha de vórtices reportados por Priour (2003), reportando velocidades mayores a υ = 1,8x105 m/s en películas de YBCO. Para la entrada del vórtice en el defecto encontramos una velocidad significativamente mayor que para la red de vórtices de Abrikosov Δt = 17,279t0, Δy = 4,125ξ(0), lo cual conduce a υAB = 6,8x103 m/s, puede esto atribuirse a la atracción adicional ejercida por el defecto.
4. Conclusiones
Investigamos teóricamente la distribución espacial de los vórtices en una muestra superconductora cuadrada con dos defectos o huecos llenos de un material aislante. La presencia de los huecos afecta la distribución de vórtices, los vórtices que no se localizan en ellos están ubicados principalmente en la región superconductora opuesta a los mismos. Cuando estudiamos la muestra con un defecto metálico asimétrico vemos que el número de vórtices incrementa al aumentar el carácter metálico el hueco. Un defecto metálico cuadrado centrado en la muestra afecta fuertemente la velocidad del par vórtice antivórtice. Al aumentar el carácter metálico del mismo la colisión vórtice antivórtice ocurre más cerca de él y la velocidad del antivórtice tiende a crecer fuertemente.
Referencias
Barba, J. J. & Aguiar J. A., (2010a); Two dimensional vortex structures in a superconductor slab at low temperatures. Physica C: Superconductivity and its applications, 470, 225-230. [ Links ]
Barba, J. J., Sardella, E., & Aguiar, J. A., (2010b); Temperature-dependent vortex matter in a superconducting mesoscopic circular sector. Physica C: Superconductivity and its applications, 470, 1964-1967. [ Links ]
Barba, J. J., Sardella, E., & Aguiar, J. A., (2011); Superconducting boundary conditions for mesoscopic circular samples. Superconductor, Science & Technology, 24, 015001-015007. [ Links ]
Berdiyorov, G., Milosevic, M. & Peeters F. M., (2006); Novel commensurability effects in superconducting films with antidot arrays. Phys. Rev. Lett, 96, 207001-1-207001-4. [ Links ]
Bolech, A. C., Buscaglia, G. C. & Lopez, A., (2000); Connectivity and Superconductivity, J. Berger and J. Rubinstein. (Eds) Springer. [ Links ]
Cabral, L. R. E., Barba, J. J., Souza, C. C. & Aguiar, J. A.,( 2010); Vortex properties of mesoscopic superconducting samples. Physica C: Superconductivity and its applications, 470, 786-790. [ Links ]
Chibotaru, L. F., Ceulemans, V., Bruyndonck. & Moshchalkov, V. V., (2000); Symmetry-induced formation of antivortices in mesoscopic superconductors. Nature (London), 408, 833-835. [ Links ]
Geurts, R., Milosevic, M. & Peeters F. M., (2006); Symmetric and AsymmetricVortex-Antivortex Molecules in a Fourfold Superconducting Geometry. Phys. Rev. Lett, 97, 137002-1-137002-4. [ Links ]
Gropp, D., Kaper, H. D., Leaf, G. K., Levine, D. M., Palumbo, M. & Vinokur, V. M., (1996); Vortex properties of mesoscopic superconducting samples. J. Comput. Phys, 123, 54. [ Links ]
Gillijns, W., Aladyshkin, A., Lange, M., Van Bael, M. J. & Moshchalkov, V. V., (2005); Domain-Wall Guided Nucleation of Superconductivity in Hybrid Ferromagnet-Superconductor-Ferromagnet Layered Structures. Phys. Rev. Lett, 95, 227003-1-227003-4. [ Links ]
Lange, M., Bael, M., Bruynseraede. & Moshchalkov, V. V., (2003); Nanoengineered Magnetic-Field-Induced Superconductivity. Phys. Rev. Lett, 90, 197006-1-197006-4. [ Links ]
Misko, V., Fomin, V., Devreese, J. T. & Moshchalkov, V. V., (2003); Stable Vortex-Antivortex Molecules in Mesoscopic Superconducting Triangles. Phys. Rev. Lett, 90, 147003-1-147003-4. [ Links ]
Moshchalkov, V. V., Gielen, L., Strunk, C., Jonckheere, R., Qiu, X., Van Haesendonck, C. & Bruynseraede, Y. (1995); Effect of sample topology on the critical fields of mesoscopic superconductors. Nature (London), 373, 319-322. [ Links ]
Moshchalkov, V. V., Bruynseraede, Y., Van Look, Y., Grigorenko, A. N. & Tonomura, A. (1999); Handbook of Nanostructured Materials and Nanotechnology, edited by, H. S. Naywa (Academic San Diego, Vol 3, Chap 9, p. 451. [ Links ]
Priour, D. J. & Fertig, H. A. (2003); Deformation and depinning of superconducting vortices from artificial defects: A Ginzburg-Landau study. Phys. Rev. B 67, 054504-1-054504-9. [ Links ]
Sardella, E., Lisboa, P., Souza, C. C., Cabral, L. R. E. & Ortiz, W. (2009); Vortex-antivortex annihilation dynamics in a square mesoscopic superconducting cylinder. Phys. Rev. B. 80, 012506-1-012506-4. [ Links ]
Souza, C. C., Van de Vondel, J., Zhu, B. Y., Morelle, M. & Moshchalkov. (2006); Vortex ratchet effects in films with a periodic array of antidots. Phys. Rev. B 73, 014507-1-14507-10. [ Links ]
Sivakov, A. G., Glukhov, A. M., Omelyanchouk, A. N., Koval, Y., Muller, P. & Ustinov, A. V. (2003); Josephson Behavior of Phase-Slip Lines in Wide Superconducting Strips. Phys. Rev. Lett. 91, 267001-1-267001-4. [ Links ]
Tinkham, M. (1996); Introduction to Superconductivity, McGraw Hill, New York. [ Links ]