Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
TecnoLógicas
versão impressa ISSN 0123-7799versão On-line ISSN 2256-5337
TecnoL. no.29 Medellín jul./dez. 2012
Artículo de Investigación/Research Article
Simulación de Propiedades Mecánicas de Películas Delgadas de Carburo de Tungsteno a Partir del Modelo Monte Carlo
Simulation on Mechanical Properties of Tungsten Carbide Thin Films Using Monte Carlo Model
Liliam C. Agudelo-Morimitsu1, Elisabeth Restrepo-Parra2, Jhonattan De La Roche-Yepes3
1Laboratorio de Física del Plasma, Universidad Nacional de Colombia, Manizales-Colombia, licagudelom@unal.edu.co
2Laboratorio de Física del Plasma, PCM Computational Applications, Universidad Nacional de Colombia, Manizales-Colombia, erestrepop@unal.edu.co
3Laboratorio de Física del Plasma, PCM Computational Applications, Universidad Nacional de Colombia, Manizales-Colombia, jdey@unal.edu.co
Fecha de recepción: 10 de septiembre de 2012 / Fecha de aceptación: 30 de noviembre de 2012
Resumen
El objetivo de este trabajo es estudiar a partir de simulaciones el comportamiento mecánico de un sistema sustrato/recubrimiento. Se analizan los esfuerzos de contacto y la deformación elástica, al aplicar una carga normal a la superficie de un sistema compuesto por una película delgada resistente al desgaste de Carburo de Tungsteno (WC) y un sustrato de acero inoxidable. El análisis se basa en simulaciones utilizando el método Monte Carlo a partir del algoritmo de Metrópolis; el fenómeno fue simulado a partir de una estructura cristalina centrada en las caras fcc, tanto para el recubrimiento como para el sustrato, asumiendo el plano de deformación uniaxial en el eje z. Los resultados fueron obtenidos para diferentes valores de carga normal aplicada a la superficie del recubrimiento, obteniendo así la curva Esfuerzo vs Deformación del sistema. A partir de la curva se calculó el módulo de Young, obteniéndose un valor de 600 GPa, la cual concuerda con resultados experimentales.
Palabras clave: Películas delgadas, WC, método Montecarlo, algoritmo de metrópolis, curvas esfuerzo-deformación.
Abstract
The aim of this paper is to study the mechanical behavior of a system composed by substrate-coating using simulation methods. The contact stresses and the elastic deformation were analyzed by applying a normal load to the surface of the system consisting of a tungsten carbide (WC) thin film, which is used as a wear resistant material and a stainless steel substrate. The analysis is based on Monte Carlo simulations using the Metropolis algorithm. The phenomenon was simulated from a fcc face-centered crystalline structure, for both, the coating and the substrate, assuming that the uniaxial strain is taken in the z-axis. Results were obtained for different values of normal applied load to the surface of the coating, obtaining the Strain-stress curves. From this curve, the Young´s modulus was obtained with a value of 600 Gpa, similar to the reports.
Keywords: Thin films, WC, Monte Carlo method, metropolis algorithm, stress-strain curves.
1. Introducción
Los recubrimientos superficiales son en la actualidad un método eficaz para mejorar la durabilidad de los materiales utilizados en ambientes agresivos, además de generar aumentos en el valor comercial de los productos (Arias et al., 2006). Los materiales cerámicos son muy utilizados en la aplicación de recubrimientos, especialmente en los ámbitos relacionados con la ingeniería, ya que permiten mejorar la resistencia al desgaste y la corrosión de los elementos mecánicos involucrados, sin afectar las propiedades internas. De esta manera, el sistema sustrato/recubrimiento alcanza un mayor rendimiento y una mayor versatilidad en sus aplicaciones (Mateos et al., 2000). Entre los recubrimientos duros protectores se destaca el carburo de tungsteno (WC), debido a su alta temperatura de fusión, alta dureza, relativamente baja conductividad y excelente estabilidad química (Taylor, 1977; Neuville & Matthews, 2007; Bewilogua, et. al., 2009). Estas propiedades son utilizadas para mejorar el rendimiento y durabilidad de piezas de materiales expuestas a prácticas de carga, laminación o diferentes condiciones tribológicas (fricción, desgate y lubricación).
Además, el WC también cuenta con otras propiedades como alta resistencia a la corrosión, alta resistencia al desgaste y relativo bajo coeficiente de fricción (Voevodin et al., 1999; Abad, et al., 2010). Recientemente, este material ha aumentado su interés tecnológico debido a su uso en recubrimientos de materiales nanoestructurados WC-C (Esteve et al., 1999). Hoy en día, gracias al interés de la industria por hacer más eficientes los sistemas tribológicos, se hace necesario el estudio del comportamiento mecánico de los materiales de los elementos de máquina que intervienen en estos sistemas; el análisis de esfuerzos y deformaciones bajo condiciones de contacto y deslizamiento juega un papel importante, ya que mediante estudios experimentales y recientemente de simulación, se puede llegar a analizar características mecánicas de sustratos y de materiales de protección superficial para una determinada aplicación industrial.
De otro lado, se han empleado diferentes métodos de simulación numérica, para el entendimiento de los procesos de deformación, generados en los materiales metálicos durante procesos de conformación (Dejun et al., 1998; Souza et al., 2001). Así mismo, la simulación numérica ha sido utilizada en el estudio del comportamiento de determinadas propiedades mecánicas de materiales y recubrimientos, para lo cual se ha estudiado la simulación del proceso de indentación (Malzbender & de With, 2000) y de indentación y rayado simultáneo (Holmberg et al., 2003). A pesar del gran número de trabajos que realizan estudios de propiedades mecánicas para sistemas sustrato/recubrimiento reportados en la literatura, empleando métodos como elementos finitos, no existen reportes en estudios de este tipo empleando la técnica Monte Carlo.
En el presente trabajo se desarrolla un modelo y se llevan a cabo simulaciones para estudiar del fenómeno de deformación que se presenta al ser aplicada una carga variable sobre la superficie del sistema sustrato/recubrimiento (Acero/WC), usando simulación numérica por medio del método Monte Carlo y el algoritmo de metrópolis.
2. Metodología
2.1 Método Monte Carlo
Monte Carlo es uno de los métodos numéricos mas utilizados para solucionar problemas físico-estadísticos. La idea básica de este método es simular aleatoriamente las fluctuaciones térmicas del sistema de interés, pasando de un estado a otro por medio de una cadena de Markov a través del espacio de configuraciones. En el método de Monte Carlo se simula directamente el proceso en estudio, creando un modelo del sistema y haciéndolo pasar sobre una gran cantidad de estados posibles que se calculan estadísticamente. Esto se hace de acuerdo a una cierta distribución probabilística que calcula los valores esperados de los observables físicos deseados. Para encontrar la distribución probabilística, se exige que esta modele al sistema en el caso real, es decir cuando el sistema se encuentre en equilibrio termodinámico (Cossio, 2007). Para nuestro estudio de películas delgadas la distribución probabilística, en el equilibrio, está dada por la distribución de Boltzmann, (1).

Donde Z es la función de partición del sistema, Eμ la energía del estado μ y β=1/(kBT) siendo kB la constante de Boltzmann y T la temperatura.
Una gran ventaja del uso del método Monte Carlo, consiste en que no es necesario conocer todos los estados de un sistema para encontrar estimativos de los observables físicos; sin embargo, este método conlleva errores estadísticos y otros generados por la correlación entre los datos consecutivos cuando se genera una cadena de Markov (Cossio, 2007; Barco et al., 2011).
2.2 Descripción del modelo
Inicialmente, el sistema de la muestra fue construido como se aprecia en la Fig. 1. Este sistema está compuesto por una capa de sustrato de acero inoxidable con una estructura cubica FCC, y una capa de la película delgada de WC en la parte superior del sustrato, igualmente, con estructura cubica FCC. Para el modelo planteado se uso como energía potencial de interacción entre las partículas del sistema, un potencial de tipo Lennard-Jones (2).

Donde γ es la profundidad del pozo de energía (esfuerzo de interacción), do es el diámetro característico de las partículas (la distancia a la cual dos partículas se encuentran en equilibrio) y d es la distancia entre dos átomos vecinos, para la cual el valor del Hamiltoniano es cero, F es la fuerza aplicada y δ es el desplazamiento respecto a la posición de equilibrio de cada partícula.
El programa aplica el método Monte Carlo para hallar la configuración de mínima energía. Esto se lleva a cabo seleccionando de manera aleatoria cada una de las partículas para desplazarlas. El movimiento de una partícula se hace en la dirección de la fuerza resultante que actúa sobre ella, desplazando todo el plano transversal al que pertenece, para evitar el desordenamiento de la muestra (amorfización) y el movimiento de esta se haga efectivo; si dicho desplazamiento hace disminuir la energía de deformación del sistema. La deformación de la muestra (ε) se calcula como la relación de la suma de todos los desplazamientos sufridos en la dirección de la fuerza, dividida entre la longitud de la muestra. Este procedimiento se lleva a cabo durante un número determinado de pasos de Monte Carlo, para determinada fuerza (F); en este punto de equilibrio se considera que el sistema ha alcanzado su mínimo de energía y se ha relajado (Áñez, et al., 2009).
Las simulaciones se llevaron a cabo siguiendo los siguientes pasos:
1. Construcción de la muestra
2. Designar un estado inicial Ei
3. Designar un estado temporal Ef
4. ΔE = Ef - Ei, si ΔE < 0 el sistema permanece en el estado final
5. se obtiene un numero aleatorio r
6. Calcular la probabilidad w = e-ΔE/kT
7. Si r ≤ w el sistema configura el estado actual como estado final
Por otro lado, la teoría matemática de elasticidad, desarrollada para cuerpos que se deforman gradualmente, a temperatura constante, desde un estado inicial de cero esfuerzo hasta un estado final que difiere infinitesimalmente del estado inicial, explica la respuesta mecánica de un sólido a través del tensor de constantes de rigidez elástica (Cijkl), el cual constituye la constante de proporcionalidad entre el tensor de esfuerzos (σij) y el tensor de deformaciones específicas (εkl), que depende de cada material, en la Ley de Hooke generalizada (Koerber, 1962), (3):

En los cálculos efectuados se condicionó el sistema para que únicamente se aplique una deformación normal en una dirección arbitraria, impidiendo cualquier otra deformación normal o cortante en otra dirección, por lo que la expresión (3) se reduce a (4). Este análisis abre la posibilidad de usar las relaciones de la teoría matemática de la elasticidad en el cálculo del módulo de elasticidad mediante simulación computacional.

Siendo C la constante equivalente al módulo de elasticidad E del material. σ=F/A, siendo A el área transversal de la muestra y ε=δ/L, siendo L la longitud de la muestra en la dirección de aplicación de la muestra.
3. Resultados y discusión
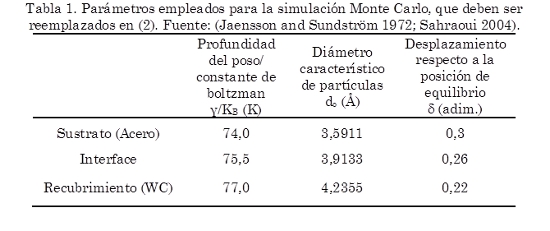
Utilizando el método Monte Carlo, por medio del algoritmo Metrópolis se realizó la curva de esfuerzo-deformación del sistema sustrato/recubrimiento (Acero/WC), el cual fue modelado como un sistema en capas con estructura cubica FCC, para un número total de partículas N=1728; a este sistema se le aplicó una carga variable normal a la superficie de la capa de WC. Los parámetros empleados, para ser reemplazados en (2) se muestran en la Tabla 1.
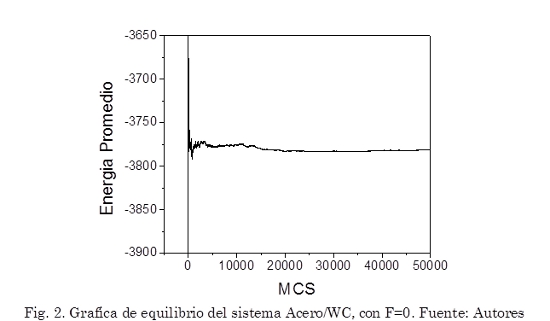
Inicialmente, se obtuvo una curva para la energía de relajación del sistema Acero/WC en función de los pasos de Monte Carlo (MCS), como se muestra en la Fig. 2. Para este caso no se aplicó ningún valor de fuerza externa al sistema, solo se hizo iterar el modelo que incluye el potencial de Lenard-Jones, para asegurar que el sistema estuviera en el estado de menor energía, antes de aplicar una carga a la superficie de la capa.
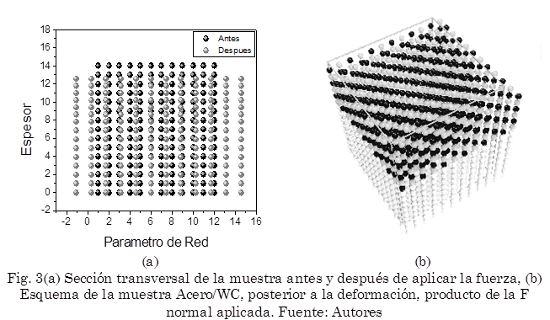
Posteriormente, se aplicó una fuerza normal a la superficie de la muestra, la cual varió de 0 a 100 nN, con pasos de 2 nN, durante 50000 MCS a una temperatura T = 300 °K (cercana a la temperatura ambiente). Como era de esperarse, la muestra presentó una deformación súbita a lo largo de sus ejes, proporcional a la fuerza normal aplicada (Fig. 3). En esta figura se observa además de la deformación en la dirección de la fuerza, una deformación transversal en el plano x-y, que se determina empleando el coeficiente de Poisson (ν = -dx/dz), siendo dx = dy (suponiendo que la muestra es isotrópica) la deformación en la dirección x y dz la deformación en la dirección z.
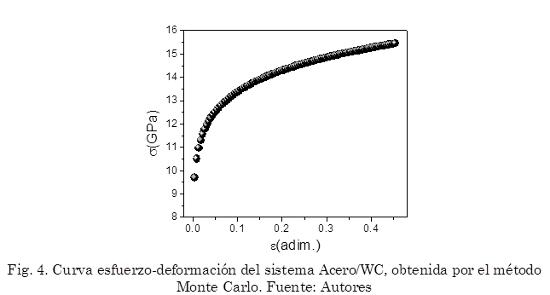
La Fig. 4 muestra la curva de Esfuerzo-Deformación, obtenida para el sistema sustrato/recubrimiento. De acuerdo con los datos utilizados en el método Monte Carlo, coincide con las curvas obtenidas en algunos ensayos experimentales. Se puede observar inicialmente una zona elástica, presentando una dependencia lineal, después de cierta fuerza aplicada, aparece la zona plástica del material, la cual es una característica de este tipo de sistemas. De esta curva se puede obtener el módulo de Young para el sistema muestra recubrimiento, teniendo en cuenta que E= σ/ε a partir de (4), calculado de la parte lineal de la curva, con σ = 12 GPa y ε = 0.02. El valor obtenido es de 600 GPa, similar a 627 GPa reportado por (Swamy, 2011).
4. Conclusiones
El método de Monte Carlo fue utilizado para modelar el comportamiento esfuerzo-deformación de un sistema compuesto por un sustrato de acero inoxidable y una película de WC. El modelo se basó en el potencial de Lennard-Jones y la ley de Hook. Los resultados mostraron el efecto de compresión de la muestra en la dirección z y la expansión en el plano xy. La curva de esfuerzo-deformación obtenida evidencio tanto la zona elástica, como la zona plástica característica del sistema, lo cual esta en coherencia con el fenómeno que sucede normalmente en los materiales reales. Además, pudimos identificar el papel que desempeña la geometría de un cuerpo en sus propiedades efectivas tales como su respuesta mecánica, la cual permite explicar y predecir el comportamiento mecánico de un material conociendo su geometría o incluso sintetizar materiales con requerimiento de propiedades mecánicas específicas mediante el control de su geometría. Ya que tradicionalmente el estudio de la interacción entre las propiedades mecánicas y los parámetros texturales o geométricos de un medio se lleva a cabo a través de una gran cantidad y variedad de experimentos, pero el uso de sistemas modelos de geometría conocida permite analizar de forma sistemática los efectos de las diferentes propiedades texturales en el medio, por lo que se convierte en una alternativa eficaz para abordar el problema.
5. Agradecimientos
Los autores queremos dar gracias a la Facultad de Ciencias Exactas y Naturales de la Universidad Nacional de Colombia sede Manizales y a la Dirección de Investigación (DIMA), por su apoyo económico y administrativo en esta investigación, a través del proyecto “Efecto del dopaje de titanio en recubrimientos de bisulfuro de tungsteno (WS2) producidos por la técnica de Magnetrón Co-Sputtering no reactivo para aplicaciones en lubricantes sólidos”, y a Colciencias por su apoyo bajo la convocatoria Jóvenes Investigadores 2011 bajo el proyecto Modelamiento de propiedades mecánicas de películas delgadas de nitruros metálicos por el método de dinámica molecular.
Referencias
Abad, M.D., Muñoz-Márquez, M.A., El Mrabet, S., Justo, A. & Sánchez-López, J.C. (2010). Tailored synthesis of nanostructured WC/a-C coatings by dual magnetron sputtering, Surface & Coatings Technology, 204, 3490-3500. [ Links ]
Áñez, L. M., Primera, J. C., Hasmy, A., Franceschini, P., Sánchez, N., & Woignier, T. (2009). Método de Monte Carlo para el cálculo computacional de las propiedades mecánicas de un medio poroso, CIENCIA, 17(1), 80-86. [ Links ]
Arias, D. F., Arango, Y.C. & Devia, A. (2006). Study of TiN and ZrN thin films grown by cathodic arc technique, Applied Surface Science, 253, 1683-1690. [ Links ]
Barco, H., Rojas-Calderón, E. & Restrepo-Parra, E. (2011). Graphic User Interface for Monte Carlo Simulation of Ferromagnetic/Antiferromagnetic Manganite Bilayers, Rev. Tecno Lógicas, 26,133-143. [ Links ]
Bewilogua, K., Bräuer, G., Dietz, A., Gäbler, J., Goch, G., Karpuschewski, B. & Szyszka, B. (2009). Surface technology for automotive engineering,CIRP Annals - Manufacturing Technology, 58, 608-627. [ Links ]
Cossio, P. (2007). Simulación Monte Carlo de sistemas de películas delgadas magnéticas, tesis pregrado, Universidad de Antioquia Sede Medellín, Facultad de Ciencias Exactas y Naturales, Instituto de Física, Colombia. [ Links ]
Dejun, M., Kewei, X. & Jiawen, H. (1998). Numerical simulation for determining the mechanical properties of thin metal films using depth-sensing indentation technique, Thin Solids Films, 323, 183-187. [ Links ]
Esteve, J., Martínez, E., Zambrano, G., Prieto, P., Rincon, C. & Galindo, H. (1999). Mechanical and tribological properties of tungsten carbide sputtered coatings, Superficies y Vacío, 9, 276-279. [ Links ]
Holmberg, K., Laukkanen, A., Ronkainen, H., Wallin, K. & Varjus, S. (2003). A model for stresses, crack generation and fracture toughness calculation in scratched TiN-coated steel surfaces, Wear, 254, 278-291. [ Links ]
Jaensson, B. O. & Sundström, B. O. (1972). Determination of Young's modulus and poisson's ratio for WC-Co alloys by the finite element method, Materials Science and Engineering, 9, 217-222. [ Links ]
Koerber, G. (1962). Properties of Solids, Editorial Prentice-Hall, Estados Unidos de América. [ Links ]
Malzbender, J. & De With, D. (2000). Modeling of the fracture of a coating under sliding indentation, Wear, 239, 21-26. [ Links ]
Mateos, J., Cuetos, J.M., Fernández, E. & Vijande, R. (2000); Tribological behaviour of plasma-sprayed WC coatings with and without laser remelting, Wear, 239, 274-281. [ Links ]
Neuville, S. & Matthews, A. (2007). A perspective on the optimisation of hard carbon and related coatings for engineering applications, Thin Solid Films, 515, 6619-6653. [ Links ]
Sahraoui, T., Kellou, A., Faraoun, H.I., Fenineche, N., Aourag, H., Coddet C. (2004). Ab initio calculations and experimental studies of site substitution of ternary elements in WC, Materials Science and Engineering, B107, 1-7 [ Links ]
Souza, R.M, Sinatora, A., Mustoe, G. & Moore, J. (2001). Numerical and experimental study of the circular cracks observed at the contact edges of the indentations of coated systems with soft substrates, Wear,251, 1337-1346. [ Links ]
Swamy, A. R. K., Ramesha, A., Veeresh, G.B., Prakash, J. N. (2011). Effect of Particulate Reinforcements on the Mechanical Properties of Al6061-WC and Al6061-Gr MMCs, Journal of Minerals & Materials Characterization & Engineering, 10, 1141-1152. [ Links ]
Taylor, K.A. (1977). Ancillary properties of vapor-deposited carbide coatings, Thin Solid Films, 40, 201-209. [ Links ]
Voevodin, A.A., O´Neill, J.P., Prasad, S.V. & Zabinski, J.S. (1999). Nanocrystalline WC and WC/a-C composite coatings produced from intersected plasma fluxes at low deposition temperatures, Journal of Vacuum Science and Technology, A17 986-992. [ Links ]