Artículo de Investigación/Research Article

Evaluación del Desempeño de un Modelo Autosimilar para el Tráfico en Redes 802.11

Performance Evaluation of a Self-Similar Model for Traffic on IEEE 802.11 Networks

Evelio Astaiza-Hoyos¹, Héctor F. Bermúdez-Orozco², Diego A. Méndez-Suárez³

¹Magíster en Ingeniería, Docente Programa de Ingeniería Electrónica, Universidad del Quindío, Armenia-Colombia, eastaiza@uniquindio.edu.co

²Magíster en Electrónica y Telecomunicaciones, Docente Programa de Ingeniería Electrónica Universidad del Quindío, Armenia-Colombia, hfbermudez@uniquindio.edu.co

³Ingeniero en Electrónica, Universidad del Quindío, Armenia-Colombia, dialemen@hotmail.com

Fecha de recepción: 03 de septiembre de 2012 / Fecha de aceptación: 02 de agosto de 2013

Resumen

Desde el descubrimiento de las propiedades fractales (“escalado”) del tráfico en las redes de conmutación de paquetes, se han realizado numerosos estudios y se ha detectado esta propiedad en diversas redes de datos. En esta investigación se evalúa experimentalmente un modelo basado en procesos autosimilares en redes 802.11, para la caracterización del tráfico de nivel 2. La validación del modelo se realiza en dos etapas. En la primera etapa, se obtienen las características estadísticas del tráfico real que cursa en la red. En la segunda etapa, se define una medida de desempeño la cual se aplica tanto a los datos reales obtenidos como al modelo evaluado para verificar el ajuste del desempeño del modelo al desempeño real de la red a través de simulación y cálculo de la correlación existente entre los desempeños real y propuesto por el modelo. Los resultados permiten evidenciar la existencia de una adecuada aproximación de las estimaciones realizadas a partir del modelo evaluado, generando un aporte significativo para el diseño, planificación y dimensionamiento de la capacidad de este tipo de redes, para las cuales en general se realiza el diseño, planificación y dimensionamiento solo basado en su cobertura y no necesariamente en la capacidad requerida dadas las restricciones de operación.

Palabras clave:WLAN, MAC, ranura de tiempo, ventana de contienda, autosimilitud, validación, modelo de planificación de capacidad, correlación.

Abstract

Since the discovery of the traffic fractal properties ("scaling") in packet switched networks, there have been numerous studies and has been found this property in various data networks. This research evaluates experimentally a model based on self-similar processes in 802.11 networks, to characterize the Layer 2 traffic. Model validation is performed in two stages. In the first stage, we obtain the statistical characteristics of the actual traffic coursing on the network. In the second stage, we define a performance measure which applies to the actual data and the model tested to verify the performance of the model fit to the actual network performance through simulation and calculation of the correlation between actual performance and performance estimated by the model; generating a significant contribution to the design, planning and dimensioning of the capacity of this kind of networks, for which usually the design, planning and dimensioning takes place based only in coverage and not necessarily in the required capacity given the operation constraints.

Keywords:WLAN, MAC, time slot, contention window, selfsimilar, validation, capacity planning model, correlation.

1. Introducción

En años recientes, se ha generado mucho interés en el diseño de redes inalámbricas para las redes de acceso dadas las bondades que ellas presentan (Florwick et al., 2011); en particular se puede apreciar que el estándar 802.11 ha presentado una gran aceptación y por consiguiente es fundamental el estudio detallado de su comportamiento para realizar el diseño, dimensionamiento y planificación de este tipo de redes de manera adecuada, y que permitan satisfacer las necesidades del manejo de la información y servicios requeridos por usuarios y organizaciones. En este documento se realiza la validación de un modelo basado en características de tráfico autosimilar (Ge et al., 2009) para calcular el rendimiento o Throughput de la función de coordinación distribuida (DCF) para el mecanismo de acceso estándar (acceso básico), y así poder contrastar su ajuste al tráfico real de nivel 2 obtenido de la red QRD (Quindío Región Digital).

En el protocolo 802.11, el mecanismo fundamental para acceder al medio, es llamado función de coordinación distribuida (DCF). Este es un esquema de acceso aleatorio, basado en el protocolo CSMA/CA. La retransmisión de los paquetes colisionados es manejada de acuerdo a la norma exponencial y binaria de la etapa de backoff. El estándar también define la función de coordinación puntual (PCF) que es el protocolo centralizado de la capa MAC, capaz de soportar cero colisiones y un tiempo de servicio específico (Bianchi, 2000). Este trabajo está enfocado en la investigación del régimen DCF.

El DCF describe dos técnicas a emplear para la transmisión de paquetes. El esquema predeterminado es un protocolo de enlace de dos vías, la técnica Hand shacking o (mecanismo de acceso básico) y el mecanismo Request to Send Clear to Send (RTS/CTS), en este último, se especifica que antes de transmitir un paquete, una estación que opera en el modo RTS/CTS, “Reserva” el canal mandando una trama pequeña llamada “solicitud para enviar” o (RTS). La estación de destino confirma la recepción de la trama RTS devolviendo una trama “Listo para enviar” (CTS).

El objetivo del presente trabajo es identificar si el modelo autosimilar evaluado se ajusta a las condiciones de operación real de las redes inalámbricas 802.11 y de tráfico agregado. Así mismo se busca validar el modelo identificado mediante la definición de una métrica de desempeño del modelo contra el desempeño real de la red, con miras a identificar la precisión de la estimación realizada por el modelo evaluado, para de esta forma evidenciar la factibilidad de incorporar el modelo seleccionado a una posible metodología de dimensionamiento de capacidad para redes inalámbricas 802.11, dado que en la actualidad las metodologías de diseño, planificación y dimensionamiento de este tipo de redes solo contemplan aspectos referentes a la planificación de cobertura y a la parametrización de dispositivos de red, lo cual evidencia una ausencia total de criterios de planificación de capacidad.

El documento se encuentra organizado de la siguiente manera: en la sección 2 se presenta la metodología y se definen los dos mecanismos de acceso al medio en DCF: mecanismo de acceso básico y mecanismo RTS/CTS así como una combinación de los dos. En la sección 3 se muestran los resultados obtenidos del tráfico real en la red QRD y la estadística del mismo, se realiza el análisis del modelo autosimilar considerado y se muestran los resultados de simulación que permiten evidenciar el desempeño del modelo seleccionado con respecto al comportamiento de la red QRD, y se ilustra como el modelo validado podría utilizarse para realizar dimensionamiento de capacidad en las redes 802.11 y finalmente en la sección 4 se muestran las conclusiones.

2. Metodología

En este documento se compara y analiza un método que tuvo mucha acogida a finales de la década de los 90 y a principios de la década del 2000, esta técnica es llamada Autosimilitud (Hayes & Ganesh, 2004; Fiche & Hebuterne, 1988) y es utilizada para modelar redes WLAN 802.11. En este trabajo se evalúa el desempeño de un modelo que obtiene todas las características de este tipo de tráfico y está enfocado en la capa MAC de este tipo de redes (Ge et al., 2009), en donde se evalúan por separado cada una de las tramas de tráfico agregado como lo son las de gestión, de control y de datos, donde se encontró que cada una de las tramas aporta un porcentaje de autosimilitud representado por el parámetro de Hurst y finalmente determina el grado de autosimilitud de la trama de tráfico agregado, parámetro que según Ge et al. (2009) puede ser descrito como una combinación lineal de los parámetros de Hurst de los diferentes tipos de trama (gestión, control y datos). El modelo también tiene en cuenta todos los detalles del protocolo de Backoff exponencial y evalúa la red en condiciones de no saturación y con flujos de tráfico heterogéneo para calcular el rendimiento o Throughput del DCF para el mecanismo de acceso estándar (acceso básico).

2.1 Captura y Estadística del Tráfico en QRD

Con un analizador de protocolos (Lamping et al., 2004) se obtuvo la información de los paquetes capturados, y se discriminó el tiempo en que llega cada paquete y el tamaño de cada paquete, para posteriormente a través de histogramas y pruebas de ajuste obtener las estadísticas que permiten caracterizar este tipo de tráfico y de esta manera realizar la respectiva caracterización del comportamiento de la red QRD.

El analizador de protocolos wireshark-win32-1.4.0 se instaló en el servidor de la red QRD y se efectuaron capturas del tráfico a partir del 24 de enero del 2011 hasta el 24 de junio del 2011 en sesiones diarias de cuatro horas cada una en diferentes horarios, tomando de esta manera en total del orden de 365 millones de datos (paquetes). Con el wireshark se pudo obtener información muy importante de todos y cada uno de los paquetes capturados, entre otros el tiempo en que llega cada paquete y el tamaño de cada paquete además de la estadística de la razón de llegada de paquetes por segundo para realizar la respectiva caracterización del comportamiento de la red QRD.

Teniendo en cuenta los tipos de datos representativos para este estudio y arrojados por la herramienta de análisis de protocolos, del total de los paquetes capturados en la sesión, se establece el tiempo de llegada y el tamaño de cada uno de los paquetes, el resto de la información suministrada por la herramienta se descarta, y la información de interés es analizada estadísticamente.

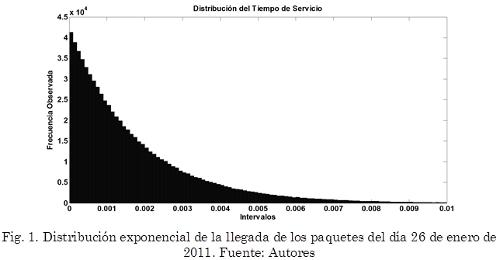
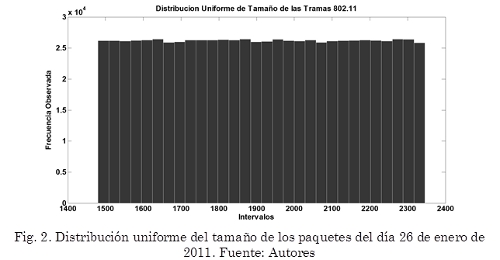
La metodología de la prueba de bondad de ajuste de Kolmogorov-Smirnov es mostrada en Astaiza et al. (2007), que al aplicarla a los datos arrojados por el wireshark, se obtiene como resultado la distribución del tiempo entre llegadas y la distribución del tamaño de la carga útil de los paquetes, estas pruebas fueron implementadas en MATLAB, generando los histogramas que permiten visualizar las distribuciones obtenidas; los cuales se muestran en las Fig. 1 y Fig. 2.

En la Fig. 1 se puede observar que el histograma de la llegada de los paquetes corresponde a una distribución exponencial con media de 0,0076 segundos. En la Fig. 2, se puede observar que el histograma del tamaño de los paquetes corresponde a una distribución uniforme con media de 1452,76 bytes. Cabe destacar que la gráfica de la distribución de los paquetes fue adquirida a partir de realizarle a todos los datos el siguiente ajuste.

Inicialmente hay que tener en cuenta que se debe trabajar únicamente con los paquetes que contienen la carga útil, por lo que se excluyeron o filtraron los paquetes con un tamaño menor a 1480 bytes, ya que dichos paquetes son tramas de gestión y tramas de control que pueden ser vistas como peticiones de broadcast, entre otras, para acceder al medio. Como se debe trabajar con los bits de carga útil, se debe tener en cuenta que las tramas de datos capturados por el analizador de protocolos tienen un encabezado físico PHY header y un encabezado MAC header, las cuales son tramas que van asociadas a las tramas de datos y que se transmiten a diferente tasa, pero no son bits de carga útil. Por lo tanto, estos bits deben ser restados a las tramas de datos. Por ejemplo, una trama de datos capturada que se muestra como una trama de tamaño 1512 bytes, a este valor se le debe restar la trama de encabezado físico PHY header que es de 34 bytes y la trama de encabezado MAC header que es de 28 bytes.

2.2 Función de Coordinación Distribuida 802.11

En esta sección se resume brevemente la función de coordinación distribuida (DCF) normalizada por el protocolo 802.11. Para una presentación más completa y detallada referirse al estándar 802.11 (P802.11, 1997).

Una estación con un nuevo paquete para transmitir supervisa la actividad del canal, si el canal está inactivo por un periodo de tiempo igual al espacio intertrama distribuido (DIFS), la estación transmite. De lo contrario, si el canal se censa ocupado, la estación persiste en monitorear el canal hasta que se encuentre libre durante un DIFS (inactivo). En este punto, la estación genera un intervalo de backoff aleatorio antes de transmitir (esta es la función anticolisión del protocolo), para minimizar la probabilidad de colisión con los paquetes que son transmitidos por otras estaciones. Además para evitar la captura de canal, una estación debe esperar un tiempo de backoff aleatorio entre dos transmisiones consecutivas de un nuevo paquete, incluso si el medio se censa inactivo en un tiempo DIFS. Por razones de eficiencia, el DCF emplea una escala de Backoff de tiempo discreto. El tiempo inmediatamente después de una inactividad DIFS se ranura y una estación puede transmitir solo al comienzo de cada ranura de tiempo. El tamaño de la ranura de tiempo “σ” se fija igual al tiempo necesario en cualquier estación para detectar la transmisión de un paquete de cualquier otra estación (Bellalta, Oliver, Meo, & Guerrero, 2005; Duffy et al., 2005).

Como se muestra en la Tabla 1, el tamaño de la ranura de tiempo “σ” depende de la capa física, y representa el retardo de propagación, durante el tiempo necesario para pasar de la recepción al estado de transmisión (RX TX tiempo de vuelta), y por el tiempo para señalar a la capa MAC el estado del canal (detectar tiempo ocupado). DCF adopta un régimen de Backoff exponencial.

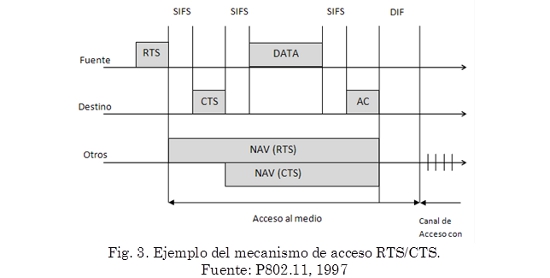
En cada transmisión de paquetes, el tiempo de Backoff es elegido de manera uniforme en el rango (0.W-1), el valor W es llamado ventana de contención (Contention Windows), y depende del número de transmisiones fracasadas por el paquete. El DCF define una técnica de cuatro vías para ser utilizada opcionalmente para una transmisión de paquetes. Este mecanismo conocido con el nombre de RTS/CTS, se muestra en la Fig. 3. La estación que quiere transmitir un paquete espera hasta que el canal es censado inactivo durante un DIFS, siguiendo las reglas del Backoff explicadas anteriormente, y a continuación, en lugar del paquete, se transmite de manera preliminar una trama corta especial llamada “solicitud de envío” (RTS). Cuando la estación de destino detecta una trama RTS, esta responde, después de un SIFS, con una trama “clear to send” CTS. A la estación transmisora se le permite transmitir su paquete solo si una trama CTS es recibida correctamente.

Las tramas RTS y CTS llevan la información del tamaño del paquete que va a ser transmitido. Esta información puede ser leída por cualquiera de los transmisores escuchantes, que luego es capaz de actualizar el vector de asignación de la red (NAV) que contiene la información del periodo de tiempo en el que el canal seguirá siendo ocupado. Por lo tanto, cuando una estación se oculta, ya sea del emisor o de la estación receptora, la estación oculta mediante la detección de una sola trama RTS o CTS evita la colisión.

El mecanismo RTS/CTS es muy efectivo en términos del desempeño del sistema, especialmente cuando se consideran paquetes grandes, ya que reduce la duración de las tramas que participan en el proceso de contención. De hecho, en el supuesto de canal perfecto detectado por cada estación, la colisión puede ocurrir solamente cuando dos (o más) paquetes se transmiten en la misma ranura de tiempo. Si las dos estaciones de transmisión emplean el mecanismo RTS/CTS la colisión se produce solo en la trama RTS y es rápidamente detectado por las estaciones que transmiten por la falta de respuesta CTS (Bianchi, 2000).

2.3 Obtención de la Expresión del Throughput

Es importante resaltar que debe existir una manera de hacer una comparación real y efectiva del modelo de tráfico autosimilar con el tráfico real que pasa por la red QRD. Esta comparación se hace mediante la definición de un valor de rendimiento del sistema también llamado en inglés como performance o Throughput, esta cifra de rendimiento se puede obtener de innumerables formas (Fiche & Hebuterne, 1988; Grote et al., 2007), en este caso se define como se muestra en (1); para de esta manera realizar una comparación adecuada del modelo autosimilar con el tráfico real.

Esta expresión puede ser representada como:

Dónde:

ρ_k: Es el tráfico ofrecido en el nodo k y en el caso real es el valor medio de la llegada de los paquetes obtenidos en la captura del tráfico.
L_k: Es el tamaño de la carga útil de los paquetes que son transmitidos y el cual es el mismo para cada modelo.
X_k: Es el tiempo necesario para que un paquete sea transmitido correctamente, este depende fundamentalmente de la ventana de contienda, así como del número de colisiones, del número de estaciones que hay en la red y de la probabilidad de colisión. Además este tiempo de servicio es el mismo para el modelo de tráfico autosimilar y para el tráfico real.

2.4 Throughput del Tráfico Real

De la captura en QRD se puede observar que la media promedio de los paquetes es 0,0076 segundos lo que quiere decir que el tráfico ofrecido real es λ_k = 7,6 ms.

Ahora, como se ve en la Fig. 2, que es la gráfica de la distribución uniforme del tamaño de los bits de carga útil de los paquetes, la media es igual a 1452,76 bytes. Por lo tanto L_k = 1452,76 bytes. Lo único que falta es el tiempo de servicio, el cual se calcula en (3):

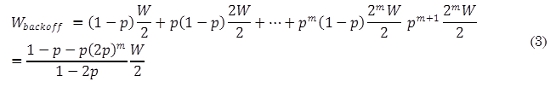
Donde W_backoff es el tamaño promedio de la ventana de backoff.
El temporizador de Backoff se decrementa después de cada ranura de tiempo a menos que haya una contención. Por ejemplo: la transmisión de otra estación causa la suspensión del temporizador. La contención entonces divide el backoff entre (n_contention + 1) ranuras de tiempo denominadas Tslice (Tay & Chua, 2001), como se aprecia en (4).

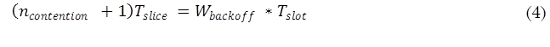
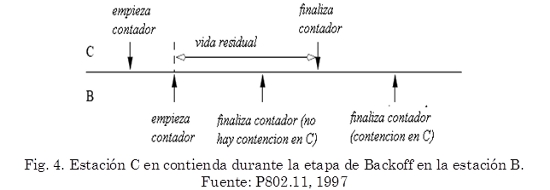
Ahora, se estima la probabilidad de contención causada por la estación C transmitiendo mientras que la estación B está en Backoff. En saturación, cada estación se alterna entre una transmisión y Backoff. Por lo tanto, cuando el contador de la estación B disminuye, C está en Backoff (como se aprecia en la Fig. 4) y el promedio residual de vida del contador de la estación es W_backoff / 3. (La vida residual esperada es m₂ / 2m₁, donde mi es el i-ésimo momento de la distribución del contador. Para una distribución uniforme, m₂ = W_backoff² / 3 y m₁ = W_backoff / 2. Ahora hay contención para C si solo si el contador de la estación B expira después de la estación C, donde esta tiene una probabilidad dada en (5):

Una estación en el contador de Backoff puede por lo tanto esperar más o menos 2/3(n-1) interrupciones de las otras n-1 estaciones. Esto es subestimado, siempre que el contador de la estación B puede ser interrumpido más de una vez por la estación C:

Sustituyendo en (4) se tiene:

Dado que la probabilidad de colisión p es menor a 0,5, las mayores transmisiones son primeramente atendidas precedidas por una detección de portadora. Por lo tanto, ocurren mayores colisiones porque una estación detecta el canal desocupado en la ranura justo antes de la transmisión, por eso p puede ser aproximado por T_slot / T_slice. Sin embargo, esto está subestimado por que no se han excluido las transmisiones que pertenecen a la estación misma. El factor utilizado fuera de esta transmisión es:

Esto es similar a la aproximación de Schwitzer para redes de colas, y correctamente dado por p = 0 para n = 1. Eliminando T_slice y el W_backoff de (5), (7) y (8) se tiene que:

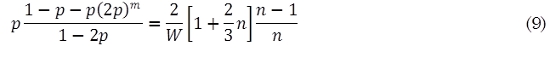
Teniendo W, m y n, esta ecuación puede ser resuelta para p. Donde p es la raíz cuadrada de la aproximación (9). En la Tabla 2 se muestran todos los parámetros utilizados en las corridas de simulación y que son básicamente especificaciones del estándar IEEE 802.11b. Siempre que la etapa de Backoff sigue una distribución uniforme entre 0,1,…W-1, el contador de Backoff es W/2 (ranuras) por simplicidad.

Por lo tanto y como se muestra en la Tabla 1 el valor de Wmin es de 32 ranuras, lo que quiere decir que el valor promedio de ranuras en el que un paquete permanece en la etapa de Backoff en una transmisión exitosa es:

Ahora en el caso a analizar según la Tabla 1 se toma un valor de tres colisiones m = 3, lo que quiere decir que un paquete dura en promedio:

Lo que indica que cuando un paquete ha colisionado tres veces este escogerá el tiempo de Backoff ranurado entre 0 y 256 T_slot. Por lo tanto el valor es escogido debido a su distribución uniforme de 256 / 2 ranuras de tiempo o T_slot.

Ahora, en el caso puntual de la red inalámbrica QRD se trabajarán las simulaciones con un máximo de 20 estaciones porque se supone esta una red pequeña que no superará este número de estaciones. A continuación se presentan los resultados numéricos para validar el modelo donde se tiene que:

n = 20 estaciones, Wmin=32σ y Wmax = 256σ, donde σ es una ranura de tiempo y su valor está especificado en la Tabla 1, y m = 3, es el número de colisiones. Por lo tanto:

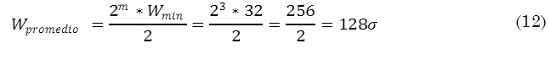
Con estos valores se dispone a hallar la probabilidad de colisión:

Se sabe que el tiempo de servicio es el tiempo que dura una transmisión exitosa. Cabe remarcar que no se tuvo en cuenta el tiempo de propagación de la onda por ser muy pequeño casi imperceptible el cual toma un valor de 1*10-6 segundos.

El tiempo de servicio X_K(n) es aquel que necesita un nodo para poder transmitir un paquete correctamente teniendo en cuenta el número de colisiones promedio que se pueden presentar en dicha transmisión y su valor depende del número de estaciones que en el caso particular varia de 1 a 20 estaciones.

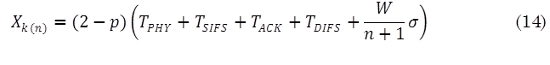
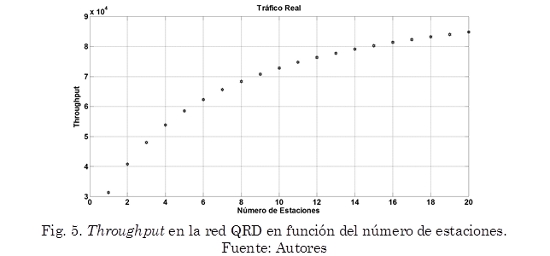
Por lo tanto, la gráfica del Throughput en Mbps contra el número de estaciones de la red, se obtiene a partir de la implementación de (2) en un script de MATLAB, la cual se muestra en la Fig. 5. Aplicando aritmética se puede determinar cuál es el máximo Throughput que podría tener una red de varios terminales, ya que esencialmente hay que dividir este valor por el número de terminales. Así, si se considera que se transmiten paquetes de 1452,76 bytes en promedio a cualquier tasa ya sea a 1, 2, 11 y 54 Mbps. De la misma manera, de la Fig. 5 se desprende que en la red QRD, 20 terminales podrían tener un máximo Throughput de 90 Kbps, por lo tanto, cada terminal tendría una tasa efectiva de 4,5 kbps.

2.5 Throughput del Modelo Autosimilar

En Ge et al. (2009), se realiza un estudio sobre la autosimilitud que presenta el tráfico agregado de una red inalámbrica a partir del parámetro de Hurst con características similares a la red QRD teniendo en cuenta que el grado de autosimilitud fue obtenido como una combinación lineal del grado de autosimilitud que presenta cada trama de tráfico analizada independientemente, es decir, se obtuvo el parámetro de Hurst para la trama de tráfico agregado. Para efectos prácticos, se debe hallar una dependencia entre el parámetro de Hurst que el modelo permite calcular y el tráfico ofrecido, para poder hacer una comparación acertada del modelo autosimilar con el tráfico real de la red QRD. Por lo tanto, de Sheluhin et al. (2007) y de Iversen (2001) se puede observar que el tráfico autosimilar para redes WLAN puede ser modelado mediante una cola M / G / ∞, análisis del cual se deriva la siguiente definición y lema.

Definición (Sheluhin et al., 2007)
Un proceso {X(t), t Є R} es llamado H_-sssi si este es autosimilar con un parámetro H y posee incrementos estacionarios.

Lema (Sheluhin et al.,2007)
Se asume que {X(t), t Є R} es el proceso H_-sssi (no degenerativo) con una varianza infinita. Entonces 0 < H ≤ 1, X(0) = 0 está casi en todas partes y la covarianza es definida de la expresión:

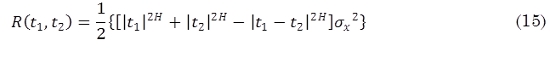
Si X(t) es un proceso H_-sssi (no degenerativo) con una dispersión finita, entonces 0 < H ≤ 1. Durante la simulación del tráfico, el rango 0,5 < H < 1 es de especial interés siempre que el proceso H_-sssi X(t) con H < 0 no puede ser medido y corresponde a un caso patológico, mientras que el caso H > 1 es prohibido debido a la condición estacionaria en el proceso incrementativo. El rango 0 < H ≤ 0.5 puede ser excluido en la práctica dada la premisa de autosimilitud planteada y trabajada en Ge et al. (2009). Para fines prácticos solo el rango 0,5 < H < 1 es importante. En este rango el factor de correlación para el proceso incrementativo Y(t) es:

Y tiene la siguiente forma:

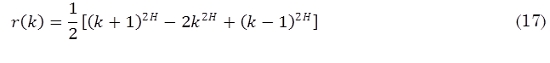
Cola M / G / ∞
El proceso M / G / ∞ es definido de la siguiente manera, se considera la cola M / G / ∞ con tiempo discreto con algunas ranuras de tiempo “σ” como unidad de intervalo de tiempo. Todas las llegadas de tipo Poisson durante la ranura de tiempo se utilizan para el servicio antes del comienzo de la siguiente ranura; W(s=k), k=1,2…, designa la función de densidad de probabilidad (PDF) del tiempo de servicio S en unidades de ranuras de tiempo o slot times “σ”. Es conocido que la distribución del tamaño de la cola en este sistema podría ser tipo Poisson al final de cada ranura con media λ = λo*M(s), donde λo es el número de llegadas promedio hasta el intervalo de tiempo en la cola M / G / ∞. Sin embargo, las longitudes de cola al final de las ranuras que se suceden se correlacionan con la función de autocorrelacion r(k) = P(S > k), igual a la distribución del tiempo adicional a la izquierda al final del servicio. Por lo tanto, si tal proceso de longitud de la cola es usado para generar las llegadas para el sistema analizado, el siguiente proceso de llegada A se obtiene de la distribución marginal de A que es un proceso discreto de Poisson con intensidad λ por ranura (intervalo) y donde P(S > k) desempeña el papel de la función de correlación. En la práctica, podría ser necesario obtener la función de autocorrelacion dada r(k), la cual puede ser usada para calcular la distribución requerida del tiempo de servicio. En particular:

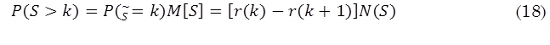
De acuerdo a que P (S > 0) = 1 y r(0) = 1, por definición, M(S) = 1 / (1-r(1)). Entonces se puede asumir dependencia a largo plazo (LRD).

Donde α = r(1) = 1 – M(S). Como resultado, el proceso de llegadas generado es asintóticamente autosimilar con el exponente Hurst H = 1 – β / 2.

Dado que el sistema M / G / ∞ describe un proceso de llegadas discreto únicamente, el próximo paso es la generación de tiempos de llegada separados. Esto se puede lograr por medio de la agregación de llegadas con K = 1 ranuras, seguidas unas con otras y su redistribución sobre todos los intervalos to = σk segundos de tamaño.

Sea N el que designa el número total de llegadas en k intervalos de tiempo. Como N es un proceso tipo Poisson, la asignación de cada llegada al punto del intervalo corresponde a una distribución uniforme, se daría unos momentos de tiempo exponencialmente distribuidos entre las llegadas con las ranuras (intervalos). La distribución de los momentos de tiempos entre llegadas sigue siendo no exponencial. Esto forma las bases de la comparación y creación de los procesos de solicitud de las páginas web, la cual es un proceso asintóticamente autosimilar con incrementos exponencialmente distribuidos.

De igualar (17) y (19) se puede hallar el tráfico ofrecido en forma de la correlación r(k) sabiendo que k es el valor promedio que dura el paquete en la etapa de backoff, por lo tanto:

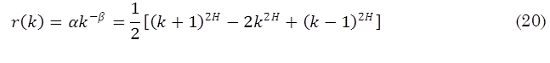
Como:

Entonces:

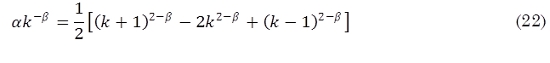
De (12) se tiene que W_promedio es el tiempo promedio que dura un paquete en la etapa de backoff y dado que el proceso denota una distribución uniforme, la ventana máxima de contienda es de 256 por lo tanto el valor promedio es 128, expresado en veces del tiempo de duración del time slot (20,33 µs para 802.11g).

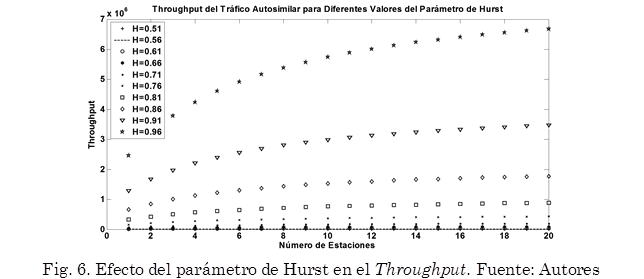
H es el parámetro de Hurst (Pezaros et al., 2007; Reyes, 2001) y en este caso con la ecuación de Throughput se varió con distintos valores entre 0,5<H<1 para encontrar el valor del parámetro de Hurst que mejor se acomoda al modelo de tráfico real, y con base a este parámetro se concluye si el modelo autosimilar es el modelo que mejor se acomoda al tráfico real de la red IEEE 802.11. Estas variaciones se pueden observar en la Fig. 6, la cual se obtiene a partir de la implementación en MATLAB del script que incorpora y grafica (20) para diferentes valores de H.

r(k) es el mismo ρ_k o sea el tráfico ofrecido y se remplaza en (2) donde se define el Throughput.

En este punto se remplazan todos los parámetros necesarios para poder resolver esta ecuación y se varía únicamente el parámetro de Hurst para saber el grado de autosimilitud del modelo para poder obtener las características del tráfico real.

En la Fig. 6, se puede observar que el valor del parámetro de Hurst que mejor se acomoda al tráfico real es H = 0,61, lo que quiere decir que es poco autosimilar debido a que entre más cercano este a 1 es más autosimilar y en este caso se puede observar que el valor es más cercano a 0,5, valor para el cual se considera el tráfico no presenta características autosimilares.

3. Resultados

Inicialmente, se mostrarán los resultados gráficamente, los cuales demostrarán si el modelo autosimilar evaluado representa de manera adecuada el comportamiento del tráfico de la red QRD que es una red WLAN IEEE 802.11g. Obviamente estos resultados son impresiones inicialmente ópticas que tienen que tener un soporte numérico que ratifique que efectivamente el modelo se ajusta o no a las características del tráfico real de la red WLAN QRD.

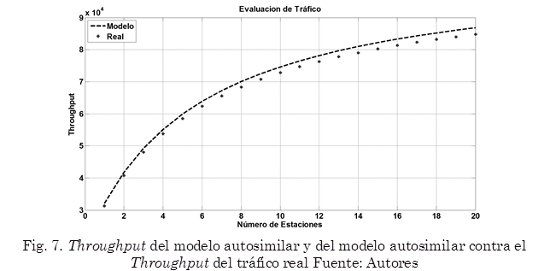
En la Fig. 7 se puede observar el gráfico del modelo autosimilar superpuestos con el tráfico real, el Throughput del tráfico real está descrito con el signo +, y el Throughput del modelo autosimilar está en línea discontinua. Esta gráfica se obtiene de manera similar a las anteriores, mediante la implementación del script en MATLAB que permite graficar simultáneamente el Throughput del tráfico real y del tráfico estimado por el modelo.

Se puede observar que el modelo autosimilar sigue de manera aceptable el comportamiento real del tráfico 802.11 pero cabe destacar que este modelo autosimilar tiene un parámetro de Hurst igual a 0,61 lo cual evidencia unas características de autosimilitud del tráfico agregado en redes 802.11g. Confirmando los resultados obtenidos gráficamente mediante un análisis de correlación se obtiene que:

La correlación de tráfico real con el modelo autosimilar es de 0,941. Donde se observa una fuerte correlación directa y positiva ya que el valor es cercano a uno. Este resultado permite observar sin lugar a dudas que el modelo captura las características del tráfico IEEE 802.11. Sin embargo, debido a que el valor del parámetro de Hurst que mejor describe el tráfico real es más cercano a 0,5 que a 1, se puede decir que el proceso es poco autosimilar, lo cual permite concluir que este tipo de modelos se aproximan de buena manera a la descripción de las características de tráfico en este tipo de redes, pero dicha aproximación no necesariamente es la más adecuada dado el valor que adopta el parámetro de Hurst que mejor se ajusta al tráfico real.

Los resultados obtenidos pueden utilizarse con el fin de realizar dimensionamiento de capacidad que garantice una determinada calidad del servicio QoS en redes 802.11, ya que en la actualidad las metodologías de diseño, planificación y dimensionamiento de este tipo de redes solo contemplan aspectos referentes a la planificación de cobertura y a la parametrización de dispositivos de red.

La metodología de mayor aceptación para realizar dimensionamiento de redes de área local es la Top Down de Cisco (Oppenheimer, 2011), la cual fue utilizada en Astaiza et al. (2011) para evaluar su aplicación al diseño de redes inalámbricas 802.11, trabajo en el cual se identifica que permite realizar un dimensionamiento primario de capacidad para redes de datos en general, pero no permite dimensionar adecuadamente la carga de tráfico ofrecida orientada a garantizar QoS en redes inalámbricas 802.11, dado que los resultados de carga de tráfico obtenidos son sobredimensionados, dado que se presume la totalidad de los usuarios requieren la totalidad de servicios usados de manera permanente (caso similar al de red operando en saturación).

De otro lado la metodología de Cisco, no contempla aspectos como el mecanismo de acceso al medio utilizado por las redes 802.11, lo cual deriva en lo identificado en Astaiza et al. (2011), como lo es la limitada cantidad de usuarios que puede soportar un punto de acceso inalámbrico (AP) antes de que se degrade su desempeño respecto a la tasa de transferencia de información y a la confiabilidad de la conexión.

En orden a que los aspectos mencionados anteriormente implican incurrir en incrementos posiblemente considerables (dependiendo del tamaño de la red) en los costos de infraestructura de la red (sobredimensionamiento) y posibles fallos en el desempeño (degradación de la QoS, dada la cantidad de usuarios por AP), y en concordancia con los resultados obtenidos, se considera el modelo propuesto en Ge et al. (2009) se adapta a las características del tráfico en redes 802.11, y por consiguiente se espera funcione mejor en el dimensionamiento de este tipo de redes, lo anterior se evidencia retomando el estudio de capacidad realizado en Astaiza et al. (2011), donde se estima la carga de tráfico por usuario es de 497 kbps, estimación con la cual se realiza el diseño, dando lugar a una estimación total de tráfico de 20,04 Mbps, tasa que no es alcanzable en enlaces de larga distancia (mayores a 100 m) en redes 802.11g, los cuales en promedio alcanzan tasas del orden de 10 Mbps (Guladrón & Diaz, 2012) y verificada en Astaiza et al. (2011). Sin embargo, el enlace se encuentra en operación satisfaciendo las necesidades de la organización, lo cual indica que con una capacidad inferior a la estimada mediante la metodología Top Down, es posible garantizar soportar los servicios y cargas de tráfico impuestas por los usuarios.

Realizando la estimación del tráfico por usuario y posteriormente del total requerido en la red diseñada en Astaiza et al. (2011) utilizando el modelo de tráfico propuesto en Ge et al. (2009), y dado que según Gualdrón & Diaz, (2012) y Astaiza et al. (2011), el tiempo promedio de servicio en este tipo de redes es del orden de 0,00225 s (uniformemente distribuida entre 1500 y 3000 milisegundos), al aplicar (20) donde K=128σ =128*(20,33 µs) = 2,6 ms y H=0,61. Luego:

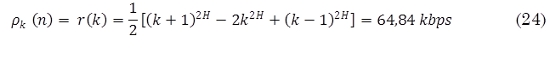
Por lo tanto, para los 40 usuarios referidos en Astaiza et al. (2011) se tiene que la carga total estimada de tráfico del enlace será ρ(n)= 2,59 Mbps. Lo cual se aproxima a las mediciones realizadas posteriormente a la implementación de la red diseñada en Astaiza et al. (2011) y corresponde con un valor inferior a los 10 Mbps esperados como máxima tasa promedio de transferencia de información para enlaces de larga distancia 802.11 y que puede ser satisfecha con este valor promedio.

4. Conclusiones

La autosimilitud en este tipo de tráfico fue cogiendo fuerza a medida que el proceso estocástico se hacía extremadamente parecido a distintas escalas, pero tal y como se presenta en este artículo, esta técnica fue perdiendo popularidad debido al alto nivel matemático y probabilístico que existe detrás de la misma, además que se hace un poco engorroso el proceso de determinar el grado de autosimilitud obtenido a partir del parámetro de Hurst debido a que hay que separar cada una de las tramas agregadas y hallar el parámetro de Hurst por separado para después poder unificarlo y obtener el grado de autosimilitud total del tráfico agregado.

Para poder realizar una comparación adecuada con el tráfico real, se debió definir una expresión de rendimiento que permitiera medir de manera cuantitativa que tan preciso es el modelo autosimilar con respecto al tráfico real capturado en la red WLAN IEEE 802.11 QRD. Esta expresión precisaba una dependencia directa entre el parámetro de Hurst y el tráfico ofrecido, debido a que el tiempo de servicio es aquel que necesita un nodo para transmitir un paquete correctamente, este no permitía una relación del parámetro de Hurst con dicha expresión, ya que este tiempo promedio es el mismo para la expresión del throughput del tráfico real y del modelo autosimilar.

Finalmente, se concluye que el modelo obtenido en Ge et al. (2009) se ajusta a las condiciones reales de funcionamiento y de tráfico agregado ya que se puede apreciar que existe un alto grado de precisión en la comparación con un tráfico real; y la evaluación realizada sobre este modelo, bajo la medida de desempeño definida, permite concluir que es adecuado para ser incorporado en una futura metodología de dimensionamiento de capacidad en redes inalámbricas 802.11.

5. Referencias

Astaiza, E., Bermúdez, H. F., & Muñoz, P. A. (2007). Simulación de sistemas de telecomunicaciones. Armenia: Padilla Bejarano, Ferney.         [ Links ]

Bellalta, B., Oliver, M., Meo, M., & Guerrero, M. (2005). A simple model of the IEEE 802.11 MAC Protocol with Heterogeneous Traffic Flows. The International Conference on Computer as a Tool, Belgrade, Serbia and Montenegro.         [ Links ]

Bianchi, G. (2000). Performance Analysis of the IEEE 802.111 Distributed Coordination Function. IEEE Journal on Selected Areas in Communications, 18(3), 535-547.         [ Links ]

Duffy, K., Malone, D., & Leith, D. J. (2005). Modeling the 802.11 Distributed Coordination Function in Non-Saturated Conditions. IEEE Communications Letters, 9(8), 715-717.         [ Links ]

Fiche, G., & Hebuterne, G. (1988). Communicating systems and networks: traffic and performance. London and Sterling.         [ Links ]

Ge, X., Yang, Y., Wang, C., Lui, Y.Z., Liu, C. & Xiang, L. (2010). Characteristics analysis and modeling of frame traffic in 802.11 wireless networks. Wireless Communications and Mobile Computing, 10(4) 584-592.         [ Links ]

Grote, W., Ávila, C., & Molina, A. (2007). Análisis de máximo desempeño para WLAN operando a tasas fijas o adaptivas usando el estándar IEEE 802.11 a/b/g. Ingeniare. Revista chilena de ingeniería, 15(3), 320-327.         [ Links ]

Hayes, J. F., & Ganesh, T. V. (2004). Modeling and analysis of telecommunications networks. New Jersey: John Wiley & Sons, Inc.         [ Links ]

Iversen, V. B. (2001). Teletraffic engineering handbook. Technical university of Denmark.         [ Links ]

Lamping, U., Sharpe, R., & Warnicke, E. (2004). Wireshark User's Guide. 35094 for Wireshark 1.4.         [ Links ]

P802.11. (1997). IEEE Standard for Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications.         [ Links ]

Pezaros, D., Sifalakis, M., & Hutchison, D. (2007). On the long range dependent behavior of unidirectional packet delay of Wireless Traffic. IEEE Global Telecommunications Conference (IEEE GLOBECOM).         [ Links ]

Reyes, A. (2001). Modelado de tráfico de clientes WWW. Reyes Lecuona, Arcadio: Universidad de Málaga, Servicio de publicaciones. Tesis doctoral.         [ Links ]

Sheluhin, O. I., Smolskiy, S. M., & Osin, A. V. (2007). Self-similar processes in telecommunication. New York: John Wiley & Sons, Ltd.         [ Links ]

Tay, Y., & Chua, K. (2001). A capacity analysis for the IEEE 802.11 MAC Protocol. Wireless Networks, 7(2), 159-171.         [ Links ]