Artículo de revisión/Review Article

Teoría cristalográfica de la transformación martensítica

Crystallographic theory of the martensitic transformation

Edwar A. Torres-López¹, Juan J. Arbeláez-Toro², Diego A. Hincapié-Zuluaga³

¹Ph.D en ingeniería mecánica, Departamento de Mecatrónica y Electromecánica, Facultad de Ingeniería, Instituto Tecnológico Metropolitano, Medellín-Colombia, edwartorres@itm.edu.co

²M.Sc en ingeniería mecánica, Departamento de Mecatrónica y Electromecánica, Facultad de Ingeniería, Instituto Tecnológico Metropolitano, Medellín-Colombia, juanarbelaez@itm.edu.co

³M.Sc en ciencias-Física, Departamento de Mecatrónica y Electromecánica, Facultad de Ingeniería, Instituto Tecnológico Metropolitano, Medellín-Colombia, diegohincapie@itm.edu.co

Fecha de recepción: 11 de diciembre de 2013 / Fecha de aceptación: 19 de mayo de 2014

Cómo citar / How to cite

E. A. Torres-López, J. J. Arbeláez-Toro y D. A. Hincapié-Zuluaga, "Teoría cristalográfica de la transformación martensítica", Tecno Lógicas, vol. 17, no. 33, pp. 77-90, 2014.

Resumen

La transformación martensítica es uno de los temas más investigados en la ciencia de los materiales durante el siglo XX. Precisamente la segunda parte de ese siglo se destacó por el desarrollo de diversas teorías relacionadas con la cinética de la transformación de esta fase, los mecanismos de nucleación y la forma como se produce el cambio de la estructura cristalina. En este trabajo se realiza la descripción de los diferentes conceptos que definen la cristalografía de la transformación martensítica, centrándose en la construcción y aplicación de los modelos cristalográficos más destacados: el modelo de Bain; el modelo de Wechsler, Lieberman y Read; y el modelo de Bowles y Mackenzie. Este desarrollo será realizado con base en características particulares de la transformación martensítica como su carácter no difusional, el tipo de intercara entre la fase madre (austenita) y la fase producto (martensita), la formación de la subestructura de defectos y el cambio de forma; todas estas descritas por medio de ecuaciones matemáticas que buscan predecir cómo se dará la transformación, más que en explicar el movimiento real de los átomos dentro de la estructura. Este desarrollo es conocido como la Teoría Fenomenológica de la Cristalografía de la Martensita (TFCM).

Palabras clave: Modelo de Bain, teoría fenomenológica, deformación invariante, cambio de forma, intercara austenita-martensita.

Abstract

The martensitic transformation is one of the most researched topics in the materials science during the 20th century. The second half of this century was mainly remembered by the development of several theories related with the kinetics of phase transformation, the mechanisms involved in the nucleation phenomenon, and the way as the crystallographic change is produced. In this paper are described the fundamental concepts that are defined in the crystallographic framework of the martensitic transformation. The study is focused on the application of the most outstanding crystallographic models: the Bain; the Wechsler, Lieberman & Read; and the Bowles & Mackenzie. The topic is presented based upon the particular features of the martensitic transformation, such as its non-diffusional character, type of interface between parent (austenite) and product (martensite) phases, the formation of substructural defects, and the shape change; all of these features are mathematically described by equations aimed to predict how the transformation will take place rather than to explain the actual movement of the atoms within the structure. This mathematical development is known as the Phenomenological Theory of Martensite Crystallography (PTMC).

Keywords: Bain Model, phenomenological theory, invariant strains, shape change, austenite-martensite interface.

1. Introducción

Una parte fundamental del estudio de la martensita busca entender el cambio de estructura cristalina durante la trasformación, mediante modelos fenomenológicos que, a pesar de no describir el movimiento real de los átomos, permitieron determinar algunas de sus características morfológicas, cristalográficas y cinéticas.

Los modelos cristalográficos abrieron la puerta a la predicción de características como la determinación del plano de hábito, las relaciones de orientación, los parámetros de red y la magnitud de la deformación. Este modelo matemático es conocido como la Teoría Fenomenológica de la Cristalografía de la Martensita (TFCM) o PTMC, por sus siglas en inglés. Las herramientas matemáticas desarrolladas, para este fenómeno, han sido extrapoladas a otras trasformaciones de fase como la ferrítica, la bainítica y la formación de compuestos intermetálicos [1], [2].

Este artículo corresponde a la segunda parte de un trabajo anteriormente publicado acerca de la transformación martensítica, donde fueron descritos diferentes rasgos propios de esta transformación de fase [3]. Esta segunda parte explica la construcción matemática de la TFCM, estableciendo cómo y por qué fueron descartadas y adaptadas diferentes hipótesis, a medida que surgían nuevas evidencias y se comprendía mejor el fenómeno en sí mismo. Con este fin, al inicio de este trabajo se establecerán cuáles son las condiciones que deben ser cumplidas por cualquier modelo cristalográfico.

A seguir, se describe uno de los primeros trabajos alrededor de la cristalografía de la transformación martensítica, destacando sus contribuciones y las razones por las que fue descartado. Finalmente, será descrita la plataforma matemática de la TFCM y los dos modelos cristalográficos actuales: el modelo de Wechsler, Lieberman y Read, y el modelo de Bowles y Mackenzie [4]-[7].

2. Condiciones para la transformación martensítica

Gracias al estudio del fenómeno martensítico y al avance en las técnicas de caracterización se pudieron definir las características que, según Veroheven [8], todo modelo cristalográfico debe considerar: La intercara austenita-martensita puede ser de tipo coherente o semicoherente; a escala macroscópica el plano de hábito es un plano invariable; a escala macroscópica el cambio de forma en la transformación martensítica es una deformación plana invariante; a escala microscópica la martensita contiene una alta densidad de dislocaciones o de maclas.

Estas características deben ser reflejadas por medio de artefactos matemáticos en un modelo que pretenda ser aceptado. Partiendo del modelo de Bain hasta los modelos de la TFCM, este artículo revisará los pasos dados para la construcción de la teoría que hoy en día es aceptada, finalizando con una revisión del estado del arte de los modelos más modernos de esta teoría.

3. Modelo de Bain

En este modelo, su principal aporte fue describir la transformación de la estructura cristalina en los aceros al pasar de austenita, con estructura cúbica centrada en las caras (ccca), a martensita, cuya estructura es tetragonal centrada en el cuerpo (tccu); además, este modelo aportó dos conceptos fundamentales a la teoría cristalográfica: correspondencia de retícula y deformación pura de retícula o deformación de Bain, descritas en [9].

3.1 Correspondencia de retícula

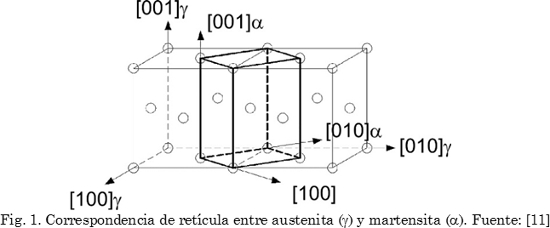
El punto de partida para toda transformación martensítica envuelve una relación entre las estructuras de la fase madre y producto, donde puntos reticulares en la fase madre deben conectarse, uno a uno, con puntos reticulares de la fase producto [10]-[12]. Esta condición se denomina correspondencia y se considera su existencia cuando un grupo de planos, con un apilamiento determinado, forman una celda unitaria en la fase madre y en la fase producto [13], [14]. Esto se verifica en la Fig. 1, donde la estructura ccca (líneas finas) contiene simultáneamente una estructura tccu (líneas gruesas).

La correspondencia entre la fase madre (ccca) y la martensita (tccu), permite construir una matriz de transformación de coordenadas denominada matriz de correspondencia (αC_γ), donde el paralelismo de planos y vectores presentados en la Fig. 1 no puede entenderse como relaciones de orientación ente γ y α [15].

3.2 Deformación de Bain

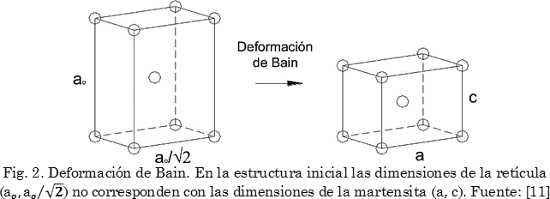
La correspondencia de retícula facilita la obtención de una estructura cristalina similar a la martensita a partir de la retícula de la fase madre. Sin embargo, esta estructura (líneas gruesas en la Fig. 1) no tiene las dimensiones correctas de la celda unitaria de la martensita; por lo tanto, se debe aplicar una deformación donde la tccu inicial pase a la tccu con las dimensiones correctas, como la presentada en la Fig. 2. La deformación que permite la obtención de las dimensiones correctas de la estructura cristalina es conocida como la deformación de Bain [16].

Esta se genera por la tracción y compresión de la retícula, con la condición que las líneas permanezcan rectas y los planos como planos. Este tipo de deformación es conocida como deformación homogénea de retícula [7], [17].

3.3 Deformación homogénea

Según Bhadeshia [6] y Yeddu et al [18], una transformación homogénea es aquella donde los puntos colineales permanecen colineales, y las líneas coplanares permanecen coplanares. Para el caso particular de la correspondencia de Bain, una compresión a lo largo del eje [001]_α, junto a una expansión a lo largo de [100]_α y [010]_α, como se presenta en (1 ), permite la transformación de la red cristalina.

Donde η₁ es la deformación a lo largo de [100]_γ, η₂ es la deformación a lo largo de [010]_γ, η₃ es la deformación a lo largo de [001]_γ, a_γ es el parámetro de red de la fase madre y a_α es el parámetro de red de la martensita.

Si la retícula madre se define como A, vectorialmente se tiene: [A;v] = (ASA)[A;u]. Donde (ASA) es la matriz que convierte el vector [A;u] en el vector [A;v], como representado matemáticamente en (2). Esta deformación, representada por la matriz (ASA), corresponde a una deformación pura, pues es posible encontrar tres vectores ortogonales invariantes, después de la deformación [7].

A pesar de los importantes aportes del modelo de Bain, este modelo presenta dos vicios: 1) El modelo sólo es válido para transformaciones martensíticas de ccca a tccu. 2) La deformación de Bain produce la transformación de la estructura cristalina mas no explica la formación del plano de hábito [3], [17]. Estas incongruencias llevaron a la puesta en escena de nuevas formulaciones matemáticas que posteriormente constituirían la TFCM.

3.4 Deformación Plana Invariante (Invariant Plane Strain, IPS)

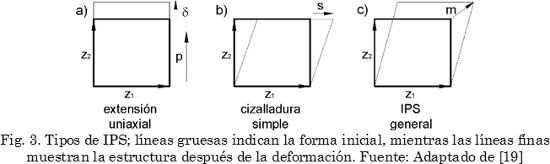
Otro concepto importante es el de deformación plana invariante. Para su construcción se considera que existen varios tipos de desplazamientos atómicos, en bloque, los cuales no producen cambio en la posición relativa entre los átomos y son capaces de conservar un plano sin distorsión ni rotación [19]. El plano conservado se conoce como plano invariante, que a nivel microestructural no es otro que el plano de hábito [20]. Por lo tanto, se tienen tres tipos de IPS, como se muestra en la Fig. 3.

Partiendo de una base Z, definida por la estructura cristalina de la fase producto, y una muestra con la misma forma, rectángulo en líneas gruesas (Fig. 3), se obtiene un cambio en la forma, donde p es el vector unitario paralelo a z₃, δ es la magnitud de la dilatación, s es la magnitud de la cizalladura paralela a z₁ y m es la magnitud del desplazamiento total.

La Fig. 3a muestra una IPS de dilatación pura; se conoce así pues a pesar que se produce alargamiento en una dirección, en la dirección perpendicular no se registra reducción de sus dimensiones; lo que implica un cambio de volumen debido a la deformación. La Fig. 3b describe una IPS por cizalladura simple, en la cual no se registra ningún cambio volumétrico. El caso más general de IPS es el representado en la Fig. 3c, que resulta de la combinación de las dos deformaciones anteriores, y que matemáticamente se representa en (3).

Donde z_i es el vector unitario de la base definida por los de la celda cristalina de la fase producto, md es el vector desplazamiento, d es el vector unitario con la dirección de desplazamiento, sz₁ es la magnitud de la cizalladura y δz₃: es la magnitud de la dilatación. La representación en matrices de cada IPS de la Fig. 3, se presenta en (4), (5) y (6) :

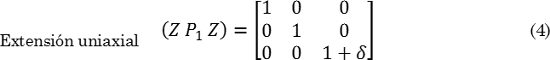
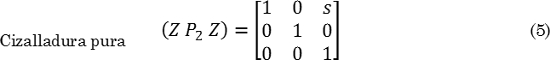
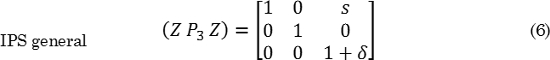
4. Construcción de los modelos actuales

4.1 Cambio de forma

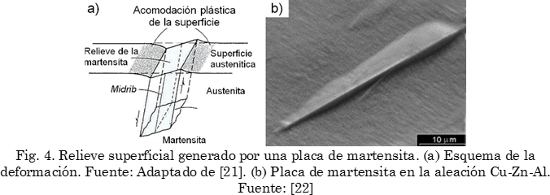
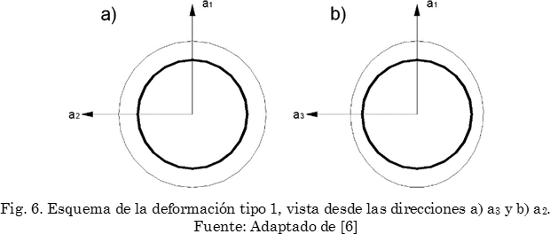
Como la transformación martensítica involucra el movimiento coordinado de átomos sin difusión, esto genera un cambio físico que se manifiesta macroscópicamente con la formación de un relieve (Fig. 4a) en el lugar donde crecen las placas (Fig. 4b).

En la Fig. 5 se muestra como en las transformaciones de fase sin difusión (como la transformación martensítica) se mantiene el ordenamiento atómico, pese al desplazamiento producto de la deformación plana invariante, que para el caso de la Fig. 5b se trata de una cizalladura simple (Fig. 3b).

Esta deformación produce el cambio de forma, evidente por el relieve superficial derivado de la transformación (Fig. 4). Igualmente la Fig. 5 destaca como las transformaciones por difusión no producen cambio de forma, a pesar del cambio en el ordenamiento atómico (Fig. 5c).

El cambio de forma es uno de los elementos más destacados de la teoría, pues ofrece información sobre el mecanismo atómico involucrado en la transformación [23], [24], información que se hace extensiva al estudio cristalográfico de la bainita [25]-[27].

El cambio de forma es importante porque indica que se produjo una deformación por cizalladura, siendo posible asociar dicha trasformación a una correspondencia de retícula y a una transformación de fase sin difusión, que se considera invariante [13], [28]. Pero los cambios de forma varían con el tipo de deformación aplicada. Para estudiar este punto considere una región de la fase madre definida por una esfera unitaria, sometida a diferentes deformaciones a lo largo de sus ejes principales, definidas en (7), transformando la esfera en elipsoide.

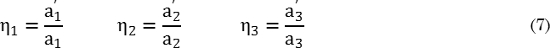
Donde a₁, a₂, a₃ y a´₁, a´₂, a´₃ son los ejes principales de la esfera unitaria y la elipsoide. El cambio de longitud de los vectores base se define como εi = ηi-1. A partir de estas definiciones se consideran cuatro tipos de deformaciones [29].

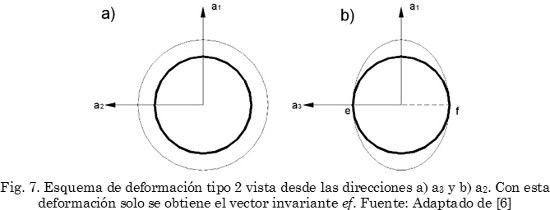
Cuando los alargamientos ei son todos positivos o negativos (Fig. 6), no se produce ningún punto de contacto entre la esfera unitaria y el elipsoide, lo que indica que todos los vectores sufrieron deformación y/o rotación, lo que implica que no se produce un plano invariante. Esta deformación se denomina deformación tipo 1.

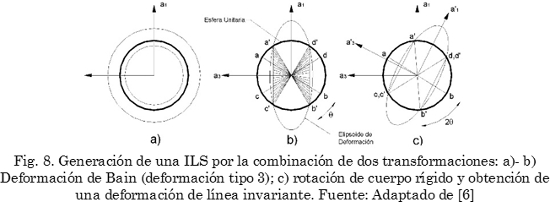
Para la deformación tipo 2, uno de los ejes principales permanece sin deformación (eje a₃ en la Fig. 7), mientras los otros dos presentan ei positivas o negativas. En estas condiciones la esfera y el elipsoide hacen contacto a lo largo del eje sin deformación, generando un único vector invariante (línea ef en la Fig. 7b), pues este vector no se deforma ni rota. Este tipo de deformación, es denominada deformación de línea invariante (Invariant Line Strain, ILS) [30].

La deformación tipo 3 es el caso donde dos de los ejes principales son deformados positiva o negativamente, mientras el tercero lo hace en sentido contrario a los dos primeros (Fig. 8a-b). Del contacto entre la esfera unitaria y el elipsoide se generan dos superficies cónicas que contienen todos los vectores no deformados (Fig. 8b); sin embargo estos vectores han cambiado de dirección; por ejemplo, los vectores iniciales ab y cd, rotan hasta los puntos a’b’ y c’d’. Por lo tanto, no existen vectores invariantes, ya que a pesar de no deformarse sí sufren rotación.

Regresando a la transformación de Bain, recuerde el lector que esta corresponde a la tracción y compresión de la estructura en sus ejes principales, descrita por (1) ; por lo tanto, la deformación de Bain es un caso específico de la deformación de tipo 3. Las implicaciones de esta observación son significativas, pues esto implica que una deformación tipo 3 está en capacidad de generar el cambio de estructura cristalina. Sin embargo, esta deformación continúa fallando, pues a pesar de generar la estructura cristalina, sigue replicando el segundo defecto descrito en la deformación homogénea, ya que no consigue generar el plano de hábito.

Adicionalmente, el modelo debe reproducir el cambio de forma y explicar la formación de una sub-estructura de maclas o dislocaciones, lo cual no se consigue con esta propuesta de deformación. A pesar de estas falencias el modelo de Bain (deformación tipo 3, Fig. 8a-b) todavía es útil, pues al combinarse con una rotación de cuerpo rígido (Fig. 8c), uno de los vectores sin deformación es llevado a su posición original (vector c’d’) produciendo una ILS.

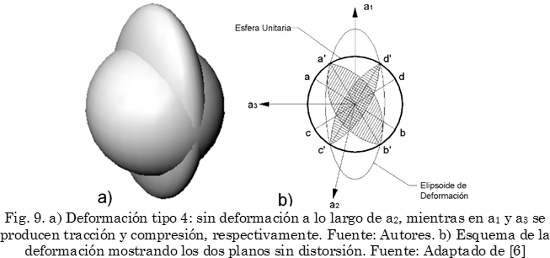
Por último, en la deformación tipo 4, uno de los ejes principales permanece intacto y los otros dos se deforman cada uno con signo contrario (Fig. 9a); entonces, dos planos en la retícula se mantienen sin deformación, como lo muestra la Fig. 9b.

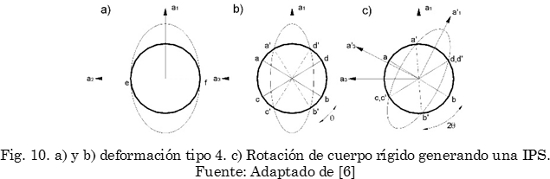
Cuando se habla de planos sin deformación se considera que ninguno de los vectores contenidos sufre cambio en sus dimensiones; a pesar de ello se produce un cambio de dirección, pasando de las posiciones ab-cd a a’b’-c’d’ (Fig. 9b). Por lo tanto, la deformación tipo 4 no puede ser considerada como una IPS. Sin embargo, de la misma forma que se obtiene una ILS (Fig. 8c), si se combina la deformación tipo 4 con una rotación de cuerpo rígido, uno de los planos sin deformación se convierte en un plano invariante, generando una IPS, como se muestra en la Fig. 10.

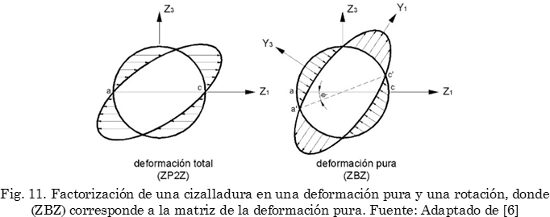
Algunas martensitas presentan intercaras austenita-martensita coherentes [3 ], pues durante la transformación no se produce cambio volumétrico, lo que implica que no hay componente de dilatación en la deformación. Estas martensitas se forman por medio de una IPS, la que corresponde específicamente a una deformación por cizalladura simple [7]. La cizalladura simple resulta de la combinación de una deformación pura (tracción y compresión sobre los vectores base) y una rotación de cuerpo rígido, representada gráficamente en la Fig. 11, donde la deformación pura debe ser del tipo 4, ya que es la única capaz producir planos sin deformaciones.

Por lo tanto, para martensitas coherentes, la IPS puede ser factorizada como:

Donde P es el cambio de forma o IPS, R es la rotación de cuerpo rígido y B es la deformación pura (tipo 4).

No obstante, en la mayoría de los casos la transformación martensítica presenta cambio volumétrico, donde la deformación que mejor describe la trasformación corresponde a la IPS de la Fig. 3c. En este la intercara austenita-martensita es semi-coherente, con presencia de dislocaciones o maclas [3]. Debido a estas características no es posible obtener la trasformación mediante la factorización descrita en (8).

La mejor opción, es obtener el cambio de estructura cristalina mediante una ILS, resultante de la combinación entre la deformación de Bain (deformación tipo 3) y una rotación de cuerpo rígido, como se presenta en la Fig. 8. Sin embargo, aún persiste un problema para representar la transformación martensítica con intercaras austenita-martensita semicoherentes, pues es necesario producir el plano invariante, que es el mismo plano de hábito de la trasformación. Ahora es necesario determinar cómo generar un plano invariante, similar al generado durante la IPS (deformación tipo 4), a partir de la ILS que produjo el cambio de estructura cristalina. Este es el problema fundamental de la TFCM.

5. Teoría fenomenológica de la cristalografía de la martensita

La solución al problema anteriormente establecido fue planteada por dos grupos diferentes: el primero formado por M. S. Wechsler, D. S. Lieberman y T. A. Read en 1953; y el segundo por J. S. Bowles y J.K. Mackenzie en 1954. La teoría formal busca ajustar la intercara entre la fase madre y la martensita, para formar el plano de hábito, sin modificar la estructura cristalina generada mediante la deformación de línea invariante (Fig. 8c). La solución propuesta se basa en el ajuste de la intercara aplicando una nueva deformación, no continua, sino periódica, que corrija dicho desajuste generado por la ILS [13]. Esta deformación escalonada genera la impresión que macroscópicamente el plano es invariante, a pesar que a nivel atómico el plano de hábito presente discontinuidades. Sin embargo, se debe cumplir la siguiente condición: como la estructura cristalina se produjo mediante una ILS, la operación de ajuste no debe generar ningún cambio en la retícula; por lo tanto, la nueva deformación debe ser una deformación de retícula invariante.

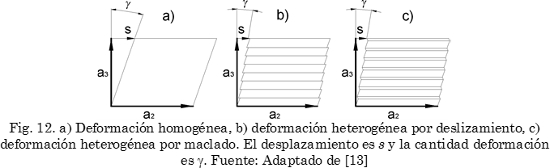
Una deformación por deslizamiento (cizalladura) permite realizar tal ajuste sin cambio en la retícula. Sin embargo, presenta un inconveniente: si la cizalladura es homogénea (Fig. 12a) la magnitud del desplazamiento (s), o cambio de forma, es proporcional a la cantidad de planos deslizados, resultando casi casual que se obtenga la deformación (s) necesaria que permita que uno de los ejes principales (de la deformación tipo 3, Fig. 8a-b) regrese a su posición en la esfera unitaria, condición ineludible para generar los planos sin distorsión (deformación tipo 4, Fig. 9a).

Pero si el deslizamiento se realiza de forma escalonada (Fig. 12b) el desplazamiento entre cada bloque desplazado no cumple ninguna regla; por lo tanto, el desplazamiento (s) puede tener cualquier magnitud, incluso la requerida para el ajuste necesario; esta operación se denomina deformación heterogénea por deslizamiento.

El maclado es otro mecanismo apto para producir el mismo efecto (Fig. 12c); este último se conoce como deformación heterogénea por maclado. Ambos mecanismos, además de permitir el ajuste de la intercara, sin cambios en la estructura cristalina, explican la existencia de la sub-estructuras de dislocaciones o maclas al interior y en el plano de hábito [31]-[34].

Por lo tanto, una deformación de línea invariante, compuesta por la deformación pura de retícula (B) y una rotación de cuerpo rígido (R), combinada con una deformación heterogénea de retícula invariante (Q), producen el cambio de forma (P), el plano de hábito (a nivel macroscópico) y las discontinuidades en la microestructura. Toda esta transformación se expresa matemáticamente como:

Donde P es el cambio de forma, definido por una matriz 3x3 del tipo (ZP3Z), R es la rotación de cuerpo rígido (ZRZ), Q es la deformación de retícula invariante (ZBZ), igual a la matriz (ASA), B es la deformación pura de retícula (ZQZ), matriz similar a la matriz (ASA) y Z es la base construida a partir de la estructura cristalina de la fase producto.

5.1 Formulación de la teoría

Para las teorías actualmente aceptadas, la primera parte del desarrollo del modelo se inicia con la identificación de una correspondencia de retícula, la cual se lleva a cabo por inspección de las estructuras de las fases madre y producto. Después se define la deformación pura de retícula (B) que produce el cambio de estructura cristalina y convierte al vector u en Bu, donde B, es la matriz (ASA) representada en (2) . A partir de este punto los dos modelos aceptados, a pesar de ser equivalentes, presentan ligeras diferencias en su planteamiento. Los modelos serán descritos a continuación.

5.2 Modelo de Wechsler, Lieberman y Read [35]

En este modelo, denominado WLR, el paso a seguir después de la transformación de la estructura cristalina es determinar el sistema de deslizamiento o de maclado para la deformación invariante de la retícula, teniendo presente que el cambio de volumen por esta deformación tiene que ser cero. Si Q es la deformación de retícula invariante, esta no produce cambios significativos en vectores pequeños (Bu), donde la transformación es descrita en (10), donde F representa la combinación de las deformaciones B y Q, equivalente a la deformación tipo 4 de la Fig. 10. Por otro lado, para vectores grandes (mBu), donde mu es un vector paralelo a u pero m veces más grande, la transformación es descrita por (11).

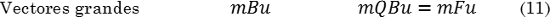
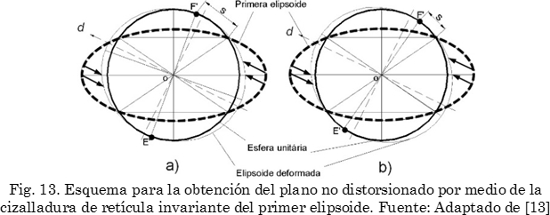
La deformación Q es aplicada sobre un plano en una dirección específica; solo que los sistemas de deslizamiento o maclado, de la estructura madre y producto, son múltiples; por lo tanto, hay varias alternativas, cada una capaz de producir un resultado diferente. Para disminuir el número de posibilidades, se debe tener en cuenta que la cantidad de deformación (s) debe ser tal que garantice que se producirán dos planos sin deformación (Fig. 9b). La magnitud de la deformación Q es desconocida; pero la cantidad de cizalladura puede ser establecida teniendo en cuenta que sólo existen dos magnitudes capaces de transformar el elipsoide producido por la deformación de Bain, o tipo 3 (Fig. 8a-b), en el elipsoide tipo 4 (Fig. 9a). Las dos posibilidades son presentadas en la Fig. 13, donde para ambos esquemas la magnitud s es diferente.

En la Fig. 13, el círculo en líneas gruesas corresponde a la esfera inicial, la cual es convertida en el primer elipsoide (líneas punteadas) por la trasformación de Bain. Este primer elipsoide es posteriormente transformado en el elipsoide deformado (línea clara) mediante la aplicación de Q (indicado por las flechas), el cual desplaza los puntos de intersección, entre este y la esfera, a la posición E’ y F’ (puntos negros). Por lo tanto, en la elipsoide deformada se producen dos planos invariantes, pues en la esfera uno de los ejes principales no sufre deformación (eje E’F’).

Así, al aplicar Q, representado por las flechas en la dirección d y con las magnitudes s, según la Fig. 13a-b, se genera el plano sin distorsión. En este punto se ha generado tanto el cambio de estructura como el plano sin deformación mediante la operación F (combinación de QB). Ahora se aplica la rotación de cuerpo rígido (R) para llevar el plano sin deformación a la orientación original, formando el plano macroscópicamente invariante (Fig. 10c). El modelo se expresa como:

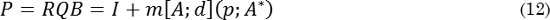
Donde I es la matriz identidad de 3x3, m es la magnitud del desplazamiento total (Fig. 3c), d es el vector unitario con la dirección de desplazamiento, p es el vector unitario normal del plano invariante, A es la base definida por los vectores unitarios a₁, a₂, a₃ y A* es la base recíproca de A definida por los vectores unitarios a₁*, a₂*, a₃*.

5.3 Modelo de Bowles y Mackenzie [36]

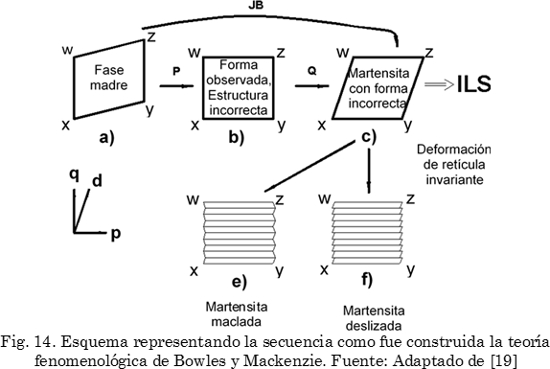
El modelo de Bowles y Mackenzie (BM) fue desarrollado en los 50’s en paralelo al WLR; a diferencia del modelo WLR, el modelo BM comienza generando el cambio de forma en lugar de iniciar con la trasformación de la estructura cristalina (Fig. 14a). En primer lugar sobre la fase madre se aplica una IPS para producir el cambio de forma (P), donde el plano invariante es wx, normal a p, y la magnitud y la dirección de la deformación son m y d; esta trasformación no involucra mudanza en la estructura cristalina, pero sí el cambio volumétrico correspondiente (Fig. 14b). Para producir el cambio de estructura cristalina, se aplica otra IPS (Q), cuyo plano invariante es xy, normal a q, con magnitud s y dirección n, pero sin cambio volumétrico. La intersección de los planos invariantes generados por las deformaciones P y Q corresponde a una ILS, representada por la línea invariante x (Fig. 14).

Desafortunadamente la deformación Q produce un nuevo cambio de forma, el cual no corresponde con el esperado [35]-[37]. En este punto es donde la teoría es ingeniosa, pues supone que la deformación Q debe ser macroscópicamente invisible para no producir el cambio de forma observado en la Fig. 14c. Por lo tanto, para que Q sea invisible es necesario cancelarla con otra deformación tal que la forma observada pase de la Fig. 14c a la de Fig. 14e-d, sin generar cambio en la estructura cristalina. La deformación que anula a Q es entonces una deformación invariante de retícula denominada Q’.

En resumen el modelo formula: Se aplica una IPS (P) para producir el cambio de forma a la fase madre (Fig. 14b), el cual es representado matemáticamente por (13):

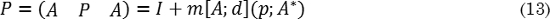
P se combina con una deformación Q para producir una ILS (Fig. 14c), que en términos matemáticos se describe en (14):

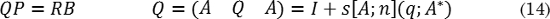
Se aplica una deformación Q’ para anular el cambio de forma generado por Q, y así retornar a la forma correcta generada por P (Fig. 14e-d), como descrito en (15):

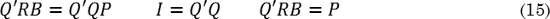
Así las teorías WLR y BM, presentadas en (12) y (15), son formalmente equivalentes.

6. El modelo cristalográfico en la actualidad

En los últimos cincuenta años, la TFCM no ha sufrido cambios significativos en su estructura matemática [38]-[40]. Sin embargo, están siendo desarrolladas nuevas propuestas integrando los cambios cristalográficos y la cinética de la trasformación. Por ejemplo, Ledbettera & Dunn [41] proponen un modelo que estima la deformación, los esfuerzos y la energía de deformación producida durante la formación de una placa, cuyas predicciones del plano de hábito y el cambio de forma coinciden con las realizadas por los modelos WLR y BM, además de ser corroboradas por medida realizadas en una aleación Fe-31Ni.
Algunas variantes de los modelos apuntan a la incorporación de efectos como la fuerza impulsora mecánica, en los modelos tradicionales. En algunos de estos trabajos son determinadas las relaciones de orientación en aleaciones no ferrosas, a partir de datos generados por medio de difracción de electrones retrodispersados (Electron Backscatter Diffraction, EBSD). Esta herramienta permitió ubicar los planos de hábito de las martensitas resultantes de trasformaciones ccca/cccu y hcp/cccu en un cono similar al mostrado en el esquema de la Fig. 8b, revalidando los modelos clásicos [42]-[44].

Algunos desarrollos analíticos relacionados con características cristalográficas como las relaciones de orientación, la orientación del plano de hábito y la configuración de las dislocaciones en el plano de hábito, basados en derivaciones en dos dimensiones de los espacios reciproco y directo, han sido puestos en escena [45]. Uno de los trabajos más sobresalientes es el de Wu et al [46] quienes desarrollaron una metodología que evita las dificultades que representa el hecho que la línea invariante esté contenida en el espacio 2D, generando un tratamiento más simple de las variables y resultados consistentes. Este tipo de modelos busca su aplicación en trasformaciones con y sin difusión atómica; siendo posible su uso en estudios como la cristalografía de la austenita Widmanstatten para develar evidencias que permitan apuntar a los mecanismos para su formación [47]. Sin embargo, las mejoras en las predicciones de los modelos actuales está supeditada la integración a los modelos de las fuerzas química y mecánica [19].

Algunos casos han tratado de construir modelos más amplios que comprendan tanto la cristalografía como la cinética de la transformación martensítica, encontrando serias dificultades, debido principalmente a que los modelos cristalográficos no pretenden simular el movimiento atómico durante la transformación [48]. No obstante, el éxito de las teorías WLR y BM se ha visto ratificado en el estudio de nuevos materiales y fenómenos donde parte o todo el planteamiento teórico concuerda de forma precisa con las observaciones experimentales. El alcance de esto modelos inclusive ha llevado a propuestas donde se considera el efecto de la deformación de la matriz y de la composición química, siendo aplicados a otros mecanismos de transformación como la transformación bainítica [49], [50].

7. Conclusiones

La teoría cristalográfica de la trasformación martensítica define dos modelos matemáticos: uno para martensitas con intercara coherente austenita-martensita y otro para martensitas con intercara semi-coherente. Para el primero la trasformación de fase no involucra cambio volumétrico, luego la transformación puede ser concebida como la combinación de una deformación plana invariante (deformación tipo 4) y una rotación de cuerpo rígido. En el segundo caso existe un cambio volumétrico asociado al cambio de fase, por lo tanto el modelo requiere de una trasformación de línea invariante (deformación de Bain o tipo 3, sumada a una rotación de cuerpo rígido), donde se genera el cambio de estructura cristalina, junto a una deformación invariante de retícula, la cual debe ser heterogénea, y que responde por la generación de plano invariante, aunque sea invariante solo a nivel macro.

Referencias

[1] M.-X. Zhang and P. M. Kelly, "Crystallographic features of phase transformations in solids," Prog. Mater. Sci., vol. 54, no. 8, pp. 1101-1170, Nov. 2009.         [ Links ]

[2] C. M. Wayman, "Phase Transformations, Nondiffusive," in Physical Metallurgy, Amsterdam: North Hollan Publishing Corp., 1983, pp. 1031-1073.         [ Links ]

[3] E. A. Torres, J. J. Arbelaez, and D. A. Hincapié, "Aspectos generales acerca de la transformación martensítica," Tecno Lógicas, no. 31, pp. 151-179, 2013.         [ Links ]

[4] J. K. Mackenzie and J. S. Bowles, "The crystallography of martensite transformations II," Acta Metall., vol. 2, no. 1, pp. 138-147, Jan. 1954.         [ Links ]

[5] J. W. Christian, The theory of transformations in metals and alloys: Part 1 - Equilibrium and general kinetic theory, 3rd ed. Oxford: Pergamon Press, 1975, p. 794.         [ Links ]

[6] H. K. D. H. Bhadeshia, Worked examples in the geometry of crystals, 2nd ed. Carlton House Terrace: The Institute of Metals, 2001, p. 109.         [ Links ]

[7] E. A. Torres, "Cristalografía de la transformación martensítica," Universidad Nacional de Colombia - Medellín, 2004.         [ Links ]

[8] J. D. Verhoeven, Fundamentos de metalurgia física, 1st ed. México: Limusa, 1987, p. 547.         [ Links ]

[9] E. C. Bain, "The nature of martensite," Trans. Am. Inst. Min. Met. Eng., vol. 70, pp. 25-47, 1924.         [ Links ]

[10] C. M. Wayman, "The phenomenological theory of martensite crystallography: Interrelationships," Metall. Mater. Trans. A, vol. 25, no. 9, pp. 1787-1795, Sep. 1994.         [ Links ]

[11] J. . Morris, C. . Krenn, D. Roundy, and M. L. Cohen, "Deformation at the limit of elastic stability," Mater. Sci. Eng. A, vol. 309-310, pp. 121-124, Jul. 2001.         [ Links ]

[12] J. B. Yang, Z. G. Yang, Y. Nagai, and M. Hasegawa, "A crystallographic model of fcc/bcc martensitic nucleation and growth," Acta Mater., vol. 58, no. 5, pp. 1599-1606, Mar. 2010.         [ Links ]

[13] J. W. Christian, "Basic crystallography and kinetics," in Martensite: fundamentals and technology, E. R. Petty, Ed. London: Longman Ltda., 1970, pp. 11-41.         [ Links ]

[14] P. M. Kelly and L. R. Francis Rose, "The martensitic transformation in ceramics - its role in transformation toughening," Prog. Mater. Sci., vol. 47, no. 5, pp. 463-557, Jan. 2002.         [ Links ]

[15] S. Morito, X. Huang, T. Furuhara, T. Maki, and N. Hansen, "The morphology and crystallography of lath martensite in alloy steels," Acta Mater., vol. 54, no. 19, pp. 5323-5331, Nov. 2006.         [ Links ]

[16] Y. M. Jin, A. G. Khachaturyan, Y. U. Wang, C. R. Krenn, and A. J. Schwartz, "Crystallography of the δ→α martensitic transformation in plutonium alloys," Metall. Mater. Trans. A, vol. 36, no. 8, pp. 2031-2047, Aug. 2005.         [ Links ]

[17] R. Reed-Hill, Physical metallurgy principles, 2nd ed. New York: Van Nostrand, 1973, p. 920.         [ Links ]

[18] H. K. Yeddu, V. I. Razumovskiy, A. Borgenstam, P. A. Korzhavyi, A. V Ruban, and J. Ågren, "Multi-length scale modeling of martensitic transformations in stainless steels," Acta Mater., vol. 60, no. 19, pp. 6508-6517, Nov. 2012.         [ Links ]

[19] H. K. D. H. Bhadeshia, S. Kundu, and H. Abreu, "Mathematics of crystallographic texture in martensitic and related transformations," in Microstructure and Texture in Steels, D. B. A. Haldar, S. Suwas, Ed. London: Springer, 2009, pp. 19-31.         [ Links ]

[20] V. D. Blank and B. A. Kulnitskiy, "The habit plane of martensite at BCC-HCP phase transformation," Scr. Mater., vol. 37, no. 3, pp. 373-376, Aug. 1997.         [ Links ]

[21] G. R. Speich and W. C. Leslie, "Tempering of steel," Metall. Trans., vol. 3, no. 5, pp. 1043-1054, May 1972.         [ Links ]

[22] G. Bertolino, P. A. Larochette, E. M. Castrodeza, C. Mapelli, A. Baruj, and H. E. Troiani, "Mechanical properties of martensitic Cu-Zn-Al foams in the pseudoelastic regime," Mater. Lett., vol. 64, no. 13, pp. 1448-1450, Jul. 2010.         [ Links ]

[23] J. W. Christian, "The origin of surface relief effect in phase transformations," in Decomposition of austenite by diffusional processes, H. I. A. V. F. Zackay, Ed. New York: Interscience Publishers, 1962, pp. 371-386.         [ Links ]

[24] U. Dahmen, "Surface relief and the mechanism of a phase transformation," Scr. Metall., vol. 21, no. 8, pp. 1029-1034, Aug. 1987.         [ Links ]

[25] G. . Srinivasan and C. . Wayman, "The crystallography of the bainite transformation - I," Acta Metall., vol. 16, no. 5, pp. 621-636, May 1968.         [ Links ]

[26] H. Kawata, K. Sakamoto, T. Moritani, S. Morito, T. Furuhara, and T. Maki, "Crystallography of ausformed upper bainite structure in Fe-9Ni-C alloys," Mater. Sci. Eng. A, vol. 438-440, pp. 140-144, Nov. 2006.         [ Links ]

[27] T. Furuhara, H. Kawata, S. Morito, and T. Maki, "Crystallography of upper bainite in Fe-Ni-C alloys," Mater. Sci. Eng. A, vol. 431, no. 1-2, pp. 228-236, Sep. 2006.         [ Links ]

[28] P. M. Kelly, "Martensite crystallography - The role of the shape strain," Mater. Sci. Eng. A, vol. 438-440, pp. 43-47, Nov. 2006.         [ Links ]

[29] S. . Xiao and J. . Howe, "Analysis of a two-dimensional invariant line interface for the case of a general transformation strain and application to thin-film interfaces," Acta Mater., vol. 48, no. 12, pp. 3253-3260, Jul. 2000.         [ Links ]

[30] D. Qiu, Y.-X. Shen, and W.-Z. Zhang, "An extended invariant line analysis for fcc/bcc precipitation systems," Acta Mater., vol. 54, no. 2, pp. 339-347, Jan. 2006.         [ Links ]

[31] A. Shibata, S. Morito, T. Furuhara, and T. Maki, "Local orientation change inside lenticular martensite plate in Fe-33Ni alloy," Scr. Mater., vol. 53, no. 5, pp. 597-602, Sep. 2005.         [ Links ]

[32] H. Kitahara, R. Ueji, N. Tsuji, and Y. Minamino, "Crystallographic features of lath martensite in low-carbon steel," Acta Mater., vol. 54, no. 5, pp. 1279-1288, Mar. 2006.         [ Links ]

[33] A. Shibata, T. Murakami, T. Furuhara, and T. Maki, "The Origin of Midrib in Lenticular Martensite," Mater. Trans., vol. 49, no. 6, pp. 1242-1248, 2008.         [ Links ]

[34] Z. Li, Y. Zhang, C. Esling, X. Zhao, and L. Zuo, "Twin relationships of 5M modulated martensite in Ni-Mn-Ga alloy," Acta Mater., vol. 59, no. 9, pp. 3390-3397, May 2011.         [ Links ]

[35] P. M. Kelly, "Crystallography of lath martensite in steels," Mater. Trans. JIM(Japan), vol. 33, no. 3, pp. 235-242, 1992.         [ Links ]

[36] W.-Z. Zhang and G. C. Weatherly, "Why do the solutions of the habit plane of lath martensite converge? An application of decomposition of the transformation displacement field," Scr. Mater., vol. 37, no. 10, pp. 1569-1574, Nov. 1997.         [ Links ]

[37] C. P. Luo and J. Liu, "Crystallography of lath martensite and lower bainite in alloy steels," Mater. Sci. Eng. A, vol. 438-440, pp. 149-152, Nov. 2006.         [ Links ]

[38] Y. Ohmori, "Crystallographic aspects of bainite transformation in steels," Scr. Mater., vol. 47, no. 3, pp. 201-206, Aug. 2002.         [ Links ]

[39] D. Y. Cong, Y. D. Zhang, Y. D. Wang, M. Humbert, X. Zhao, T. Watanabe, L. Zuo, and C. Esling, "Experiment and theoretical prediction of martensitic transformation crystallography in a Ni-Mn-Ga ferromagnetic shape memory alloy," Acta Mater., vol. 55, no. 14, pp. 4731-4740, Aug. 2007.         [ Links ]

[40] A. Dogan, Y. Havvatoglu, and H. Arslan, "Rigorous version of ınfinitesimal deformation approach to the crystallography of fcc ® bcc martensitic phase transformation observed in Fe-31 wt % Ni and zirconia alloys," Int. J. Phys. Sci., vol. 7, no. 20, May 2012.         [ Links ]

[41] H. Ledbetter and M. L. Dunn, "Equivalence of Eshelby inclusion theory and Wechsler-Lieberman-Read, Bowles-Mackenzie martensite-crystallography theories," Mater. Sci. Eng. A, vol. 285, no. 1-2, pp. 180-185, Jun. 2000.         [ Links ]

[42] D. J. Rowenhorst, A. Gupta, C. R. Feng, and G. Spanos, "3D Crystallographic and morphological analysis of coarse martensite: Combining EBSD and serial sectioning," Scr. Mater., vol. 55, no. 1, pp. 11-16, Jul. 2006.         [ Links ]

[43] P. P. Suikkanen, C. Cayron, A. J. DeArdo, and L. P. Karjalainen, "Crystallographic Analysis of Martensite in 0.2C-2.0Mn-1.5Si-0.6Cr Steel using EBSD," J. Mater. Sci. Technol., vol. 27, no. 10, pp. 920-930, Oct. 2011.         [ Links ]

[44] S. Kundu, A. K. Verma, and V. Sharma, "Quantitative Analysis of Variant Selection for Displacive Transformations Under Stress," Metall. Mater. Trans. A, vol. 43, no. 7, pp. 2552-2565, Jan. 2012.         [ Links ]

[45] G. Miyamoto, A. Shibata, T. Maki, and T. Furuhara, "Precise measurement of strain accommodation in austenite matrix surrounding martensite in ferrous alloys by electron backscatter diffraction analysis," Acta Mater., vol. 57, no. 4, pp. 1120-1131, Feb. 2009.         [ Links ]

[46] J. WU, W. ZHANG, and X. GU, "A two-dimensional analytical approach for phase transformations involving an invariant line strain," Acta Mater., vol. 57, no. 3, pp. 635-645, Feb. 2009.         [ Links ]

[47] A. J. W. Menezes, H. Abreu, S. Kundu, H. K. D. H. Bhadeshia, and P. M. Kelly, "Crystallography of Widmanstätten austenite in duplex stainless steel weld metal," Sci. Technol. Weld. Join., vol. 14, no. 1, pp. 4-10, Jan. 2009.         [ Links ]

[48] J.-Y. Li, C.-H. Lei, L.-J. Li, Y.-C. Shu, and Y.-Y. Liu, "Unconventional phase field simulations of transforming materials with evolving microstructures," Acta Mech. Sin., vol. 28, no. 4, pp. 915-927, Sep. 2012.         [ Links ]

[49] M. J. Peet and H. K. D. H. Bhadeshia, "Surface Relief Due to Bainite Transformation at 473 K (200 °C)," Metall. Mater. Trans. A, vol. 42, no. 11, pp. 3344-3348, Jun. 2011.         [ Links ]

[50] T. Teramoto, M. Tahara, T. Inamura, H. Hosoda, and S. Miyazaki, "Composition Dependence of Compatibility in Self-Accommodation Microstructure of β-Titanium Shape Memory Alloy," Adv. Sci. Technol., vol. 78, pp. 25-30, Sep. 2012.         [ Links ]