Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
TecnoLógicas
Print version ISSN 0123-7799On-line version ISSN 2256-5337
TecnoL. vol.18 no.35 Medellín July/Dec. 2015
Artículo de investigación/Research article
Cambios del patrón de radiación en arreglos lineales de dipolos de microcinta a 2,4 GHz en presencia de elementos parásitos
Radiation pattern changes in linear arrays of dipoles microstrip at 2.4 GHz in the presence of parasitic elements
Héctor F. Bermúdez-Orozco1, Evelio Astaiza-Hoyos2, Luis F. Muñoz-Sanabria-Otro3
1M.Sc. Electrónica y Telecomunicaciones, Grupo de Investigación GITUQ, Facultad de Ingeniería, Universidad del Quindío, Armenia- Colombia, hfbermudez@uniquindio.edu.co
2Ph.D. (c) Ciencias de la Electrónica, Grupo de Investigación GITUQ, Facultad de Ingeniería, Universidad del Quindío, Armenia- Colombia, eastaiza@uniquindio.edu.co
3M.Sc. en Computación, Grupo de Investigación LOGICIEL, Fundación Universitaria de Popayán, Popayán-Colombia, lfreddyms@fup.edu.co
Fecha de recepción: 20 de agosto de 2014 / Fecha de aceptación: 16 de enero de 2015
Como citar / How to cite
H. F. Bermúdez-Orozco, E. Astaiza-Hoyos y L. F. Muñoz-Sanabria, “Cambios del patrón de radiación en arreglos lineales de dipolos de microcinta a 2,4 GHz en presencia de elementos parásitos”, Tecno Lógicas, vol. 18, no. 35, pp. 21-34, 2015.
Resumen
En este artículo se presenta uno de los resultados de la investigación realizada para estudiar los cambios producidos en los parámetros de impedancia de entrada y patrón de radiación de los sistemas radiantes cuando son sometidos a la presencia de elementos parásitos. Específicamente, se utilizan arreglos lineales de dipolos de microcinta y se escoge como parámetro de estudio el patrón de radiación; el parámetro de impedancia de entrada será presentado en otra publicación. Para su estudio, el sistema es modelado mediante técnicas numéricas con la ayuda del método de los momentos, en la conformación de la malla del arreglo se utiliza la función base propuesta por Rao-Wilton y Glisson. El modelo es simulado con la herramienta Matlab®, se determina el patrón de radiación para un dipolo tipo parche y para un arreglo de estos elementos; se ubican elementos parásitos (dipolos) a diferentes distancias del dipolo y del arreglo original y se calculan nuevamente los patrones de radiación, los cuales son comparado con los inicialmente encontrados. Finalmente, se presentan los resultados y se evidencia la ventaja que tienen estos estudios para la manipulación del patrón de radiación en sistemas radiantes. Adicionalmente, se evidencia en el presente estudio la presencia de un elemento de simetría, lo cual permite disminuir en un alto porcentaje las simulaciones, ya que el efecto producido por los elementos parásitos ubicados a un lado del arreglo de dipolos es similar al efecto que se produce cuando se ubican los elementos parásitos al lado opuesto.
Palabras clave: Antenas, arreglos, elemento parásito, patrón de radiación, microcinta.
Abstract
This paper presents one of the results of research conducted to study the changes in the impedance input and radiation pattern parameters of the antenna systems, specifically linear arrays of microstrip dipoles are used; it is chosen as a parameter study the radiation pattern, the input impedance parameter will be presented in another publication. For their study, the system is modeled using numerical techniques with the help of the method of moments, in the conformation of the mesh array is used basis function given by Rao-Wilton and Glisson. The model is simulated with the Matlab® tool, the radiation pattern is determined for a dipole type patch and an array of these; the parasitic elements (dipoles) are located at different distances from the original array dipole and calculates the radiation pattern again, which are compared to those originally found. Finally, the results are presented and the advantage of these studies for handling radiation pattern in radiant systems is evident. Additionally, the presence of an element of symmetry is evident, this situation allows a considerable decrease the number of simulations, since the effect of the parasitic elements located on one side of the array of dipoles is similar to the effect that occurs when the parasitic elements are located on the opposite side.
Keywords: Antennas, arrays, parasitic elements, radiation pattern, microstrip.
1. Introducción
La selección adecuada del patrón de radiación de los sistemas radiantes es un factor determinante para la correcta prestación de los servicios inalámbricos que actualmente tienen mayor demanda por parte de los usuarios, los cuales requieren cada vez mayor movilidad, mayor alcance, menor tamaño, menor costo y menos consumo energético. Es por eso que se hace necesario poder conocer los parámetros que rigen el comportamiento de los sistemas radiantes, entre los cuales se encuentra el patrón de radiación [1], [2]. En [3] y [4] se presenta un estudio de los efectos causados por elementos parásitos sobre el parámetro de impedancia de un dipolo y un arreglo de dipolos de microcintas, lo que determina el punto de partida del presente estudio; ya que se utiliza la misma estructura y se modela de igual forma el sistema radiante en estudio. El uso de arreglos en sistemas radiantes mejora significativamente algunos parámetros tales como la ganancia, la directividad, etc. [2], donde el efecto que los elementos parásitos causan en el patrón de radiación es algo que no está determinado, lo cual se constituye en el objetivo del presente artículo. Para evaluar computacionalmente las integrales de superficie que se presentan con la técnica de la ecuación integral de campo eléctrico (EFIE) cuando se aplica el método de los momentos, se utiliza el método de subdivisión de baricentros presentadas en [4] y [5], cuya finalidad es la de aumentar la eficiencia computacional.
En el modelamiento del sistema radiante usado en el presente artículo, se utiliza, al igual que en [4] técnicas numéricas, específicamente el método de los momentos MoM, adicionalmente, para simplificar dicho modelado se asume que el espacio entre el parche y el plano de masa es aire. En la primera parte del artículo se presentan los conceptos básicos de la tecnología de microcintas y tipos de arreglos, en la segunda parte se explica el modelo numérico para representar un dipolo y un arreglo de dipolos tipo microcinta, seguidamente se consignan los resultados obtenidos; por último se muestran las conclusiones y se resalta la utilización de elementos parásitos para manipular el patrón de radiación en un sistema radiante construido con tecnología de microcinta.
2. Metodología
2.1 Análisis de antenas de microcinta
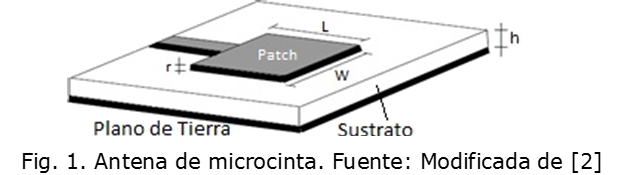
Una antena de microcinta o parche consiste en una delgada capa metálica sobre la superficie de un dieléctrico con un plano de tierra, la cual radia potencia en un haz perpendicular al plano de la antena y muestra una impedancia de entrada similar a un circuito resonante paralelo cerca de su frecuencia de operación [2], [5], [6].
Una antena de microcinta puede tomar diferentes formas, de las cuales el parche rectangular es uno de los más populares. En la Fig. 1 se observan las dimensiones características, L, W, h y r; en donde L es el largo del parche, usualmente su valor varía entre 0,003 λ0 ≤ L ≤ 0,5 λ0, λ0 es la longitud de onda en el espacio libre, para el caso de 2,4 GHz corresponde a 125 mm; W es el ancho; r es el grosor del parche (r<<λ0); h, es el espesor del dieléctrico, su valor varía entre 0,003 λ0 y 0,5 λ0; εr es la constante dieléctrica del sustrato (2,2 ≤ εr ≤ 12) [2], [3].
Las antenas construidas con dipolos de microcinta o también conocidas como antenas de microtira, se diferencian geométricamente de las antenas tipo parche rectangular en la relación ancho - largo (W-L); el ancho W de un dipolo es, por lo general, menor a 0,05 λ0. Los patrones de radiación de un dipolo y de un parche son similares debido a que poseen distribuciones iguales de corrientes longitudinales. Sin embargo, la resistencia de radiación, ancho de banda y radiación en polaridad cruzada difieren ampliamente [5].
Existen varios métodos de análisis para antenas de microcinta, entre los modelos más utilizados se tienen: el de línea de transmisión, el de cavidad y el de onda completa (incluye ecuación integral de campos y método de los momentos) los cuales se encuentran definidos y se aplican en una extensa bibliografía [2], [6]-[15], entre otras.
2.2 Arreglos de antenas
Para ciertas aplicaciones en comunicaciones es necesario el uso de antenas de alta directividad (alta ganancia) lo cual no es posible de obtener con solo un elemento radiante. Lo anterior se puede lograr con el uso de arreglos, que son agrupaciones de elementos radiantes (antenas), generalmente del mismo tipo y que se encuentran orientadas en una misma dirección. Son acomodadas de una forma física determinada relativamente cercanas unas con otras y son capaces de concentrar la radiación en la dirección deseada. Para que se generen patrones muy directivos, es necesario que los campos de los diferentes elementos interfieran constructivamente en la dirección deseada [4].
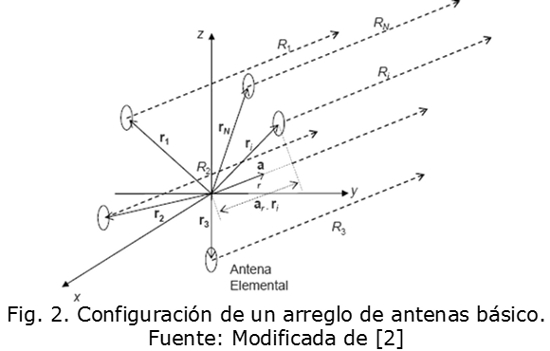
En un arreglo de antenas básico, como el mostrado en la Fig. 2, el campo eléctrico E en una posición arbitraria (r, θ, φ), expresado por (1), es dado por la suma de campo eléctrico Ei de cada elemento que compone el arreglo (asumiendo que no hay acoplamiento entre los elementos). Teniendo en cuenta el teorema de multiplicación de patrones presentado en [2], [6], [8] el campo eléctrico total dado en (1) se puede expresar en (2):
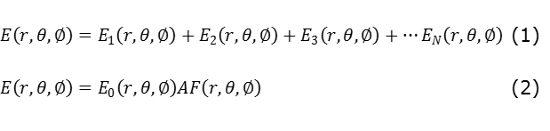
Donde AF es el factor de arreglo, el cual indica la variación del patrón de radiación y la relación con los ceros en el plano imaginario.
2.3 Arreglo de antena lineal uniforme (ULA)
Un arreglo lineal uniforme se define como un arreglo en donde todos los elementos son idénticos con igual magnitud y cada uno es alimentado con una fase progresiva [2]. En [2] y [5] se muestra que para el caso específico del ULA el factor de arreglo está dado por (3):

Donde el término ψ se define como (4):

N corresponde a cada uno de los elementos radiantes del arreglo, K0 corresponde a 2π/λ, di la distancia al i-ésimo elemento, βi es la fase entre las corrientes de los elementos.
Con este tipo de arreglo, se obtiene una antena altamente directiva, que consiste en un arreglo lineal de pequeños elementos de antena radiantes, cada uno alimentado con señales idénticas (igual amplitud) desde un transmisor. Con el incremento del ancho total del arreglo, el haz central se hace más estrecho, y con el aumento del número de elementos, los lóbulos laterales se harán más pequeños. Así mismo, si se incrementa la distancia entre los elementos de la antena de un arreglo lineal aparecerá un mayor número de lóbulos laterales, y el haz central se hará aún más estrecho (la longitud de la antena se incrementa).
Para evitar la aparición de los lóbulos laterales y estrechar el haz central se debe aumentar la longitud de la antena, pero manteniendo una distancia pequeña entre elementos, es decir, aumentando su número. Los arreglos lineales uniformes de antenas permiten la generación de patrones de radiación que no se pueden obtener con antenas simples [10], [16], [17].
2.4 Modelo numérico
Para la solución de problemas electromagnéticos (EM) se utilizan algunas técnicas tales como: técnicas analíticas (separación de variables, expansión de series, mapeo conformal (conformal mapping), solución integral, métodos de perturbación) y técnicas numéricas (método de diferencias finitas FDM, métodos de elementos finitos FEM, método de pesos residuales, método de los momentos MoM, modelamiento de línea de transmisión, método de Monte Carlo, método de líneas, entre otros). La adecuada selección del modelo a usar depende de la clasificación del problema EM, los cuales se puede analizar dependiendo de la aplicación en particular en: la región de la solución del problema, la naturaleza de la ecuación que describe el problema y las condiciones de contorno asociadas [18], [19].
Para su estudio, el sistema radiante es clasificado de acuerdo a la naturaleza de las ecuaciones que lo describen, para lo cual en (5) se define:

Donde F es el operador (diferencial, integral o integro-diferencial), h es la excitación o fuente conocida y g es la función desconocida [5].
La solución del problema EM consiste en encontrar la función desconocida g. El hecho que g satisfaga (5) para una determinada solución dentro de una región R, implica que g debe cumplir con ciertas condiciones de S (el contorno de R). Típicamente, esas condiciones de contorno son del tipo Dirichlet, cuando se desea encontrar una función armónica sobre un dominio de ℝn que tome valores prescritos sobre el contorno de dicho dominio, o Neumann cuando no se tiene en cuenta el contorno del dominio; o una mezcla de ambas [20], [21].
Para encontrar el parámetro de impedancia de entrada del sistema radiante en estudio, se aplica la técnica numérica del método de los momentos MoM. El objetivo es modelar la solución de la densidad de corriente desconocida, la cual es inducida sobre la superficie de una antena de transmisión o recepción, en forma de una ecuación integral, en donde la densidad de corriente inducida hace parte de la integral [2], [11], [19].
El MoM es un procedimiento general para encontrar la solución de (5) con operadores integrales o diferenciales. En [22] se muestra que cualquier función desconocida se puede representar en forma de serie, por lo tanto, la función incógnita g se aproxima a una combinación lineal de funciones base bn dada en (6) como:

Donde gn son muestras de la discretización de g, y además son las incógnitas del problema a resolver. Sustituyendo (6) en (5) se obtiene (7) como:

En [5] se demuestra que (7) se puede representar en forma matricial como (8):

Donde Zmn = F(bn), In = gn y Vm = hm, Los coeficientes desconocidos de gn se pueden encontrar usando técnicas de inversión de matriz [2], [3].
2.5 Método numérico de subdivisión de baricentros
El método de subdivisión de baricentros [4], permite que las integrales correspondientes se puedan evaluar numéricamente en términos de sumas finitas y se aproximen al punto medio de los subtriángulos. Dicha técnica evalúa las integrales correspondientes directamente en el plano cartesiano en lugar de realizar la transformación a coordenadas de área normalizada; se divide cada parche triangular de la superficie conductora en un número finito de triángulos más pequeños, lo cual permite que el total de las integrales dobles generadas con el método de evaluación inicial, sean remplazadas en menor número por sumas finitas, disminuyendo así considerablemente el tiempo computacional para obtener la distribución de corriente sobre la superficie en estudio, sin afectar la exactitud de los resultados.
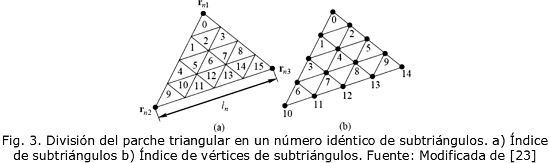
Para aplicar dicho método, un parche triangular se divide en un número idéntico de subtriángulos, como se puede ver en la Fig. 3, Esto se logra dividiendo cada lado del triángulo inicial en s segmentos y trazando líneas paralelas a los lados del triángulo. Este procedimiento, divide el parche triangular en s2 subtriángulos idénticos [23].
Este método asume que el integrando es constante dentro de cada subtriángulo, por lo tanto la integral de una función g sobre el triángulo general Tm está dada por (9):

Donde los puntos rkc, k =1,2…s2 corresponden a los puntos medios de los subtriángulos.
2.6 Estructura del sistema radiante
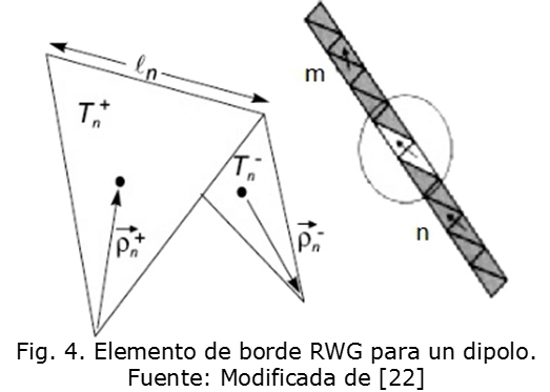
El primer paso en la simulación del sistema de radiación es el de modelar la superficie de la antena, para lo cual se selecciona la división en triángulos de dicha superficie que corresponde a una estructura de dos dimensiones [18], [24], dicha división permitirá trabajar con la función base propuesta en [25], en donde cada par de triángulos denotados T+ y T- tienen un borde en común que conforma el elemento de borde RWG correspondiente como se muestra en la Fig. 4. A cada elemento de borde se le asigna una función base bn(r) mostrada en [3] y [5].
El arreglo está conformado por dipolos de microcinta lineales uniformes, los cuales se utilizan como elementos activos y pasivos; los elementos activos poseen alimentación y los elementos pasivo o parásitos no. Para modelar la alimentación de los elementos activos se escoge el modelo de delta gap propuesto en [2], ya que este se ajusta al modelo de borde mostrado en la Fig. 4 y que permite definir una línea de transmisión a través de dos terminales eléctricamente cerrados, lo cual representa un generador de voltaje ideal conectado a la antena a través de un gap con un ancho muy pequeño.
La división de la estructura de la antena en elementos de borde RWG corresponde a la división de la antena en pequeños dipolos eléctricos, como se puede apreciar en la Fig. 3 Por simplicidad, se utiliza el método de Galerking, definido en [6] y [18], en donde la función base y la función de prueba son las mismas, lo cual genera una matriz Z de impedancia simétrica definida en [3] y [5] como se observa en (10):
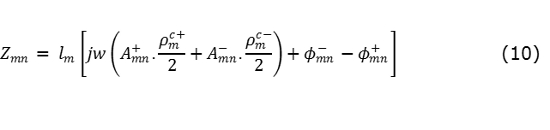
Donde 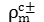 representan los vectores de los vértices libres al centro de los dos los triángulos
representan los vectores de los vértices libres al centro de los dos los triángulos 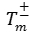 del elemento de borde
del elemento de borde 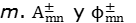 representan el vector de potencial magnético y el potencial escalar, los cuales son definidos en [3] y [5]. Para considerar el método numérico de subdivisión de baricentro, el vector potencial magnético y el potencial escalar se redefinen en (11) y (12):
representan el vector de potencial magnético y el potencial escalar, los cuales son definidos en [3] y [5]. Para considerar el método numérico de subdivisión de baricentro, el vector potencial magnético y el potencial escalar se redefinen en (11) y (12):
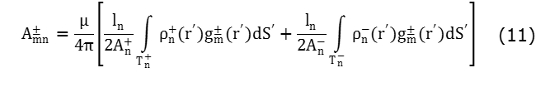
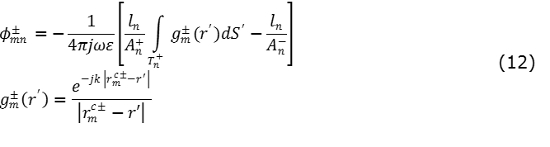
Con los resultados de la matriz de impedancia y la definición del voltaje de alimentación, es posible obtener los coeficientes de expansión desconocidos para la densidad de corriente superficial J sobre la superficie del dipolo con el uso de la función base RWG sobre un borde M como se muestra en (13):
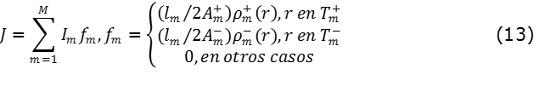
Los coeficientes de expansión Im forman el vector I, el cual es la única solución de la ecuación de impedancia dada por (8).
Impedancia de entrada: la impedancia de entrada se define como la relación entre el voltaje y la corriente en los terminales de entrada de la antena [2]. De acuerdo con el modelo de bordes RWG, la impedancia de entrada es la relación del voltaje de alimentación y la corriente normal en el borde de alimentación. Por lo anterior, de (13) se puede concluir que solo las funciones base RWG donde fn = m contribuirán al cálculo de la impedancia de entrada.
Patrón de radiación: la densidad de corriente superficial J sobre la superficie de la antena, radia una señal electromagnética en el espacio libre, dicha señal dependiendo del punto en el espacio en donde sea calculada o medida (en campo cercano o lejano) permitirá calcular el diagrama o patrón de radiación.
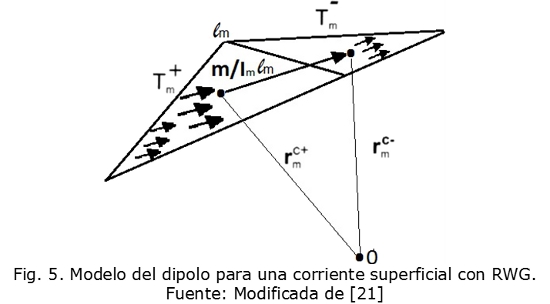
Para calcular el patrón de radiación, es necesario calcular el campo eléctrico, E, y el campo magnético, H, en un punto espacial. Si se hace en campo cercano, E y H son independientes y deben ser calculados por separado, lo cual tomaría más tiempo para su solución. Una forma de encontrar el patrón de radiación independientemente de si el punto de observación está ubicado en campo cercano o lejano es mediante el modelo del dipolo propuesto en [22]. En dicho modelo, la distribución de corriente superficial para cada elemento de borde RWG contiene dos triángulos, los cuales son reemplazados por un dipolo infinitesimal, el cual tiene un momento de dipolo equivalente. La expresión analítica del campo radiado por dicho dipolo infinitesimal se encuentra en [2]. El campo radiado total se obtiene de la suma de las contribuciones de todos los dipolos infinitesimales. El momento del dipolo m equivalente, considerando un elemento RWG, con dos triángulos internos 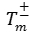 adyacentes al borde de longitud lm, como se aprecia en la Fig. 5, se obtiene mediante (14) que corresponde a la integral de la corriente superficial, correspondiente al elemento de borde m, sobre el elemento de superficie.
adyacentes al borde de longitud lm, como se aprecia en la Fig. 5, se obtiene mediante (14) que corresponde a la integral de la corriente superficial, correspondiente al elemento de borde m, sobre el elemento de superficie.
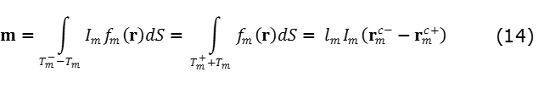
Donde fm(r) corresponde a la función base RWG del elemento m. Los coeficientes de corriente superficial Im, son conocidos y se encuentran con la solución de la ecuación de momentos. El producto lmIm se asocia con la corriente del dipolo, mientras que la longitud efectiva del dipolo lm, es dada por 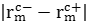 como se puede apreciar en la Fig. 4 [6]. El campo eléctrico y magnético radiado por un dipolo infinitesimal localizado en el origen, es expresado en un punto r, utilizando notación vectorial (15) y (16):
como se puede apreciar en la Fig. 4 [6]. El campo eléctrico y magnético radiado por un dipolo infinitesimal localizado en el origen, es expresado en un punto r, utilizando notación vectorial (15) y (16):
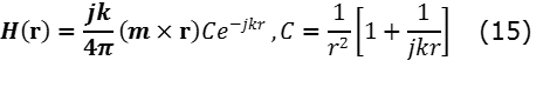
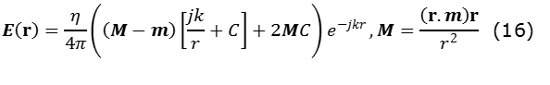
Donde r = │r│;η = √µ/ε = 377Ω que corresponde a la impedancia de espacio libre. Las ecuaciones (15) y (16) son las expresiones exactas, sin ningún tipo de aproximación para campo lejano, por lo tanto son válidas tanto para campo cercano como lejano. El campo eléctrico y magnético total en un punto r se obtiene como la suma (17) y (18):
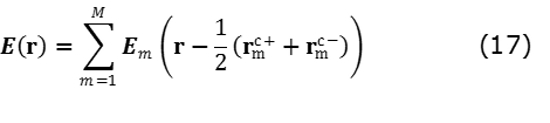
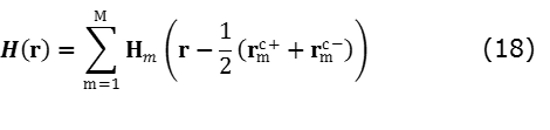
La potencia media radiada del campo por unidad de área en cualquier punto r, es obtenida mediante el vector de Poynting mediante (19) en unidades con unidades W/m2.
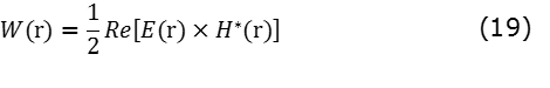
2.7 Algoritmo para el arreglo de dipolos
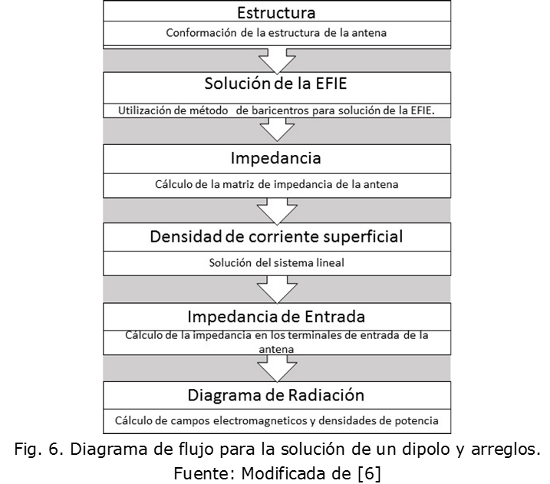
En la Fig. 6 se presenta el diagrama de flujo empleado en los algoritmos de cálculo de la matriz de impedancia, la densidad de corriente, la impedancia de entrada de un dipolo y arreglos de dipolos con tecnología de microcintas y la ayuda de la herramienta Matlab.
2.8 Modelo dieléctrico de la microcinta
Para encontrar la solución a uno o varios elementos de microcinta, al cual se le aplica el método de los momentos MoM, se requiere que la formulación de la EFIE se realice considerando la estructura no como una superficie, como es el caso del dipolo elemental, sino como un volumen. En este caso, es necesario encontrar la corriente de polarización J [A/m2] del volumen equivalente, la cual se define en [26] y [27] como (20):

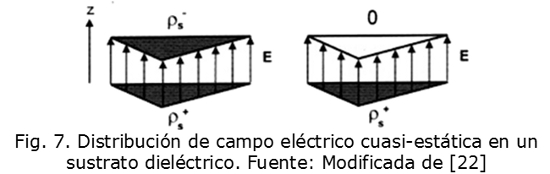
Donde, ε es la permitividad dieléctrica del vacío, εR es la permitividad relativa, y E es el campo eléctrico del segmento triangular. Para aplicar el método RWG, se divide el volumen total del dieléctrico en elementos de volumen triangulares como se observa en la Fig. 7, se asume que el campo eléctrico dentro de cada elemento de volumen solo tiene una componente vertical; dicha componente vertical es definida en (21) por la carga superficial en la parte superior e inferior del parche para cada elemento de volumen [28]:

Donde, 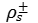 es la densidad de carga superficial sobre el metal del plano de tierra y el metal del parche. La ecuación (21) corresponde a la relación cuasi-estática para el capacitor de láminas paralelas. Esas son las densidades de carga para los elementos RWG sobre la superficie del metal. En (8) el MoM para el dipolo elemental aplicado a un dipolo de microcinta, toma la forma de (22) [29]:
es la densidad de carga superficial sobre el metal del plano de tierra y el metal del parche. La ecuación (21) corresponde a la relación cuasi-estática para el capacitor de láminas paralelas. Esas son las densidades de carga para los elementos RWG sobre la superficie del metal. En (8) el MoM para el dipolo elemental aplicado a un dipolo de microcinta, toma la forma de (22) [29]:

Donde, ID es el vector de la corriente de volumen desconocida. Las matrices ZDS y ZDD (matriz de auto-iteración) son obtenidas usando el modelo del dipolo. El subíndice S se refiere al metal y el subíndice D al dieléctrico. En la simulación de los arreglos lineales uniformes ULA se debe tener en cuenta que estos deben ser orientados a los largo del eje z, el eje del arreglo es x, y en los cuales es posible modificar la distancia de separación d de los dipolos.
3. Resultados
Las variaciones del patrón de radiación para un dipolo y para un arreglo de dipolos de microcinta con el método RWG cuando se someten a la presencia de un elemento parásito se presentan a continuación. Como se plantea al inicio del presente artículo, la configuración geométrica es lineal, con una distancia constante entre los elementos, con igual amplitud de excitación para cada elemento y sin cambio de fase. Lo anterior corresponde a la clase de arreglos de antenas lineales uniformes ULA, específicamente se trabajarán con arreglos Broadside [2].
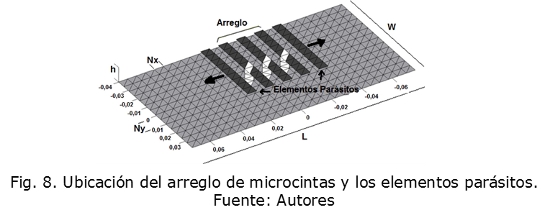
Es necesario determinar parámetros para simular un dipolo o un arreglo de dipolos de microcinta con el método RWG, los cuales se muestran en la Fig. 8, estos son: longitud del plano de tierra L (a lo largo del eje x), ancho del plano de tierra W (a lo largo del eje y), parámetro de discretización Nx (longitud), parámetro de discretización Ny (ancho), separación entre plano de tierra y conductor h, permitividad dieléctrica del sustrato. Los cálculos de estos valores son explicados en [5].
Inicialmente se calcula el patrón de radiación para un dipolo, luego para un arreglos de 3 y 5 dipolos de microcinta, posteriormente se incorporan los elementos parásitos. En primera instancia se van ubicando elementos parásitos a distancia fijas a la derecha y luego a la izquierda; para cada caso se grafica el efecto causado por éstos en el patrón de radiación del sistema radiante.
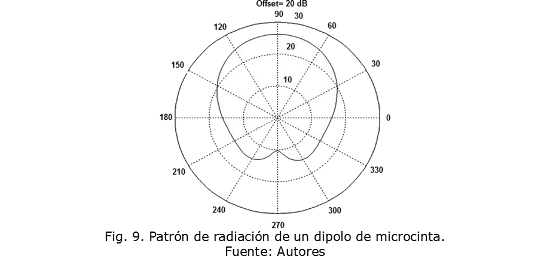
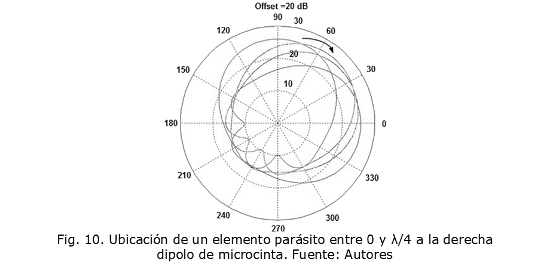
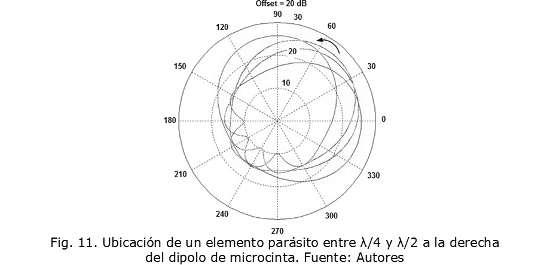
En la Fig. 9 se muestra el patrón de radiación de un dipolo de microcinta. Se comienza a ubicar un elemento parásito a la derecha del dipolo a una distancia en longitudes de onda de 0 a λ/4. En la Fig. 10 se puede observar que el patrón va girando en esa misma dirección hasta 90°, cuando la distancia del elemento parásito varía entre λ/4 y λ/2. Se observa en la Fig. 11 que el patrón de radiación vuelve a la posición inicial del patrón del dipolo.
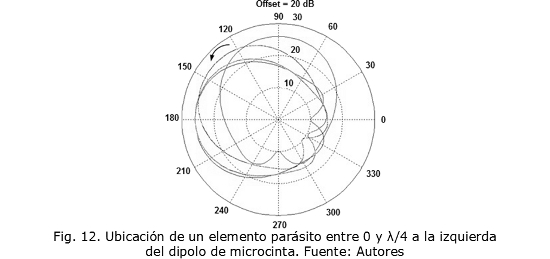
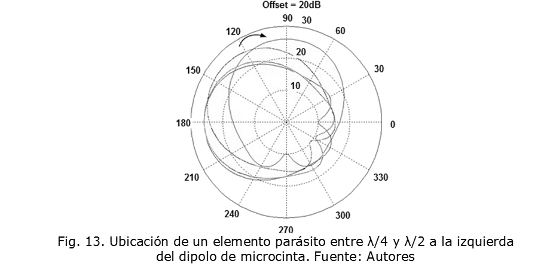
Análogo a la ubicación del elemento parásito a la derecha del dipolo de microcinta, se ubica un elemento parásito a la izquierda, las Fig. 12 y 13 describen un comportamiento similar de giro del patrón, pero esta vez en sentido contrario.
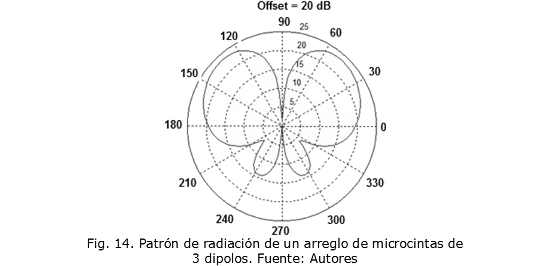
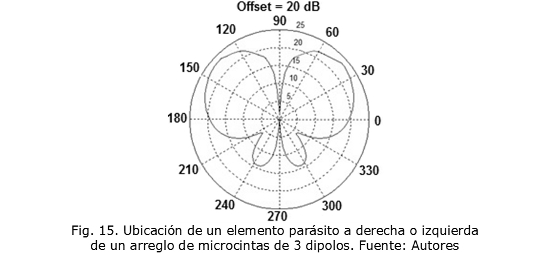
A continuación se presentan los resultados encontrados cuando se ubica un elemento parásito a la derecha o a la izquierda de un arreglo de 3 dipolos de microcinta. La Fig. 14 muestra el patrón de radiación del arreglo, la Fig. 15 muestra el efecto causado por la ubicación del elemento parásito a derecha o a izquierda del arreglo.
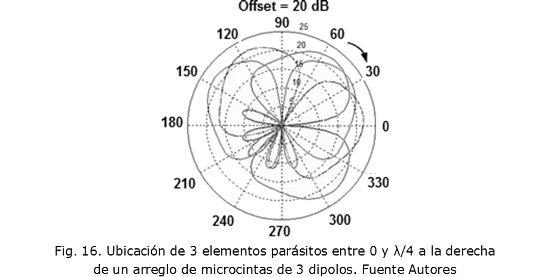
Como se puede apreciar en la Fig. 15, el elemento parásito ubicado a derecha o izquierda no afecta considerablemente al patrón, ni cambia su posición; solo se aprecia una pequeña variación en la forma del patrón de radiación. La Fig. 16 muestra el patrón de radiación de un arreglo de 3 dipolos de microcinta cuando se ubican 3 elementos parásitos a la derecha del arreglo, la distancia de ubicación de los elementos parásitos varía de 0 a λ/4. Cuando la distancia de ubicación de los elementos parásitos varía entre λ/4 y λ/2, el patrón de radiación gira en sentido contrario a las manecillas del reloj y recupera su posición inicial.
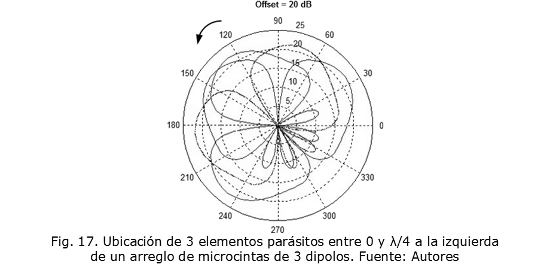
El mismo comportamiento de giro se evidencia cuando se ubican los elementos parásitos a la izquierda del arreglo; entre 0 a λ/4 el patrón gira en sentido anti-horario hasta los 90°, como se muestra en la Fig. 17; en una ubicación del arreglo comprendida λ/4 y λ/2 el patrón cambia el sentido de giro y recupera su posición inicial.
Un comportamiento similar sucede cuando se simulan arreglos de 5 dipolos de microcinta en presencia de 5 elementos parásitos ubicados a derecha o a izquierda del arreglo.
4. Conclusiones
El patrón de radiación ante la presencia de elementos parásitos presenta un giro a derecha o izquierda, el cual depende de la ubicación del elemento parásito dentro del sistema radiante, se observa un ángulo máximo de giro y luego el patrón retorna a su ubicación original. Se observa que el giro en mención, tiene una dependencia de la distancia d a la cual se encuentra ubicado el elemento o elementos parásitos; para el presente trabajo, se fija dicha distancia d = 5,58 mm. Representando en longitudes de onda la distancia d, donde λ = 0,125 m para la frecuencia de 2,4 GHz, se puede observar como el patrón de radiación alcanza el mayor ángulo a una distancia de 6d, lo cual equivale aproximadamente a λ/4, al aumentar dicha distancia el patrón comienza a retornar a su posición original, lo cual se observa a una distancia de 12d, que equivale aproximadamente a λ/2.
Realizando una analogía con el comportamiento de una línea de transmisión, lo cual en últimas representa una antena, la distancia entre dos máximos o mínimos consecutivos es λ/2, por lo tanto, se podría augurar que el giro del patrón de radiación tendría ciclos de repetición con respecto a la ubicación del elemento parásito cada (n+1) λ/4 con n = 0,1,2,…, para n impar y el máximo ángulo de giro aparece cada (n+1) λ/4 para n par.
Se establece en los diferentes casos de simulación que existe una simetría muy bien definida en el giro del patrón de radiación cuando se introduce un elemento parásito a igual distancia a la izquierda o a la derecha del sistema radiante analizado. Esta apreciación permite simplificar el número de simulaciones realizadas, ya que solamente basta con realizar la simulación ubicando elementos parásitos a un lado del arreglo de microcinta y se conocerá de antemano el comportamiento por simetría del otro lado.
Los resultados brindan la posibilidad de modificar el patrón de radiación de un sistema radiante dependiendo de la ubicación de elementos parásitos, lo cual permite que en aplicaciones de sistemas de comunicaciones inalámbricos, los patrones fijos de antenas puedan ser manipulados con la ubicación de una forma estratégica de estos, convirtiéndose en una alternativa de diseño y operación de dichos sistemas cuando por variaciones significativas de tráfico o cobertura los elementos radiantes deban modificar sus patrón de radiación para aumentar la calidad de servicio a los usuarios finales.
Referencias
[1] H. F. Bermúdez, S. Botero, and M. A. Gómez, “Construcción y evaluación de un dipolo en la banda de 2.4 GHz utilizando tecnología de microcintas,” Sci. Tech., vol. 1, no. 44, pp. 25-30, 2010. [ Links ]
[2] C. Balanis, Antenna Theory Analysis and Design. New York: John Wiley and Sons Inc., 1997. [ Links ]
[3] H. F. Bermúdez, E. Astaiza, and G. Agredo, “Efectos en la impedancia de entrada en un dipolo de microcinta en presencia de elementos parásitos,” ITECKNE, vol. 9, no. 1, pp. 51-56, 2012. [ Links ]
[4] H. F. Bermúdez, “Efectos en la impedancia de entrada de un arreglo lineal uniforme de dipolos de microcinta en presencia de elementos parásitos,” Sci. Tech., vol. 18, no. 3, pp. 463-470, 2013. [ Links ]
[5] Y. Kamen and L. Shirman, “Triangle rendering using adaptive subdivision,” IEEE Comput. Graph. Appl., vol. 18, no. 2, pp. 95-103, 1998. [ Links ]
[6] H. F. Bermúdez, “Efecto del acoplamiento mutuo en antenas tipo parche en la banda de 2.4 GHz,” Universidad del Cauca, Popayán - Colombia, 2010. [ Links ]
[7] A. Cardama, L. Jofre, and J. M. Rius, Antenas. Barcelona: UPC, 1998. [ Links ]
[8] W. Stutzman and G. A. Thiele, Antenna Theory and Design, 3 edition. Hoboken, {NJ}: Wiley, 2012. [ Links ]
[9] S. N. Orfanidis, Electromagnetic Waves and Antennas. New Jersey: {ECE} Department Rutgers University. Piscataway, 2006. [ Links ]
[10] M. Martínez, “Diseño de Arreglos de Antenas con Aplicación en Sistemas de Antenas Inteligentes,” Universidad de Guadalajara, México D.F:, 2006. [ Links ]
[11] C. Ángel and J. Tisnés, “Diseño e Implementación de Arreglos de Antenas,” Universidad del Quindío, Armenia - Colombia, 2007. [ Links ]
[12] J. T. Aberle and D. M. Pozar, “Analysis of infinite arrays of one- and two-probe-fed circular patches,” IEEE Trans. Antennas Propag., vol. 38, no. 4, pp. 421-432, Apr. 1990. [ Links ]
[13] M. Sadiku, Numerical Techniques in Electromagnetics, Second Edi. New York: {CRC} Press {LLC}, 2000. [ Links ]
[14] N. A. Valero, “Resolución de problemas electromagnéticos complejos mediante análisis circuital generalizado,” Universidad Politécnica de Valencia, Valencia, 1997. [ Links ]
[15] R. Selfridge and D. Arnold, “Electromagnetics,” Proc. Inst. Elec. Eng., vol. 142, no. 4, pp. 326-332, 1995. [ Links ]
[16] D. Cheng, Field and Wave Electromagnetics, 2nd Editio. New York: Pearson Education, 1989. [ Links ]
[17] R. S. Elliott, Antenna Theory and Design, Revised Edition. New Jersey: John Wiley & Sons. Inc. Hoboken, 2003. [ Links ]
[18] F. Ulaby, Fundamentals of Applied Electromagnetics. New York: Person, 2006. [ Links ]
[19] K. F. A. Hussein, “Fast computational algorithm for EFIE applied to arbitrarily-shaped conducting surfaces,” Prog. Electromagn. Res., vol. 68, pp. 339-357, 2007. [ Links ]
[20] K. Lonngren, S. Savov, and R. Jost, Fundamentals of electromagnetics with matlab. Taiwan: {SciTech} Publishing, Inc., 2007. [ Links ]
[21] S. Rao, D. Wilton, and A. Glisson, “Electromagnetic scattering by surfaces of arbitrary shape,” IEEE Trans. Antennas Propag., vol. 30, no. 3, pp. 409-418, May 1982. [ Links ]
[22] S. N. Makarov, Antenna and EM Modeling with Matlab. New York: John Wiley & Sons Inc., 2002. [ Links ]
[23] R. Garg, Analytical and Computational Methods in Electromagnetics. Boston: Artech House, Inc., 2008. [ Links ]
[24] B. G. Salman, “The CFIE technique applied to finite-size planar and non-planar microstrip antenna,” in 3rd International Conference on Computation in Electromagnetics (CEM 96), 1996, vol. 1996, pp. 338-341. [ Links ]
[25] T. K. Sarkar, S. M. Rao, and A. R. Djordjevic, “Electromagnetic scattering and radiation from finite microstrip structures,” IEEE Trans. Microw. Theory Tech., vol. 38, no. 11, pp. 1568-1575, Nov. 1990. [ Links ]
[26] J. D. Krauss and R. J. Marhefka, Antennas for all applications, Third Edit. New York: {McGraw}-Hill, 2001. [ Links ]
[27] D. M. Pozar and D. H. Schaubert, Microstrip Antennas: The Analysis and Design of Microstrip Antennas and Arrays. New York: {IEEE} press, 1995. [ Links ]
[28] K. Carver and J. Mink, “Microstrip antenna technology,” IEEE Trans. Antennas Propag., vol. 29, no. 1, pp. 2-24, Jan. 1981. [ Links ]
[29] J. James and P. Hall, Handbook of microstrip antennas. Vols 1 and 2. London, {UK}.: Peter Peregrinus Ltd., 1989. [ Links ]