Artículo de investigación/Research article

Interfaz Gráfica de Usuario para la Simulación por Dinámica Molecular de Películas Delgadas

Graphic User Interface for Molecular Dynamics Simulation of Thin Films

Héctor Barco-Ríos¹, Héctor D. Aristizábal-Soto², Elisabeth Restrepo-Parra³

¹MSc. en Física, Departamento de Física y Química, Universidad Nacional de Colombia Sede Manizales, Manizales-Colombia, hsbarcor@unal.edu.co

²Ingeniero Físico, PCM-Computational Applications, Departamento de Física y Química, Universidad Nacional de Colombia Sede Manizales, Manizales-Colombia, hdaristizabals@unal.edu.co

³PhD. en Ingeniería, Línea Automática, PCM-Computational Applications, Departamento de Física y Química, Universidad Nacional de Colombia Sede Manizales, Manizales-Colombia, erestrepopa@unal.edu.co

Fecha de recepción: 9 de noviembre de 2015/ Fecha de aceptación: 25 de diciembre de 2015

Como citar / How to cite

H. Barco-Ríos, H. D. Aristizábal-Soto y E. Restrepo-Parra, “Interfaz gráfica de usuario para la simulación por dinámica molecular de películas delgadas”, Tecno Lógicas, vol. 19, no. 36, pp. 113-123, 2016.

Resumen

En este trabajo se implementó el software de simulación para la nanoindentación de películas delgadas. El software desarrollado empleó la técnica de Dinámica Molecular. El modelo con el cual opera la interfaz gráfica (software), es un modelo aproximado, que reproduce las tendencias de las curvas características en pruebas de dureza de materiales. Por otro lado, el programa se diseñó y construyó con un entorno amigable, donde el usuario puede construir sus propias películas delgadas, tanto en monocapas como en bicapas. La interfaz permite controlar el espesor de la película, el número de capas y otras propiedades físicas tales como energía de disociación o parámetros de energía en la esfera; además, se puede tener control de los pasos de tiempo de dinámica. Para comprobar el funcionamiento del software se realizaron una serie de simulaciones utilizando los parámetros del cromo como material de referencia. Los resultados obtenidos, demostraron que el software puede reproducir las tendencias y curvas características en pruebas de dureza de materiales. Se espera mejorar este software para que sea una herramienta que permita realizar comparaciones con futuras investigaciones experimentales.

Palabras clave: Dinámica Molecular, interface gráfica, energía de disociación, simulación, software

Abstract

In this work, a software for simulating nanoindentation in thin films was implemented. For the software constructions, the Molecular Dynamics technique was used. The model applied for the graphic interface (software) is an approximation that reproduces the characteristic curves tendencies in test of materials hardness; on the other hand, the software was designed and built in a friendly environment, where the user can develop its own thin films, not only in monolayers, but also in multilayers. This interface allows to control the film thickness, the number of layers and other physical properties as the dissociation energy or the energy parameter in the sphere; furthermore, it is possible to control the steps of the dynamical time. For ensuring the proper working of the software, several simulations using the chromium parameters as the reference material were carried out, reproducing experimental tendencies.

Keywords: Thin films, Molecular Dynamic, dissociation energy, simulations, Software.

1. Introducción

Las herramientas de simulación han evolucionado a través del tiempo; este adelanto se ha visto influenciado positivamente debido al crecimiento y desarrollo de los sistemas informáticos y a la capacidad de procesamiento de los ordenadores. La implementación actual de este tipo de herramientas es de gran interés y ayuda para el crecimiento y avance tecnológico [1]-[5]. A través de estas aplicaciones se logra estudiar el comportamiento dinámico y estático de sistemas complejos y se ha podido alcanzar una mayor comprensión y entendimiento de los fenómenos físicos estudiados.

Existen en el mercado diversos softwares que permiten realizar simulaciones por Dinámica Molecular; algunos de estos programas son de carácter libre, mientras que otros requieren de una licencia para su uso. Dale y sus colaboradores  [6] muestran el uso de LAMMPS como un componente de simulación que puede manejar varios modos al invocar librerías especiales. Spoel y sus colaboradores [7] describen el software GROMACS y afirman que es una herramienta rápida para simulaciones por Dinámica Molecular. Nagata [8] explica las características del software de modelado gráfico molecular (Molby) que puede ser usado como una herramienta de apoyo en química experimental. Popov y sus colaboradores [9] describen el programa multiplataforma de código abierto: analizador y lector de trayectorias por Dinámica Molecular (MDTRA) asistido con una interfaz gráfica de usuario. Aunque se han desarrollado diversos programas que permiten simular sistemas empleando la técnica de dinámica molecular, ninguno de estos lo hace de manera específica para el estudio de películas delgadas, y a través de una interfaz gráfica de usuario que requiera de conocimientos mínimos para su uso. 

En esta investigación se expone el software asistido por una interfaz gráfica de usuario que pueda ser usado para la simulación del comportamiento mecánico de películas delgadas. Para lograr esto, se ha diseñado un programa de simulación utilizando los principios de la Dinámica Molecular, con el manejo de potenciales interatómicos, integradores numéricos y parámetros teóricos; además, se llevaron a cabo simulaciones de cromo como material de prueba, el cual nos ayudará a comprobar si las tendencias en las curvas se aproximan a las que se obtienen en la vida real y de esta manera tener un soporte que valide las simulaciones hechas con la interfaz gráfica de usuario.

2. Materiales y Métodos

2.1 Interfaz Gráfica

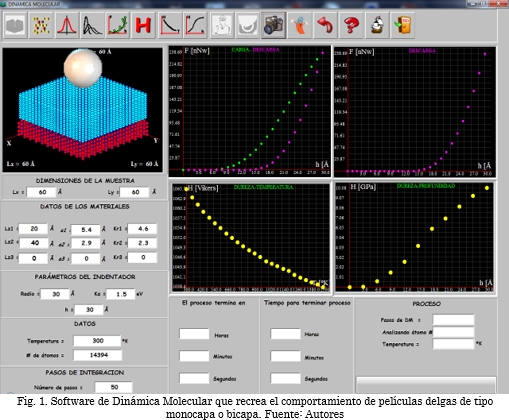
La Fig. 1, muestra el software asistido por una interfaz gráfica del usuario. El menú superior consiste de varios botones que permiten realizar el proceso de corrida de una simulación, capturar imágenes, observar tipos de distribución (gaussiana, Maxwell-Boltzman), corregir curvas mediante una aproximación de tipo gauss-ampere y de tipo polinómico, grabar información, borrar para limpiar la pantalla y ayuda para ejecutar el software. En la esquina superior izquierda, se puede apreciar una ventana donde se muestra el sustrato - recubrimiento que se está simulando, además, en tiempo real se observa cómo se va deformando la película delgada a medida que el indentador la penetra. En el panel inferior izquierdo se localizan los espacios correspondientes para entrada de datos del sistema, como dimensiones de la muestra Lx y Ly en las componentes vectoriales x y y en Amstrongs (Å), dimensión de espesor del sustrato especificado en Lz1, dimensión de espesor de la capa 1 en Lz2, de igual forma, si se está trabajando con una bicapa, se introduce su espesor en Lz3. a1, a2 y a3 representan los parámetros de red del sustrato, capa 1 y capa 2, Kr1, Kr2 y Kr3 corresponden a las relaciones entre el parámetro de red y el radio atómico. La dimensión del indentador se define en parámetros de indentador, donde Radio representa el radio de la esfera sólida, Ka la constante de energía de la esfera indeformable y h la profundidad de penetración del indentador sobre la muestra. Los datos hacen referencia a la temperatura a la cual se desea estabilizar el sistema. Esta temperatura está dada en °K. El número de pasos de integración representa los pasos de dinámica durante los cuales va a transcurrir la simulación. En el panel inferior derecho se pueden apreciar dos casillas, una donde se indica el tiempo de simulación en horas, minutos y segundos y otra donde se muestra el tiempo restante de simulación. Por último, en el panel superior derecho, se encuentran cuatro ventanas, donde: la primera hace referencia a la gráfica de carga-descarga, la segunda indica la curva de descarga con la cual se realiza el análisis de dureza, la ventana tres muestra la relación de dureza contra temperatura de penetración y, por último, en la ventana cuatro se observa la relación existente entre la dureza y la profundidad.

2.2 Modelo Empleado

El modelo teórico que permite el funcionamiento del software asistido por la interfaz gráfica posee las siguientes características: un potencial (potencial de Morse) que se ajusta adecuadamente a sistemas metálicos [10]-[14]. La forma del potencial es la siguiente:

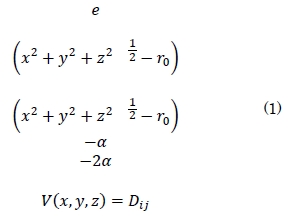
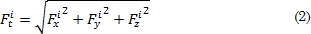
De la ecuación (1) D_ij representa la energía de disociación, r_ij la distancia entre dos átomos del sistema (r_ij = x² + y² + z^{2 1/2}) α es una constante del material que es obtenida del módulo de elasticidad y r_o la distancia de equilibrio de dos átomos del sistema. La derivada parcial de este potencial permite calcular la fuerza que ejerce el sistema sobre cada átomo en todas sus componentes vectoriales (Fⁱ_x, Fⁱ_y y Fⁱ_z). Fⁱ_t en la ecuación (2) corresponde a la magnitud de la fuerza sobre el i-esimo átomo debida a sus átomos vecinos [15].

Por otro lado, la interacción indentador - superficie se calcula a partir de un potencial esférico repulsivo [16]-[20] que recrea el fenómeno físico de interacción cuando el indentador penetra la muestra. Matemáticamente se representa de acuerdo con la ecuación (3):

En la expresión, la constante Ka representa la energía de la esfera indeformable, R el radio y r_ij la distancia de la esfera a un átomo. Al sistema se le asigna una velocidad con una distribución tipo Maxwell [21]-[25]. Esta velocidad es ajustada para mantener constante la temperatura del sistema a partir de un factor de escalamiento:

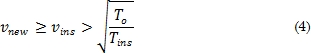
Este factor de escala aproxima las velocidades de tal forma que el sistema aumenta o disminuye su energía cinética llevándolo a un equilibrio térmico. En la ecuación (4), v_new es la velocidad, de acuerdo con la temperatura deseada, v_ins representa la velocidad instantánea a la cual se encuentra el sistema [10], T₀ es la temperatura de equilibrio a la cual se pretende llegar y T_ins es la temperatura instantánea. Después de tener la fuerza calculada en cada átomo, el paso siguiente consiste en integrar la ecuación del movimiento de Newton utilizando el algoritmo de integración en el tiempo de Verlet [26]-[28]. Se inicia con una expansión de Taylor de las coordenadas de un átomo en un intervalo de tiempo de la siguiente forma,

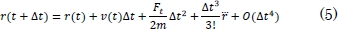
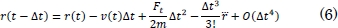
Sumando (5) y (6) se obtiene,

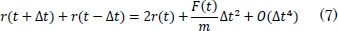
También se puede expresar así:

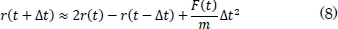
En la ecuación (5), m representa la masa atómica, O el error de truncamiento y Δt el cambio en el tiempo. A partir de la ecuación (7) se puede integrar la ecuación del movimiento de Newton, para encontrar las nuevas posiciones de los átomos.

2.3 Cálculo de la Dureza

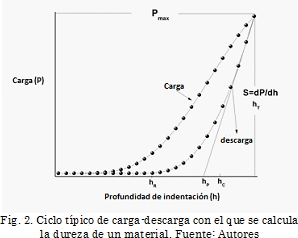
carga-descarga en el régimen elástico [29]. Se pueden obtener dos valores a partir de estas curvas: la penetración bajo carga máxima (hT) y la penetración final (hR) que se mide cuando el indentador está fuera de contacto con la muestra o material analizado. Este valor corresponde a la profundidad de la huella residual, el cual indica la deformación plástica del material después del proceso de carga-descarga. La curva de descarga muestra un comportamiento no lineal, lo que implica un límite de recuperación que deforma la huella residual. La profundidad hR permite obtener una superficie de contacto menor a la profundidad máxima [30]. En la Fig. 2 se observa la curva tangente que se traza desde el punto de inicio de descarga. La intersección entre la tangente y el eje de las abscisas permite obtener hp que se refiere a la profundidad máxima que puede alcanzar la huella residual. A partir de la forma de la huella residual producida por el indentador esférico se puede determinar la profundidad de penetración hc, correspondiente a la profundidad entre la punta del indentador y la curva límite de contacto bajo carga máxima. La penetración real es entonces:

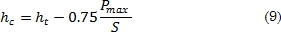
En esta ecuación, S representa la rigidez máxima:

De forma general se puede expresar la ecuación (9) así:

En donde ℇ representa el parámetro de forma del indentador; de esta manera se tiene que:

ℇ = 1paraunidadunidentadorplano

ℇ = 0,75paraunidadunidentadoresfericodeformaparabólica

ℇ = 0,72paraunpunzónperfectamentecónico

Para calcular la dureza se debe considerar el área de contacto que viene dada por:

Así, la dureza se determina mediante la siguiente ecuación:

Según el sistema internacional de unidades SI, la dureza calculada mediante la ecuación (13) se obtiene en GPa; análogamente la dureza se puede presentar en Vickers (HV) [31] teniendo en cuenta la siguiente conversión  [31], [32]:

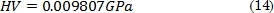
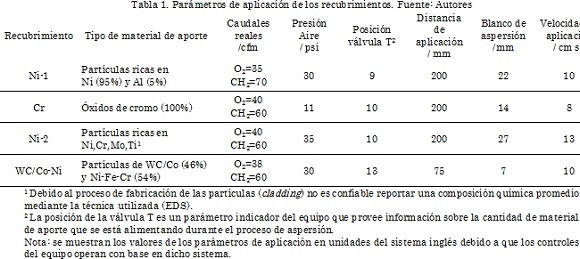
Para la validación del software asistido por la interfaz gráfica de usuario se llevaron a cabo una serie de simulaciones que consistieron en recrear las tendencias de las curvas características en pruebas de nanoindentación. El material que se simuló está conformado por un sustrato de silicio con estructura FCC tipo diamante, y una película delgada de cromo con estructura BCC, ambas orientadas en la dirección (100). El modelo de simulación está compuesto por 14400 átomos, que se distribuyen en 3810 átomos de silicio y 10584 átomos de cromo. El indentador es una esfera sólida indeformable, es decir, esta no sufre alteraciones al indentar el material; el radio de la esfera es 30 Å. En la construcción del modelo se tuvieron en cuenta condiciones de frontera libres a lo largo de la dirección z y condiciones de contorno a lo largo de la dirección x-z y y-z, ya que la cantidad de átomos en la simulación no superó el orden de 106 átomos, requisito indispensable para evadir los efectos de borde [33].

3. Resultados y Discusión

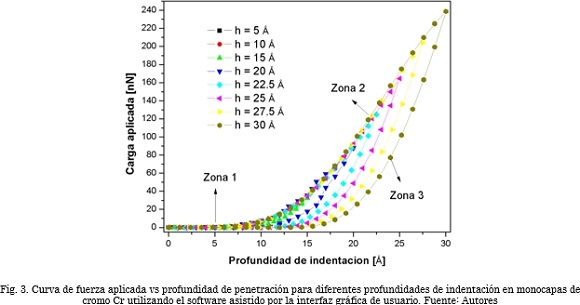
La Fig. 3 muestra los resultados de simulación obtenidos utilizando la interfaz gráfica. En esta figura se aprecia la curva de carga aplicada vs profundidad de indentación para diferentes profundidades de indentación en monocapas de Cr. Las profundidades asumidas fueron 5, 10, 15, 20, 22.5, 25, 27.5 y 30 Å [34]-[39]. Los parámetros del potencial de Morse como son: energía de disociación, distancia de enlace de equilibrio y constante de fuerza se encuentran en la Tabla 1

Estos valores fueron ingresados al programa antes de correr las simulaciones. Al comienzo de la nanoindentación, en la zona de carga, los átomos se encuentran relajados en su posición más estable, permitiendo que el indentador avance sin ninguna oposición (zona 1); a partir de cierta profundidad, la fuerza aplicada comienza a incrementarse generando deformaciones de carácter elásticas; después de esto, se observa un incremento constante en la fuerza aplicada. En este punto los átomos del material inician el proceso de dislocación, que conlleva a una deformación elasto-plástica (zona 2). Por último, en la zona de descarga se observa cómo a medida que el indentador retrocede, el material se recupera elásticamente (zona 3). La pendiente de la curva indica qué tanto se puede recuperar elásticamente el material [40]. Es claro entonces, que los resultados observados a partir de las simulaciones desarrolladas utilizando la interfaz gráfica, presentan un comportamiento coherente con lo que se observa en pruebas experimentales, reproduciéndose, de este modo, las tendencias de las curvas características de carga-descarga.

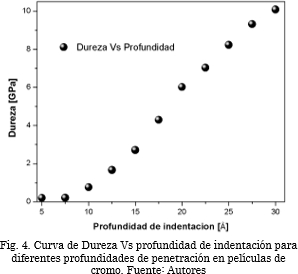
Por otro lado, en la Fig. 4 se aprecia la curva de dureza Vs profundidad de indentación. El material, al ser penetrado a mayor profundidad, exhibe un incremento en la fuerza que debe ser aplicada para que se mantenga un avance constante de penetración; este comportamiento es debido al aglomeramiento de átomos en la dirección normal, donde, se presenta acumulación de tensión que incrementa localmente la fuerza de opción del material [41]-[43].

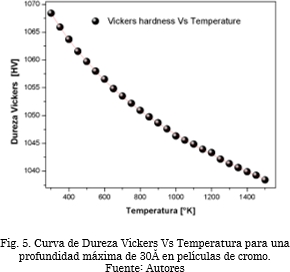
La Fig. 5 muestra la curva de dureza Vs temperatura [44], [45]. Se observa claramente cómo el material comienza a presentar cambios en sus propiedades mecánicas a medida que se incrementa la temperatura. Esto ocurre debido al aumento en la energía interna del material, que es de tipo cinética y se representa mediante la vibración de las partículas en el cristal. Al aumentar las vibraciones a causa de un incremento en la temperatura, la entropía del material aumenta al punto de debilitar los enlaces cristalinos, perdiéndose de esta forma la energía de cohesión que mantiene unida las partículas y que hace al material más duro.

Se ha mostrado un ejemplo del uso práctico del software asistido por una interfaz gráfica de usuario para la simulación de películas delgadas. Los resultados de la simulación revelan la capacidad que posee el programa para reproducir tendencias de las curvas características de dureza, ya sea variando la profundidad de indentación o la temperatura. Es de gran relevancia aclarar que el software es un paquete de prueba que debe ser optimizado en cuanto a diseño y estructura de código, para ser implementado en lenguajes de programación más avanzados.

4. Conclusiones

En este estudio se usó la técnica de dinámica molecular para construir un software asistido por una interfaz gráfica usuario, el cual se validó mediante la simulación de un recubrimiento, utilizando los parámetros del cromo. De las simulaciones realizadas y de los resultados calculados se obtuvieron las siguientes conclusiones:

1). Se desarrolló una interfaz gráfica de simulación capaz de reproducir las tendencias de las curvas características en pruebas de nanoindentación.

2). El software de simulación funcionó adecuadamente cuando se modelaron monocapas de cromo con estructura BCC, sobre un sustrato de silicio con estructura FCC-Diamante. Los ensayos que se realizaron inicialmente para este material fueron pruebas de nanoindentación. Pudo comprobarse que el comportamiento es coherente con relación con los reportados en la literatura, ya que se observó que, a partir de cierta profundidad, la fuerza aplicada comienza a incrementarse, generando deformaciones de carácter elásticas y reproduciendo muy acertadamente las tendencias de las curvas de carga-descarga.

3). Los resultados obtenidos para el cálculo de la dureza muestran que las tendencias de las curvas se aproximan a las reportadas en pruebas experimentales, dándose de esta forma un soporte de validación cualitativo del software.

Referencias

[1] B. H. Toby, “EXPGUI , a graphical user interface for GSAS,” J. Appl. Crystallogr., vol. 34, no. 2, pp. 210-213, Apr. 2001.         [ Links ]

[2] A. Kokalj, “Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale,” Comput. Mater. Sci., vol. 28, no. 2, pp. 155-168, Oct. 2003.         [ Links ]

[3] K. Hinsen, “The molecular modeling toolkit: A new approach to molecular simulations,” J. Comput. Chem., vol. 21, no. 2, pp. 79-85, Jan. 2000.         [ Links ]

[4] P. Eastman and V. Pande, “OpenMM: A Hardware-Independent Framework for Molecular Simulations,” Comput. Sci. Eng., vol. 12, no. 4, pp. 34-39, Jul. 2010.         [ Links ]

[5] M. S. Friedrichs, P. Eastman, V. Vaidyanathan, M. Houston, S. Legrand, A. L. Beberg, D. L. Ensign, C. M. Bruns, and V. S. Pande, “Accelerating molecular dynamic simulation on graphics processing units,” J. Comput. Chem., vol. 30, no. 6, pp. 864-872, Apr. 2009.         [ Links ]

[6] B. FrantzDale, S. J. Plimpton, and M. S. Shephard, “Software components for parallel multiscale simulation: an example with LAMMPS,” Eng. Comput., vol. 26, no. 2, pp. 205-211, Apr. 2010.         [ Links ]

[7] A. E. M. D. Spoel, E. Lindahl, B. Hess, G. Groenhof and J. C. Berendsen, “GROMACS: Fast, Flexible, and Free,” J. Comput. Chem, vol. 26, no. 16, pp. 1701-1718, 2005.         [ Links ]

[8] T. Nagata, “Molby: Graphical Molecular Modeling Software with Integrated Ruby Interpreter,” Bull. Chem. Soc. Jpn., vol. 87, no. 8, pp. 902-904, 2014.         [ Links ]

[9] A. V. Popov, Y. N. Vorobjev, and D. O. Zharkov, “MDTRA: A molecular dynamics trajectory analyzer with a graphical user interface,” J. Comput. Chem., vol. 34, no. 4, pp. 319-325, Feb. 2013.         [ Links ]

[10] R. Komanduri, N. Chandrasekaran, and L. M. Raff, “MD simulation of indentation and scratching of single crystal aluminum,” Wear, vol. 240, no. 1-2, pp. 113-143, May 2000.         [ Links ]

[11] M. B. Cai, X. P. Li, and M. Rahman, “Study of the mechanism of nanoscale ductile mode cutting of silicon using molecular dynamics simulation,” Int. J. Mach. Tools Manuf., vol. 47, no. 1, pp. 75-80, Jan. 2007.         [ Links ]

[12] R. T. Allen and P. Feuer, “Vibrational Energy Exchange for a Morse Potential Interaction,” J. Chem. Phys., vol. 40, no. 10, p. 2810, 1964.         [ Links ]

[13] H. Taseli, “Exact solutions for vibrational levels of the Morse potential,” J. Phys. A. Math. Gen., vol. 31, no. 2, pp. 779-788, Jan. 1998.         [ Links ]

[14] B. Molnár, P. Földi, M. G. Benedict, and F. Bartha, “Time evolution in the Morse potential using supersymmetry: Dissociation of the NO molecule,” Europhys. Lett., vol. 61, no. 4, pp. 445-451, Feb. 2003.         [ Links ]

[15] E. T. Lilleodden, J. A. Zimmerman, S. M. Foiles, and W. D. Nix, “Atomistic simulations of elastic deformation and dislocation nucleation during nanoindentation,” J. Mech. Phys. Solids, vol. 51, no. 5, pp. 901-920, May 2003.         [ Links ]

[16]T.-H. Fang, C.-I. Weng, and J.-G. Chang, “Molecular dynamics simulation of nano-lithography process using atomic force microscopy,” Surf. Sci., vol. 501, no. 1-2, pp. 138-147, Mar. 2002.         [ Links ]

[17] J. de Boer, "The non spherical potential field between two hydrogen molecules," Physica, vol. 9, no. 3, pp. 363-382, Mar. 1942.         [ Links ]

[18] Y. Wang, D. Raabe, C. Klüber, and F. Roters, “Orientation dependence of nanoindentation pile-up patterns and of nanoindentation microtextures in copper single crystals,” Acta Mater., vol. 52, no. 8, pp. 2229-2238, May 2004.         [ Links ]

[19] R. E. Miller, L. Shilkrot, and W. A. Curtin, “A coupled atomistics and discrete dislocation plasticity simulation of nanoindentation into single crystal thin films,” Acta Mater., vol. 52, no. 2, pp. 271-284, Jan. 2004.         [ Links ]

[20] G. S. Smith, E. B. Tadmor, N. Bernstein, and E. Kaxiras, “Multiscale simulations of silicon nanoindentation,” Acta Mater., vol. 49, no. 19, pp. 4089-4101, Nov. 2001.         [ Links ]

[21] A. Upadhyaya, J.-P. Rieu, J. A. Glazier, and Y. Sawada, “Anomalous diffusion and non-Gaussian velocity distribution of Hydra cells in cellular aggregates,” Phys. A Stat. Mech. its Appl., vol. 293, no. 3-4, pp. 549-558, Apr. 2001.         [ Links ]

[22] J. D. Vergados, S. H. Hansen, and O. Host, “Impact of going beyond the Maxwell distribution in direct dark matter detection rates,” Phys. Rev. D, vol. 77, no. 2, p. 023509, Jan. 2008.         [ Links ]

[23] L. V. Zhigilei and B. J. Garrison, “Velocity distributions of molecules ejected in laser ablation,” Appl. Phys. Lett., vol. 71, no. 4, p. 551, 1997.         [ Links ]

[24] A. M. Kapral and R. Kapral, “Continuous-velocity lattice-gas model for fluid flow,” Eur. Lett, vol. 44, no. 5, pp. 552-558, 1998.         [ Links ]

[25] S. van Zon and F. C. MacKintosh, “Velocity Distributions in Dissipative Granular Gases,” Phys. Rev. Lett., vol. 93, no. 3, p. 038001, Jul. 2004.         [ Links ]

[26] K. Sun, L. Fang, Z. Yan, and J. Sun, “Atomistic scale tribological behaviors in nano-grained and single crystal copper systems,” Wear, vol. 303, no. 1-2, pp. 191-201, Jun. 2013.         [ Links ]

[27] T. Hilbig, W. Brostow, and R. Simoes, “Simulating scratch behavior of polymers with mesoscopic molecular dynamics,” Mater. Chem. Phys., vol. 139, no. 1, pp. 118-124, Apr. 2013.         [ Links ]

[28] L. Verlet, “Computer 'Experiments' on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules,” Phys. Rev., vol. 159, no. 1, pp. 98-103, Jul. 1967.         [ Links ]

[29] J. M. Meza, M. C. M. Farias, R. M. de Souza, and L. J. C. Riaño, “Using the ratio: maximum load over unload stiffness squared, Pm/Su2, on the evaluation of machine stiffness and area function of blunt indenters on depth-sensing indentation equipment,” Mater. Res., vol. 10, no. 4, pp. 437-447, Dec. 2007.         [ Links ]

[30] A. Bolshakov and G. M. Pharr, “Influences of pileup on the measurement of mechanical properties by load and depth sensing indentation techniques,” J. Mater. Res., vol. 13, no. 04, pp. 1049-1058, Apr. 1998.         [ Links ]

[31] A. G. B. J. C. Caicedo, P. Prieto, J. M. Caicedo, R. G. Bejarano and S. Gottschalk, “Deposición de películas de Zirconio/nitruro de zirconio en forma de multicapas por magnetrón sputtering reactivo,” Rev. Colomb. Fis, vol. 37, no. 2, pp. 388-392, 2005.         [ Links ]

[32] O. Z. V. Di Graci, M. Torres and E. S. Puchi, “Dureza en aceros aisi 304 laminados en tibio y en caliente,” Rev. Lat. Met. Mater, vol. 1, pp. 237-248, 2009.         [ Links ]

[33] Q. H. Tang, “MD simulation of dislocation mobility during cutting with diamond tip on silicon,” Mater. Sci. Semicond. Process., vol. 10, no. 6, pp. 270-275, Dec. 2007.         [ Links ]

[34] A. K. Nair, E. Parker, P. Gaudreau, D. Farkas, and R. D. Kriz, “Size effects in indentation response of thin films at the nanoscale: A molecular dynamics study,” Int. J. Plast., vol. 24, no. 11, pp. 2016-2031, Nov. 2008.         [ Links ]

[35] M. Shell De Guzman, G. Neubauer, P. Flinn, and W. D. Nix, “The Role of Indentation Depth on the Measured Hardness of Materials,” MRS Proc., vol. 308, p. 613, Jan. 1993.         [ Links ]

[36] J. R. Tuck, A. M. Korsunsky, S. J. Bull, and R. I. Davidson, “On the application of the work-of-indentation approach to depth-sensing indentation experiments in coated systems,” Surf. Coatings Technol., vol. 137, no. 2-3, pp. 217-224, Mar. 2001.         [ Links ]

[37] N. Chollacoop, M. Dao, and S. Suresh, “Depth-sensing instrumented indentation with dual sharp indenters,” Acta Mater., vol. 51, no. 13, pp. 3713-3729, Aug. 2003.         [ Links ]

[38] W. C. Oliver and G. M. Pharr, “Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology,” J. Mater. Res., vol. 19, no. 01, pp. 3-20, Jan. 2004.         [ Links ]

[39] A. H. W. Ngan and B. Tang, “Viscoelastic effects during unloading in depth-sensing indentation,” J. Mater. Res., vol. 17, no. 10, pp. 2604-2610, Oct. 2002.         [ Links ]

[40] P. Peng, G. Liao, T. Shi, Z. Tang, and Y. Gao, “Molecular dynamic simulations of nanoindentation in aluminum thin film on silicon substrate,” Appl. Surf. Sci., vol. 256, no. 21, pp. 6284-6290, Aug. 2010.         [ Links ]

[41] Y. Gao, C. J. Ruestes, and H. M. Urbassek, “Nanoindentation and nanoscratching of iron: Atomistic simulation of dislocation generation and reactions,” Comput. Mater. Sci., vol. 90, pp. 232-240, Jul. 2014.         [ Links ]

[42] J. V. Y. Gaillard, E. Jiménez-Piqué, J. A. Muñoz and M. Anglada, “Nanoindentación de circona dopada con itria expuesta a degradación hidrotérmica,” An. la Mecánica Fract., vol. 1, pp. 283-288, 2007.         [ Links ]

[43] J. Gubicza, A. Juhász, and J. Lendvai, “A new method for hardness determination from depth sensing indentation tests,” J. Mater. Res., vol. 11, no. 12, pp. 2964-2967, Dec. 1996.         [ Links ]

[44] B. Evans and C. Goetze, “The temperature variation of hardness of olivine and its implication for polycrystalline yield stress,” J. Geophys. Res., vol. 84, no. B10, p. 5505, 1979.         [ Links ]

[45] Y. Milman, S. Luyckx, and I. Northrop, “Influence of temperature, grain size and cobalt content on the hardness of WC-Co alloys,” Int. J. Refract. Met. Hard Mater., vol. 17, no. 1-3, pp. 39-44, May 1999.         [ Links ]