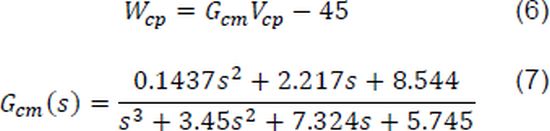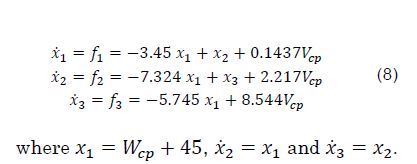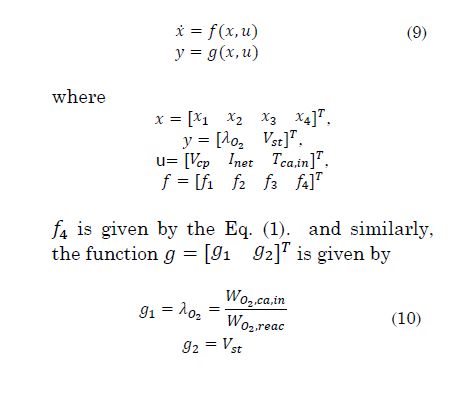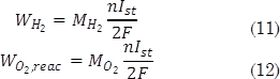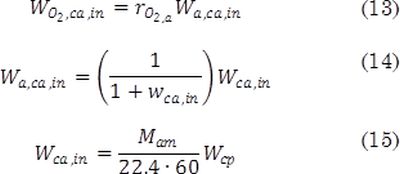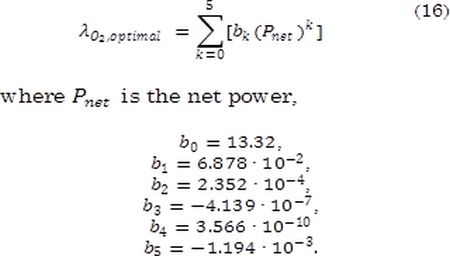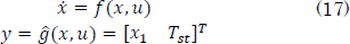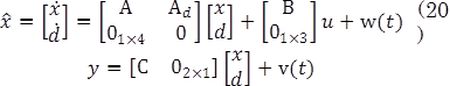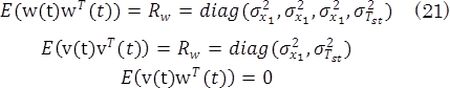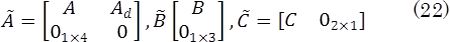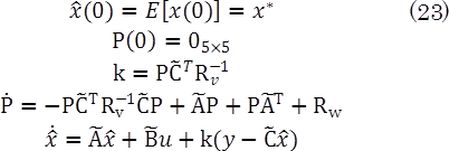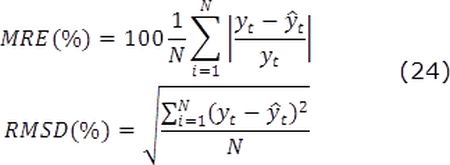Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
TecnoLógicas
Print version ISSN 0123-7799On-line version ISSN 2256-5337
TecnoL. vol.19 no.37 Medellín July/Dec. 2016
Artículo de investigación/Research article
A control system for reducing the hydrogen consumption of PEM fuel cells under parametric uncertainties
Sistema de control para reducir el consumo de hidrógeno en celdas de combustible PEM considerando incertidumbres paramétricas
Richard Ríos 1, Carlos A. Ramos-Paja 2 y Jairo J. Espinosa 3
1 Ingeniero de Control, M.Sc. en Matemáticas, Departamento de Energía Eléctrica y Automática, Facultad de Minas, Universidad Nacional de Colombia, Medellín-Colombia, rriospa@unal.edu.co
2 Ingeniero Electrónico, M.Sc. en Ingeniería Automática y Ph.D. en Electrónica, Automática y Comunicaciones, Departamento de Energía Eléctrica y Automática, Facultad de Minas, Universidad Nacional de Colombia, Medellín-Colombia, caramosp@unal.edu.co
3 Ingeniero Electrónico, M.Sc. en Ingeniería de Control y Ph.D. en Ciencias Aplicadas, Departamento de Energía Eléctrica y Automática, Facultad de Minas, Universidad Nacional de Colombia, Medellín-Colombia, jespinov@unal.edu.co
Fecha de recepción: 01 de septiembre de 2015/ Fecha de aceptación: 16 de junio de 2016
Como citar / How to cite
R. Ríos-Patiño, C.A. Ramos-Paja y J.J. Espinosa-Oviedo, "A control system for reducing the hydrogen consumption of PEM fuel cells under parametric uncertainties", Tecno Lógicas, vol. 19, no. 37, pp. 45-59, 2016
Abstract
This paper presents a control system for reducing the hydrogen consumption for a Polymer Electrolyte Membrane fuel cell, also considering parametric uncertainties. The control system is based on a non-linear state space model of the fuel cell, a Kalman filter/estimator, a linear state feedback controller and a Maximum Power Point (MPP) tracking algorithm. The control objective is to supply the requested load power, avoiding oxygen starvation with minimum fuel consumption using a Perturb and Observe (P&O) algorithm.
The performance of the control system was assessed under parametric uncertainties by simulating a performance degradation of the compressor due to aging. Thus, two cases were simulated: first, a mismatch between the system and the linear model in the (open-loop) air compressor gain; and second, a mismatch between the system and the linear model in the current compressor and losses. The simulation results showed that the Kalman filter/estimator overcome the uncertainties produced by the parametrical variations. Besides, the P&O algorithm accomplished to provide the suitable compressor voltage without identifying an optimal profile under ideal operating conditions and empirical data.
Keywords: PEM fuel cells; oxygen excess ratio; Kalman filter; parametric uncertainty; Perturb & Observe.
Resumen
Este artículo presenta un sistema de control para reducir el consumo de hidrógeno para una celda de combustible de Membrana de Intercambio Protónico, considerando incertidumbres paramétricas. El sistema de control incluye un modelo no lineal en el espacio de estado para la celda de combustible, un filtro de Kalman/estimador, un regulador óptimo cuadrático y algoritmo de seguimiento de puntos de máxima potencia (MPP). El objetivo de control es suministrar la potencia de carga demandada, evitando el agotamiento del oxígeno y minimizando el consumo de hidrógeno por medio de un algoritmo de Perturbación y Observación (P&O).
El desempeño del sistema de control es evaluado ante incertidumbres paramétricas al simular escenarios de pérdida de desempeño como producto del envejecimiento del compresor. De esta forma, dos escenarios fueron simulados: un primer escenario simula un error entre la ganancia (de lazo abierto) del compresor de la celda de combustible y la del modelo; y un segundo escenario, con un error entre la corriente de pérdidas y del compresor de la celda de combustible con respecto al modelo. Los resultados de simulación muestran que el filtro Kalman/estimador logra contrarrestar las incertidumbres producidas por los cambios paramétricos del sistema. Igualmente, el algoritmo MPP logra suministrar el voltaje del compresor adecuado sin necesidad de un perfil óptimo en condiciones ideales.
Palabras clave: Celdas de Combustible de Membrana de Intercambio Protónico-PEM; exceso de razón de oxígeno; filtro de Kalman; incertidumbre paramétrica; Perturbación & Observación.
1. Introduction
Currently, there is a growing interest in developing alternative energy sources that can be cleaner than those based on fossil fuel. In addition, fuel cells are devices that produce electri-cal current with almost null pollutant emissions by reacting oxygen with an oxidizing agent. Therefore, these devices have been earning a huge interest as alternative energy sources with strong research efforts and intensive development by several manufacturers. One of the most developed fuel cell technologies is the Proton Exchange Membrane (PEM) based on hydrogen as an oxidizing agent. These fuel cells have low operating temperature, high power efficiency, long cell life and low electrolyte corrosion [1]. However, PEM fuel cell operating conditions must be regulated to achieve high power efficiency and to avoid degradation of the device [2].
Therefore, two important operating conditions must be regulated: the stoichiometric relation between oxygen and hydrogen, supplied to the stack, and the consumed oxygen. Otherwise, a mismatch between the supplied and demanded oxygen to produce the stack current may arise, yielding to undesirable phenomenon like oxygen starvation, which could to generate the degradation of the fuel cell, the decrement of the output power, and frequently the shut-down of the fuel cell [2], [3].
Although the oxygen starvation is a phenomenon that varies spatially, regulation of the oxy-gen excess ratio is the most common solution. The oxygen excess ratio gives the fraction between the oxygen flow supplied to the cathode and the consumed in the electrochemical reaction, and it must be higher than one for a proper performance of the fuel cell [2]. Few works have used model-based control systems [2]â[8] or MPP methods [9]â[13] for regulat-ing the oxygen excess ratio. In particular, two kinds of MPP approaches can be found in the literature: a first group maximizes the power generation by tracking the optimal stack current for the demanded power; and a second group maximizes the power generation by regulating the optimal compressor voltage, keeping the oxygen excess ratio constant at any operating condition. However, an optimal stack current does not imply an optimal value in the compres-sor voltage.
Therefore, it is not possible to guarantee an optimal fuel cell operation [11]. Other works have been devoted to model and regulate PEM fuel cells, such as empirical polynomial based approximations [14], performance models based on interpolation and experimental characterization [15], control-oriented models [16]â[18], and models that consider the stack with its auxiliary systems [19].
However, these not necessarily were focused on the oxygen starvation In the above groundwork, model parameters have been estimated under ideal operating conditions and assumed being constants in the complete operating range. However, these parameters vary over time due to different events like fuel cell degradation by aging (clog-ging of air filters or contamination of gas diffusion layers), or changes in the environmental conditions (temperature and humidity), among others. Therefore, robust controls have been proposed to regulate oxygen excess ratio under disturbances and uncertainties [5]â[8]. How-ever, these works have used an optimal load profile to determine the reference of the oxy-gen excess ratio. These optimal profiles are usually identified under ideal operating conditions from experimental results as a polynomial depending on the net power. These profiles there-by require being parameterized specifically for each PEM fuel, and they should be re-identified when the ideal operating conditions differ significantly from the actual operating conditions.
Previously, in [4] a linear control system and a non-linear state space model were proposed to deliver the requested load power by tracking an optimal profile, while the oxygen starva-tion is avoided and the fuel consumption is minimized. The optimal load profile was obtained from a set of maximum power points under ideal operating conditions parameterized using a polynomial function [2]. The modeled dynamics were the temperature of the stack and the airflow in the compressor for predicting the stack voltage and the behavior of the oxygen excess ratio. The model was validated using a set of experimental data obtained from a 1.2 kW NEXA Power Module [10]. The control system was designed using a linear-quadratic state feedback regulator and a linear Kalman filter. Both, controller and observer were designed using a linearized representation of the model around an operating point.
However, modeling errors introduced by parametric uncertainties and their effect on the fuel cell performance have not been analyzed in detail. For example, fuel cell degradation by aging may be an important source of modeling errors, yielding to mismatches in the system variables between the process and the model like the air compressor open-loop gain, optimal load power profiles or the compressor current and losses. To address these issues, this paper proposes a cascade control scheme combining a P&O algorithm and an LQR with a Kalman filter/estimator.
The P&O is proposed for determining the reference value of the oxygen starvation to minimize the fuel consumption and to supply the demanded load power. As in [11], it determines the compressor voltage that keeps the oxygen excess ratio constant, but the observed variable is the net power and the perturbed variable is the oxygen excess ratio. Then, for regulating oxygen starvation, the P&O algorithm provides the suitable compressor voltage without identifying an optimal profile under ideal operating conditions and empirical data. The term Kalman filter/estimator refers to a classic Kalman filter together with the estimation of a non-physical variable that eliminates steady-state error. Finally, the design of the proposed cascade control system is based on the mathematical model presented in [20].
The rest of paper is organized as follows: In the second section, it is described the architec-ture of a PEM fuel cell and it is summarized the non-linear model reported in [20] for predict-ing the oxygen excess ratio, stack voltage, thermal effects and compressor dynamics. Then, it is described the proposed cascade control scheme to overcome the uncertainty effects. In the third section, it is evaluated the performance of the proposed solution in comparison with the former optimal load profile by analyzing the delivered net power versus the fuel con-sumption. Finally, the conclusions of the work are given in section four.
2. Methods
2.1 Mathematical model of PEM fuel cell systems
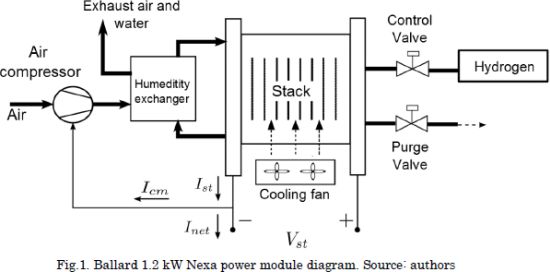
Fig. 1 depicts the physical configuration of a typical PEM fuel cell and the interaction among all its elements. The PEM fuel cell considered in this work is the Ballard 1.2 kW Nexa Power module, which uses hydrogen as fuel. The Nexa system provides run-time measures of stack temperature, air flow, stack current, and hydrogen consumption, among others.
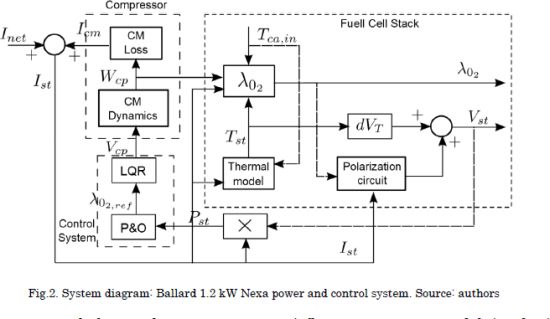
The non-linear state-space model used in this work for designing the control system is published in [20]. The model structure is depicted in Fig. 2. Since the design of the Kalman filter/estimator proposed in this work strongly depends on the model structure, this section summarizes the model using the same equations and analyses reported in [20]. However, a more detailed description of the model, and its experimental validation, is available in [20].
The model dynamics are the temperature of the stack Tst and the air flow generated by the compressor Wcp. Such system is modeled using the equations given in (1-7).
Using an energy balance, the temperature of the stack Tst is given by the Eq. (1), where Tca,in is the ambient temperature, Vst is the stack voltage, Inet is the load by the compressor and losses, while Ist= Inet+Icm is the stack current obtained by adding both currents. The stack voltage and compressor current are given by the Equations (2-5), where Isc is a virtual short-circuit current.
Equations (3-5) are identified from the 1.2kW Nexa prototype by using experimental curves, where dVstis a deviation factor of the stack voltage that considers the changes of the stack temperature from the reference temperature T0=35C. An airflow compressor model is obtained by using experimental data taken from the Ballard NEXA 1.2 kW system, following the Reaction Curve Method [6] and described as follows:
where Vcp is the compressor control signal. A linear state space model for the air compressor is proposed by deriving a time domain representation of Gcms
Considering the stack temperature Tst as an additional state X4′ , a non-linear state space model for the PEM fuel cell is defined, whose inputs are the compressor control signal Vcp within [0%-100%], the load current Inet and the ambient temperature Tca,in -. The model outputs are the oxygen excess ratio λO2 and the stack voltage Vst-. The state-space model is given as follows:
WO2,ca,in is the oxygen flow that reaches the cathode, and WO2,reac is the oxygen flow consumed in the reaction. The hydrogen and oxygen flows consumed in the electrochemical reaction are given as follows:
and the inlet dry air flow WO2,ca,in is given by:
where MO2 = 0.032 is the molecular mass of the oxygen, n=46 is the number of cells in the stack, F= 96485 is the Faraday constant, rO2,a = 0.2330is the molar mass relation between oxygen and dry air, which relates the oxygen flow available in the inlet dry air flow W a,ca,in In addition, w ca,in is the inlet air flow, Mam = 0.0288 is the humidity ratio, Mam = 0.0288 is the inlet air molar mass. Finally, it is worth to mention that in the Eq. (15) is used to transform Wca,in from [Kgâs^(-1) ] to [SLPM], because Wcp is expressed in this unit. The non-linear model was validated through a set of experimental data from a 1.2 kW NEXA Power Module. Table 1 describes each variable and parameter with respective units.
2.2 Control system and parametric uncertainty
In [20] a linear control system was designed, whose control objective was to regulate the oxygen excess ratio λO2 by tracking an optimal profile, while the requested net power is delivered and fuel consumption is minimized. The control system consisted in a Linear Quadratic Regulator (LQR), a linear Kalman filter and the following parameterization of the optimal profile:
However, such linear control system was designed for ideal conditions, where coefficients of the parametric equations were identified with empirical data, e.g. (3-7) and (16). Thus, modeling errors introduced by parametric uncertainties were not considered in [20]. In fact, the analyses reported in [20] and [9] show that detecting the optimal operating point of the fuel cell using classical control approaches must be performed off-line, which is subjected to parametric uncertainties.
In such a way, two types of parametric uncertainties are considered in this paper: first, a mismatch between the (open-loop) air compressor gain in the fuel cell and control system; and second, a mismatch between the compressor current and losses Icm in the full cell and control system. In addition, the aim is to determine the optimal reference value of oxygen excess ratio λO2 based on a method that is free of ideal operating condition. Thus, two solutions are considered for overcoming parametric uncertainties: first, a P&O algorithm for tracking on-line the optimal operating point, and second, a Kalman filter/estimator to eliminate the residual steady-state error produced by modeling errors. Fig. 2 illustrates the connection of the proposed control structure.
The P&O algorithm is a technique used in photovoltaic applications for maximizing the output power by tracking the MPPs, which defines a hill climbing optimization problem in dynamic optimization [21]-[22]. The P&O algorithm tracks the optimum value of a variable of a dynamic system by repeatedly changing the value of another suitable variable, i.e. the perturbed variable. To find this value, it relies on the assumption that the variable to be optimized has a single optimum in the range of values of the perturbed variable.
In this paper, it is aimed to supply the requested load power with minimum Ist, i.e. with minimum fuel consumption as derived in the Eq. (11), because reductions in Ist produce diminution on the hydrogen flow required to supply the load power. Thus, the perturbed variable is the oxygen excess ratio λO2 and the variable to be optimized is the net power Pnet= Pst - Pcm, where Pst stands for the stack power, while Pcm represents the compressor power. As a result, the P&O method behaves as a master controller that fix the reference value of λO2, and the LQR behaves as a slave system that manipulates the compressor voltage Vcp to obtain such reference value of λO2 under perturbations.
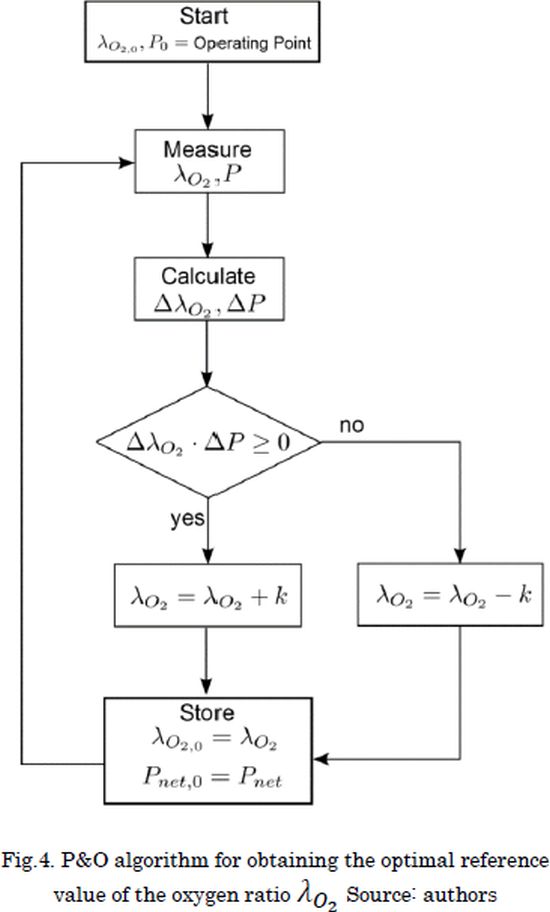
Then, the basic idea of the P&O algorithm is: starting from an initial value of the oxygen excess ratio λO2 and net power Pnet,0 given by an arbitrary operating point, the value of Pnet is increased, if the slope on the Pnet vs λO2 curve is positive; or decreased, if the slope is negative; or remains constant, if the slope is zero, see Fig. 3. Thus, performing such strategy, an algorithm could be stated as follows: the process starts with initial values of λO2 and Pnet,0, both variables are measured and deltas values (i.e. increments or decrements) are calculated; if both variables change in the same direction or remain equal λO2 - Pnet ≥ 0, the value of λO2 is increased with a constant slope k. Similarly, if both variables change in different direction (λO2 - Pnet < 0), the value of λO2 is decreased with a constant slope k. Finally, the new values of λO2and P_net are stored as λO2 and Pnet,0, respectively, for a further iteration, see the proposed flow chart in Fig. 4.
For overcoming modeling errors, the linear control is adjusted by introducing a linear Kalman filter with an additional non-physical variable used to properly estimate the state space variables [23]. Thus, since the measurable states are X1 and Tst, a non-linear model is defined from the Eq. (9), with output variables y = [ x1 Tst] T , as follows:
A linear version of the model given in the Eq.(17) is obtained around the operating point defined by
This operating point is defined by taking the values of v19n37a04ec1012 as the average in the experimental range. The remaining variables are found by solving numerically the system of nonlinear equations described by (9-10). It is worth to mention that such linear system is observable, i.e. the matrix observability has full rank. Then, a continuous-time linear Kalman filter with an addition non-physical variable is proposed by extending the linear system in Equations (18)and(19) to:
where the matrices A, B, C and D are given in the Eq. (19). The variable d is a non-physical state added in order to eliminate any possible offset that can be presented in steady state, i.e. it introduces an integral term to the Kalman filter. The signals w and v are the plant and measurement noise, and both are assumed to be zero-mean Gaussian process, that is
where o-2x1=33.185 Kgs-1 and o-2Tst=1.1608•10-3C are the variance of the experimental data of Wcp and Tst, respectively. Defining the matrices, Ã, B˜ and C˜as:
Equations of the Kalman filter are given as follows
3. Results and discussion
Aiming to assess the performance of the control system against uncertainties produced by the model parameters, two cases were simulated: first, a mismatch between the system and the linear model in the (open-loop) air compressor gain; and second, a mismatch between the system and the linear model in the current compressor and losses. Both parametric uncertainties are considered as consequences of the device aging, and they were simulated with exponential behavior, i.e. v = vnominal+vnominal Δ(1-e-(t-t0)/Ï)) where t0 = 50s, r = 100s, Δ = 10% and v represents the compressor gain or the current compressor.
The remaining variables of the system were considered constants at the operating point. Then, the first case was mainly focused in to assess the performance of the Kalman filter/estimator in comparison with the former filter proposed in [20]; and the second case was aimed to assess the performance of the MPP method for determining the reference value of λO2 in comparison with the optimal profile used in [20].
The simulations were performed in Matlab/Simulink software using the following parameters: solver ode23s of step-variable with relative tolerance of 1e -2.
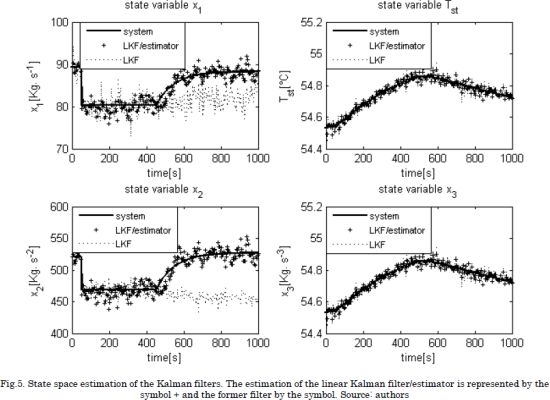
The first scenario was simulated by adding a step of 10% below the nominal value of the compressor voltage voltage Vcp at t = 50s, while the compressor gains changes with time. Fig. 5 illustrates the performance of the Kalman filter/estimator (LKF/estimator) against the observer proposed in [9]. In addition, an error analysis was carried out using both the mean relative error-(MRE) and root-mean-square deviation-(RMSD) for providing a measure of the error between the system and the observers.
The first scenario was simulated by adding a step of 10% below the nominal value of the compressor voltage Vcp at t = 50s, while the compressor gains changes with time. Fig. 5 illustrates the performance of the Kalman filter/estimator (LKF/estimator) against the observer proposed in [20]. In addition, an error analysis was carried out using both the mean relative error-(MRE) and root-mean-square deviation-(RMSD) for providing a measure of the error between the system and the observers:
In such expressions N is the number of samples, while yt and y^t are the system and estimated data, respectively. The values of these metric errors are given in Tables 2 and 3. It must be point out that the RMSD error quantifies the standard deviation of the state estimations value from the real state value.
The simulation results showed an improved performance of the Kalman filter/estimator in the estimation of the non-measurable variables, e.g. when a step change was made in the compressor voltage. It is observed that the linear Kalman filter could not detect this gain change, which produces a deficient estimation of the non-measurable variables. Meanwhile, the Kalman filter/estimator overcome such condition thanks to the virtual stated, which behaves as an integral term contributing to eliminate the instantaneous error over time. In addition, metric values in Tables 2 and 3 agree with the performance of the filters observed in Fig. 5. It is worth mentioning that the RMSD values cannot be compared to variables because it is scale-dependent.
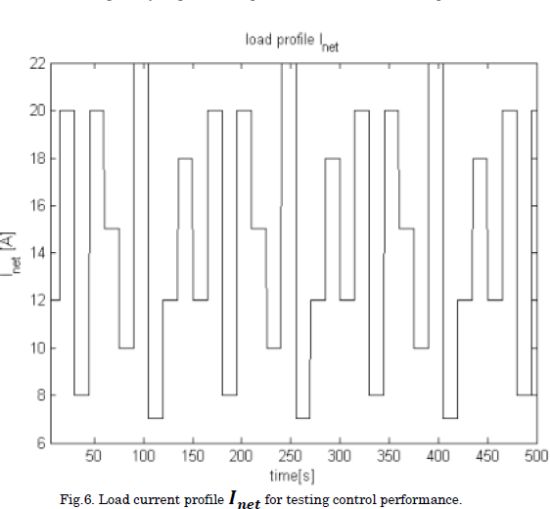
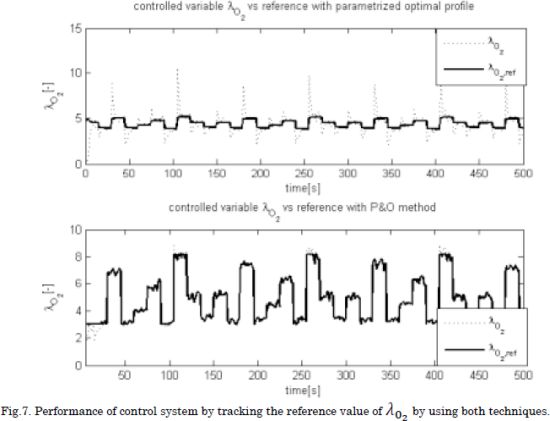
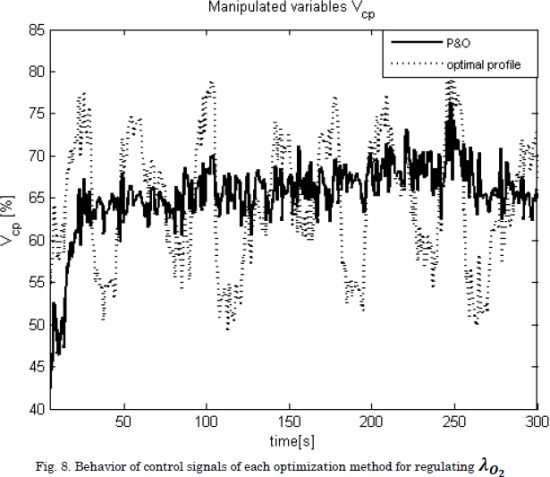
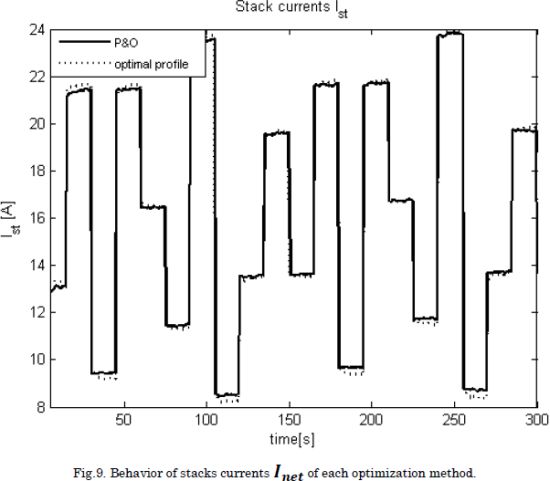
Considering that changes in the environmental temperature are neglected, the Tca,in was kept constant at the operating point. The performance of the control system was tested under a current demand profile Inet depicted in Fig. 6, while the compressor current increases with time due to aging of the fuel cell. The simulation performance of the control system with the P&O algorithm and the parametrized optimal profile is observed in Figs. 7, 8 and 9. In addition, for assessing quantitatively the performance of both techniques, MRE errors for λ02, and mean values of net powers and stack currents were obtained from the simulation and reported in Table 4.
According to the results, the slave LQR accomplished to track the reference value given by each technique for determining the optimal value of λ02, see Fig. 6.
Although the P&O does not obtain an improved performance against the optimal profile, it is observed that both techniques obtained the same tradeoff regarding fuel consumption and delivered net power. However, a significant advantage of the P&O algorithm concerns its robustness to parameter changes, which enable it to be used for any fuel cell without performing an off-line identification of an optimal profile for λO2. Instead, solutions like the optimal load profile proposed in [2] require to be parameterized specifically for the PEM fuel cell used in a particular solution. Moreover, such an optimal profile could change due to aging, equipment repairing/replacement, among others without any prior off-line parametrization.
4. Conclusions
This paper presents a control system for reducing the hydrogen consumption in PEM fuel cells considering parametric uncertainties. The control system consisted in a LQR, a Kalman filter/estimator and a P&O algorithm for determining the optimal value of the oxygen excess ratio that reaches the minimum fuel cell consumption for the delivered power. The performance of the Kalman filter/estimator was assessed under modeling errors generated by parametric uncertainties. This proposed solution provided better estimation in comparison with the traditional Kalman filter. Moreover, the P&O algorithm provided a run-time procedure that accomplishes to supply the net power Pnet requested by the load with the minimum hydrogen consumption regardless the PEM fuel cell device and operating conditions.
The main disadvantage of the P&O algorithm is the small oscillation around the steady-state operation condition, which introduces small deviations from the optimal operating point. This can be addressed by using non-oscillating MPPT algorithms such as the incremental conductance. However, due to the high sensitivity to measurement noise of those approaches, such a solution requires further investigation. Similarly, non-linear control strategies with higher robustness to uncertainties, such as the sliding-mode approach, could be used to improve the regulation of the oxygen excess ratio.
5. Acknowledgements
The authors acknowledge the scholarship 511 de Doctorados Nacionales Generación Bicente-nario 2010 granted by the Departamento Administrativo de Ciencia, Tecnología e Innovación (COLCIENCIAS). This work was also supported by COLCIENCIAS and the Universidad Nacional de Colombia under the project "Desarrollo de Nuevas Líneas de Servicios Tecnológicos Basa-das en Celdas de Combustibles" with code 121056236765.
References
[1] J. T. Pukrushpan, A. G. Stefanopoulou, and Huei Peng, “Control of fuel cell breathing,” IEEE Control Syst. Mag., vol. 24, no. 2, pp. 30-46, Apr. 2004. [ Links ]
[2] C. A. Ramos-Paja, C. Bordons, A. Romero, R. Giral, and L. Martinez-Salamero, “Minimum Fuel Consumption Strategy for PEM Fuel Cells,” IEEE Trans. Ind. Electron., vol. 56, no. 3, pp. 685-696, Mar. 2009. [ Links ]
[3] C. Bordons, A. Arce, and A. J. del Real, “Constrained predictive control strategies for PEM fuel cells,” in 2006 American Control Conference, 2006, p. 6 pp. [ Links ]
[4] M. A. Danzer, J. Wilhelm, H. Aschemann, and E. P. Hofer, “Model-based control of cathode pressure and oxygen excess ratio of a PEM fuel cell system,” J. Power Sources, vol. 176, no. 2, pp. 515-522, Feb. 2008. [ Links ]
[5] I. Matraji, S. Laghrouche, S. Jemei, and M. Wack, “Robust control of the PEM fuel cell air-feed system via sub-optimal second order sliding mode,” Appl. Energy, vol. 104, pp. 945-957, Apr. 2013. [ Links ]
[6] W. García-Gabin, F. Dorado, and C. Bordons, “Real-time implementation of a sliding mode controller for air supply on a PEM fuel cell,” J. Process Control, vol. 20, no. 3, pp. 325-336, Mar. 2010. [ Links ]
[7] S. Laghrouche, M. Harmouche, F. S. Ahmed, and Y. Chitour, “Control of PEMFC Air-Feed System Using Lyapunov-Based Robust and Adaptive Higher Order Sliding Mode Control,” IEEE Trans. Control Syst. Technol., vol. 23, no. 4, pp. 1594-1601, Jul. 2015. [ Links ]
[8] J. K. Gruber, C. Bordons, and A. Oliva, “Nonlinear MPC for the airflow in a PEM fuel cell using a Volterra series model,” Control Eng. Pract., vol. 20, no. 2, pp. 205-217, Feb. 2012. [ Links ]
[9] C. A. Ramos-Paja, R. Giral, L. Martínez-Salamero, J. Romano, A. Romero, and G. Spagnuolo, “A PEM Fuel-Cell Model Featuring Oxygen-Excess-Ratio Estimation and Power-Electronics Interaction,” IEEE Trans. Ind. Electron., vol. 57, no. 6, pp. 1914-1924, Jun. 2010. [ Links ]
[10] C. A. Ramos-Paja, G. Spagnuolo, G. Petrone, R. Giral, and A. Romero, “Fuel cell MPPT for fuel consumption optimization,” in Proceedings of 2010 IEEE International Symposium on Circuits and Systems, 2010, pp. 2199-2202. [ Links ]
[11] C. A. Ramos-Paja, G. Spagnuolo, G. Petrone, and E. Mamarelis, “A perturbation strategy for fuel consumption minimization in polymer electrolyte membrane fuel cells: Analysis, Design and FPGA implementation,” Appl. Energy, vol. 119, pp. 21-32, Apr. 2014. [ Links ]
[12] A. Giustiniani, G. Petrone, C. Pianese, M. Sorrentino, G. Spagnuolo, and M. Vitelli, “PEM Fuel Cells Control by means of the Perturb and Observe Technique,” in IECON 2006 - 32nd Annual Conference on IEEE Industrial Electronics, 2006, pp. 4349-4354. [ Links ]
[13] J. Lu and A. Zahedi, “Air supply control for maximum efficiency point tracking in fuel cell systems,” J. Renew. Sustain. Energy, vol. 4, no. 3, p. 33-106, May 2012. [ Links ]
[14] X. D. Xue, K. W. E. Cheng, and D. Sutanto, “Unified mathematical modelling of steady-state and dynamic voltage-current characteristics for PEM fuel cells,” Electrochim. Acta, vol. 52, no. 3, pp. 1135-1144, Nov. 2006. [ Links ]
[15] S. O. T. Ogaji, R. Singh, P. Pilidis, and M. Diacakis, “Modelling fuel cell performance using artificial intelligence,” J. Power Sources, vol. 154, no. 1, pp. 192-197, Mar. 2006. [ Links ]
[16] A. Hernandez, D. Hissel, and R. Outbib, “Non Linear State Space Modelling of a PEMFC,” Fuel Cells, vol. 6, no. 1, pp. 38-46, Feb. 2006. [ Links ]
[17] J. Golbert and D. R. Lewin, “Model-based control of fuel cells: (1) Regulatory control,” J. Power Sources, vol. 135, no. 1-2, pp. 135-151, Sep. 2004. [ Links ]
[18] J. Golbert and D. R. Lewin, “Model-based control of fuel cells (2): Optimal efficiency,” J. Power Sources, vol. 173, no. 1, pp. 298-309, Nov. 2007. [ Links ]
[19] M. J. Khan and M. T. Iqbal, “Modelling and Analysis of Electro-chemical, Thermal, and Reactant Flow Dynamics for a PEM Fuel Cell System,” Fuel Cells, vol. 5, no. 4, pp. 463-475, Dec. 2005. [ Links ]
[20] R. Rios, C. Ramos, and J. Espinosa, “Non-Linear State Space Model and Control Strategy for Pem Fuel Cell Systems,” Dyna, vol. 78, no. 166, pp. 60-67, 2011. [ Links ]
[21] N. Femia, G. Petrone, G. Spagnuolo, and M. Vitelli, “Optimization of Perturb and Observe Maximum Power Point Tracking Method,” IEEE Trans. Power Electron., vol. 20, no. 4, pp. 963-973, Jul. 2005. [ Links ]
[22] N. Femia, P. G., G. Spagnuolo, and M. Vitelli, “Power Electronics and Control Techniques for Maximum Energy Harvesting in Photovoltaic Systems (Femia, N. et al; 2013) [Book News],” IEEE Ind. Electron. Mag., vol. 7, no. 3, pp. 66-67, Sep. 2013. [ Links ]
[23] D. Simon, Optimal state estimation: Kalman, H infinity, and nonlinear approaches, 1st ed. Hoboken, N.J.: Wiley-Interscience, 2006. [ Links ]