Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
TecnoLógicas
Print version ISSN 0123-7799On-line version ISSN 2256-5337
TecnoL. vol.19 no.37 Medellín July/Dec. 2016
Artículo de investigación/Research article
Planeamiento de la expansión integrada generación-transmisión: una revisión del estado del arte
Integrated generation-transmission expansion planning: a review of the state of the art
Sergio D. Saldarriaga-Zuluaga 1, Jesús M. López-Lezama 2 y Nicolás M. Galeano 3
1 Ingeniero Electricista, Facultad de Ingeniería, Departamento de Ingeniería Eléctrica, Universidad de Antioquia, Medellín-Colombia, sergio.saldarriaga@udea.edu.co
2 Ph.D. en Ingeniería Eléctrica, Dpto. de Ingeniería Eléctrica, Facultad de Ingeniería, Universidad de Antioquia, Medellín-Colombia, jmaria.lopez@udea.edu.co
3 Ph.D. en Ingeniería Electrónica, Facultad de Ingeniería, Departamento de Ingeniería Eléctrica, Universidad de Antioquia, Medellín-Colombia, nicolas.munoz@udea.edu.co
Fecha de recepción: 30 de enero de 2016/ Fecha de aceptación: 8 de mayo de 2016
Como citar / How to cite
S. D. Saldarriaga-Zuluaga, J. M. López-Lezama y N.M. Galeano, "Planeamiento de la expansión integrada generación-transmisión: una revisión del estado del arte", Tecno Lógicas, vol. 19, no. 37, pp. 79-92, 2016
Resumen
En la última década, un gran número de trabajos de investigación han abordado el problema de la expansión de los sistemas de potencia, coordinando en un solo problema de optimización el planeamiento de expansión de la generación (GEP, Generation Expansion Planning) y el planeamiento de expansión de la transmisión (TEP, Transmission Expansion Planning). El GEP normalmente se lleva a cabo sin tener en cuenta las restricciones de red y desde una perspectiva energética. Por otro lado, el TEP busca encontrar los refuerzos en la red, que atiendan una demanda futura de forma económica y confiable. La integración de estos problemas ha sido abordada utilizando diferentes métodos, modelos y funciones objetivo. En este artículo se presenta una revisión bibliográfica del problema del planeamiento integrado GEP-TEP desde diferentes puntos de vista como su modelado, métodos de solución, consideraciones de confiabilidad, entre otros. En la literatura especializada se encuentran artículos de revisión que caracterizan de forma independiente los problemas GEP y TEP. Sin embargo, no se encuentran revisiones que aborden problema GEP-TEP integrado. Surge entonces la necesidad de caracterizar los aspectos del planeamiento de la expansión integrada de los sistemas de potencia, con el propósito de proporcionar herramientas de consulta para los investigadores en este campo.
Palabras clave: Planeamiento de la generación, planeamiento de la transmisión, mercados eléctricos, métodos de optimización, planeamiento integrado.
Abstract
In the last decade a great number of research works have approached the power systems planning problem by coordinating in a single optimization problem the generation expansion planning (GEP) and the transmission expansion planning (TEP). GEP is usually carried out disregarding network constraints and under an energetic perspective. On the other hand, TEP aims to find network reinforcements that meet the expected demand in an economical and reliable way. The integration of these problems has been approached using different methods, models, and objective functions. This paper presents an exhaustive review of the integrated GEP-TEP problem from different points of view such as modeling, solving methods, reliability considerations, among others. There are review papers in the specialized literature that characterize the GEP and TEP problem independently. However, there are no reviews regarding the integrated GEP-TEP problem. So, it is needed to characterize aspects of the power systems integrated planning problem with the aim to provide consulting tools for researchers in this field.
Keywords: Generation planning, transmission planning, electricity markets, optimization methods, integrated planning.
1. Introducción
El planeamiento de la expansión de los sistemas eléctricos de potencia tiene como objetivo suplir las necesidades de demanda eléctrica que tendrá determinada región en el futuro. La atención de la demanda en el horizonte de planeación debe hacerse de manera económica, cumpliendo con criterios de confiabilidad y seguridad [1], [2]. En la búsqueda de soluciones para el planeamiento se deben considerar diversas variables que inciden en la toma de decisiones como, proyección de la demanda en el horizonte de planeación, hidrología, costo de los combustibles, fuentes de recursos energéticos y contaminación ambiental entre otras. La alta complejidad del problema de planeación de la expansión de los sistemas de potencia y la liberación de los mercados eléctricos han generado que el problema del planeamiento de la expansión de los sistemas de potencia se trabaje de forma separada. En una primera etapa se realiza el GEP. Luego, considerando el resultado de la primera etapa se procede a realizar una segunda etapa donde se desarrolla el TEP [3]. Sin embargo, recientemente el problema de planeación de la expansión integrando generación-transmisión (GEP-TEP) ha atraído más atención. Varios investigadores han venido desarrollando trabajos sobre este tema, considerando escenarios de operación orientados a la competencia y no orientados a la competencia.
La optimización coordinada del GEP-TEP es un problema de gran complejidad en la planeación de los sistemas de potencia [2]. Tres razones dan cuenta de la separación de los problemas GEP y TEP: 1) Más del 80% del costo total de la planificación de la expansión está relacionado al GEP. Por lo tanto, solucionar el problema del GEP primero y luego utilizar la solución obtenida como un punto inicial para el problema TEP no causa una desviación considerable de la solución óptima del problema integrado. Sin embargo, a pesar de que el GEP-TEP resulta en un porcentaje muy pequeño de ahorro con respecto a la GEP separado del TEP, este es significativo debido a la enorme financiación invertida en la expansión de los sistemas de potencia. 2) El problema combinatorio necesita un gran esfuerzo computacional [3]. 3) La elección de las unidades generadoras está fuertemente influenciada por la distancia de estas a los recursos de combustible y centros de consumo [4].
En este artículo se realiza una revisión bibliográfica sobre el planeamiento integrado genera-ción-transmisión. Vale la pena destacar que la bibliografía sobre temas de expansión en sistemas de potencia es bastante extensa. Por este motivo la búsqueda bibliográfica para este artículo se centra principalmente en artículos publicados después del año 2000 y que aborden el problema de la expansión conjunta de la generación y la transmisión. Existen muchos trabajos que abordan únicamente el TEP [5], [6] o el GEP [7], [8], bajo diferentes aspectos. De hecho, en la literatura técnica se encuentran artículos de revisión sobre el problema del GEP como se reporta en [9] y [10]; artículos que solo hablan del TEP como [1], [11] - 14]; y artículos que abordan los aspectos importantes del GEP y TEP, pero cuando se abordan de forma separada como en [15]. A diferencia de los artículos ya mencionados, en este se realiza una revisión de modelos que resuelven el problema de planeamiento de la expansión integrando el GEP y el TEP.
2. Metodología
2.1 GEP-TEP considerando aspectos de mercado
Los mercados eléctricos pueden agruparse en orientados a la competencia y no orientados a la competencia. Los modelos de planificación que se basan en un modelo de mercado no orientado a la competencia, utilizan una herramienta integrada verticalmente para determinar el plan de instalación de nuevos recursos [16]. La planificación de la expansión basada en el mercado considera participantes con intereses propios, así que coordina las estrategias que planten los participantes y analiza los riesgos asociados basándose en las incertidumbres que prevalecen [16].
Los modelos de planeamiento que consideran mercados eléctricos basados en libre competencia abordan el problema desde distintas perspectivas que incluyen teoría de juegos y teoría microeconómica. Los enfoques más comunes trabajan en torno a los modelos de equilibrio, en los cuales se busca una condición o solución que posee la propiedad de que ningún participante quiere alterar sus estrategias unilateralmente, lo que es conocido como equilibrio de Nash [17], [18]. En [2] y [19] se formuló el modelo de equilibrio como un problema com-plementario mixto (MCP). En [20]-[22] se formuló el modelo de equilibrio como un programa matemático con restricciones de equilibrio (MPEC). En [23], [24] se formuló el modelo de equilibrio como un MPEC y se utiliza una técnica para convertirlo en un problema lineal. En [25] también se formula el problema de equilibrio como un MPEC y se resuelve reformulán-dose como un MCP y utilizando un método de diagonalización.
2.2 Modelos utilizados
El GEP-TEP se puede dividir en dos enfoques: anticipativo e integrado. El modelo integrado asume que un organismo centralizado se encargada de definir qué plantas generadoras y qué líneas de transmisión se requieren en el sistema. El objetivo es maximizar el beneficio social y reducir los costos de inversión y operación [23]. El modelo anticipativo se basa en el hecho de que el agente transmisor tiene que anticipar los resultados del mercado al momento de decidir sobre la inversión en transmisión, adelantándose al portafolio de inversión del agente generador. Las decisiones en el planeamiento de la generación son hechas por empresas rivales en un mercado eléctrico competitivo, lo que implica que puede formularse como un problema de optimización que maximiza el bienestar social o la ganancia del productor. La decisión de inversión en transmisión está influenciada por las expectativas de desarrollo del mercado y viceversa, debido a la relación que existe entre el agente transmisor y el mercado eléctrico [23].
En la literatura técnica se han encontrado artículos que resuelven el problema utilizando cualquiera de los dos enfoques. En [4], [26], [27] se ha resuelto el GEP-TEP utilizando el modelo Integrado. Por otro lado, en [20], [24] y [25] se ha resuelto el problema utilizando un modelo anticipativo de expansión generación-transmisión. Finalmente en [23] se resuelve el problema utilizando los dos enfoques, integrado y anticipativo.
2.3 Métodos de solución
De forma general, se puede decir que los métodos usados para solucionar el GEP-TEP se dividen en tres grupos: las técnicas de programación matemática, las técnicas heurísticas y las técnicas metaheurísticas [12]. Estos métodos se describen a continuación.
2.3.1 Técnicas de programación matemática
Las técnicas de programación matemática son herramientas de optimización utilizadas para facilitar la toma de decisiones en problemas que presentan múltiples alternativas. Estas técnicas presentan tres aspectos principales. El primero consiste en definir las posibles decisiones que puedan tomarse en el problema, representado por medio de variables de decisión. El segundo consiste en especificar el conjunto de valores que pueden tomar las variables de decisión, representado por medio de restricciones. Por último, el tercero consiste en determinar el beneficio asociado a cada variable de decisión, representado por medio de la función objetivo [11].
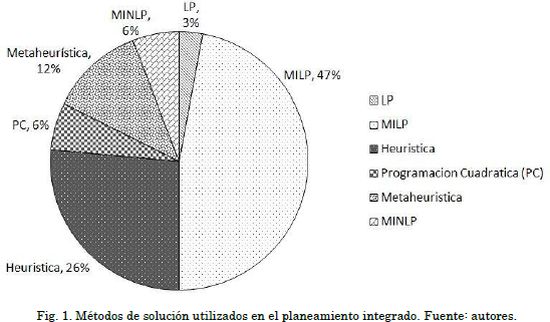
En la formulación de estos modelos, la planificación se plantea como un problema de optimización con una función objetivo, sujeto a un conjunto de restricciones. Estas restricciones tratan de modelar gran parte de los criterios técnicos, económicos y de confiabilidad impuestas a la expansión del sistema eléctrico [11]. Diferentes métodos se han propuesto para resolver el GEP-TEP mediante programación matemática. En [28] se resolvió el problema utilizando Programación Lineal (PL), en [4], [16], [24] y [29]-[32] se usó programación lineal entera mixta (MILP, Mixed Integer Linear Programming), en [3]también se usó MILP y se adicionó el cálculo de confiabilidad por medio de una técnica heurística, en [2] se resolvió el problema utilizando programación cuadrática, en [23] y [33] se resuelve de dos formas con MILP y con programación no lineal entera mixta (MINLP, Mixed Integer NonLinear Program-ming) verificando las condiciones de optimalidad de Karush-Kuhn-Tucker (KKT), y en [34]-[37][34] se usa descomposición de Benders.
2.3.2 Técnicas heurísticas
Los métodos heurísticos son la alternativa cuando no es posible utilizar los métodos de optimización matemática. El término "heurística" se utiliza para describir todas aquellas técnicas que utilizan un procedimiento paso a paso para la generación, evaluación y selección de opciones de expansión, con o sin la ayuda del usuario. Para ello, los modelos heurísticos realizan búsquedas locales con la guía de reglas empíricas o lógicas. Estas reglas se utilizan para generar y clasificar las opciones durante la búsqueda. El proceso heurístico se lleva a cabo hasta que el algoritmo no es capaz de encontrar ya una mejor solución, teniendo en cuenta los criterios de evaluación que se establecieron. Estos criterios suelen incluir los costos de operación de inversión, sobrecargas en los elementos del sistema y potencia no suministrada [11].
Varios autores han propuestos técnicas heurísticas para resolver el GEP-TEP. Las característi-cas de estas técnicas son diversas y varían de acuerdo al tipo de sistema en el que se implementen y a las consideraciones de cada autor. En [27] se calcula una solución inicial sin tener en cuenta las restricciones para luego ir mejorando la solución. En [38] se calcula una solución inicial considerando algunas restricciones, esta solución se convierte en un límite inferior del problema para luego por medio de un algoritmo constructivo mejorar la solución. En [39] se implementa un algoritmo constructivo e introduce generación distribuida en el GEP-TEP. En [25] se incorpora un algoritmo que resuelve un modelo estático tri-nivel de planeamiento (transmision, genracion y operación del mercado). En [20] se propone un algoritmo basado en agentes y se utiliza una técnica de optimización basada en búsqueda local para encontrar soluciones al GEP-TEP. En [26] y [40] se proponen algoritmos heurísticos que en sus etapas resuelven problemas que son formulados como MILP y PL.
2.3.3 Técnicas metaheurísticas
Las metaheurísticas pueden concebirse como estrategias generales de diseño de procedimientos heurísticos para la resolución de problemas de alta complejidad. Las estrategias metaheurísticas normalmente son utilizadas en problema que no tienen un algoritmo específico que entregue una solución satisfactoria [41]. Estas técnicas integran las características de la programación matemática y los métodos heurísticos. Las metaheurísticas, en menor medida, también han sido utilizadas para abordar el GEP-TEP. En [42] se propone un algoritmo NSGA-II (Non-dominated Sorting Genetic Algorithm II) para resolver el planeamiento integrado multiobjetivo.
En este caso, se consideran dos funciones objetivo, la primera minimiza la expectativa de energía no suministrada y la segunda minimiza los costos de operación e inversión más los costos de emisiones. En [43] se utiliza el método NBI (Normal Boundary Intersection) en un abordaje multiobjetivo similar para obtener la solución óptima de Pareto y luego se utiliza un proceso de toma de decisiones difusa para seleccionar una de las soluciones óptimas. En [21] se implementa una técnica heurística que combina un algoritmo genético embebido con un algoritmo genético isla paralela (IPGA, Island parallel genetic algorithm).
2.4 Representación de la red de transmisión
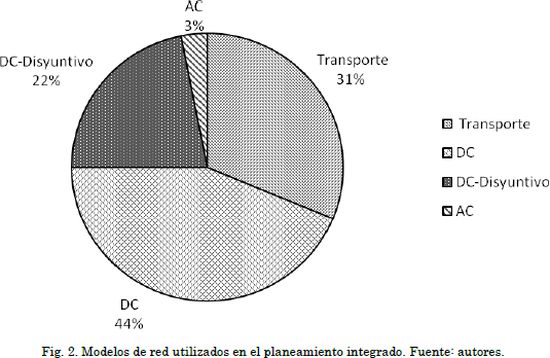
En los modelos que resuelven el GEP-TEP encontrados en la literatura se han utilizado diferentes formas para representar la red de transmisión. Se ha usado el modelo de transporte, el modelo DC, el modelo DC disyuntivo y el modelo AC.
El modelo de transporte es una aproximación del modelo DC. Considera las ecuaciones de balance en los nodos o primera ley de Kirchhoff, pero no considera la segunda ley de Kirchhoff (ignora la reactancia de las líneas). Este tipo de simplificaciones presenta facilidad de solución, pero los resultados se pueden alejar de la realidad. En [2], [24], [28], [31], [35] y [38]-[40] se representa la red de transmisión con el modelo de transporte.
El modelo DC considera las ecuaciones de balance en los nodos o primera ley de Kirchhoff y las ecuaciones de las ramas o segunda ley de Kirchhoff. En esta representación los resultados se aproximan más a la realidad que con el modelo de transporte. En [16], [20], [22], [25], [27], [29], [29], [33], [34], [42], [43] se representa la red de transmisión con el mo-delo de DC. El modelo DC disyuntivo considera la primera y segunda ley de Kirchhoff como el modelo DC normal. Pero este es una versión lineal del modelo DC. Este modelo es utilizado cuando el GEP-TEP se formula como un problema de programación lineal entera mixta. En [3], [4], [23], [26], [30], [36], [37] se representa la red de transmisión con el modelo de DC disyuntivo.
El modelo AC considera la potencia activa, la potencia reactiva y las pérdidas. Este es el modelo que más se aproxima a la realidad, pero puede presentar problemas de convergencia. Muchos escenarios pueden no converger, ya sea porque no tengan solución, el punto inicial no sea factible, las referencias de generadores, trasformadores y elementos de compensación no sean adecuados o los perfiles de tensión no sean compatibles [44]. En [45] se representa la red de transmisión con el modelo AC.
2.5 Consideraciones de confiabilidad
En la literatura especializada se han propuesto diferentes métodos para el cálculo de confiabilidad aplicados al GEP-TEP. Estos métodos se basan en el cálculo de índices, los cuales permi-ten identificar el grado de confiabilidad de los planes de expansión. Los índices propuestos se pueden clasificar en dos grupos: probabilísticos y deterministas [46]. Los probabilísticos permiten la evaluación cuantitativa de las alternativas del sistema, tomando directamente en consideración los parámetros que influyen en la confiablidad, tales como las capacidades de las unidades generadoras individuales y la tasa de interrupción forzada de cada unidad. Los índices deterministas son más limitados, pero son comunes debido a que su cálculo es simple y requiere poca o ninguna información [46].
Dentro de los índices deterministas el índice de Margen de Reserva (MR) permite identificar cuanta capacidad de generación se tiene disponible. Este índice es utilizado en [31], [35]. El índice LU (Largest Unit) permite identificar la capacidad de generación que se tiene disponible, pero considerando la pérdida de la unidad generadora más grande del sistema. En sistemas donde predomina la generación hidráulica se aplica un método denominado día seco. Este consiste en identificar con base en datos históricos el día más seco que se tendrá en el horizonte de planeación para validar en este si el plan de expansión propuesto es capaz de ga-rantizar la atención de la demanda.
En cuanto a índices probabilísticos, uno de los más utilizados es el índice de probabilidad de pérdida de carga (LOLP, Loss of Load Probability). El índice LOLP indica la probabilidad de que una parte de la carga no sea atendida debido a que no se cuenta con la generación disponible adecuada [3]. El índice de expectativa de pérdida de carga (LOLE, Loss of Load Expectation) definido como la suma del LOLP en el tiempo, es utilizado en [3], [16]. Otros índices como el índice Energía Esperada No Suministrada (EENS) o el índice de pérdida de energía esperada (LOEE, Loss of Energy Expectation) miden la cantidad de energía esperada que no se suministra al año, por no contar con capacidad de generación adecuada o por no suministrar energía debido a fallas en el sistema. Estos índices son utilizados en 29], [33], [36] y [42]. El índice de probabilidad de pérdida de energía (LOEP, Loss of Energy Probability) es utilizado en [33] y [37].
2.6 Incertidumbre
En los sistemas de potencia no se conocen con certeza las condiciones que se presentarán en el futuro. Diversas variables como la demanda, el costo de los combustibles, el clima y las políticas de Estado son difíciles de predecir. Lo que genera una variedad de incertidumbres que se deben considerar en la selección de un plan de expansión [47].
En [48] se plantea una clasificación de incertidumbres de acuerdo al impacto que estas tienen sobre el sistema. Las de alto impacto son clasificadas como incertidumbres globales, y aquellas que su impacto es menor son clasificadas como locales. En [22], [24], [26], [27] y [40], se considera incertidumbre en la demanda. En [22], [29], [33] y [37] se considera incertidumbre respecto a la salida de equipos en el sistema de potencia, esto con el propósito de calcular la confiabilidad. En [24], [26] y [40] se considera incertidumbre en el costo de los combustibles y disponibilidad de los recursos energéticos. En [27] se considera incertidumbre en la demanda y en la generación eólica.
2.7 Nuevas tecnologías
La generación producida por la quema de hidrocarburos en todo el mundo continúa impactan-do negativamente el medio ambiente. Esto ha dado lugar a varias regulaciones ambientales para reducir los gases de efecto invernadero. Por ejemplo, a través de la imposición de los costos de mitigación de emisiones y normas que faciliten el ingreso de generación con fuentes renovables [40]. Acorde con lo anterior, en [49] se propone un modelo de GEP-TEP que considera restricciones para las emisiones de CO2.
La generación con recursos renovables y la generación distribuida han llamado mucho la atención en los últimos años a causa de la presión ambiental y el alto precio del gas natural y del petróleo. Muchos países han adoptado normas que incentivan el uso de energías renovables [50].
Por otro lado, la utilización de generación distribuida en el GEP-TEP puede contribuir a la reducción de pérdidas de transmisión y eventualmente a posponer la construcción de nuevas líneas [51]. Algunos modelos de planeación de GEP-TEP consideran estas tecnologías. En [39] se propone un modelo del planeamiento de la expansión integrando la generación y la transmisión considerando generación distribuida. En [27], [30] y [35] se propone un modelo de planeamiento de la expansión integrando la generación y la transmisión considerando parques eólicos. En [52] se estudia la confiabilidad de la planeación y operación del sistema de potencia integrando generación eólica.
2.8 Resumen general de los modelos
En la Tabla 1 se presenta un resumen da las principales características de algunos de los modelos citados en este artículo. Adicionalmente, en la Fig. 1 se presentan los métodos de solución. Se puede evidenciar que el método de solución más utilizado en la literatura es la programación lineal entera mixta (MILP), seguido por las técnicas heurísticas.
En la Fig. 2 se presenta el porcentaje de utilización de los modelos de flujo de carga. Se puede observar que el más utilizado es el modelo DC dado que es lineal y presenta resultados que se aproximan bien a la realidad.
3. Conclusiones
En este trabajo se presenta una caracterización de aspectos importantes en el planeamiento coordinado de la expansión generación - transmisión. Esta caracterización sirve de guía para investigadores que quieran incursionar en este campo de estudio. Los autores citados muestran la importancia que tiene el problema de planeamiento coordinado para garantizar la atención de la demanda en el futuro de manera confiable, segura y económica. Lo anterior se evidencia con el aumento de número de artículos publicados en este tema en los últimos años.
En futuras investigaciones se deben construir modelos que incorporen nuevas tendencias en el planeamiento, tales como generación solar, baterías, y respuesta de la demanda. Además, se debe profundizar en la incorporación de tecnologías como generación distribuida, generación eólica a pequeña y gran escala y el efecto de considerar redes de diferente nivel de tensión en la expansión. Los modelos citados no consideran escenarios hidrológicos, análisis detallados de contingencias, planeamiento de potencia reactiva y aumento de capacidad de circuitos existentes.
En cuanto a los métodos de solución este artículo realiza una descripción de los que son utilizados actualmente en la literatura. Debido a la naturaleza del problema se evidenció que el método de solución más utilizado es la programación lineal entera mixta, ya que permite obtener soluciones óptimas. Sin embargo, requieren de simplificaciones en el modelado del sistema. Por otro lado, técnicas como las heurísticas y metaheurísticas permiten consideraciones de modelaje más precisas y se han implementado como una opción importante de solución para modelos multiobjetivos. La principal desventaja de estas últimas técnicas radica en que no garantizan la obtención del óptimo global del problema bajo estudio.
4. Agradecimientos
Los autores agradecen al programa de Sostenibilidad 2016-2017 de la Universidad de Antioquia.
Referencias
[1] A. K. Reza Hemmati, Rahmat-Allah Hooshmand, “State-of-the-art of transmission expansion planning:Comprehensive review,” Renew. Sustain. Energy Rev., vol. 23, pp. 312-319, 2013. [ Links ]
[2] L. Xiaotong, L. Yimei, Z. Xiaoli, and Z. Ming, “Generation and Transmission Expansion Planning Based on Game Theory in Power Engineering,” Syst. Eng. Procedia, vol. 4, no. 2011, pp. 79-86, 2012. [ Links ]
[3] B. Alizadeh and S. Jadid, “Reliability constrained coordination of generation and transmission expansion planning in power systems using mixed integer programming,” IET Gener. Transm. Distrib., vol. 5, no. 9, p. 948, 2011. [ Links ]
[4] I. Sharan and R. Balasubramanian, “Integrated generation and transmission expansion planning including power and fuel transportation constraints,” Energy Policy, vol. 43, pp. 275-284, 2012. [ Links ]
[5] R. A. Gallego, A. Monticelli, and R. Romero, “Transmision system expansion planning by an extended genetic algorithm,” IEE Proc. - Gener. Transm. Distrib., vol. 145, no. 3, p. 329, 1998. [ Links ]
[6] M. Moradi, H. Abdi, S. Lumbreras, A. Ramos, and S. Karimi, “Transmission Expansion Planning in the presence of wind farms with a mixed AC and DC power flow model using an Imperialist Competitive Algorithm,” Electr. Power Syst. Res., p. --, 2016. [ Links ]
[7] G. Mavrotas, D. Diakoulaki, and L. Papayannakis, “An energy planning approach based on mixed 0-1 Multiple Objective Linear Programming,” Int. Trans. Oper. Res., vol. 6, no. 2, pp. 231-244, 1999. [ Links ]
[8] S. Li, D. W. Coit, and F. Felder, “Stochastic optimization for electric power generation expansion planning with discrete climate change scenarios,” Electr. Power Syst. Res., p. --, 2016. [ Links ]
[9] Jinxiang Zhu and Mo-yuen Chow, “A review of emerging techniques on generation expansion planning,” IEEE Trans. Power Syst., vol. 12, no. 4, pp. 1722-1728, 1997. [ Links ]
[10] V. Phupha, T. Lantharthong, and N. Rugthaicharoencheep, “Generation Expansion Planning Strategies on Power System: A Review,” IEEE Trans. Power Syst, vol. 6, no. 4, pp. 436-439, 2012. [ Links ]
[11] G. Latorre, J. M. Areiza, A. Villegas, and R. D. Cruz, “Classification of Publications and Models on Transmission Expansion Planning,” IEEE Trans. Power Syst., vol. 18, no. 2, pp. 938-946, 2003. [ Links ]
[12] J. D. Molina and H. Rudnick, “Transmission of electric energy: A bibliographic review,” IEEE Lat. Am. Trans., vol. 8, no. 3, pp. 245-258, 2010. [ Links ]
[13] J. Quintero, H. Zhang, S. Member, and Y. Chakhchoukh, “Next Generation Transmission Expansion Planning Framework: Models , Tools , and Educational Opportunities,” IEEE Trans. Power Syst., vol. 29, no. 4, pp. 1911-1918, 2014. [ Links ]
[14] R. Romero, A. Monticelli, A. V García, and S. Haffner, “Test systems and mathematical models for transmission network expansion planning,” IEE Proc. Gener. Transm. Distrib., vol. 149, no. 1, pp. 27-36, 2002. [ Links ]
[15] R. Hemmati, R. A. Hooshmand, and A. Khodabakhshian, “Comprehensive review of generation and transmission expansion planning,” IET Gener. Transm. Distrib., vol. 7, no. 9, pp. 955-964, 2013. [ Links ]
[16] A. Khodaei, M. Shahidehpour, L. Wu, and Z. Li, “Coordination of short-term operation constraints in multi-area expansion planning,” IEEE Trans. Power Syst., vol. 27, no. 4, pp. 2242-2250, 2012. [ Links ]
[17] L. Eduardo, G. Vega, L. Eduardo, and G. Vega, “Estimación y análisis de precios nodales como efecto de las restricciones de transmisión en el mercado mayorista de Colombia Assessment and analysis of local marginal prices as an effect of electric transmission constraints in the Colombian power market,” Ing. e Investig., vol. 30, no. 3, pp. 71-85, 2010. [ Links ]
[18] S. Wogrin, B. F. Hobbs, D. Ralph, E. Centeno, and J. Barquín, “Open versus closed loop capacity equilibria in electricity markets under perfect and oligopolistic competition,” Math. Program., vol. 140, no. 2, pp. 295-322, 2013. [ Links ]
[19] L. Tang and M. C. Ferris, “A Hierarchical Framework for Long-Term Power Planning Models,” IEEE Trans. Power Syst., vol. 30, no. 1, pp. 46-56, 2015. [ Links ]
[20] A. Motamedi, H. Zareipour, M. O. Buygi, and W. D. Rosehart, “A transmission planning framework considering future generation expansions in electricity markets,” IEEE Trans. Power Syst., vol. 25, no. 4, pp. 1987-1995, 2010. [ Links ]
[21] M. R. Hesamzadeh, D. R. Biggar, N. Hosseinzadeh, and P. J. Wolfs, “Transmission augmentation with mathematical modeling of market power and strategic generation expansion - Part II,” IEEE Trans. Power Syst., vol. 26, no. 4, pp. 2040-2048, 2011. [ Links ]
[22] E. E. Sauma and S. S. Oren, “Proactive planning and valuation of transmission investments in restructured electricity markets,” J. Regul. Econ., vol. 30, no. 3, pp. 261-290, 2006. [ Links ]
[23] M. Jenabi, S. M. T. Fatemi Ghomi, and Y. Smeers, “Bi-level game approaches for coordination of generation and transmission expansion planning within a market environment,” IEEE Trans. Power Syst., vol. 28, no. 3, pp. 2639-2650, 2013. [ Links ]
[24] D. Pozo, E. Sauma, and J. Contreras, “A Three-Level Static MILP Model for Generation and Transmission Expansion Planning,” IEEE Trans. Power Syst., vol. 28, no. 1, pp. 202-210, 2013. [ Links ]
[25] S. Jin and S. M. Ryan, “A tri-level model of centralized transmission and decentralized generation expansion planning for an electricity market-Part II,” IEEE Trans. Power Syst., vol. 29, no. 1, pp. 142-148, 2014. [ Links ]
[26] G. H. Moon, S. K. Joo, D. Hur, H. S. Jeong, H. S. Ryu, and K. W. Cho, “Stochastic integrated generation and transmission planning method with gradient radar step (GRS),” Transm. Distrib. Conf. Expo. Asia Pacific, T D Asia 2009, pp. 1-4, 2009. [ Links ]
[27] X. Ma and Y. Zhou, “Coordination of Generation and Transmission Planning for Power System with Large Wind Farms,” Energy Procedia, vol. 16, pp. 1979-1985, 2012. [ Links ]
[28] B. Graeber, R. Spalding-Fecher, and B. Gonah, “Optimising trans-national power generation and transmission investments: A Southern African example,” Energy Policy, vol. 33, no. 18, pp. 2337-2349, 2005. [ Links ]
[29] A. Khodaei and M. Shahidehpour, “Microgrid-based co-optimization of generation and transmission planning in power systems,” IEEE Trans. Power Syst., vol. 28, no. 2, pp. 1582-1590, 2013. [ Links ]
[30] H. Saboori, M. Mohammadi, and R. Taghe, “Composite Generation and Transmission Expansion Planning Considering the Impact of Wind Power Penetration,” 2011 Asia-Pacific Power Energy Eng. Conf., pp. 1-6, 2011. [ Links ]
[31] G. Liu, H. Sasaki, and N. Yorino, “Application of network topology to long range composite expansion planning of generation and transmission lines,” Electr. Power Syst. Res., vol. 57, no. 3, pp. 157-162, 2001. [ Links ]
[32] M. Benidris, S. Elsaiah, and J. Mitra, “An emission-constrained approach to power system expansion planning,” Int. J. Electr. Power Energy Syst., vol. 81, pp. 78-86, 2016. [ Links ]
[33] J. Aghaei, N. Amjady, A. Baharvandi, and M. Akbari, “Generation and Transmission Expansion Planning: MILP-Based Probabilistic Model,” IEEE Trans. Power Syst, vol. 29, no. 4, pp. 1592-1601, 2014. [ Links ]
[34] B. Alizadeh and S. Jadid, “A dynamic model for coordination of generation and transmission expansion planning in power systems,” Int. J. Electr. Power Energy Syst., vol. 65, pp. 408-418, 2015. [ Links ]
[35] Y. Gu, J. D. McCalley, and M. Ni, “Coordinating Large-Scale Wind Integration and Transmission Planning,” IEEE Trans. Sustain. Energy, vol. 3, no. 4, pp. 652-659, 2012. [ Links ]
[36] J. H. Roh, M. Shahidehpour, and Y. Fu, “Market-based coordination of transmission and generation capacity planning,” IEEE Trans. Power Syst., vol. 22, no. 4, pp. 1406-1419, 2007. [ Links ]
[37] J. H. Roh, M. Shahidehpour, and L. Wu, “Market-based generation and transmission planning with uncertainties,” IEEE Trans. Power Syst., vol. 24, no. 3, pp. 1587-1598, 2009. [ Links ]
[38] B. Kūςūkyazici, L. Ōzdamar, and S. Pokharel, “Developing concurrent investment plans for power generation and transmission,” Eur. J. Oper. Res., vol. 166, no. 2, pp. 449-468, 2005. [ Links ]
[39] A. Rouhani, S. H. Hosseini, and M. Raoofat, “Composite generation and transmission expansion planning considering distributed generation,” Int. J. Electr. Power Energy Syst., vol. 62, pp. 792-805, 2014. [ Links ]
[40] T. S. Ng and C. Sy, “An affine adjustable robust model for generation and transmission network planning,” Int. J. Electr. Power Energy Syst., vol. 60, pp. 141-152, 2014. [ Links ]
[41] B. Melián, J. A. Moreno Pérez, and J. Marcos Moreno-Vega, “Metaheuristics: A global view,” Intel. Artif., vol. 7, no. 19, pp. 7-28, 2003. [ Links ]
[42] M. S. Javadi, M. Saniei, H. R. Mashhadi, and G. Gutiérrez-Alcaraz, “Multi-objective expansion planning approach: distant wind farms and limited energy resources integration,” IET Renew. Power Gener., vol. 7, no. 6, pp. 652-668, 2013. [ Links ]
[43] A. Heidari, H. Mavalizadeh, and A. Ahmadi, “Probabilistic multi-objective generation and transmission expansion planning problem using normal boundary intersection,” IET Gener. Transm. Distrib., vol. 9, no. 6, pp. 560-570, 2015. [ Links ]
[44] K. Uhlen and L. Warland, “A Comparison of AC and DC Power Flow Models for Contingency and Reliability Analysis,” Power Syst. Comput. Conf. PSCC, pp. 1-7, 2014. [ Links ]
[45] H. Kim and W. Kim, “Integrated Optimization of Combined Generation and Transmission Expansion Planning Considering Bus Voltage Limits,” J. Electr. Eng. Technol., vol. 9, pp. 742-749, 2014. [ Links ]
[46] IAEA, “Expansion Planning for Electrical Generating Systems: A Guidebook - Technical Report Series No. 241,” Int. At. Energy Agency-IAEA, ..., no. 241, pp. 1-642, 1984. [ Links ]
[47] S. Hossein and S. S. Mohammad, Electric Power System Planning. 2011. [ Links ]
[48] D. Mejía-Giraldo, “Robust and flexible planning of power system generation capacity,” Iowa State University, 2013. [ Links ]
[49] O. J. Guerra, D. A. Tejada, and G. V Reklaitis, “An optimization framework for the integrated planning of generation and transmission expansion in interconnected power systems,” Appl. Energy, vol. 170, pp. 1-21, 2016. [ Links ]
[50] Y. Zhang, S. Zhu, and A. A. Chowdhury, “Reliability modeling and control schemes of composite energy storage and wind generation system with adequate transmission upgrades,” IEEE Trans. Sustain. Energy, vol. 2, no. 4, pp. 520-526, 2011. [ Links ]
[51] A. P. Agalgaonkar, S. V. Kulkarni, and S. A. Khaparde, “Evaluation of configuration plans for DGs in developing countries using advanced planning techniques,” Power Syst. IEEE Trans., vol. 21, no. 2, pp. 973-981, 2006. [ Links ]
[52] J. Lin, L. Cheng, Y. Chang, K. Zhang, B. Shu, and G. Liu, “Reliability based power systems planning and operation with wind power integration: A review to models, algorithms and applications,” Renew. Sustain. Energy Rev., vol. 31, pp. 921-934, 2014. [ Links ]