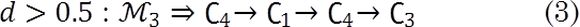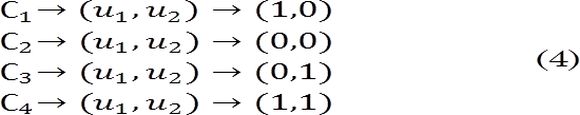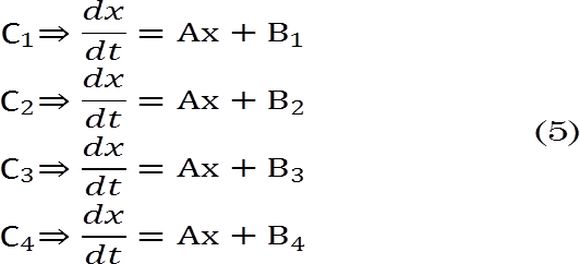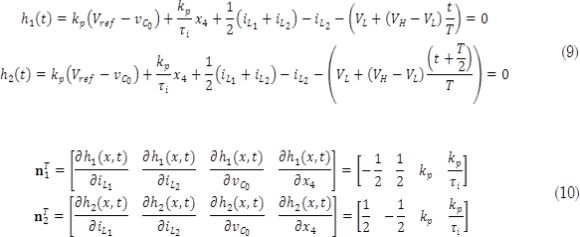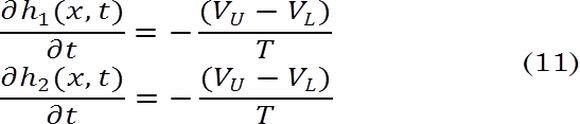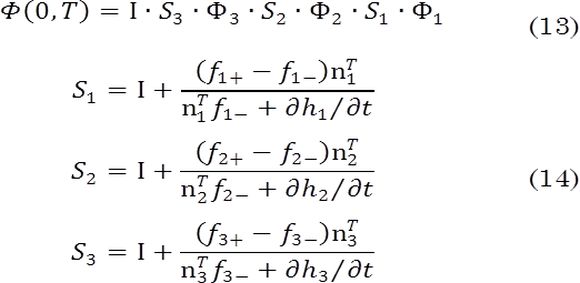Artículo de investigación/Research article

Análisis de la estabilidad de alto orden de un convertidor buck entrelazado basado en el método de Filippov

Subharmonic ripple analysis of an interleaved buck converter based on the Filippov method

Julián Peláez-Restrepo¹, Sergio I. Serna-Garcés², Carlos A. Ramos-Paja³ y Daniel González-Montoya⁴

¹ PhD. Ingeniería Electrónica, Profesor Ocasional, Departamento de Electrónica y Telecomunicaciones, Instituto Tecnológico Metropolitano, Medellín-Colombia, julianpelaez@itm.edu.co

² MSc. Ingeniería, Departamento de Electrónica y Telecomunicaciones, Instituto Tecnológico Metropolitano, Medellín-Colombia, sergioserna@itm.edu.co

³ PhD. Ingeniería Electrónica, Automática y Comunicaciones, Profesor Asociado, Departamento de Energía Eléctrica y Automática, Universidad Nacional de Colombia, Medellín-Colombia, caramosp@unal.edu.co

⁴ MSc. Ingeniería - Automatización Industrial, Profesor Ocasional, Departamento de Electrónica y Telecomunicaciones, Instituto Tecnológico Metropolitano, Medellín-Colombia, danielgonzalez@itm.edu.co

Fecha de recepción: 05 de mayo de 2016 / Fecha de aceptación: 28 de octubre de 2016

Como citar / How to cite

J. Peláez-Restrepo, S. I. Serna-Garcés, C. A. Ramos-Paja y D. González-Montoya, “Análisis de la estabilidad de alto orden de un convertidor buck entrelazado basado en el método de Filippov”, Tecno Lógicas, vol. 20, no. 38, pp. 55 - 69 enero-junio, 2017

Resumen

El diseño de convertidores conmutados en gran parte de la literatura científica está realizado desde el modelo promediado, debido a la facilidad de obtener las funciones de transferencia lineales. Asimismo, la conmutación en los convertidores de potencia causa un rizado en las variables de estado que no es considerado en el modelo promediado. El componente de frecuencia de una de las variables de estado está compuesto por un espectro de potencia con un único pico de nivel DC (valor promedio), un único pico a la frecuencia de conmutación (componente de rizado) y en un número finito de picos en cada sub-armónico (inestabilidades). El método de Filippov es utilizado para la predicción de inestabilidades debidas a las dinámicas rápidas, este método predice el rango de los parámetros que evitan la primera bifurcación en las dinámicas rápidas. En el presente artículo se presenta una predicción de un espacio de parámetros estables para el controlador PI (K_p , T_i), estimados por el método de Filippov para un convertidor buck de dos fases con regulación de voltaje. Finalmente, los resultados presentados son validados mediante simulaciones de Matlab y Psim.

Palabras clave: Convertidor multifase, diseño de controladores, método de Filippov, rizado de conmutación, sistemas lineales a tramos.

Abstract

In many papers, the averaged model of power switching converters is used to design the control system due to its simple manipulation, which can be approximated by linear transfer functions. Therefore, the power converter commutation causes a state variable ripple that is not considered on the averaged model. The component frequency of the state variables is composed by a power spectrum with a unique peak at the DC level (average variable), a unique peak at the switching frequency (ripple component) and a finite number of peaks in each sub-harmonic (instabilities). The Filippov method is used for instability predictions due to fast dynamics, this method predicts the parameters range that avoids the first bifurcation of the fast dynamics. In this paper a stable space of parameters (K_p , T_i) for a PI controller is presented, it estimated with the Filippov method, for a buck converter with voltage regulation. Finally, the presented results are validated using both Matlab and Psim simulations.

Keywords: Multi-phase converter, controller design, method of Filippov, instability, bifurcations, piecewise linear systems.

1. Introducción

El procesamiento de potencia eléctrica se realiza, principalmente, utilizando convertidores conmutados debido a su alta eficiencia, rápida respuesta, alta confiabilidad y capacidad de transformación de tensión, corriente y frecuencia (elevar, reducir, etc.) [1]. Estos convertidores son controlados por semiconductores que conmutan entre condiciones de conducción y no-conducción, lo que genera la existencia de múltiples circuitos eléctricos en diferentes instantes de tiempo. Debido a esta condición se les denomina sistemas de estructura variable (Variable Structure System - VSS) [2], [3].

A nivel operativo, los convertidores conmutados exhiben dinámicas muy rápidas, en comparación con los reguladores lineales clásicos [4]. De esta forma, los convertidores conmutados, controlados apropiadamente, tienen la capacidad de garantizar amplios anchos de banda y pequeños tiempos de respuesta requeridos por cargas modernas tales como microprocesadores, motores, vehículos, sistemas de comunicación, etc. [5]-[9]. Tradicionalmente, el diseño de controladores lineales para este tipo de convertidores se realiza utilizando un modelo promediado del convertidor [10] [11], el cual elimina la condición de conmutación para proveer un modelo continuo, lo que simplifica el diseño del controlador. Sin embargo, el modelo conmutado desprecia las variaciones de alta frecuencia, lo que limita su validez a fracciones de la frecuencia de conmutación.

Las dinámicas debidas a la conmutación, conocidas en la literatura como dinámicas rápidas [12], introducen a la forma de onda de las variables de estado un rizado con frecuencia igual a la frecuencia de conmutación, siempre y cuando el sistema sea estable. Debido a su naturaleza no-lineal, el convertidor conmutado es susceptible de operar en una condición caótica [13], [14], en la cual el rizado exhibe una forma de onda con un periodo mayor al periodo de conmutación debido a que el convertidor bifurca a una órbita periódica de mayor orden [15].

La bifurcación a una órbita periódica es indeseable, ya que introduce armónicos que incrementan la magnitud del rizado de tensión y corriente, dispersando la potencia a lo largo del espectro de frecuencia, lo que genera mayores pérdidas y menor eficiencia [16]. Por lo tanto, la operación deseada del convertidor conmutado tienen un espectro de frecuencia compuesto por un nivel DC y una componente de rizado [15] a la frecuencia de conmutación, es decir, sin armónicos adicionales debido a fenómenos de bifurcación. Finalmente, estos fenómenos de bifurcación pueden ocurrir por resonancias dentro del lazo de control [17], [18], por lo que es necesario disponer de una técnica que permita predecir la ocurrencia de la primera oscilación sub-armónica, así como el rango de parámetros del controlador dentro de los cuales el sistema es estable.

Por otra parte, los convertidores tradicionales (de una fase) se han utilizado ampliamente en aplicaciones de regulación de cargas [19]. En el caso particular de cargas de baja tensión (Point-Of-Load [19]), los convertidores tradicionales se deben construir con elementos pasivos (capacitores e inductores) excesivamente grandes para proveer los niveles de rizado requeridos por la carga, p. ej. 1% en la tensión de alimentación de microprocesadores, lo que genera un dispositivo de gran tamaño, peso y costo. Como alternativa, se desarrollaron los convertidores buck multi-fase con conmutación entrelazada, los cuales requieren elementos pasivos significativamente más pequeños [19]. Estos convertidores entrelazados requieren de un mayor número de semiconductores, lo que incrementa su complejidad de análisis y control. Este artículo presenta un método de análisis de sistemas continuos a tramos de Filippov para estimar la estabilidad de un convertidor buck entrelazado [20]-[25]. El método de análisis propuesto permite diseñar controladores para regulación de baja tensión evitando la bifurcación a una órbita indeseable.

El artículo está organizado así: en la siguiente sección se presenta el modelo matemático del convertidor buck entrelazado; posteriormente se introduce la técnica de Filippov para predecir el desdoblamiento de periodo. La aplicación de la técnica propuesta se ilustra con un ejemplo práctico; y finalmente se presentan las conclusiones y el trabajo futuro a desarrollar.

2. Convertidor buck entrelazado

El convertidor buck entrelazado (interleaved) está basada en la conexión en paralelo de convertidores buck con sus señales de control desfasadas. El principal objetivo de esta estructura es incrementar la frecuencia de trabajo efectiva en los elementos pasivos, sin incrementar la frecuencia de conmutación de las distintas células canónicas [26]. El convertidor buck entrelazado de dos fases se presenta en la Fig. 1

Un convertidor entrelazado en estado estable tiene una órbita periódica: parte de un estado inicial, y después de un tiempo igual al periodo de conmutación, regresa a ese mismo estado. Sin embargo, a lo largo del periodo de conmutación el sistema describe una trayectoria continua a tramos, donde la cantidad de tramos depende del número de fases del convertidor [27]. Para un convertidor balanceado se tiene que d₁ = d₂ = ... d_n , siendo n el número de fases. Si el ciclo de trabajo es d ≠ 1/n existirán 2_n tramos, mientras que si d = 1/n existen n tramos.

Para un convertidor buck entrelazado de dos fases (n = 2) operando en modo de conducción continua (CCM), se tienen tres posibilidades de operación: d < 1/2 , d = 1/2 y d > 1/2 , lo que define los tres modos de operación, donde C₁ , C₂ ,C₃ y C₄ representan las diferentes configuraciones eléctricas que resultan de la conmutación de los semiconductores:

Modo de operación para

Modo de operación para

Modo de operación para

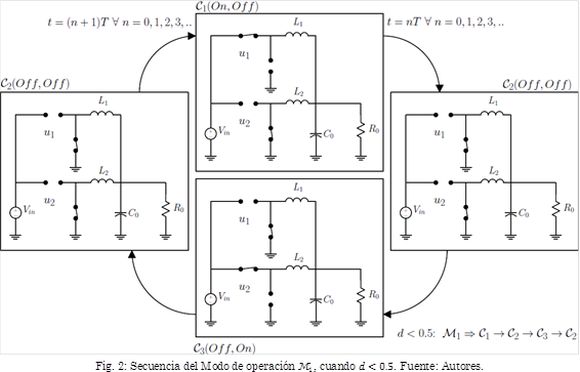
Cada configuración está determinada por las señales de conmutación de los transistores de acuerdo con (4)(véase Fig. 2).

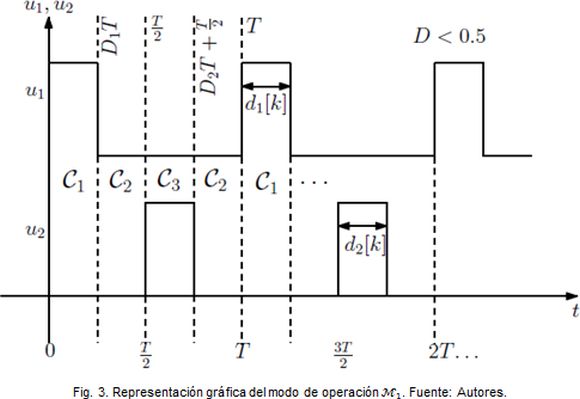
Gráficamente, el modo de operación M₁ se presenta en las Fig. 2 y Fig. 3, donde u₁(t) y u₂(t) representan las señales de activación de los transistores de la primera y segunda fase, respectivamente.

Asimismo, d₁ y d₂ representan los ciclos de trabajo de las fases, T es el periodo de conmutación, D es el valor de los ciclos de trabajo cuando el convertidor esta balanceado.

Las configuraciones se modelan matemáticamente como sistemas en espacio de estados, donde cada configuración representa la estructura topológica del convertidor después de la conmutación de uno de los transistores. Los modelos de las configuraciones del convertidor se presentan en (5).

La matriz de estados A, las cuatro matrices de entrada B₁ , B₂ ,B₃ y B₄ , y el vector de estados x, se presentan en (6). En estos espacios de estado se introduce una cuarta variable de estado x₄ para representar la integral del error de voltaje. Esta variable se requiere para estimar la parte integral del controlador PI con el cual se regulará la tensión de salida.

2.1 Método de Filippov

Si un sistema se encuentra en una condición inicial x(t₀) en un tiempo t₀, y si ese sistema tiene cuatro posibles tramos, entonces el comportamiento del sistema en un tiempo futuro t puede describirse como x(t) = Φ₄.S₃.Φ₃.S₂.Φ₂.S₁.Φ₁.x(t₀), donde Φ_n es la matriz de transición de estados y S_n es la matriz de saltación [20]. Si el sistema es continuo, y continuamente derivable, la matriz total de transición de estados es Φ = Φ₄.Φ₃.Φ₂.Φ₁. Sin embargo, debido a que el convertidor buck entrelazado presenta discontinuidades en los tiempos de conmutación, su modelo es continuo a tramos y la matriz total de transición de estados se convierte en Φ = Φ₄.S₃.Φ₃.S₂.Φ₂.S₁.Φ₁.

La matriz de transición de estado es función de los tiempos inicial y final, por lo que la matriz de transición de estados se define como (7).

En (5) A es la matriz del sistema en el espacio de estados representado como ẋ = A_n^x + B_n. Definiendo la matriz de saltación como la matriz que relaciona la perturbación antes y después del instante de conmutación, se obtiene (8).

donde I es la matriz identidad con un orden proporcional al número de variables de estado del modelo del convertidor. En este caso, h(x,t) = 0 representa la condición de conmutación, la cual sucede cuando el voltaje de control y la señal diente de sierra del modulador de ancho de pulso [20] son iguales (ver Fig. 1): h(x,t) = v_con(t) - v_tri(t) = 0, siendo v_tri = V_L + (V_H - V_L)mod(t/T, 1). Típicamente V_H = 1 y V_L = 0 debido a que el ciclo de trabajo siempre está restringido por esos valores. Mientras que el periodo de conmutación se representa por T.

Para el caso de un convertidor buck entrelazado existen n señales de control, es decir una señal de control por cada fase, donde las señales diente de sierra tienen un desfase de Φ = 2_Πk/n con k = 1, 2, 3, ..., (n-1). Esto implica que el convertidor buck entrelazado de dos fases tiene las siguientes condiciones de conmutación, donde n^T es un vector normal con respecto a cada una de las variables de estado reportado en (10).

Finalmente, ∂h(x,t)/∂t es la tasa de cambio de la condición de conmutación con respecto al tiempo reportada en (11).

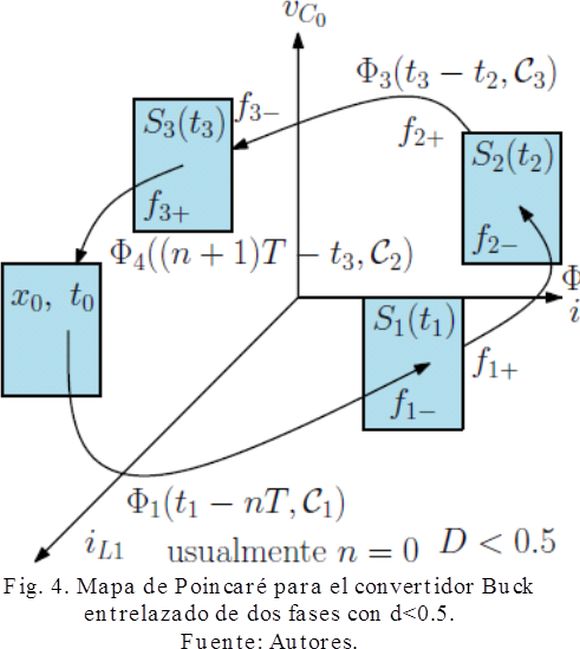
El mapa de Poincaré para el convertidor buck entrelazado de dos fases con d < 0.5 se presenta en la Fig. 4, el cual describe la evolución del sistema. En este mapa t₀, t₁, t₂, t₃ son los instantes de conmutación, es decir, los puntos de trabajo donde el sistema cambia de estructura. Asimismo, S1, S2 y S3 son las matrices de saltación.

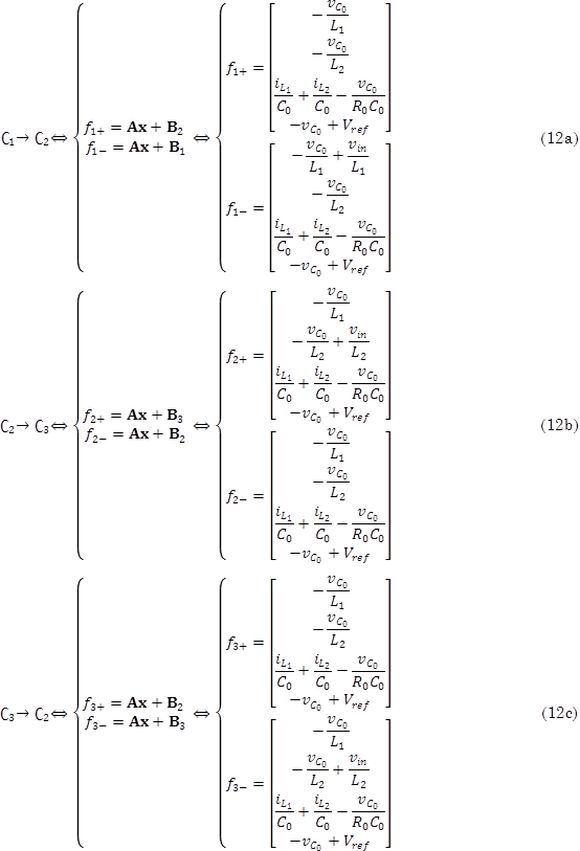
A partir de este mapa se definen las fronteras de conmutación, donde f_n+ representa el valor hacia donde tiende el límite del modelo antes de un cambio de estructura por la derecha, y f_n- representa un cambio de estructura por la izquierda, con C_n siendo una configuración dada por (12a) a (12c).

Finalmente, la matriz de monodromía para un el convertidor buck entrelazado de dos celdas se define como se muestra en (13).

La matriz de monodromía se compone de varias matrices de transición de estados, las cuales modelan el comportamiento dinámico suave del sistema, y las matrices de saltación modelan el comportamiento dinámico debido a la conmutación (14). Si el sistema no cambiara bruscamente (debido a las discontinuidades) la matriz de monodromía solo tendría matrices de transición de estados.

Si la magnitud de los auto valores de la matriz de monodromía es menor que la unidad, el sistema es estable [20]-[24]. En todo caso, al considerar un controlador tradicional PI, el integrador puro impone uno de los auto valores con magnitud igual a +1, pero la estabilidad del sistema se asegura al imponer los auto valores restantes una magnitud menor a la unidad.

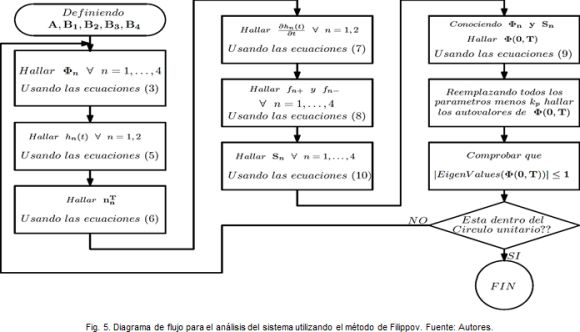
En la Fig. 5 se puede observar un diagrama de flujo que representa todos los cálculos que se deben realizar con el fin de analizar el sistema bajo los criterios del método de Filippov.

3. Ejemplo de aplicación

Para ilustrar la aplicabilidad del método presentado anteriormente, se considera un convertidor buck entrelazado controlado por un controlador PI G_PI(s) = k_p(1+1/(t_i s)). Inicialmente se analiza la estabilidad con un controlador PI dado, para luego presentar el diseño de un controlador PI que asegure la ausencia de bifurcación (estabilidad).

Considerando el convertidor buck entrelazado de dos fases de la Fig. 1 con los valores de parámetros dados en (15), cuyo punto de equilibrio es dado por (16). Asimismo, los parámetros del control PI a evaluar son [k_p = 40 , t_i = 0.1].

Los auto-valores del sistema deben tener una magnitud menor que la unidad para que el sistema sea estable, como se muestra en (20) y (21).

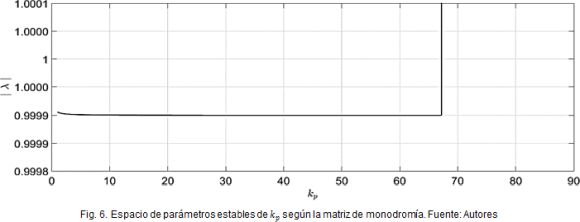
Para analizar la sensibilidad de la ganancia k_p se evalúa el mayor auto-valor, el cual debe tener una magnitud menor que la unidad. La Fig. 6 presenta la variación de ese auto valor con respecto a k_p, donde se predice el espacio de valores de k_p que garantizan estabilidad (evitan bifurcación).

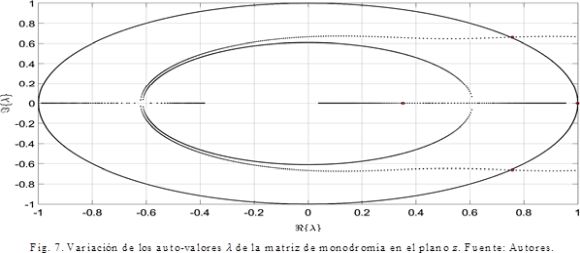
La Fig. 7 presenta todos los auto-valores de la matriz de monodromía en el plano complejo, los cuales residen dentro del circulo unitario siempre que k_p < 67.3. Si k_p = 67.3 los auto-valores llegan a la frontera del circulo unitario (frontera de estabilidad), y para k_p > 67.3 los auto-valores salen del circulo unitario.

Finalmente, con el objetivo de diseñar un controlador PI que asegure estabilidad de baja frecuencia y de rizado (esto es, se evite la bifurcación), se varían los parámetros k_p y t_i del controlador PI. El resultado de ese procedimiento se observa en la Fig. 8, donde la línea representa la frontera de estabilidad, y todo controlador cuyos parámetros estén con valores incluidos bajo esa curva aseguran la estabilidad general.

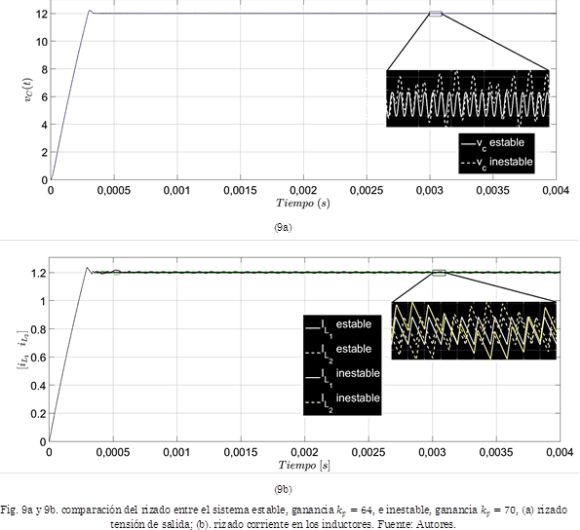
La validez del análisis presentado en la Fig. 8 se verifica con las simulaciones presentadas en las Fig. 9a y 9b: en la Fig. 9a se observa el rizado de tensión de un convertidor con control de tensión PI en la zona estable (k_p = 64 y t_i = 0.1 _s), línea continua, y un controlador en la zona inestable (k_p = 70 y t_i = 0.1 _s), línea discontinua. Se puede evidenciar claramente que el rizado del convertidor con control en la zona estable tiene forma sinusoidal, mientras que el rizado del convertidor en la zona inestable es bastante irregular, lo que evidencia la existencia de armónicos diferentes a los de la frecuencia de conmutación aparente, 200 kHz. Estos armónicos son los introducidos por la bifurcación. En la Fig. 9b se observa la misma comparación, pero para el rizado de corriente de cada una de las fases del convertidor entrelazado (línea blanca convertidor en zona estable y línea amarilla convertidor en zona inestable). Los rizados de corriente de cada fase son complementarias para el caso estable, lo que no se cumple para el caso inestable. Esto evidencia los armónicos introducidos por la bifurcación.

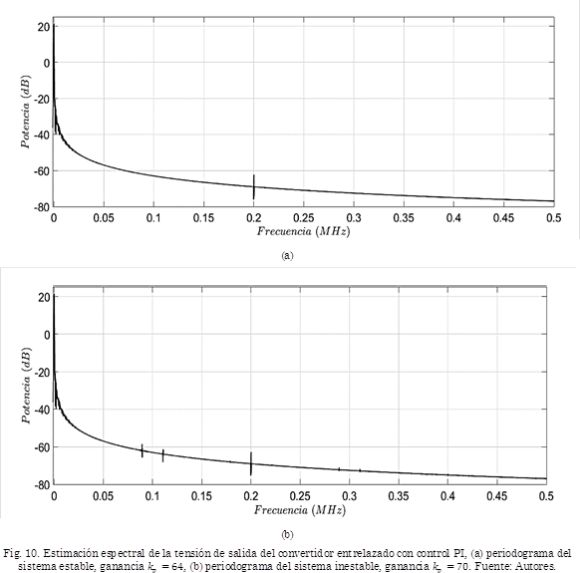
En las Fig. 10a y 10b se observan los espectros de la tensión de salida del sistema en la zona estable e inestable, respectivamente. El sistema estable muestra el rizado únicamente en 200 kHz, lo que se corresponde con la señal temporal de la Fig. 9a, donde se muestra que el rizado de tensión del sistema estable tiene forma sinusoidal pura. Por otra parte, en la Fig. 10b se evidencian las dinámicas caóticas subarmónicas que se presentan en el rizado debido a las bifurcaciones, por ejemplo, existe un armónico en 100 kHz y alrededor de este una doble banda lateral. Además, se presentan armónicos de orden superior, en 300 kHz y 40 kHz, aunque de mucha menor amplitud. Esta energía que se dispersa a través del espectro es parte de las pérdidas debido a la bifurcación, lo que hace al sistema con esta inestabilidad, menos eficiente.

Finalmente, este ejemplo hace evidente la utilidad del método de análisis para diseñar controladores que eviten la degradación de las señales de rizado (bifurcación), lo cual permite la operación eficiente y segura del convertidor.

4. Conclusiones

Se realizó un análisis de la estabilidad de un convertidor buck entrelazado de dos fases con un controlador PI en modo de voltaje, y se demostró como los valores de los parámetros del convertidor pueden afectar la estabilidad del sistema. En este caso particular, se escogió como parámetros la ganancia proporcional y el tiempo integral del control PI, y aplicando el método de Filippov, se determinó un espacio de parámetros que aseguran la estabilidad del sistema. A medida que se incrementa la ganancia proporcional del controlador PI las oscilaciones del rizado y la dispersión de la potencia a través del espectro es mucho mayor, lo que deteriora la calidad, la estabilidad y la eficiencia del sistema. Este análisis demuestra que el diseño de un controlador debe considerar tanto las dinámicas de regulación y conmutación para asegurar un correcto funcionamiento con el menor número de armónicos posible. Finalmente, este método puede extenderse a un mayor número de fases, así como a otras topologías de convertidores.

5. Agradecimientos

Este trabajo fue soportado por el Instituto Tecnológico Metropolitano, la Universidad Nacional de Colombia y Colciencias (Fondo nacional de financiamiento para la ciencia, la tecnología y la innovación, Francisco José de Caldas) a través de los proyectos P14105, P14215, UNAL-ITM-26283 y MicroRENIZ-25439 (Código 1118-669-46197) y de la beca doctoral 012-567.

Referencias

[1] R. W. Erickson and D. Maksimoviċ, Fundamentals of Power Electronics. Boston, MA: Springer US, 2001.         [ Links ]

[2] D. Biel, E. Fossas, and R. Ramos, “Sliding mode control multiphase Buck converter implementation issues,” in 2010 11th International Workshop on Variable Structure Systems (VSS), 2010, pp. 434-439.         [ Links ]

[3]C.M. Liaw, Y.M. Lin, and K.H. Chao, “A VSS speed controller with model reference response for induction\nmotor drive,” IEEE Trans. Ind. Electron., vol. 48, no. 6, pp. 1136-1147, 2001.         [ Links ]

[4] H. J. Zhang, “Basic Concepts of Linear Regulator and Switching Mode Power Supplies,” Milpitas, CA, 2013.         [ Links ]

[5] M. Orabi and A. Shawky, “Proposed Switching Losses Model for Integrated Point-of-Load Synchronous Buck Converters,” IEEE Trans. Power Electron., vol. 30, no. 9, pp. 5136-5150, Sep. 2015.         [ Links ]

[6] V. Bist and B. Singh, “A reduced sensor PFC BL-Zeta converter based VSI fed BLDC motor drive,” Electr. Power Syst. Res., vol. 98, pp. 11-18, May 2013.         [ Links ]

[7] A. Mansour, B. Faouzi, G. Jamel, and E. Ismahen, “Design and analysis of a high frequency DC-DC converters for fuel cell and super-capacitor used in electrical vehicle,” Int. J. Hydrogen Energy, vol. 39, no. 3, pp. 1580-1592, Jan. 2014.         [ Links ]

[8] Z. Wang, B. Liu, Y. Zhang, M. Cheng, K. Chu, and L. Xu, “The Chaotic-Based Control of Three-Port Isolated Bidirectional DC/DC Converters for Electric and Hybrid Vehicles,” Energies, vol. 9, no. 2, p. 83, Jan. 2016.         [ Links ]

[9] A. D. Martin, J. M. Cano, J. F. A. Silva, and J. R. Vázquez, “Backstepping Control of Smart Grid-Connected Distributed Photovoltaic Power Supplies for Telecom Equipment,” IEEE Trans. Energy Convers., vol. 30, no. 4, pp. 1496-1504, Dec. 2015.         [ Links ]

[10] R. Priewasser, M. Agostinelli, C. Unterrieder, S. Marsili, and M. Huemer, “Modeling, Control, and Implementation of DC - DC Converters for Variable Frequency Operation,” IEEE Trans. Power Electron., vol. 29, no. 1, pp. 287-301, Jan. 2014.         [ Links ]

[11] L. Guo, J. Y. Hung, and R. M. Nelms, “Comparative evaluation of sliding mode fuzzy controller and PID controller for a boost converter,” Electr. Power Syst. Res., vol. 81, no. 1, pp. 99-106, Jan. 2011.         [ Links ]

[12] Yanfeng Chen, C. K. Tse, Shui-Sheng Qiu, L. Lindenmuller, and W. Schwarz, “Coexisting Fast-Scale and Slow-Scale Instability in Current-Mode Controlled DC/DC Converters: Analysis, Simulation and Experimental Results,” IEEE Trans. Circuits Syst. I Regul. Pap., vol. 55, no. 10, pp. 3335-3348, Nov. 2008.         [ Links ]

[13] J. D. Morcillo-Bastidas, “Analysis and bifurcations of a dc-dc buck converter controlled by sine wave,” Universidad Nacional de Colombia - Sede Manizales, 2012.         [ Links ]

[14] C. Yfoulis, D. Giaouris, F. Stergiopoulos, C. Ziogou, S. Voutetakis, and S. Papadopoulou, “Robust constrained stabilization of boost DC-DC converters through bifurcation analysis,” Control Eng. Pract., vol. 35, pp. 67-82, Feb. 2015.         [ Links ]

[15] J. K. Hunter, Introduction to Dynamical Systems, 1st ed. Davis, CA 95616: Department of Mathematics, University of California at Davis, 2011.         [ Links ]

[16] J. H. B. Deane and D. C. Hamill, “Instability, subharmonics, and chaos in power electronic systems,” IEEE Trans. Power Electron., vol. 5, no. 3, pp. 260-268, Jul. 1990.         [ Links ]

[17] L. Wei-Guo, X. Ping-Ye, Z. Luo-Wei, and L. Quan-Ming, “Bifurcation Control of Current-Mode Buck Converter via TDFC,” Chinese Phys. Lett., vol. 27, no. 3, p. 30501, Mar. 2010.         [ Links ]

[18] M. Kamyar, “Modeling and stability analysis of closed loop current-mode controlled Cuk converter using Takagi-Sugeno fuzzy approach,” in 2nd IFAC Conference on Analysis and Control of Chaotic Systems, 2009, pp. 223-228.         [ Links ]

[19] S. I. Serna-Garcés, R. E. Jiménez, and C. A. Ramos-Paja, “Sliding-Mode Control of a Dc/Dc Postfilter for Ripple Reduction and Efficiency Improvement in POL Applications,” J. Appl. Math., vol. 2013, no. Article ID 915146, p. 10 pages, 2013.         [ Links ]

[20] D. Giaouris, S. Banerjee, B. Zahawi, and V. Pickert, “Stability Analysis of the Continuous-Conduction-Mode Buck Converter Via Filippov's Method,” IEEE Trans. Circuits Syst. I Regul. Pap., vol. 55, no. 4, pp. 1084-1096, May 2008.         [ Links ]

[21] D. Giaouris, S. Maity, S. Banerjee, V. Pickert, and B. Zahawi, “Application of Filippov Method For The Analisys Of Subharmonic Instability in DC-DC Converters,” Int. J. Circuit Theory Appl., no. 37, pp. 899-919, 2008.         [ Links ]

[22] I. Daho, D. Giaouris, B. Zahawi, V. Picker, and S. Banerjee, “Stability analysis and bifurcation control of hysteresis current controlled CUK converter using Filippov's method,” in 4th IET International Conference on Power Electronics, Machines and Drives (PEMD 2008), 2008, pp. 381-385.         [ Links ]

[23] O. Imrayed, I. Daho, and H. M. Amreiz, “Controlling Nonlinear Behavior in Current Mode Controlled Boost Converter Based on the Monodromy Matrix,” Conf. Pap. Eng., vol. 2013, pp. 1-7, 2013.         [ Links ]

[24] B. Zahawi, N. C. Okafor, S. Banerjee, and D. Giaouris, “Analysis of fast-scale instability in dc drives with full-bridge converter using Filippov's method,” in 5th IET International Conference on Power Electronics, Machines and Drives (PEMD 2010), 2010, pp. 235-235.         [ Links ]

[25] R.A. A. López and G.O. Londoño, “Stability analysis of a photovoltaic system with DC/DC flyback converter using Filippov's method,” in Alternative Energies and Energy Quality (SIFAE), 2012 IEEE International Symposium on, 2012, pp. 1-4.         [ Links ]