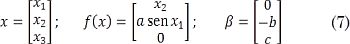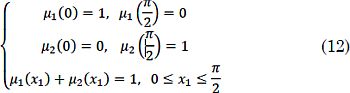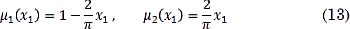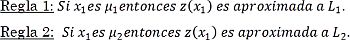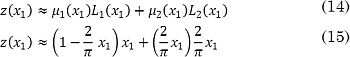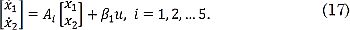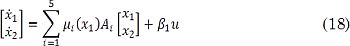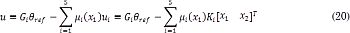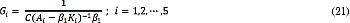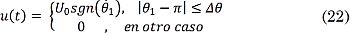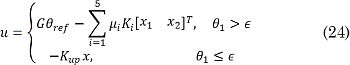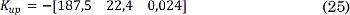Artículo de investigación/Research article

Control difuso del péndulo invertido con rueda de reacción usando seguimiento de trayectoria

Fuzzy control of an inverted pendulum Driven by a reaction wheel using a trajectory tracking scheme

Víctor Daniel Correa-Ramírez¹, Didier Giraldo-Buitrago² y Andrés Escobar-Mejía³

¹ MSc en Ingeniería Eléctrica, Facultad de Ingenierías Eléctrica, Electrónica, Física y Ciencias de la Computación, Programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira, Pereira-Colombia, victordc@utp.edu.co

² MSc en Ingeniería Eléctrica, Facultad de Ingenierías Eléctrica, Electrónica, Física y Ciencias de la Computación, Programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira, Pereira-Colombia, dgiraldo@utp.edu.co

³ PhD en Ingeniería Eléctrica, Facultad de Ingenierías Eléctrica, Electrónica, Física y Ciencias de la Computación, Programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira, Pereira-Colombia, andreses1@utp.edu.co

Fecha de recepción: 18 de agosto de 2016 / Fecha de aceptación: 15 de marzo de 2017

Como citar / How to cite

V.D. Correa-Ramírez, D. Giraldo-Buitrago y A. Escobar-Mejía, “Control difuso del péndulo invertido con rueda de reacción usando seguimiento de trayectoria”, TecnoLógicas, vol. 20, no. 39, mayo - agosto, 2017.

Resumen

En este trabajo se presenta el diseño de un controlador difuso Takagi-Sugeno (T-S), con un esquema de seguimiento de trayectoria para el sistema conocido como péndulo con rueda de reacción. A partir del modelo de estados no lineal, se definen los puntos de operación donde el sistema funcionará y se aplica la técnica de linealización por no linealidad sectorial con el fin de implementar reguladores lineales locales. Con los modelos linealizados reducidos y con base en las características dinámicas deseadas de lazo cerrado, se diseñan los reguladores locales que, al ser combinados, usando las funciones de pertenencia del modelo difuso, generan la señal de control global que contiene dos términos: el regulador y el seguimiento simple de la referencia.

El controlador difuso propuesto logra llevar el péndulo desde su posición de equilibrio natural a la posición invertida de forma gradual, con oscilaciones de amplitud creciente y con mínimo error de seguimiento. Cuando el péndulo alcanza la posición deseada invertida, se usa un regulador sobre el modelo linealizado completo alrededor del punto de operación. Los resultados de simulación muestran el seguimiento de la trayectoria angular (del péndulo) y el desempeño del controlador ante pequeñas perturbaciones. La señal de control y la velocidad angular de la rueda son presentadas con el fin de verificar que se mantienen dentro de los límites de operación establecidos. Si bien se presenta saturación en la señal de control, se obtiene un error de seguimiento menor a 0,22 radianes.

Palabras clave: Péndulo con rueda de reacción, no-linealidad sectorial, control difuso Takagi-Sugeno, compensación distribuida paralela, seguimiento de trayectoria.

Abstract

In this work, the design of a Takagi-Sugeno Fuzzy controller with a trajectory-tracking scheme for the reaction wheel pendulum is presented. By using the nonlinear state-space model, the system’s operating points are defined, then, the sector nonlinearity method is applied to obtain a linearized model of the system in order to implement linear local regulators. Once the reduced linearized models are obtained, and based on the desired closed loop response, local regulators are designed to generate the global control signal. This signal comprises two terms: The regulator and the reference tracking term.

The proposed Fuzzy controller allows the pendulum to reach the upright position from its natural state by swinging it up with minimum tracking error. Once the upright position is reached, a regulator is implemented to operate over the linearized model around the operating point (i.e., upright position). Simulation results present both, the tracking of the angular trajectory and the controller behavior during small perturbations. It is shown that the control signal and the wheel speed remain within their boundaries. Although the control signal saturates, a tracking error less than 0.22 radians is observed.

Keywords:Reaction wheel pendulum, sector nonlinearity, Takagi-Sugeno fuzzy control, parallel distributed compensation, trajectory tracking.

1. Introducción

Los sistemas mecánicos tipo péndulo invertido son ampliamente empleados como prototipos de prueba para validar la funcionalidad de diversas estrategias de control lineales y no lineales. Entre sus diferentes variantes se encuentran el modelo clásico de péndulo sobre un carro con desplazamiento lineal, el péndulo con base rotacional de Furuta, modelos con dos y tres barras, Pendubot, Acrobot, etc. [1]. Aplicaciones prácticas como los robots caminantes, los cohetes y el dispositivo de transporte personal Segway, entre otros, tienen dinámicas similares a la del péndulo invertido. Algunos trabajos, como [1] y [2], han propuesto un tratamiento integrado de dichos sistemas.

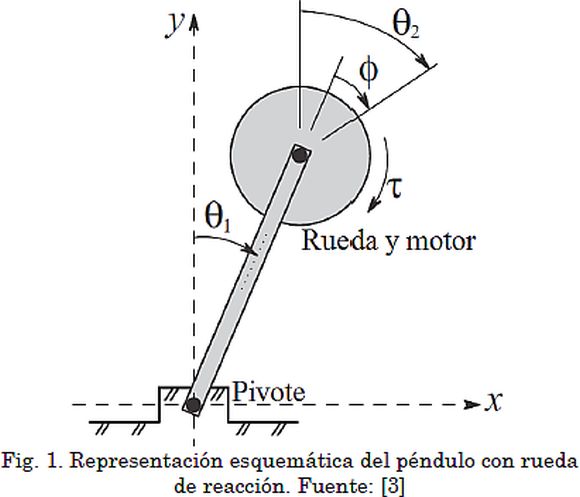
El péndulo con rueda de reacción consta de una barra que puede girar libremente alrededor del punto de apoyo (pivote) en uno de sus extremos, como se muestra en la Fig. 1. El motor acoplado al extremo opuesto del pivote actúa sobre una rueda de inercia con la cual se controlan las oscilaciones de la barra, debido al torque de reacción. El ángulo θ₁ del péndulo (respecto a la vertical) y el ángulo φ entre el péndulo y la rueda se miden con sensores ubicados en ambos ejes de giro. La rueda de inercia forma con la vertical un ángulo (absoluto) θ₂ que se obtiene como θ₂= φ + θ₁. El torque τ se obtiene de la acción directa del motor sobre la rueda.

Debido a la naturaleza altamente no lineal de estos sistemas, las estrategias de control lineal convencionales solo son efectivas cuando el sistema empieza a operar alrededor de valores cercanos a su punto de operación y cuando solo suceden pequeñas perturbaciones alrededor de los puntos de equilibrio. Al ser sistemas subactuados (i.e., el número de entradas de control es inferior a sus grados de libertad), no es posible mantener la barra (o barras) en posiciones diferentes a la vertical, lo que implica que los ángulos solo pueden ser llevados a los valores de equilibrio estable o inestable en estado estacionario. La tarea de llevar automáticamente un péndulo desde su posición de equilibrio natural (θ₁ = ± π) a la posición invertida (θ₁ = 0, ± 2π...), implica el uso de técnicas no lineales, debido a que las variables del sistema toman valores en rangos amplios y no alrededor de un punto de operación. En la mayoría de implementaciones, las limitaciones prácticas (valores límite de la señal de control, torque máximo del motor, etc.) hacen que no sea posible llevar el péndulo desde su posición de equilibrio natural a la posición invertida de forma directa, a menos que se haga manualmente. Entre las estrategias más usadas para lograr una subida gradual con oscilaciones de amplitud creciente, se encuentran el seguimiento de trayectoria [3], [4] (donde los autores implementan la técnica de linealización parcial por realimentación) y la regulación de energía, como en [5]. En contraste, en el presente trabajo se propone un método alterno de linealización, la no linealidad sectorial, y se usa un modelo difuso tipo T-S para combinar los diferentes reguladores lineales que permiten alcanzar la posición invertida de manera gradual. El control difuso para el péndulo invertido ha sido ampliamente implementado con resultados satisfactorios, tanto simulados como prácticos, recientemente, para el péndulo con rueda de reacción se pueden mencionar trabajos como [6], en el que los autores implementan un controlador difuso local con base en el error y la derivada del error en el ángulo del péndulo (desviación de la posición cero), la señal de control s define con base en una memoria asociativa difusa. En [7] se consideran varios modelos del sistema y dentro de las estrategias de control local implementadas los autores muestran resultados experimentales y de simulación de un controlador difuso.  Se puede resaltar del actual trabajo la idea de seguir una trayectoria en todo el rango de operación, con lo que el control no es local. Un análisis histórico y del estado del arte para el control del péndulo de Furuta y otros modelos, incluyendo el péndulo con rueda de reacción se puede observar en [8].

En este artículo se presentan el modelo de la planta y la estrategia de control difuso implementada en la sección 2 (Metodología). Posteriormente en la sección 3 se muestran y analizan los resultados obtenidos, finalmente se establecen las conclusiones con base en dichos resultados en la sección 4.

2. Metodología

El esquema de control que se propone se basa en el modelo no lineal del sistema, del cual se obtienen linealizaciones alrededor de distintos puntos de operación con el enfoque de no linealidad sectorial (sector nonlinearity) propuesto en [9]. El objetivo de generar modelos de estado lineales locales es aprovechar la relativa facilidad con que se diseñan reguladores de la forma u = -K_x [10], [11], siendo K un vector fila de ganancias. Estos reguladores tienen también una validez local, pero su combinación difusa resulta en un controlador para todo el rango de operación establecido.

En la literatura analizada, los autores usan la mecánica de Lagrange para obtener modelos de los diferentes sistemas tipo péndulo, con esto se evita el uso de vectores necesario cuando se aplica la mecánica newtoniana. Las ecuaciones dinámicas que se obtienen según lo desarrollado en [3] son:

En donde las constantes a, b y c, dependen de los parámetros físicos del sistema, tales como las masas, inercias, longitudes, parámetros del motor, etc. La señal de control u se establece como un valor proporcional a la corriente aplicada al motor. No se incluye la fricción en los ejes de rotación, ya que normalmente es muy baja y puede despreciarse para simplificar el modelo. La rueda de inercia es simétrica con respecto a su eje y por tanto el valor del ángulo θ₂ no tiene efecto sobre la dinámica del sistema o sus condiciones de equilibrio. Este hecho permite proponer un modelo de estados de orden tres con las variables x₁ = θ₁ (ángulo del péndulo), x₂ = θ'₁ (velocidad angular del péndulo) y x₃ = θ'₂ (velocidad angular de la rueda). Al derivar estas variables y usando (1) y (2) se obtiene el modelo no lineal de estados para el péndulo con rueda de reacción:

Se observa además que (3) y (4) están desacopladas de (5) con respecto a las variables de estado, este hecho se usa posteriormente para diseñar reguladores reducidos. La representación vectorial del anterior modelo se escribe de la forma:

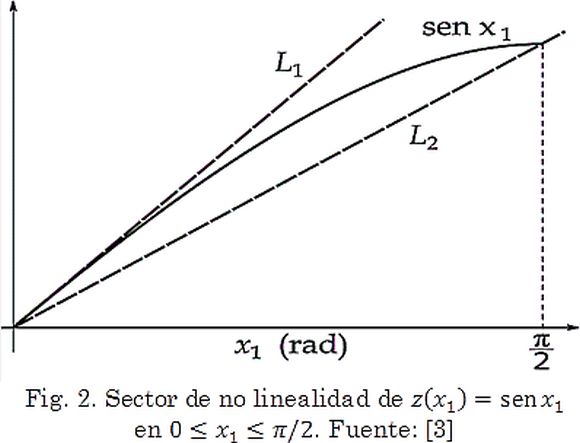
Cuando un sistema admite este tipo de modelo se dice que es lineal en el control o “afín” [12], [13]. En (6), x es el vector de estados, f(x) es una función no lineal de x (debido al término sen x₁) y β un vector constante. Entonces:

De manera intuitiva se puede establecer que los puntos de equilibrio del péndulo son su posición natural abajo (θ₁ = ± π) y su posición invertida (θ₁ = 0, ± 2π) siendo la primera estable y la segunda inestable respectivamente. El procedimiento para obtener estos puntos consiste en resolver (como se expone en [13]):

ya que con una señal de entrada nula (u = 0), esta condición será, según (6), equivalente a x' = 0, lo que implica que los estados tendrán un valor fijo. Las soluciones de (8) para la función f(x) de (7) son las dadas en (9):

Con estos resultados y revisando la Fig. 1, se concluye que los puntos de equilibrio del péndulo son exactamente las dos posiciones verticales (natural e invertida).

2.2 Método de linealización y modelo difuso

La linealización clásica usando el polinomio de Taylor de primer orden (hiperplano tangente) [10], genera modelos válidos alrededor de un punto de operación con expresiones como:

En las que Δx = x - x₀ y Δu = u - u₀, son las desviaciones de los estados y de la señal de control de sus valores en el punto de operación respectivamente. La matriz A el vector β contienen las sensibilidades de las no linealidades con respecto a x y u evaluadas en el punto de operación.

En este trabajo se usa el enfoque alternativo propuesto en [9], en el cual el hiperplano usado pasa por el punto de operación deseado y por el origen, con base en el sector que ocupan las no linealidades del modelo. Como ilustración, considere la función z(x₁) = sen x₁ en 0 ≤ x₁ ≤ π/2. Tomando las rectas L₁(x₁)= x₁(que es tangente a z(x₁) en el origen), y L₂(x₁) = 2x₁/π (que pasa por el origen y el punto ( π/2, 1)), se puede comprobar, como lo ilustra la Fig. 2, que en el intervalo establecido se cumple la desigualdad:

Para obtener una aproximación difusa de z(χ₁) con las rectas L1 y L2, se definen las etiquetas “x1 es cercano a cero” y “x1 es cercano a π/2” con funciones de pertenencia μ₁(x₁) y μ₂(x₁) respectivamente, las cuales deben cumplir las condiciones que se establecen en:

Estas funciones pueden definirse de diversas formas, por simplicidad se usaron rectas y sus ecuaciones se obtienen de (12), las cuales se presentan en (13), con un rango de validez 0 ≤ x₁ ≤ π/2.

Las reglas para el modelo difuso se plantean como:

El modelo T-S resultante para aproximar la función no lineal , con una defusificación tipo suma de productos, se expresa como:

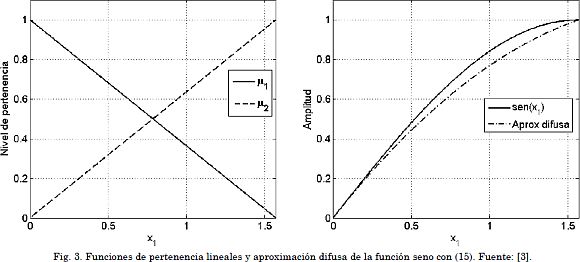
En la Fig. 3 se presentan las funciones de pertenencia μ₁(x₁) y μ₂(x₁) definidas en (13), así como la comparación entre la función sen x₁ y la aproximación propuesta en (15). Aunque el nivel de aproximación es aceptable, es posible mejorarlo definiendo rectas y funciones de pertenencia intermedias en el rango de trabajo 0 ≤ x₁ ≤ π/2.

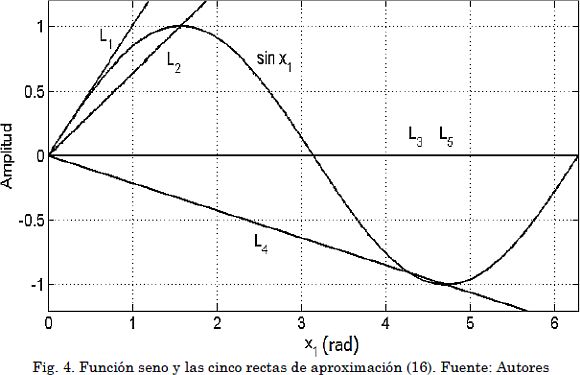
El enfoque de seguimiento de trayectoria que se propone más adelante, requiere un rango amplio de operación (0 ≤ x₁ ≤ π/2 o incluso ángulos negativos), por lo cual se aplica el método de linealización descrito en los ángulos cuadrantales, es decir, en los valores x⁰₁ = 0, π/2, π, 3π/2, 2π. Alrededor de cada ángulo, la función seno se aproxima por una recta que pasa por (0,0) y el punto (x₁⁰, sen x₁⁰). En x₁⁰ = 0 se usa la recta tangente y la aproximación general se obtiene con la combinación difusa de las anteriores. La Fig. 4 presenta la función seno y las rectas de aproximación en el rango 0 ≤ x₁ ≤ 2π. Las ecuaciones de dichas rectas se especifican como:

Del modelo de estados (3), (4) y (5), se puede observar que las dos primeras ecuaciones son independientes de x₃. Este hecho es utilizado para implementar el seguimiento de trayectoria, con base en (3) y (4), para el levantamiento del péndulo. Cuando este haya alcanzado la posición invertida, se utiliza regulación lineal sobre todas las variables de estado. Para cada uno de los cinco puntos de operación definidos, se obtienen los modelos de estado lineales reducidos (para las variables x₁ y x₂) que tienen la forma general dada:

El vector β=[0 = -b]^T es común a todos los modelos, las matrices Ai asociadas a los puntos de operación se presentan en la Tabla 1, donde también se especifican las aproximaciones correspondientes a la no linealidad.z

El modelo de estados global aproximado resulta de la combinación difusa de los cinco modelos anteriores, como se presenta en [9]:

En la cual las funciones de pertenencia μ₁(x₁) tienenla etiqueta “ x₁ es cercana a (i - 1)π/2 ”, i = 1, 2,... 5. El conjunto de reglas para la construcción de los modelos tiene la siguiente forma general:

Las funciones μ₁(x₁) usadas tienen forma triangular simétrica, como se ilustra en la Fig. 5, con base Δx₁ = π y están centradas en los diferentes puntos de linealización, μ₁ y μ₅ son solo mitades de triángulo por estar en los extremos del intervalo de trabajo 0 ≤ x₁ ≤ 2π.

2.3 Compensación distribuida paralela

Por simplicidad, se definieron polos de lazo cerrado comunes a todos los modelos representados en (17), con base en parámetros de sobrepaso (M_p) y tiempo de establecimiento (t_s) ajustados en la etapa de diseño. De igual forma, se trata de mantener la señal de control dentro de sus valores límites garantizando siempre una respuesta aceptable. Para cada uno de los modelos en (17), se calculan las ganancias de los reguladores u_i = -K_i[x₁ x₂]^T (con base en los polos deseados) usando la fórmula de Ackerman [10], que para el caso de segundo orden tiene la expresión (19):

En la cual W_i = [β₁ A_iβ₁] es la matriz de controlabilidad de cada modelo y Δ(s) es el polinomio deseado de lazo cerrado. Usando las funciones de pertenencia descritas en la Fig. 5, la expresión global para la señal de control puede escribirse como en (20), donde se realiza la defusificación por suma de productos.

La componente G_iθ_ref se incluye como un esquema simple de seguimiento de la trayectoria θ_ref que se especifica en el siguiente apartado. El valor de las ganancias G_i, que permiten seguir sin error una referencia constante, se obtienen como en (21) según [10].

Aunque en este caso el ángulo de referencia no es constante, estas ganancias permiten su seguimiento con un grado de error aceptable. Para los diferentes modelos lineales se obtiene el mismo valor G si se definen polos de lazo cerrado comunes.

2.4 Diseño de la trayectoria

En teoría, el regulador difuso lleva los estados del sistema desde una condición inicial dada a cero de forma directa. En la práctica, dado que la señal de control tiene limitaciones en sus valores extremos, en este trabajo se implementa un seguimiento de trayectoria. En el modelo propuesto, se toma la posición invertida (θ₁ = 0) como referencia para la medida del ángulo del péndulo. La posición de equilibrio natural se establece como θ₁ = ± π de forma general θ₁ = (2_n - 1)π; n ∈ Ζ.

Considerando la posición inicial θ₁ = π (equilibrio natural), se genera mediante simulación la trayectoria a seguir teniendo en cuenta que es posible hacer oscilar, el péndulo con una amplitud creciente si se aplica una señal de control constante y cuyo signo depende de la velocidad de la barra [14]. Esta entrada se aplica al sistema en una vecindad de tamaño ajustable Δθ alrededor del ángulo inicial. La entrada de control que permite dicha oscilación, según la descripción anterior, tiene la expresión (22):

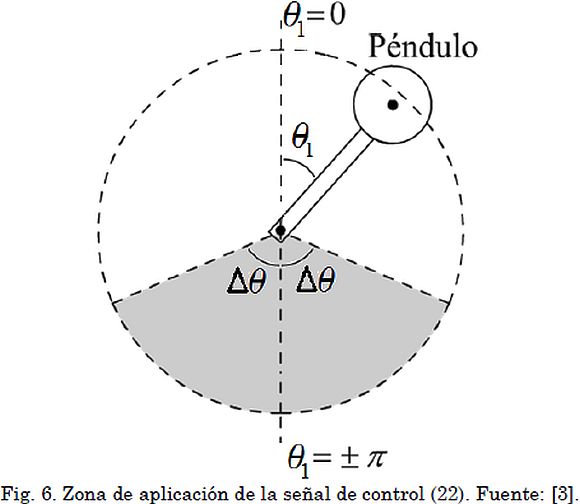
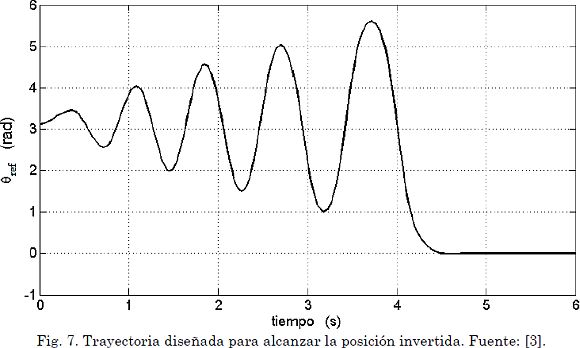
Siendo U₀ una constante menor al máximo valor posible de la señal de control y sgn(.) la función signo. Ajustando el tamaño Δθ de la zona de aplicación de la entrada (π - Δθ ≤ θ ≤ π + Δθ), que se presenta sombreada en la Fig. 6, se puede variar el tiempo que el péndulo tarda en alcanzar la posición invertida (zonas más amplias reducen el tiempo de subida). Este proceso es necesario ya que para lograr una subida directa se requieren valores muy elevados de la señal de control. Cuando el péndulo llega a puntos suficientemente cercanos al equilibrio inestable, un controlador (regulador) lineal se encarga de llevar al sistema hasta esa posición (x₁ = 0) y mantenerlo allí, regulando pequeñas perturbaciones. En la Fig. 7 se presenta la trayectoria de referencia obtenida.

Dado que dicha trayectoria se obtiene con base en el modelo del sistema y considerando sus limitaciones (que serán definidas en la sección siguiente), se espera que el péndulo logre seguirla con un error aceptable, aunque se presente cierto nivel de saturación en la señal de control.

3. Resultados y Discusión

Se realizaron simulaciones en el dominio de tiempo, con el fin de validar la efectividad del controlador sobre el sistema no lineal estudiado. El esquema de control descrito anteriormente es simulado en el entorno Matlab, asignando a los coeficientes a, b y c los valores correspondientes a los parámetros físicos del sistema de prueba presentado en [3] (Mechatronics Control Kit). Dichos valores son: a = 78,4 rad/s²; b = 1,08 rad/s²; c = 198 rad/s². La señal de control se debe limitar al rango normalizado -10 ≤ u ≤ 10 UI (unidades de ingeniería), que luego de la etapa de amplificación corresponde al rango de voltajes aplicado al motor.

Con los valores asignados a los coeficientes, se diseñaron reguladores Ki para cada uno de los modelos lineales (17) y la ganancia común G para el seguimiento. Se definieron los parámetros de respuesta deseada t_s = 0,15 s (tiempo de establecimiento) y M_p = 5% (sobrepaso), de los cuales resultan los polos de lazo cerrado s_1,2 = -26,7 ± j 27,2 (raíces del polinomio característico típico Δ(s) = s² + 2ζω_ns + ;ω_n²). Las ganancias obtenidas usando (19) con estos polos y cada uno de los modelos de la Tabla 1 se presentan en (23).

Usando (21) y los parámetros descritos, el valor de la ganancia de seguimiento resulta ser G = -1343,7 (común a todos los modelos). Con las ganancias (23) y G se puede implementar el regulador (19), que actúa sobre las variables de estado x₁ = θ₁ y x₂ = θ'₁. La tercera variable de estado, x₂ = θ'₂ , no se realimenta, corriendo el riesgo de que se presente un aumento progresivo de la velocidad de giro de la rueda de reacción al alcanzar la posición invertida (en la etapa de subida del péndulo esta velocidad es oscilante y dicho inconveniente no se presenta). Una forma de resolver este inconveniente es la siguiente: al detectar que el ángulo θ1 es cercano a cero (posición invertida, inestable), se cambia el controlador (20) por un regulador local que realimenta las tres variables de estado, u_up = -K_upx , siendo x el vector de estados completo; K_up = [K_up1 K_up2 K_up3] es el vector de ganancias de dicho regulador. La señal de control global implementada se presenta en (24)

El ángulo ∈ debe ser menor a 5° con el fin de evitar cambios bruscos en la señal de control en el instante de conmutación. Para el regulador K_up se definieron los polos de lazo cerrado s_1,2 = -4 ± j4,1 y s₃ = -11,4. Con estos polos y el modelo linealizado alrededor de x₁ = θ₁ = 0 se obtuvo el vector de ganancias presentado en (25)

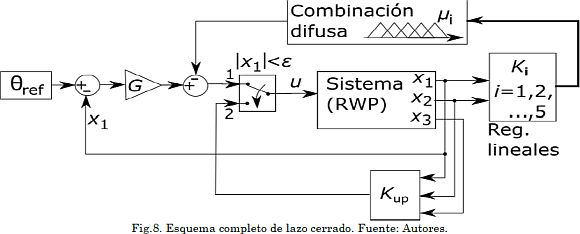
El esquema completo de lazo cerrado se ilustra en la Fig. 8. En la etapa de levantamiento del péndulo, la señal de control resulta de la combinación difusa de los reguladores lineales obtenidos para los modelos reducidos. Cuando se detecta que la barra se encuentra cerca de la posición invertida (|θ₁| ≤ ∈) se realiza la conmutación al regulador del vector de variables de estado completo (u = K_upx), como se describe en (24).

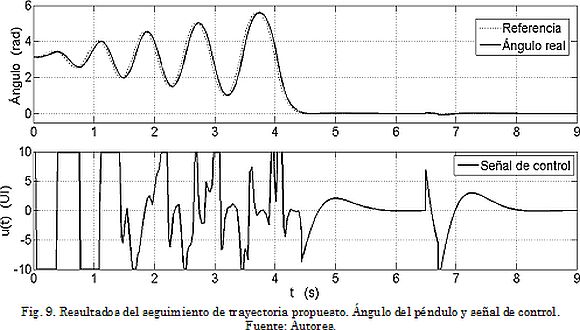
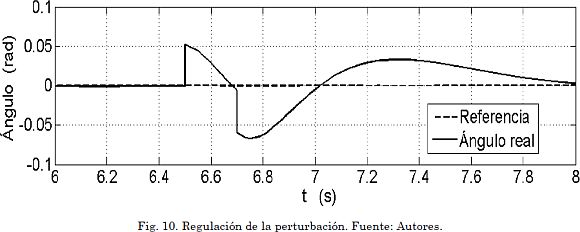
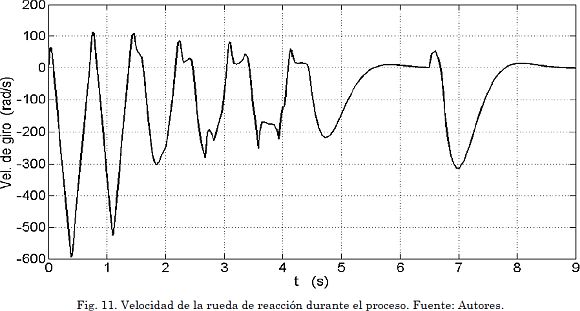
En la Fig. 9 se muestran los resultados de simulación. Se observa que hay saturación en la señal de control, pero aun así se logra el seguimiento de la referencia con un grado de desfase aceptable. Debido a dicha saturación, resulta muy difícil reducir el tiempo de subida a un valor menor al obtenido (t_up ≈ 4,5 s). Se incluye el efecto de una perturbación de tres grados (3°) en el ángulo del péndulo aplicada durante Δt = 0,2 s en el instante t = 6,5 s. Se observa cómo el regulador elimina dicha desviación. En la Fig. 10 se presenta en detalle el efecto sobre la variable de estado x1 debida a la perturbación. Finalmente, la velocidad angular de la rueda se presenta en la Fig. 11.

4. Conclusiones

Se presentaron de forma detallada el diseño del controlador y los resultados de simulación para llevar el péndulo desde su posición natural de equilibrio a la posición invertida. Los reguladores locales obtenidos actúan alrededor de los puntos de operación para los cuales fueron diseñados, y la señal de control global resultó de la combinación difusa de dichos reguladores. Aunque se presentó saturación de la señal de control, fue posible el seguimiento de la trayectoria con lo cual el péndulo alcanzó su posición invertida con oscilaciones de amplitud creciente en un tiempo cercano a 4,5s y con error de seguimiento menor a 0,22 rad. Se comprobó la capacidad del regulador para atenuar pequeñas perturbaciones alrededor la posición invertida.

La validez de la técnica de linealización usada (no-linealidad sectorial), quedó establecida gracias a la respuesta satisfactoria del sistema ante la técnica de control que se implementó, ya que los parámetros del controlador fueron calculados con base en los modelos lineales obtenidos.

La estrategia de control difuso con base en modelos T-S, permitió el uso de las técnicas conocidas de control por realimentación lineal de las variables de estado. Aunque los reguladores locales son en efecto lineales, su combinación difusa usando las funciones de pertenencia definidas, genera un controlador global no lineal.

Referencias

[1] O. O. Gutiérrez-Frías, “Diseño de Controladores para Sistemas Subactuados del Tipo Péndulo Invertido,” Instituto Politécnico Nacional, 2010.         [ Links ]

[2] R. Olfati-Saber, “Nonlinear control of underactuated mechanical systems with application to robotics and aerospace vehicles,” MASSACHUSETTS INSTITUTE OF TECHNOLOGY, 2000.         [ Links ]

[3] V. D. Correa-Ramírez, “Control de un sistema no lineal usando técnicas inteligentes. El péndulo con rueda de reacción,” Universidad Tecnológica de Pereira, 2016.         [ Links ]

[4] A. Molina, D. Buitrago, and V. Correa, “Control global para el péndulo con rueda de reacción,” Sci. Tech., pp. 95-99, 2007.         [ Links ]

[5] O. D. Montoya Giraldo, L. F. Grisales Noreña, V. D. Correa Ramírez, and D. Giraldo Buitrago, “Control global del péndulo con rueda de reacción mediante regulación de energía y linealización extendida de las variables de estado,” Tecno Lógicas, vol. 17, no. 32, pp. 33-46, 2014.         [ Links ]

[6] J. G. Valenzuela-Hernández, O. D. Montoya-Giraldo, and D. Giraldo-Buitrago, “Lógica Difusa Aplicada al Control Local del Péndulo Invertido con Rueda de Reacción,” Sci. Tech., vol. 18, no. 4, pp. 623-632, 2013.         [ Links ]

[7] B. Bapiraju, K. N. Srinivas, P. Kumar P, and L. Behera, “On balancing control strategies for a reaction wheel pendulum,” in Proceedings of the IEEE INDICON 2004. First India Annual Conference, 2004., 2004, pp. 199-204.         [ Links ]

[8] R. J. M., Triana García Giovanni , Buitrago José Tomás, “Control de un péndulo de furuta. Una revisión del estado del arte.,” Sci. Tech., vol. 20, no. 4, pp. 326-334, 2015.         [ Links ]

[9] K. Tanaka and H. O. Wang, Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach, 1st ed. New York, USA: John Wiley & Sons, Inc., 2001.         [ Links ]

[10] D. Giraldo-Buitrago and E. Giraldo-Suárez, Teoría de Control Análogo. Universidad Tecnológica de Pereira, 2010.         [ Links ]

[11] W. J. Terrell, “Some Fundamental Control Theory I: Controllability, Observability, and Duality,” Am. Math. Mon., vol. 106, no. 8, p. 705, Oct. 1999.         [ Links ]

[12] A. Isidori, Nonlinear Control Systems, 2nd ed. Berlin, Heidelberg: Springer Berlin Heidelberg, 1989.         [ Links ]

[13] Jean Jacques, E. Slotine and, and L. Weiping, Applied nonlinear control, 1st ed., vol. 199, no. 1. Englewood Cliffs, New Jersey 07632: prentice-Hall Englewood Cliffs, NJ, 1991.         [ Links ]

[14] V. M. Hernández and H. Sira-Ramírez, “Generalized PI control for swinging up and balancing the inertia wheel pendulum,” in Proceedings of the 2003 American Control Conference, 2003., 2003, vol. 4, pp. 2809-2814.         [ Links ]