Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
TecnoLógicas
Print version ISSN 0123-7799On-line version ISSN 2256-5337
TecnoL. vol.20 no.40 Medellín Dec. 2017
Artículo de investigación/Research article
Flujo de potencia óptimo para redes radiales y enmalladas empleando programación semidefinida
Optimal Power Flow for radial and mesh grids using semidefinite programming
Oscar D. Montoya-Giraldo1, Walter J. Gil-González2, y Alejandro Garcés-Ruíz3
1 MSc en Ingeniería Eléctrica, Facultad de Ingenierías Eléctrica, Electrónica, Física y de Sistemas y Computación, Universidad Tecnológica de Pereira, Pereira -Colombia, odmontoya@utp.edu.co
2 MSc en Ingeniería Eléctrica, Facultad de Ingenierías Eléctrica, Electrónica, Física y de Sistemas y Computación, Universidad Tecnológica de Pereira, Pereira -Colombia, wjgil@utp.edu.co
3 PhD en Ingeniería Eléctrica, Facultad de Ingenierías Eléctrica, Electrónica, Física y de Sistemas y Computación, Universidad Tecnológica de Pereira, Pereira-Colombia, alejandro.garces@utp.edu.co
Fecha de recepción: 14 de septiembre de 2016/ Fecha de aceptación: 24 de julio de 2017
Como citar / How to cite
O. D. Montoya-Giraldo, W. J. Gil-González, y A. Garcés-Ruíz, Flujo de potencia óptimo para redes radiales y enmalladas empleando programación semidefinida. TecnoLógicas, vol. 20, no. 40, pp. 29-42, 2017.
Resumen
Este artículo presenta una formulación convexa para el problema de flujo de potencia óptimo (Optimal Power Flow-OPF) en sistemas de potencia radiales y enmallados, a través de un modelo matemático basado en programación semidefinida (Semidefinite Programming-SDP), el cual trasforma el modelo cuadrático no convexo del OPF en un modelo convexo relajado, que puede ser solucionado de forma mucho más eficiente. El modelo es implementado en MATLAB usando el paquete de optimización convexa CVX. Los resultados obtenidos son comparados con el modelo no lineal del problema implementado en GAMS y MATPOWER usando cuatro sistemas típicos de la literatura especializada, dos de tipo radial y dos enmallado. Las soluciones encontradas por esta aproximación convexa, son muy cercanas a las respuestas presentadas en la literatura especializada para el modelo no lineal. Este tipo de aproximación permite obtener soluciones de muy buena calidad, muy cercanas a la solución óptima del problema en tiempos computacionales menores y susceptibles de aplicarse en problemas de operación y control en tiempo real.
Palabras clave: Aproximación convexa, flujo de potencia, flujo de potencia óptimo, programación semidefinida, redes radiales, redes malladas.
Abstract
This paper presents a convex formulation for optimal power flow (OPF) in both radial and meshed grids. A semidefinite programming (SDP) approximation transforms the quadratic non-convex model into a relaxed convex quadratic model, which can be more efficiently solved. This model is implemented in MATLAB using the CVX package for convex optimization. The results obtained are compared to the non-linear model of the problem implemented in GAMS and MATPOWER by using four typical systems in specialized literature (two radial and two meshed). SDP approximation demonstrated to provide accurate solutions that are close to an optimal solution of the problem in shorter computational times. Such solutions are applicable to real-time operation and control problems.
Keywords: Convex approximation, power flow, optimal power flow, semidefinite programming, radial grids, mesh grids.
Nomenclatura
A continuación, se describe la simbología matemática empleada en este artículo para los modelos matemáticos desarrollados:

1. Introducción
El flujo de carga óptimo u OPF por sus siglas en inglés (Optimal Power Flow) es una metodología clave para la operación en tiempo real de sistemas eléctricos en el contexto de las redes inteligentes, en donde la demanda y la generación son altamente variables en el tiempo [1]-[4]. Así mismo, el OPF puede ser una subrutina de otras metodologías de optimización asociadas a problemas de planeamiento. En uno u otro caso (operación o planeamiento) es necesario desarrollar algoritmos eficientes que reduzcan el tiempo de cálculo y que, de ser posible, sean independientes de la condición inicial, características propias de los modelos convexos. Aunque el OPF no es un modelo convexo, es posible planear aproximaciones convexas altamente eficientes y cercanas al modelo original. Este es el principal objetivo de este artículo.
Históricamente, el OPF fue formulado como la minimización de pérdidas de potencia considerando tanto la potencia activa como reactiva en los generadores. En este sentido, el problema está relacionado estrechamente con el problema de despacho económico y por tanto, en la literatura moderna se suele usar ambos conceptos de forma intercambiable. Así pues, la función objetivo puede ser minimizar las pérdidas del sistema, los costos de operación, o la maximización de un beneficio neto. Las restricciones del OPF corresponden a los límites operativos de las centrales generadoras, límites de regulación de tensión y flujos de potencia por las líneas [1]-[4]. Adicionalmente, el OPF se puede plantear como un problema de factibilidad sin función objetivo, con lo cual se obtienen un conjunto de ecuaciones no lineales, no convexas que permiten resolver el problema clásico de flujo de potencia (PF).
El OPF es un problema matemático complejo de resolver, debido a que corresponde a formulaciones matemáticas no lineales y no convexas [2], lo que implica esfuerzos computacionales altos para su solución; adicionalmente, debido a la no convexidad del problema, la solución obtenida es dependiente del punto de arranque empleado por el algoritmo que sea implementado [5], [6].
La solución del problema de OPF está relacionada con la solución del flujo de carga y este, a su vez, de las características intrínsecas del sistema [6],[7]. En redes de potencia enmalladas, se ha empleado el algoritmo como Newton-Raphson con resultados de buena calidad para sistemas altamente mallados [1]-[3], [8]. Esto se debe a que existe una baja relación r/x en las redes de potencia con lo cual se simplifica la construcción del jacobiano. De otro lado, existen métodos alternativos para redes radiales que evitan la inversión de matrices y mejoran notablemente los tiempos de convergencia, aprovechando la topología radial del sistema[9]. Estos algoritmos son integrados para resolver el OPF mediante técnicas de optimización matemática de tipo combinatorial, como algoritmos genéticos[10]-[12], colonia de hormigas [13] u optimización por enjambre de partículas [14], [15]; así como técnicas exactas entre las que se destaca el método de punto interior [16], además de algoritmos de optimización clásicos, como el gradiente descendente [6], modelos de linealización aproximada [17], [18], programación cuadrática [19] y SDP [9], [20], entre otros. Sin embargo, ninguno de estos algoritmos garantiza el óptimo global debido a la no convexidad del modelo. Así mismo, es importante destacar la dependencia de los métodos de solución en relación con el punto inicial.
Para eliminar los problemas asociados a la clasificación de las redes, es decir, redes radiales o redes enmalladas y la necesidad de emplear distintas estrategias de optimización matemática para resolver el OPF, se propone una formulación matemática por medio de programación semidefinida (SDP) que resuelve estos problemas a través de una aproximación convexa de fácil solución [21]. Mediante está relajación se pueden obtener soluciones de muy buena calidad, que están muy cerca de la solución óptima y son factibles de ser empleados como inicializadores de algoritmos que requieran operación en tiempo real [9], [20]. La programación convexa es altamente eficiente, además de no depender del punto inicial. Estas características son clave para la operación en tiempo real de sistemas de potencia.
A diferencia de los trabajos anteriores, en este artículo se propone un modelo de SDP para resolver los problemas de PF y OPF en redes radiales y enmalladas, con una aproximación convexa que presenta resultados comparables a los obtenidos con el modelo exacto, evaluado en paquetes de optimización comercial como GAMS o MATPOWER. Adicionalmente, se propone una función objetivo para la regulación de tensión, por medio de un modelo de desviación promedio del perfil de tensión en todas las barras del sistema de potencia, que puede ser aplicada en metodologías orientadas a la mejora de la regulación de tensión. La relajación SDP para modelos de optimización no convexos es usualmente estudiada bajo dos enfoques: desempeño computacional y precisión. En este trabajo se estudiará únicamente el segundo aspecto.
Este artículo está dividido en siete secciones. La siguiente sección se presenta algunas generalidades asociados a la optimización convexa y en particular a la SDP. En la sección tres se muestran y se modelan el OPF. En la sección cuatro se discute la aplicación de la metodología, en la sección cinco se muestran los circuitos de prueba utilizados para comprobar la metodología, y los resultados obtenidos se muestran la sección seis. Finalmente, la sección siete presenta las conclusiones más importantes de la investigación.
2. Materiales y métodos
2.1 Programación semidefinida
La optimización convexa es una clase de optimización matemática, sobre la cual se ha desarrollado una teoría de dualidad que garantiza condiciones de optimalidad global. Los problemas convexos presentan dos grandes ventajas: primero, se resuelven numéricamente de manera eficiente; y segundo, siempre alcanzan soluciones globales [9]. Estos modelos incluyen los problemas de programación lineal, programación cuadrática, programación geométrica y programación semidefinida, entre otros.
La SDP ha sido de amplio interés en las últimas décadas debido a sus aplicaciones prácticas (en sistemas de comunicación, sistemas de control, sistemas de potencia) y su velocidad de convergencia en tiempos polinomiales [21]. En esencia, la SDP es una reformulación matemática para problemas no lineales con características similares a las de la programación lineal, ya que pueden ser resueltos con métodos de punto interior usando el determinante como barrera logarítmica [9], [20].
En algunos problemas particulares es posible afirmar que las aproximaciones SDP alcanzan la solución óptima del problema; esto no se puede generalizar para todos los problemas. No obstante, se puede garantizar que se encuentran soluciones de buena calidad, las cuales pueden ser implementadas como puntos de inicialización para algoritmos de optimización no lineales, mejorando los tiempos de convergencia globales de dichos algoritmos. Finalmente, es posible afirmar qué en relación con los problemas no lineales, la SDP presenta una formulación con mayor facilidad de implementación sin importar el número de variables asociadas al modelo [21].
De forma general, un problema SDP se puede formular según el modelo presentado en (1):
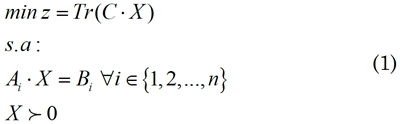
Es de notarse que el modelo es muy similar a la formulación clásica para problemas de programación lineal; de hecho, los problemas de programación lineal son un caso especial de la SDP [22]. Para el modelo presentado en (1) hay que tener en cuenta que la variable de optimización corresponde a una matriz (X ∈ ℝ nxn);y el operador X ≻ 0 implica que la matriz X es semidefinida positiva. Adicionalmente, la función Tr(C · X) corresponde a la traza de la matriz, es decir, la suma de los elementos de la diagonal de la matriz resultante al multiplicar C · X.
2.2 Modelado del flujo de potencia óptimo
El flujo de potencia se puede formular usando modelos matemáticos en coordenadas polares o rectangulares, ya que su operación en régimen sinusoidal permanente permite esta descomposición. La formulación acorde al modelo propuesto en la SDP es esencia un modelo polinomial de segundo grado, en el cual las coordenadas rectangulares se ajustan correctamente. La función objetivo se puede formular como un problema de minimización en el cual se pueden considerar diferentes funciones, dentro de las que se destacan la minimización del costo de generación de potencia activa y la minimización de pérdidas de potencia activa o de potencia reactiva [9], [20]. En este trabajo, dado que el objetivo central es modelar y resolver el problema de OPF, considerando como funciones objetivo la minimización de las pérdidas técnicas de potencia activa (Z1) y la minimización del error medio cuadrático de los perfiles de tensión en cada nodo, respecto a la referencia(Z2). El modelo matemático propuesto corresponde a un modelo de optimización mono-objetivo de minimización sujeto a condiciones técnicas y operativas clásicas de la operación de sistemas eléctricos.
Las posibles funciones objetivo consideradas se muestran en (2) y (3).
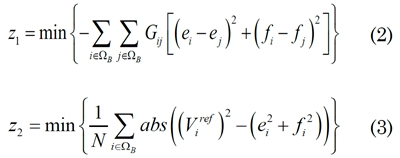
La función objetivo dada en (2) corresponde a la minimización de las pérdidas técnicas en las líneas del sistema; mientras que la función objetivo definida en (3) representa la minimización de la desviación en los perfiles de tensión para cada barra del sistema, respecto a su nivel de referencia.
Las restricciones generales del OPF que modelan el balance de potencia activa y reactiva en cada barra del sistema son representados por (4) y (5).
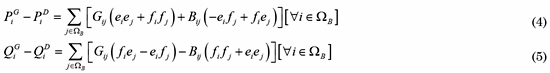
Para generar un punto de referencia es escogido un nodo arbitrario como referencia, el cual típicamente corresponde al generador con mayor capacidad. Esta restricción se modela en (6). Adicionalmente, (7) garantiza que para todos los nodos se cumpla la regulación de tensión.
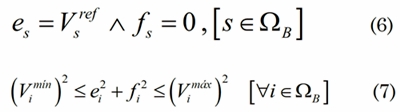
Por último, las centrales de generación, que operan con energéticos convencionales o energías alternativas (incluidos compensadores reactivos) deben garantizar en sus máquinas los límites operativos asociados a la capacidad de generación de potencia activa y reactiva según (8) y (9).
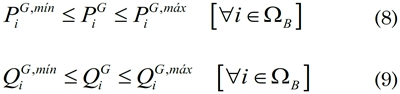
Es de notarse que para convertir el problema de OPF en un problema de PF solo es necesario fijar los valores de generación de potencia activa y la tensión de referencia en los nodos del tipo PV (nodos que controlan tensión y potencia activa), y fijar la capacidad de generación de potencia activa de los generadores distribuidos y la potencia reactiva en los compensadores reactivos, en caso de que estos existan [20].
2.3 Formulación del OPF como un problema de SDP
2.3.1 Reformulación del problema
Para transformar el problema de OPF en un problema de SDP es necesario emplear una formulación matricial, que permita trasformar el problema de OPF presentado de (2) a (9) a la forma canónica de la formulación mediante SDP definida en (1). Se define entonces la matriz de variables X ∈ ℝnxn como (10).
X =V . VT (10)
Donde, V = [e1 f1 e2 f2··· ei fi ··· eN fN]T corresponde al vector que contiene las componentes real e imaginaria de las tensiones en cada nodo i de la red. La dimensión de este vector fila corresponde a dos veces el número total de nodos del sistema (2N). Las funciones objetivas (Z1) y (Z2) definidas en (2) y (3) respectivamente, pueden ser reescritas como (11) y (12).

Donde, las matrices C1 C2 son matrices de coeficientes constantes en función de los parámetros de la red. Estas matrices pueden ser fácilmente calculadas como se presenta en (13).

Las restricciones de balance de potencia en cada nodo pueden ser escritas según (14) y (15).
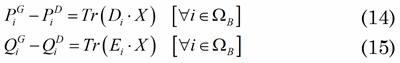
Donde, las matrices Di y E1 están definidas en función de los parámetros de la red y tienen dimensión (2N x 2N). Para calcular de forma general estas matrices para cualquier nodo del sistema, considere el nodo i, al cual le corresponderán las filas y columnas 2i - 1 y 2i. La expresión (16) presenta el cálculo de las matrices Di y E1.

Para determinar la tensión del nodo de referencia, según lo planteado en (6), se define como barra de referencia al nodo s, con lo que se llega a (17).
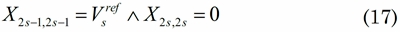
Con el fin de garantizar el cumplimiento de la regulación de tensión en cada nodo del sistema, es necesario reescribir (7) para un nodo genérico i, como (18).
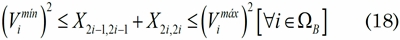
Las ecuaciones (8) y (9) que garantizan que la potencia activa y reactiva generada en cada nodo se encuentren dentro de los límites permitidos, no requieren de ninguna modificación; por lo cual, en aras de claridad estas son nuevamente presentadas en (19) y (20).
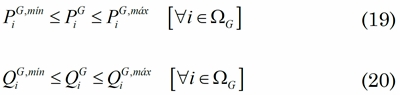
Finalmente, para obtener una representación exacta del problema de OPF se requiere que se cumplan (21) y (22).

Según la reformulación anterior, el modelo completo para representar los problemas de PF y OPF a través de un modelo de optimización empleado SDP corresponde a las funciones objetivo mostradas en (11) y (12) y el conjunto de restricciones definido por (13) y (14) y (17) a (22).
En general, para un problema modelado a través de SDP la matriz presenta en (10) es de rango completo, por lo cual el rango sería igual 2N en el caso OPF. Para obtener de forma general el vector de variables de interés V desde la matriz X se emplea el método de descomposición por medio de valores propios y vectores propios [22], como se muestran en (23).

Donde, λ representa a los valores propios y W los vectores propios. Si la representación del problema como un modelo de SDP es lo suficientemente buena, se espera que 2N-1 valores propios sean muy cercanos a cero y exista por lo menos un valor propio de magnitud superior a los demás. Lo cual quiere decir que el rango de la matriz X es unitario y la expresión (23) puede ser rescrita como (24).

Donde, λm representa el máximo valor propio y Wm el vector propio asociado a este. Bajo este escenario es posible recuperar el vector de variables V según (25).

2.4 Sistemas de prueba
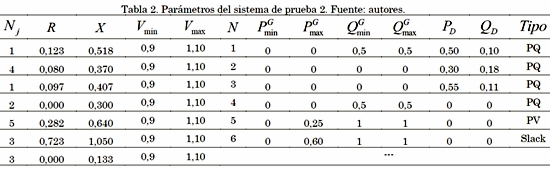
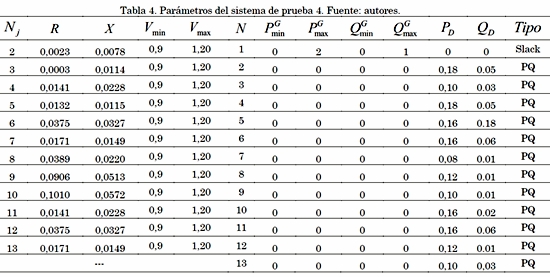
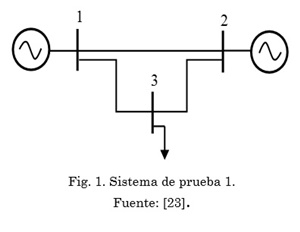
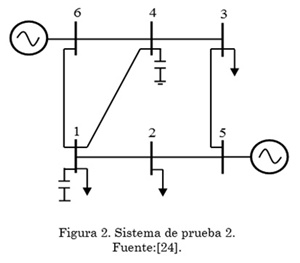
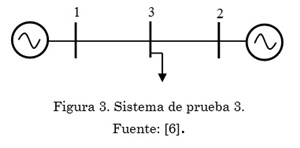
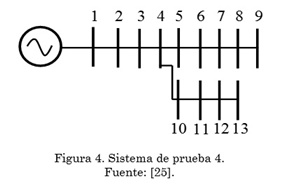
Para verificar la validez de la formulación matemática propuesta en los problemas de PF y OPF, empleando un modelo basado en SDP, son usados cuatro sistemas de prueba comunes de la literatura especializada. Los dos primeros sistemas de prueba corresponden a redes malladas con 3 y 6 barras, respectivamente. Los otros dos sistemas de prueba corresponden a redes radiales con 3 y 9 barras, respectivamente. En las Tabla 1 a 4 se presentan los datos de demanda, impedancia de línea, demandas, y límites operativos para cada sistema de prueba con valores en por unidad, y en las Figs. 1 a 4 se presenta su topología.
3. Resultados y Discusión
Para validar la formulación de los problemas de OPF y PF son empleados el software MATLAB, con el paquete de optimización CVX para problemas formulados como SDP, el MATPOWER para evaluar flujos de potencia con el método de Newton-Raphson y el paquete de optimización comercial GAMS para modelado matemático.
En la primera parte de esta sección, se presentan los resultados obtenidos al analizar el problema de OPF usando CVX, los resultados presentados en la literatura especializada y GAMS; la segunda parte, muestra los resultados obtenidos al analizar el problema de PF usando CVX y MATPOWER.
3.1 Resultados OPF
Para simular cada uno de los sistemas de prueba se tienen en cuenta los datos presentados en las Tablas 1 a 4, asignando ángulo de referencia a cada nodo slack y dejando libres las tensiones en los generadores.
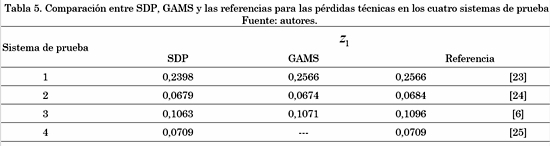
La Tabla 5 se presenta los resultados obtenidos para el problema OPF considerando como función objetivo la minimización de las pérdidas de potencia activa empleado SDP definida en (2). Esto resultados son comparados con los resultados obtenidos en GAMS para el modelo no lineal y los resultados presentados en la literatura especializada.
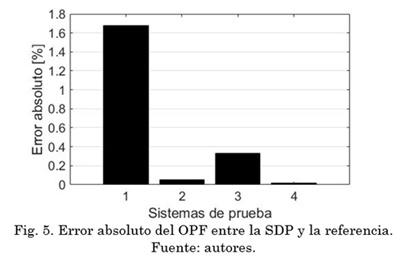
La Fig. 5 presenta el error absoluto del modelo empleado SDP con respecto a los resultados presentados en las referencias.
Los resultados presentados en la Tabla 5 y la Fig. 5 muestran claramente cómo el modelo empleando SDP es una aproximación de muy buena calidad para resolver el problema de OPF, en sistemas radiales y enmallados.
Para el caso particular de los sistemas de prueba presentados, se observó que el mayor error de estimación fue de 1,68 % para el sistema de prueba 1, lo cual garantiza una aproximación de muy buena calidad. Adicionalmente, de la Tabla 5 se puede observar que para los cuatro sistemas de prueba el modelo de SDP encontró soluciones de mejor calidad para las pérdidas técnicas, lo que ratifica su eficiencia. Por otro lado, los resultados dados por el modelo desarrollado en GAMS, se observa que en el caso del cuarto sistema de prueba no encuentra convergencia, y en los demás casos sus resultados son muy similares a los arrojados por la SDP.
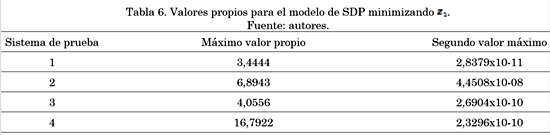
La Tabla 6 muestra cómo son los dos primeros valores propios de cada uno de los sistemas de prueba (valores máximos), lo cual ratifica que la aproximación lineal empleando SDP se ajusta perfectamente a la respuesta no lineal del problema de OPF, según se definió en (25).
Para el caso de mejorar el perfil de tensión, se trabajó con la función objetivo presentado en (3). Esta función objetivo corresponde a la minimización de la desviación promedio de los perfiles de tensión en cada nodo, respecto de la referencia. Para simular este caso, se supone que la referencia para todos los sistemas de prueba corresponde a una tensión 1,0 en p.u.
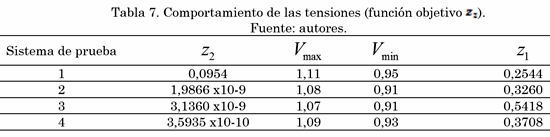
La Tabla 7 presenta el valor de esta función objetivo, el máximo y el mínimo valor de tensión registrado en para cada sistema de prueba, además de las pérdidas técnicas en este escenario.
La función objetivo presentada en la Tabla 7, muestra que se ha alcanzado el mínimo posible para esta función, la cual orresponde a valores cercanos a cero (excepto para el sistema de prueba 1); sin embargo, se observa que el mínimo perfil de tensión para cada sistema está en sus valores mínimos permitidos, y por tanto las pérdidas incrementan enormemente en relación con el resultado obtenido para la función objetivo definida en (2).
Este resultado parece contraintuitivo a primera vista, pues se espera que las tensiones estén todos cercanos al valor 1,0 en p.u, ya que, se supone que allí estaría el mínimo; sin embargo, existe una combinación que eleva los perfiles de tensión en algunos nodos y la disminuye en otros, tal que se obtiene un mejor resultado para dicha función objetivo.
Los resultados de la Tabla 7 permiten afirmar que no es recomendable emplear una función objetivo que pretenda minimizar la desviación de tensión en cada nodo, ya que se presentan combinaciones de tensiones que, aunque alejadas del resultado esperado, garantizan un mínimo global, que es nada deseable en la operación real de sistemas de potencia.
3.2 Resultados PF
Para evaluar el comportamiento del modelo formulado con SDP para PF, se considerará que: el nodo slack será la referencia para el ángulo de la tensión y se le asignará un voltaje magnitud 1,1 en p.u. Los generadores PV serán fijados con una potencia activa equivalente al 60 % de su valor máximo y con un control de tensión equivalente a 1,1 en p.u. La función objetivo considerada es la minimización de las pérdidas técnicas definida en (2) y finalmente, si existen compensadores reactivos, estos se fijarán en su valor máximo.
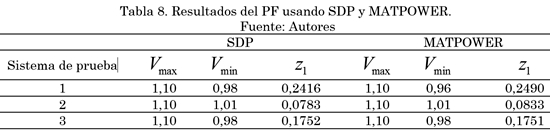
La Tabla 8 muestra los resultados del SDP y MATPOWER (disponible para MATLAB), del valor máximo y mínimo de la tensión para cada sistema de prueba, así como sus pérdidas técnicas.
Al comparar los resultados de la Tabla 8, es posible afirmar que los perfiles de tensión obtenidos al resolver el problema de PF empleado el modelo de SDP son iguales para los sistemas de prueba 2, 3 y 4. Para el sistema de prueba 1 aunque se presenta una diferencia porcentual del 2 %, esta está dentro de los límites de regulación establecidos en la operación normal del sistema.
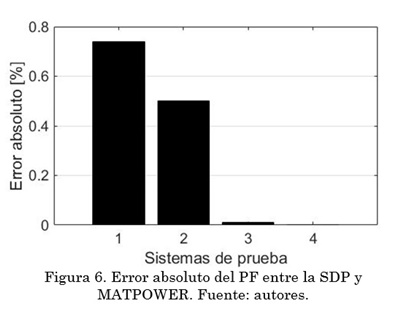
Tomando como referencia, los datos de pérdidas de potencia activa que arroja el MATPOWER, se obtienen los errores absolutos presentados en la Fig. 6, donde se puede observar que el máximo error se presenta en el caso del sistema de prueba 1 y corresponde 0,74 %; lo cual es un error entre el modelo empleando SDP y el modelo clásico de Newton-Raphson que usa el MATPOWER.
4. Conclusiones
Se desarrolló una aproximación matemática para formular los problemas de OPF y PF en redes radiales y enmalladas, a través de un modelo matemático de SDP. Esta formulación permite transformar la no linealidad y no convexidad de ambos problemas, en una aproximación lineal convexa de fácil implementación en software especializado, como es el caso del CVX de MATLAB.
La formulación presentada permite trabajar con redes radiales y enmalladas, por lo cual puede ser aplicada a redes de transmisión, subtransmisión y distribución, solo conociendo la matriz de admitancia nodal correspondiente y sin necesidad de preocuparse por la topología y condicionamiento de la red. Esta característica permite olvidarse de la clasificación entre métodos derivados de Newton-Raphson (redes malladas) y derivados del barrido iterativo (redes radiales), para concentrase en las condiciones operativas de la red; resultando muy útil para los operadores de red, ya que, no será necesario distinguir entre estas dos topologías.
Los resultados obtenidos para los problemas de OPF y PF usando el modelo de SDP, muestran claramente que las soluciones encontradas por esta aproximación lineal, son muy cercanas a las respuestas presentadas en la literatura especializada para el modelo no lineal, al igual que acercan enormemente a los resultados obtenidos con GAMS y MATPOWER, por lo que es susceptible de ser aplicada en problemas de planeación y operación de redes eléctricas con buen nivel de precisión, reduciendo el esfuerzo computacional en la solución del problema tratado.
Se propone como un trabajo derivado de este, realizar una formulación mediante SDP para los problemas de OPF y PF en sistemas radiales y enmallados considerando la integración de redes AC y DC, es decir, con interconexiones en HVDC o microrredes en DC. Adicionalmente, se propone incluir elementos de compensación de potencia activa y reactiva, lo que podría ser útil para trabajar en redes con alta penetración de energéticos renovables y almacenamiento de energía.
5. Agradecimientos
Al programa de Becas Doctorados Nacionales del Departamento Administrativo de Ciencia, Tecnología e Innovación de Colombia (COLCIENCIAS), según convocatoria 727 de 2015 y al programa de Doctorado en Ingeniería de la Universidad Tecnológica de Pereira.
Referencias
[1] D. Wu, D. K. Molzahn, B. C. Lesieutre, and K. Dvijotham, “A Deterministic Method to Identify Multiple Local Extrema for the AC Optimal Power Flow Problem,” IEEE Trans. Power Syst., pp. 1-13, 2017. [ Links ]
[2] J. Gunda, G. Harrison, and S. Z. Djokic, “Analysis of Infeasible Cases in Optimal Power Flow Problem,” IFAC-PapersOnLine, vol. 49, no. 27, pp. 23-28, 2016. [ Links ]
[3] Y. Tang, K. Dvijotham, and S. Low, “Real-time Optimal Power Flow,” IEEE Trans. Smart Grid, pp. 1-11, 2017. [ Links ]
[4] M. B. Cain, R. P. Oneill, and A. Castillo, “History of Optimal Power Flow and Formulations,” Fed. Energy Regul. Comm., vol. 1, pp. 1-36, 2012. [ Links ]
[5] M. F. Bedrinana, M. J. Rider, and C. A. Castro, “Ill-conditioned Optimal Power Flow solutions and performance of non-linear programming solvers,” in 2009 IEEE Bucharest PowerTech, 2009, pp. 1-7. [ Links ]
[6] J. M. L. Lezama and L. A. G. Pareja, “Flujo de potencia óptimo usando el método del gradiente para reducción de pérdidas en sistemas de potencia,” Ing. y Cienc., vol. 4, no. 7, pp. 71-85, 2008. [ Links ]
[7] A. R. Baran and T. S. P. Fernandes, “A three-phase optimal power flow applied to the planning of unbalanced distribution networks,” Int. J. Electr. Power Energy Syst., vol. 74, pp. 301-309, Jan. 2016. [ Links ]
[8] J. Zhu, “Power Flow Analysis,” in Optimization of power system operation, Hoboken, NJ, USA: John Wiley & Sons, Inc, 2015, pp. 13-50. [ Links ]
[9] X. Bai and H. Wei, “A semidefinite programming method with graph partitioning technique for optimal power flow problems,” Int. J. Electr. Power Energy Syst., vol. 33, no. 7, pp. 1309-1314, Sep. 2011. [ Links ]
[10] A. K. M. R. Rahman, M. S. Alam, M. Z. Hossain, and M. Shahjahan, “Localization of FACTS devices for optimal power flow using Genetic Algorithm,” in 2013 International Conference on Electrical Information and Communication Technology (EICT), 2014, pp. 1-6. [ Links ]
[11] J. Rahul, Y. Sharma, and D. Birla, “A New Attempt to Optimize Optimal Power Flow Based Transmission Losses Using Genetic Algorithm,” in 2012 Fourth International Conference on Computational Intelligence and Communication Networks, 2012, pp. 566-570. [ Links ]
[12] S. Balasubramanian, R. V Gokhale, and A. Sekar, “A new AC optimal power flow formulation and solution using Genetic Algorithm based on P-Q decomposition,” in 2015 North American Power Symposium (NAPS), 2015, pp. 1-5. [ Links ]
[13] J. Soares, T. Sousa, Z. A. Vale, H. Morais, and P. Faria, “Ant Colony Search algorithm for the optimal power flow problem,” in 2011 IEEE Power and Energy Society General Meeting, 2011, pp. 1-8. [ Links ]
[14] U. Leeton, D. Uthitsunthorn, U. Kwannetr, N. Sinsuphun, and T. Kulworawanichpong, “Power loss minimization using optimal power flow based on particle swarm optimization,” in Electr. Eng. Comput. Telecommun. Inf. Technol., 2010, pp. 440-444. [ Links ]
[15] J. Praveen and B. S. Rao, “Multi objective optimization for optimal power flow with IPFC using PSO,” in 2016 3rd International Conference on Electrical Energy Systems (ICEES), 2016, pp. 85-90. [ Links ]
[16] Liang Xie and Hsiao-Dong Chiang, “A enhanced multiple predictor-corrector interior point method for optimal power flow,” in IEEE PES General Meeting, 2010, pp. 1-8. [ Links ]
[17] J. R. Marti, H. Ahmadi, and L. Bashualdo, “Linear Power-Flow Formulation Based on a Voltage-Dependent Load Model,” IEEE Trans. Power Deliv., vol. 28, no. 3, pp. 1682-1690, Jul. 2013. [ Links ]
[18] A. Garces, “A Linear Three-Phase Load Flow for Power Distribution Systems,” IEEE Trans. Power Syst., vol. 31, no. 1, pp. 827-828, Jan. 2016. [ Links ]
[19] A. Garces, “A quadratic approximation for the optimal power flow in power distribution systems,” Electr. Power Syst. Res., vol. 130, pp. 222-229, Jan. 2016. [ Links ]
[20] X. Bai, H. Wei, K. Fujisawa, and Y. Wang, “Semidefinite programming for optimal power flow problems,” Int. J. Electr. Power Energy Syst., vol. 30, no. 6-7, pp. 383-392, Jul. 2008. [ Links ]
[21] M. Laurent and F. Rendl, “Semidefinite Programming and Integer Programming,” in Handbooks Oper. Res. Manag. Sci., vol. 12, 2005, pp. 393-514. [ Links ]
[22] Z. Luo, W. Ma, A. So, Y. Ye, and S. Zhang, “Semidefinite Relaxation of Quadratic Optimization Problems,” IEEE Signal Process. Mag., vol. 27, no. 3, pp. 20-34, May 2010. [ Links ]
[23] E. Castillo, A. J. Conejo, P. Pedregal, R. García, and N. Alguacil, “Programación no lineal,” in Formulación y Resolución de Modelos de Programación Matemática en Ingeniería y Cienc., 1 ed., Real, Espa{ñ}a, 2002, pp. 47-72. [ Links ]
[24] S. S. Sharif, J. H. Taylor, and E. F. Hill, “On-line optimal reactive power flow by energy loss minimization,” in Proceedings of 35th IEEE Conference on Decision and Control, vol. 4, pp. 3851-3856. [ Links ]
[25] M. Granada, “Flujo de potencia para sistemas radiales de distribución usando el método de la cadena,” Sci. Tecnhnica, vol. 20, pp. 183-188, 2002. [ Links ]