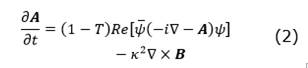1. INTRODUCTION
One way to modify the magnetic response of superconducting samples at low temperature is controlling their boundary conditions. Several theoretical physics models enable to simulate different kinds of material in contact with the sample by varying the deGennes extrapolation length b in the boundary conditions, thus allowing controlling the superconducting critical parameters [1]-[2]. In a recent work, we studied the magnetic response of a superconducting film in absence of a magnetic field, under a continuous electric current, and subjected to different boundary conditions; we found that the critical current for which the first vortex-anti-vortex penetrates the sample, depends strongly with the material in contact with the superconductor [3]. Flux trapping and boundary effects in superconducting slabs and circular geometries have been studied by several authors who found that a superconductor-dielectric interface leads to Bean-Livingston surface barrier, which is responsible for the hysteresis in the magnetization curve. Additionally, a superconductor in contact with another superconductor at different critical temperature T c increases the second critical field [4]-[7]. Fink et al. studied the effect of the presence of another material in contact with the superconducting sample (simulated by b) [3,5] on T c for various geometries. They found that the deGennes parameter is useful to analyze the variation of Tc in mesoscopic superconductors [8]. Other authors found that the T c of the sample is very sensitive to electrical fields in a reversible way [9]-[11]. In order to study the b(T), we used a TDGLM in a mesoscopic square where temperature T is locally modified. Ti is the temperature in the internal points of the sample, while its lateral surface remains at Ts. We changed the boundary conditions until we found a b value that mimicked the magnetization curve at Ts and Ti = 0 in a single vortex state.
This paper is organized as follows. Section 2 introduces the dimensionless time-dependent Ginzburg-Landau equations [12]-[15] taking into account the general boundary conditions. Section 3 presents the results of the computational simulations for certain temperatures and the deGennes parameter of a superconducting square at Ts.
2. THEORETICAL FORMALISM
In this work, a mesoscopic superconducting square immersed in an external magnetic field H = Hz is simulated with the TDGLM for the order parameter 𝜓(𝑥,𝑦) and the potential vector 𝑨(𝑥𝑦), where 𝑩 = 𝛻 x 𝑨 is the magnetic induction. The time-dependent Ginzburg-Landau equations are written as [16]:
The equations are complemented with specific boundary conditions for the order parameter 𝒏· (𝑖 𝛻 + 𝑨)𝜓 = 𝑖 𝜓/ b, is the deGennes parameter and it is characteristic of a superconducting interface with any kind of material. 𝑘 is the Ginzburg-Landau parameter, which is material dependent. For convenience, we selected the parameter 𝛾 = 1 - 𝛿/b, where 𝛿 is the size of the grid used to solve Eqs. (1) and (2) computationally. (i) 𝛾 = 0 simulates an interface at the normal state, (b = 0, where ?? = 0); (ii) 0 ˂ 𝛾 ˂ 1, a superconductor/metal interface (b ˃ 𝛿); (iii) 𝛾 = 1, a superconductor/vacuum interface (b→∞); and (iv) a superconductor/superconductor interface is described by 𝛾 ˃ (b < 0) [12]-[17].
We chose a square with dimensions Lx = Ly = 3 𝜉(0), 𝛿 = 0.1, k = 𝜆𝜉 = 5.0.
(typical values for an Pb-In alloy) [18]-[22]. 𝜉(0) is the coherence length at zero temperature. In this study, we do not consider the heat equation (thermal dissipation), which is associated with the relaxation of the Cooper pair density and it is very important in measurements of magnetization as a function of time [23].
3. RESULTS AND DISCUSSION
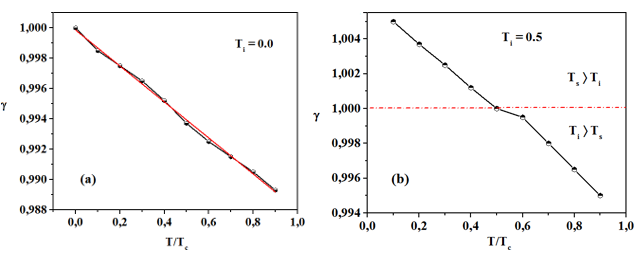
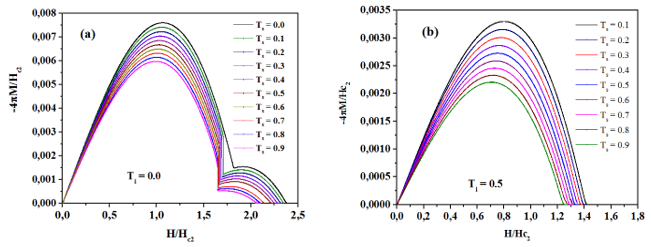
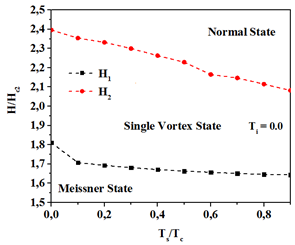
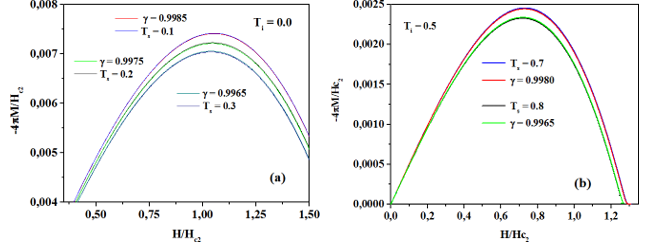
We analyzed the magnetization curves of the deGennes parameter in the single-vortex state using several values. Fig. 1 shows magnetization -4𝜋𝛭 as a function of applied magnetic field 𝛨 for a superconducting/vacuum interface in a single vortex state at 𝛵 = 0.0 (Fig. 1a) and Meissner state at Τ𝑐 = 0.5𝛵𝑐 (Fig. 1b). It is widely known that magnetization decreases as Ti increases and the sample becomes less diamagnetic. It can be seen from the plots that the lower critical field 𝛨 ∼ 1.726𝛨c2 is practically independent of Ts, and the upper field depends on Ts (see Fig. 2). The Meissner state is presented for the case with Τ𝑖 = 0.5𝛵𝑐, and a slow superconductor/normal state occurs due to the temperature dependence with vortex size [2]. In Fig. 3, we plot magnetization as a function of 𝐻 for several values of 𝛾 and Ts. Fig. 3(a): Ti = 0.0 and 𝛾 = 0.9985, Ts = 0.1 T c , (red and blue lines), 𝛾 = 0.9975, Ts = 0.2T c , (green and black lines) and 𝛾 = 0.9965, Ts = 0.3 T c , (dark cyan and navy blue lines). Fig. 3(b): Ti = 0.5T c and 𝛾 = 0.998, Ts = 0.7 T c (red and blue lines), 𝛾 = 0.9965, (Ts = 0.8T c green and black lines).
Source: Authors’ own work.
Fig. 1 (Color online) Magnetization curves for Ts/T c = 0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9 and 𝛾 = 1.0, for (a) the single vortex state at Ti = 0.0 and (b) the Meissner state at Ti = 0.5T c .
Source: Authors’ own work.
Fig. 2 (Color online) Phase diagram H - T showing the first vortex penetration field H1 and superconducting-normal transition field H2 at Ti = 0.0 and 𝛾 = 1.0.
Source: Authors’ own work.
Fig. 3 (Color online) Magnetization curves for (a) Ti = 0.0 and 𝛾 = 09985, Ts = 0.1 (red and blue lines), 𝛾 = 0.9975, Ts = 0.2 (green and black lines) and 𝛾 = 0.9965, Ts = 0.3 (dark cyan and navy blue lines). (b) Ti = 0.5 and 𝛾 = 0.9980, Ts = 0.7 (red and blue lines), 𝛾 = 0.9965, Ts = 0.8 (green and black lines).
We calculated the error in the maximum difference of the magnetization curves by comparing all cases with 𝛾 = 1.0 and Ti = Ts = 0.0. We thus found a percentual error 𝐸 ∼ 1% and, based on this criterion, we can say that the curves are very similar. We also established that 𝛾 presents an analytical dependence with 𝛵 = Ts, as 𝛾(𝛵) = 09980 - 0.118𝛵 (see Fig. 3, left). In Fig. 4, we plot 𝛾 as a function of Ts when the magnetization curves are similar for Fig. 4(a) Ti = 0.0 and Fig. 4(b) Ti = 0.5 As we can see in Fig. 4(b), there is a deflection in the slope of 𝛾(𝛵) when Ts ˃ Ti from 𝛾 (𝛵) = 1.0062 - 0.0125𝛵 for 𝛾 ˃ 1.0 to 𝛾(𝛵) = 1.0085 - 0.0150𝛵 for 𝛾 ˂ 1.0. This is due to a super conductor-superconductor (superconductor-metal) interface. The surface barrier is enhanced (suppressed) and, consequently, diamagnetism increases (decreases) and an interface with 𝛾 > 1.0 (0 ˂ 𝛾 ˂ 1.0 must be chosen. Our results show dependence for the critical temperature with the boundary simulated by the deGennes parameter 𝑏.
4. CONCLUSIONS
In summary, we analyzed the numerical results of the magnetization curves of a mesoscopic superconducting square sample embedded in a thermal bath at different temperatures 𝛵 and boundary conditions 𝛾. A metallic (superconducting) material in contact with the sample suppressed (enhanced) the surface superconductivity. Therefore, we could find a temperature of the surface for which Ts 𝛵𝑖 when 𝛾 = 1, mimicking the result for Ts 𝛵𝑖 when 𝛾 ≠1. We found a highly possible value for 𝛾 at Ti = Ts = 0.0 at which the magnetization curve is similar to the one simulated with each Ts. We found that, for a square sample surrounded by different kinds of materials, in the Ginzburg-Landau model, the critical temperature of these materials for the studied samples at T = 0.0 exhibits a dependence 𝛾 (T) = 0.998 - 0.0118T. In terms of the deGennes parameter, we have b(T)=(0.085-0.15T)^(-1) 𝜉(0).