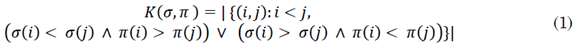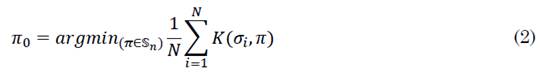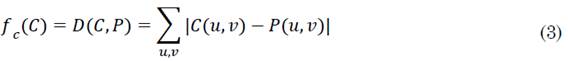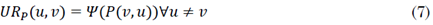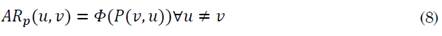1. INTRODUCCIÓN
En la actualidad se generan grandes cantidades de datos a cada segundo. Las técnicas para el manejo de grandes volúmenes de información surgen con el nombre de minería de datos y se constituyen como la alternativa ideal en estos casos.
La minería de datos comprende un conjunto de técnicas tendientes a “realzar” o descubrir comportamientos y patrones presentes dentro de un conjunto de datos con la finalidad de generar conocimiento que proporcione soluciones a un problema determinado [1]. Como gran parte de estos datos son presentados siguiendo algún orden de preferencia, temas como la agregación de rankings han llamado la atención de numerosos investigadores y ya cuentan con diferentes aplicaciones en variados temas que van desde la calidad educativa [2] hasta la biología computacional [3]-[7].
Debido a su popularidad en la comunidad científica, y la amplia gama de aplicaciones que presenta el tema, se han desarrollado además numerosas herramientas para facilitar su uso [8], [9].
Dado un conjunto de elementos (u objetos), para ser ordenados por jueces, según su criterio de preferencias (por ejemplo, los mejores delante y los peores al final), los rankings proporcionados por cada juez, que ordenan todos los elementos, (o algunos de ellos), podrían ser combinados para obtener un ranking de consenso (agregación). El problema de encontrar dicho ranking es conocido en la literatura como Problema de Agregación de Rankings (RAP, por sus siglas en inglés) [10].
Existen diferentes tipos de RAP. Por ejemplo, cuando los rankings a agregar no tienen empates ni ausencias de algún elemento, entonces los rankings son permutaciones (rankings completos sin empates) y el RAP se reduce al Problema de Kemeny (KRP) [11].
Una variante más reciente del RAP es el Problema de Ordenamiento Óptimo de Rankings con Empates (OBOP, por sus siglas en ingles), cuya solución consiste en un ranking con empates, a diferencia del KRP [12] - [14].
En el RAP, para instancias de gran tamaño no es posible, en general, obtener la solución exacta. Sin embargo, se puede abordar mediante el uso de algoritmos heurísticos codiciosos (por ejemplo, Borda), los cuales encuentran una solución aproximada del problema. Estos algoritmos son rápidos, pero las soluciones así obtenidas están lejos de ser óptimas. Las metaheurísticas han mostrado un buen equilibrio entre la eficiencia y la precisión en problemas de este tipo [15], [16].
En [14] se introducen dos nuevo conceptos, la Matriz Utópica y la Anti Utópica, que se asocian a una matriz de orden de pares que representa las precedencias en un conjunto de rankings. Siguiendo la investigación presentada en [14], en este trabajo se replantean los conceptos de Matriz Utópica y de Matriz Anti Utópica para RAP. De esta forma, estas idealizaciones constituyen soluciones súper-óptimas para el RAP, que se pueden utilizar como valores extremos. Además, se muestran los resultados experimentales de la relación entre el Valor Utópico y la solución óptima de 47 modelos de Programación Lineal Entera (PLE) resueltos con la ayuda del software de código abierto SCIP.
El resto del documento está estructurado de la siguiente manera. A continuación, se definen el RAP y OBOP, así como se presentan los conceptos de Matriz Utópica, Matriz Anti utópica, Valor Utópico y Valor Anti Utópico para OBOP planteados en [14]. Seguidamente, se introducen los conceptos nuevos relacionados con los Valores Utópicos y Anti Utópicos para RAP. Posteriormente se muestran los resultados de los experimentos realizados. Finalmente, se dan a conocer las conclusiones del presente trabajo.
2. ANTECEDENTES
2.1 Problema de Agregación de Rankings (RAP)
Informalmente, el Problema de Agregación de Rankings (RAP) consiste en combinar varios rankings (que ordenan el mismo conjunto de candidatos, o alternativas), para obtener un ordenamiento que exprese un consenso entre todos ellos. La agregación de rankings se ha estudiado en muchas disciplinas, principalmente en el contexto de la teoría de la elección social, donde existe una rica literatura que data de la segunda mitad del siglo XVIII [17].
Entonces, formalmente, dado un conjunto [[n]] = {1, ..., n} de elementos, un ranking π es un orden de preferencia de estos (o algunos de estos) elementos. Los rankings que ordenan todos los elementos de [[n]] se denominan completos, mientras que los que ordenan los elementos de un subconjunto de [[n]] se denominan rankings parciales. Por otro lado, los rankings que establecen una preferencia entre cada par de elementos ordenados se denominan sin empates, mientras que los que presentan empates son rankings con empates.
Conceptualmente, un empate puede entenderse como una falta de información de preferencia entre algunos elementos clasificados. Los elementos empatados forman un bucket. Entonces, un ranking también puede entenderse como un orden de preferencia (disjunto) entre sus buckets [18].
Para identificar el ranking que será el que mejor represente ese conjunto, es importante medir cuan diferentes son dos de ellos [4]. Las distancias son la forma común de medir la diferencia entre dos rankings.
A pesar de existir diferentes formas de calcular la distancia entre dos rankings, la más popular es la distancia de Kendall-Tau.
La distancia de Kendall [19], entre dos rankings π y σ, se define en (1) como el número total de pares de elementos en desacuerdo. Hay desacuerdo sobre un par de elementos (i; j) si el orden relativo de i y j es diferente en π y. σ Más precisamente:
Donde σ(i) y π (i) indican la posición del elemento i dentro de las permutaciones σ y π, respectivamente. Además, debe notarse que los rankings se expresan como permutaciones y no hay empates entre los elementos.
Una propiedad interesante de la Distancia de Kendall es que su valor máximo entre dos rankings de n elementos es
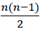 .
.
Entonces, según [20] dado un conjunto de N rankings, Σ= {σ1, σ2, …, σ N } que ordenan n elementos 1, 2, …, n, con σi ∈ Sn, donde Sn es un grupo que contiene todas las permutaciones de los n elementos, el RAP consiste en encontrar la permutación π 0 que satisface (2):
K(σ i , π,) corresponde a la distancia Kendall-Tau entre los rankings σ i y la permutación π.
2.2 Problema de Ordenamiento Óptimo de Rankings con Empates (OBOP)
Nuevamente, el objetivo del OBOP es encontrar un ranking de consenso que ordene cada uno de los rankings de entrada, pero en este caso la respuesta puede contener empates entre varios elementos del ranking.
Más formalmente, dado un conjunto de elementos [[n]] = {1, ..., n}, un ranking completo con empates β es una partición ordenada de [[n]] [14]. Más precisamente, se trata de una ordenación lineal de subconjuntos disjuntos (buckets) B1, B2, ...,B k de [[n]], 1 ≤ k ≤ n, con ⋃ k i =1 B i =[[n]]. Por lo tanto, teniendo en cuenta dos buckets Bi, B j en β,se escribe B i ≺ β B j , para indicar que B j precede a B j de acuerdo con el orden de bucket β. Análogamente, dados dos objetos u ∈ B i , v ∈ B j , se escribe u≺ β v si B i ≺β B j . Todos los elementos que pertenecen al mismo bucket se consideran empatados. Por lo tanto, si u y v están empatados con respecto a B, se escribe u ~ β v [14].
Se puede representar B como una matriz C n x n, donde C(u, v) = 1 si u ≺ B v, C(u, v) = 0 si v ≺ B u y C(u, v) = 0,5 si u ∼ B v. Debe notarse, además, que C(u, v)+ C(v, u) = 1 [21].
La entrada del problema es un conjunto de rankings (completos o parciales) que se representan en una matriz de precedencias P de dimensiones n x n con valores en el intervalo [0,1] tal que P(u, v) + P(v, u) = 1 para todo u, v ∈ [[n]], u ≠ v, y P(u, u) = 0,5 para todo u ∈ [[n]]. Usualmente P (u, v) es interpretado como la fracción de permutaciones de la muestra en las que el elemento u ha sido ordenado antes del elemento v [14].
Entonces, el objetivo del OBOP consiste encontrar el orden de buckets tal que la distancia entre las matrices C y P sea mínima. En otras palabras, el valor óptimo del OBOP para la matriz P consiste en encontrar una Matriz de Bucket C n x n que minimice la función (3):
Esto quiere decir, que la distancia D(C, P) es el valor modular o absoluto de las diferencias sumadas entre cada par de elementos de la matriz de entrada (matriz de precedencias) y la forma matricial de representar un ranking usada en el OBOP.
Es importante notar que la matriz de precedencia puede representar tanto rankings completos, incompletos como con empates. En [22] se demuestra que la distancia D(C, P) es en realidad una extensión de la distancia de Kendall, formulada en (1) con anterioridad, con la diferencia que permite la comparación entre cualquier par de rankings.
Por lo tanto, el OBOP tiene una matriz de entrada P y una salida formada por la permutación de los conjuntos de partición. Así, se clasifican los elementos del ranking inicial en buckets que contienen subconjuntos con propiedades homogéneas, y proporciona la permutación de buckets que mejor los represente [21].
2.3 La Matriz Utópica (UP) y el Valor Utópico (uP) para OBOP
Según [14], dada una Matriz de Precedencia P, la Matriz Utópica asociada a P es la matriz n × n definido en (4) como:
Donde:
Debe notarse que cada celda de la Matriz Utópica toma uno de los valores posibles de precedencia cuando se permiten empates (0, 0,5 o 1) escogiendo el que está más cerca de la matriz de precedencia de entrada.
Siendo así, no puede existir ninguna representación matricial de un ranking que tenga una celda con distancia menor a la matriz de precedencia que el valor presente en la Matriz Utópica. Entonces el Valor Utópico U P asociado con P es u P =D(UP, P).
Con base en lo anterior, el Valor Utópico U P es una cota del valor óptimo del problema OBOP asociada a la matriz de precedencia P. Debe notarse que no siempre la Matriz Utópica representa una solución factible para el OBOP [14].
Debe tenerse en cuenta además que:
- Para cualquier Matriz de Precedencia P, la distancia máxima entre una salida en particular y la correspondiente en la Matriz Utópica es 0,25, y sucede cuando el valor en la matriz de precedencia de entrada es 0,25 o 0,75.
- P(u , u)= U P (u, u)=0,5
- Para una matriz de dimensión n, el mayor Valor Utópico es u (n)=0,25n(n-1). Este valor de utopía corresponde a una matriz P con valores en {0,25, 0,75} en todas las celdas, excepto en las de la diagonal principal.
- Si P(u, v)= U P (u, v) ∈{0 , 0,5, 1} para todo u, v ∈ M entonces el Valor Utópico u P asociado a P es 0. Es los demás casos, no es posible encontrar una solución con distancia 0.
Por otro lado, la utopicidad U(P) de una matriz P se puede definir como se muestra en (5):
La utopicidad U(P) puede considerarse como una normalización en el intervalo [ 0,1 ] de la similitud entre P y su Matriz Utópica U P . En particular, si U(P)=1 entonces U P =P. Es decir, P es utópica.
2.4 La Matriz Anti Utópica (AP) y el Valor Anti Utópico (AP) para OBOP
Según [14], dada una Matriz de Precedencia P, la Matriz Anti Utópica asociada a P es la matriz n × n definido en (6):
Donde:
Entonces el Valor Anti Utópico a P asociado con P es a P =D(A P , P).
Definido de esta manera, es una idealización a la peor solución posible al OBOP, y podría ser útil como límite superior para D(•, P). En otras palabras, dado una Matriz de Precedencia arbitraria P, D(B, P) está en el intervalo [u P , a P ] para cualquier orden de bucket B. Esto quiere decir que con los conceptos anteriores es posible determinar cotas superiores e inferiores para el problema OBOP. En la sección siguiente se mostrará cómo pueden extenderse estos conceptos para el problema RAP donde no es posible que haya empates en el ranking de consenso que brinda como salida.
3. EXTENSIÓN DEL CONCEPTO DE UTOPÍA PARA RAP
3.1 La Matriz Utópica (URP) y el Valor Utópico (urP) para RAP
Dada una Matriz de Precedencia P, la Matriz Utópica asociada a P es la matriz n × n definida como (7):
Donde:
Entonces el Valor Utópico ur P asociado con P es ur P =D(UR P , P).
Debe notarse que, para una matriz E, no se puede obtener una solución que tenga valor de función objetivo menor que ur P , pues es una cota inferior que solo se alcanza en algunos casos.
3.2 La Matriz Anti Utópica (ARP) y el Valor Anti Utópico (arP) para RAP
Análogamente a la Matriz Anti Utópica y al Valor Anti Utópico del OBOP, se pueden definir estos conceptos para RAP, entonces, dada una Matriz de Precedencia P, la Matriz Anti Utópica asociada a P es la matriz n × n definida como (8):
Donde:
Entonces el Valor Anti Utópico ar P asociado con P es ar P = D(AR P , P).
Definido de esta manera, es una idealización a la peor solución posible al RAP, y podría ser útil como límite superior para D(•, P). En otras palabras, dado una Matriz de Precedencia arbitraria P, D(B, P) está en el intervalo [ur P ,ar P ] para cualquier ranking sin empates.
Es interesante notar que el espacio de solución del problema RAP es un subconjunto del espacio de soluciones del problema OBOP. Por esta razón, no es posible encontrar una solución del RAP que no sea solución del OBOP. De esta manera, el intervalo [ur P , ar P ] de los posibles valores de las soluciones del RAP está contenido en el intervalo [u P , a P ] de posibles soluciones para el OBOP. Así, las cotas definidas por el intervalo [ur P , ar P ] para el RAP están más ajustadas. Esto resalta la importancia la extensión del concepto de Utopía para el RAP, ya que permite un mejor ajuste que si se usara el intervalo [u P , a P ].
4. RESULTADOS Y DISCUSIÓN
En esta sección se presenta un estudio experimental de la relación entre el Valor Utópico del RAP y los valores óptimos reales para esas instancias. Esto es posible, debido a la existencia de una formulación de PLE para el problema RAP que fue presentada en [10].
Por esta razón, dada una matriz de precedencia es posible encontrar su solución óptima usando una herramienta de solución de problemas de PLE. En este caso, se empleará la herramienta libre SCIP.
SCIP es un framework para la Programación Entera con Restricciones (CIP), un novedoso paradigma que integra la Programación con Restricciones (CP), la Programación Mixta-Entera (MIP) y las técnicas de modelado y solución de satisfacción (SAT) [23]. SCIP está disponible gratuitamente en código fuente para uso comercial y se puede descargar desde [24].
Es importante estudiar la relación que existe entre la solución óptima y la solución utópica en problemas en los cuales es posible encontrar su solución óptima en un tiempo prudencial, ya que puede servir de referencia para estimar lo que ocurriría en instancias mayores cuya solución óptima se desconozca, aprovechando que la obtención de las cotas utópicas es computable en muy poco tiempo.
Todos los experimentos fueron realizados en un ordenador personal con un procesador Intel i7 - 4790, 3,60 GHz, 4 núcleos y 4GB de memoria RAM.
Para los experimentos se usaron 47 conjuntos de datos (dataset) de rankings reales disponibles en [25]. En particular, se descargaron ficheros pwg asociados a los siguientes conjuntos de “Datos de Elección”: ED-00006-Skate Data(3-4, 11-12, 18, 28, 46, 48), ED-00011-Web Search(1), ED-00014-Sushi Data(1) and ED-00015-Clean Web Search (1-2, 7, 9,12, 14, 16-20, 23-25, 27, 29-30, 32, 34, 40-42, 44, 46, 48, 50, 54, 55,57, 59, 65-66, 67, 69, 73, 74, 77). Estos ficheros han sido utilizados previamente en experimentos de OBOP publicados en [14].
Todos los ficheros pws usados para los experimentos, así como los modelos de PLE y las herramientas con las que se ejecutaron los modelos [26] para poder ser analizados y replicados. Una descripción general de los 47 conjuntos de datos utilizados se muestra en la Tabla 1.
Tabla 1 Descripción de los conjuntos de rankings usados en los experimentos

Fuente: elaboración propia.
Por cada conjunto de datos, se muestra el promedio (Pro), la mediana (Med), los valores mínimos (Min) y máximos (Max) y la desviación estándar (Des Est.) del número de elementos del conjunto de rankings a agregar (n), cantidad de votantes (v), Valor Utópico para OBOP (u P ) y el Valor Utópico para RAP (ur P ).
4.1 Relación entre el Valor Utópico y el valor óptimo en el RAP
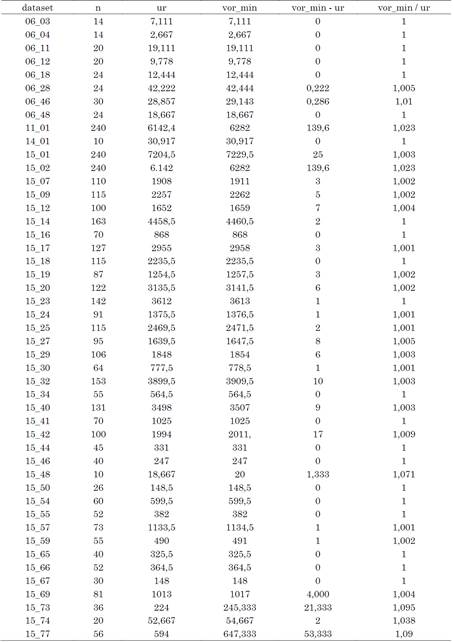
La Tabla 2 muestra una comparación entre los valores utópicos para RAP (ur) para cada instancia y su valor óptimo real (vor_min). Además, se muestra la diferencia entre ambos valores. A partir de la Tabla 2 se puede apreciar que entre el valor óptimo real y su Valor Utópico correspondiente, normalizado teniendo en cuenta el tamaño de cada instancia, existe un desfasaje promedio de aproximadamente 0,083.
Como se muestra en la Figura 1, fue factible el Valor Utópico en 19 de los 47 modelos, resultando un 40,43 % de factibilidad aproximadamente.
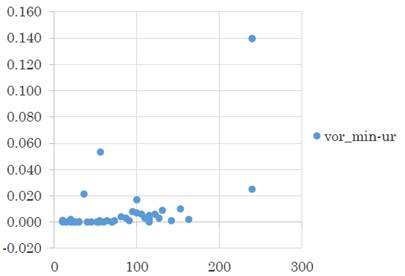
Fuente: elaboración propia.
Figura 1 Comportamiento del desfasaje entre el Valor Utópico y el valor óptimo real según crecen los elementos a ordenar
Además, se puede apreciar que, en varios modelos, ambos valores coinciden porque la solución utópica es factible y por tanto la mínima diferencia proporcional es 1, sin embargo, es más interesante notar que el promedio es de 1,01 y el mayor valor es 1,10. Esto quiere decir que nunca en los modelos la solución óptima fue más de 10 % peor que el Valor Utópico.
La Figura 2 muestra un gráfico con la diferencia proporcional. Es interesante notar que en estos resultados la matriz utópica fue factible (se correspondió con la solución óptima) en una cantidad de instancias mucho mayor que las reportadas en [14]. Aunque este resultado merece un estudio a fondo, creemos que hay aspectos que favorecen esta diferencia.
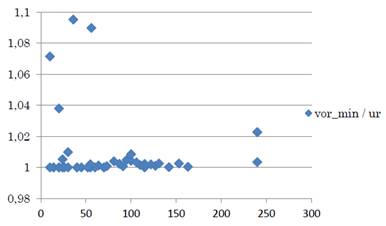
Fuente: elaboración propia.
Figura 2 Diferencia proporcional entre el Valor Utópico y el valor óptimo real
Por una parte, aquí se ha usado un algoritmo exacto que garantiza el óptimo, mientras que en [14] se reporta el resultado promedio de algoritmos aproximados.
Adicionalmente, el problema OBOP tiene un espacio de búsqueda mucho mayor que el del RAP y con una mayor complejidad en las restricciones a cumplir. Por ejemplo, el primer ejemplo mostrado en [14] cuya solución utópica para el OBOP no es factible, sí tiene una solución utópica que se corresponde con el ranking 1|2|3 que es factible para el RAP. Estos aspectos pueden explicar las diferencias.
4.2 Relación entre el Valor Anti Utópico y el valor óptimo en el RAP
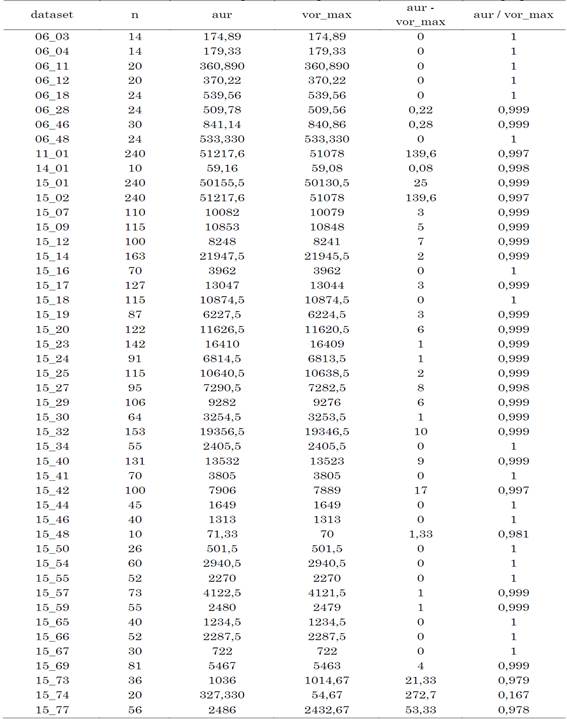
Para obtener la relación entre los valores anti utópicos y el valor óptimo real en el RAP se maximizó la función objetivo. La Tabla 3 muestra una comparación entre los valores anti utópicos para RAP (aur) para cada instancia y su valor óptimo real (vor_max). Además, se muestra la diferencia entre ambos valores.
En la Tabla 3 se pueden apreciar los resultados obtenidos para el valor óptimo real, en general, se encuentran muy próximos a su Valor Anti Utópico correspondiente, existiendo un desfasaje promedio aproximado de tan solo 0,37, normalizado teniendo en cuenta el tamaño de cada instancia.
Para una mejor comprensión se muestra la Figura 3. Además, fue factible el Valor Anti Utópico en 18 de los 47 modelos, resultando un 38 % de factibilidad aproximadamente.
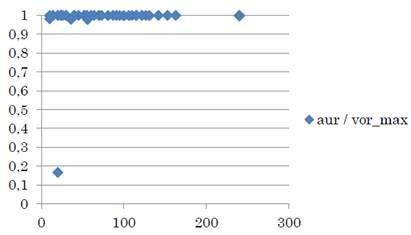
Fuente: elaboración propia.
Figura 3 Comportamiento del desfasaje entre Valor Anti Utópico - valor óptimo real, maximizando, según crecen los elementos a ordenar
Además, se puede apreciar que, como promedio, el óptimo es 0,98 del anti utópico por tanto se logró una muy buena estimación del óptimo. La Figura 4 muestra estos resultados.
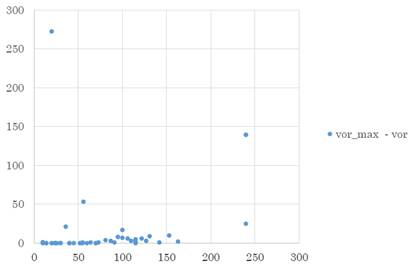
Fuente: elaboración propia.
Figura 4 Diferencia proporcional entre el Valor Anti Utópico y el valor óptimo real
La Figura 5 representa la relación entre los valores utópicos, anti utópico y óptimos reales.
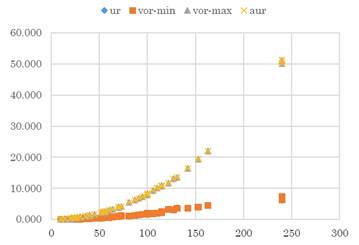
Fuente: elaboración propia.
Figura 5 Relación entre Valor Utópico, Valor Anti Utópico, valor óptimo real minimizando y valor óptimo real maximizando
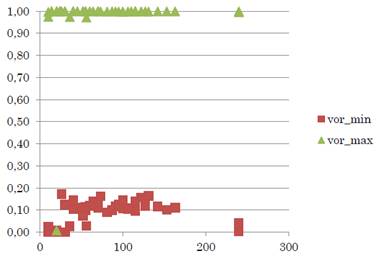
En la Figura 6 se realiza una proporción llevando los valores utópicos, anti utópicos y reales a una escala [0,1], donde 0 es el Valor Utópico, 1 el anti utópico y ubica según la proporción el valor óptimo, lo cual permite ver con claridad que están acotados bien con respecto a los valores utópicos.
5. CONCLUSIONES
En este trabajo, se extiende la investigación realizada en [14] y se realizó una nueva reformulación de los conceptos de Matriz Utópica y Anti Utópicas para el problema RAP.
En los experimentos se compararon los valores obtenidos de la matrices utópicas y anti utópicas con los valores óptimos del problema, donde se pudo demostrar la efectividad de los valores utópicos y anti utópicos como valores óptimos extremos (mínimos y máximos), y en ocasiones factibles, para medir el valor de calidad de la solución (ranking de consenso) del RAP sin empates.
La Matriz Utópica y la Matriz Anti Utópica son conceptos que se puede utilizar para evaluar las matrices de precedencia, que son la entrada de los RAP, por tanto, obtener una solución factible a partir de una matriz utópica es un problema interesante y abierto.
Además, es necesario conocer los casos en los que la Matriz Utópica y la Matriz Anti Utópica no son factibles, ya que ambos factores se vinculan directamente a la toma de decisiones, con el objetivo de ayudar a seleccionar los algoritmos correctos de acuerdo con las instancias del problema a resolver.
Además, encontrar rápidamente, con solo recorrer la matriz de entrada, una buena cota de los valores óptimos es muy interesante cuando se quiere resolver este tipo de problemas.
El hecho de que en algunos casos la Matriz Utópica refleje una matriz factible tiene varias implicaciones, y una importante es que el proceso de construir la Matriz Utópica se convierte en algunos casos en un algoritmo de solución del RAP, lo cual debe analizarse a profundidad en trabajos futuros.