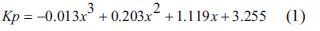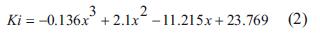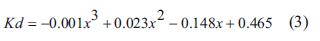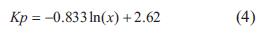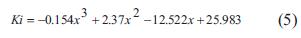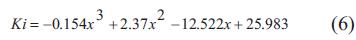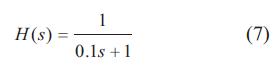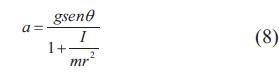Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Tecnura
Print version ISSN 0123-921X
Tecnura vol.15 no.30 Bogotá July/Dec. 2011
Control de posición de un sistema bola y viga con actuadores magnéticos
Position control ball and beam system with magnetic actuator
Francy López1, Paola Monroy2, José Danilo Rairán Antolines3
1 Tecnóloga en electricidad, investigadora de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. francylilo@gmail.com
2 Tecnóloga en electricidad, investigadora de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. pamv98@gmail.com
3 Ingeniero electricista, magister en Control. Docente de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. drairan@udistrital.edu.co
Fecha de Recepción: 28 de mayo de 2011 Fecha de aceptación: 29 de agosto de 2011
Resumen
En este artículo se realiza un control de doble lazo para el sistema bola y viga con actuadores magnéticos, además, se presenta el diseño y la construcción del prototipo correspondiente. El control se hace en tiempo real, por medio de una tarjeta de adquisición de datos y Simulink, mediante los cuales se implementan filtros y se linealizan las señales de cuatro sensores. De otra parte, se crean los algoritmos de control para los lazos, uno, de inclinación de la viga, y dos, de posición de la bola. Se trabajan dos alternativas para la estrategia de control del lazo interno, éstas son: un PID con ganancias fijas y otro con variables. Este último entrega un mejor resultado y además permite obtener un modelo del sistema, mientras que en el lazo externo (el cual se encarga de la posición de la bola), se trabaja con un PID tradicional. La experimentación con el prototipo construido muestra que no es fácil lograr la estabilización del lazo externo, debido a la latencia del actuador magnético.
Palabras clave: Actuador magnético, controlador PID variable, linealización, sistema bola y viga.
Abstract
This paper makes a double loop to control the ball and beam system with magnetic actuators also presents the design and construction of the corresponding prototype. The control is done in real time through a data acquisition card and Simulink, which are implemented by filters and linearized signals of 4 sensors. On the other hand, it creates the control algorithms for loops, one of inclination of the beam, and two, ball position. We work on two alternatives for the strategy to control inner loop, these are: a fixed PID gains and variables. The latter delivers better results and also allows a system model, while the outer loop (which takes care of the ball position), working with a traditional PID. Experimentation with the prototype built shows that it is not easy to achieve stabilization of the outer loop, because the latency of the magnetic actuator.
Key words: Magnetic actuators, PID controller variable, linearization, ball and beam system.
1. Introducción
El sistema bola y viga es un caso de estudio típico en la ingeniería de control, puesto que introduce el tema de sistemas no lineales e inestables, como se expresa en [1]. Esto se debe a que en lazo abierto la salida del sistema, es decir, la posición de la bola en la viga aumenta indefinidamente hasta encontrar un final de la viga, cuando el ángulo de la viga permanece constante en cualquier valor distinto de cero, lo que puede asociarse con una señal de entrada al sistema de tipo escalón, como se explica en [2].
En este trabajo se realiza un doble lazo de control, en el cual el lazo externo controla la posición de la bola. La variable de corrección generada por el controlador externo sirve como entrada al controlador interno, de la misma forma en que se explica en [3]. El lazo interno se encarga de fijar el ángulo de inclinación de la viga.
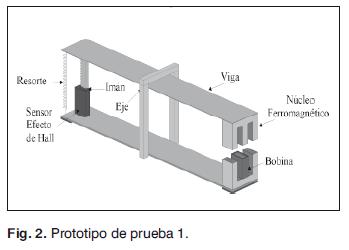
Usualmente el actuador para el lazo interno es un motor, sin embargo, en este artículo es un circuito magnético, como se realiza en [4], lo cual aumenta la complejidad del sistema, principalmente por dos cosas: 1) la construcción misma de la planta y 2), el comportamiento no lineal que presentan los dispositivos magnéticos [5], a lo cual debe agregarse que se desconocen los parámetros del modelo matemático del prototipo. Estas razones obligan a que sólo se calcule un modelo aproximado del sistema. Aún así se genera un modelo para el prototipo de prueba, el cual se denominará en adelante como prototipo 1, en la Fig. 2, utilizado como referencia para iniciar el proceso de sintonización del controlador de lazo interno.
En el prototipo de prueba denominado prototipo 2, en la Fig. 3, se trabaja con dos actuadores magnéticos, los cuales garantizan la condición de equilibrio de la planta y se construye una viga, la cual limita el desplazamiento de la bola a un sólo eje. El sistema entonces tiene dos grados de libertad, según se trabaja en [1] y en [6], los cuales corresponden a la inclinación de la viga y al desplazamiento de la bola. El primer grado de libertad se retroalimenta con la medida de sensores de efecto Hall, mientras que el segundo se establece a través de sensores ópticos, los cuales son sometidos a un proceso de linealización, como se explicará en detalle.
La sintonización del control PID del lazo interno tiene como punto de partida el modelo obtenido con la planta de prueba 1. Al no conseguir un control experimental igual al que se logra en la simulación con el modelo, se decide trabajar con los parámetros expuestos por Ziegler-Nichols, pero aún así no se consiguen los resultados que este método promete, principalmente debido a que el modelo que se construyó es útil en el único punto de trabajo, al ser lineal mientras el sistema no lo es. Finalmente, el controlador se sintoniza por ensayo y error. En primer lugar se establece un proceso de linealización en el punto medio del entrehierro, no obstante, los resultados de este proceso no son satisfactorios, puesto que las ganancias del controlador solo funcionan para esa posición, por esa razón se decide encontrar las constantes para varias distancias, y generar una función que represente el comportamiento de las constantes. Esa función describe el valor de la constante con la multiplicación entre la entrada y el error, lo cual hace al PID variable. Con el fn de observar la respuesta en frecuencia del lazo interno se construye el diagrama de Bode, del cual se obtiene un modelo de la planta y la frecuencia de corte del lazo.
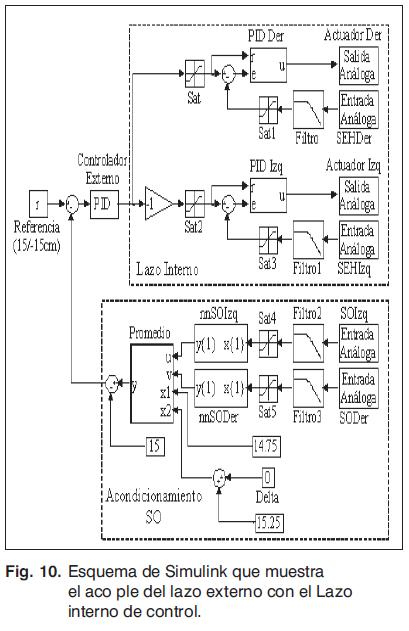
En el prototipo final se realiza el acople mecánico de los dos lazos, como se indica en la Fig. 3, y se establece el esquema de trabajo mediante Simulink, como en la Fig. 10. Con base en la literatura sobre el sistema bola y viga, se decide implementar un control PD para el lazo externo. Este resultado es adecuado cuando el actuador es un motor, dado que éste presenta dos polos, uno de los cuales se encuentra ubicado en S = 0, y actúa a manera de la integral del controlador cuando se trabaja en lazo cerrado.
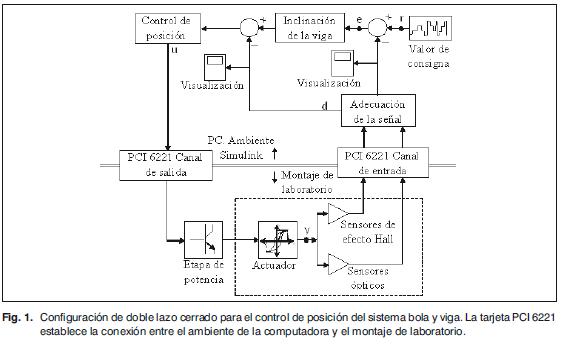
En la Fig. 1 se visualiza el diagrama general del control de doble lazo del prototipo, la tarjeta de adquisición permite el acople entre el PC (ambiente Simulink) y la planta (montaje de laboratorio); los procesos de adecuación de sensores y los algoritmos de control se establecen en Matlab, mediante Simulink.
Hay que adelantar que los resultados de la aplicación de los dos lazos de control no son los esperados, puesto que aunque el control de lazo externo genera variables de corrección con la rapidez adecuada, el lazo interno no responde con la misma velocidad, por tanto no es posible que la bola se estabilice en la posición que el usuario desea.
El artículo está organizado de la siguiente manera, la sección dos habla sobre el diseño y la construcción mecánica de la planta. La tercera sección trata sobre la implementación del lazo interno y en ésta se incluye el trabajo hecho con los sensores de efecto Hall y los modelos que se consiguen para ese subsistema. La cuarta sección corresponde a la presentación de los resultados, en la que se enfatiza el trabajo realizado con el lazo externo, por último, se presentan las conclusiones del trabajo.
2. Metodología
El sistema bola y viga tradicionalmente se implementa teniendo como actuador un motor [3], sin embargo, en este trabajo, al igual que en [4], se genera el torque a través de un actuador magnético, el cual está compuesto por dos núcleos ferromagnéticos en forma de E, con una bobina por núcleo como se muestra en la Fig. 3.
2.1 Prototipos de prueba
Para definir el entrehierro entre los núcleos y otras características del sistema se desarrollan dos prototipos de prueba. El primero, el cual se visualiza en la Fig. 2, es una viga que tiene en un extremo un actuador y en el otro un sensor de efecto Hall, acoplado con un imán, además, tiene un resorte, el cual garantiza la condición de equilibrio del sistema, con este prototipo se establece la distancia entre los núcleos ferromagnéticos, la cual es cercana a 6 mm. Esta distancia corresponde a la existente entre el sensor de efecto Hall y el imán; además, este prototipo permite hacer las primeras pruebas del control de lazo interno.
Con los resultados se construye el siguiente prototipo, en el cual se realizan dos modificaciones. La primera consiste en garantizar la condición de equilibrio, por medio de otro núcleo ferromagnético. No obstante, para precisar la ubicación de los núcleos es indispensable fijar la posición del eje, ya que éste determina la amplitud del movimiento angular que deben realizar los núcleos superiores de los actuadores. Con el fin de determinar dicha posición, se ejecutan varias pruebas hasta obtener como resultado un eje principal, el cual consta de dos partes insertadas en la mitad de los laterales de la viga, esta disposición permite que la bola se mueva libremente.
Las características mecánicas de los electroimanes limitan su desplazamiento angular, debido a esto se construye un soporte, del cual se sujeta el núcleo inferior del actuador, éste presenta una inclinación de 5,5º, lo que permite el contacto adecuado entre los núcleos, cuando el entrehierro es cero. Al definir esta parte del sistema, se opta por acoplar el conjunto sensor-imán en paralelo con los actuadores.
La segunda modificación radica en la adecuación de la viga y el acople entre ésta, la bola y los sensores ópticos. En este caso, los sensores ópticos se ubican en los extremos de la viga y determinan los materiales de ésta y de la bola, puesto que el color de los materiales influye en la medida de los sensores, como se indica en [7]. Además, si el diámetro de la esfera es pequeño, la superficie no es suficiente para que el sensor haga una medida adecuada. A través de varias pruebas se establece que para el sistema propuesto, el material de la viga sea translúcido, mientras que la bola debe ser de color blanco y tener un diámetro de 4 cm.
2.2 Prototipo final
El prototipo final se construye principalmente en acrílico, elemento ideal para trabajar con los sensores ópticos, los cuales se disponen de la misma manera que en el prototipo de prueba 2, además, la viga tiene forma de U, lo que permite que la bola se desplace en un sólo eje. A este desplazamiento por un solo eje se lo denomina un grado de libertad, como en [2].
Se construyen piezas, las que se insertan en los laterales de la viga, con el propósito de limitar el movimiento de la bola y garantizar el rango de funcionamiento de los sensores ópticos, los cuales deben estar alejados como mínimo 3 cm de la superficie refectora.
Por otro lado, los sensores de efecto Hall están dentro de una caja de acrílico, que se ensambla a la planta por medio de tornillos de bronce. Este metal es diamagnético, lo cual permite realizar la medida indirecta de la inclinación de la viga. Otro material predominante en la planta es el aluminio, que no interfiere en la medida de los sensores, debido a su naturaleza paramagnética, éste se usa en los soportes de la viga y de los núcleos inferiores de los actuadores, además en una caja en la que se introducen los imanes, que se ubican en paralelo con los actuadores. En la Fig. 3 está una fotografía del prototipo final.
2.3 Implementación del lazo interno
Para realizar la implementación del lazo interno se llevan a cabo tres procesos, los cuales se describen a continuación. El primero es el acondicionamiento de los sensores de efecto Hall, luego el modelado inicial, y un modelado final.
2.3.1 Acondicionamiento de los sensores de efecto Hall (SEH)
La posición angular del sistema bola y viga es determinada de manera indirecta por los SEH UGN3503, los cuales se caracterizan por un grado de sensibilidad alto, lo que les permite detectar cambios pequeños en el flujo magnético. Al determinar la distancia del entrehierro se obtiene el rango de medida del sensor, el cual es aproximadamente un voltio. No obstante, este rango es pequeño, razón por la cual, mediante un circuito electrónico se adecua la señal para que varíe entre 0 y 10 V, lo cual se establece como parámetro de trabajo debido a las características de la tarjeta PCI-6221.
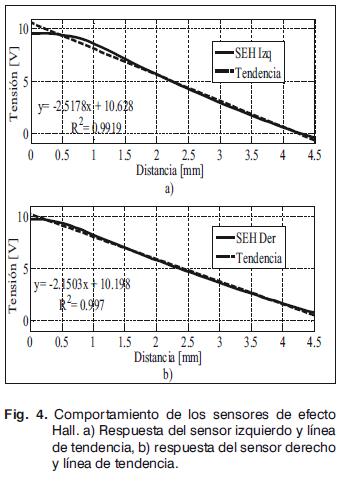
El patronamiento de los sensores se realizó tomando como distancia de muestreo 0,1 mm y se obtuvo una tendencia lineal, como se observa en la Fig. 4. Sin embargo, las señales presentaban un nivel de ruido considerable, razón por la cual se diseñó un filtro pasabajos, el proceso se realiza como en [8], el filtro más adecuado es Butterworth, de orden 3 y frecuencia de corte 50 Hz.
2.3.2 Modelo inicial
En el modelado de la planta se utiliza la descripción del sistema que se hace en [9]. El modelo matemático resulta complejo, por esta razón se decide realizar la simplificación que hacen en [6] y [2], sin embargo, el desconocimiento de algunos parámetros de la planta hace necesario la implementación de un modelo inicial aproximado, el cual se obtiene con la planta de prueba 1, Fig. 2, la cual tiene como fin describir el comportamiento del actuador.
La primera dificultad que la planta presenta es que la tensión de alimentación y la fuerza electromagnética no tienen una relación lineal como en [5], por ende, sólo al alcanzar un valor mínimo de tensión se logra que haya fuerza de atracción entre los núcleos de los contactores. Además, si la diferencia de potencial se disminuye, el magnetismo remanente en los núcleos lleva a que la parte móvil y fija del contactor se peguen, por lo que, si se desea separar los núcleos se debe alimentar con 0 V, lo cual significa que hay histéresis en el sistema. La forma de controlar el entrehierro entre la parte fija y móvil del contactor es mediante un controlador PID.
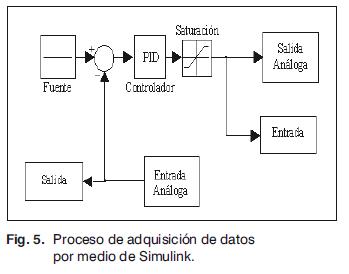
La Fig. 5 presenta el esquema con el que se realizó la adquisición de datos, con los cuales se halla el modelo. La herramienta para generar el modelo de la planta es System Identification Toolbox de Matlab. Sin embargo, hay que decir que no fue posible encontrar un modelo con un coeficiente de correlación superior al 90%, por lo cual se abandonó este procedimiento de modelado, y en su lugar se utilizó una red neuronal backpropagation feedforward. Ésta aprende los patrones entrada-salida, con base en los ejemplos. Algunas características de la red son: una capa de entrada con 6 neuronas y función de activación tansig, una capa intermedia y una capa de salida, las cuales trabajan con la función de activación purelin, El algoritmo de entrenamiento se conoce como trainlm de Matlab.
2.3.3 Sintonización del controlador PID para el lazo interno
Debido a los resultados obtenidos con el prototipo 2, se decide trabajar con el prototipo final, puesto que el acople mecánico ha sido mejorado, lo que permite fiabilidad en las pruebas. Para Ssintonizar el controlador PID del lazo interno se trabaja con las reglas de Ziegler-Nichols [10], puesto que éstas son usadas cuando no se conoce el modelo matemático de la planta; sin embargo, al no conseguir el comportamiento esperado se optó por sintonizar el controlador a ensayo y error, mediante el método descrito a continuación:
Sintonización en la mitad del rango (ref 5 V)
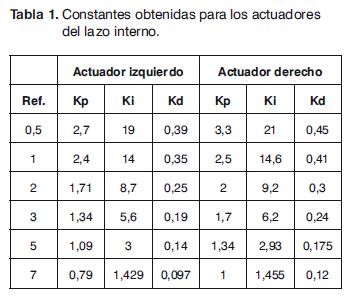
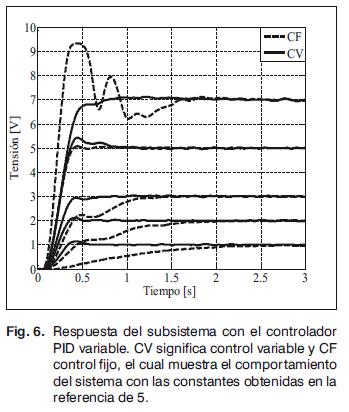
Primero se linealiza, como se explica en [11], alrededor de una referencia igual a 5 V, la cual corresponde al punto medio del rango del entre-hierro, es decir, 2,5 mm. El resultado es bueno puesto que el sistema no presenta sobrepico, tiene un tiempo de subida menor a 0,3 s y un tiempo de estabilización menor a 0,5 s. El valor de las constantes del controlador se puede observar en la tabla 1. Esta sintonización de las constantes sólo sirve para la referencia de 5 V, ya que al probar con referencias menores, el tiempo de respuesta del sistema es lento, pero para referencias mayores presenta sobrepico y tiempos de estabilización altos, como se muestra en las curvas punteadas de la Fig. 6.
El procedimiento descrito anteriormente se genera para los dos actuadores del sistema, la diferencia entre estos es que el actuador derecho tiene un tiempo de respuesta mayor al izquierdo, no obstante, en ambos casos es menor a 0,5 s. En vista del resultado se busca implementar un controlador PID variable.
Sintonización variable
El proceso de sintonización que se realiza para obtener las constantes en la referencia 5 V se repite para 0,5, 1, 2, 3 y 7 V. Las constantes resultantes se consignan en la tabla 1, y con ellas se establece un patrón, es decir, una función que describe el comportamiento de cada una de las constantes del controlador.
A continuación se relacionan las ecuaciones de las constantes del controlador izquierdo:
y las ecuaciones de las constantes del controlador derecho:
Estas ecuaciones conforman el controlador PID variable, el cual garantiza que todo el rango del entrehierro tenga un comportamiento deseable, es decir, la salida no presenta sobrepico, con un tiempo de subida menor a 0,3 s y un tiempo de estabilización menor a 0,5 s como indica la Fig. 6.
Se decide implementar el PID variable debido a que el comportamiento del lazo interno es uniforme a lo largo de las posibles referencias para el entrehierro.
2.3.4 Modelo final
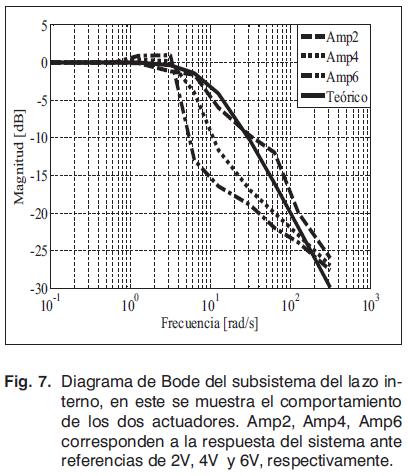
Para conocer la respuesta en frecuencia del lazo interno (acople de los actuadores), se aplica una fuente sinusoidal, realizando cambios en amplitud y frecuencia. A partir de los resultados se construye la gráfica de magnitud del diagrama de Bode, Fig. 7, éste indica que el comportamiento del subsistema es equivalente al de un filtro pasa-bajos, como se puede observar en algunos ejemplos en [11].
Según las respuestas en la Fig. 7, puede considerarse que la función de transferencia del subsistema es de orden uno, en lazo cerrado. El tao se establece al observar que la frecuencia de corte es 10 rad/s aproximadamente. A continuación se presenta el modelo aproximado, el cual surge de la respuesta en frecuencia del lazo interno, ante tres referencias.
No obstante, el modelo obtenido es más acertado para referencias pequeñas, es decir, menores a 2 V, lo cual no se considera como error, dado que la mayoría del tiempo el sistema estará cerca del punto de referencia, o cercano a la condición de equilibrio.
3. Resultados
Esta sección de resultados se dedica a presentar la implementación del lazo externo, para lo cual es necesario realizar un trabajo previo con los sensores ópticos, los cuales se deben acondicionar y linealizar como se muestra a continuación.
3.1 Acondicionamiento de los sensores ópticos
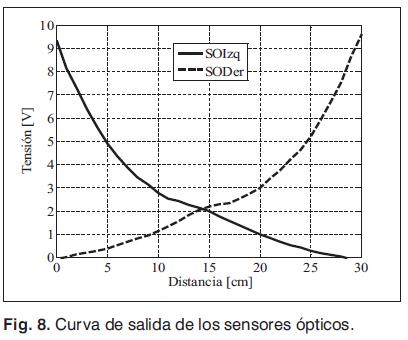
La posición de la bola es medida a través de dos sensores ópticos (SO) tipo GP2D120, los cuales se adecuan de la misma manera que los sensores de efecto Hall, es decir, se implementa un circuito para ampliar el rango de medida de 0 a 10 V. La diferencia radica en que la distancia de muestreo es 1 cm y la tendencia obtenida es exponencial, a su vez, la implementación del filtro pasabajos tiene una frecuencia de corte de 20 Hz. Debido a la tendencia de los sensores Fig. 8, se hace necesario un proceso de linealización.
Este proceso se hace mediante el entrenamiento de otra red neuronal tipo feedforward, compuesta por tres capas: la primera es la de entrada; la segunda es una capa intermedia, con 30 neuronas, la cual trabaja con la función de activación tansig y; la tercera es la capa de salida, la cual tiene una función de activación purelin. El entrenamiento se efectúa con 1.000 épocas, con el algoritmo Levenberg-Marquart, el cual es un algoritmo back propagation modificado. La red neuronal aprende los datos del patronamiento y su relación con una salida lineal, es decir, el resultado que se espera de las redes. Al obtener un error aceptable entre la salida y el objetivo se exporta la red a Simulink. Para este caso se crean dos redes, las cuales son entrenadas de la misma manera y corresponden a la salida de cada sensor.
La salida conseguida para cada sensor es aceptable para el rango total de desplazamiento de la bola, por tanto, un solo sensor podría realizar la realimentación del lazo externo. Sin embargo, el comportamiento de los sensores es óptimo para un rango más pequeño, ya que a distancias mayores presentan una distorsión considerable (ruido) que afecta la medida de posición de la bola.
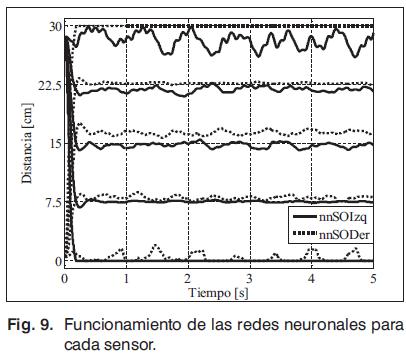
Dado el ruido en parte del rango de funcionamiento, se realizan varias pruebas con el objetivo de establecer el rango de funcionamiento de cada red, como se visualiza en la Fig. 9. Allí se nota que si bien el sensor izquierdo aproxima la lectura real en todo el rango de funcionamiento del sensor, tiene un comportamiento mejor entre 0 y 15 cm; de una manera equivalente para el sensor derecho, pero entre 15 y 30 cm. Entonces, la salida de posición para valores pequeños es la salida del SO izquierdo, para valores grandes es la salida del SO derecho, y para valores cercanos a 15, se realiza un promedio entre la salida de las dos redes. Por ende, la señal de salida tiene una pendiente de 0,983 y el coefciente de correlación es del 99,9 %. Un esquema de la descripción del tratamiento de las señales de los sensores ópticos está en la Fig. 10, en el bloque llamado Acondicionamiento SO.
3.2 Sintonización del controlador externo
Para realizar el proceso de sintonización del controlador externo es necesario crear un esquema en Simulink, en el cual se acople el lazo externo con el lazo interno, este esquema se expone en la Fig. 10.
Dada la evidencia bibliográfica, como en [2], se busca implementar un controlador PD, el cual es usado para controlar el sistema bola y viga, partiendo de un modelo lineal aproximado. Se fija la ganancia proporcional, y se hacen variaciones de la ganancia derivativa, en un rango amplio; luego se cambia la ganancia proporcional, y se retoman las ganancias derivativas, y se observa el comportamiento en cada caso. Esto genera una matriz de comportamiento, de la cual se esperó seleccionar el mejor conjunto de ganancias.
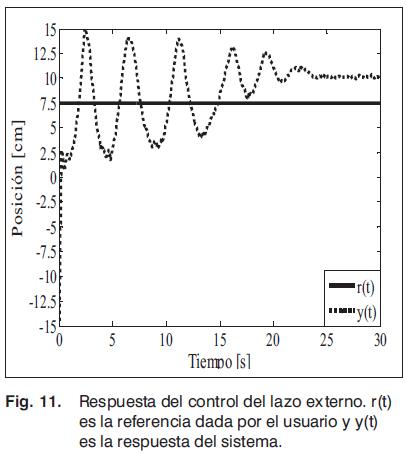
La conclusión más evidente es que si bien algunos conjuntos de ganancias parecen dirigir la esfera al valor de referencia, en realidad ningún conjunto de ganancias logra el control, por tanto el mejor de los casos es una oscilación alrededor del punto de referencia, como se indica en la Fig. 11.
Con el fin de justificar el comportamiento mostrado en la Fig. 11, se realiza un proceso teórico en el que se obtiene la frecuencia de corte del lazo externo, el cual se describe a continuación:
Tomando como referencia las ecuaciones del movimiento rectilíneo uniformemente acelerado,
Donde αes la aceleración, g es la gravedad, θ es el ángulo de inclinación de la viga, I es el momento de inercia de la bola, m es la masa de la bola, r es el radio de la bola, Vf es la velocidad final, Vo es la velocidad inicial, x es la distancia recorrida por la bola, y h es la altura. Teniendo en cuenta que la bola parte del reposo, Vo =0 m/s y reemplazando (8) y (9) en (10), se obtiene (11). Se decide trabajar con la altura, debido a que ésta se puede obtener mediante la resta del entrehierro máximo y el valor obtenido de las ecuaciones que describen el comportamiento de los SEH Fig. 4, para un valor de referencia de dos voltios, del cual se obtuvo la frecuencia de corte del lazo interno. A partir de la ecuación (11) se halla la velocidad promedio teniendo como resultado 0,1103 m/s.
Para calcular la aceleración se implementa (8), la cual equivale a 0,6709 m/s2, utilizando el ángulo correspondiente a la inclinación máxima de la viga. Como la bola se desplaza sobre un plano inclinado la aceleración es constante. Con los datos de velocidad y aceleración, se halla el tiempo, el cual se despeja de (12), dando como resultado 0,1644 s.
La ecuación (13) se utiliza para determinar la frecuencia de corte del lazo externo, la cual es 19,1 rad/s.
El problema radica en que la frecuencia de corte del lazo externo es superior a la del lazo interno. Si bien el control del lazo externo genera las correcciones adecuadas, el lazo interno demora demasiado en obedecer e ir a la referencia indicada. Esto se puede comprobar a partir del Diagrama de Bode, en la Fig. 7, pues allí se observa cuál es la frecuencia máxima de respuesta del lazo interno, luego de lo cual la amplitud de salida es cada vez más pequeña que la amplitud de entrada. Para este prototipo el tiempo de respuesta es mayor a 0,5 s en el lazo interno de control, por ende, al exigir un tiempo menor el sistema no es capaz de responder ante esa conmutación.
4. Conclusiones
El diseño del controlador PID con ganancias variables supera las falencias del PID tradicional, sintonizado en un solo punto de funcionamiento de la planta, ya que se asegura que la respuesta del sistema sea comparable en todo el rango de funcionamiento del sistema. Aún así, a entrehierros pequeños, persiste un problema, este es que no se logra que la viga se mantenga en una referencia dada, debido al flujo remanente presente en los actuadores magnéticos.
El controlador del lazo externo no se logra sintonizar debido a que la velocidad de la bola supera el tiempo de respuesta del lazo interno, lo cual se puede comprobar al revisar la frecuencia de corte del Diagrama de Bode.
Un inconveniente que se presenta a nivel mecánico es la fricción entre la bola y la viga, lo cual hace que aún cuando la viga esté inclinada la bola sigue pegada, por la fricción estática, y cuando se vence esa fricción, entonces el ángulo de inclinación es muy grande y hace que la bola vaya rápido hacia el extremo más bajo. Este es uno de los aspectos más importantes que se deben tener en cuenta en trabajos posteriores.
Referencias
[1] W. Hongui, T. Yantao, F. Siyan and S. Zhen, "Nonlinear control for output regulation of ball and plate system," Proceedings of the 27th Chinese Control Conference, Kun ming, July. 2008. [ Links ]
[2] W. Yu and F Ortiz, "Stability analysis of PD regutation for ball and beam system," IEEE Conference on Control Applications, Toronto, Aug. 2007. [ Links ]
[3] H. Wang, Y. Tian, Z. Sui, X. Zang and C. Ding, "Tracking control of ball and plate system with a double feedback loop structure," Proceedings of the International Conference on Mechatronics and Automation, Kunming, July. 2008. [ Links ]
[4] C. E. Lin, C. Ker and R. Wang, "Magnetic suspension actuador in ball and beam system demonstration," JSME International Journal Series C, vol. 49, no. 4 pp. 1018-1026. Apr. 2006. [ Links ]
[5] C. Lin, H. Jou and Y. Sheu, "Exact model identification for magnetic suspension system via magnetic field measurement," Instrumentation and Measurement Technology Conference, Taiwan, 1992. [ Links ]
[6] A. Knuplez, A. Chowdhury and R. Svecko, "Modeling and control design for the ball and plate system," University of Maribor. Faculty of Electrical Engineering and Computer Science, Dec. 2003. [ Links ]
[7] J. Rairán, J. Pérez y J. Osorio, "Implementación de una red neuronal para la medición indirecta de posición," Revista Avances en Sistemas e Informática, vol. 6. no. 3, pp 79-85, Slovenia, Dec. 2009. [ Links ]
[8] J. Rairán, Y. Sierra y N. Moreno, "Implementación de dos estrategias de control para la velocidad de un motor DC," Revista Ingeniería e Investigación, vol. 29, no. 2, pp 100-106, Agu. 2009. [ Links ]
[9] J. Yi, N. Yubazaki and K. Hirota, "Stabilization control of ball and beam systems," IFSA World Congress and 20th NAFIPS International Conference, Vancouver, 2001. [ Links ]
[10] C. Sanabria and O. Hernández, "Control de un péndulo invertido simple por métodos de realimentación de estados", Tecnura, vol. 13, no. 25, pp. 59-69, Dic. 2009. [ Links ]
[11] J. Rairán. Análisis de sistemas dinámicos y control PID, primera edición, Colombia: Universidad Distrital Francisco José de Caldas, 2007. [ Links ]