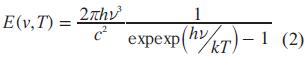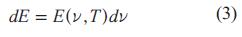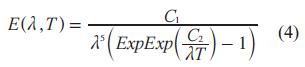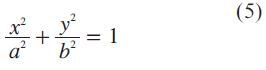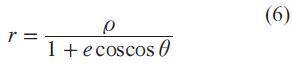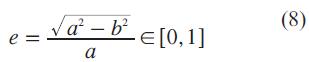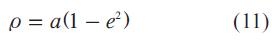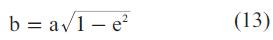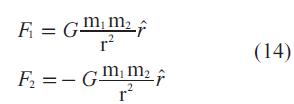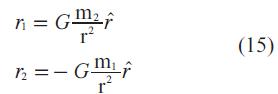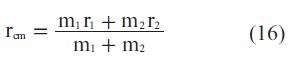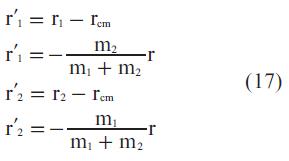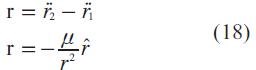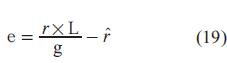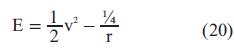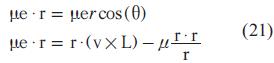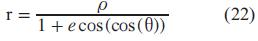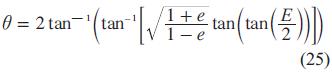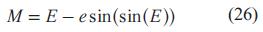Evaluación del desempeño de la radiación emitida por el sol como sistema de suministro de energía a un pico-satélite "CUBESAT"

Outstanding evaluation of radiation emitted by the sun as a power supplysystem for a pico-satellite "CUBESAT"

Sergio Hernández R¹, Ernesto Gómez V², Diego F. Rocha A³

¹ Licenciado en Matemáticas y Física, Especialista en Matemáticas Avanzadas. Estudiante de la Maestría en Ciencias de la Información y las Comunicaciones de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. sergioehr@gmail.com
² Ingeniero electrónico, especialista en Telecomunicaciones Móviles, magíster en Teleinformática, estudiante de Doctorado en Ingeniería. Docente de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. egomez@udistrital.edu.co
³ Ingeniero electrónico, estudiante de Maestría de Ciencias de la Información y las Comunicaciones de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. dfrochaa@correo.udistrital.edu.co.

Fecha de recepción: 4 de Agosto de 2011 Fecha de aceptación: 28 de Noviembre de 2011

Resumen

En la operación de un satélite es de vital importancia la energía eléctrica, ya que esta debe alimentar todos los sistemas del mismo, tales como el de control y comando, el de comunicaciones, el de control de actitud, entre otros. Esta energía puede ser obtenida, básicamente, en el espacio exterior a la Tierra de diferentes formas, ya bien sea a partir de reacciones nucleares (EN), o a partir de reacciones químicas (EQ), o bien a partir de la transformación de la energía proveniente del sol (EF).

Sin importar el tipo de misión que deba ejecutar la nave espacial (comercial, militar o científica), el tamaño del satélite y el tipo de fuente de energía, se debe tener presente que esta es un recurso limitado tanto en tiempo de vida como en su valor, y que mientras más pequeño sea el satélite estas dos magnitudes decrecen de manera dramática, siendo el escenario más crítico el de un pico satélite, en donde las restricciones de tamaño y peso impiden el uso de la EN y la EQ, quedando como única opción el uso la EF. A esto se ha de agregar que las dimensiones de las caras del mismo (10 cm x 10 cm) solo permiten ubicar, a lo máximo, dos celdas solares por cara.

Con el propósito de determinar la energía que puede suministrar el sol a un pico satélite a continuación, y de manera rápida, se estudiará la radiación emitida por el sol y la cantidad posible de esta que se encuentra disponible a la altura de la órbita del pico satélite, para lo cual se hace uso de una simulación de la misma en MATLAB.

Palabras clave: Energía solar, fotocelda, fotón, orbita, pico-satélite, radiación.

Abstract

In the operation of a satellite is vital electricity, as this should feed all the same systems, such as command and control, that of communications, attitude control, among others. This energy can be obtained, basically, in outer space to Earth in different forms, either from nuclear reactions (EN), or from chemical reactions (EQ) or from the transformation of energy from the sun (EF).

Regardless of the type of mission need to run the spacecraft (commercial, military or scientific), the size of the satellite and the type of energy source, be aware that this is a limited resource in time of life and in his value, and that the smaller the satellite these two quantities decrease dramatically, being the most critical stage of a satellite peak, where size and weight restrictions prevent the use of EN and EQ, as the only remaining option using the EF. To this must be added that the dimensions of the faces of the same (10 cm x 10 cm) only allow us to locate, at most, two solar cells per side.

In order to determine the energy that the sun can supply a satellite peak below, and quickly, we will study the radiation emitted by the sun and the possible amount of this which is available at the height of the orbit of the peak satellite, for which one uses the same simulation in MATLAB.

Keywords: Solar energy, photocell, photon, orbits, pico-satellite, radiation.

1. Introducción

La estrella más cercana a la Tierra es el Sol, que en promedio se encuentra a aproximadamente 149.597'870.700(3) m de distancia [1] de la tierra y posee un radio de 6,9551(3)x108m [1]. La masa del sol es aproximadamente de 1,9884(2)x1030 kilogramos [1], lo que equivale a 333000 veces la masa de la Tierra, que es de 5,9722(6)x1024 Kg, según AMSLER et ál [1]. La temperatura del núcleo del Sol es de aproximadamente 1,57x107 millones de grados Kelvin, la cual disminuye hasta llegar a ser aproximadamente 5.778°K en su superficie [2].

En el núcleo del Sol, el cual contiene cerca del 40% de la masa de esta estrella y ocupa menos del 2% del volumen total de la misma [3], se llevan a cabo reacciones de fusión nuclear, por medio de las cuales se unen los núcleos de átomos ligeros para formar átomos más pesados; por ejemplo, dos núcleos de deuterio (un isótopo del hidrógeno) se fusionan transformándose en un núcleo de helio, lo que equivale a una pérdida de masa, ya que el hidrógeno consumido pesa más que el helio producido. Esta diferencia de masa, de acuerdo con la ecuación fundamental de la relatividad restringida (E = mc2), se transforma en energía, liberándose así grandes cantidades de energía [4]. "En este proceso, cada segundo, una masa aproximada de 4,4 millones de toneladas, que irradia 3,96x1026 W, se transforma en energía" [3].

La energía liberada en el núcleo debe atravesar la zona radiactiva del Sol, que se encuentra a una temperatura promedio aproximada de 130.000 °Ky que es tan densa que los fotones y la radiación electromagnética proveniente del núcleo tarda miles de años en atravesarla. Luego, dicha energía debe pasar por la zona conectiva que tiene mucha agitación debido a la ascensión de gases muy calientes que luego de enfriarse descienden. Finalmente, la energía alcanza la fotosfera, la cual se caracteriza por poseer una baja densidad, una temperatura promedio de aproximadamente 5.762°K [3], y porque sus gases se encuentran fuertemente ionizados.

Para modelar el proceso de radiación de energía del Sol, y como una aproximación inicial, este puede considerarse como un cuerpo negro sometido a una temperatura T, medida en grados Kelvin. Así, el Sol emite energía electromagnética que se propaga radialmente por el espacio a la velocidad de la luz y cuya intensidad disminuye con el cuadrado de la distancia. Es importante aclarar que en su propagación hacia la tierra, la energía del Sol casi no interactúa con la materia debido a que la densidad de esta en el espacio extraterrestre es muy pequeña (10-8 kg/m3) [3].

2. Estado Del Arte

2.1. Ley de Stefan-Boltzmann

El concepto de cuerpo negro no es más que la idealización de lo que ocurre en la realidad y por tanto es útil para ayudar a explicar cómo un cuerpo absorbe o irradia energía electromagnética. Se define cuerpo negro como aquel que absorbe toda la energía electromagnética que incide sobre él sin permitir que parte de esta radiación sea reflejada o pase a través de él. Este concepto fue propuesto por Kirchhoff en 1862 al estudiar la emisión de energía de un cuerpo. Igualmente, Kirchhoff probó experimentalmente que "en condiciones de equilibrio termodinámico, la relación entre el poder emisivo y el poder absorbente es para todos los cuerpos, una misma función de la longitud de onda y la temperatura del cuerpo".
En 1879, Josef Stefan, a partir de los resultados obtenidos por John Tyndall (1865) al medir la emisión total de energía de un alambre de platino a diferentes temperaturas concluyó que el total de energía radiada por un cuerpo negro es proporcional a la cuarta potencia de la temperatura absoluta a la que este se encuentre sometido. Este resultado fue verificado posteriormente por otros investigadores y en 1984, Ludwig Boltzmann realizó una justificación teórica de este resultado, al cual se le conoce con el nombre de Ley de Stefan-Boltzmann [5]. Así, esta ley se puede expresar como:

Donde, 0 < ε ≤ 1 es una constante adimensional que depende de las características del cuerpo (para un cuerpo negro ε = 1), conocida como constante de emisividad del cuerpo; y es la constante de Stefan-Boltzmann cuyo valor es 5,670400(40)x10^-8 Wm^-2 K^-4 [6].

De acuerdo con la Ec. 1 y tomando como temperatura aproximada de la superficie del Sol 5.779°K, este emite un total de energía de cerca de. 6,3245x10⁷ W m^-2Se tomó el presente valor para la temperatura superficial del Sol, teniendo en cuenta que al escalar el valor del total de energía radiada por el Sol al borde de la atmósfera terrestre, este valor coincida aproximadamente con el valor de la constante solar, dado por el estándar E-490-0a.

2.2. Ley de radiación de cuerpo negro

Según Max Planck (1900), la cantidad de energía radiante emitida por un cuerpo, por unidad de superficie y de tiempo, es una función (E) de la frecuencia (v) y la temperatura (T), dada por la Ec. 2:

Donde:

h: constante de Planck con un valor de 6,62606896(33)x10^-34Jul/seg,
c: velocidad de la luz en el vacío cuyo valor es 299'792.458 m/seg,
k: constante de Boltzmann cuyo valor es 1,3806504(24)x10^-23 Jul/K
E(v,T): poder emisivo espectral en función de la frecuencia [6].

Considerando el intervalo de frecuencias entre v y v+dv. El poder emisivo del cuerpo dE en dicho intervalo de frecuencias será como la Ec. 3.

Evaluación del desempeño de la radiación emitida por el sol como sistema de suministro de energía a un pico-satélite "CUBESAT"

Como v = c / λ, luego dv = (-c / λ²) dλ y por lo tanto se tiene que el poder emisivo espectral en función de la longitud de onda se obtiene a partir de la Ec. 4.

Dónde,

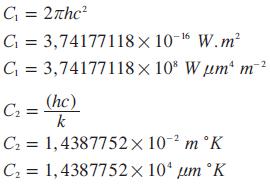
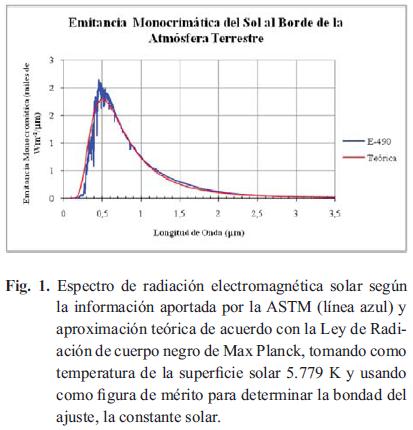
Según el Standard Extraterrestrial Spectrum Reference E-490-00a, de la American Society for Testing and Materials (ASTM) [7], el Sol emite radiación electromagnética en el rango de aproximadamente de 100 nm a un milímetro. La Fig 1 muestra la comparación, sobre la porción más representativa del espectro solar a una masa de aire cero (borde de la atmósfera terrestre), entre los valores experimentales suministrados por la ASTM en el estándar E-490-00 y los calculados a partir de la Ec. 4.

El espectro de radiación electromagnética solar se pude subdividir en: la banda del ultravioleta, la banda de la luz visible y la banda del infrarrojo. A continuación se describe cada una de estas bandas de acuerdo con las definiciones establecidas en el estándar ISO 21348 [8]

• A la banda del ultravioleta pertenece la radiación electromagnética cuya longitud de onda es tal que 0,1 µm ≤ λ < 0,4 µm.

• En el rango visible se encuentra la radiación electromagnética con longitud de onda en el rango de 0,38 µm ≤ λ < 0,76 µm., que es la parte del espectro electromagnético que estimula las células especializadas encargadas de la visión humana. Este rango se subdivide en seis colores: el violeta, radiación con longitud de onda l tal que 0,36 !m : l < 0,45 !m; el azul radiación con longitud de onda entre 0,45 µm ≤ λ < 0,57 µm; el verde radiación con longitud de onda en el rango de 0,5 µm ≤ λ < 0,57 µm; el amarillo que corresponde a radiación con longitud de onda en el intervalo 0,57 µm ≤ λ < 0,591 µm; el naranja que comprende la radiación con longitud de onda tal que 0.591 µm ≤ λ <0,61 µm; y, el rojo que es radiación con longitud de onda en el intervalo 0,61 µm ≤ λ < 0,76 µm.

• La banda del infrarrojo cubre la radiación electromagnética con longitudes de onda entre 0,76 µm y 1 mm. A veces se subdivide en tres categorías espectrales. El infrarrojo A (IR-A) caracterizado por tener longitud de onda en el rango 0,76 µm ≤ λ < 1,4 µm; el infrarrojo B (IR-B) con longitud de onda en el intervalo 1,4 µm ≤ λ < 3,0 µm; y, el infrarrojo C (IR-C) con longitudes de onda que oscilan entre 3,0 µm a un milímetro.

Es de resaltar que de acuerdo con este estándar hay solapamiento entre las bandas de radiación ultravioleta y la visible. Con el ánimo de solucionar este impase y teniendo en cuenta que, como se verá más adelante, la radiación ultravioleta que más afecta al módulo de potencia, y en especial a las celdas solares, son aquellas con longitudes de onda menores a 0,3 µm, en el presente trabajo se tomaran como rangos de longitud de onda para cada tipo de radiación electromagnética los mostrados en la Tabla 1.

Teniendo en cuenta los rangos definidos en la Tabla 1 y el estándar E-490-0a, del total de la radiación en el borde de la atmósfera terrestre, conocida como la constante solar (1.366,1 W/m²), 85,80 W/m² corresponden al ultravioleta, lo que equivale al 6,28%; 714,78 - 85,80 = 628,98 W/m² a la banda de la luz visible, es decir, el 46,04%; y, 1.366,1 - 714,78 = 651,32 W/m² a la banda del infrarrojo, el 47,68%.

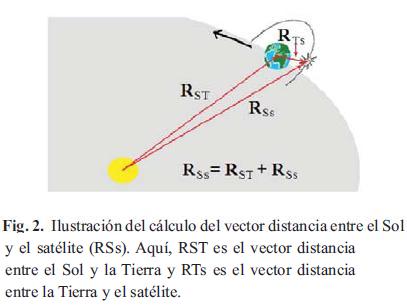
Con de propósito de simular la cantidad de energía disponible a la altura del satélite es necesario conocer la distancia a la cual este se encuentra del Sol. Por tanto es importante calcular la distancia de la Tierra al Sol y la distancia del satélite a la Tierra para sumarlas vectorialmente y así poder determinar la distancia del satélite al Sol, tal como se ilustra en la Fig. 2. Esta última distancia no permanece constante en el tiempo, debido a que la Tierra se mueve sobre una órbita elíptica alrededor del Sol, e igualmente el satélite lo hace alrededor de la Tierra.

Con el propósito de describir tanto el movimiento de la Tierra alrededor del Sol como el del satélite alrededor de la Tierra, inicialmente, se dará un breve vistazo a las propiedades matemáticas de la elipse.

2.3. La elipse

La elipse se define como el lugar geométrico de los puntos tales que la suma de la distancia a dos puntos fijos, denominados focos, es constante. En coordenadas cartesianas la ecuación de la elipse está dada por la Ec. 5:

Donde, α es el semieje mayor y b es el semieje menor. El punto donde estos se cortan se denomina centro (O) [9]. La elipse pertenece a una familia de curvas denominadas cónicas (parábola, elipse e hipérbola), las cuales fueron estudiadas por Apolonio en el siglo II a.C. y que se obtienen al intersecar un cono circular recto con un plano oblicuo a su eje. La ecuación general de una cónica, en coordenadas polares esta dada por la ecuación 6.

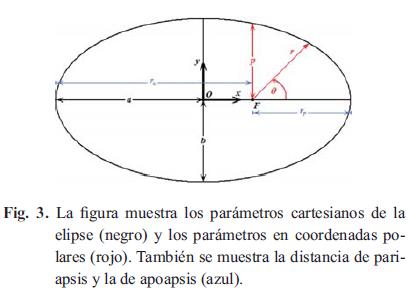
Donde ρ > 0 se conoce como el semilatus-rectum o parámetro focal y e es la excentricidad. En el caso de la elipse, el parámetro focal es la mitad de la cuerda trazada por uno de los focos y paralela al eje menor, tal a como se ilustra en la Fig.3, la cual está dada por la Ec. 7.

La excentricidad mide el porcentaje de diferencia entre la elipse y la circunferencia; su valor se obtiene a partir de la Ec. 8:

La Fig. 3 ilustra los parámetros de la elipse tanto en coordenadas cartesianas como en coordenadas polares.

Se define el punto de periapsis (simplemente, periapsis) como el de mínima distancia al foco; en tal caso, θ = 0 y de la Ec. 6 se deduce la Ec. 9 para la distancia de pariapsis.

De otro lado se define el punto de apoapsis (simplemente, apoapsis) como el de máxima distancia al foco; en tal caso, θ = π y nuevamente de la Ec. 6 se obtiene la Ec. 10 para la distancia de apoapsisestá.

Los parámetro de la elipse pueden ser expresados como una función del semieje mayor (α) y la excentricidad (e). Para esto se debe tener en cuenta que la suma de r_p y r_aes igual al eje mayor (2a). Así, la Ec. 11 es el resultado de sumar las Ec. 9 y 10.

En la Fig. 3 se puede observar que r_p - r_a=20F, luego restando de la Ec. 10 la Ec. 9 y reemplazando la Ec. 11 el resultado final es la Ec. 12.

Finalmente, puesto que 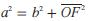, despejando b y reemplazando en el resultado la Ec. 12, obtenemos la Ec. 13.

2.4. Sistemas de referencia

Con el propósito de describir el movimiento de un planeta o de un vehículo espacial se hace necesario el uso de uno o más sistemas de referencia, los cuales se seleccionan de acuerdo con las exigencias de la situación que se desea describir. Estos sistemas referenciales pueden ser inerciales o no inerciales.

Un sistema de referencia se considera inercial si el origen de coordenadas (lugar donde se supone se encuentra ubicado el observador) se encuentra en reposo absoluto o se mueve con velocidad constante, es decir, no se encuentra sometido a la acción de fuerza alguna [10]. Así, en astrofísica un sistema de referencia inercial supone que el observador se encuentra ubicado en el centro de un cuerpo del sistema solar, despreciando el efecto que sobre él tienen fuerzas tales como las de arrastre y las de Coriolis, entre otras. Los sistemas de referencia inerciales más usados son: el sistema de referencia cartesiano heliocéntrico eclíptico, el sistema de referencia cartesiano geocéntrico ecuatorial y el sistema de referencia cartesiano geocéntrico eclíptico.

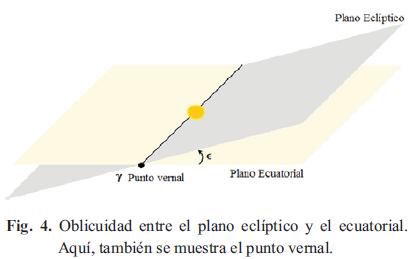
Antes de entrar a la descripción de estos sistemas de referencia de debe anotar que hay dos planos de suma importancia: el plano eclíptico y el plano ecuatorial terrestre. Se denomina plano eclíptico a aquel que contiene la órbita de la Tierra alrededor del Sol [11]; y, se denomina plano ecuatorial terrestre aquel, que como su nombre lo indica, contiene al ecuador terrestre [11]. Estos dos planos no son paralelos, si no que por el contrario, forman entre sí un ángulo, denominado oblicuidad (ε), cuyo valor es 23° 26' 29" [8], tal como se muestra en la Fig.4. Igualmente, es de resaltar que la línea de corte de estos dos planos al interceptarse con la trayectoria de la Tierra determina el punto vernal o punto Aries (γ) que es aquel que ocupa la Tierra, en su órbita alrededor del Sol, el 21 de marzo (equinoccio vernal). Este punto también es conocido como nodo ascendente y la línea de corte de estos dos planos se denomina línea de nodos. El nodo ascendente es un vector cuya dirección está determinada por la línea Sol- Tierra del 21 de marzo [8].

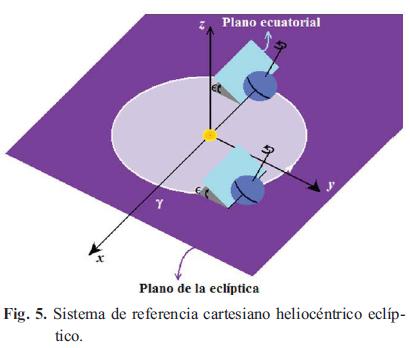
2.4.1. Sistema de referencia cartesiano heliocéntrico eclíptico

El origen O del sistema de referencia cartesiano heliocéntrico eclíptico es el centro del Sol, de tal manera que el plano xy es el plano de la eclíptica. La dirección positiva del eje de las x es la determinada por el Sol y la Tierra en el equinoccio vernal. El eje z pasa por el centro del Sol y es perpendicular al plano eclíptico. Este sistema de referencia se ilustra en la Fig.5, y tal como allí se ve este es un sistema de referencia cartesiano derecho. Este sistema de referencia es útil para el estudio del movimiento planetario y para el análisis y diseño de misiones interplanetarias [2].

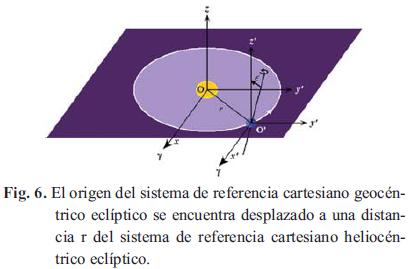
2.4.2. Sistema de referencia cartesiano geocéntrico eclíptico

El origen de coordenadas O' se encuentra ubicado en el centro de la Tierra, de tal manera que el plano x'y' es el plano de la eclíptica. El eje x' apunta hacia el punto, el eje y' es perpendicular al eje x' y el eje z' es perpendicular al plano x'y' o plano de la eclíptica, tal como se muestra en la Fig.6. Se debe anotar que el eje z' no coincide con el eje de rotación de la tierra y que este sistema de referencia resulta de desplazar el origen de referencia del sistema cartesiano heliocéntrico eclíptico. Este sistema de referencia es de gran utilidad en el estudio del movimiento de naves espaciales cercanas a la Tierra y como sistema de referencia intermedio. [2]

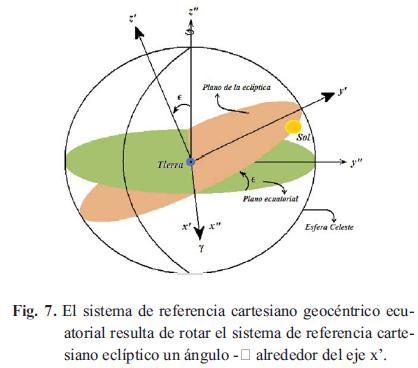
2.4.3. Sistema de referencia cartesiano geocéntrico ecuatorial

Tiene como origen de coordenadas el centro de la Tierra, O", y el plano x"y" coincide con el plano ecuatorial terrestre de manera tal que la dirección positiva del eje x" apunta en la dirección. Aquí, el eje z" coincide con el eje de rotación de la Tierra. Este sistema de referencia resulta de rotar el plano y"z", sobre el eje x', del sistema de referencia cartesiano geocéntrico eclíptico un ángulo -E con el propósito de hacer coincidir el eje z' con el eje rotación de la Tierra z". Ambos sistemas de referencia comparten el mismo eje de las x. Es de utilidad para el estudio del movimiento de cuerpos orbitando la Tierra y se ilustra en la Fig. 7 [7].

2.5. El problema de dos cuerpos

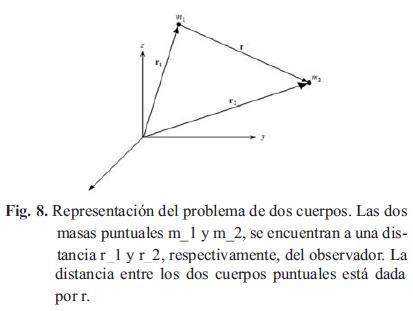
El estudio de dos cuerpos masivos en el espacio, sometidos a la fuerza de la gravedad, es conocido como el problema de dos cuerpos. Para esto se considera el sistema formado por los dos cuerpos como aislado del resto de Universo, es decir, que no intervienen más fuerzas que la atracción gravitatoria mutua entre ellos. Para simplificar el problema, además se supone, que los dos cuerpos son esféricos y de densidad constante, de manera que una partícula con la misma masa del cuerpo genere el mismo campo gravitatorio; y así poder considerar las masas como puntuales y localizadas en el centro de masa de cada uno de los cuerpos, tal como se ilustra en la Fig. 8. Se aclara que las cantidades vectoriales se anotaran con letras minúsculas en negrilla y las matrices con letras mayúsculas en negrilla.

Como ya se mencionó, la fuerza sobre cada partícula es la debida a la atracción gravitatoria ejercida por la otra partícula, las cuales, de acuerdo con los postulados de Newton, están dadas por la Ec. 14

Donde:

G: constante de gravitación universal cuyo valor es 6,67428(67)x10^-11m³kg^-1s^-2.

r: vector unitario en la dirección del vector r = r₂ - r_1, dado po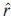r = r/r

Teniendo en cuenta la segunda ley de Newton (F=mr)¹ , se puede concluir:

Que son las ecuaciones que describen la aceleración de los dos cuerpos o simplemente las ecuaciones de movimiento de cada una de las partículas.

La posición del centro de masa del sistema está dada por la siguiente ecuación:

Encontrando la segunda derivada del centro de masa del sistema, es fácil comprobar que la aceleración del mismo es cero y por tanto no se encuentra sometido a la acción de fuerza alguna. Así se puede desplazar el origen del sistema de referencia al centro de masas y el nuevo sistema de referencia seguirá siendo inercial. En este nuevo sistema de referencia la posición de los cuerpos está dada por los vectores r₁ y r₂, de acuerdo a:

Cuando m₁>>m₂, r₁ tiende a ser cero. Por lo tanto r₁ tiende a ser cero. Por lo tanto r₁→r_cm y r₂ →r, lo que en este caso significa que el movimiento de estos dos cuerpos se aproxima al problema de un cuerpo alrededor de un cuerpo masivo. Esto ocurre cuando, por ejemplo, se trata de describir el movimiento de cuerpos tales como el de la Tierra alrededor del Sol, o el de un satélite alrededor de la tierra. Así, recordando que r = r₂ -r₁ y haciendo uso de las Ec. 15, se tiene que la ecuación de movimiento está dada por:

Donde:

µ: parámetro gravitacional de las masas combinadas el cual es igual a G(m₁ + m₂) [2]. En el caso en que m₁>>m₂, µ se aproxima a Gm₁. Así en el caso del movimiento de la Tierra alrededor del Sol tenemos:

µ = µ

µ = Gm

µ = 1,3271 x 10²⁰ m³ seg^-1

Y para el caso del movimiento de un satélite alrededor de la tierra tenemos

µ = µ

µ = Gm

µ = 3,9860 x 10¹⁴ m³ seg^-1

Aquí m_D es la masa del Sol y m es la masa de la Tierra, cuyos valores ya fueron dados en la Sección 1.

Antes de continuar, es bueno estudiar algunas de las características del movimiento sin entrar a solucionar la Ecuación del movimiento de un cuerpo alrededor de otro masivo, dada por la Ec. 18.

Tal como lo demuestra Martínez et ál [11] el momentum angular (L=mrxr) del cuerpo menos masivo respecto al de mayor masa es constante, lo que significa que la órbita del cuerpo de menor masa se encuentra confinada en un plano perpendicular a que pasa por el origen del sistema de referencia (en este caso, el centro del cuerpo de mayor masa).

Otra cantidad de gran importancia en el estudio del movimiento de un cuerpo alrededor de otro masivo es el vector de Laplace-Runge-Lenz (e), o de manera simplificada el vector LRL, el cual es usado para describir la forma y orientación de la órbita de un cuerpo que gira alrededor de otro. Para dos cuerpos que interactúan por medio de una fuerza conservativa proporcional al inverso del cuadrado de la distancia que los separa, tal como la fuerza de la gravedad, se ha demostrado que el vector LRL es una constante del movimiento (ver Goldstein [10] y Arnold [12]). Estos problemas reciben el nombre de problemas de Kepler.

Según Goldstein [10], para una partícula sobre la que actúa una fuerza central proporcional al inverso del cuadrado de la distancia, descrita por la ecuación, 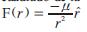el vector se definido por la Ec. 19.

Donde:

D: velocidad de la partícula puntual que se mueve bajo la acción de la fuerza central, L=rxp es la cantidad de movimiento angular, µ es un parámetro que describe el poder de la fuerza central vector unitario en la dirección de ; esto es, donde r es la magnitud de 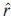= r/r, donde r es la magnitud de r.

e: El vector perpendicular al vector cantidad de movimiento angular L, debido a que pxL y r son perpendiculares a L. De esto se sigue que e está en el plano de la órbita.

Es bueno recordar que el lagrangiano describe el movimiento de ambos cuerpos mide la energía total. Como la fuerza de la gravedad es conservativa, la energía total es una constante de movimiento. Así, si se está interesado en el movimiento relativo de una de las partículas respecto a la otra, digamos en el movimiento de m₂ respecto a m₁, la lagrangiana de dicho sistema queda como la Ec. 20 [13].

2.6. Forma de la órbita resultante del problema de Kepler

La forma y la orientación de la órbita resultante del problema de Kepler se pueden obtener a partir del vector e [12]. Al tomar el producto escalar de e con el vector posición r se obtiene:

Donde θ es el ángulo entre r y e denominado anomalía principal. Teniendo en cuenta que r. (v x L) = L.(r x v) = L² se obtiene que µer cosθ = L²- µr. Despejando r se obtiene la ecuación 22.

Donde la excentricidad es la magnitud del vector 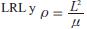es el semilatusrectum.

La Ec. 21 corresponde a la ecuación en coordenadas polares de una elipse.

2.7. Ley horaria

Hasta este momento se ha demostrado que las trayectorias orbitales en el caso de la Tierra alrededor del Sol y de un satélite alrededor de la tierra son elípticas. Pero, al resolver de la ecuación del movimiento se ha eliminado la dependencia del tiempo, la cual es necesaria para localizar a un cuerpo en su órbita en un instante dado. Resolver este problema en el caso circular en más fácil que hacerlo en el caso elíptico.

Se debe tener en cuenta que T = 2π/n y por lo tanto el tiempo que tarda un cuerpo en ir del punto de periapsis al de apoapsis es igual al semiperiodo de la órbita, es decir, 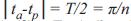. Igualmente, cuando 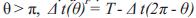por lo que se puede suponer siempre la anomalía principal entre 0 y π.

De otro lado, se define la (M) anomalía media (Ec. 24) como el ángulo barrido un tiempo, si el cuerpo se moviera sobre una órbita circular con una velocidad angular equivalente a la velocidad orbital media.

De esta manera M = θ, solamente cuando el cuerpo pasa por el punto de periapsiso de apoapsis.

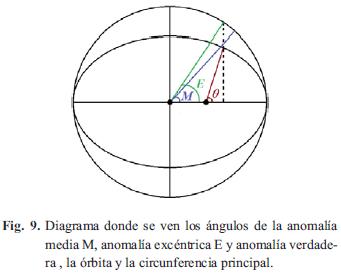
Finalmente, considérese una elipse de semieje mayor a circunscrita en una circunferencia de radio a, tal como se ilustra en la Fig. 9. Se define la (E) anomalía excéntrica como el ángulo subtendido entre el semieje de la elipse y el radio que pasa por la proyección del planeta sobre la circunferencia.

La anomalía verdadera y la excéntrica se encuentran relacionadas (ver [13]) mediante la la Ec. 25.

De otro lado, la anomalía media y la excéntrica están relacionadas por medio de la llamada ecuación de Kepler (Ec. 26) [13], [14], [2].

Si la variable que se desea despejar de la Ec. 26 es, para hallar el valor de esta variable se debe usar un método numérico.

2.8. Elementos orbitales

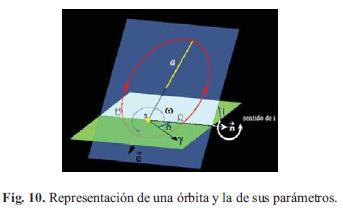
Para una órbita arbitraria en el espacio es necesario ubicar el plano orbital respecto a un plano de referencia. Es bueno recordar que la intersección entre el plano orbital y el de referencia determina la llamada línea de nodos. La órbita corta la línea de nodos en dos puntos cada uno de ellos conocido con el nombre de nodo [8]. Aquel en donde la trayectoria "asciende" (de abajo a arriba) es el nodo ascendente (Ω); [15] el otro es el nodo descendente (Ω), tal como se ilustra en la Fig. 10. El vector nodo nv es un vector unitario en la dirección de Ω.

Para orbitas heliocéntricas, como la de la tierra alrededor del sol, el plano de referencia es el plano de la eclíptica. En este caso la línea de corte de estos dos planos al interceptarse con la trayectoria de la Tierra determina el nodo ascendente o punto vernal Aries (γ). De otro lado, Para orbitas planetocéntricas el plano de referencia será el plano ecuatorial del planeta.

Un ápside es el punto de una órbita elíptica de mayor o menor distancia a su centro de atracción, que generalmente también el centro de masas y el cual se encuentra ubicado en uno de los focos de la órbita. El punto de menor distancia a su centro de atracción se llama periápside y el de mayor distancia a este se denomina apoápside. La línea recta trazada desde el periápside hasta el apoápside se denomina línea de ápsides y corresponde al eje mayor de la órbita elíptica [16].

Cuando se hace referencia a una órbita alrededor de un cuerpo en particular se emplean términos equivalentes. De esta forma, para el caso de una órbita alrededor del Sol se usan los términos de perihelio y afelio, en lugar de periápside y apoápside; y para órbitas alrededor de la Tierra se usan los términos de perigeo y el apogeo, respectivamente.

Dado el plano de la órbita y un sistema de referencia Oxyz centrado en el foco de la misma, de tal manera que el plano Oxy coincida con el plano de la órbita, son necesarios seis parámetros para determinar la órbita, los cuales reciben el nombre de elementos orbitales [2].

Le geometría de la órbita queda determinada por el conjunto de parámetros {a,e} o en su defecto por {p,e}. El parámetro define la forma de la órbita, es decir, el tipo de cónica, mientras que el parámetro a, o en su lugar p , establece su tamaño [15].

El parámetro ω, llamado el argumento de periapsis (de perigeo/de perihelio/de periastro) orienta la línea de ápsides en la dirección del vector excentricidad e, el cual apunta hacia el perigeo. Es el ángulo, sobre el plano orbital, entre y , medido en la dirección del movimiento [2] (Fig. 10). Para órbitas ecuatoriales, en los que no hay nodo ascendente, y para órbitas circulares, que no tienen periastro, este parámetro no está definido

Un cuarto parámetro, que bien puede serla anomalía verdadera e, o bien la anomalía media θ, o la anomalía excéntrica E, o un Δt que nos permita calcular cualquiera de las anteriores, permite determinar la posición del cuerpo sobre la trayectoria.

El quinto parámetro mide la inclinación del plano de la órbita respecto al plano de referencia y recibe el nombre de i/eli/aeió/ de la órbita (i). De esta manera, la inclinación de la órbita mide el ángulo entre el plano de referencia y el plano orbital, de manera que 0 ≤ i ≤π, en el sentido indicado por [16].

El sexto parámetro, la ascensión recta del nodo ascendente (RAAN) es un ángulo que específica la orientación del plano de la órbita del cuerpo con respecto a la esfera celeste. Así, la ascensión recta del nodo ascendente (Ω) es el ángulo, medido en el sentido contrario al de las agujas del reloj, entre γ y [11].

3. Metodología

Para la presente investigación se diseñó un programa que para cada deltat calculara al mismo tiempo la posición, tanto de la Tierra en su órbita alrededor del Sol como la del satélite en su órbita alrededor de la Tierra, esto con el propósito de determinar la distancia existente entre el Sol y el satélite, dato con el cual se puede calcular cada deltat la potencia disponible en ese punto. Como se muestra en la Fig. 2, la distancia existente entre el Sol y el satélite es el vector que resulta de sumar el vector distancia Sol-Tierra con el vector distancia Tierra-satélite.

Como el vector distancia Sol-Tierra se encuentra dado en un sistema de coordenadas heliocéntrico eclíptico y el vector distancia se expresa en un sistema de coordenadas geocéntrico ecuatorial, este último vector debe cambiar de base, de manera que se exprese en un sistema de coordenadas heliocéntrico. Así, el programa diseñado debe realizar el cambio de base del vector distancia Tierra-satélite, para poder sumarlo con el vector distancia Sol-Tierra. Finalmente conocida la distancia Sol-satélite el programa debe calcular la energía emitida por el Sol en este punto. Es bueno aclarar que se tomó como época de la tierra el primero de enero del 2000 a las 00:00:00 y como época del satélite la misma fecha.

Para lo anterior el software permite el ingreso de los elementos orbitales del satélite y de la Tierra.

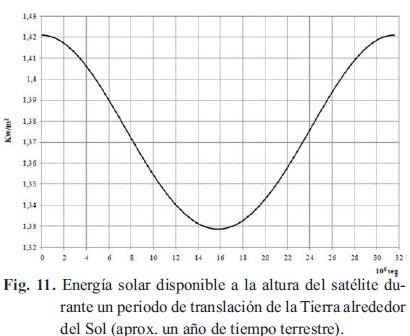
Suponiendo que la vida del satélite es el tiempo que tarda la tierra en completar una órbita alrededor del sol, se obtiene la gráfica que se muestra en la Fig. 11. Aquí se puede observar que la energía disponible a la altura del satélite oscila entre aproximadamente 1421,06 y 1328,66 w/m². Así, alrededor de un año ocurre un cambio de 92,40 w/ m². Este cabio en la energía se debe al constante cambio en la distancia al Sol durante el año, en donde el mayor valor corresponde al perihelio y el menor valor al afelio.

4. Resultados

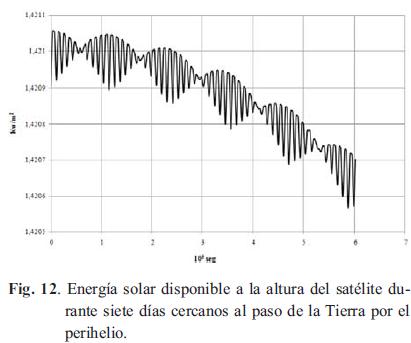
Tomando siete días alrededor de la fecha en el que la tierra alcanza el perihelio, el afelio y el punto Aries, se construyeron las gráficas que se muestran en las Fig. 12, 13 y 14. En el caso de la Fig. 12, que corresponde a cuando la tierra alcanza el perihelio, la energía disponible a la altura del satélite pasa de un valor máximo de 1421,06 a uno mínimo de 1420,57 w/m², lo que da una diferencia de 0,49 w/m². Es de anotar que debido al movimiento del satélite alrededor de la tierra el cambio en el valor de la energía es oscilatorio con una envolvente del tipo coseno.

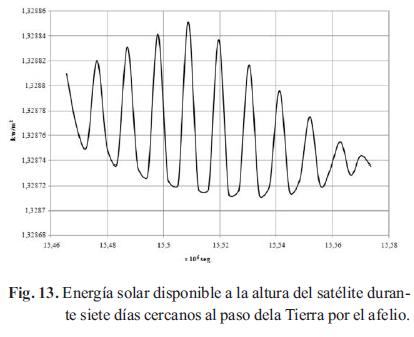
En el segundo caso, el correspondiente al paso por el afelio, la Fig. 13 muestra que la energía disponible pasa de un valor máximo de 1328,85 al mínimo de 1328,66 w/m², con una diferencia de 0,19 w/m². A diferencia de la Fig. 14, durante estos siete días se forma un único ciclo de oscilación de la energía disponible. Esto se explica a que la tierra en cercanías de este punto cuenta con menor velocidad, a la que tenía cuando estaba pasando por el perihelio.

En el tercer caso, que corresponde a cuando la Tierra pasa por el punto Aries (equinoccio de primavera) se pasa de un máximo de energía disponible de 1384,33 a un mínimo de 1378,84 w/m², produciéndo se una diferencia de 5,49 w/m². También se debe hacer notar que la gráfica de la energía disponible durante estos siete días disminuye oscilando sobre una envolvente lineal.

5. Conclusiones

Queda claro que la energía solar disponible a la altura del satélite cambia de acuerdo con la ubicación de la Tierra sobre su órbita alrededor del Sol, en un rango que va desde 1421,06 a 1328,66 w/m² con un ancho de 92,40 w/m². Es de anotar que este cambio ocurre en un tiempo equivalente al periodo de translación de la Tierra. De esta manera se puede afirmar que en promedio se encuentra disponibles 1374,86 w/m². Así, se puede afirmar que en promedio se cuenta con 0,137486 w/cm².

Teniendo en cuenta que un pico-satélite es un cubo con una arista de 10 cm, cada cara lateral del mismo tendría un área de 100 cm² y suponiendo que siempre tiene dos caras expuestas al Sol, el área susceptible a la exposición solar es de 200 cm². Suponiendo celdas solares de 3,5 cm x10 cm, el área efectiva de los colectores de energía sería del 70% de estas dos caras, lo que arroja un resultado de 140 cm2. Suponiendo una eficiencia del 29,5%, [17] esta superficie podría colectar un máximo de 5,68 watts, ya que en realidad esta cantidad puede ser mucho menos, debido a que la eficiencia depende del ángulo de incidencia de la luz sobre la superficie de la fotocelda. Así, debido al movimiento de rotación del pico-satélite sobre su eje, la potencia producida no permanecerá constante, si no que por el contrario oscilará.

También debe quedar claro, que la energía suministrada por las fotoceldas oscilara debido movimiento de translación sobre su órbita alrededor de la Tierra y a la translación de la Tierra sobre su órbita alrededor del Sol.

Referencias

[1] C. Amsler, Physics Letters B667, 1, 2008. [En línea]. Disponible en: http://pdg.lbl.gov/2008/reviews/rpp2008-rev-astrophysical-constants.pdf        [ Links ]

[2] V. Valenzuela, Astronáutica y vehículos espaciales. Departamento de Ingeniería Aeroespacial. Escuela Superior de Ingenieros, Universidad de Sevilla, septiembre, 2008.        [ Links ]

[3] UPME, IDEAM, Atlas de Radiación Solar de Colombia, pp. 115, Bogotá, 2005. [En línea]. Disponible en: http://www. upme.gov.co/Index4.htm        [ Links ]

[4] E. Burbidge, G. Burbidge, W. Fowler y F. Hoyle, Synthesis of the Elements in Stars. Mod. Phys. 29, 1957, 547. [En línea]. Disponible en: http://prola.aps.org/pdf/RMP/v29/i4/p547_1        [ Links ]

[5] E. Braun, Una faceta desconocida de Ei/stei/. Fo/do de Cultura Eeo/ómiea. Segunda Edición. México, 1997.        [ Links ]

[6] CODATA, Internationally Recommened Values of the Fu/dame/tal Physieal Constants. [En línea]. Disponible en: http://physics.nist.gov/cuu/Constants/index.html. Visitada el 21-05-2009.        [ Links ]

[7] American Society for Testing Materials. Standard Extraterrestrial Spectrum Reference E-490-00a, 2006.        [ Links ]

[8] International Standard. "Space Environment (Natural and Artificial)", Process for Determining Solar Irradiances. ISO 21348. First Edition, 2007.        [ Links ]

[9] I. Bronshtein y K. Semendiaev, Manual de Matemáticas para Ingenieros y Estudiantes. Moscú: Editorial MIR, 1971.        [ Links ]

[10] H. Goldstein, Classical Mechanics, Addison Wesley, 1980.        [ Links ]

[11] J. Martínez, J. Miralles and M. Galadí-Enríquez, Astronomía Fundamental, Publicaciones Universidad de Valencia, 2005.        [ Links ]

[12] V. Arnold, Mathematical Methods of Classical Mechanics, Second Edition, New York: Springer-Verlag, 1989.        [ Links ]

[13] B. Portilla, Estudio analítico de las perturbaciones a la solución exacta del problema de los dos euerpos post-newtoniano (1PN). Universidad Nacional de Colombia. Facultad de Ciencias. Programa Curricular de Física.        [ Links ]

[14] D. Stern, De astrónomos a astronaves, [En línea]. Disponible en: http://www.phy6.org/stargaze/Mintro.htm.        [ Links ]

[15] S. Roncero y F. Gavilán, Aeronaves y vehículos espaciales. Departamento de Ingeniería Aeroespacial y Mecánica de Fluidos. Escuela Superior de Ingenieros. Universidad de Sevilla, 2009.        [ Links ]

[16] I. Ridpath, Diccionario de Astronomía. Oxford University Press, Primera Edición, Editorial Complutense, 2004.        [ Links ]

[17] Emcore, CTJ Photovoltaic Cell Triple-Junction Solar Cell for Terrestrial Applications, [En línea]. Disponible en: http://www.emcore.com/assets/photovoltaics/CTJ_B_Web.pdf.        [ Links ]